Plan zajęć

Wstęp teoretyczny
Optymalizacja struktury produkcji

Wstęp teoretyczny

Zagadnienia mieszanek
Wybór procesu technologicznego
Simpleks
Zagadnienie transportowe
Problemy przydziału
Kolokwium I
Programowanie sieciowe
Kolokwium II

CPM

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Metody programowania sieciowego można zdefiniować jako techniki, które umożliwiają sprawne planowanie i
prowadzenie przedsięwzięć. Przedsięwzięcie jest to działanie człowieka, które zmierza do określonego celu,
jest zawarte w skończonym przedziale czasu, z wyraźnie zaznaczonym początkiem i końcem i realizowane
przy użyciu różnych zasobów (ludzkich, rzeczowych, finansowych itp.). Na przedsięwzięcie składa się szereg
czynności, które są ze sobą wzajemnie powiązane i są wykonywane w określonej kolejności. Zależność między
czynnościami i zdarzeniami określa strukturę logiczną modelu sieciowego.

Budowa modelu sieciowego składa się z następujących etapów:

+ sporządza się listę czynności, ustala relację między nimi oraz czas ich trwania (dla metod sieciowych
deterministycznych czas określony jest jednoznacznie, dla metod stochastycznych czas trwania czynności
określony jest z pewnym prawdopodobieństwem).
+ rysuje się wykres sieciowy, używając następujących graficznych symboli:

Czynność, część przedsięwzięcia cechująca się czasem trwania i zużywaniem zasobów,

Czynność pozorna, typ czynność, która nie zużywa czasu ani zasobów, a służy jedynie do
pokazania zależności między czynnościami,

Zdarzenie, określa stan zaawansowania prac. To moment rozpoczęcia lub zakończenia jednej lub
więcej czynności.

Dla zdarzeń przypisuje się kolejne numery identyfikacyjne, natomiast czynności porządkowane są parą
wskaźników i-j (i-numer zdarzenia rozpoczynającego czynność; j-numer zdarzenia kończącego czynność).

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Zasady konstrukcji sieci (za chwilę kontynuacja etapów):

Wymagane jest, aby:

- istniał dokładnie jeden wierzchołek (zdarzenie) początkowy i jeden wierzchołek (zdarzenie) końcowy (zasadę
można spełnić wprowadzając czynności pozorne),

- wierzchołki i krawędzie (zdarzenia i czynności) były odpowiednio uporządkowane, poprzednik ma mniejszy
numer lub wcześniejszą literę od następnika,

- dwa zdarzenia miały połączenie tylko jedną czynnością, jeżeli kilka czynności wykonywanych równolegle jest
poprzednikami jednej, to należy wtedy wprowadzić czynności pozorne,

- strzałki, symbolizujące czynności, się nie przecinały.

Kolejne etapy:

+ wyznacza się podstawowe charakterystyki sieci dla poszczególnych czynności i zdarzeń (najwcześniejsze
możliwe i najpóźniejsze dopuszczalne momenty zaistnienia zdarzeń, zapasy czasu dla zdarzeń i czynności).,

+ wyznaczenie terminu końcowego dla przedsięwzięcia oraz ścieżki krytycznej.

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

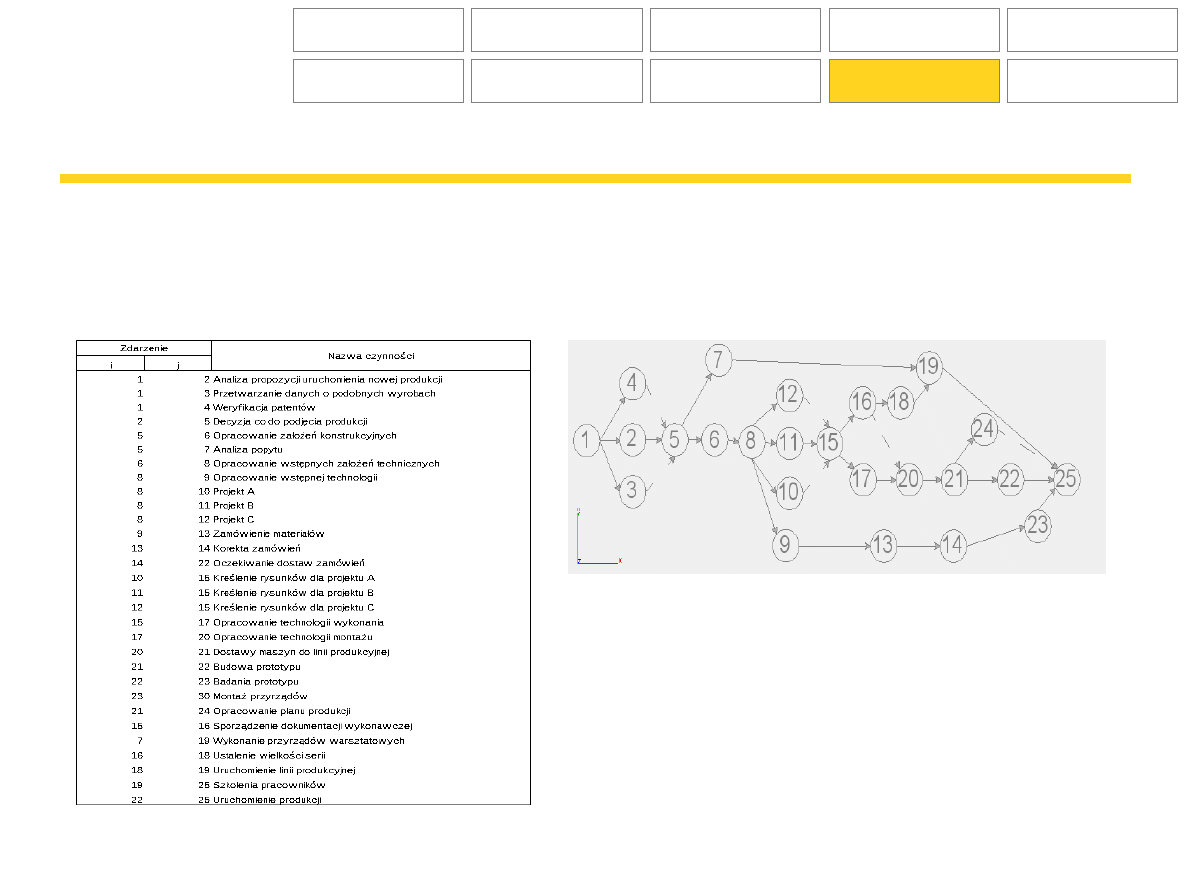
Przykładowa sieć:

Wykaz czynności

Zdarzenia: Sieć:

Przykład pochodzi z książki: „Metody ilościowe w organizacji i zarządzaniu”
Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

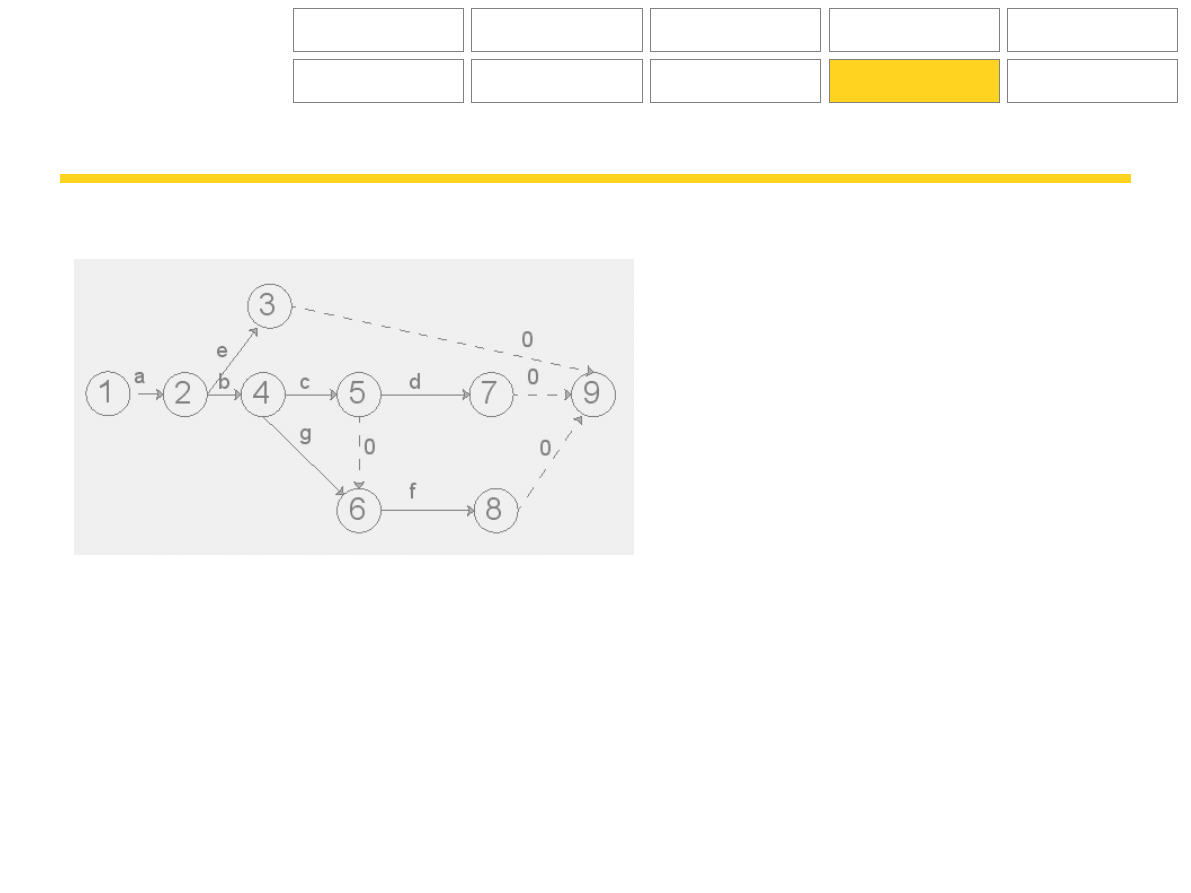
Zadanie:

Narysować wykres sieciowy znając następujące zależności między czynnościami:

- czynności e i b rozpoczynają się po zakończeniu czynności a,
- czynności c,g rozpoczynają się po zakończeniu czynności b,
- czynność d rozpoczyna się po zakończeniu czynności c,
- czynność f rozpoczyna się po zakończeniu czynności g, ale nie wcześniej niż przed zakończeniem czynności
c.

Przykład pochodzi z książki: „Metody ilościowe w organizacji i zarządzaniu”

Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

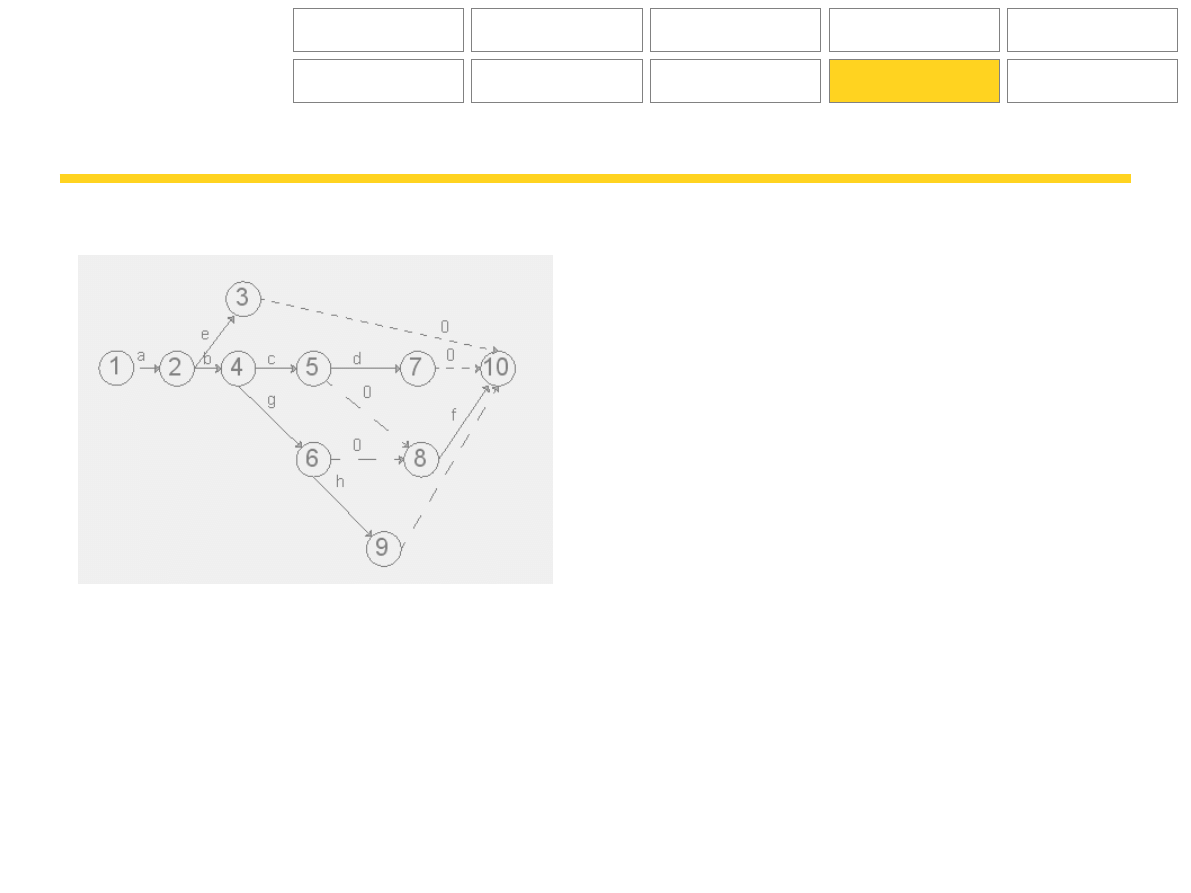
Rozwiązanie zadania:

Jak zmieni się wykres sieciowy, gdy uwzględnimy zależność, że czynność h rozpoczyna się po zakończeniu
czynności g?

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Rozwiązanie zadania:

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

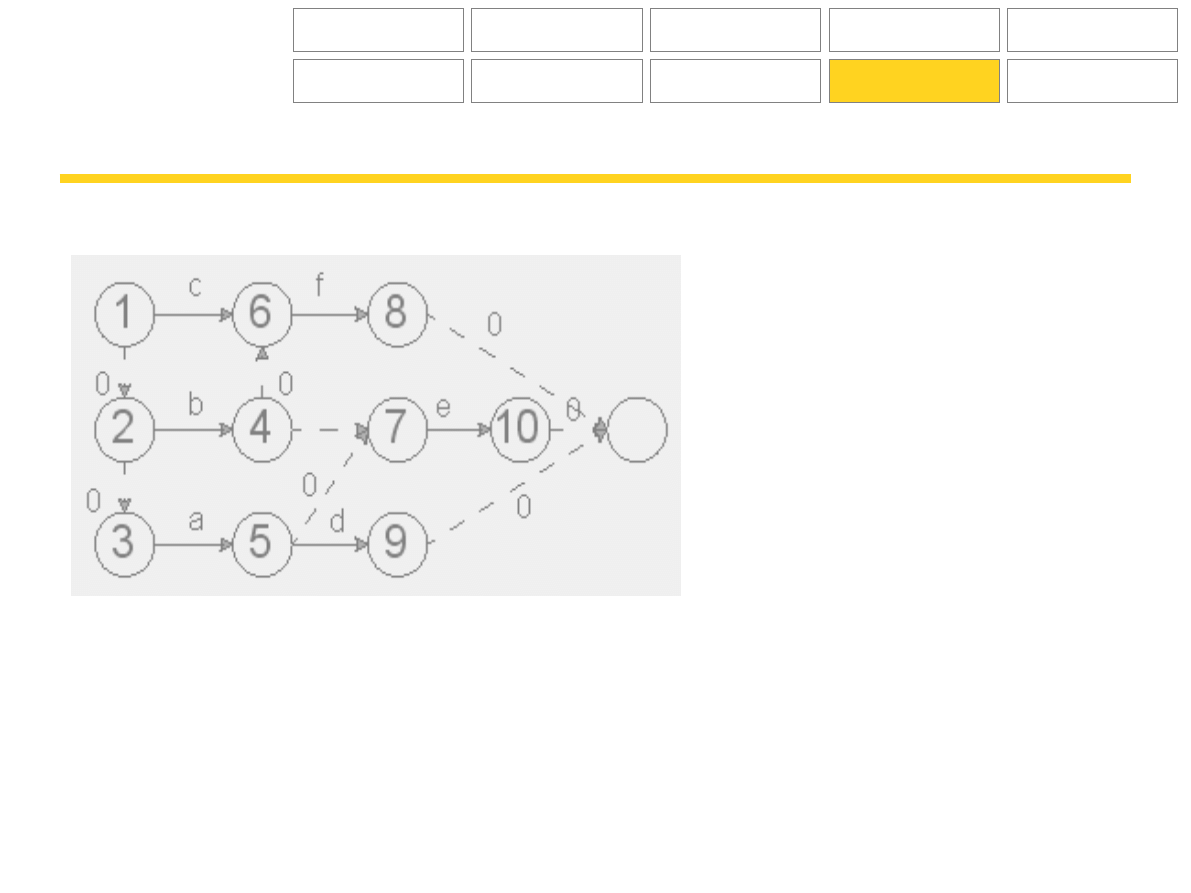
Zadanie:

Narysować wykres sieciowy znając następujące zależności między czynnościami:

- czynność f rozpoczyna się po zakończeniu czynności b,c,
- czynność e rozpoczyna się po zakończeniu czynności a,b,
- czynność d rozpoczyna się po zakończeniu czynności a.

Przykład pochodzi z książki: „Metody ilościowe w organizacji i zarządzaniu”

Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Rozwiązanie zadania:

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Analiza grafów sieciowych:

Analiza taka polega na:

- obliczeniu najkrótszego czasu wykonania programu pracy – określenie tzw. drogi krytycznej,
- wyznaczeniu drogi krytycznej (jej przebiegu) i czynności krytycznych (leżących na tej drodze), biegnących od
początkowego wierzchołka grafu do wierzchołka końcowego,
- określeniu czasów rozpoczęcia i ukończenia czynności – najwcześniejszych i najpóźniejszych terminów dla
czynności, będących składowymi grafu.

Analizę można przeprowadzić graficznie (na diagramie sieciowym) albo analitycznie (posługując się
algorytmami).

Co to jest droga krytyczna?

Drogą krytyczną nazywamy łańcuch czynności, które ma początek w zdarzeniu rozpoczynającym sieć, a koniec
w zdarzeniu ją kończącym, pozwalający na realizację wszystkich czynności zawartych w sieci. Jest to
najdłuższa droga przejścia przez sieć, zgodnie ze zwrotem czynności, rozpoczynając od zdarzenia
początkowego, a kończąc na końcowym. Na wykresie może być wiele dróg krytycznych, jedna droga może się
rozgałęzić na wiele dróg lub wiele dróg może się zbiegać w jedną.

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Metoda CPA – Critical Path Analysis

Drogę krytyczną możemy wyznaczyć posługując się dwiema metodami, które bazują na analizie czasowej
wykresu sieciowego.

Pierwsza metoda polega na przeanalizowaniu łącznego czasu trwania wszystkich czynności leżących na
możliwych do utworzenia ścieżkach. Ścieżki te prowadzą od początku wykresu do jego końca, a
przemieszczanie się musi być zgodne ze zwrotami linii łączących zdarzenia. Droga, która posiada najdłuższy
czas przewidziany na wykonanie wszystkich czynności w niej zawartych, stanowi drogę krytyczną.

Druga metoda bazuje na obliczeniach, do których używa się najwcześniejszych możliwych i najpóźniejszych
dopuszczalnych terminów zajścia zdarzeń. Wielkości te obliczane są początkowo i na ich podstawie wyznacza
się zapas całkowity czasu, jakim dysponuje każda czynność. Po obliczeniu zapasu czasu dla każdej czynności,
czynnościami krytycznymi będą te, które mają wartość zapasu całkowitego równą 0. Czynności krytyczne łączą
się w łańcuchy (łańcuch), które stanowią drogę krytyczną.

Opóźnienie jakiejkolwiek czynności krytycznej, powoduje opóźnienie całego przedsięwzięcia wyrażonego
wykresem sieciowym.

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

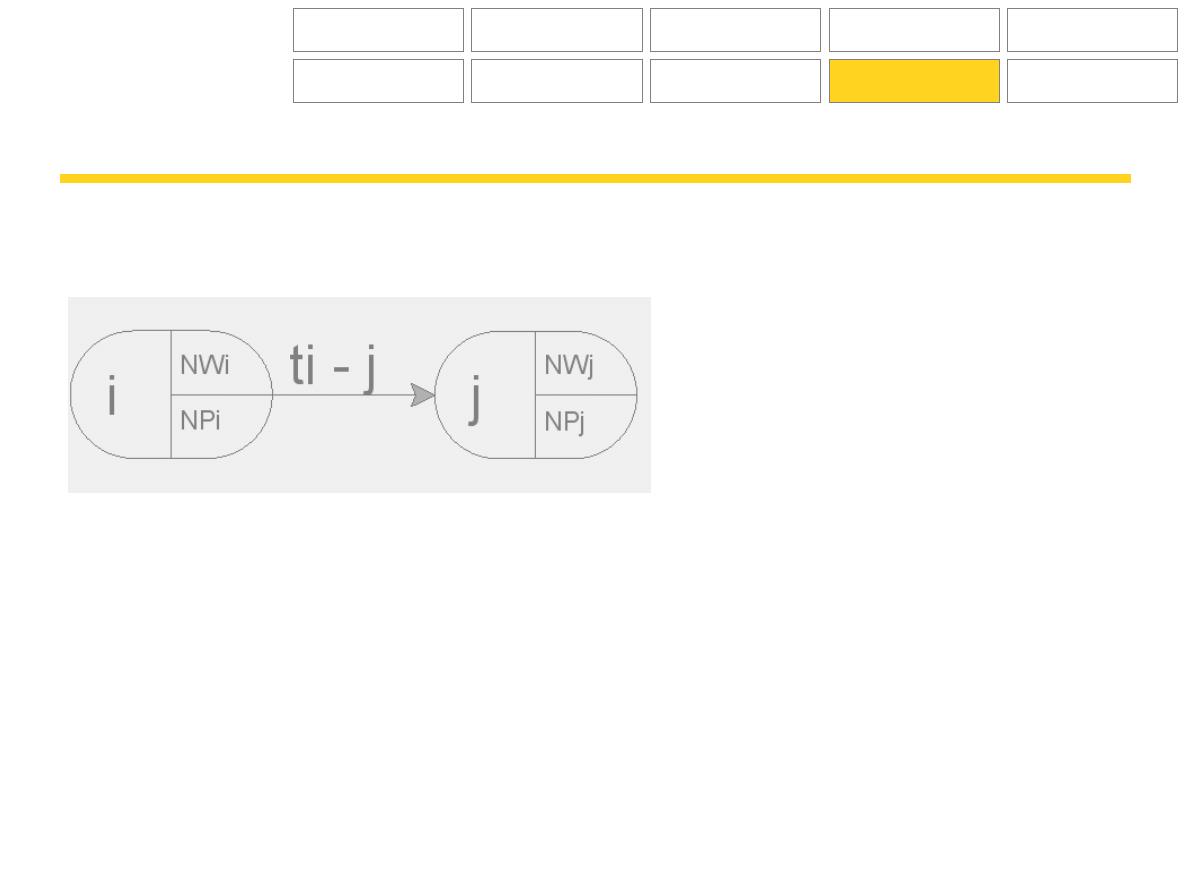
Metoda CPA – Critical Path Analysis

Graficznie:

gdzie:

i-j – dowolna czynność na wykresie sieciowym
i – numer zdarzenia rozpoczynającego czynność
j – numer zdarzenia kończącego czynność
ti-j – czas trwania czynności i-j
NWi, NWj – najwcześniejsze możliwe terminy zaistnienia zdarzeń i,j
NPi, NPj – najpóźniejsze dopuszczalne terminy zaistnienia zdarzeń i,j

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Metoda CPA – Critical Path Analysis

Obliczanie terminów:

Dla zdarzenia rozpoczynającego wykres przyjmuje się NW = 0.

Terminy następnych zdarzeń oblicza się korzystając z następującego wzoru:

NWj = max(NWi + ti-j)

Obliczenia terminów najwcześniejszych dokonuje się „w przód” wykresu sieciowego.

Gdy znany jest już termin najwcześniejszy zdarzenia ostatniego, zaczyna się obliczenia „wstecz” terminów
najpóźniejszych. Przyjmuje się jeszcze, że termin najpóźniejszy zdarzenia kończącego jest terminem
najwcześniejszym tego zdarzenia. Kolejne terminy oblicza się tak:

NPi = min(NPj - ti-j)

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Metoda CPA – Critical Path Analysis

Zapasy - obliczanie:

Zapas całkowity – jest to czas, o który może być opóźnione rozpoczęcie danej czynności bez wpływu na termin
końcowy całego przedsięwzięcia. Wykorzystanie całego zapasu (ZC = 0) powoduje, że czynność staje się
czynnością krytyczną:

ZCi-j = NPj – NWi – ti-j ; (ZCi-j ≥0)

(zapasy dotyczące pozostałych, poza krytycznymi, czynności)

Zapas swobodny – mówi, o ile maksymalnie można opóźnić termin zakończenia czynności rozpoczętej w jej
terminie najwcześniejszym bez naruszenia najwcześniejszego możliwego terminu rozpoczęcia czynności
następnej:

ZSi-j = NWj – NWi – ti-j ; (ZSi-j ≥0)

Zapas krytyczny – wskazuje, o ile maksymalnie można opóźnić termin zakończenia czynności rozpoczętej w
terminie najpóźniejszym, bez naruszenia najpóźniejszego terminu rozpoczęcia czynności następnej:

ZKi-j = NPj – NPi – ti-j ; (ZKi-j ≥0)

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Metoda CPA – Critical Path Analysis

Zapasy - obliczanie:

Zapas niezależny – mówi, o ile można maksymalnie opóźnić termin zakończenia czynności rozpoczętej w jej
terminie najpóźniejszym bez naruszenia najwcześniejszego terminu rozpoczęcia czynności następnej:

ZNi-j = NWj – NPi – ti-j

Zapas warunkowy – różnica zapasu całkowitego i swobodnego czasu dla czynności:

ZWi-j = ZCi-j – ZSi-j = NPj – NWj

Jest to wielkość czasu, która będąc wykorzystaną do opóźnienia danej czynności, wpłynie na opóźnienie
rozpoczęcia czynności następnej, ale bez wpływu na opóźnienie całego zadania.

Luz czasowy – określany jest dla zdarzeń niekrytycznych, wyrażony jako różnica pomiędzy terminem
najpóźniejszym i najwcześniejszym danej czynności:

Li = NPi – NWi

Lj = NPj– NWj

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Przykład

Narysować wykres sieciowy znając zależności między czynnościami:

- czynności c,d rozpoczynają się po czynności b,
- czynność e rozpoczyna się po zakończeniu czynności a,
- czynności f,g rozpoczynają się po zakończeniu czynności e,c,
- czynność h rozpoczyna się po zakończeniu czynności f,d,

Wykres sieciowy ma jedno zdarzenie rozpoczynające i jedno kończące.

Określić terminy najwcześniejsze, najpóźniejsze zaistnienia zdarzeń, obliczyć zapasy czasu dla każdej
czynności przy następujących czasach ich trwania:

ta = 3, tb = 2, tc = 3, td = 4, te = 4, tf = 5, tg = 3, th = 3

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

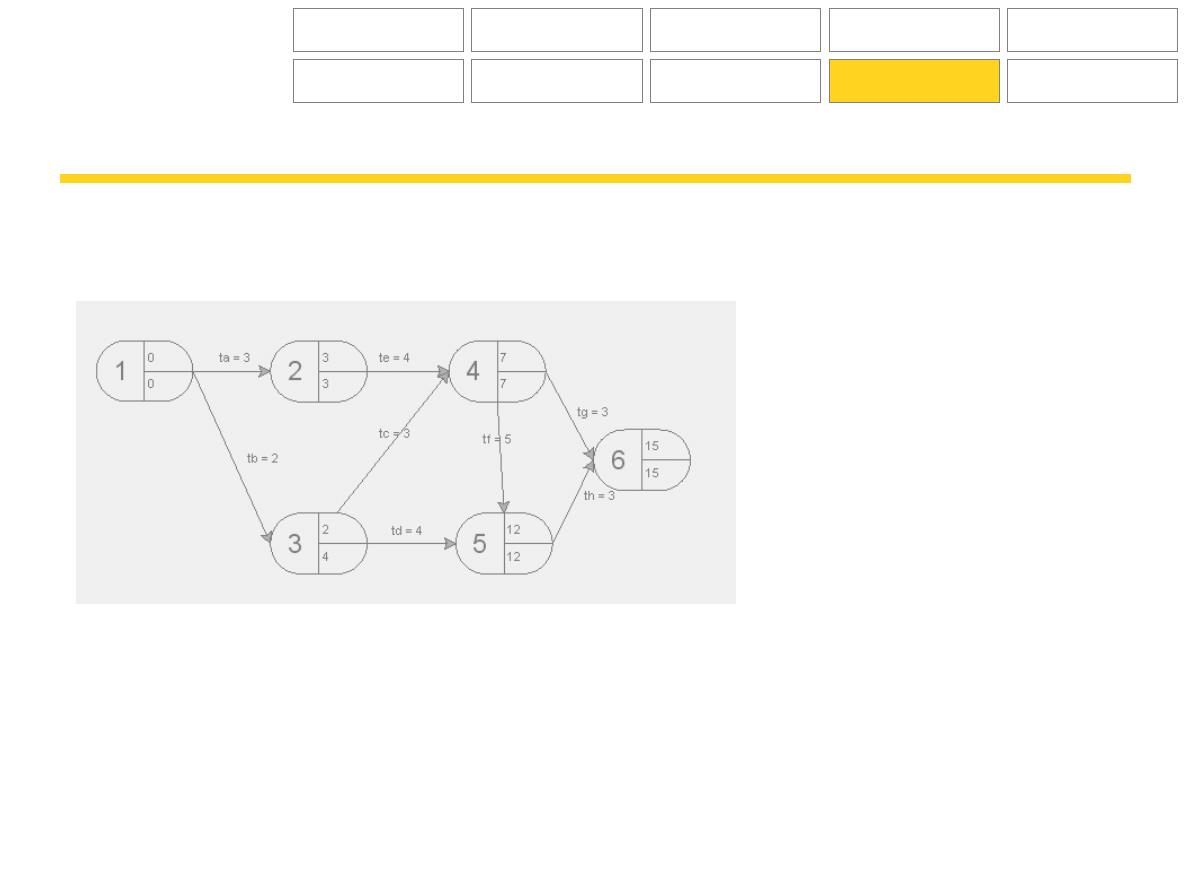
Rozwiązanie:

Wykres:

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Rozwiązanie:

Metoda pierwsza wyznaczania ścieżki krytycznej:

Określa się wszystkie możliwe drogi przejścia pomiędzy zdarzeniem 1-6, wraz z ich łącznymi czasami.

1) 1 – 2 – 4 – 6 t

1

= 10

2) 1 – 2 – 4 – 5 – 6 t

2

= 15 – droga krytyczna

3) 1 – 3 – 4 – 6 t

3

= 8

4) 1 – 3 – 4 – 5 – 6 t

4

=13

5) 1 – 3 – 5 – 6 t

5

= 9

Metoda druga:

Określa się najwcześniejsze i najpóźniejsze terminy (są już na wcześniejszym wykresie).
Określa się zapas całkowity czasu dla wszystkich czynności:

ZC1-2 = NP2 – NW1 - t1-2 = 3 – 0 -3 = 0
ZC1-3 = NP3 – NW1 - t1-3 = 4 – 0 -2 = 2
ZC2-4 = NP4 – NW2 - t2-4 = 7 – 3 -4 = 0
ZC3-4 = NP4 – NW3 - t3-4 = 7 – 2 -3 = 2
ZC3-5 = NP5 – NW3 - t3-5 = 12 – 2 -4 = 6
ZC4-5 = NP5 – NW4 - t4-5 = 12 – 7 -5 = 0
ZC4-6 = NP6 – NW4 - t4-6 = 15 – 7 -3 = 5
ZC5-6 = NP6 – NW5 - t5-6 = 15 – 12 -3 = 0

W przypadku, gdy wynik wynosi 0, mamy do czynienia z czynnością krytyczną.

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Rozwiązanie:

Zapasy czasu:

ZS1-2 = NW2 – NW1 - t1-2 = 0
ZS1-3 = NW3 – NW1 - t1-3 = 0
ZS2-4 = NW4 – NW2 - t2-4 = 0
ZS3-4 = NW4 – NW3 - t3-4 = 2
ZS3-5 = NW5 – NW3 - t3-5 = 6
ZS4-5 = NW5 – NW4 - t4-5 = 0
ZS4-6 = NW6 – NW4 - t4-6 = 5
ZS5-6 = NW6 – NW5 - t5-6 = 0

ZK1-2 = NP2 – NP1 - t1-2 = 0
ZK1-3 = NP3 – NP1 - t1-3 = 2
ZK2-4 = NP4 – NP2 - t2-4 = 0
ZK3-4 = NP4 – NP3 - t3-4 = 0
ZK3-5 = NP5 – NP3 - t3-5 = 0
ZK4-5 = NP5 – NP4 - t4-5 = 0
ZK4-6 = NP6 – NP4 - t4-6 = 5
ZK5-6 = NP6 – NP5 - t5-6 = 0

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

ZN1-2 = NW2 – NP1 - t1-2 = 0
ZN1-3 = NW3 – NP1 - t1-3 = 0
ZN2-4 = NW4 – NP2 - t2-4 = 0
ZN3-4 = NW4 – NP3 - t3-4 = 0
ZN3-5 = NW5 – NP3 - t3-5 = 4
ZN4-5 = NW5 – NP4 - t4-5 = 0
ZN4-6 = NW6 – NP4 - t4-6 = 5
ZN5-6 = NW6 – NP5 - t5-6 = 0

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

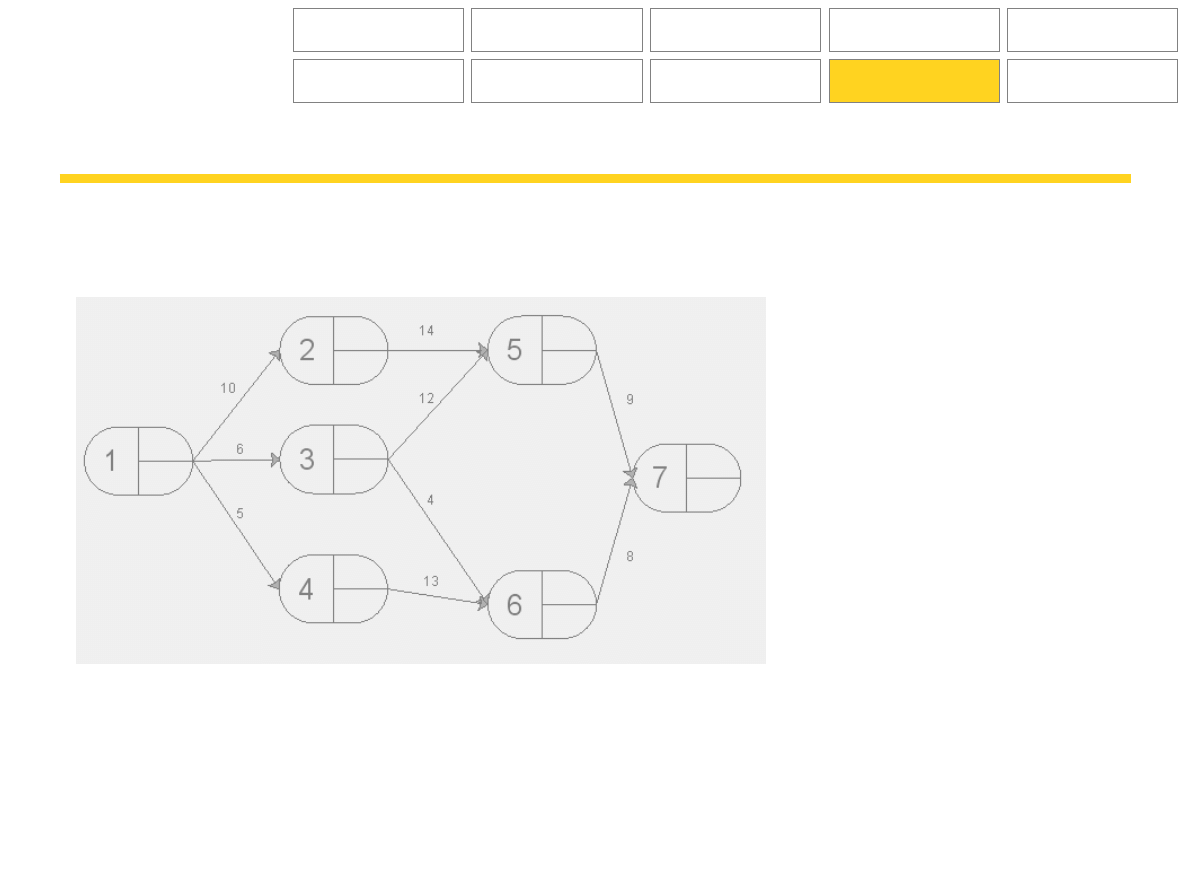
Zadania

Na poniższych wykresach wskaż drogę krytyczną, określ terminy najpóźniejsze i najwcześniejsze zdarzeń.

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

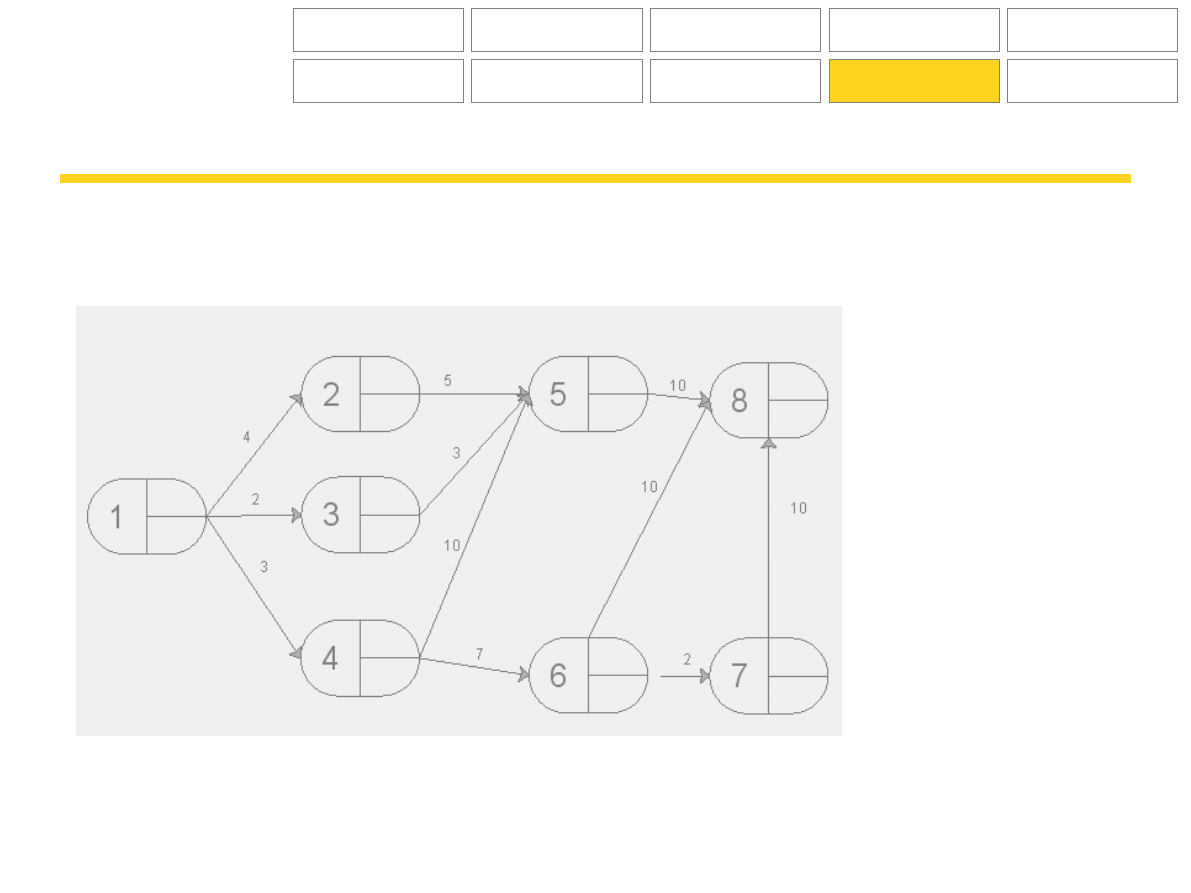
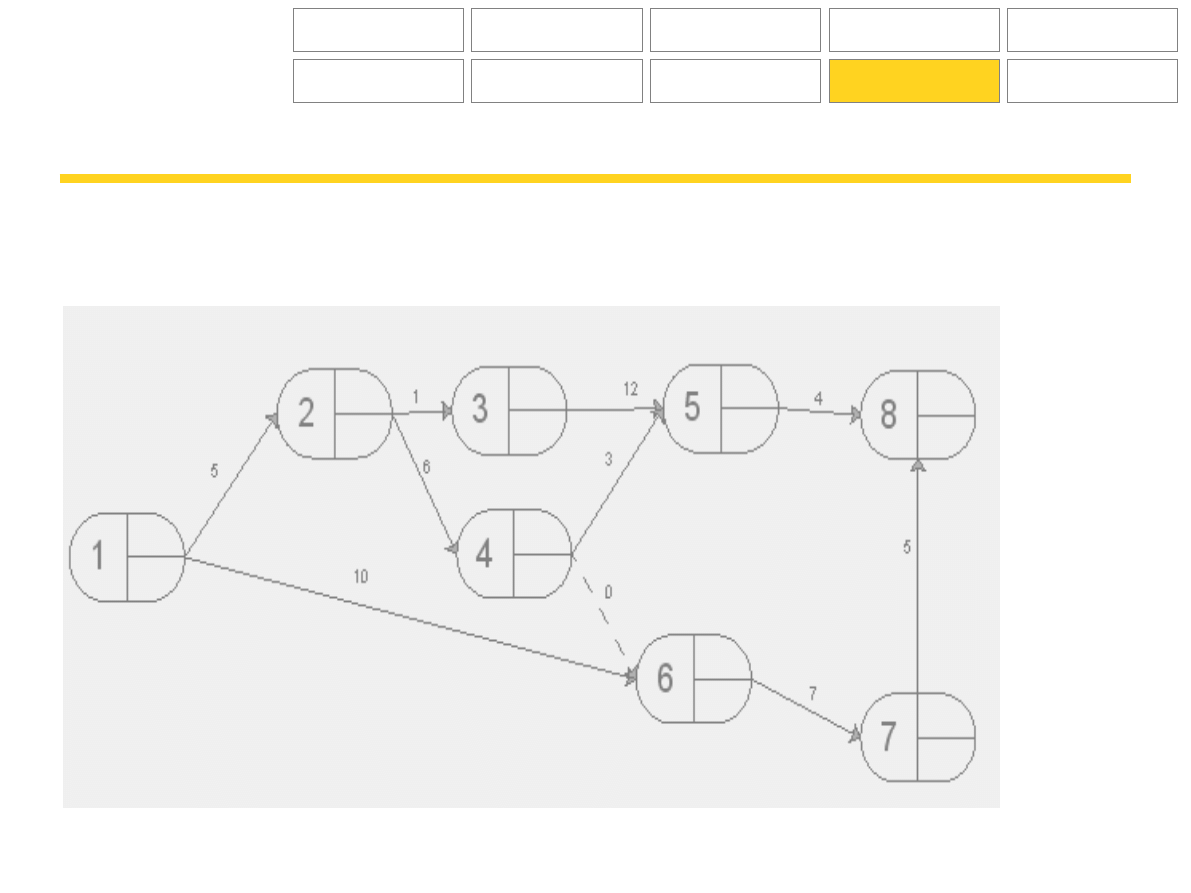
Zadania

Na poniższych wykresach wskaż drogę krytyczną, określ terminy najpóźniejsze i najwcześniejsze zdarzeń.

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

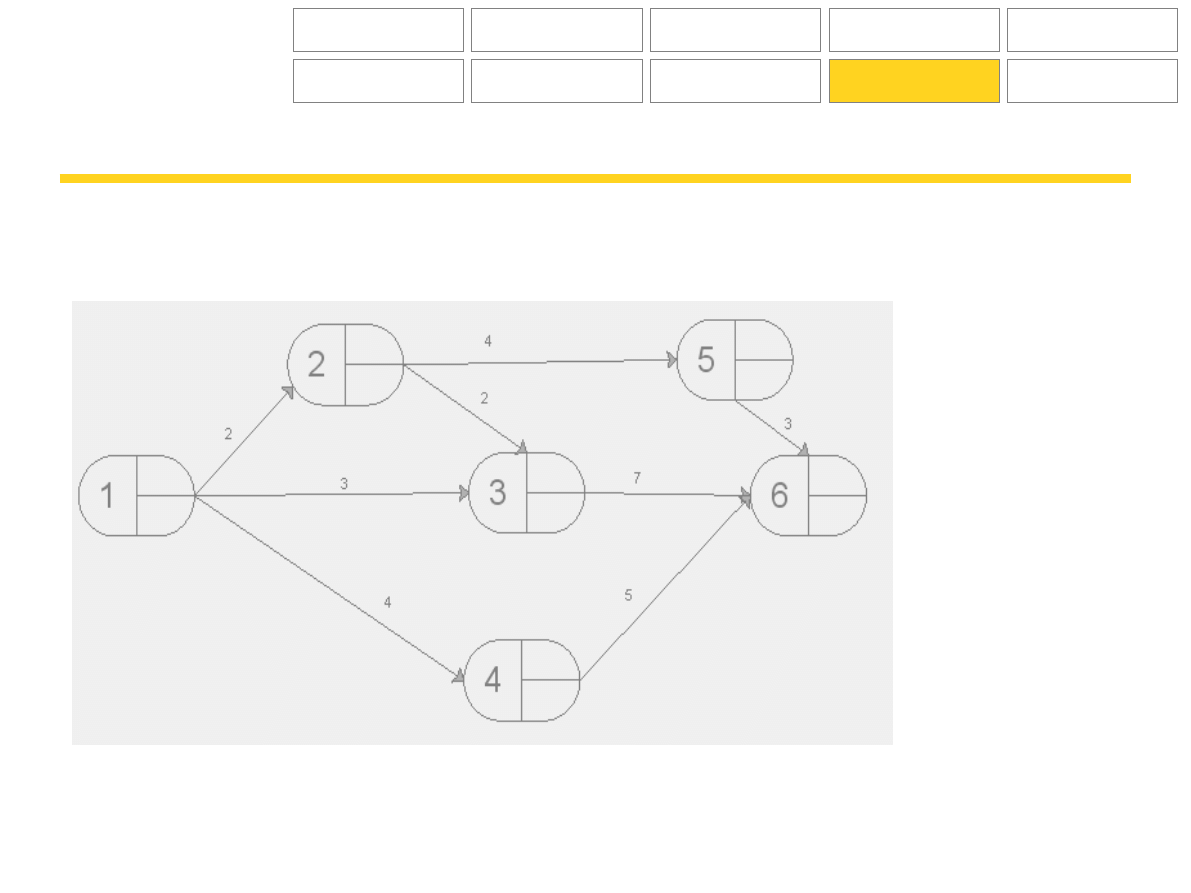
Zadania

Na poniższych wykresach wskaż drogę krytyczną, określ terminy najpóźniejsze i najwcześniejsze zdarzeń.

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

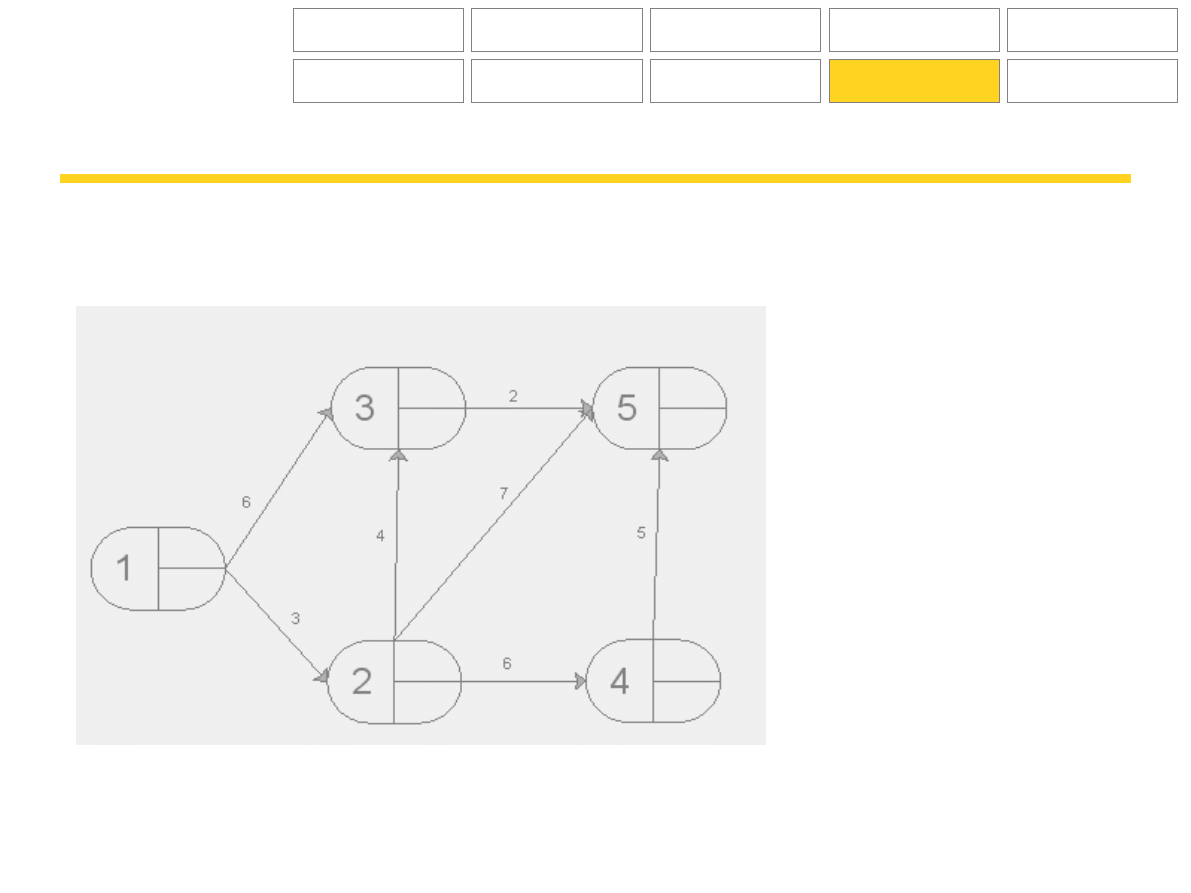
Zadania

Na poniższych wykresach wskaż drogę krytyczną, określ terminy najpóźniejsze i najwcześniejsze zdarzeń.

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

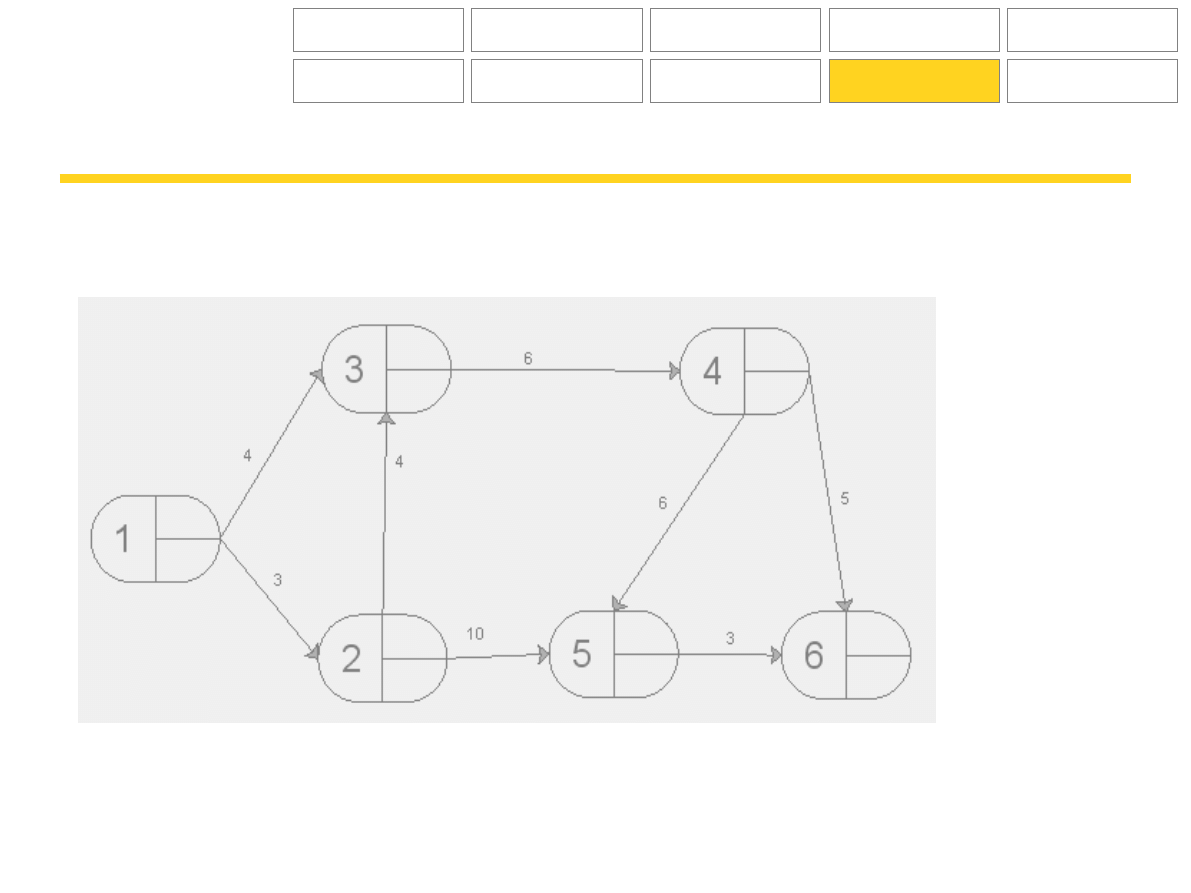
Zadania

Na poniższych wykresach wskaż drogę krytyczną, określ terminy najpóźniejsze i najwcześniejsze zdarzeń.

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Zadania

Na poniższych wykresach wskaż drogę krytyczną, określ terminy najpóźniejsze i najwcześniejsze zdarzeń.

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

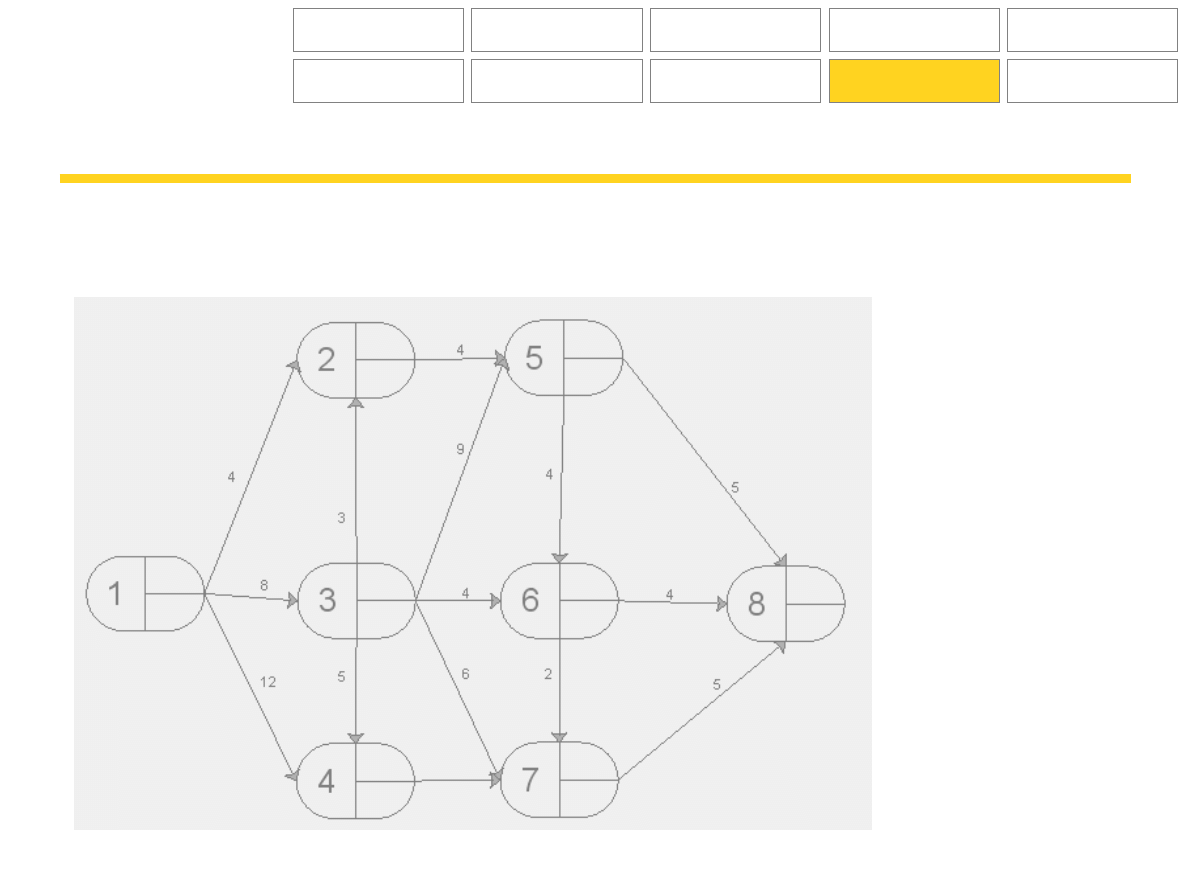
Zadania

Na poniższych wykresach wskaż drogę krytyczną, określ terminy najpóźniejsze i najwcześniejsze zdarzeń.

Zagadnienia teoretyczne pochodzą z książki: „Metody ilościowe w organizacji

i zarządzaniu” Pani Prof. L.Zawadzkiej

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Metoda PERT:

W metodzie PERT czasy trwania poszczególnych czynności są zmiennymi losowymi. Rozkład
prawdopodobieństwa występowania różnych czasów trwania odpowiada znanemu w probabilistyce rozkładowi
beta, którego szczególnym przypadkiem jest rozkład normalny.

Dla każdej czynności znane są trzy oceny czasu jej trwania:

a – czas optymistyczny (tyle może trwać czynność w najbardziej sprzyjających warunkach)
b – czas pesymistyczny (czas trwania czynność w niesprzyjających warunkach)
m – czas modalny – najbardziej prawdopodobny, czas najczęściej występujący przy wielokrotnym powtarzaniu
czynności

Między ocenami zachodzi relacja: a ≤ m ≤ b.

Oczekiwany czas trwania czynności oblicza się ze wzoru:

natomiast odchylenie (wariancję) rzeczywistego czasu trwania czynności od wyznaczonego czasu
oczekiwanego:

t

e

=

a +4m+b

6

σ

ij

2

=

(

b−a

6

)

2

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

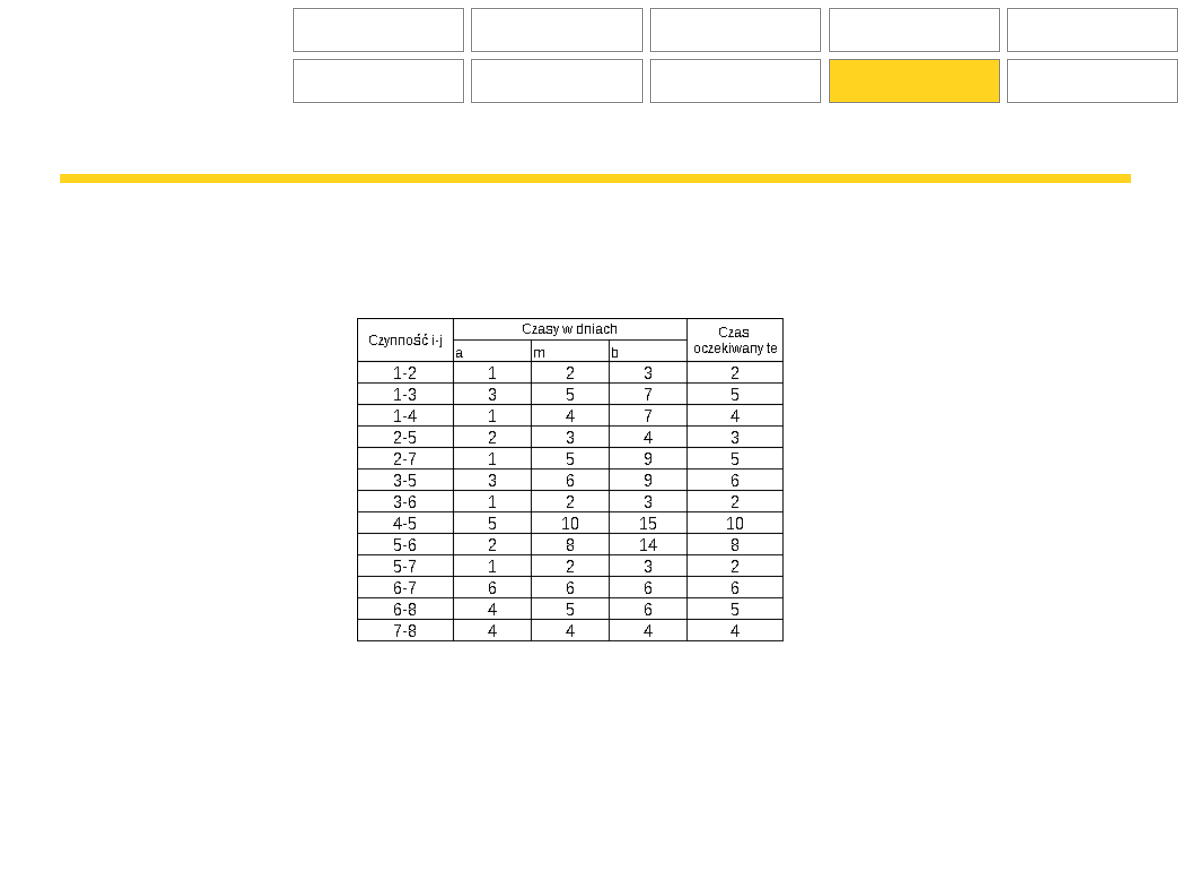
Zadanie:

Mając dane czynności składające się na przedsięwzięcie P, ich następstwo oraz czasy trwania określ:

a) czas oczekiwany t

e

b) najkrótszy czas trwania przedsięwzięcia
c) prawdopodobieństwo dotrzymania założonego terminu t

d

= 30 dni

Narysuj wykres sieciowy i wyznacz drogę krytyczną.

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

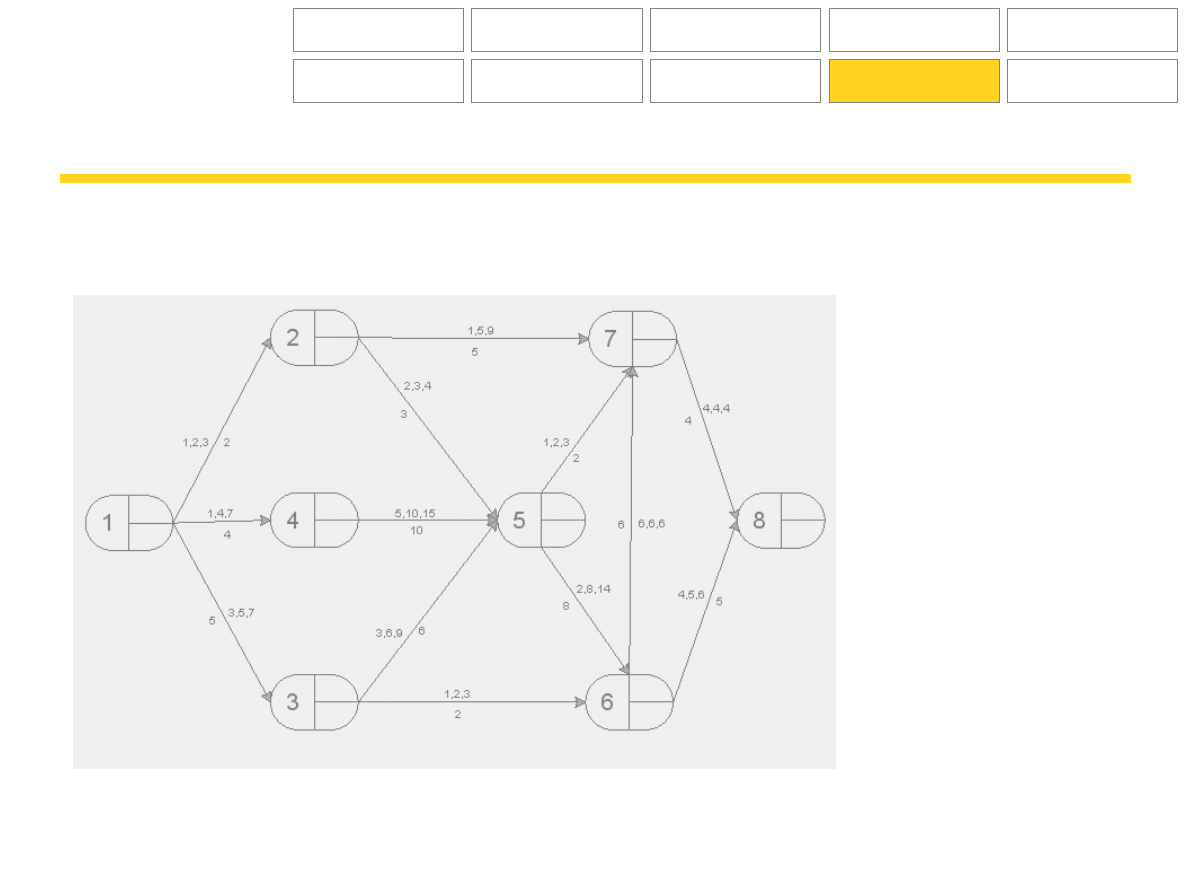
Rozwiązanie zadania:

Czasy oczekiwane t

e

:

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Rozwiązanie zadania:

Wykres sieciowy:

:

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

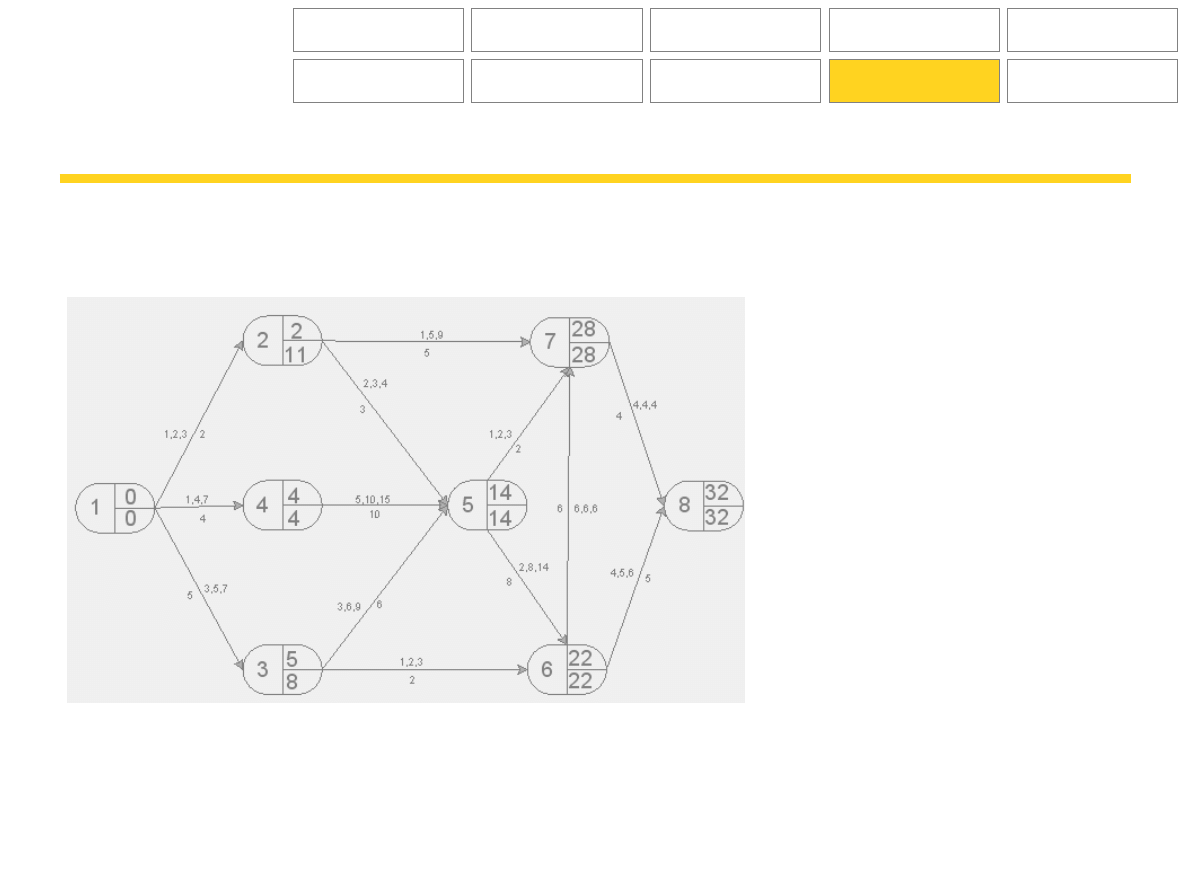
Rozwiązanie zadania:

Wykres sieciowy:

Najwcześniejszy oczekiwany termin zakończenia przedsięwzięcia wynosi 32 dni.

Droga krytyczna prowadzi przez czynności: 1-4-5-6-7-8

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Rozwiązanie zadania:

W naszej sytuacji termin zakończenia przedsięwzięcia jest wielkością losową, może się różnić od terminu
rzeczywistego. Dlatego też potrzebujemy znać odchylenie od tego terminu. W tym celu posłużymy się wariancją
terminu wykonania (σ

2

Tw

), która jest sumą wariancji czynności krytycznych.

Obliczamy wariancje dla czynności krytycznych:

Sumujemy poszczególne wariancje:

σ

14

2

=

(

7−1

6

)

2

=

1

σ

45

2

=

(

15−5

6

)

2

=

25

9

σ

56

2

=

(

14−2

6

)

2

=

4

σ

67

2

=

(

6−6

6

)

2

=

0

σ

78

2

=

(

4−4

6

)

2

=

0

σ

Tw

2

=

1+

25

9

+

4+0+0=

70

9

zatem σ=2,78

Programowanie sieciowe

Optymalizacja

struktury produkcj

i

Zagadnienia

mieszanek

Wybór procesu

technologicznego

Simpleks

Wstęp teoretyczny

Problem przydziału

Kolokwium I

Programowanie

sieciowe

Kolokwium II

Zagadnienie
transportowe

Rozwiązanie zadania:

Obliczmy prawdopodobieństwo, że przedsięwzięcie będzie zakończone w pewnym narzucanym z góry terminie
t

d

(30 dni z treści zadania).

Skorzystamy ze wzoru:

td – narzucony z góry termin,

tw – oczekiwany termin wykonania przedsięwzięcia – najwcześniejszy możliwy termin zakończenia zdarzenia
końcowego (z naszej sieci 32 dni)

σ

2

Tw

wariancja terminu wykonania

Dla obliczonego współczynnika x = -0,71 z tablic dystrybuanty standaryzowanego rozkładu normalnego
odczytujemy prawdopodobieństwo dotrzymania narzuconego z góry terminu:

W praktyce przyjmuje się, że gdy wartość F(x) (dla naszego zadania F(-0,71) = 0,23885) jest w przedziale
(0,25;0,6), to termin dyrektywny nie jest zagrożony. Gdy jest ≤0,25 termin dyrektywny jest zagrożony, natomiast
gdy ≥0,6, to w przedsięwzięciu występuje duży zapas czasu.

:

x=

(

t

d

−

t

w

)

√

σ

TW

2

P

{

t

d

⩽

t

w

}

=

F ( x)