Twierdzenie Plancherela

Helena Gawrońska

Alina Maląg

10 czerwca 2015

1

Transformata Fouriera

Postawimy definicję transformaty Fouriera dla funkcji o argumentach wektorowych. Dla danej
funkcji f ∈ L

1

(R

n

) ∩ L

2

(R

n

) , jej transformatę Fouriera definiujemy jako:

ˆ

f (ξ) := (2π)

−n/2

Z

R

n

f (x)e

iξx

dx.

Oznaczmy odwzorowanie f → ˆ

f jako F

Stosuje się również alternatywną definicję transformaty: Transformacja z dziedziny czasu t w
dziedzinę pulsacji (częstości kołowej)

ω : ˆ

f (ω) =

∞

Z

−∞

f (t)e

−iωt

dt

gdzie

• f (t) - funkcja (oryginał) w dziedzinie czasu

• ˆ

f (ω)- transformata (widmo Fouriera) w dziedzinie pulsacji

• ω =

2π

T

= 2πν - pulsacją proporcjonalną do częstotliwości oscylacji ν

Zdefiniujemy także unitarną transformację z dziedziny czasu t w dziedzinę pulsacji (częstości
kołowej)

ω : ˆ

f (ω) =

1

√

2π

∞

Z

−∞

f (t)e

−iωt

dt

i transformację odwrotną:

f (t) =

1

√

2π

∞

Z

−∞

ˆ

f (ω)e

iωt

dω

Czynnik

1

√

2π

przed transformacją i transformacją odwrotną występuje umownie - zamiast takiej

postaci może występować czynnik

1

2π

przed transformacją prostą, albo (częściej) przed trans-

formacją odwrotną Jeżeli jednak czynnik wynosi

1

√

2π

, wtedy transformacja i transformacja

odwrotna są izometriami przestrzeni L

2

(R) Pierwsza z dwu powyższych definicji jest popular-

niejsza, nie posiada jednak własności unitarności.

1

2

Twierdzenie Plancherela

Ponieważ miara Lebesgue’a zbioru R jest nieskończona, zatem L

2

nie jest podprzestrzenią prze-

strzeni L

1

, a więc nie można zastosować definicji transformaty Fouriera do każdej funkcji f ∈ L

2

(Definicję tę można stosować, gdy f ∈ L

2

∩ L

1

) Okazuje się wówczas, że wówczas ˆ

f ∈ L

2

.

Co więcej || ˆ

f ||

2

= ||f ||

2

. Transformacja Fouriera jest więc izometrią przestrzeni L

1

∩ L

2

w L

2

.

Izometrię tę rozszerza się do izometrii przestrzeni L

2

na siebie. Rozszerzenie to określa transfor-

matę Fouriera (zwaną czasem transformatą Plancherela) dowolnej funkcji f ∈ L

2

. Otrzymana w

ten sposób teoria w przestrzeni L

2

ma o wiele wyższy stopień symetrii niż teoria transformacji

Fouriera w przestrzeni L

1

. W przestrzeni L

2

funkcje f i ˆ

f odgrywają dokładnie tę samą rolę.

Twierdzenie Plancherela:
Każdej funkcji f∈L

2

można przyporządkować funkcję ˆ

f w taki sposób, że spełnione będą na-

stępujące warunki:

1. Jeżeli f ∈ L

2

∩ L

1

to ˆ

f jest transformatą Fouriera w sensie definicji alternatywnej

2. Dla każdego f∈L

2

zachodzi równość || ˆ

f ||

2

= ||f ||

2

.

3. Przekształcenie F jest izomorfizmem przestrzeni Hilberta na siebie

4. Niech f ∈ L

1

(R

n

) ∩ L

2

(R

n

) Na podstawie alternatywnej definicji mamy,że:

f (x) =

1

√

2π

Z

∞

−∞

F (k)e

ikx

dk ⇔ F (k) =

1

√

2π

Z

∞

−∞

f (x)e

ikx

dx,

gdzie F(k) jest transformatą Fouriera z f(x) i f(x) jest odwrotną transformatą z F(k).
Twierdzenie w takiej postaci będziemy udowadniać.

3

Dowód twierdzenia

Dowód twierdzenia przeprowadzimy w kilku krokach, sprawdzając po kolei założenia twierdze-
nia:

3.1

Krok 1

Na początku sprawdzimy, że funkcja f(x) na przedziale [-a,a] może być rozszerzona w szereg
Fouriera

f (x) =

∞

X

n=0

[a

n

sin(

nΠx

a

) + b

n

cos(

nΠx

a

)]

(1)

f(x) może być zapisana równoważnie jako :

f (x) =

∞

X

n=−∞

c

n

e

inΠx

a

(2)

Pokażemy teraz, jak c

n

zapisać w zależności od a

n

i b

n

. Dla n=0 (1) przyjmuje postać: f (x) = b

n

Stosując wzór Eulera, możemy zapisać (1) jako:

f (x) = b

0

+

∞

X

n=1

[

a

n

2i

(e

inΠx

a

− e

−inΠx

a

)) +

∞

X

n=1

[

b

n

2

(e

inΠx

a

− e

−inΠx

a

)

f (x) = b

0

+

∞

X

n=1

[

a

n

2i

(e

inΠx

a

− e

−inΠx

a

)) + [

b

n

2

(e

inΠx

a

− e

−inΠx

a

)

2

f (x) = b

0

+

∞

X

n=1

[

a

n

2i

e

inΠx

a

−

a

n

2i

e

−inΠx

a

)) + [

b

n

2

e

inΠx

a

−

b

n

2

e

−inΠx

a

)

Grupując:

f (x) = b

0

+

∞

X

n=1

[(

a

n

2i

+

b

n

2

e

−inπx

a

) +

∞

X

n=1

(

−a

n

2i

+

b

n

2

e

−inΠx

a

)

(3)

Dla n=1 powyższe równanie przyjmuje postać:

f (x) =

1

2

(−ia

1

+ b − 1)e

iπx

a

+

1

2

(ia

1

+ b − 1)e

−iπx

a

(4)

Sprawdźmy, jak zachowa się (2) dla n=-1 i n=1:

dla n=-1

f (x) = c

1

e

iπx

a

dla n=-1

f (x) = c

−

1e

−iπx

a

Zauważmy podobieństwo powyższych wyrażeń do (4), gdy :

c

1

=

1

2

(−a

1

+ b

1

)

i

c

−

1 =

1

2

(a

1

+ b

1

)

Zatem, w ogólności:

f (x) =

∞

X

n=0

[a

n

sin(

nΠx

a

) + b

n

cos(

nΠx

a

)]

może być zapisana jako:

f (x) =

∞

X

n=−∞

c

n

e

inΠx

a

,

gdzie c

0

= b

0

, c

1

=

1
2

(−a

1

+ b

1

)ic

−

1 =

1
2

(a

1

+ b

1

)

3.2

Krok 2

Wykażemy teraz, że:

c

n

=

1

2a

Z

+a

−a

f (x)e

−inπx

a

dx

(5)

W tym celu pomnożymy obie strony równania (2) przez

φ

∗
m

, przy czym

φ

n

= e

nπix

a

Z

a

−a

φ

∗
m

(x)f (x)dx =

∞

X

−∞

c

n

Z

a

−a

φ

∗
m

(x)φ

n

(x)dx =

∞

X

−∞

2ac

n

δmn = 2ac

m

Ortonormalność φ

n

i φ

∗
m

wybija wszystkie wyrażenia oprócz n = m, a więc odpowiednich dla

delty Kroneckera. Zatem mamy:

Z

a

−a

φ

∗
m

(x)f (x)dx = 2ac

m

3

Zamieniając indeksy z m na n otrzymujemy:

Z

a

−a

φ

∗
n

(x)f (x)dx = 2ac

n

Wyliczając c

n

i pamiętając, że

φ

n

= e

inπx

a

ostatecznie otrzymujemy, że:

c

n

=

1

2a

Z

+a

−a

f (x)e

−inπx

a

dx

3.3

Krok 3

Teraz wyeliminujemy n i c

n

oraz zastosujemy podstawienie: k =

nπ

a

oraz F (k) =

q

2

π

ac

n

Wtedy (2) ma postać:

f (x) =

1

2π

∞

X

−∞

F (k)e

ikx

∆k

oraz (5) (z kroku 2):

F (k) =

1

2π

Z

a

−a

f (x)e

−iks

dx

Wyliczając c

n

z

F (k) =

s

2

π

ac

n

mamy:

c

n

=

1

a

F (k)

r

π

2

Dodatkowo wiemy, że

∆k =

∆nπ

a

∆n = 1

∆k

π

=

1

a

Podstawiając powyższe do (2) otrzymujemy:

f (x) =

∆k

π

1

a

r

π

2

∞

X

−∞

F (k)e

ikx

=

s

1

2π

F (k)e

ikx

∆k

Z drugiej strony dla F(k) otrzymujemy (5). Ale c

n

=

1
a

F (k)

q

π

2

, zatem :

1

a

F (k)

r

π

2

=

1

2a

Z

a

−a

f (x)e

inπx

a

dx

Po przekształceniu i podstawieniu

∆k =

nπ

a

otrzymujemy:

F (k) =

1

2π

Z

a

−a

f (x)e

−iks

dx

4

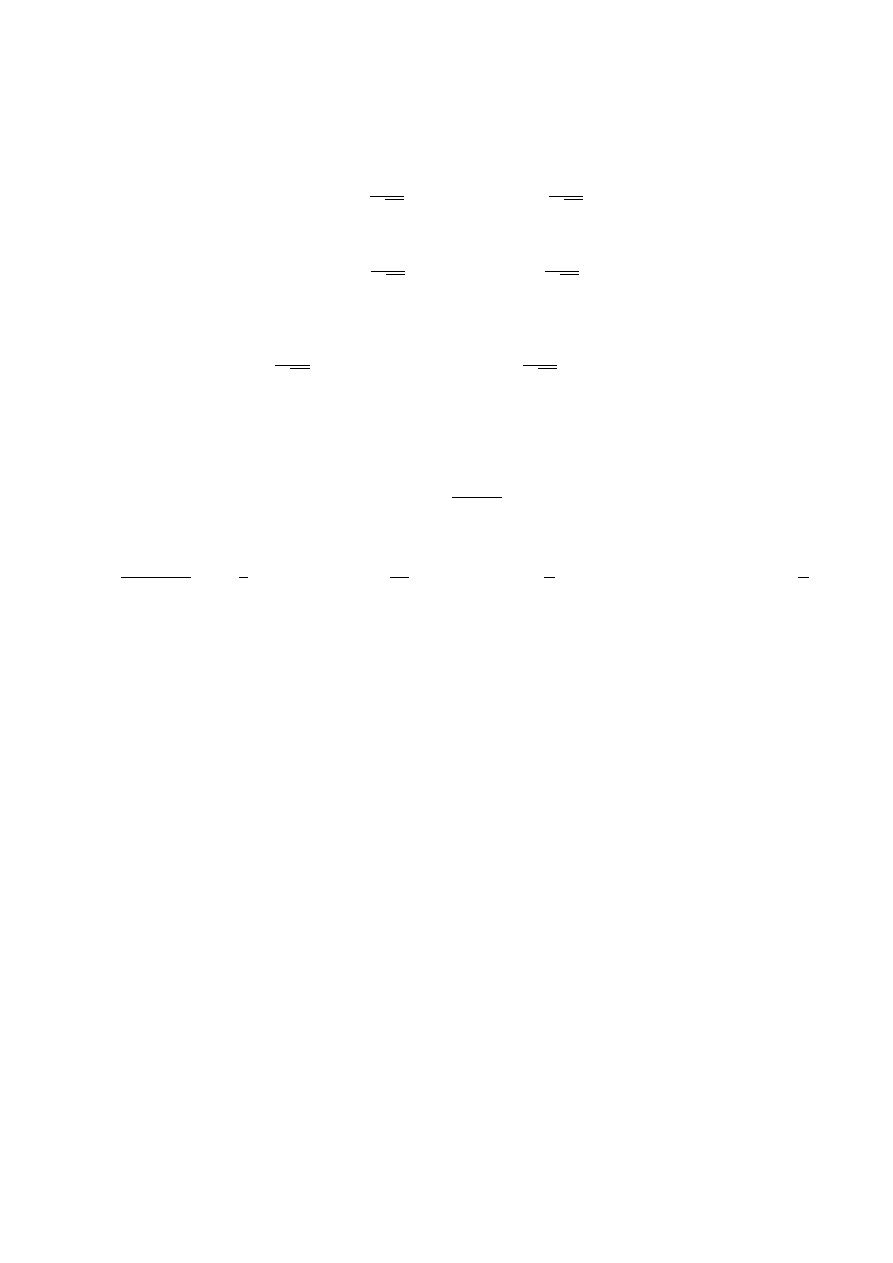
3.4

Krok 4

Aby zakończyć dowód należy rozważyć granicę przy a→ ∞ dla dwóch rezultactów z kroku 3:

1.

lim

∆k→0

f (x) = lim

∆k→0

1

√

2π

∞

X

−∞

F (k)e

ikx

∆k =

1

√

2π

Z

∞

−∞

F (k)e

ikx

dk

2.

lim

a→∞

F (k) = lim

a→∞

1

√

2π

Z

a

−a

f (x)e

ikx

dx =

1

√

2π

Z

∞

−∞

f (x)e

ikx

dx

Stąd otrzymujemy tezę:

f (x) =

1

√

2π

Z

∞

−∞

F (k)e

ikx

dk ⇔ F (k) =

1

√

2π

Z

∞

−∞

f (x)e

ikx

dx

4

Przykład

Niech f (x) = e

−|x|

. Wówczas

F (x) =

2

1 + ω

2

Zatem:

Z

∞

−∞

1

(1 + ω

2

)

2

dω =

1

4

Z

∞

−∞

|F (ω)|

2

dω =

2π

4

Z

∞

−∞

|f (x)|

2

dx =

π

2

Z

∞

−∞

e

−2|x|

dx = π

Z

∞

0

e

−2x

dx =

π

2

5