Zakład Sensorów i Systemów Pomiarowych

Instytut Metrologii i Systemów Pomiarowych

Politechniki Warszawskiej

Laboratorium

Podstaw Metrologii

2

Spis treści

1.

Harmonogram wykonywanych ćwiczeń laboratoryjnych

2.

Instrukcje wykonawcze do ćwiczeń

a) Ćwiczenie 1: Metody pomiarowe na przykładzie pomiarów masy

b) Ćwiczenie 2: Wyznaczanie właściwości metrologicznych wagi elektromechanicznej

c) Ćwiczenie 3: Eliminacja błędów dodatkowych przyrządu na przykładzie korektora

wskazań gazomierza

d) Ćwiczenie 4: Wyznaczanie niepewności pomiarów pośrednich na przykładzie

przepływomierza zwężkowego

e) Ćwiczenie 5: Wpływ temperatury na wskazanie manometrów i przetworników

ciśnienia

f) Ćwiczenie 6: Metody dyfrakcyjne w pomiarach średnicy drutów

3.

Regulamin Laboratorium Podstaw Metrologii

3

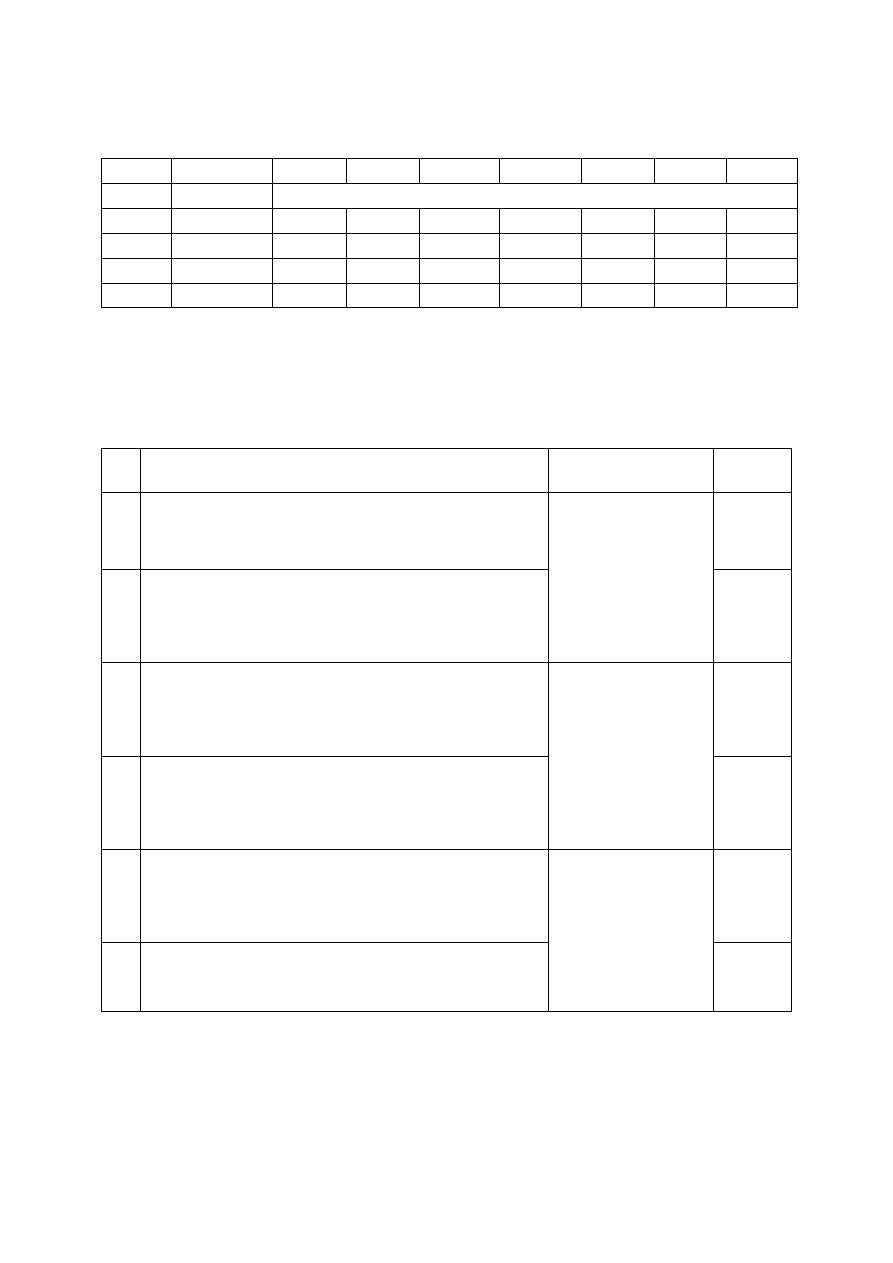
Grupa 11

Data

22.11.07 29.11.07 6.12.07

13.12.07 20.12.07 10.1.08 17.1.08

Zespół

1

Ćwiczenie

W

5

6

1

2

3

4

2

Ćwiczenie

W

6

5

2

1

4

3

3

Ćwiczenie

W

1

2

3

4

5

6

4

Ćwiczenie

W

2

1

4

3

6

5

Grupa 12

Data

23.11.07 30.11.07 7.12.07

14.12.07 21.12.07 11.1.08 18.1.08

Zespół

1

Ćwiczenie

W

5

6

1

2

3

4

2

Ćwiczenie

W

6

5

2

1

4

3

3

Ćwiczenie

W

1

2

3

4

5

6

4

Ćwiczenie

W

2

1

4

3

6

5

Grupa 13

Data

20.11.07 27.11.07 4.12.07

11.12.07 18.12.07 08.1.08 15.1.08

Zespół

1

Ćwiczenie

W

5

6

1

2

3

4

2

Ćwiczenie

W

6

5

2

1

4

3

3

Ćwiczenie

W

1

2

3

4

5

6

4

Ćwiczenie

W

2

1

4

3

6

5

Grupa 14

Data

22.11.07 29.11.07 6.12.07

13.12.07 20.12.07 10.1.08 17.1.08

Zespół

1

Ćwiczenie

W

5

6

1

2

3

4

2

Ćwiczenie

W

6

5

2

1

4

3

3

Ćwiczenie

W

1

2

3

4

5

6

4

Ćwiczenie

W

2

1

4

3

6

5

4

Grupa 15

Data

21.11.07 28.11.07 5.12.07

12.12.07 19.12.07 9.1.08

16.1.08

Zespół

1

Ćwiczenie

W

5

6

1

2

3

4

2

Ćwiczenie

W

6

5

2

1

4

3

3

Ćwiczenie

W

1

2

3

4

5

6

4

Ćwiczenie

W

2

1

4

3

6

5

Grupa 16

Data

21.11.07 28.11.07 5.12.07

12.12.07 19.12.07 9.1.08

16.1.08

Zespół

1

Ćwiczenie

W

5

6

1

2

3

4

2

Ćwiczenie

W

6

5

2

1

4

3

3

Ćwiczenie

W

1

2

3

4

5

6

4

Ćwiczenie

W

2

1

4

3

6

5

Grupa 17

Data

21.11.07 28.11.07 5.12.07

12.12.07 19.12.07 9.1.08

16.1.08

Zespół

1

Ćwiczenie

W

5

6

1

2

3

4

2

Ćwiczenie

W

6

5

2

1

4

3

3

Ćwiczenie

W

1

2

3

4

5

6

4

Ćwiczenie

W

2

1

4

3

6

5

Grupa 18

Data

21.11.07 28.11.07 5.12.07

12.12.07 19.12.07 9.1.08

16.1.08

Zespół

1

Ćwiczenie

W

5

6

1

2

3

4

2

Ćwiczenie

W

6

5

2

1

4

3

3

Ćwiczenie

W

1

2

3

4

5

6

4

Ćwiczenie

W

2

1

4

3

6

5

5

Grupa 19

Data

22.11.07 29.11.07 6.12.07

13.12.07 20.12.07 10.1.08 17.1.08

Zespół

1

Ćwiczenie

W

5

6

1

2

3

4

2

Ćwiczenie

W

6

5

2

1

4

3

3

Ćwiczenie

W

1

2

3

4

5

6

4

Ćwiczenie

W

2

1

4

3

6

5

Wykaz

ć

wicze

ń

laboratoryjnych

nr

Tytuł

prowadz

ą

cy

sala

1

Metody pomiarowe na przykładzie

pomiarów masy

239

2

Wyznaczanie wła

ś

ciwo

ś

ci

metrologicznych wagi

elektromechanicznej

Dr in

ż

.

Eugeniusz

Sukiennik

/

mgr in

ż

.

Jacek Salach

239

3

Eliminacja bł

ę

dów dodatkowych

przyrz

ą

du na przykładzie korektora

wskaza

ń

gazomierza

33

4

Wyznaczanie niepewno

ś

ci pomiarów

po

ś

rednich na przykładzie

przepływomierza zw

ęż

kowego

dr hab. in

ż

.

Mateusz

Turkowski

34

5

Wpływ temperatury na wskazanie

manometrów i przetworników

ci

ś

nienia

237

6

Metody dyfrakcyjne w pomiarach

ś

rednicy drutów

mgr in

ż

.

Jacek Salach

/

mgr in

ż

. Piotr

Orzechowski

226

6

Materiały do ćwiczeń laboratoryjnych

7

INSTYTUT METROLOGII I SYSTEMÓW POMIAROWYCH

Politechniki Warszawskiej

Laboratorium Podstaw Metrologii

Semestr I

Ć

wiczenie nr 1

Metody pomiarowe na przykładzie pomiarów masy

Warszawa

8

Metody pomiarowe na przykładzie pomiarów masy

Opracowanie: mgr inż. Tadeusz Czwal, prof. Janusz Jankowski, dr inż. Roman Szewczyk

1. Cel ćwiczenia
Celem ćwiczenia jest praktyczne poznanie metod pomiarowych na przykładzie metod
stosowanych w pomiarach masy oraz ocena ich wad i zalet.


2. Wprowadzenie

Metodą pomiarową nazywamy sposób wykonania pomiaru uwzględniający przede wszystkim
sposób porównania nieznanej wartości wielkości mierzonej (np. masy) ze znaną wartością
wzorcową (np. odważnikami) tej wielkości.

Poszczególne metody pomiarowe różnią się czynnościami wykonywanymi podczas pomiaru i
algorytmem wyznaczania wyniku.

Metody pomiarowe dzielimy na:

•

bezpośrednie,

•

pośrednie.

Metoda bezpośrednia (bezpośredniego porównania) - polega na zrównoważeniu masy ciała
znaną masą odważników.

Metoda pośrednia - polega na porównaniu skutku oddziaływania masy ciała z inną znaną
wielkością (np. siłą, napięciem lub natężeniem prądu, kątem obrotu, przemieszczeniem
liniowym).

Stosowane w pomiarach masy metody pomiarowe zostaną kolejno omówione.

Metoda zerowa - polega na zrównoważeniu masy ciała za pomocą odważników, aż do
doprowadzenia wskazówki wagi do zerowego położenia równowagi.
Przebieg ważenia jest następujący:

•

wyzerowanie wagi nieobciążonej,

•

zrównoważenie masy ciała odpowiednią ilością odważników,

•

odczytanie wyniku ważenia

Równanie ważenia ma postać następującą:

m

c

g l

1

= m

o

g l

2

gdzie: m

c

- masa ważonego ciała, m

o

- masa odważników, l

1

i 1

2

- długości ramion dźwigni

wagi.

Stąd:

m = m

0

l

1

/ l

2

Ponieważ ważenie jest dokonywane na wadze równoramiennej, przyjmuje się że 1

1

= 1

2

(lub l

1

/l

2

=1), a więc ostatecznie:

m

c

= m

0

9

Wadą tej metody jest to, że nie uwzględnia się błędu nierównoramienności, gdyż w
rzeczywistości zawsze występuje drobna różnica w długościach ramion i 1

1

/l

2

≠

1.

Metoda ta jest stosowana w przypadkach ważeń na dźwigniowych wagach równoramiennych
o mniejszych dokładnościach ważenia (np. technicznych).

Aby uniknąć błędu nierównoramienności, stosujemy metodę podstawienia (tzw. Bordy) lub
przestawienia (tzw. Gaussa). Oczywiście, obie te metody można stosować ważąc również na
dźwigniowych wagach równoramiennych, ale o wyższych dokładnościach ważenia (np.
analitycznych).

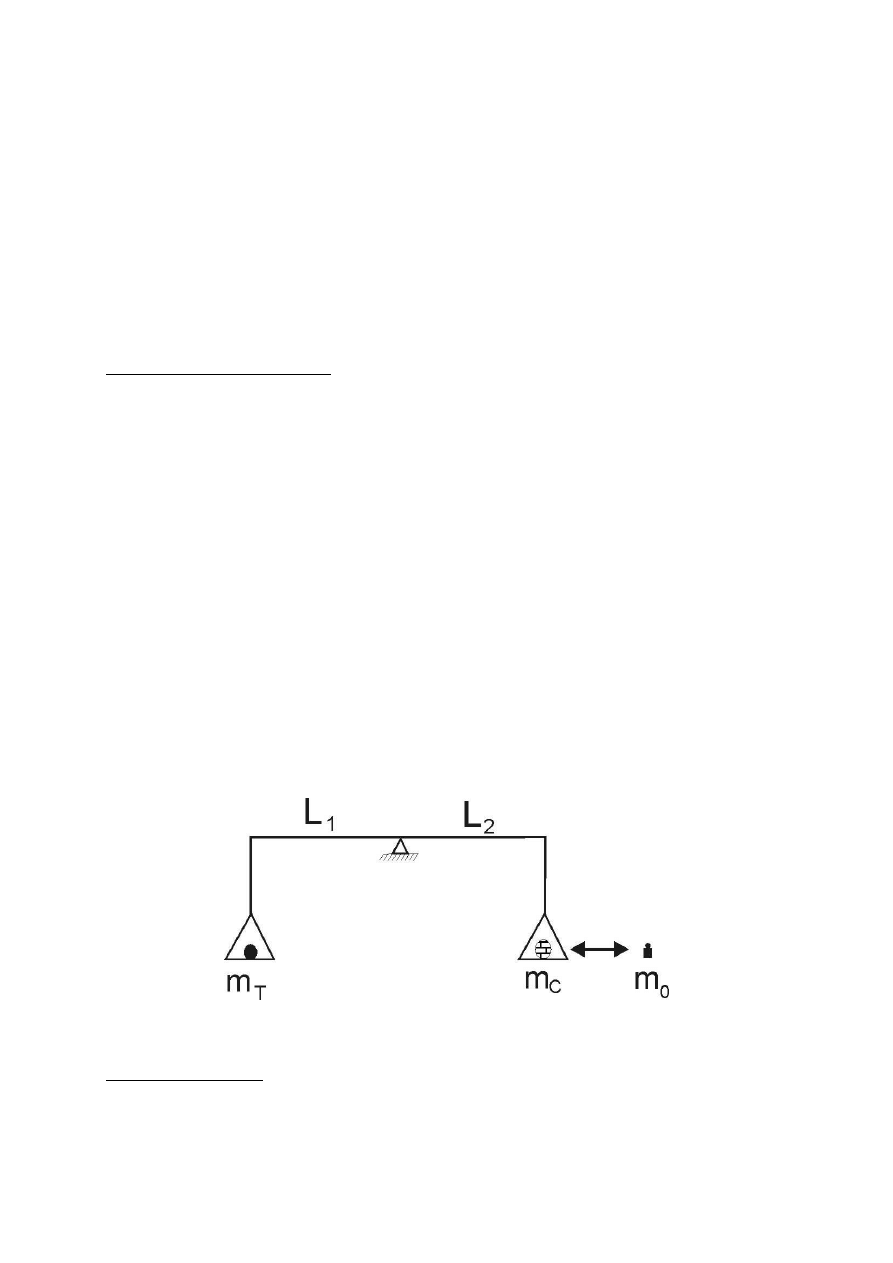
Metoda podstawienia (Bordy) zwana również metodą tary polega na użyciu do ważenia
jednego ramienia dźwigni wagi i wyeliminowania w ten sposób błędy nierównoramienności.

Przebieg ważeń jest następujący:

•

wyzerowanie wagi nieobciążonej,

•

nałożenie na szalkę ważonego ciała i zrównoważenie go masą tary,

•

zdjęcie z szalki ważonego ciała i zrównoważenie odważnikami masy tary,

•

odczytanie wyniku ważenia

Układ ważeń ma postać:

m

T

l

1

g = m

c

l

2

g ⇒ m

c

= m

T

l

1

/ l

2

m

T

l

1

g = m

o

l

2

g ⇒ m

o

= m

T

l

1

/ l

2

stąd

m

c

= m

o

tj. masa ciała m

c

jest równa masie odważników m

o

Metoda przestawienia (Gaussa) zwana również metodą zamiany obciążeń polega na zważeniu
ciała na obu ramionach wagi i wyeliminowaniu w ten sposób błędu nierównoramienności.
Przebieg ważeń jest następujący:

10

•

wyzerowanie wagi nieobciążonej,

•

nałożenie na szalkę (np. lewą) ważonego ciała i zrównoważenie go masą
odważników m

01

,

•

przestawienie ważonego ciała na szalkę prawą i zrównoważenie go masą
odważników m

02

,

•

odczytanie i obliczenie wyniku pomiaru

Układ ważeń ma postać:

m

c

l

1

g = m

0

l

2

g

m

c

l

2

g = m

02

l

1

h

Stąd:

02

01

m

m

m

c

⋅

=

Zależność ta nie jest dogodna w użyciu i w praktyce można się posługiwać zależnością
przybliżoną (lecz dostatecznie dokładną)

m

c

= m

01

+

∆

m

0

/ 2

gdzie

∆

m

0

= m

02

–m

01

- różnica mas obu ważeń (

∆

m

0

może by dodatnie lub ujemne).

Metoda wychyłową - polega na wyznaczeniu masy ciała na podstawie kąta wychylenia
wskazówki przyrządu analogowego:

mc = f(

∆ϕ

)

lub wskazania przyrządu cufrowego.

Metoda ta jest stosowana w wagach uchylnych. Aby uzyskać poprawny wynik ważenia, waga
musi być uprzednio wywzorcowana w jednostkach masy.

Metoda kompensacyjna - polega na skompensowaniu masy ciała tą samą lub inną wielkością
tak, aby układ zerowy wskazywał ponownie zero.

Metoda ta jest stosowana głównie w wagach dźwigniowych jednoramiennych i
elektronicznych - elektromagnetycznych, w których masa ważona jest proporcjonalna do
prądu kompensacyjnego I płynącego przez cewkę

m

c

= k* I

skąd

m

0

= I*k/g

Aby uzyskać poprawny wynik ważenia, waga musi być uprzednio wywzorcowana dla uzyskania
zależności pomiędzy wartością masy a prądem kompensacyjnym (i wyeliminowania g).

11

3. Opis stanowiska

W skład stanowiska wchodzą:

•

dźwigniowa waga równoramienna z bezpośrednim odczytywaniem wskazań,

•

waga włącznikowo-uchylna z optycznym odczytywaniem wskazań,

•

waga elektroniczna pomostowa,

•

waga analityczna jednoramienna (tzw. dwunożowa),

•

komplet odważników,

•

próbka do zważenia.

Waga dźwigniowa jest wagą techniczną o maksymalnym obciążeniu 500 g. Na wadze tej można
stosować bezpośrednie metody pomiarowe:

•

zerowa,

•

podstawienia (Bordy lub tary),

•

przestawienia (Gaussa lub zamiany obciążeń).

Waga włącznikowo-uchylna jest wagą techniczną o maksymalnym obciążeniu 160 g z
mechanizmem włącznikowym umożliwiającym zdejmowanie odważników włącznikowych o
masie 150 g, co 10 g. Na wadze tej można stosować metodę pomiarową - wychyłową, w
zakresie ważenia do 10 g. Przy ważeniu większych mas stosujemy odważniki włącznikowe,
stanowiące integralną część wagi.

Waga elektroniczna jest wagą techniczną o maksymalnym obciążeniu 2000 g. Na wadze tej
można ważyć metodą kompensacyjną.

Waga analityczna jest wagą włącznikowo-uchylna wysokiej dokładności o maksymalnym
obciążeniu 200 g, służącą do bezpośrednich pomiarów masy, a tylko w niewielkim stopniu (w
zakresie 10 mg) - umożliwiająca ważenie metodą wychyłową.


4. Wykonanie ćwiczenia

Dla wykonania ćwiczenia należy zważyć tą samą próbkę na wszystkich wagach, stosując
różne metody pomiarów.

a) Dźwigniowa waga równoramienna

Na wadze równoramiennej należy zważyć próbkę o masie mp metodą zerową za pomocą
odważników o masie m

0

i metodą podstawieniową (tary) dla wyeliminowania błędu

nierównoramienności.

Następnie należy wyznaczyć błąd nierównoramienności

∆

i i rozrzut wskazań wagi

∆

w.

Ważenia przeprowadzamy zgodnie z podanymi tabelami

12

Metoda zerowa

Obciążenie lewego

ramienia dźwigni

Obciążenie prawego

ramienia dźwigni

Wskazanie

0

m

0

0

m

0

0
0

m

p

= m

0

= ....... g

Metoda tary

Obciążenie lewego

ramienia dźwigni

Obciążenie prawego

ramienia dźwigni

Wskazanie

0

m

T

m

T

0

m

p

m

0

0
0
0

m

p

= m

0

= ....... g

Błąd nierównoramienności

∆

i możemy wyznaczyć stosując np. dwa odważniki o tej samej

masie (tzw. bliźniacze) odpowiadające maksymalnemu obciążeniu wagi. W przypadku gdy
nie mamy odważników bliźniaczych, możemy zastosować metodę przestawienia (zamiany
obciążeni Gaussa

Błąd nierównoramienności

Obciążenie lewego

ramienia dźwigni

Obciążenie prawego

ramienia dźwigni

Wskazanie

0

mB

0

m

B

±

∆

i

0
0

∆

i = ....... g

Błąd nierównoramienności odnosimy do lewego ramienia dźwigni, tj. prawe ramię może być
dłuższe lub krótsze od lewego (a więc dodatkową masę

∆

i możemy dołożyć na lewe lub

prawe ramię wagi).

Dla określenia rozrzutu wskazań wagi

∆

w należy pięciokrotnie zważyć tę samą próbkę.

Rozrzut wskazań

∆

w jest równy różnicy między maksymalnym a minimalnym wynikiem

pomiaru.

Zakres rozrzutu wskazań

∆

w daje nam informację, z jaką dokładnością możemy ważyć na

wadze.


b) Waga techniczna włącznikowo-uchylna z optycznym odczytywaniem wskazań

13

Na wadze należy zważyć próbkę o masie m

p

metodą wychyłową posługując się w razie

potrzeby odważnikami włącznikowymi dla zrównoważenia części masy próbki. Całkowita
masa próbki jest suma masy odważników włącznikowych i wskazania uchylnego (układu
optycznego).

m

p

= ........... g

c) Waga elektroniczna
Na wadze należy zważyć próbkę o masie m

p

metodą kompensacyjną

m

p

= ........... g

d) Waga analityczna
Na wadze można zważyć próbki o masie m

p

równoważąc jej znaczną część masy

odważnikami włącznikowymi (metoda zerowa), a pozostałą (b. małą) wartość masy odczytać
z układu uchylnego (optycznego) metodą wychyłową

m

p

= ........... g

5) Opracowanie wyników pomiarów

Wyniki pomiarów należy opracować zgodnie z tabelkami, podając wyniki pomiarów masy próbek
uzyskanych na:

1. wadze technicznej dźwigniowej (metodą zerową i tary),
2. wadze technicznej włącznikowo-uchylnej,
3. wadze analitycznej.

Należy dokonać analizy uzyskanych wyników odnośnie ich dokładności. Ponadto, biorąc pod
uwagę ważenie na wadze elektronicznej, należy podać wnioski dotyczące czasu ważenia
poszczególnymi metodami, tj.;

•

zerową,

•

tary,

•

wychyłową,

•

kompensacyjną.

5. Treść sprawozdania

W sprawozdaniu należy zamieścić:

•

wyniki ważeń próbki poszczególnymi metodami,

•

wartość błędu nierównoramienności

∆

i dźwigniowej wagi technicznej,

•

zakres rozrzutu wskazań

∆

w dźwigniowej wagi technicznej

•

oraz przedstawić wnioski odnośnie dokładności pomiarów poszczególnymi
metodami i czasu ważenia na poszczególnych wagach

14

Literatura

Jankowski J.: Wagi i ważenie wysokiej dokładności. WNT, Warszawa 1982
Obalski J.: Podstawy metrologii. WPW, Warszawa 1970
Piotrowski J.: Podstawy metrologii. PWN, Warszawa 1979

15

INSTYTUT METROLOGII I SYSTEMÓW POMIAROWYCH

Politechniki Warszawskiej

Laboratorium Podstaw Metrologii

Semestr I

Ć

wiczenie nr 2

Wyznaczanie właściwości metrologicznych wagi

elektromechanicznej

Warszawa

16

Wyznaczanie właściwości metrologicznych wagi elektromechanicznej

Opracował: prof. Janusz Jankowski

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z właściwościami metrologicznymi przyrządów
pomiarowych na przykładzie wagi elektromechanicznej oraz wyznaczenie właściwości
metrologicznych wagi pomostowej.

2. Wprowadzenie

Waga elektromechaniczna (nazywana potocznie wagą elektroniczną) jest wagą której
podstawowym elementem jest elektromechaniczny przetwornik pomiarowy (lub zespół
przetworników - zwykle 1

÷

6), służący do przetworzenia wielkości mierzonej m (masy), na

równoważny sygnał elektryczny V (napięcie). Analogowy sygnał wyjściowy po wzmocnieniu
i przetworzeniu na postać cyfrową (w przetworniku a/c) jest wyświetlany na mierniku w
jednostkach masy.

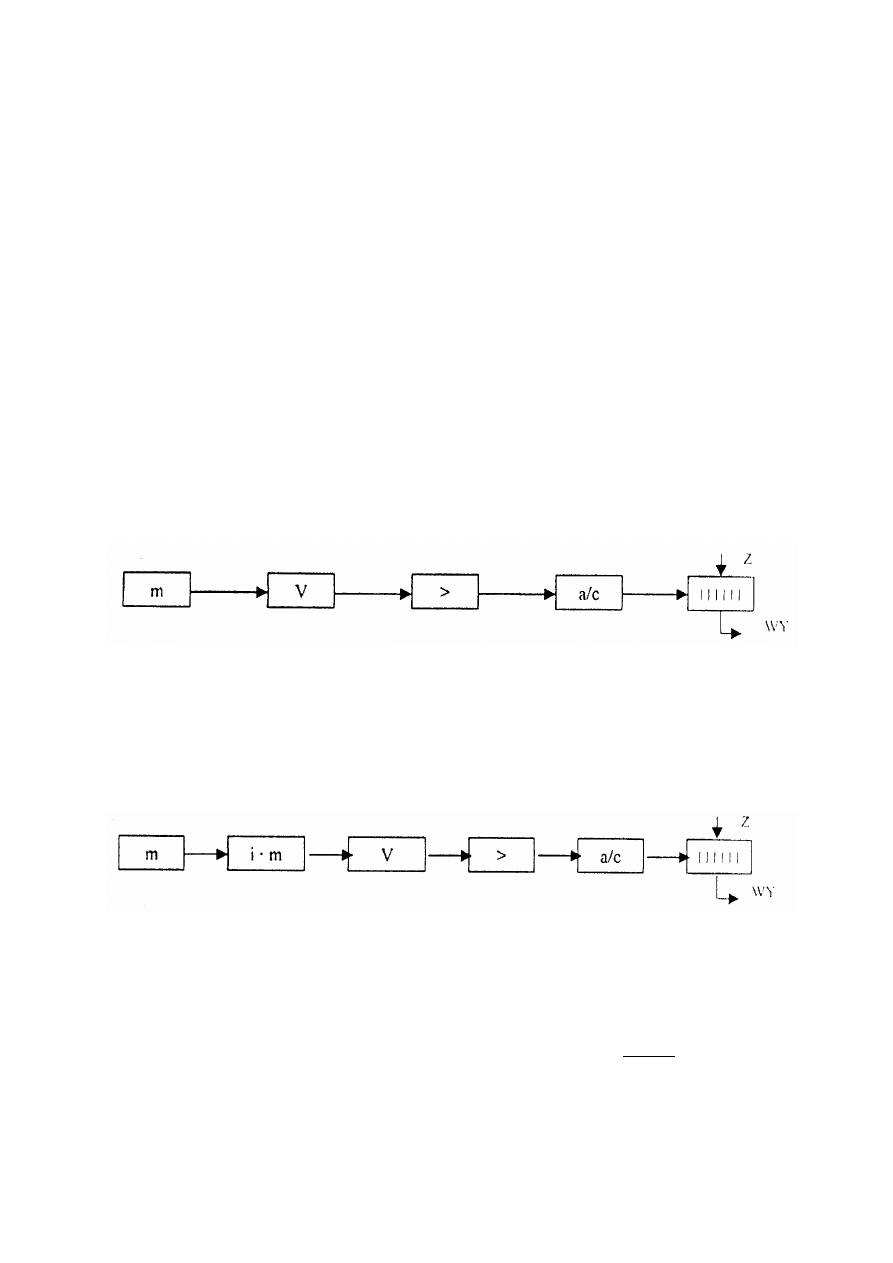
Tor przetwarzania w wadze elektromechanicznej można przedstawić następująco:

Rys. 1. Tor przetwarzania w wadze elektromechanicznej

Przy dużych wymiarach gabarytowych pomostu wagi trzeba użyć kilku
przetworników, albo też zastosować pomocniczy układ dźwigniowy, który przekazuje
zredukowaną wartość m na jeden przetwornik - co obniża koszt wykonania wagi. Tor
przetwarzania będzie miał wtedy postać:

Rys. 2. Tor przetwarzania w wadze elektromechanicznej hybrydowej (z pomocniczym
układem dźwigni pomostowych o przełożeniu i)

Stosowane przełożenia i mają zwykle wartości od 1:2 do 1:200.

Wagi elektromechaniczne (elektroniczne) pomostowe budowane są w różnych odmianach
jako wagi:

•

stołowe,

•

podłogowe,

•

samochodowe,

17

•

kolejowe (wagonowe).

o zróżnicowanych obciążeniach, poczynając od 0

÷

3 kg (najmniejsze wagi stołowe), aż do 0

÷

120 t (wagi kolejowe).

Do budowy wag pomostowych stosowane są zwykle przetworniki:

•

tensometryczne,

•

rezonansowe (z rezonatorem w postaci drgającej struny),

•

magnetosprężyste (tzw. pressduktory).

Najczęściej w wagach pomostowych stosowane są przetworniki tensometryczne.
W elemencie sprężystym przetwornika tensometrycznego, w zakresie sprężystości materiału
odkształcenie względne

ε

określa prawo Hooke'a:

E

σ

ε

=

gdzie:

σ

- naprężenie w materiale elementu sprężystego,

E - moduł sprężystości wzdłużnej (moduł Younga).

Wielkością wyjściową tensometru jest zmiana jego oporu elektrycznego R (rezystancji)
zgodnie z zależnością:

ε

⋅

=

∆

K

R

R

gdzie K - współczynnik czułości odkształceniowej (tzw. stała tensometru).

Sygnał wyjściowy

∆

V przetwornika tensometrycznego jest równy:

ε

z

V

n

K

V

=

∆

gdzie: n = 2 w układzie pełnego mostka, lub n=4 w układzie połowy mostka, V

z

– napięcie

zasilania.

Do właściwości metrologicznych należy zaliczyć:

•

maksymalne obciążenie wagi m

max

,

•

minimalne obciążenie wagi m

min

,

•

wartość działki elementarnej d,

•

dokładność wagi,

•

czułość wagi,

•

próg pobudliwości wagi.

Najważniejsze definicje:

m

max

- górna granica zakresu pomiarowego wagi. odpowiadająca największej dopuszczalnej

masie, którą można zważyć na wadze.

18

m

min

- dolna granica zakresu pomiarowego wagi, odpowiadająca najmniejszej dopuszczalnej

masie, która może być zważona na wadze.
d - wartość wyrażona w jednostkach masy, odpowiadająca działce elementarnej.

Dokładność wagi - właściwość charakteryzująca zdolność wagi do wskazywania wartości
bliskich rzeczywistej wartości mierzonej masy.

Czułość wagi - właściwość wyrażająca się ilorazem przyrostu dl obserwowanej zmiennej
przez odpowiedni przyrost dm ważonej masy

dm

dl

h

=

Czułość przetwornika -stosunek sygnału wyjściowego dy do wejściowego dx

dx

dy

k

=

Próg pobudliwości wagi - najmniejsza masa wywołująca zauważalną zmianę wskazań wagi.


3. Opis stanowiska

W skład stanowiska wchodzą:

•

pomostowa waga elektromechaniczna typu WEM50 III klasy dokładności,

•

zestaw odważników kontrolnych do sprawdzania wag.

Waga WEM50 jest pomostową wagą tensometryczną o maksymalnym obciążeniu m

max

= 50

kg. Minimalne obciążenie wagi m

min

= 20 d. Ponieważ wartość działki elementarnej d = 50 g,

to Min = 1000 g, t.j. 1 kg.

Waga WEM50 jest wagą o konstrukcji hybrydowej, tj. ma podpomostowy układ dźwigniowy
i jeden przetwornik tensomerryczny.

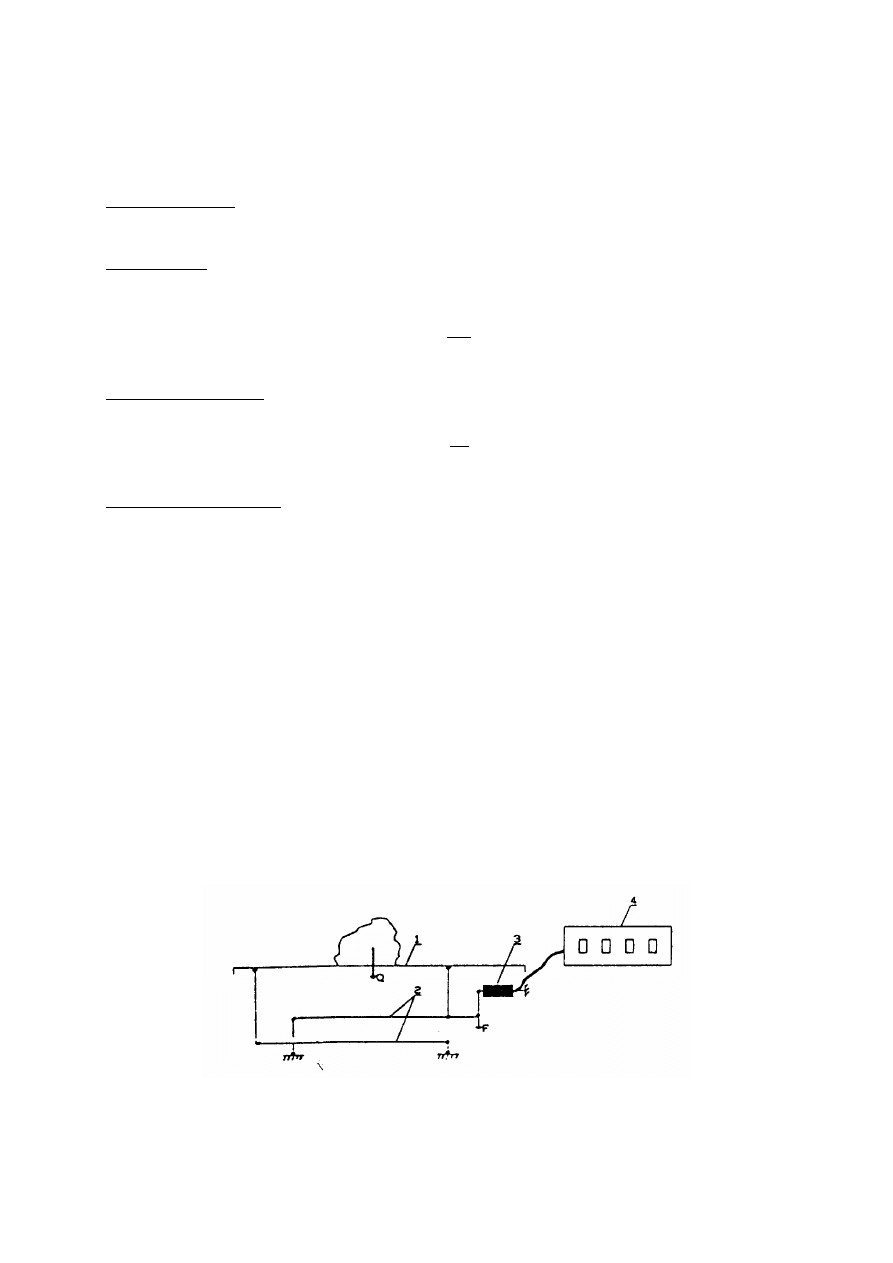
Schemat ilustrujący budowę wagi jest pokazany na rysunku 3.

Rys. 3. Schemat wagi WEM50

19

1 - pomost wagi, 2 - układ dźwigniowy, 3 - przetwornik tensometryczny (typu belka zginana),
4 - miernik cyfrowy


4. Wykonanie ćwiczenia

Dla określenia właściwości metrologicznych wagi WEM50. zgodnie z punktem 2 należy
wyznaczyć:

•

dokładność wagi,

•

czułość wagi k i jej odwrotność d = l/k, tj. wartość działki elementarnej,

•

próg pobudliwości wagi.

Dokładność wagi określimy wyznaczając:

•

błąd wskazania,

•

odchylenie standardowe.

Sprawdzenie dokładności wagi powinno być przeprowadzone przy użyciu odważników
kontrolnych (tzw. do sprawdzania wag), w warunkach zbliżonych do warunków odniesienia.
Istotna jest zwłaszcza temperatura otoczenia, która powinna wynosić 20 ± 2

o

C, a jej zmiana

podczas sprawdzania nie powinna przekraczać l

o

C/h. Błąd wskazania należy wyznaczyć w co

najmniej 8 punktach pomiarowych, obejmujących cały zakres wskazań wagi, poczynając od 0
aż do maksymalnego obciążenia, wykonując kilka serii pomiarów (np. 3) przy obciążeniu
rosnącym i malejącym.

Istotne jest sprawdzenie wagi przy obciążeniu równym 500 d, przy którym zmieniają się
dopuszczalne błędy wskazań wagi.

Odchylenie standardowe wyznaczamy przez wielokrotne obciążenie pomostu wagi
obciążeniami równymi 50 % i 100 % maksymalnego obciążenia wagi m

max

.

Ilość obciążeń w każdym punkcie pomiarowym nie powinna być mniejsza niż 10 (lecz nie
większa niż 30).

Jako wynik sprawdzenia wagi należy sporządzić protokół pomiarów, zgodnie z
załączonym wzorem.

Jako błąd wskazania należy przyjąć maksymalna różnicę odczytanych wskazań wagi w

1

-w

6

oraz wartości obciążenia nominalnego w

c

e

w max

= w

i

- w

c

Zgodnie z obowiązującymi przepisami [2] GUM (Głównego Urzędu Miar), dla wag III klasy
dokładności, dopuszczalny błąd graniczny wynosi:

± 0,5 d - w zakresie obciążeń 500 d > Q > 0
± 1 d - w zakresie obciążeń 500 d < Q < 2000 d

Zgodnie z obowiązującymi przepisami, dopuszczalna wartość odchylenia standardowego,
będąca miarą rozrzutu wskazań może wynosić:

20

s = 1/3 d

a błąd graniczny wagi spowodowany rozrzutem wskazań wynosi

e

gr

= ±3s

Możemy również określić zakres rozrzutu wskazań w zależności

W = W

max

- W

min

tj. jako różnicę wskazań pomiędzy największym i najmniejszym spośród wskazań danej serii
pomiarów.

Czułość wagi k należy wyznaczyć w kilku punktach zakresu pomiarowego wagi (np. przy
obciążeniach równych 0; 15; 30 i 45 kg) nakładając na pomost wagi dodatkowe obciążenie,
aby uzyskać przyrost wskazania równy co najmniej kilkanaście działek elementarnych d.

Czułość wagi k określamy jako liczbę działek na jednostkę masy. Na przykład przy zmianie
obciążenia o 1 kg, zmiana wskazań wyniosła 20 działek, stąd:

kg

d

k

20

1

20

=

=

a wartość działki elementarnej d:

d

g

d

kg

k

d

50

05

,

0

20

1

1

=

=

=

=

Próg pobudliwości wyznaczamy przy tych samych obciążeniach jak czułość wagi. Zgodnie z
przepisami, stwierdzamy jedynie jego zgodność z wymaganiami. Przy dodatkowym
obciążeniu pomosty masą równa od 1 do 1,4 d (tj. od 50 g do 70 g) musi nastąpić zmiana
wskazania wagi o wartości 1 d, tj. o wartość działki elementarnej. Na podstawie
przeprowadzonych badań wagi można stwierdzić, czy jej właściwości metrologiczne spełniają
wymagania przepisów GUM i czy waga może zostać zalegalizowana, jako waga III klasy
dokładności.

Uwaga: dla wag będących w użytkowaniu, dopuszczalne błędy są dwukrotnie większe niż
uprzednio podane, obowiązujące dla wag nowo wytwarzanych.

5. Opracowanie wyników pomiarów

Wyniki pomiarów należy opracować zgodnie z protokółem pomiarów, podając:

•

błąd wskazania e

w

mux

,

•

odchylenie standardowe s.

oraz wyznaczoną czułość wagi k i jej odwrotność, wartość działki elementarnej d, a także
stwierdzony próg pobudliwości.

21

Na zakończenie należy stwierdzić, czy waga spełnia wymagania przepisów:

a) dla wag nowowytwarzanych,
b) będących w użytkowaniu.

6. Treść sprawozdania

W sprawozdaniu należy zamieścić protokół sprawdzenia wagi oraz pozostałe wyniki badań
wagi,

a także wniosek dotyczący możności legalizacji wagi jako wagi III klasy dokładności.

Ponadto, należy zamieścić tor przetwarzania badanej wagi.

Literatura

1. Jankowski JA- Wagi i ważenie w przemyśle i handlu. Warszawa. WNT. 1983
2. Kacprzak K.: Wagi. Przepisy i komentarze. Wydawnictwa Normalizacyjne „Alfa"

Warszawa, 1986

22

23

INSTYTUT METROLOGII I SYSTEMÓW POMIAROWYCH

Politechniki Warszawskiej

Laboratorium Podstaw Metrologii

Semestr I

Ć

wiczenie nr 3

Eliminacja błędów dodatkowych przyrządu na przykładzie

korektora wskazań gazomierza

Warszawa

24

Eliminacja błędów dodatkowych na przykładzie korektora wskazań gazomierza

Opracował: dr hab. inż. Mateusz Turkowski

1.

Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z układem do eliminacji błędów dodatkowych o znanym,
dającym się opisać matematycznie charakterze. Badany układ to korektor wskazań
gazomierza wyposażonego w wyjście impulsowe, będący w istocie wyspecjalizowanym
mikrokomputerem wyposażonym w czujniki i przetworniki pomiarowe. W trakcie badań
wykonujący ćwiczenie zapoznają się także z metodyką sprawdzania przetworników ciśnienia
i temperatury, będących elementami korektora.

2. Wprowadzenie teoretyczne

Do pomiarów rozliczeniowych gazu dostarczanego dużym odbiorcom stosuje się obecnie z
reguły gazomierze, których sygnał wyjściowy ma charakter częstotliwościowy. Może to być
częstotliwość odrywania się wirów od odpowiednio ukształtowanego elementu, prędkość
obrotowa turbiny lub rotorów obracających się pod wpływem przepływającego gazu,
częstotliwość drgań oscylatora mechanicznego pobudzanego do drgań przez przepływający
gaz itp.
We wszystkich tych przypadkach łatwo jest uzyskać ciąg impulsów, których częstotliwość
jest proporcjonalna do strumienia objętości, a każdemu impulsowi można przypisać
określoną, elementarna objętość. Po odpowiednim przetworzeniu można uzyskać sygnał, w
którym jednemu impulsowi będzie odpowiadać jednostka objętości lub jej dziesiętna wielo-
lub podwielokrotność, np. 1 m

3

, 1 dm

3

, 10 m

3

, 0.1 m

3

itp. W przypadku gazomierza

turbinowego czy rotorowego można to uzyskać dobierając przełożenie przekładni zębatej
miedzy turbiną (rotorami) a nadajnikiem impulsów, można też zbudować dzielnik
elektroniczny.
Wskazania większości gazomierzy dotyczą jednak zwykle objętości w warunkach pomiaru,
zależnej od wielkości wpływających - ciśnienia i temperatury. Gazomierz wskaże więc
przykładowo tą samą wartość objętości po przepłynięciu jednego m

3

zarówno przy ciśnieniu

atmosferycznym jak i przy ciśnieniu np. 50 bar, podczas gdy w rzeczywistości ilość gazu
(jego masa lub objętość sprowadzona do warunków normalnych) w drugim przypadku będzie
kilkadziesiąt razy większa. Podobnie będzie przy zmianach temperatury. Dlatego też
podstawą rozliczeń między dostawcą a odbiorcą gazu jest objętość w metrach sześciennych,
sprowadzona do warunków normalnych lub innych tzw. warunkach odniesienia, czasem
zwanych warunkami umownymi. Są to warunki przewidziane dla danego przyrządu, dla
których przyrząd został skonstruowany, wywzorcowany, i w których występują jedynie tzw.
błędy lub niepewności podstawowe. W gazownictwie w Polsce i w Unii Europejskiej przyjęto
powszechnie jako normalne następujące warunki (nie zawsze jako warunki odniesienia
przyjmuje się warunki normalne):

- ciśnienie normalne p

n

= 101.325 kPa

- temperatura normalna t

n

= 0

°

C lub T

n

= 273.15 K

W innych krajach lub w innych dziedzinach nauki i techniki można spotkać się jednak z
innymi definicjami warunkow normalnych.
Związek miedzy objętością w warunkach pomiaru V a objętością w warunkach normalnych
V

n

można wyprowadzić z równania stanu gazu. Ma on postać:

)

1

(

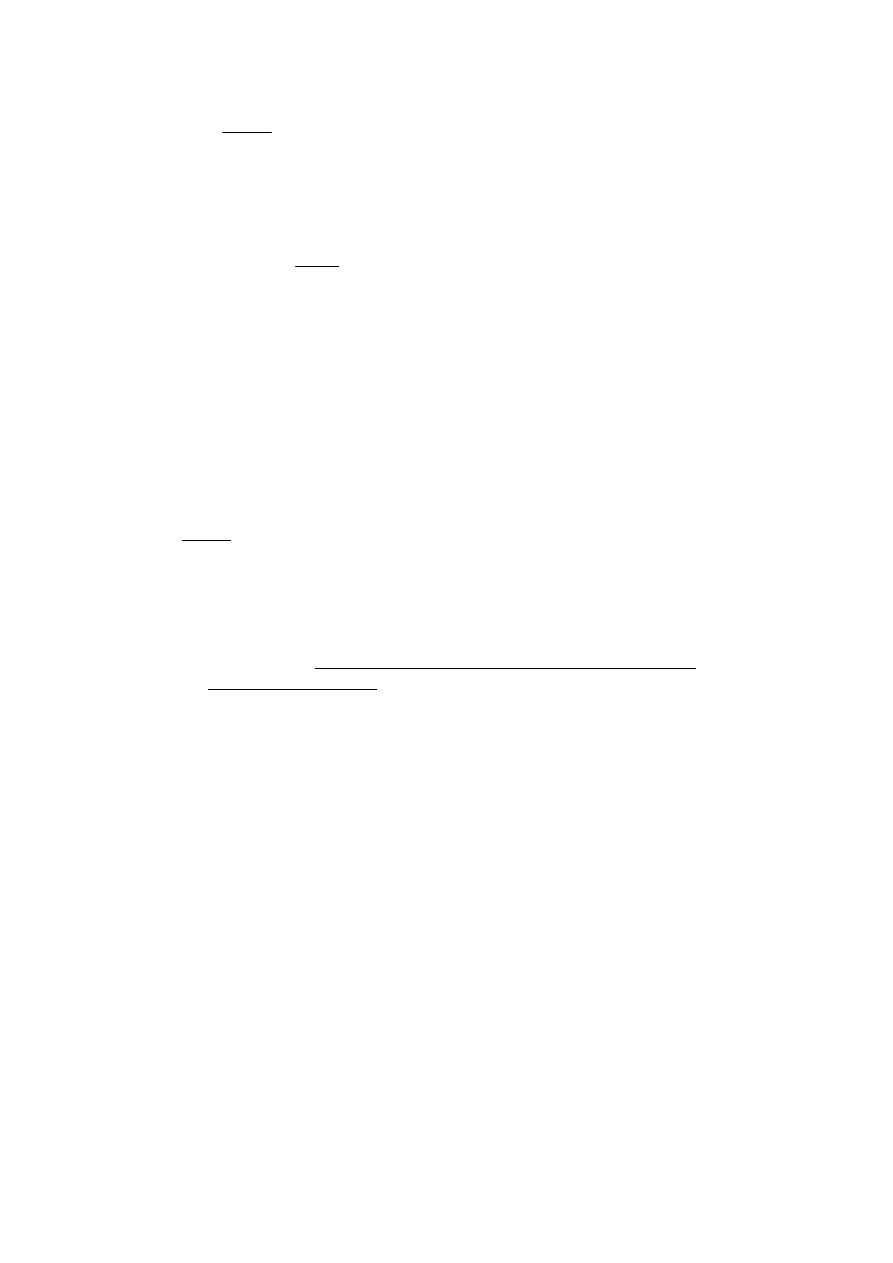
25

gdzie p - ciśnienie bezwzględne, T - temperatura bezwzględna, Z - współczynnik ściśliwości.
Brak indeksu oznacza rzeczywiste warunki pomiaru, indeks n - warunki normalne.

Czasem stosuje się pojęcie względnego współczynnika ściśliwości K=Z/Z

n

. Wzór (1)

przybierze wówczas postać

W miejsce temperatury bezwzględnej T można podstawić wartość liczbowa temperatury w
stopniach Celsjusza t plus 273.15, tj.

T = (t + 273.15) K

Współczynnik ściśliwości uwzględnia odchylenie właściwości gazu rzeczywistego od
właściwości gazu doskonałego, a więc m. in. skończony (niezerowy) wymiar cząstek
składników gazu.
Wzór (1) bywa przedstawiany w innej postaci:

V

n

= CV, gdzie

Stała C nazywana jest współczynnikiem korekcyjnym. Jeszcze dzisiaj często, zwłaszcza

gdy w grę wchodzą małe pobory gazu dla odbiorców indywidualnych (mieszkania, domy
jednorodzinne) przyjmuje się stałą wartość współczynnika korekcyjnego, opartą na
uśrednionych, wartościach odniesienia (ciśnienia i temperatury). Jeśli więc w danej chwili
temperatura czy ciśnienie nie są równe umownym wartościom odniesienia, mamy do
czynienia z błędami dodatkowymi, spowodowanymi rozbieżnością między warunkami
odniesienia a rzeczywistymi warunkami pracy gazomierza. Nie pociąga to za sobą znacznych
błędów, gdyż odbiorcy ci odbierają gaz pod tzw. niskim ciśnieniem, które jest relatywnie
stabilne. Sezonowe wahania temperatury natomiast uśredniają się w dłuższym okresie
rozliczeniowym.
Im bardziej jednak warunki rzeczywiste pomiaru (ciśnienie i temperatura) będą odbiegać od
przyjętych warunków odniesienia, tym bardziej rzeczywisty współczynnik korekcyjny
będzie się różnił od uśrednionego, przyjętego do obliczeń. Towarzyszyć będzie temu wzrost
błędu dodatkowego, spowodowanego odchyleniami warunków rzeczywistych od przyjętych
warunków odniesienia.
Urynkowienie i wzrost cen gazu spowodowały, że metoda polegająca na przyjęciu stałej
wartości współczynnika korekcyjnego jest obecnie zbyt mało dokładna, zwłaszcza w
przypadku dużych odbiorców gazu, gdy nawet niewielkie błędy wynikające z odchyleń od
przyjętych warunków odniesienia powodują straty dużych kwot dla jednej ze stron (i
oczywiście nieuzasadnione zyski drugiej strony). Dlatego też obecnie dla odbiorców tych
zawsze stosuje się automatyczną korekcję wpływu rzeczywistych warunków pracy i
sprowadzanie wskazań gazomierza do warunków normalnych na bieżąco, za pomocą
elektronicznego korektora.

2.1 Budowa i działanie korektorów wskazań gazomierzy

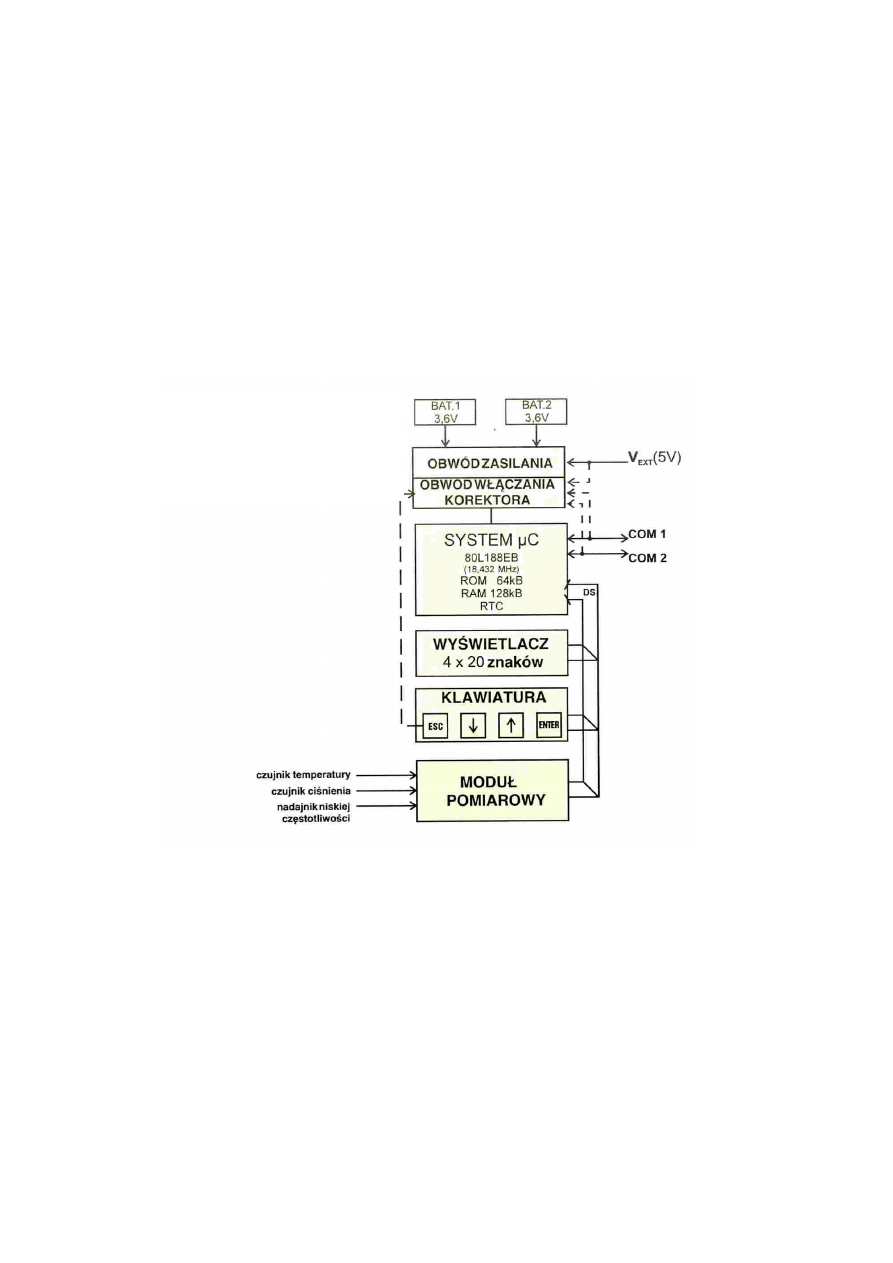
Budowę korektora wskazań gazomierzy przedstawiono schematycznie na rys. 1 i 2. Korektor
otrzymuje trzy rodzaje informacji.

TZ

p

Z

pT

V

V

n

n

n

n

=

TK

p

pT

V

V

n

n

n

=

)

2

(

TZ

p

Z

pT

C

n

n

n

=

)

3

(

26

Pierwsza to impulsy z gazomierza, każdemu z nich odpowiada "okrągła" wartość objętości,

zwykle 0.1, 1 lub 10 m

3

.

Kolejna informacja to ciśnienie gazu. Ciśnienie rurką impulsowa przekazywane jest z
rurociągu do przetwornika ciśnienia (P/U) zabudowanego wewnątrz obudowy korektora.
Przetwarza on ciśnienie na proporcjonalne do niego napięcie. Fizycznie element ten to
odpowiednio ukształtowany element krzemowy z wdyfundowanymi czujnikami naprężeń
(tensometrami).

Informacja o temperaturze jest uzyskiwana z czujnika temperatury zamontowanego w

rurocią-gu. W tym celu stosuje się czujnik półprzewodnikowy lub platynowy czujnik
rezystancyjny Pt 100, Pt500 lub Pt 1000 (o rezystancji odpowiednio 100

Ω

, 500

Ω

, lub 1000

Ω

, przy temperaturze 0

°

C; zmiany rezystancji są informacją o zmianach temperatury).

Informacje o ciśnieniu i temperaturze po wzmocnieniu i przetworzeniu zamieniane są na
informacje w postaci cyfrowej za pomocą

Rys. 1.Schemat blokowy jednego z rozwiązań korektorów

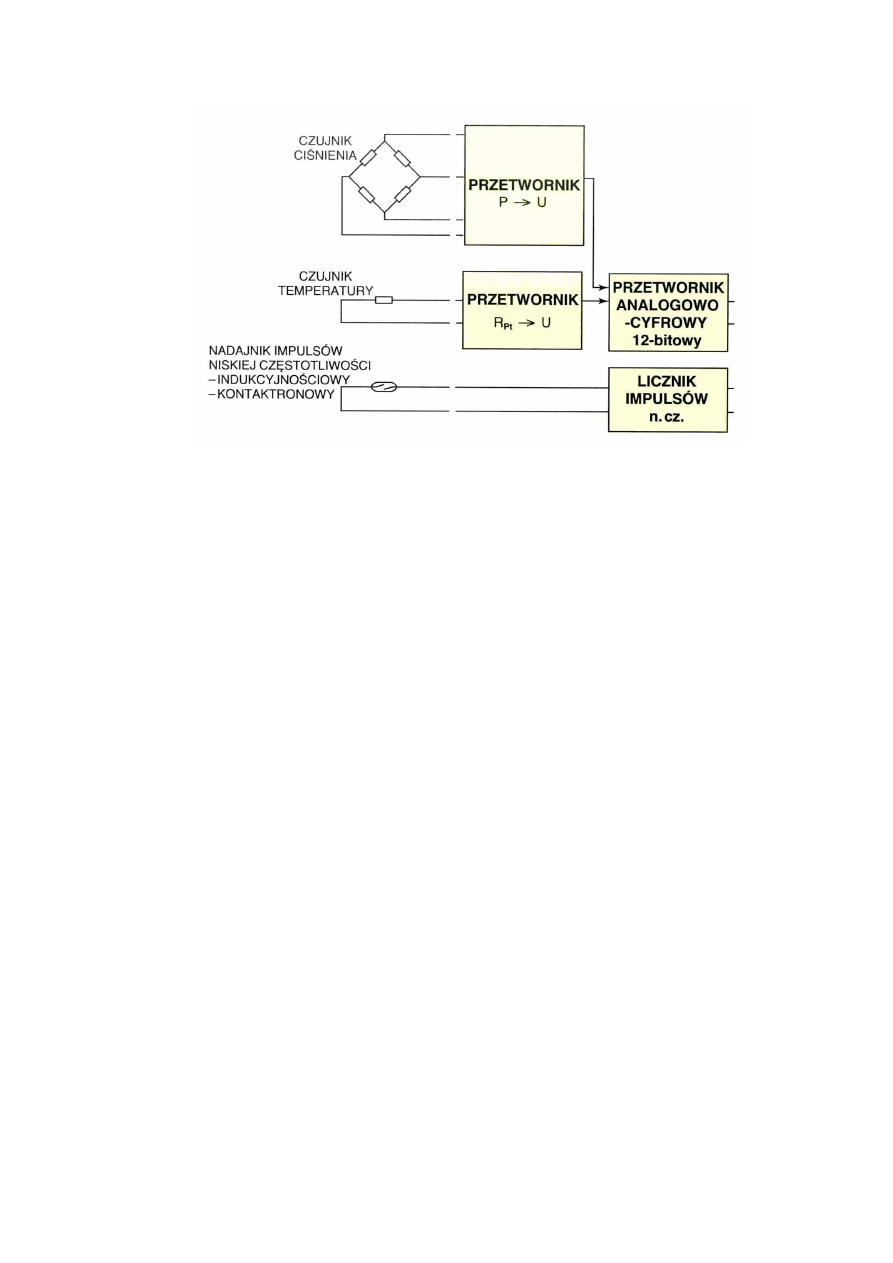
27

Rys. 2. Schemat blokowy układu pomiarowego korektora

przetwornika analogowo – cyfrowego (posiada on niezależne wejścia dla sygnału ciśnienia i
temperatury).
Przez większość czasu korektor znajduje się w stanie "uśpienia", dzięki czemu zużywa bardzo
mało energii, możliwe jest więc jego zasilanie bateryjne. Dopiero po nadejściu impulsu z
gazomierza korektor dokonuje pomiaru ciśnienia i temperatury i wykonuje obliczenia
współczynnika korekcyjnego

C (wg wzoru 2), po czym zwiększa wskazanie licznika objętości

niekorygowanej

V o odpowiednią wartość (zależnie od wagi impulsu z gazomierza, np. 0.1

m

3

), a wskazanie licznika objętości w warunkach normalnych

V

n

- o tą wartość pomnożoną

przez obliczony współczynnik korekcyjny

C.

Korektor może być wyposażony w szereg wyjść, np. wyjście impulsowe do sterowania
licznika zewnętrznego, alarmy przekroczenia dopuszczalnych ciśnień, temperatur czy
przepływów, interfejs do komunikacji z komputerem (np. RS232, USB) itp.

2.2. Wyznaczanie współczynnika ściśliwości

Z punktu widzenia cyklu obliczeniowego najtrudniejsze jest wyznaczenie współczynnika
ś

ciśliwości. Istnieją co prawda obszerne wyniki badań współczynnika ściśliwości w funkcji

ciśnienia i temperatury dla gazów o różnym składzie i wydawałoby się najprostsze
wprowadzenie ich do pamięci korektora w postaci tablicy. Byłaby ona jednak prawdziwa
tylko dla jednego gazu o określonym składzie. Skład ten, np. dla gazu ziemnego zależy silnie
od źródła gazu, może też zmieniać się w funkcji czasu.

Dużą trudność powoduje fakt, że conajmniej kilkanaście składników gazu ziemnego lub

produkowanego z węgla wpływa na współczynnik ściśliwości (CH

4

i wyższe węglowodory,

CO, CO

2

, N

2

, H

2

itp.).

Istnieje wiele procedur obliczeniowych dla wyznaczenia współczynnika ściśliwości gazu.
Podstawą ich stosowania jest znajomość zawartości metanu, azotu i dwutlenku węgla oraz
gęstości gazu. Niektóre procedury uwzględniają jeszcze ciepło spalania. Umożliwia to
uwzględnienie wpływu wyższych niż metan węglowodorów na współczynnik ściśliwości, a
wyniki są dokładniejsze.
Można wykazać, że dla ciśnień do 200 kPa przyjęcie współczynników ściśliwości

Z = Z

n

= 1 daje pomijalne błędy (pomijalne w porównaniu z błędami samego gazomierza). Dla
ciśnień w zakresie do kilkuset kPa, zwłaszcza gdy ciśnienie nie zmienia się w szerokich

28

granicach, można przyjąć stosunek

Z/Z

n

jako wartość stałą (trzeba ją wówczas wyliczyć dla

ś

redniego ciśnienia i średniej temperatury gazu).

Dla ciśnień wysokich wartość

Z odbiega jednak znacznie od jedności, np. dla gazu

wysokometanowego dla ciśnienia 6 MPa i temperatury 0

°

C wynosi ona ok. 0.86 (tak więc

przyjęcie wartości

Z = 1 spowodowałoby błąd rzędu 14 %) i silnie zmienia się z ciśnieniem i

temperaturą.
W Europie do obliczeń współczynnika ściśliwości stosuje się obecnie procedurę SGERG
(Groupe Européen des Récherches Gasieres), natomiast w USA i Kanadzie procedurę AGA
NX 19 (AGA - American Gas Association).

3. Opis stanowiska

W celu wykonania badań czujnik ciśnienia korektora został podłączony do manometru

obciążnikowo – tłokowego, umożliwiającego zadawanie z wysoką dokładnością wartości
ciśnień zgodnie z definicją ciśnienia za pomocą tłoka o znanej powierzchni obciążonego
obciążnikami o znanej masie (tzw. podstawowa lub bezwzględna metoda pomiarowa).
Czujnik temperatury umieszcza się w termostacie, który umożliwia zadawanie i pomiar
określonych wartości temperatury.

4. Wykonanie ćwiczenia

Badanie polega na zadaniu przy stałym ciśnieniu 6 wartości temperatury, a następnie przy

stałej temperaturze - 6 wartości ciśnienia w cyklu rosnącym i 6 - przy zmniejszaniu jego
wartości (w ten sposób można wychwycić zjawisko histerezy).
Dla każdego zestawu wartości ciśnienia i temperatury należy odczytać wartość ciśnienia i
temperatury zmierzoną przez korektor oraz wyliczony przez korektor współczynnik
korekcyjny.
Wielkości te można wywołać na wyświetlacz w zależności od budowy korektora wciskając
kolejno przycisk "display" lub z klawiatury, zwykle można też odczytać wszystkie istotne
informacje za pomocą komputera przy zastosowaniu odpowiedniego interfejsu.
Ostatnia czynność to sprawdzenie poprawności zliczania objętości przez korektor. Po
zadaniu wybranych, średnich wartości ciśnienia i temperatury należy zadać określoną liczbę
impulsów (z generatora impulsów lub wymuszając przepływ przez podłączony do korektora
gazomierz). Należy dokonać odczytu stanu liczników objętości nieskorygowanej i objętości
sprowadzonej do warunków normalnych przed i po zadaniu impulsów.

5. Opracowanie wyników pomiarów

W trakcie ćwiczenia wykonuje sie jedynie badania podstawowe, takie jak podczas

rutynowego sprawdzania każdego korektora w trakcie produkcji. Badania pełne obejmują
dodatkowo badania klimatyczne, odporności mechanicznej (drgania, udary) odporności na
różnego rodzaju narażenia elektryczne, elektromagnetyczne i wyładowania elektrostatyczne
(kompatybilność elektromagnetyczna).
Dla zadawanych w trakcie ćwiczenia wartości ciśnień i temperatur należy obliczyć
wartość poprawną współczynnika korekcyjnego

C

p

wg wzoru (3). Należy skorzystać z

odpowiedniego programu komputerowego do wyznaczenia poprawnej wartości
współczynnika ściśliwości wg tej samej procedury, na której bazuje korektor (informacja o
procedurze podana jest na tabliczce znamionowej korektora).
Następnie należy obliczyć błąd wyznaczenia współczynnika korekcyjnego przez korektor
z wzoru

)

4

(

29

gdzie

C - współczynnik korekcyjny wyznaczony przez korektor. Wyniki obliczeń zamieścić

w protokółach pomiaru.
Poprawność zliczania objętości można sprawdzić porównując przyrost wskazań licznika
objętości niekorygowanej

∆

V z przyrostem wskazań licznika objętości sprowadzonej do

warunków normalnych

∆

V

n

. Błąd wyznacza się z wzoru

6. Treść sprawozdania

W sprawozdaniu należy podać:
- schemat stanowiska
- protokóły pomiarów z wynikami obliczeń

- wnioski

We wnioskach uwzględnić, że zgodnie z wymaganiami przepisów metrologicznych:

-

całkowity błąd korekcji (czyli wyznaczenia współczynnika korekcyjnego) nie
powinien przekraczać 0.5%,

-

temperatury nie powinien przekraczać 0.1%,

-

maksymalny błąd pomiaru ciśnienia nie powinien przekraczać 0.2%.

Literatura:
[1] Turkowski M.: Przemysłowe sensory i przetworniki pomiarowe, OWPW, Warszawa,
2000 (wyd. 1) lub wyd. II - 2002

(%)

100

⋅

−

=

p

p

C

C

C

C

e

(%)

100

,

⋅

∆

∆

−

∆

=

V

C

V

C

V

e

p

p

n

n

V

)

5

(

30

INSTYTUT METROLOGII I SYSTEMÓW POMIAROWYCH

Politechniki Warszawskiej

Laboratorium Podstaw Metrologii

Semestr I

Ć

wiczenie nr 4

Wyznaczanie niepewności pomiarów pośrednich na przykładzie

przepływomierza zwężkowego

Warszawa

31

Wyznaczanie niepewności pomiarów pośrednich na przykładzie przepływomierza

zwężkowego

Opracował: dr hab. inż. Mateusz Turkowski

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z praktycznym wyznaczaniem niepewności pomiarów

bezpośrednich i pośrednich oraz zmniejszeniem wpływu błędów systematycznych na wynik
pomiaru poprzez wprowadzenie poprawek. Inny cel to zapoznanie się zasadą zwężkowego
pomiaru strumienia płynu.

2. Wprowadzenie teoretyczne

2.1. Wyprowadzenie wzoru umożliwiającego obliczenie strumienia płynu przy pomiarze
zwężkowym

Strumień płynu jest pojęciem ogólnym, obejmującym strumień masy i strumień objętości

cieczy lub gazu.

Strumień objętości q

v

jest to objętość płynu przepływającego przez poprzeczny przekrój

rurociągu w jednostce czasu a strumień masy q

m

– masa przepływająca przez ten przekrój w

jednostce czasu. Między q

v

a q

m

zachodzi prosty związek

q

m

=

ρ

q

v

(1)

gdzie

ρ

– gęstość płynu.

Najczęściej stosowaną zwężką pomiarową, umożliwiającą pomiar strumienia płynu, jest

kryza – płaska tarcza z okrągłym otworem o średnicy d, współosiowa z rurociągiem o
ś

rednicy wewnętrznej D. Zasadę pomiaru omówimy więc na jej przykładzie. Załóżmy na

razie, dla uproszczenia, że rozkład prędkości jest równomierny, czyli prędkość w każdym
przekroju jest stała, równa prędkości średniej w (patrz rys. 1a).

Zgodnie z zasadą ciągłości przepływu (będącą jedną z form powszechnie

obowiązującego w przyrodzie prawa zachowania masy) do każdego przekroju dopływa i
odpływa w jednostce czasu taka sama masa płynu. Obowiązuje więc, dla przekroju rurociągu
A

1

=

π

D

2

/4 i dla przekroju otworu kryzy A

2

=

π

d

2

/4 równanie ciągłości:

q

m

= A

1

ρ

1

w

1

= A

2

ρ

2

w

2

(2)

gdzie

ρ

1

,

w

1

– prędkość średnia i gęstość płynu w rurociągu przed kryzą,

ρ

2

,

w

2

– prędkość

ś

rednia i gęstość płynu w otworze kryzy. Dla płynów nieściśliwych

ρ

= const, wówczas

q

v

= A

1

w

1

= A

2

w

2

(3)

Drugie równanie wyprowadza się z zasady zachowania energii. Zgodnie z tą zasadą

wzrost energii kinetycznej (związanej z prędkością) może nastąpić tylko kosztem spadku
energii potencjalnej (ciśnienia). Zwiększeniu prędkości w okolicach kryzy towarzyszy więc
spadek ciśnienia w tej strefie, co wyraża równanie Bernoulliego:

const

p

w

p

w

=

+

=

+

2

2

2

1

2

1

2

2

ρ

ρ

(4)

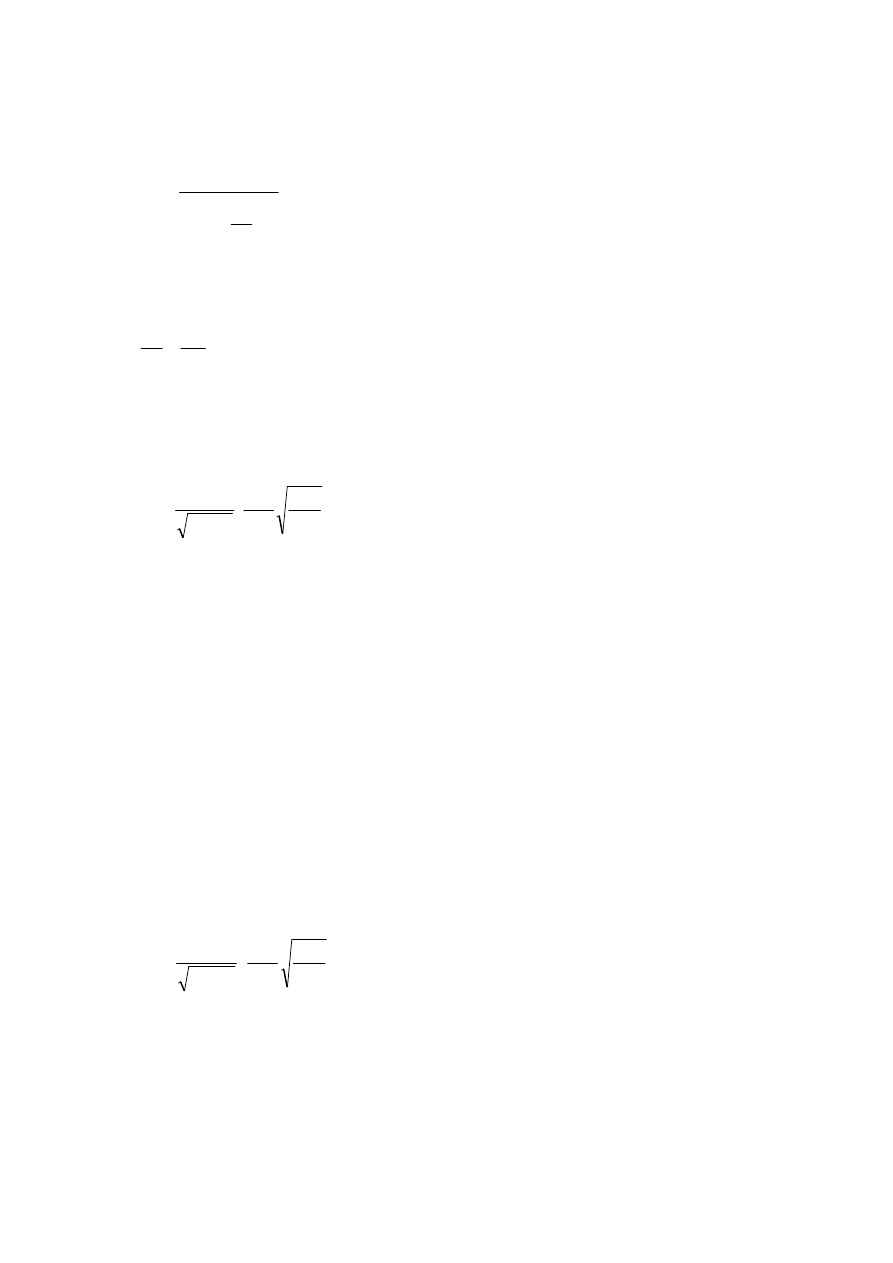
32

Rozwiązując układ dwóch równań (równanie Bornoulliego (4) i równanie ciągłości (3))

otrzymujemy

(

)



























−

−

=

2

2

1

2

1

2

2

1

2

A

A

p

p

w

ρ

(5)

Zdefiniujmy jeszcze tzw. przewężenie zwężki

β

= d/D. Wówczas

2

2

2

1

2

β

=

=

D

d

A

A

(6)

Uwzględniając jeszcze związki q

v

= F

2

w

2

oraz A

2

=

π

d

2

/4 i oznaczając różnicę

ciśnień p

1

– p

2

=

∆

p otrzymujemy uproszczony związek między strumieniem objętości a

spadkiem ciśnienia na zwężce

ρ

π

β

p

d

q

v

∆

⋅

−

=

2

4

1

1

2

4

(7)

Przy wyprowadzaniu powyższego wzoru przyjęto jednak szereg założeń upraszczających.

M.in. rozkład prędkości w otworze zwężki i rurociągu nie jest równomierny (płaski), a
wyostrzony (rys. 1b). Dla nierównomiernego rozkładu prędkości energia strumienia jest
większa niż dla płaskiego, tak więc równanie Bernoulliego nie opisuje zupełnie ściśle stanu
faktycznego.

Ponadto najsilniejsze przewężenie strumienia nie występuje w samym otworze kryzy a

poza nią, ponadto przekrój strumienia w miejscu najsilniejszego przewężenia jest mniejszy
niż w otworze kryzy. Dzieje się tak dlatego, że elementy płynu, dopływając do kryzy, mają
pewną doosiową składową prędkości, która nie może zaniknąć od razu (patrz obraz linii prądu
na rys. 1 c). Przekrój o najsilniejszym przewężeniu nazywamy „vena contracta”.

Takie przewężenie strumienia (tzw. kontrakcja) nie występuje jednak w płynnie

ukształtowanych dyszach (rys. 2 a).

Niestety, ani stopnia kontrakcji ani rzeczywistych profili prędkości nie da się wyznaczyć

z taką dokładnością, aby na drodze teoretycznej skorygować wyprowadzony powyżej,
uproszczony wzór. Dlatego wpływ wymienionych czynników (oraz szeregu innych) ujmuje
się za pomocą jednego, sumarycznego, tzw. współczynnika przepływu C. Wzór (7) przybierze
wówczas postać

ρ

π

β

p

d

C

q

v

∆

⋅

−

=

2

4

1

2

4

(8)

Współczynnik przepływu można wyznaczyć poprzez wzorcowanie szeregu podobnych

geometrycznie zwężek o różnych przewężeniach

β

. Wyznaczone wartości zależą jednak od

szeregu innych czynników, jak średnica rurociągu, prędkość przepływu czy lepkość płynu.

Dla wykorzystania w przyszłości tych wyników wzorcowań posługujemy się więc teorią

podobieństwa przepływów.

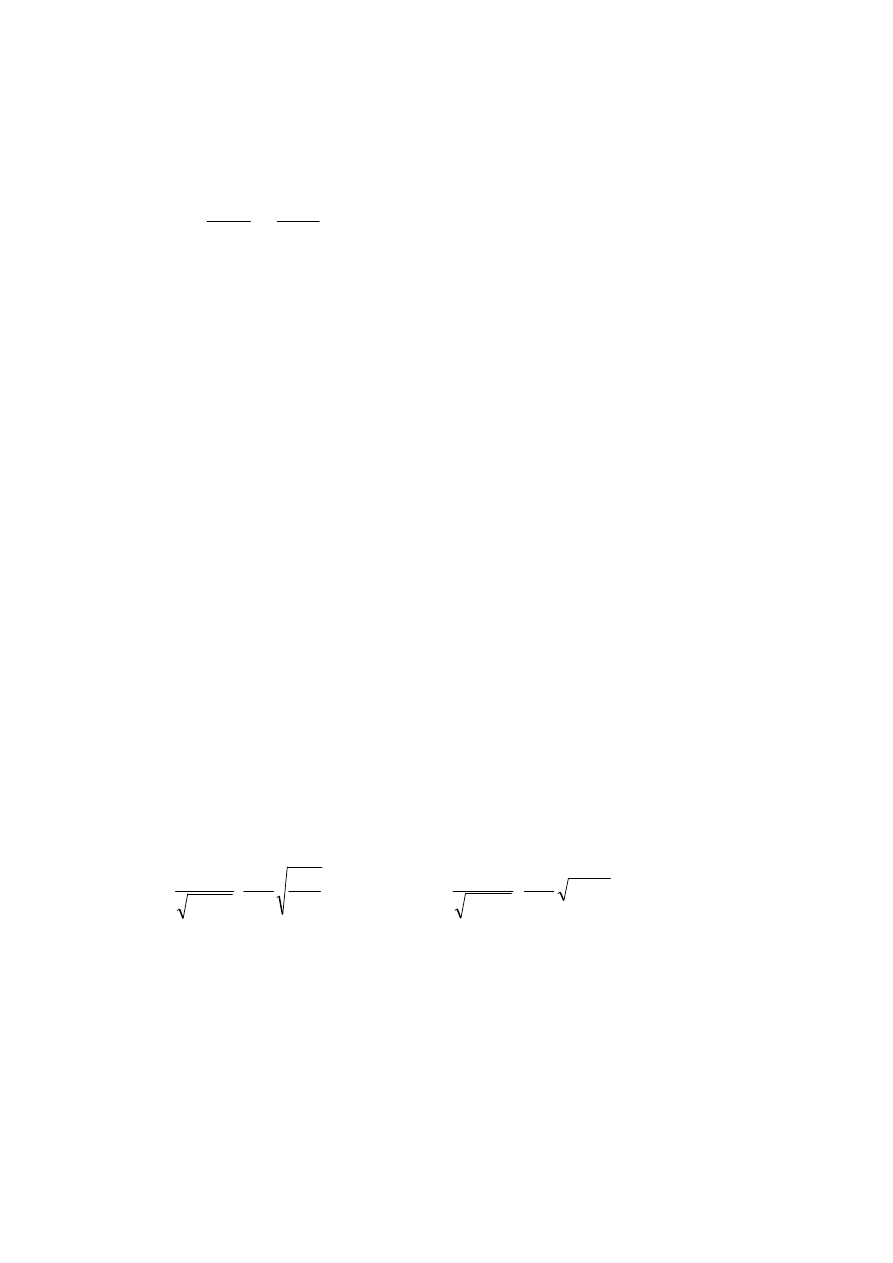
33

Wprowadźmy tzw. liczbę Reynoldsa, jedną z bezwymiarowych liczb podobieństwa

stosowanych w technice. Jest to stosunek występujących w przepływie sił bezwładności do sił
lepkości. Dla rurociągu o przekroju kołowym można ją obliczyć z jednego z wzorów:

gdzie

ν

- kinematyczny współczynnik lepkości płynu.

Zgodnie z teorią podobieństwa przepływów dla różnych rozpatrywanych przepływów,

przy podobnych geometrycznie powierzchniach opływanych (dla zwężki sprowadza się to do
równości przewężeń

β

) i dla takich samych wartości liczby Reynoldsa zachodzi podobieństwo

pól ciśnień i pól prędkości.

Podobieństwo pól prędkości zapewnia podobieństwo rozkładów prędkości i

podobieństwo linii prądu, co z kolei zapewnia taki sam stopień kontrakcji. Dzięki temu, przy
takich samych liczbach Reynoldsa taka sama będzie wartość współczynnika przepływu,
uwzględniającego wpływ tych zjawisk. Wystarczy więc wyznaczyć poprzez wzorcowanie
szeregu zwężek o różnych wartościach przewężenia

β

wartości współczynnika przepływu dla

różnych przewężeń w funkcji liczby Reynoldsa, aby móc później, wykorzystując wyniki tych
wzorcowań, przenosić ich wyniki na inne średnice rurociągów czy inne płyny, niż stosowane
podczas tych wzorcowań.

Kolejne uproszczenie jakie wprowadzono powyżej, to założenie nieściśliwości płynu

(

ρ

= const). Dla gazów uproszczenie to może być źródłem znacznych błędów pomiaru.

Wskutek spadku ciśnienia w strefie zwężki wystąpi tu rozprężanie – zmniejszenie gęstości i
dodatkowe zwiększenie prędkości. Dla uwzględnienia tych zjawisk stosowany jest mnożnik
poprawkowy

∈

∈

∈

∈

, zwany liczbą ekspansji. Wyznacza się go eksperymentalnie poprzez

porównanie charakterystyk zwężki dla praktycznie nieściśliwych cieczy z charakterystykami
dla gazów. Z termodynamiki wiadomo, że liczba ekspansji jest funkcją przewężenia

β

,

wykładnika izentropy

κ

, oraz stosunku

∆

p/p:

∈

∈

∈

∈

= f(

β

,

κ

,

∆

p/p)

(10)

Dla cieczy, które są praktycznie nieściśliwe, przyjmuje się

∈

∈

∈

∈

= 1.

Po tym uściśleniu ostateczne związki, z których korzystamy przy obliczaniu strumienia

płynu mają postać

ρ

π

β

p

d

C

q

v

∆

⋅

−

∈

=

2

4

1

2

4

lub

p

d

C

q

m

∆

⋅

−

∈

=

ρ

π

β

2

4

1

2

4

(11)

2.2. Normalizacja zwężek

Uzyskanie wystarczająco obszernych wyników badań zależności C = f(Re,

β

) i

∈

∈

∈

∈

= f(

β

,

κ

,

∆

p/p) umożliwia normalizację zwężek. Warunkiem jest jednak uzyskanie zgodności

wyników badań uzyskanych w różnych laboratoriach. W wyniku opracowania statystycznego
wyników tych badań zostaje sformułowana ostateczna postać zależności C = f(Re,

β

) i

∈

∈

∈

∈

=

f(

β

,

κ

,

∆

p/p) a z analizy statystycznej tych wyników – niepewności wyznaczenia C i

∈

∈

∈

∈

.

Normalizacja zwężek umożliwia projektowanie przepływomierzy zwężkowych i

wyznaczanie ich charakterystyki obliczeniowo, tylko na podstawie znajomości parametrów
płynu i pomiarów geometrycznych zwężki. Eliminuje się więc konieczność indywidualnego
wzorcowania, często w ogóle niemożliwego, a zawsze kosztownego i pracochłonnego.

ν

ν

1

1

A

D

q

D

w

Re

v

=

=

)

9

(

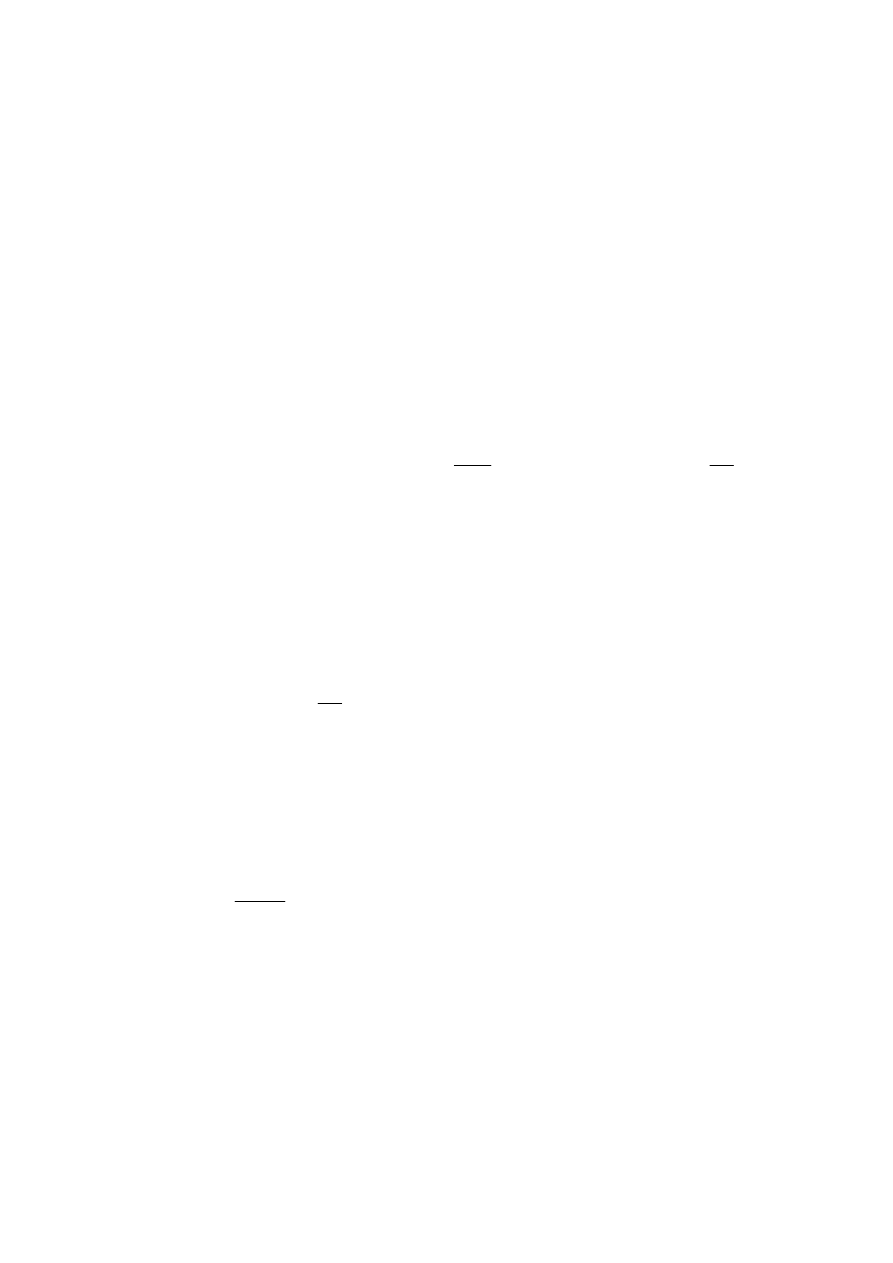
34

Polska Norma EN-ISO 5167:2005 dotycząca zwężkowych pomiarów parametrów

przepływu jest odpowiednikiem normy międzynarodowej, przyjętej powszechnie w Europie i
większości krajów świata.

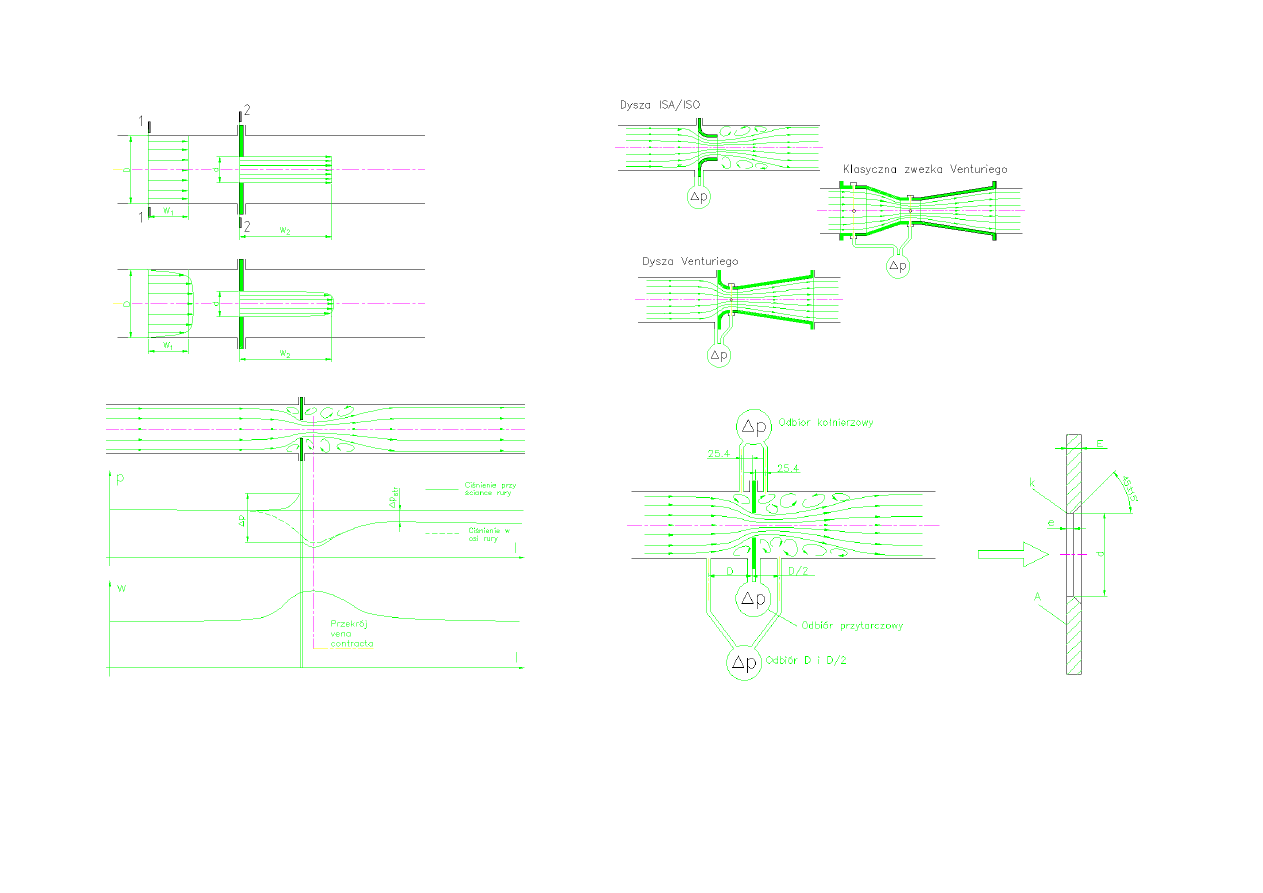
Poza kryzami znormalizowane są dysze o płynnie ukształtowanym wlocie (rys. 2 a).

Należy je stosować tam, gdzie korozyjne lub korozyjne oddziaływanie płynu powodowałoby
szybkie stępienie krawędzi kryzy.

W przypadkach gdy niedopuszczalne są duże straty ciśnienia należy stosować oraz

zwężki o małych stratach ciśnienia – dysze Venturiego (rys. 2 b) i klasyczne zwężki
Venturiego (rys. 2 c). Dzięki łagodnemu rozszerzeniu strumienia przez stożkową część
rozbieżną nie występuje tu strefa silnych zaburzeń i zawirowań, w której następują szkodliwe
straty energii potencjalnej (ciśnienia), przez co niezbędna jest większa moc pomp/sprężarek.

Na rys. 2 podano też miejsca odbioru ciśnienia różnicowego

∆

p z kryz.

Wartości C i

∈

∈

∈

∈

wyznacza się z podanych w normie równań empirycznych. Np. dla

znormalizowanej kryzy z przytarczowym odbiorem ciśnienia (patrz rys. 2) współczynnik
przepływu obliczamy z równania Reader-Harrisa

C = 0,5961+0,0261

β

2

- 0,216

β

8

+ 0,000521

7

,

0

6

10













Re

β

+ (0,0188+0,0063

A)

β

3,5

3

,

0

6

10













Re

(12)

w którym

β

= d/D jest przewężeniem kryzy;

Re jest liczbą Reynoldsa, dana wzorem (9)

Liczbę ekspansji dla znormalizowanych kryz oblicza się z wzoru empirycznego

∈

∈

∈

∈

= 1 - (0,41+0,35

β

4

)

∆

p

p

κ

1











(13)

2.3. Wyznaczenie parametrów płynu

Dla obliczenia strumienia płynu niezbędna jest znajomość gęstości i lepkości. Dla cieczy

korzystamy zwykle z danych tablicowych. W przypadku cieczy w zasadzie możemy pominąć
wpływ ciśnienia na te parametry, a jedynie uwzględnić wpływ temperatury.

Dla gazów gęstość wyznaczamy zwykle z wzoru

gdzie

ρ

n

– gęstość gazu w warunkach normalnych, tj.

T

n

= 273.15 K, p

n

= 101.325 kPa (dla

powietrza

ρ

n

= 1.2928 kg/m

3

);

p i T – ciśnienie i temperatura absolutna przed zwężką, K –

względny współczynnik ściśliwości przy ciśnieniu

p i temperaturze T (współczynnik

ś

ciśliwości uwzględnia odchylenia właściwości gazu rzeczywistego od właściwości gazu

doskonałego).

TK

p

pT

n

n

n

ρ

ρ

=

)

14

(

Rys. 1. Przepływ płynu przez kryzę: a) model uproszczony do wypro-
wadzenia wzoru, rzeczywiste profile prędkości i obraz linii prądu
przy przepływie przez kryzę.-

Rys. 2. Inne zwężki znormalizowane i linie prądu przy przepływie przez te
zwężki, pokazano miejsca odbioru ciśnienia różnicowego

∆∆∆∆

p. Sposoby

odbioru ciśnienia dla kryzy

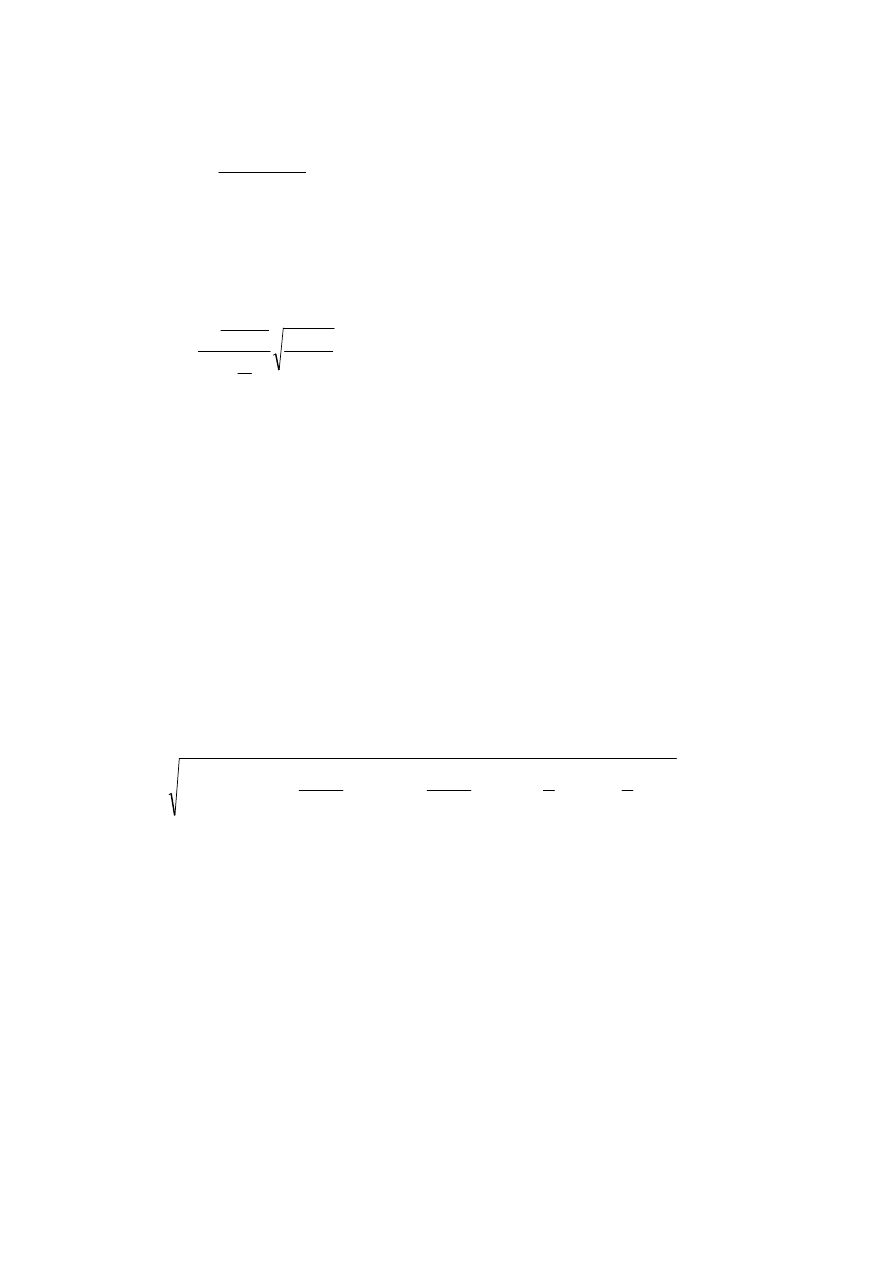
36

Jeżeli gaz jest wilgotny to wzór (16) trzeba zmodyfikować do postaci

gdzie

ϕ

- wilgotność względna,

p

p

– ciśnienie pary wodnej w temperaturze

T,

ρ

p,s

– gęstość

pary wodnej nasyconej w temperaturze

T. Wartości te można znaleźć m.in. w [4], są one

znane z niepewnościami

u( p

p

)= 0.0007 kPa;

u(

ρ

p,s

) = 0.00005 kg/m

3

.

Niezbędną do obliczenia liczby Reynoldsa wartość lepkości obliczamy dla gazów z wzoru

gdzie

C – stała Sutherlanda (dla powietrza C = 112 K),

η

0

– lepkość gazu w warunkach

normalnych (dla powietrza

η

0

= 17.1

·10

-6

kg/m

·s).

2.4. Analiza niepewności zwężkowego pomiaru strumienia płynu

Pomiar strumienia płynu za pomocą zwężki jest klasycznym pomiarem pośrednim, tj.

wartość strumienia płynu uzyskiwana jest drogą pośrednią, poprzez wstawienie do wzoru (11)
wartości innych wielkości, mierzonych bądź bezpośrednio (np.

∆

p), bądź także pośrednio; np.

gęstość

ρ

obliczana jest pośrednio, z zależności (14) lub (15).

Z wykładów Podstaw Metrologii wiadomo, że niepewność pomiaru można obliczyć jako
sumę geometryczną niepewności cząstkowych, będących iloczynami niepewności danej
wielkości przez współczynnik wrażliwości (dla wielkości niezależnych potęgę, w której
wielkość ta występuje). Do wyznaczenia współczynnika wrażliwości dla

d i D, które

dodatkowo wpływają na niepewność wyznaczenia przewężenia

β

, przyjęto postać funkcji

C

= f(

Re,

β

) w postaci

C = const + 0.5

β

4

, pomijając jako małą drugiego rzędu niepewność

obliczenia

Re. Dla pomiaru zwężkowego wzór na niepewność wyznaczenia strumienia płynu

ma przy tych założeniach postać

( )

( )

( )

( )

( )

( )

( )

ρ

β

β

β

2

2

2

2

4

2

2

4

4

2

2

4

1

4

1

1

2

1

2

u

p

u

d

u

D

u

u

C

u

q

U

v

+

∆

+













−

+













−

+

∈

+

=

(17)

W metrologii przemysłowej przyjmuje się podawanie wyniku pomiaru przy poziomie

ufności 0.95, tak więc wszystkie niepewności występujące w powyższym wzorze to
niepewności tzw. dwusigmowe, czyli ze współczynnikiem rozszerzenia równym

k = 2.

Założono też, że wszystkie błędy systematyczne pomiarów zostały wyeliminowane.

2.5. Najistotniejsze niepewności pomiaru zwężkowego

Jak wiadomo z wykładu Podstawy Metrologii niepewności najogólniej można podzielić na

dwie grupy: niepewności typu A – obliczane metodami statystycznymi i niepewności typu B
– wyznaczane innymi metodami. W trakcie ćwiczenia będą stosowane obie metody.

2.5.1. Niepewność wyznaczenia współczynnika przepływu

u(C)

Niepewność

u(C) wynosi dla kryzy (stosowanej w niniejszym ćwiczeniu):

0.6% dla

β

< 0.6 lub

β

(%) dla 0.6 <

β

< 0.75.

(

)

s

p

n

n

p

n

TK

p

T

p

p

,

ϕρ

ϕ

ρ

ρ

+

−

=

15

.

273

1

15

.

273

1

0

T

T

C

C

+

+

=

η

η

)

16

(

)

15

(

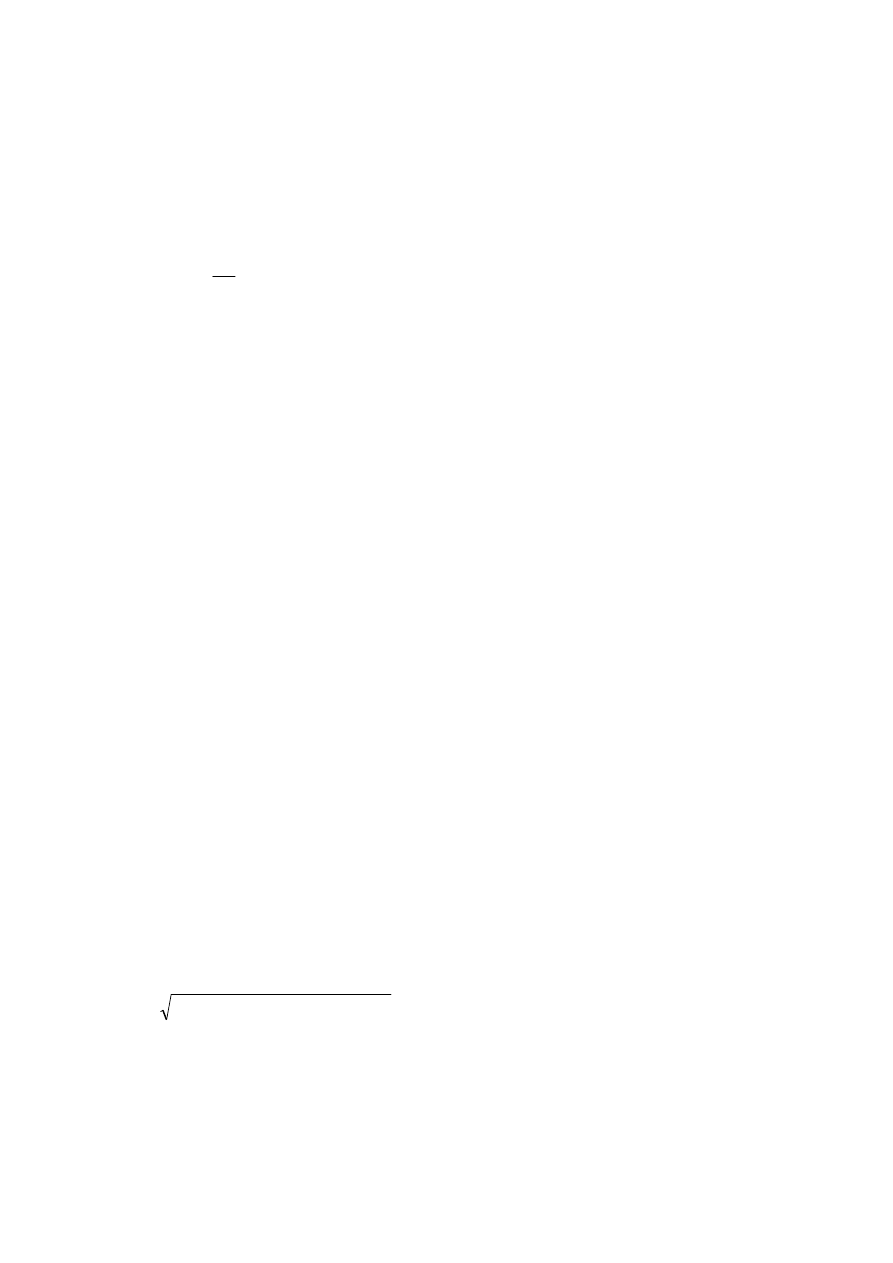
37

Informacje o tej niepewności są zaczerpnięte z normy [1], i pomimo, że przez autorów

normy były wyznaczone metodami statystycznymi, to z punktu widzenia użytkownika normy
są to niepewności typu B.

2.5.2. Niepewność wyznaczenia liczby ekspansji
Dla kryzy niepewność ta wynosi

Podobnie jak dla niepewności współczynnika przepływu jest to niepewność typu B.

2.5.3. Niepewność pomiaru parametrów geometrycznych zwężki i rurociągu
Metody pomiaru parametrów geometrycznych takich jak np. średnica otworu zostały
zmierzone w laboratorium pomiarów wielkości geometrycznych Instytutu. Niepewności u(D)
i u(d) obliczone w trakcie tych pomiarów poda prowadzący ćwiczenie, w zależności od tego,
jaki rurociąg i kryza będą wykorzystane w trakcie ćwiczenia. Należy je traktować jako
niepewności typu B, chociaż wykonujący pomiary prawdopodobnie stosował metody
statystyczne do oszacowania tych niepewności.

2.5.4. Niepewność pomiaru ciśnienia różnicowego
Niepewność pomiaru ciśnienia różnicowego u(

∆

p

) na zwężce wyznaczyć można poprzez

wykonanie serii pomiarów (co najmniej 10) tej wielkości. Będzie to więc niepewność typu
A, czyli wyznaczana metodami statystycznymi.

2.5.5. Niepewność pomiaru ciśnienia w rurociągu

Także ta niepewność u(p) będzie wyznaczona poprzez wykonanie serii pomiarów (co

najmniej 10). Będzie to więc także niepewność typu A.

2.5.6. Niepewność pomiaru temperatury

Temperatura będzie mierzona za pomocą czujnika Pt 100 (platynowy rezystor o rezystancji

100

Ω

w temperaturze 0

°

C. W temperaturze ok. 20

°

C, panującej w laboratorium, jego

niepewność wynosi 0.2

°

C. Niepewność tą określono w oparciu o tolerancje dla tych

czujników podane w normie PN-EN 60751:1995, jest to więc niepewność typu B. Również
niepewność przetwornika współpracującego z czujnikiem wynosi 0.2

°

C (dane katalogowe, a

więc także niepewność typu B). Niepewność pomiaru temperatury u(T) można wyznaczyć
sumując te wartości (zgodnie z zasadami sumowania niepewności).

2.5.7. Niepewność wyznaczenia gęstości
Gęstość gazu suchego obliczamy z wzoru (14). Jest to wiec też pomiar pośredni,
niepewność obliczenia gęstości można wyznaczyć z wzoru

( )

( )

( )

( )

)

(

2

2

2

2

K

u

T

u

p

u

u

u

n

+

+

+

=

ρ

ρ

Niepewność gęstości w warunkach normalnych z danych tablicowych (a więc typu B)

u

(

ρ

n

) = 0.002 kg/m

3

.

Niepewność względna współczynnika ściśliwości (typu B, wyznaczanego w trakcie

obliczeń z wzoru Redlicha – Kwonga) wynosi u(K) = 20(1 – K) %.

( )

(%)

4

p

p

u

∆

=

∈

38

Należy pamiętać, że p - ciśnienie absolutne w rurociągu - wyznacza się czasem (o ile nie

ma do dyspozycji przetwornika ciśnienia absolutnego) pośrednio, jako sumę ciśnienia
atmosferycznego p

b

i zmierzonego nadciśnienia w rurociągu.

Uwzględniając dodatkowe czynniki występujące we wzorze (15), tj.

ϕ

, p

p

i

ρ

p,s

, można też

uwzględnić niepewność obliczenia gęstości gazu wilgotnego.

2.6. Automatyczne opracowywanie wyników pomiarów zwężkowych
Procedura obliczenia wyniku pomiaru przepływu metodą zwężkową jest na tyle
skomplikowana i pracochłonna, że opracowano wiele programów komputerowych,
umożliwiających obliczenie strumienia płynu lub, co jeszcze ważniejsze, zaprojektowanie
przepływomierza zwężkowego. Polega ono na takim doborze średnicy otworu zwężki, aby
uzyskać pożądany zakres manometru różnicowego odpowiadający żądanemu zakresowi
zmian strumienia płynu.
W większości pomiarów przemysłowych przyjmuje się stałą wartość współczynnika
przepływu i liczby ekspansji a także gęstości. Przyjęcie stałej gęstości jest w większości
procesów technologicznych możliwe, gdyż na ogół procesy te wymagają stałego ciśnienia i
temperatury.

Zwykle też dąży się do zapewnienia stałości przepływu, zakres pomiarowy nie musi być

więc szeroki. Wówczas wzory (11) można uprościć do postaci

gdzie stała k uwzględnia uśrednione wartości czynników przyjętych za stałe. Jedyną operacją
jest wówczas pierwiastkowanie sygnału różnicy ciśnień, dlatego często przetworniki różnicy
ciśnień (m. in. stosowany w niniejszym ćwiczeniu) mają możliwość pierwiastkowania
sygnału wyjściowego. Gdy potrzebny jest tylko lokalny analogowy odczyt strumienia
wystarczy zastosować miernik z nieliniową podziałką o charakterze kwadratowym.
Zdarzają się jednak przypadki, gdy zmiany przepływu, ciśnienia i temperatury (czyli także
gęstości czy lepkości, wpływającej poprzez liczbę Reynoldsa na liczbę przepływu) są duże.
W takich przypadkach stosuje się wyspecjalizowane przeliczniki mikrokomputerowe
wykonujące program obliczeń oparty o podane powyżej wzory przy uwzględnieniu
wszystkich czynników wpływających na wynik pomiaru.
Informacja o temperaturze, ciśnieniu i spadku ciśnienia na zwężce jest doprowadzana do
przelicznika w postaci sygnałów elektrycznych, najczęściej w postaci prądu w przedziale
(4 - 20) mA proporcjonalnego do mierzonej wielkości, lub w przypadku przetworników
inteligentnych, jak np. w stanowisku stosowanym w trakcie ćwiczenia, w postaci cyfrowej.

3. Opis stanowiska

W ćwiczeniu wykorzystuje się niskociśnieniowe stanowisko powietrzne. Składa się ono z

wentylatora wymuszającego przepływ, zaworu do regulacji przepływu, zestawu gazomierzy
kontrolnych (w ćwiczeniu nie będą one wykorzystywane), komory filtrów chroniących
gazomierze kontrolne oraz z ciągu przepływomierza sprawdzanego, w którym będzie
zamontowany rurociąg z kryzą, stosowaną do pomiaru w niniejszym ćwiczeniu.

Do pomiaru ciśnienia absolutnego i ciśnienia różnicowego zastosowane zostaną

inteligentne przetworniki firmy Rosemount. Do pomiaru temperatury zastosowano platynowy
czujnik rezystancyjny Pt100 z przetwornikiem Rosemount.

4. Wykonanie ćwiczenia
Wstępne dane o instalacji i badanym płynie będą podane na ćwiczeniach przez
prowadzącego zajęcia. Dane te należy zamieścić w otrzymanym protokole.

p

k

q

∆

=

39

Następnie należy wykonać pomiary parametrów otoczenia, tj. ciśnienia atmosferycznego,
temperatury i wilgotności, określając przy tym niepewności pomiarów tych wielkości na
podstawie oznaczeń na podzielni lub świadectw przyrządów.
Kolejna czynność to sprawdzenie długości prostych odcinków pomiarowych przed i za
zwężką i porównanie ich z wymaganiami normy [1].
Następnie, po uruchomieniu wentylatora wymuszającego przepływ w rurociągu należy
dokonać serii pomiarów nadciśnienia (lub ciśnienia absolutnego) w rurociągu, ciśnienia
różnicowego i temperatury. Wyniki zapisać w otrzymanym formularzu protokołu.

5. Opracowanie wyników pomiarów
Po wykonaniu części pomiarowej należy wykonać obliczenia za pomocą odpowiednio
oprogramowanego komputera. Program umożliwia śledzenie toku obliczeń i wyników
posrednich, oblicza też, poza strumieniem płynu, niepewności pomiaru spowodowane
rożnymi czynnikami i niepewność złożoną.
Obliczenia strumienia objętości należy porównać z wynikami uzyskanymi z
mikrokomputerowego przelicznika przepływu (jeśli ta część jest wykonywana).

Jeżeli jest możliwość porównania wyniku pomiaru za pomocą zwężki z wynikiem pomiaru

wykonanym innym przepływomierzem (zainstalowanym szeregowo) to należy sprawdzić czy
wyniki te są zgodne (w granicach niepewności obu przepływomierzy)

6. Treść sprawozdania
W sprawozdaniu należy zamieścić:

1. Schemat instalacji pomiarowej
2. Protokół pomiarów
3. Wyniki obliczeń
4. Analizę niepewności wykonana na podstawie wyliczonych wartości niepewności

poszczególnych parametrów i niepewności złożonej. Analiza powinna obejmować ocenę,
które ze źródeł błędów są najistotniejsze, a wiec jakie czynności należy podjąć aby
efektywnie podwyższyć dokładność pomiaru. Ponadto należy dokonać oceny, które
niepewności (lub ich grupa) są pomijalnie małe.

5. Porównanie wyników obliczeń z wynikami z automatycznego przelicznika, analiza
przyczyn ewentualnych rozbieżności (jeżeli ta część jest wykonywana).
6. Jeżeli jest możliwość porównania wyniku pomiaru za pomocą zwężki z wynikiem pomiaru

wykonanym innym przepływomierzem (zainstalowanym szeregowo) to należy sprawdzić
czy wyniki te są zgodne (w granicach niepewności obu przepływomierzy)

Bibliografia:

[1] PN-ISO 5167:2005. Pomiar strumienia płynu za pomocą zwężek
[2] Turkowski M. Pomiary przepływów (skrypt). WPW, Warszawa, 1989
[3) Turkowski M. Przemysłowe sensory i przetworniki pomiarowe, OWPW, Warszawa, 2002
[4] Poradnik fizykochemiczny. WNT, Warszawa, 1974

40

INSTYTUT METROLOGII I SYSTEMÓW POMIAROWYCH

Politechniki Warszawskiej

Laboratorium Podstaw Metrologii

Semestr I

Ć

wiczenie nr 5

Wpływ temperatury na wskazanie manometrów i przetworników

ciśnienia

Warszawa

41

Wpływ temperatury na wskazanie manometrów i przetworników ciśnienia

Opracował: dr inż. Eugeniusz Sukiennik

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z budową manometru, wyznaczaniem błędu
temperaturowego i jego analizą.

2. Wprowadzenie teoretyczne

Wskazania każdego przyrządu pomiarowego powinny być zależne tylko od zmian wartości tej
wielkości do mierzenia której jest on przeznaczony. W szczególności wskazania manometru
sprężynowego powinny być zależne tylko od zmian mierzonego ciśnienia.
W rzeczywistości wskutek oddziaływania na przyrząd pomiarowy szeregu wielkości
wpływających takich jak temperatura, wilgotność, ciśnienie atmosferyczne itp. wskazania
jego są również funkcją zmian wartości tych wielkości wpływających. Jeżeli wartości tych
wielkości będą różniły się od wartości odpowiadających warunkom odniesienia, to
pochodzący stąd błąd wskazania narzędzia pomiarowego będziemy nazywać błędem
dodatkowym tego przyrządu.

2.1. Zagadnienia dotyczące błędu dodatkowego

Istotnym pojęciem przy analizie błędów przyrządu pomiarowego są warunki odniesienia
przewidziane do badania tego przyrządu lub do wzajemnego porównywania wyników
pomiarów. Warunki odniesienia zawierają na ogół wartości lub zakresy odniesienia dla
wielkości wpływających, oddziaływujących na przyrząd pomiarowy. Definiuje sieje
najczęściej jako zespół wartości głównych wielkości wpływających, przy których przyrząd
powinien być wzorcowany. Warunki te mogą być podane w postaci pojedynczych wartości
dla każdej wielkości wpływającej, bądź też w postaci granic, w których wartości te powinny
być zawarte dla zachowania granic błędów dopuszczalnych przyrządu pomiarowego.
Wielkość wpływająca to wielkość nie będąca wielkością mierzoną, która ma jednak wpływ na
wynik pomiaru.
Błędem podstawowym nazywamy błąd przyrządu pomiarowego wyznaczony w warunkach
odniesienia.
Błędem dodatkowym nazywamy błąd przyrządu pomiarowego powstały w wyniku
przekroczenia przez wielkości wpływające wartości określonych przez warunki odniesienia.
Warunki odniesienia są to warunki przewidziane do badania przyrządu pomiarowego
zawierające zakresy odniesienia dla wielkości wpływających, oddziaływujących na przyrząd
pomiarowy.

2.2. Zagadnienia dotyczące błędu dodatkowego

Jeżeli zmiana wskazania przyrządu pomiarowego na skutek zmiany wartości wielkości
wpływającej następuje wg dającego się zidentyfikować prawa, wtedy błąd dodatkowy ma
charakter błędu systematycznego. W szczególności może to być błąd addytywny lub błąd
multiplikatywny (zmiana czułości).

42

W ogólnym przypadku błąd dodatkowy o charakterze systematycznym można obliczyć z
zależności [Romer, 1973]:

∑

=

∂

∂

⋅

∂

∂

=

n

i

i

i

z

dz

z

g

x

f

dy

1

gdzie: wskazanie przyrządu pomiarowego

y = f(x)

a wartość wielkości mierzonej x może ulegać zmianom pod wpływem zmian wartości
wielkości wpływających z

i

wg zależności

x = g(z

i

)

gdzie:

z

i

= [z

1

, z

2

, .... , z

m

]

T

Jeżeli ze wzoru (2) przyjmiemy dla manometru sprężynowego y = f(x) =k x wówczas:

∑

=

∂

∂

⋅

∂

∂

=

n

i

i

i

z

dz

z

g

x

k

dy

1

2.3. Błąd dodatkowy pomiaru ciśnienia

W ćwiczeniu będziemy zajmować się błędem temperaturowym manometrów sprężystych, tzn.
błędem pochodzącym stąd, że temperatura otoczenia nie zachowuje wartości przewidzianych
w warunkach odniesienia.
Uwzględniając przytoczone wyżej definicje w przypadku, gdy tylko jedna wartość
wpływająca, np. temperatura, przekracza wartości określone warunkami odniesienia można
napisać:

∆

p

dt

=

∆

p

t

-

∆

p

t0

gdzie:

∆

p

dt

- błąd dodatkowy wskazania, gdy wielkość wpływająca osiąga wartość t,

∆

p

t

- całkowity błąd wskazania, gdy wielkość wpływająca osiąga wartość t,

∆

p

t0

- błąd podstawowy wskazania przyrządu pomiarowego w temperaturze odniesienia t

0

.

Wyznaczony będzie błąd temperaturowy wskazania manometru z rurkową sprężyną
Bourdona przedstawionego na rysunku 2. Końcówka 3 sprężyny rurkowej 1 przemieszcza się
pod wpływem wzrostu mierzonego ciśnienia o wartość w, jak przedstawiono na rysunku 1
według zależności:

2

2

N

r

w

w

w

+

=

43

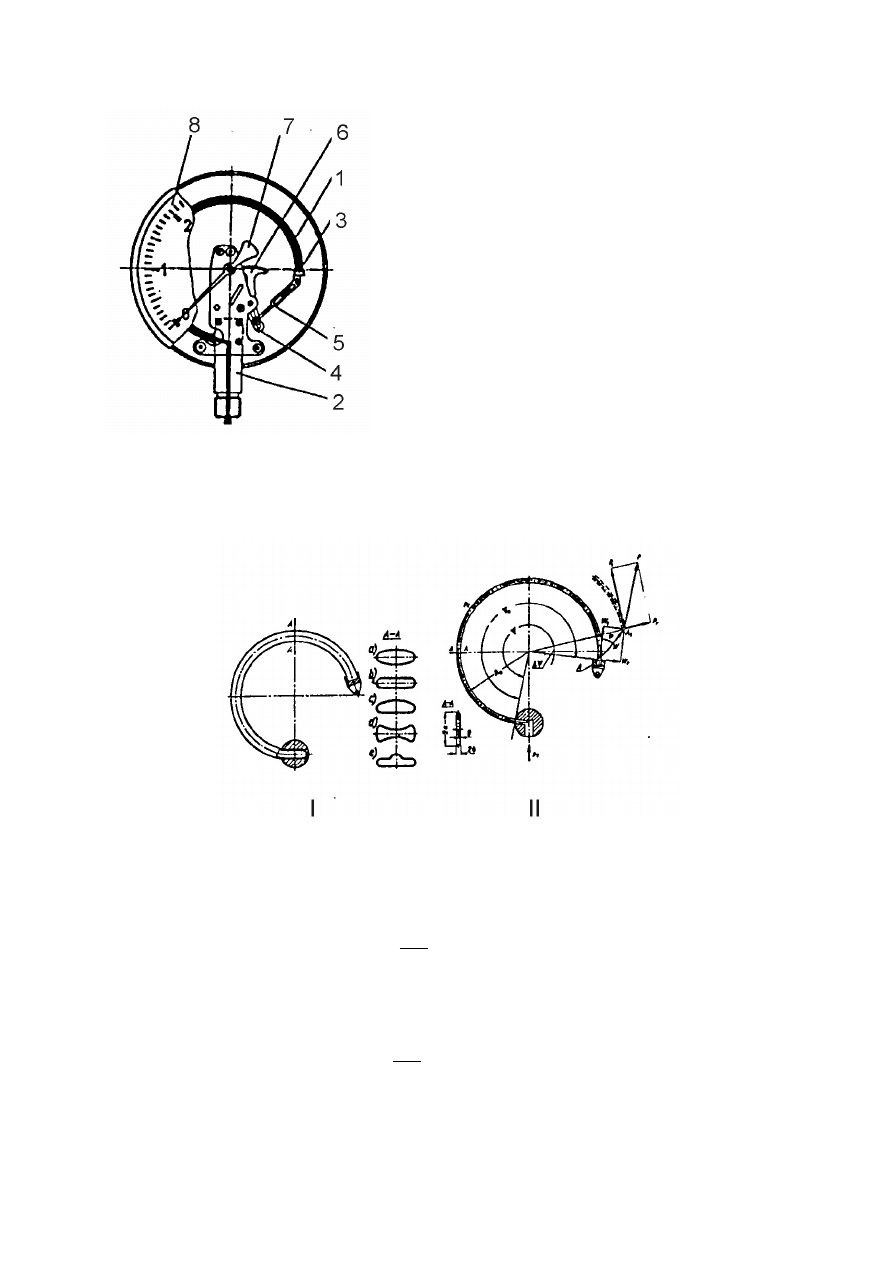
Rys. 1. Manometr z rurką sprężystą Bourdona. 1 - sprężyna, 2 - króciec, 3 - końcówki
sprężyny, 4 - końcówka segmentu zębatego, 5 - łącznik, 6 - zębatka, 7 - wskazówka,
8 - podzielnia

Rys. 2. I - Przekroje stosowane dla rurek manometrycznych cienkościennych

II - Odkształcenie rurki manometrycznej pod wpływem ciśnienia.

Przemieszczenie w

r

końca rurki w kierunku promieniowym wynosi:

)

cos

(

0

0

0

Ψ

−

Ψ

∆Ψ

=

t

R

w

r

oraz przemieszczenie

W

N

końca rurki w kierunku prostopadłym do promienia:

)

sin

(

0

0

0

0

Ψ

−

Ψ

Ψ

∆Ψ

=

R

w

r

Względna zmiana kąta odkształcenia rurki jest funkcją ciśnienia i parametrów
konstrukcyjnych tej rurki którą można opisać zależnością

44

E

g

b

a

R

h

p

s

)

,

,

,

,

,

,

(

0

0

ν

β

α

=

Ψ

∆Ψ

=

gdzie:

(

)

2

2

0

2

2

2

0

2

0

1

1

)

,

,

,

,

,

,

(













+













−

−

=

a

g

R

a

b

bg

R

g

b

a

R

h

β

α

ν

ν

β

α

Funkcja h zmienia wartości wraz ze zmianami temperatury, ale znacznie bardziej zmienia się
wartość E modułu Younga. W związku z tym zależności pomiędzy mierzonym ciśnieniem p,
a odkształceniem s elementu sprężystego, którego kształt jest tak dobrany, aby była ona
możliwie liniowa, można przedstawić ogólnym wzorem:

E

p

A

s

⋅

=

gdzie: A - współczynnik będący zawiłą funkcją kształtu i wymiarów elementu sprężystego,
E - współczynnik sprężystości materiału (moduł Younga).

Należy jednocześnie zwrócić uwagę na fakt, że manometry z elementem sprężystym mierzą
zawsze różnicę między ciśnieniem manometrycznym p

m

, a ciśnieniem otoczenia p

b

(barometrycznym). Tym samym ciśnienie mierzone p możemy wyrazić wzorem

p = p

m

- p

b

Zmiany temperatury powodują zmiany wartości modułu Younga E oraz współczynnika A.
Zmiany współczynnika sprężystości E możemy z pewnym przybliżeniem opisać wzorem

[

]

)

(

1

0

0

t

t

E

E

t

−

+

=

γ

gdzie: E

o

- moduł sprężystości w temperaturze t

o

,

E

t

- moduł sprężystości w temperaturze t,

γ

- współczynnik temperaturowy zmiany modułu sprężystości,

t

o

- temperatura odniesienia,

t - temperatura różna od temperatury odniesienia - temperatura pracy manometru.

Wartość temperaturowego współczynnika zmiany modułu sprężystości

γ

jest zawsze ujemna i

wynosi dla stopu miedzi z którego wykonywane są elementy sprężyste manometrów wynosi

γ

= -8

⋅

10

-4

1/°C

Ujemna wartość temperaturowego współczynnika zmiany modułu sprężystości powoduje
powstanie dodatkowego błędu temperaturowego.

45

Należy pamiętać, ze przemieszczenie w końcówki 3 sprężyny rurkowej 1 manometru
zamieniane jest na wychylenie s wskazówki 7 za pomocą mechanizmu dźwigniowo-zębatego
według zależności:

s = k

mech

w(p)

gdzie: k

mech

-

czułość mechanizmu manometru,

w - wychylenie końcówki 3 sprężyny rurkowej manometru.

Analizując wzór 11 łatwo stwierdzić, że błąd temperaturowy będzie funkcją nie tylko zmiany
temperatury, ale również funkcją mierzonego ciśnienia. Możemy to ogólnie wyrazić za
pomocą wzoru

∆

p

dt

= k

⋅

p

⋅

(t-t

0

)

gdzie: k - współczynnik temperaturowy charakteryzujący zmiany czułości danego
manometru,
p - mierzone ciśnienie,
t - temperatura pracy manometru,
t

0

- temperatura odniesienia,

∆

p

dt

- dodatkowy błąd wskazania spowodowany różnicą temperatury pracy i temperatury

odniesienia.

W praktyce współczynnik temperaturowy k charakteryzuje nie tylko element sprężysty
badanego manometru ale obejmuje również wpływ współczynników A i E na dodatkowy błąd
wskazania manometru.

3. Opis stanowiska

W ćwiczeniu wyznacza się dodatkowe błędy wskazań manometru z rurką Bourdona klasy
dokładności 1 (1,5) o zakresie wskazań 0

÷

10 bar (0

÷

60 bar). Jako manometry kontrolne

zostały użyte w ćwiczeniu manometry obciażnikowo-tłokowe MTU60 o zakresie
pomiarowym 0,1

÷

60 MPa i klasie dokładności 0,05. Do zadawania temperatury użyto

komorę typ KBC-G-100/250 z dwoma czujnikami do pomiaru temperatury rezystancyjnymi
PT 100 - jeden mierzy temperaturę otoczenia czujnika, drugi temperaturę rurki Bourdona oraz
komorę SML 32/250 z czujnikiem do pomiaru temperatury termoelektrycznym Fe- Konst. z
przetwornikiem napięcia MAU 92 Z, T/U = 0

÷

100 °C, Wy = 0

÷

10 V.

4. Wykonanie ćwiczenia

W celu wyznaczenia dodatkowego błędu wskazania

∆

p

dt

wykonujemy 4 serie pomiarów,

jedną w temperaturze otoczenia t

0

pozostałe w t

1

÷

t

3

przy zadawanych ciśnieniach p'

÷

p’’

(podanych przez prowadzącego ćwiczenie). Każda z serii zawiera po 6 pomiarów
wykonanych dla każdego punktu zadawanego ciśnienia. Wyniki pomiarów notujemy w
protokole sprawdzenia manometru.

5. Opracowanie wyników pomiaru

Na podstawie otrzymanych wyników obliczamy w tabeli błędy wskazania manometru

∆

p

i

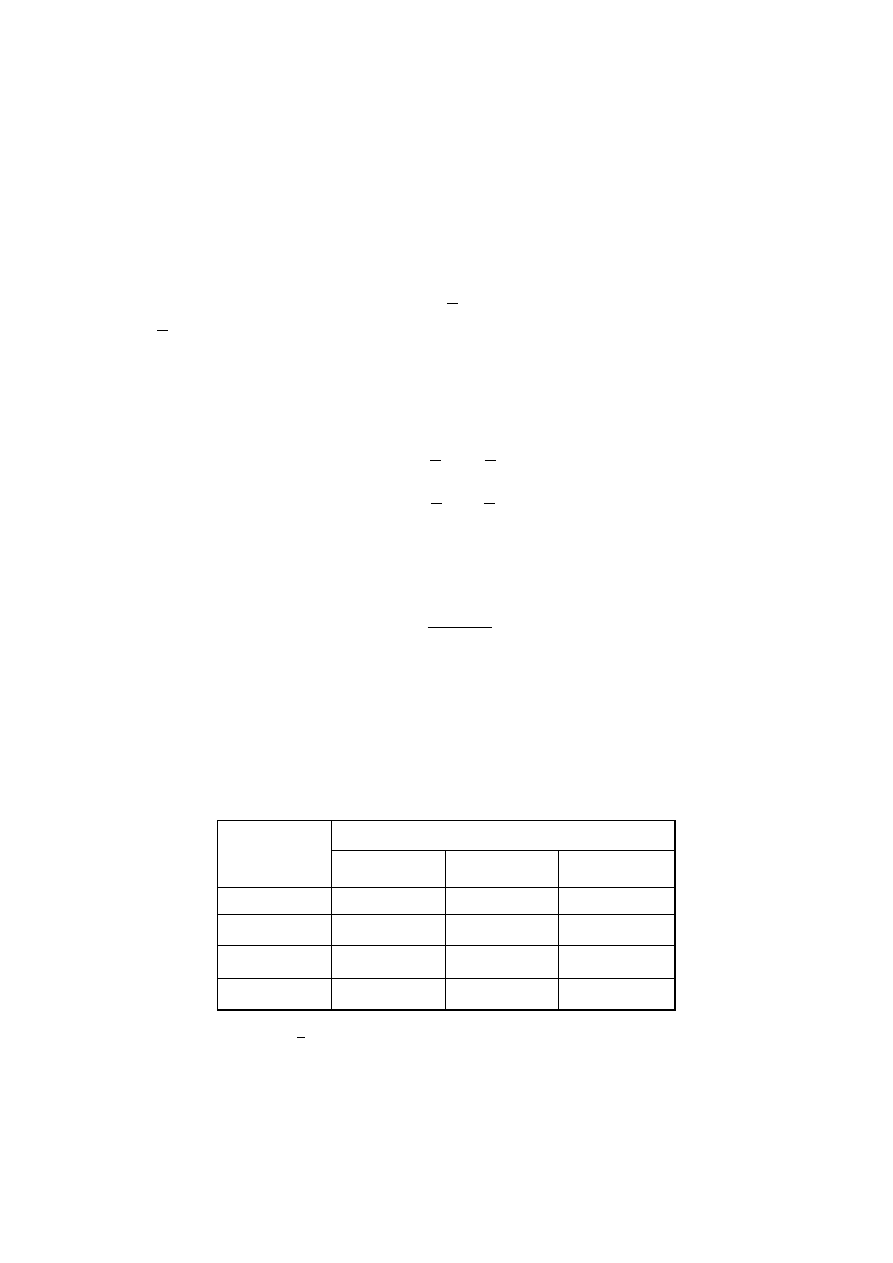
46

∆

p

0

= p

0

– p’

...................

∆

p

3

= p

3

– p’’

gdzie: p

0

÷

p

3

- wskazania manometru sprężynowego,

p’

÷

p’’ – ciśnienie otrzymane z manometru obciążnikowo-tłokowego.

Obliczamy średnie błędy wskazań manometru

i

p

∆

dla poszczególnych punktów sprawdzania.

Błąd

0

p

∆

czyli średni wskazania w temperaturze otoczenia przyjmujemy jako błąd

podstawowy wskazań.

Zgodnie z definicją błędu dodatkowego będziemy obliczać błędy dodatkowe wskazań
manometru w danej temperaturze t dla danego ciśnienia

∆

p

dt1

=

∆

p

t1

–

∆

p

t0

...................

∆

p

dt2

=

∆

p

t3

–

∆

p

t0

Wyznaczyć wartość temperaturowego współczynnika k charakteryzującego badany
manometr sprężynowy ze wzoru

)

(

0

t

t

p

p

k

dt

−

′

∆

=

Przy tym w miejsce p' podstawiamy wartości otrzymane z manometru obciążnikowo-
tłokowego, traktując je jako poprawne wartości ciśnienia

Wyniki obliczeń zestawić w tablicy 1

Tablica 1. Wartości współczynnika k

Wartości współczynnika k

ciśnienie bar

t

1

t

2

t

3

p' =

p" =

p"'=

p""=

Obliczyć wartość średnią

∑

=

12

/

)

(

k

k

ze wszystkich pomiarów.

6. Treść sprawozdania

Sprawozdanie powinno zawierać:

47

- schemat układu pomiarowego,
- schemat kinematyczny sprawdzanego manometru,
- wypełniony protokół sprawdzenia manometru,
- sporządzone na papierze milimetrowym lub komputerowe wykresy

a)

∆

p

dt

= f(

∆

t),

b)

∆

p

dt

= f(p),

c) k = f(

∆

t),

d) k = f(p).

- wnioski

1.1.1.1 Literatura

1. Jaworski J. i in.: Wstęp do metrologii i teorii eksperymentu. WNT, Warszawa 1992.
2. Międzynarodowy słownik podstawowych i ogólnych terminów metrologu.: GUM,

Warszawa 1996.

3. Przewodnik.: Wyrażenie niepewności pomiaru. GUM Warszawa, 1999.
4. Romer E.: Miernictwo przemysłowe. PWN, Warszawa 1973.

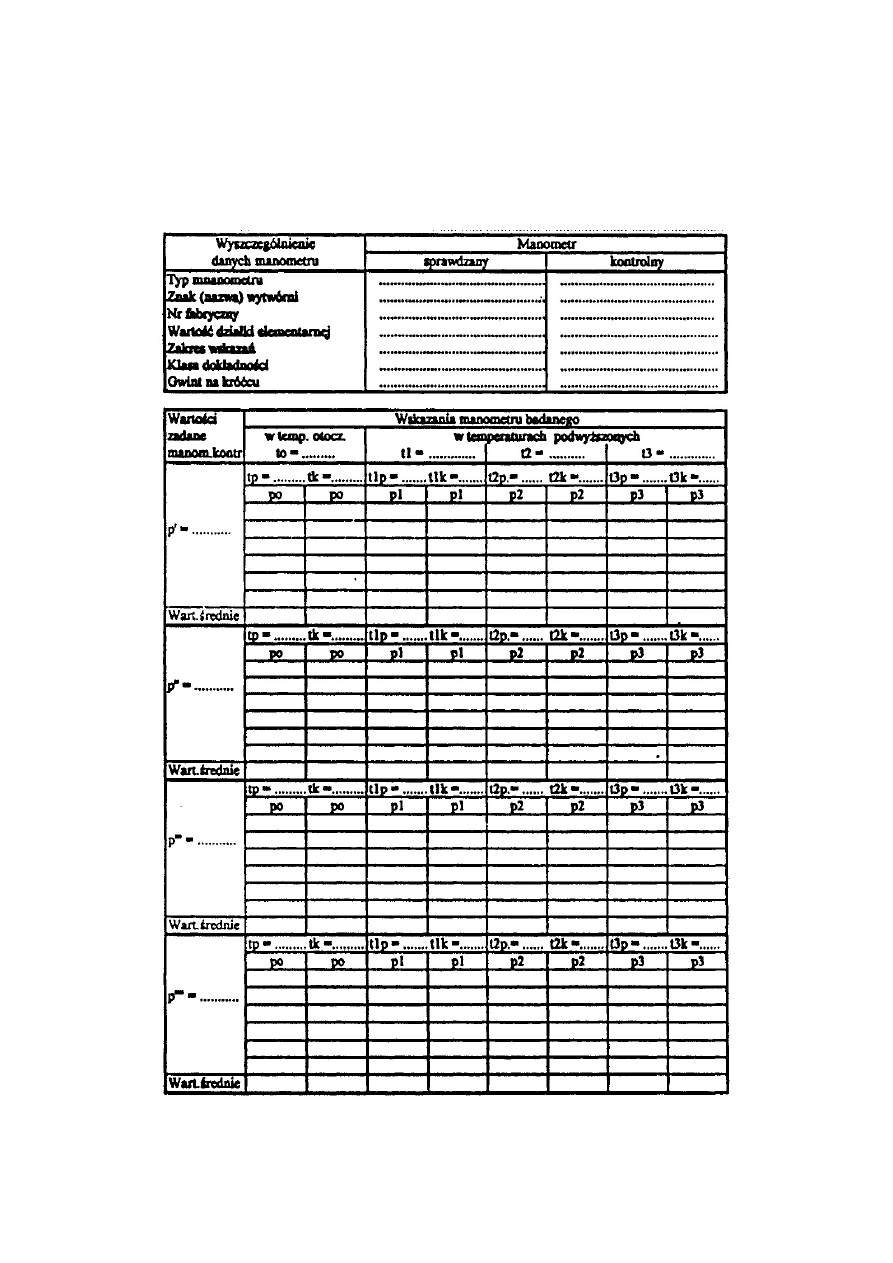
48

Protokół sprawdzenia manometru

Temperatura otoczenia: .....................

.

Wykonujący ćwiczenie:..........................

Cisnienie barometryczne: ...................
Data: ...................................................

49

INSTYTUT METROLOGII I SYSTEMÓW POMIAROWYCH

Politechniki Warszawskiej

Laboratorium Podstaw Metrologii

Semestr I

Ć

wiczenie nr 6

Metody dyfrakcyjne w pomiarach średnicy drutów

Warszawa

50

Metody dyfrakcyjne w pomiarach średnicy drutów.

Opracował: mgr inż. Piotr Orzechowski

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie studentów ze sposobem wyznaczania niepewności
pomiarów wykonywanych metodą pośrednią, tj. wtedy, gdy wielkość mierzona jest
wyznaczana na podstawie pomiaru innych wielkości związanych z wielkością mierzoną jakąś
zależnością matematyczną (np. wartość pola powierzchni prostokąta uzyskujemy mnożąc
uprzednio zmierzone długości jego boków). Innym celem ćwiczenia jest zapoznanie
studentów z metodami pomiarowymi związanymi z techniką laserową, w tym przypadku z
pomiarem średnicy cienkiego drutu i mikrootworu z zastosowaniem dyfrakcji
promieniowania (światła widzialnego) na krawędziach przeszkody.

2. Wprowadzenie teoretyczne

2.1 Przekształcenie Fouriera

Szereg funkcyjny o postaci:

(

)

(

)

nx

B

nx

A

x

B

x

A

A

n

n

sin

cos

....

sin

cos

1

1

0

+

+

+

+

+

nazywamy szeregiem trygonometrycznym.
Szereg Fouriera dla funkcji f(x) jest szczególnym przypadkiem szeregu trygonometrycznego,
którego wartości współczynników A i B wyrażają się następującymi wzorami:

( )

( )

∫

−

=

π

π

π

dx

kx

f

A

x

k

cos

1

( )

( )

∫

−

=

π

π

π

dx

kx

f

B

x

k

sin

1

Łatwo zauważyć, że współczynnik B

0

jest równy 0 (sin 0 =0), zaś współczynnik A

0

jest

równy całce z funkcji f (x) (cos 0 =1).
Zdefiniujmy sobie teraz funkcję zespoloną, zmiennej naturalnej k, której kolejnymi
wartościami są wartości współczynników szeregu Fouriera funkcji f(x):

( )

k

k

k

d

iB

A

F

+

=

__
Gdzie symbol i oznacza jednostkę urojoną tj.

√

-1 . Funkcja taka jest funkcją dyskretną tj. ma

wartości tylko dla niektórych liczb ze zbioru liczb rzeczywistych (wyłącznie dla liczb
naturalnych). Funkcję taką nazywamy dyskretną transformatą Fouriera (ang. Discrete Fourier
Transform) w skrócie DFT.
Jeżeli teraz liczby naturalne k we wzorze 3 zastąpimy przez liczby rzeczywiste

ω

, to

otrzymamy ciągłą transformatę Fouriera (lub po prostu transformatę Fouriera) F(

ω

) funkcji

f(x).

(1)

(3)

(2)

51

Możemy zatem zapisać:

( )

( )

( )

( )

(

)

dx

x

i

x

f

F

x

∫

−

⋅

+

⋅

=

π

π

ω

ω

ω

sin

cos

a wprowadzając cos(

ω

x)+i sin(

ω

x)=e

-i

ω

x

, otrzymujemy:

( )

( )

dx

e

f

F

x

i

x

∫

−

−

⋅

=

π

π

ω

ω

Funkcję f(x) nazywamy oryginałem, F(x) transformatą, zaś e

-i

ω

x

nazywamy jądrem

przekształcenia Fouriera.
Przekształcenie Fouriera często stosujemy zwłaszcza wtedy, gdy chcemy się dowiedzieć, z
jakich prostych funkcji składowych składa się funkcja uzyskana w wyniku danego
eksperymentu np. w zagadnieniach związanych z analizą sygnałów akustycznych, zaś w
mechanice przy analizie drgań obiektów. W trakcie niniejszego ćwiczenia poznamy jeszcze
jedno zastosowanie dla przekształcenia Fouriera.

2.2 Dyfrakcja fali elektromagnetycznej

Zjawisko dyfrakcji zachodzi wówczas, gdy na krawędź nieprzeźroczystej przesłony pada
wiązka promieniowania elektromagnetycznego np. światła. Obserwujemy wówczas
niezerową intensywność promieniowania, również w obszarze za przesłoną.
Ogólna teoria dyfrakcji jest zagadnieniem niezwykle skomplikowanym i jej szczegółowy opis
daleko wykraczający poza zakres tej instrukcji. Osoby zainteresowane mogą się zapoznać z
tym zagadnieniem w pracach [1] i [2]. Dla potrzeb ćwiczenia studenci powinni wiedzieć, że
opis zjawiska wynika bezpośrednio z równań Maxwella, oraz że istnieje szereg modeli
fizycznych tego zjawiska, dla których stosujemy pewne założenia upraszczające.
Jednym z modeli jest model dyfrakcji Fraunhofera. Założeniem upraszczającym w tym
przypadku jest to, że fala padająca na przeszkodę jest płaska (to oznacza, że wiązka promieni
ś

wiatła jest równoległa), obserwator znajduje się w odległości dużo większej niż wymiary

przeszkody, zaś sama przeszkoda ma wymiary większe od długości fali promieniowania.
Rozkład promieniowania elektromagnetycznego za przesłoną jest wówczas opisany wzorem:

( )

∫

∞

∞

−

−

=

ξ

ξ

ξ

d

e

E

E

x

i

x

)

(

0

Gdzie:
E(x) – rozkład promieniowania za przesłoną
E

0

(

ξ

)- rozkład promieniowania w płaszczyźnie przesłony

rect(

ξ

) jest funkcją, którą, możemy opisać (gęstość optyczną) przeźroczystość płaskiej

szczeliny, lub cienkiego drucika:







=

1

0

)

(

ξ

rect

Rozwiązaniem całki (6) dla funkcji (7) jest:

( )

x

s

x

s

E

E

x

λ

π

λ

π

)

sin(

0

=

dla

ξ

>s i

ξ

<-s

dla –s>

ξ

<s

(7)

(4)

(6)

(5)

(8)

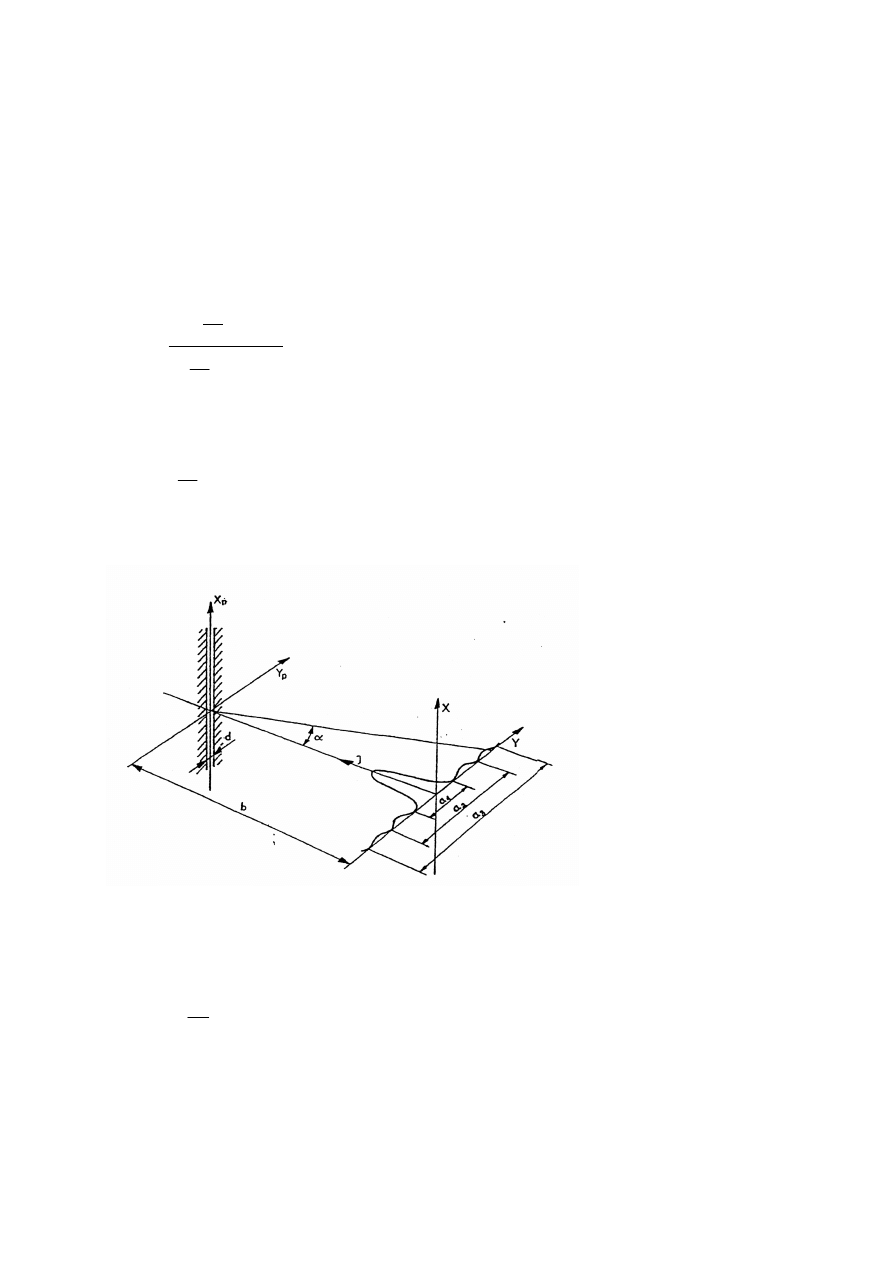
52

Gdzie:
s – jest szerokością szczeliny (grubością drucika)

λ

- jest długością fali promieniowania (światła)

Wzór (8) jest dość niewygodny w użyciu, gdyż opisuje rozkład energii, a nie intensywności
promieniowania, w dodatku opisuje rozkład energii w ściśle określonej płaszczyźnie. Aby
uzyskać rozkład intensywności promieniowania (a więc wielkość, którą możemy zmierzyć),
wystarczy wzór (8) podnieść do kwadratu, z kolei, aby uzyskiwać rozkłady w dowolnej
płaszczyźnie podstawimy x=sin

α

, gdzie

α

jest kątem dyfrakcji:

( )

2

0

)

sin(

))

sin(

sin(

























=

α

λ

π

α

λ

π

α

s

s

I

I

Wzór (9) osiąga wartość 0 wtedy, gdy licznik osiąga wartość 0 tj. wtedy gdy:

=

π

n

)

sin(

α

λ

π

s

gdzie:
n – rząd ugięcia (n jest liczbą całkowitą różną od 0)

Jak widać z Rys. 1 kąt

α

możemy wyrazić przy pomocy odległości a

n

i b:













=

b

a

arctg

n

2

α

gdzie:
a

n

– odległość pomiędzy symetrycznie położonymi minimami rozkładu rzędu n

b – odległość mierzonego elementu od ekranu, na którym obserwujemy obraz dyfrakcyjny

(11)

(10)

(9)

53

W rezultacie otrzymujemy wzór na wymiar s:

























=

b

a

arctg

n

s

n

2

sin

λ

Dla małych kątów funkcje sinus i arcus tangens, są w przybliżeniu równe swoim argumentom
(wyrażonym w radianach). W rezultacie możemy zastosować wzór uproszczony:

n

a

nb

s

λ

2

=

W przebiegu ćwiczenia zaleca się sprawdzenie różnicy w wartościach uzyskiwanych przez
zastosowanie wzoru (13) i (14), oraz porównanie ich z wartością niepewności.
Analogiczne rozumowanie możemy przeprowadzić dla otworu okrągłego z tym, że musimy
użyć dwuwymiarowej transformaty Fouriera.
Analogicznie do wzoru (6) możemy zapisać:

∫∫

+

−

=

R

y

x

i

y

x

d

d

e

E

E

η

ξ

η

ξ

π

η

ξ

)

(

2

)

,

(

0

)

,

(

gdzie R oznacza całą płaszczyznę

ξ

,

η

.

Pełne wyprowadzenie wzoru dla okrągłego otworu zamieszczone jest w pracy [2] (Rozdział
8.2 przykład 6). Wynikiem tego wyprowadzenia jest następujący wzór na rozkład
intensywności:

2

0

0

1

0

)

(

sin

sin

2





































=

α

λ

π

α

λ

π

α

d

d

J

I

I

Symbol J

1

(z) oznacza funkcję Bessla pierwszego stopnia pierwszego rodzaju. Funkcja ta

zeruje się dla następujących wartości argumentu z:
z

1

=3,83171

z

2

=7,01559

z

3

=10,17347

z

4

=13,32369

z

5

=16,47063

Analogicznie do wzoru (12) możemy zapisać:

























=

=

b

D

arctg

d

d

z

n

n

2

sin

sin

0

0

λ

π

α

λ

π

gdzie:
z

n

– n-ta wartość argumentu funkcji Bessla, dla którego J

1

(z

n

)=0

D

n

– średnica n-tego pierścienia minimum dyfrakcyjnego.

Poszukiwaną średnicę otworu wyznaczamy z zależności:

























=

b

D

arctg

z

d

n

n

2

sin

0

π

λ

(13)

(12)

(14)

(15)

(17)

(16)

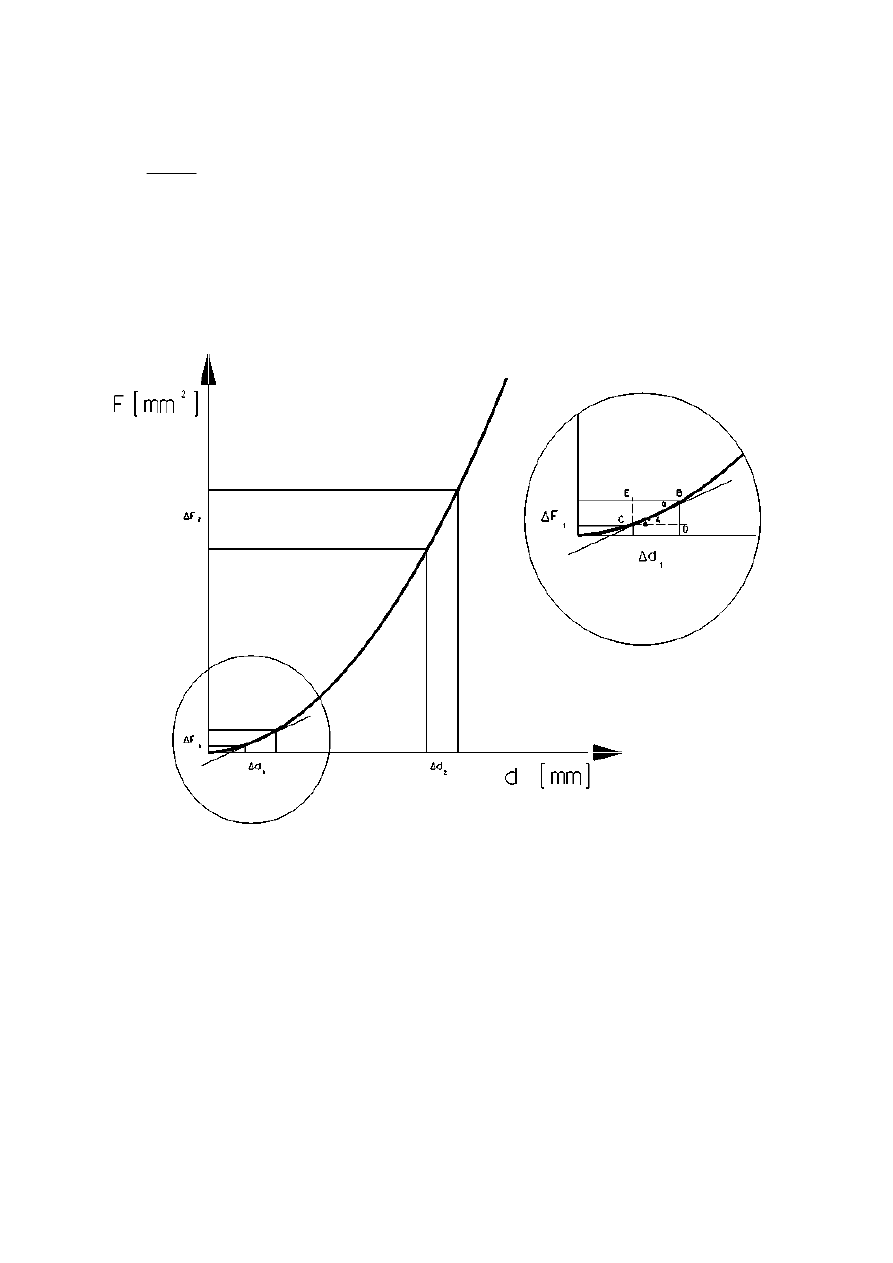
54

Podobnie jak dla wzoru (13) możemy zastosować uproszczenie wzoru (18) (pod identycznymi
warunkami) i otrzymujemy:

n

n

D

z

b

d

π

λ

2

0

=

2.3 Określanie niepewności w przypadku pomiarów pośrednich

W przypadku pomiarów pośrednich określenie całkowitej niepewności pomiaru przy pomocy
niepewności pomiarów cząstkowych nie jest sprawą prostą. Jest sprawą oczywistą, że
wyrażenie niepewności całkowitej przez proste zsumowanie niepewności cząstkowych nie
jest możliwe nawet jeśli niepewności te reprezentują jedną wielkość fizyczną (np. długość).

Wyobraźmy sobie pomiar pośredni wielkości fizycznej związanej zależnością kwadratową z
wielkością, którą rzeczywiście mierzymy, z taką sytuacją mamy np. do czynienia przy
pomiarze pola powierzchni okręgu, który dokonujemy przez pomiar jego średnicy. Na Rys. 2
przedstawiono wykres zależności pomiędzy średnicą okręgu, a jego polem powierzchni.
Łatwo zauważyć, że przy tej samej wartości niepewności pomiaru średnicy d, niepewność
pomiaru pola powierzchni rośnie. Jak zatem wyznaczyć niepewność pomiaru pola
powierzchni? Poprowadźmy styczną do paraboli w punkcie A, a następnie przesuńmy ją
równolegle do punktów przecięcia paraboli i prostych ograniczających zakres niepewności
pomiaru średnicy, oznaczymy te punkty jako B i C. Przez punkty B i C poprowadzimy teraz
dwie proste, prostopadłe do osi rzędnych (a więc osi na której odkładamy wartości pola
powierzchni), uzyskamy w ten sposób prostokąt BCDE. Bok BE (i CD) prostokąta ma

(18)

55

długość równą wartości niepewności pomiaru średnicy okręgu

∆

d, zaś bok BD (i CE) ma

długość równą wartości niepewności pola powierzchni

∆

F.

Z trygonometrii wynika, że:

( )

α

tg

BD

BE

⋅

=

a więc:

( )

α

tg

d

F

⋅

∆

=

∆

Tangens kąta

α

jest równy pochodnej z zależności pomiędzy średnicą i polem powierzchni

okręgu w punkcie A, a więc dla średniej wartości pomiaru średnicy. Mamy więc:

( )

dd

dF

d

F

d

⋅

∆

=

∆

W przypadku jeżeli wielkość wynikowa jest uzyskiwana przez pomiar wielu wielkości
pośrednich, wartość niepewności pomiaru pośredniego uzyskujemy przez sumowanie
niepewności pomiarów cząstkowych pomnożonych przez wartości bezwzględne pochodnych
cząstkowych.

(

)

( )

( )

( )

n

x

n

x

x

x

x

x

x

P

x

x

P

x

x

P

x

P

n

n

∂

∂

∆

+

+

∂

∂

∆

+

∂

∂

∆

=

∆

0

20

10

2

1

...

2

2

1

1

,...

,

gdzie:
x

1

, x

2

,..., x

n

– kolejne wielkości mierzone

∆

P – niepewność pomiaru wielkości wynikowej

∆

x

1

,

∆

x

2

,...,

∆

x

n

- kolejne niepewności wielkości mierzonych

Wyrażenie postaci (23) nazywamy różniczką zupełną.

3. Przebieg ćwiczenia

3.1 Opis stanowiska pomiarowego

Schemat stanowiska pomiarowego pokazano na Rys. 3. Składa się ono ze źródła światła 1, w
postaci lasera He-Ne; elementu mierzonego 2 (otworu lub drutu); ekranu 3; oraz detektora
obrazu 4 w postaci aparatu cyfrowego. Dane uzyskane w wyniku pomiaru są wstępnie
przetwarzane przez komputer PC 5 i drukowane na drukarce 6.

(20)

(19)

(22)

(21)

56

Ś

wiatło, emitowane przez laser 1, ulega dyfrakcji na elemencie 2. Obraz dyfrakcyjny jest

obserwowany na ekranie 3. Odczyt wyników pomiaru elementu 2 polega na pomiarze
odległości pomiędzy prążkami na ekranie 3. Wykonanie bezpośredniego odczytu wyników
(np. przez pomiar odległości przy pomocy liniału przyłożonego do ekranu 3). Jest, w
praktyce, bardzo trudny do wykonania, stąd konieczność zastosowania jakiegoś dodatkowego
sposobu odczytu wyników z ekranu 3. W ćwiczeniu zastosowano metodę, w której
wykonywane jest zdjęcie obrazu dyfrakcyjnego, a następnie odczyt wykonywany jest przez
pomiar odległości między prążkami na wydrukowanym zdjęciu. Ponieważ aparat przekształca
wymiary rejestrowanego obrazu, musimy współczynnik tego przekształcenia (powiększenia)
uwzględnić we wzorach używanych do wyznaczania wartości mierzonych. Należy zwrócić
uwagę na zachowanie stałej odległości pomiędzy aparatem cyfrowym 4 i ekranem 3 przez
cały czas trwania pomiaru, gdyż zmiana tej odległości powoduje w konsekwencji zmianę
współczynnika powiększenia obrazu prążkowego.

3.2 Przebieg ćwiczenia

Zarówno przy pomiarze średnicy otworu jak i średnicy drutu wykonywane czynności są
praktycznie identyczne stąd poniższy opis dotyczy obu przypadków.

-

Zamocować linijkę na powierzchni ekranu

-

Wykonać 5 ekspozycji obrazu linijki, a następnie wydrukować zapisane zbiory

-

Pomierzyć odległości pomiędzy kresami na obrazie linijki i ustalić współczynnik

powiększenia wraz z jego niepewnością

-

Zamocować mierzony element w oprawie

-

Ustalić odległość pomiędzy ekranem i mierzonym elementem, przez 5-krotny pomiar

-

Wykonać 5 ekspozycji obrazu prążkowego, a następnie wydrukować zapisane zbiory

-

Wykonać pomiar odległości pomiędzy symetrycznymi minimami intensywności na

obrazie prążkowym ustalić niepewność pomiaru

-

Obliczyć wartość oczekiwaną wymiaru mierzonego elementu

-

Obliczyć niepewność pomiaru wymiaru mierzonego elementu

57

Wyniki pomiaru należy zapisać w protokole, którego wzór stanowi załącznik do niniejszego
opracowania. Treść wniosków powinna zawierać:

-

Opis skrócony przebiegu ćwiczenia

-

Zestawienie obliczonych wartości wielkości wynikowych z niepewnościami

pomiarów. Co można powiedzieć o niepewnościach bezwzględnych?

-

Zestawienie wyników pomiaru obliczonych wg. wzorów dokładnych i przybliżonych

dla poszczególnych rzędów prążków. Należy porównać je z odpowiednimi
wartościami niepewności. W jakich przypadkach można stosować wzory
przybliżone?

-

Zestawienie wartości niepewności pomiarów wielkości cząstkowych. Która

niepewność cząstkowa ma największy wpływ na niepewność wynikową?

-

Własne obserwacje i wnioski.

4. Literatura

[1]

R. Jóźwicki „Optyka Instrumentalna” (rozdziały 3 i 8), WNT, Warszawa 1970

[2]

J. Petykiewicz „Optyka Falowa” (rozdział 4), PWN, Warszawa 1986

58

REGULAMIN LABORATORIUM PODSTAW METROLOGII

1. Postanowienia ogólne
1.1. Studenci wykonują ćwiczenia laboratoryjne w zespołach. Podział grupy studenckiej na

zespoły dokonywany jest przez Kierownika Laboratorium w porozumieniu ze starostami
grup na początku semestru i obowiązuje przez cały czas jego trwania.

1.2. Harmonogram wykonywania ćwiczeń dla każdego zespołu jest podany na cały semestr.

W rozkładzie tym przewiduje się dla studentów 1 semestru studiów 6 ćwiczeń
laboratoryjnych.

1.3. Zajęcia odbywają się bez przerw i trwają 1 godzinę i 45 minut. Studenci spóźnieni mogą

być niedopuszczeni do wykonywania ćwiczenia.

1.4. Studenci są obowiązani przygotować się do zajęć na podstawie wykładów oraz literatury

do poszczególnych ćwiczeń.

1.5. Nie przewiduje się oddzielnych terminów do odrobienia zajęć opuszczonych lub

niezaliczonych. W wyjątkowych wypadkach losowych wyznaczenie dodatkowych
terminów może nastąpić jedynie za zgodą Kierownika Laboratorium.

2. Przebieg zajęć
2.1. Każde ćwiczenie rozpoczyna się kollokwium ustnym lub pisemnym oraz krótkim

omówieniem ćwiczenia przez prowadzącego zajęcia.

2.2. W trakcie ćwiczenia każdy zespół prowadzi starannie protokół pomiarów. Po wykonaniu

ć

wiczenia zespół przedstawia opracowane wyniki pomiarów prowadzącemu ćwiczenie

do akceptacji.

2.3. Studenci są zobowiązani do wykonania indywidualnych sprawozdań zawierających

dyskusję otrzymanych wyników. Sprawozdanie należy oddać przed rozpoczęciem zajęć
w dniu odrabiania następnego kolejnego ćwiczenia.

3. Zasada oceniania pracy studenta w semestrze
3.1. Student za każde odrobione ćwiczenie otrzymuje ocenę w skali od 2 do 5.
3.2. Ocena za wykonanie ćwiczenia obejmuje: kollokwium wstępne, samodzielność

i sprawność w przeprowadzaniu pomiarów, sposób opracowania wyników, sprawozdanie.

3.3. Studenci nieobecni na zajęciach nie otrzymują żadnej oceny.

4. Warunki zaliczenia laboratorium
4.1. Warunkiem zaliczenia laboratorium jest:

a) wykonanie i zaliczenie 6 ćwiczeń przewidzianych programem laboratorium
b) otrzymanie przynamniej dostatecznej oceny końcowej.

4.2. Ocena końcowa obliczana jest jako suma wszystkich ocen z ćwiczeń zaliczonych

podzielona przez 6.

5. Przepisy porządkowe
5.1. Pomiary, montaż stanowiska itp. muszą być wykonywane z należytą starannością.

W szczególności studenci muszą przestrzegać zasad bezpiecznego postępowania
z aparaturą znajdującą się pod napięciem.

5.2. Uruchomienie układu pomiarowego może nastąpić jedynie po uzyskaniu zgody

prowadzącego ćwiczenie.

5.3. Wszelkie uszkodzenia stanowiska lub przyrządów pomiarowych a także wadliwe ich

działanie winno być niezwłocznie zgłaszane prowadzącemu ćwiczenie.

5.4. W czasie trwania zajęć obowiązuje studentów zachowanie odpowiadające normom

przyjętym na Uczelni.

59

5.5. Każde opuszczenie sali laboratoryjnej w czasie wykonywania ćwiczenia winno być

zgłaszane prowadzącemu ćwiczenie.

5.6. Wszelkie sprawy nie objęte regulaminem rozstrzyga Kierownik Laboratorium.