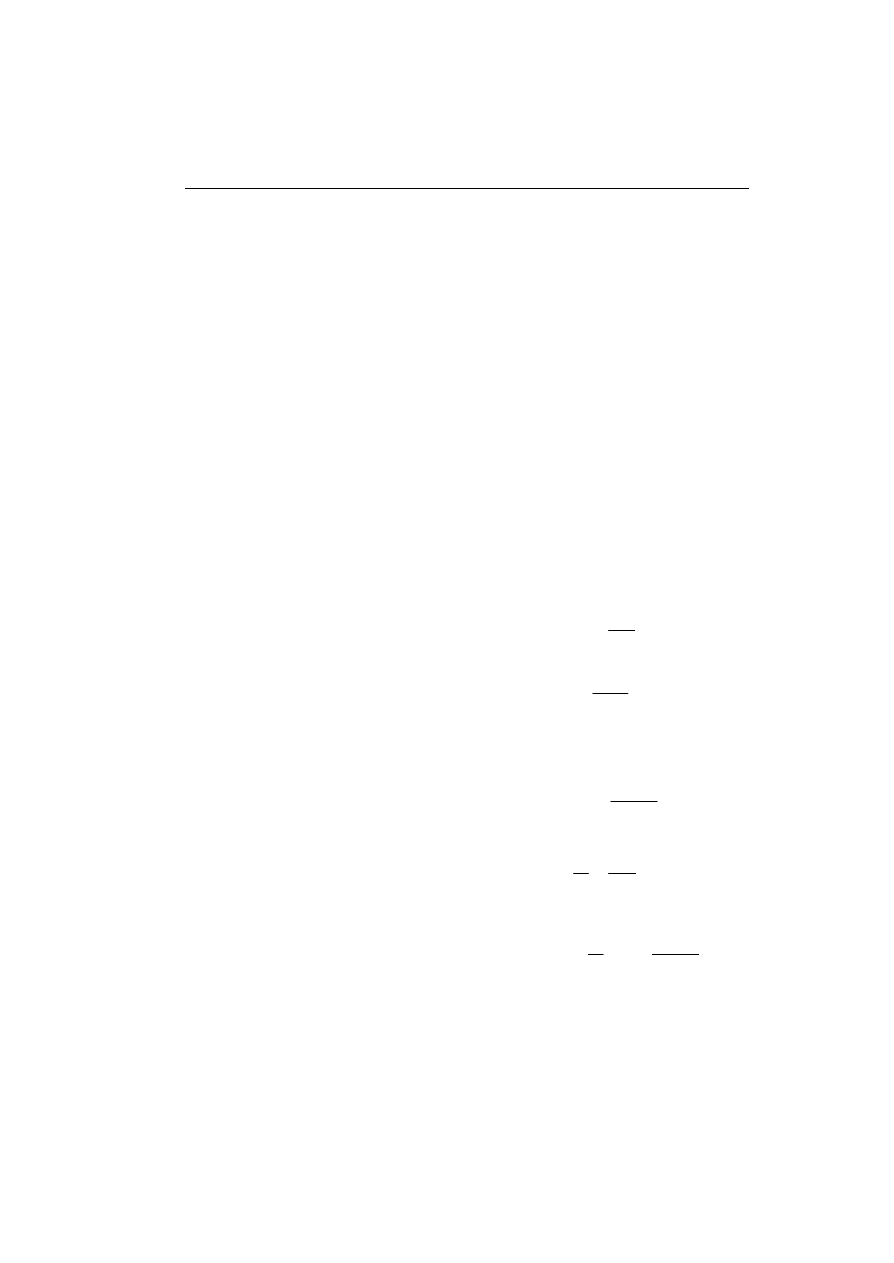
[ mm ]
Q
21000
:=
[N]
xw 4
:=
- obliczamy srednice :
Pkr
Q xw
⋅
:=
Pkr 8.4 10
4
×
=
[ N ]
σ
kr
Pkr
A
=
gdzie
A
π d
r
2
⋅
4
=
- ze wzoru Tetmajera-Jasinskiego :
σ
kr
a
b
λ
⋅
−
=
czyli po przeksztalceniach :
a
b
λ
⋅
−
4 Q
⋅
xw
⋅
π d
r
2
⋅
=
λ
lw
ix
=
4 lw
⋅
dr
=
a
4 b
⋅
lw
dr
⋅
−
4 Q
⋅
xw
π d
r
2
⋅
( )
⋅
=
- gdzie wspólczynniki dla stali St5 w równaniu Tetmajera
przyjmuje z tablic odpowiednio :
a
335
:=
a
335
:=
b
0.62
:=
b
0.62
:=
Projekt podnosnika srubowyego 1-stopniowego
.
Final version
Dane wyjsciowe
:
Q
21000
:=
[ N ]
H
115
:=
[ mm ]
Dane
:
Obliczenia :
Wyniki :
1. Obliczenia rdzenia sruby :
d
60
:=
[ mm ]
- zakladam wysokosc koronki + czesc na kolo zap. :
d
60
:=
[ mm ]
- dlugosc sruby z koronka :
l1
d
H
+
:=
l1 175
=
[ mm ]
- dlugosc wyboczeniowa :
lw 2 l1
⋅
:=
lw 350
=
-skok gwintu :
h1
5
:=
- pole przekroju rdzenia sruby :
Fr1
330.0636
:=
[ mm ]
- srednica nosna gwintu sruby :
ds1
d1 Do1
+
2
:=
ds1 23.5
=
[ mm ]
- kat wzniosu lini srubowej :
t
h1
π d
s1
⋅
:=
t
tan
γ
1
( )
=
t
0.068
=
czyli
γ
1
atan t
( )
180
π
⋅
:=
γ
1
3.874
=
- pozorny kat natarcia :
µ
0.1
:=
µ
- wspólczynnik tarcia miedzy sruba a nakretka przyjmuje
α
r
15
:=
µ
0.1
:=
a
α
r
15
:=
dla gwintu trapezowego symetrycznego
n
µ
α
π
⋅
:=
n
tan
ρ
( )
=
po przeksztalceniach otrzymujemy wzór na srednice rdzenia :
dr
1
2 a
π
⋅
( )
⋅
4 b
⋅
lw
⋅
π
⋅
4
π
⋅
b
2
lw
2
⋅
π
⋅
a Q
⋅
xw
⋅
+
⋅
+
⋅
:=
dr 19.21
=
[ mm ]
dr 19.21
=
[ mm ]
- sprawdzam smuklosc :
λ
lw
ix
=
λ
4 lw
⋅
dr
:=
λ 72.878
=
<
λ
gr
90
=
czyli korzystanie z wzoru Tetmajera bylo sluszne .
2. Dobór gwintu sruby :
Dla wyliczonej srednicy rdzenia sruby
dr 19.21
=
[ mm ]
dr1
20.5
:=
przyjmuje na podstawie PN-62/M-02017 gwint trapezowy symetryczny
Tr26x5 dla którego w [ mm ]:
[mm]
- srednica gwintu sruby :
- srednica gwintu nakretki :
- srednica rdenia sruby :
- srednica otworu nakretki:
d1
26
:=
D1
26.5
:=
dr1
20.5
:=
Do1
21
:=
D2
23.5
:=
- naprezenia skrecajace :
τ
Ms
W0
:=
τ 2.47 10
7
×
=
[Pa]
- naprezenia sciskajace :
σ
c
4 Q
⋅
π d
r1 10
3
−
⋅
(
)
2
⋅
:=
σ
c
6.362
10
7
×
=
[Pa]
- naprezenia zastepcze :
σ
z
σ
c
2
3
τ
2
⋅
+
:=
σ
z
7.667
10
7
×
=
[Pa]
- dla stali St5 kcj=100 MPa>
σ
z=76.67 MPa czyli srube dobrano prawidlowo.
4. Obliczenia dla parametrów nakretki :
Na material nakretki przyjmuje mosiadz MA58 dla którego :
pdop 12
:=
pdop 12
:=
[MPa]
[MPa]
a) obliczenia wysokosci nakretki :
- powierzchnia styku gwintów :
F
π
4
d1
2
Do1
2
+
(
)
⋅
i
⋅
=
cos
α
r
π
180
⋅
n
0.104
=
ρ
atan n
( )
180
π
⋅
:=
ρ
5.911
=
Samohamownosc gwintu jest wiec zapewniona gdyz :
γ
=3.874 <
ρ
=5.911 .
- Sprawnosc gwintu :
η
tan
γ
1
π
180
⋅
tan
γ
1
ρ
+
(
)
π
180
⋅
:=
η
0.393
=
D2 23.5
=
3. Sprawdzenie sruby na naprezenia zlozone :
[mm]
- moment skrecajacy :
Q
2.1
10
4
×
=
Ms
0.5 Q
⋅
D2
⋅
10
3
−
⋅
tan
γ
1
ρ
+
(
)
π
180
⋅
⋅
:=
Ms 42.555
=
[N*m]
[N]
dr1 20.5
=
- wskaznik wytrzymalosci przekroju na skrecanie :
[mm]
W0
0.2 dr1 10
3
−
⋅
(
)
3
⋅
:=
W0 1.723 10
6
−
×
=
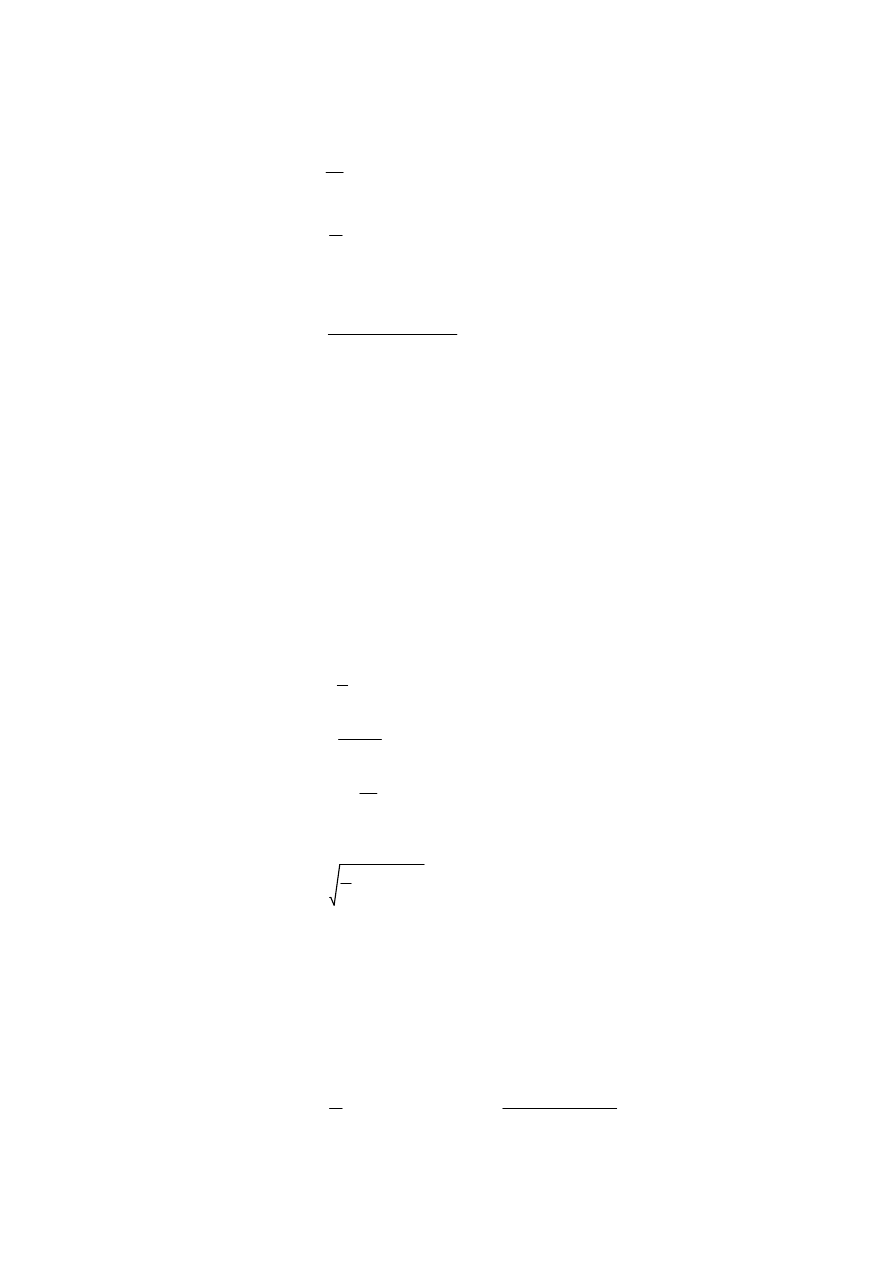
[N/mm]
En
0.9 10
5
⋅
:=
Fn
π
4
Dz1
2
Dw1
2
−
(
)
⋅
=
[N/mm]
Fr
π d
r1
2
⋅
4
:=
Fn
Fr
Es
En
⋅
:=
Fn 770.148
=
[mm]
Dw1
D1
:=
Dz1
4
π
Fn
⋅
Dw1
2
+
:=
Dz1 41.022
=
czyli przyjmuje bezpieczniejsza srednice :
Dz1
42
:=
[mm]
I srednice wewnetrzna w korpusie:
Dzw1
35
:=
[mm]
- z warunku nacisków miedzy nakretka a dnem gniazda:
Q
2.1
10
4
×
=
p
Q
F
=
czyli :
p
4 Q
⋅
π D
z1
2
Dzw1
2
−
(
)
⋅
:=
p
49.607
=
[N]
4
1
o1
(
)
i
H
h1
=
- liczba zwojów gwintu
p
Q
F
=
pdop
≤
- warunek na naciski powierzchniowe
- liczba zwojów gwintu :
i
4 Q
⋅
π d
1
2
Do1
2
−
(
)
⋅
pdop
⋅
:=
i
9.482
=
i
9.482
=
- czyli wysokosc nakretki :
teoretyczna :
Ht
i
1.5
+
(
) h1
⋅
:=
Ht 54.908
=
[ mm ]
praktyczna :
Hn1
55
:=
[ mm ]
b) Obliczenia srednicy zewnetrznej :
- z warunku na równosc odksztalcen :
Es
2.1 10
5
⋅
:=
Es
2.1 10
5
⋅
:=
[N/mm]
En
0.9 10
5
⋅
:=
[N/mm]
δ
z
2.125
=
δ
w
∆W
2
1
+
∆W
2
1
−
:=
δ
w
2.243
=
c
1
δ
z
ν
z
+
Es
δ
w
ν
w
−
En
+
:=
c
3.08
10
4
×
=
P
11.169
:=
Wcisk skuteczny W:
W
P Dz1
⋅
c
:=
W
0.015
=
Wcisk mierzony:
Wm W 1.2 0.006 0.0032
+
(
)
⋅
+
:=
Wm 0.026
=
[ mm ]
Przyjmuje pasowanie wg. stalego otworu H7:
ES
0.025
:=
ei
Wm ES
+
:=
ei
0.051
=
[ mm ]
EI
0
:=
Z PN-EN 20286-2 przyjmuje pasowanie:
φ 42H7/u6
ei
70
:=
es
85
:=
z1
zw1
(
)
pdop 95
=
[Pa]
dla mosiadzu MA58:
pdop kc
=
pdop 95
:=
[Pa]
Warunek zostal spelniony p<pdop
c) Obliczanie wcisku:
nacisk powierzchniowy:
k
2
:=
µ
0.05
:=
P
2 k
⋅
Ms
⋅
1000
⋅
µ π
⋅
Dz1
2
⋅
Hn1
⋅
:=
P
11.169
=
[ MPa ]
Dzc
70
:=
wcisk skuteczny:
ν
z
0.3
:=
∆Z
Dzc
Dz1
:=
∆Z 1.667
=
ν
w
0.36
:=
∆W
Dz1
d1
:=
∆W 1.615
=
δ
z
∆Z
2
1
+
∆Z
2
1
−
:=
dwk
7
:=
Fwk
π
Dwk
2
dwk
2
−
4
⋅
:=
Fwk 577.268
=
[mm]
[mm]
p
Q
Fwk
:=
p
36.378
=
[Pa]
p
pdop
≤
pj
=
7.Obliczenie przegubu kulistego w koronie :
ν
1
0.25
:=
E1
2.1 10
5
⋅
:=
[N/mm]
- dla St 5
ν
2
0.23
:=
E2
1.1 10
5
⋅
:=
[N/mm]
- dla brazu BK31
Przyjmuje promienie dla sruby i wkladki:
r
100
:=
R
100.08
:=
w/g wzoru Hertza :
k
1
ν
1
2
−
E1
1
ν
2
2
−
E2
+
:=
k
1.307
10
5
−
×
=
p
1
π
6
R
r
−
(
)
2
r
2
R
2
⋅
k
2
⋅
⋅
Q
⋅
1
3
⋅
:=
p
11.495
=
[N/mm]
kgj 165
:=
5. Obliczanie kolnierza oporowego sruby:
[N/mm]
- material St5 :
kgj 165
:=
[N/mm]
dr1 20.5
=
- srednice zewnetrzna przyjmuje :
Dkl
50
:=
[mm]
[mm]
Mgk
Q
Dkl dr1
−
2
⋅
0.5
⋅
:=
Mgk 1.549
×
=
[N*mm]
Wx
Mgk
kgj
=
π d
r1
⋅
hk
2
⋅
6
=
skad :
hk
6 Mgk
⋅
kgj π
⋅
dr1
⋅
:=
hk 9.351
=
[mm]
przyjmuje :
hk
10
:=
[mm]
pj 63
:=
6. Obliczanie korony podnosnika :
[MPa]
- przyjmuje material stal 35 w stanie ulepszonym :
Dwk
28
:=
[mm]
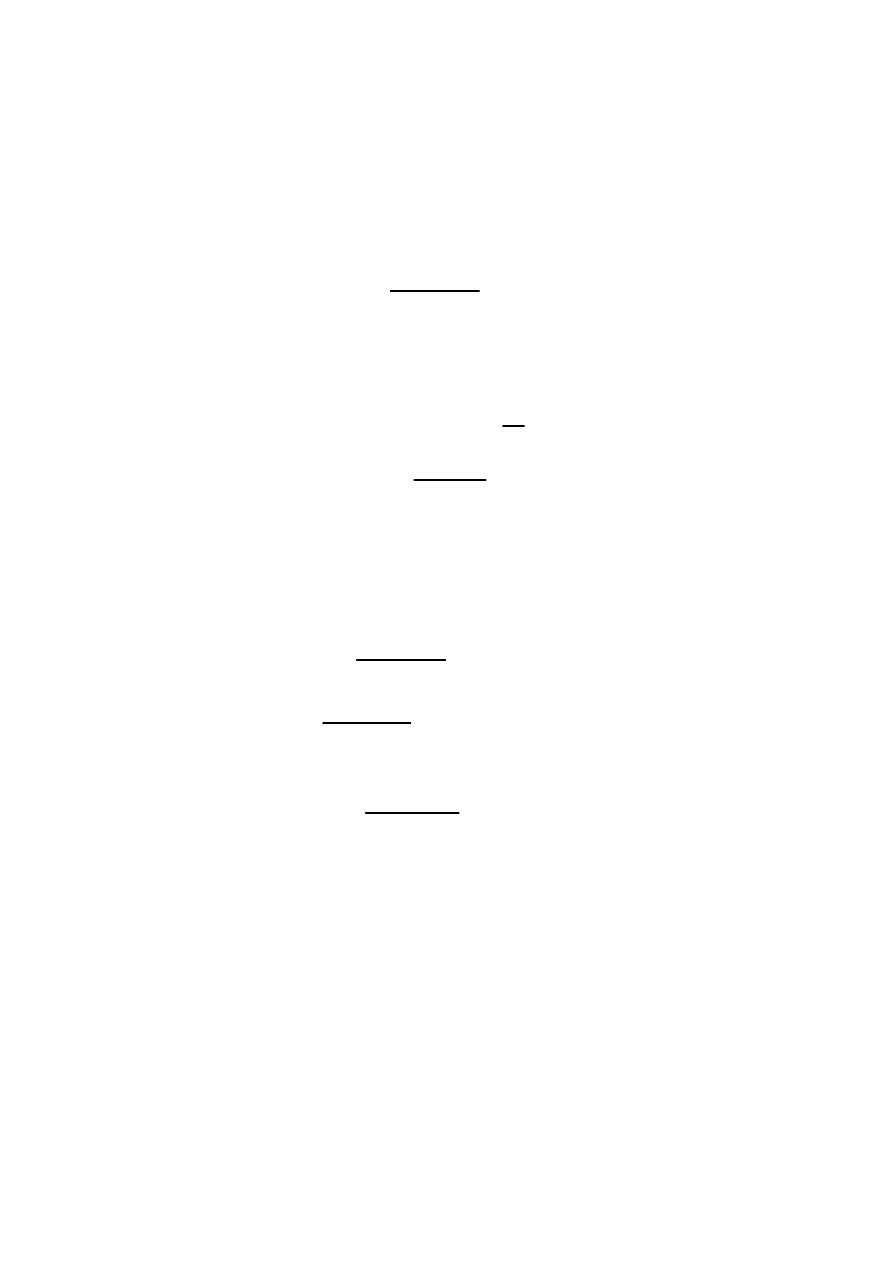
a
dz
52
:=
[mm]
Pz1
Mmax
0.25 dz dw
+
(
)
⋅
:=
Pz1 2.112 10
3
×
=
[N]
2Pz1
dz dw
−
(
)
hkz
⋅
Pdop
≤
Pdop 70
:=
[ MPa ]
Wyliczamy z tego wysokosc kola zebatego hkz:
hkz
2 Pz1
⋅
dz dw
−
(
)
Pdop
⋅
:=
hkz 10.056
=
[mm]
Zakladam material na kolo St5 dla którego przyjmuje Pdop=70MPa -
zmniejszony ze wzgledu na niedokladne przyleganie zapadki do kola.
Ostatecznie do konstrukcji przyjmuje:
kkz
12
:=
[mm]
- Obliczenia wpustów:
Dla srednicy
Dwk 28
=
przyjmuje 2 wpusty pryzmatyczne wg.
PN-70/M-85005 dla których:
n
2
:=
kcj 80
:=
[ MPa ]
Pdop 64
:=
[ MPa ]
b
8
:=
h
7
:=
Sila obwodowa na powierzchni styku czopa i kala zapadkowego:
Mmax
3
π
r R
⋅
k
⋅
p
pdop
≤
12
=
[N/mm]
Dwk 28
=
[mm]
8. Obliczenia mechanizmu zapadkowego:
Saila dzialajaca na zab kola zapadkowego:
dwk 7
=
[mm]
Q
21000
:=
[N]
Pz1
Mmax
0.25 dz dw
+
(
)
⋅
=
µ 0.05
=
γ
3.874
:=
Gdzie:
D2 23.5
=
[mm]
dw 46
:=
Zakladam ze:
[N]
Mmax 5.174 10
4
×
=
Mmax
Ms2
Mtk
+
(
)
:=
[N]
Mtk 9.188 10
3
×
=
Mtk
0.5 Q
⋅
µ
⋅
Dwk dwk
+
2
⋅
:=
[N]
Ms2 4.255 10
4
×
=
Ms2
0.5 Q
⋅
D2
⋅
tan
γ
ρ
+
(
)
π
180
⋅
⋅
:=
ρ
5.911
=
a
Mmax Ms2
Mtk
+
=
[mm]
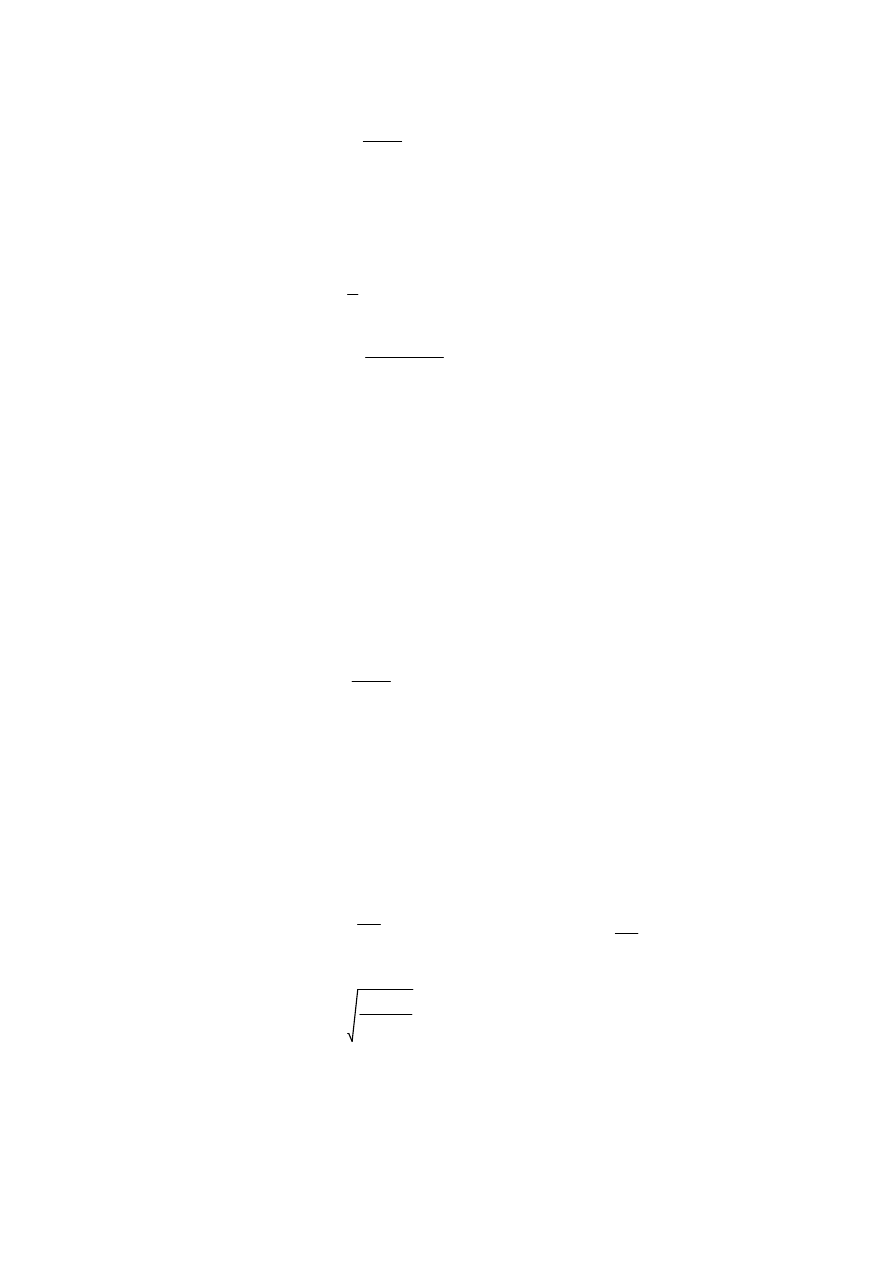
R
Mmax
Pr
:=
R
206.962
=
Do dalszych obliczen przyjmuje ramie R o dlugosci R=250 mm
R
250
:=
[ mm ]
-Obliczenia srednicy draga:
Na drag przyjmuje materaial St7 dla którego:
kgj 140
:=
[ MPa ]
Z warunków na zginanie mamy:
σ
g
Mg
Wx
=
kgj
≤
gdzie:
Wx
πd
3
32
:=
czyli :
d
3
32 Pr
⋅
R
⋅
π k
gj
⋅
:=
d
16.567
=
Ostatecznie przyjmuje wiec srednice draga na 18 mm
KONIEC
P
2
Mmax
Dwk
⋅
:=
P
3.696
10
3
×
=
F
0.5 lwp
⋅
h
⋅
n
⋅
=
lwp - dlugosc wpustu
poniewaz:
p
P
F
=
Pdop
≤
to:
lwp 2
Mmax
h Pdop
⋅
Dwk
⋅
⋅
:=
lwp 8.249
=
Ostatecznie dobieram dwa wpusty: B 8x7x10
-Obliczenia dlugosci draga:
Pr
250
:=
[ N ]
Zakladam sile reki pracownika
Pr 250
≤
[ N ]
Dlugosc ramienia bedzie wiec: