Dr inż. Janusz Dębiński

1

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.1. Zasada zesztywnienia

Rzeczywiste kratownice płaskie są zbudowane z prętów, które pod wpływem obciążenia zmieniają

swój kształt oraz wymiary.

Jednak badania tych konstrukcji udowodniły, że zmiany te są małe w porównaniu

z wymiarami kratownic płaskich.

Spostrzeżenie to pozwala nam wprowadzić zasadę zesztywnienia. Mówi ona, że reakcje na

podporach oraz siły przekrojowe w prętach kratownicy płaskiej obliczamy

dla kratownicy nieodkształconej. Pozwala to znacznie uprościć obliczenia.

Dr inż. Janusz Dębiński

2

6. Wyznaczanie sił normalnych w kratownicach płaskich

P

1

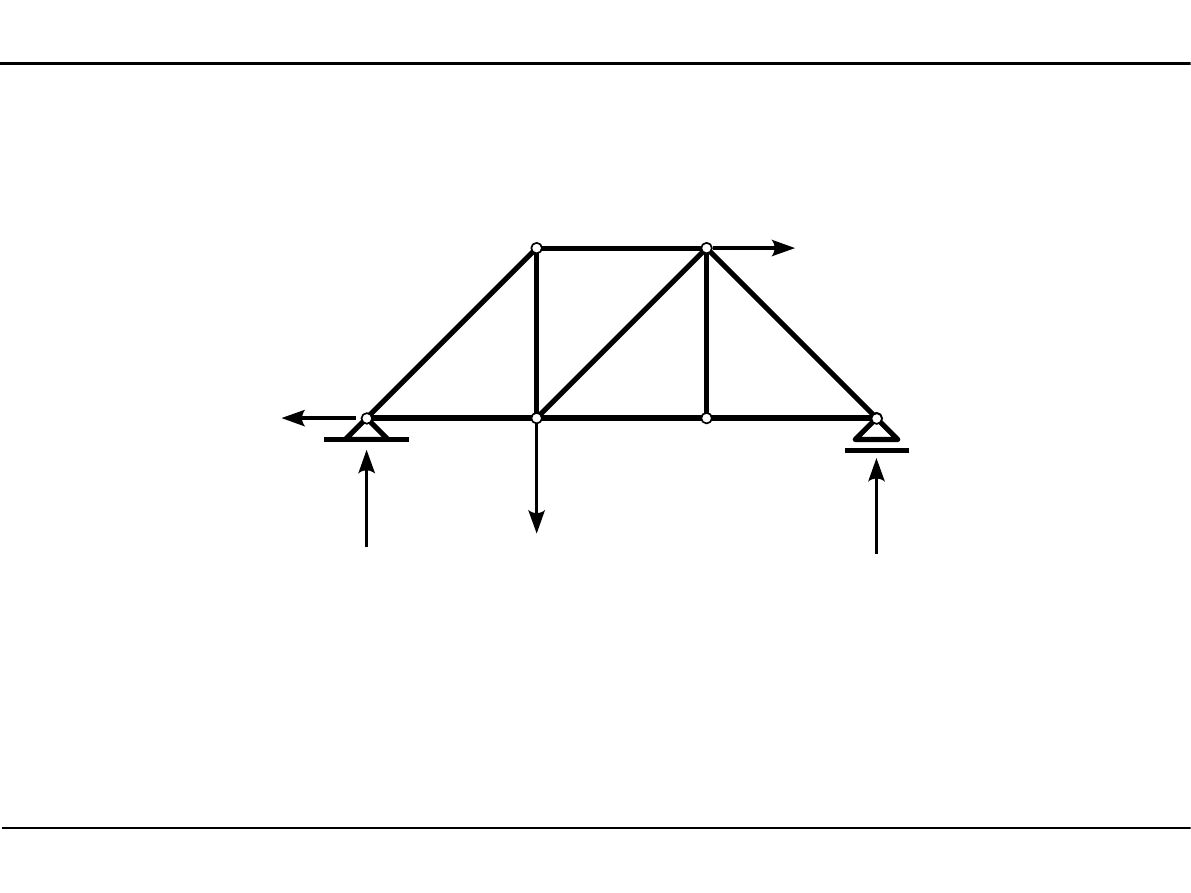
6.2. Siła normalna w kratownicy płaskiej

1

2

3

4

5

6

1

2

3

4

5

6

7

8

9

P

2

V

1

H

1

V

6

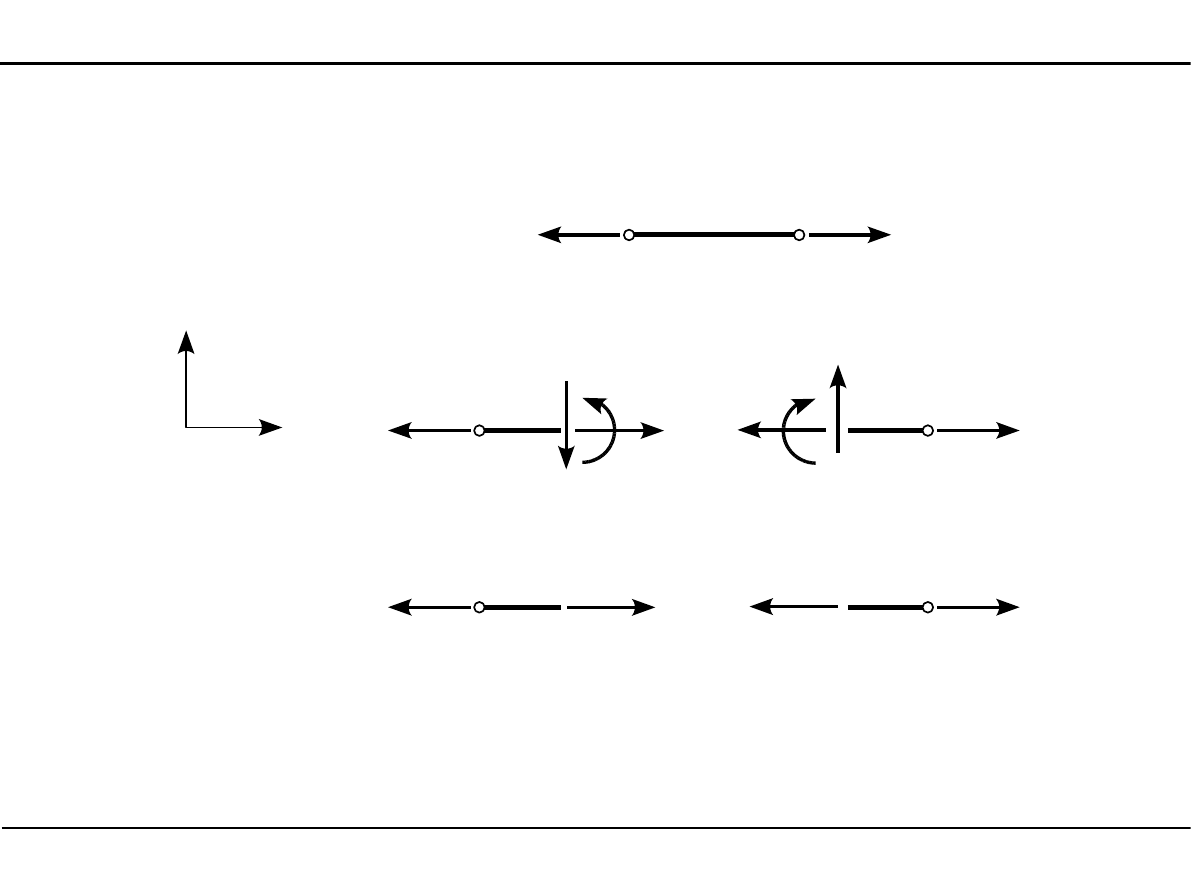
Dr inż. Janusz Dębiński

3

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.2. Siła normalna w kratownicy płaskiej

3

5

2

Aby pręt kratownicy płaskiej był w równowadze, muszą na niego działać dwie siły o tych samych

wartościach i kierunkach ale przeciwnych zwrotach.

S

S

3

5

S

S

N

T

M

N

T

M

X

Y

3

5

S

S

N

N

W prętach kratownicy płaskiej działają tylko siły normalne.

Dr inż. Janusz Dębiński

4

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.3. Metoda zrównoważenia węzłów

Dla kratownicy płaskiej o strukturze prostej zbudowanej z w węzłów podstawowa

procedura składa się z następujących kroków:

1. sprawdzenie warunku koniecznego i dostatecznych geometrycznej niezmienności

2. wyznaczyć wartości reakcji traktując kratownicę płaską jako płaski układ tarcz sztywnych,

a następnie sprawdzić je (na początku obliczeń założyć zwroty reakcji, jeżeli otrzymamy

reakcję dodatnią - ma ona zwrot założony, jeżeli ujemną - ma ona zwrot przeciwny

do założonego)

3. zaczynając od węzła, w którym schodzą się tylko dwa pręty kratownicy wyznaczyć siły

normalne w tych prętach (przyjąć na początku siły normalne we wszystkich węzłach

jako dodatnie czyli rozciągające)

4. znaleźć kolejne węzły, w których nie znamy tylko wartości sił normalnych w dwóch

prętach i wyznaczyć je

5. jedno z równań równowagi w węźle przedostatnim oraz oba równania w węźle ostatnim służą

nam do sprawdzenia poprawności obliczeń.

Dr inż. Janusz Dębiński

5

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.4. Metoda Rittera

Jest to metoda, dzięki której da się wyznaczyć siłę normalną w jednym ściśle określonym

pręcie kratownicy płaskiej. Aby ją zastosować musimy wykonać następujące kroki:

1. sprawdzić warunek konieczny i dostateczne geometrycznej niezmienności

2. wyznaczyć wartości reakcji traktując kratownicę płaską jako płaski układ tarcz sztywnych,

a następnie sprawdzić je (na początku obliczeń założyć zwroty reakcji, jeżeli otrzymamy

reakcję dodatnią - ma ona zwrot założony, jeżeli ujemną - ma ona zwrot przeciwny

do założonego)

3. przeciąć kratownicę płaską maksymalnie przez trzy pręty, w których nie znamy sił normalnych

(założyć dodatnie czyli rozciągające siły normalne)

4. z odpowiedniego równania równowagi wyznaczyć nieznaną siłę normalną w pręcie kratownicy.

Dr inż. Janusz Dębiński

6

6. Wyznaczanie sił normalnych w kratownicach płaskich

P

2

P

1

6.4. Metoda Rittera

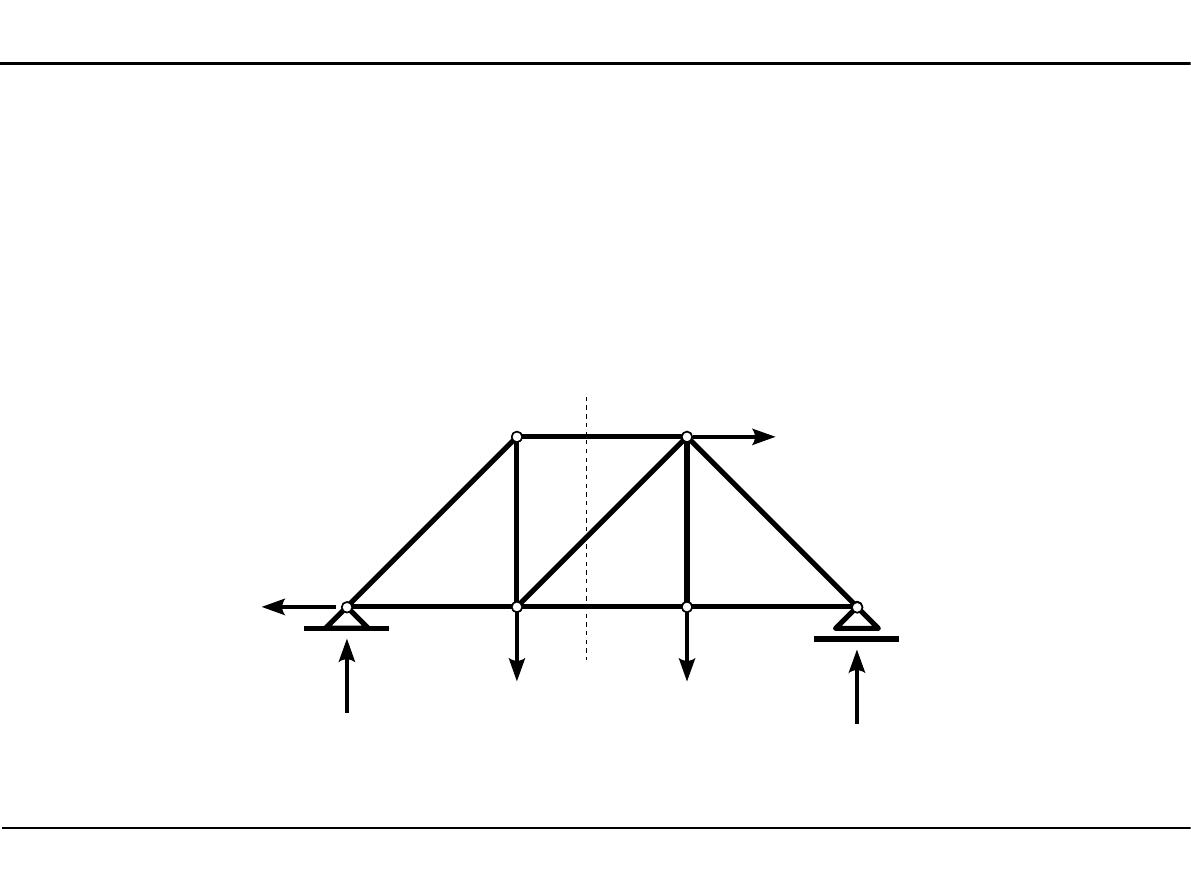
W większości przypadków tym odpowiednim równaniem równowagi jest równanie sumy

momentów wszystkich sił działających na odciętą część kratownicy płaskiej względem punktu,

który nazywamy punktem Rittera.

Jeżeli przecinamy kratownicę przez trzy pręty, to punktem Rittera dla jednego z nich jest

punkt przecięcia się kierunków pozostałych dwóch prętów.

P

3

V

1

H

1

V

6

G

D

K

α

α

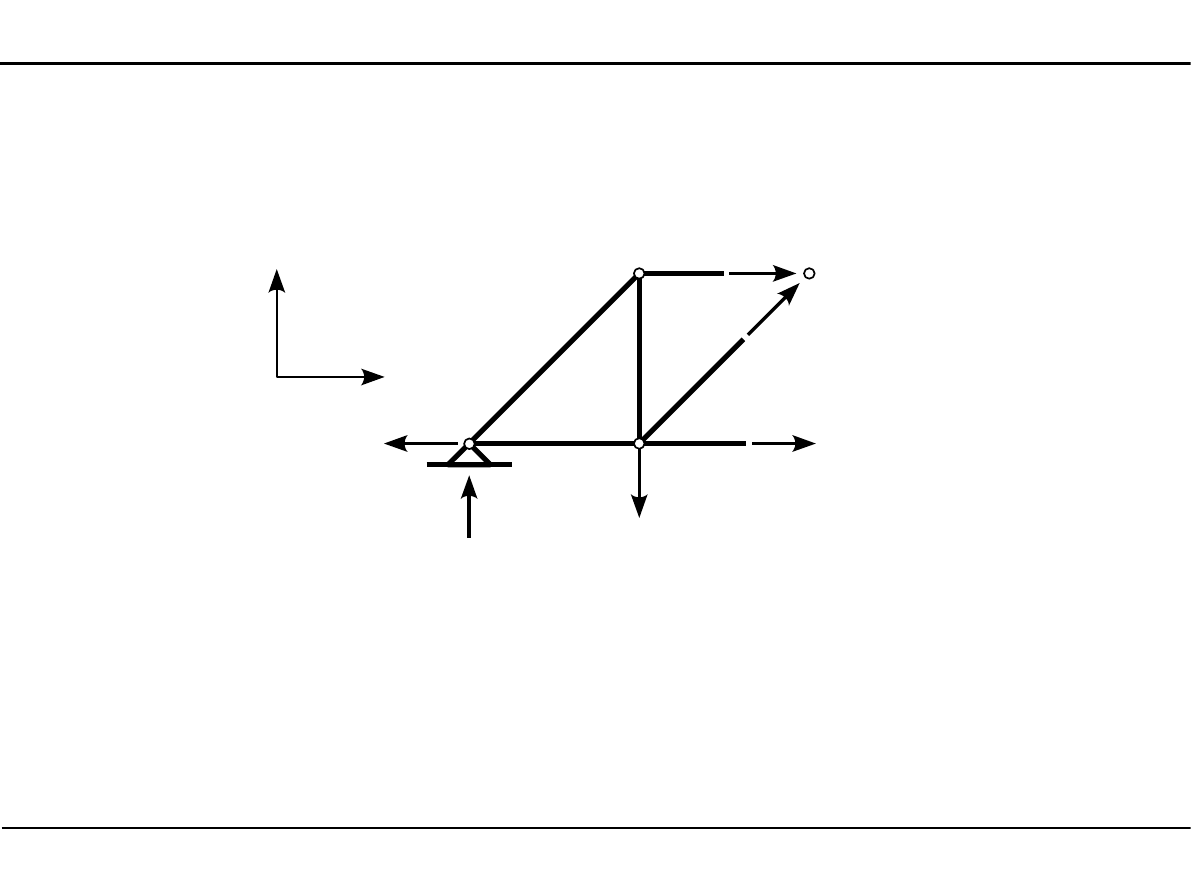
Dr inż. Janusz Dębiński

7

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.4. Metoda Rittera

P

1

H

1

V

1

G

N

G

D

N

D

K

N

K

R

G



M

RG

=

0

R

D



M

RD

=

0

X

Y



Y =0

Dr inż. Janusz Dębiński

8

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.5. Pręty zerowe

Prętem zerowym nazywamy pręt, w którym przy danej konfiguracji obciążenia czynnego oraz

reakcji, siła normalna wynosi zero.

Nie oznacza to jednak, że pręt ten jest niepotrzebny. Nie możemy go usunąć, ponieważ

wtedy nie byłyby spełniony warunek konieczny geometrycznej niezmienności,

więc kratownica byłaby geometrycznie zmienna.

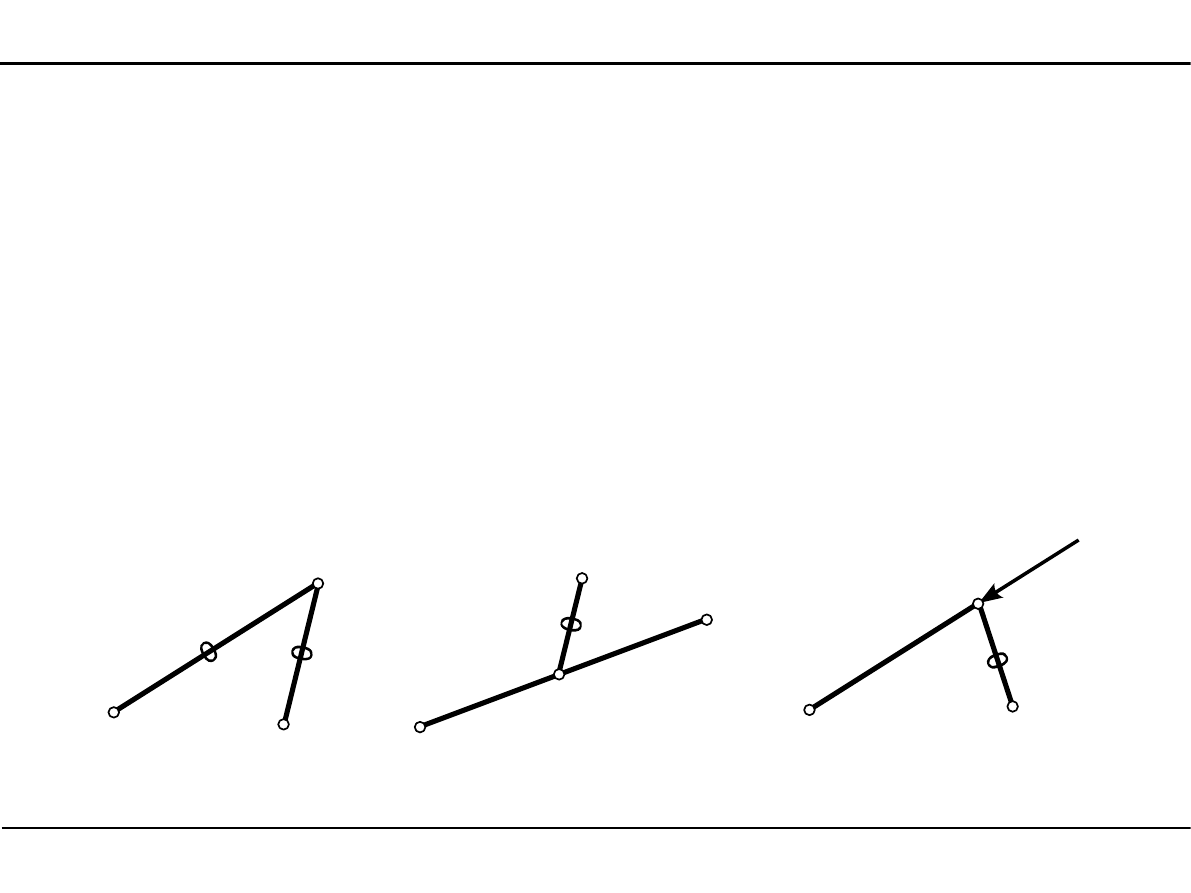
Dr inż. Janusz Dębiński

9

6. Wyznaczanie sił normalnych w kratownicach płaskich

P

6.5. Pręty zerowe

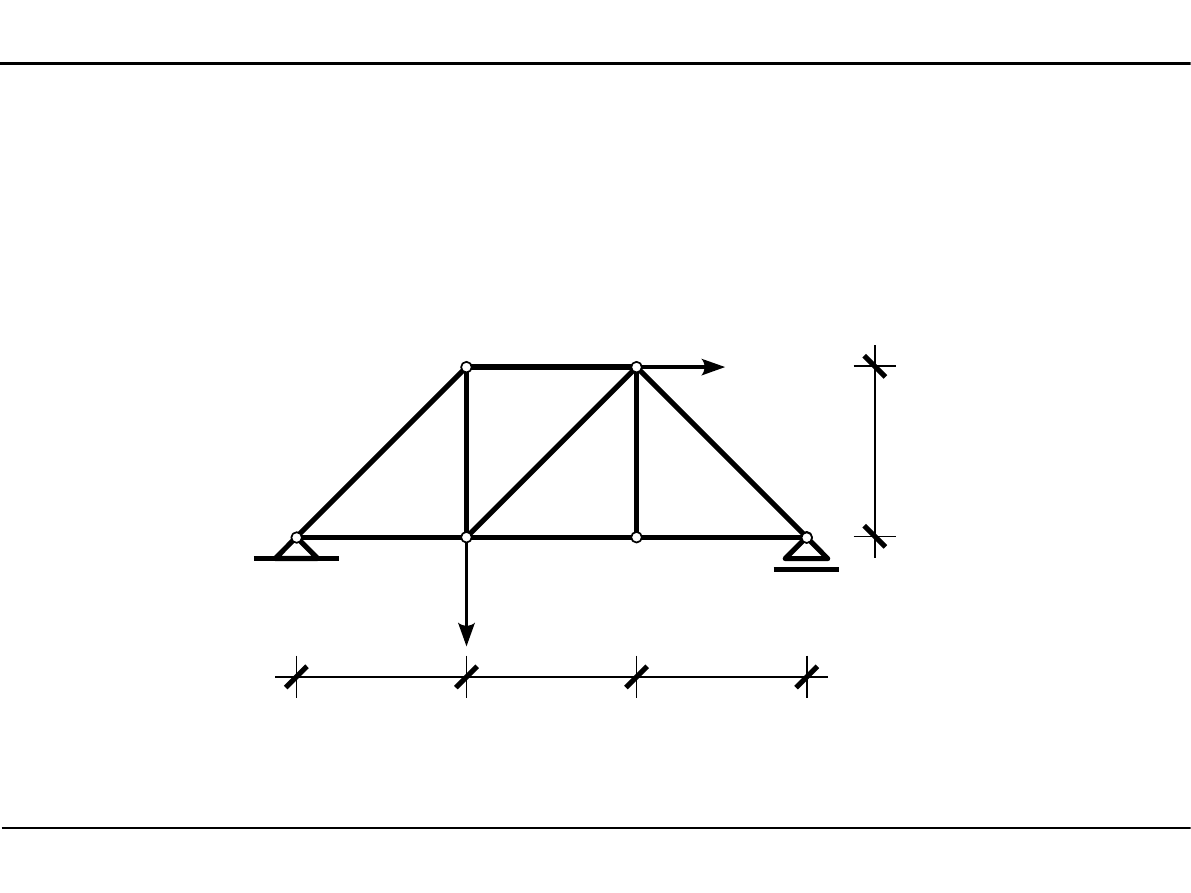
Jeżeli w nieobciążonym węźle spotykają się dwa pręty, to oba są prętami zerowymi.

Jeżeli w nieobciążonym węźle spotykają się trzy pręty i dwa z nich leżą na jednej prostej,

to trzeci z nich jest prętem zerowym

Jeżeli w obciążonym węźle spotykają się dwa pręty i siła czynna lub reakcja ma kierunek

jednego z prętów, to drugi jest prętem zerowym.

Dr inż. Janusz Dębiński

10

6. Wyznaczanie sił normalnych w kratownicach płaskich

98,0 kN

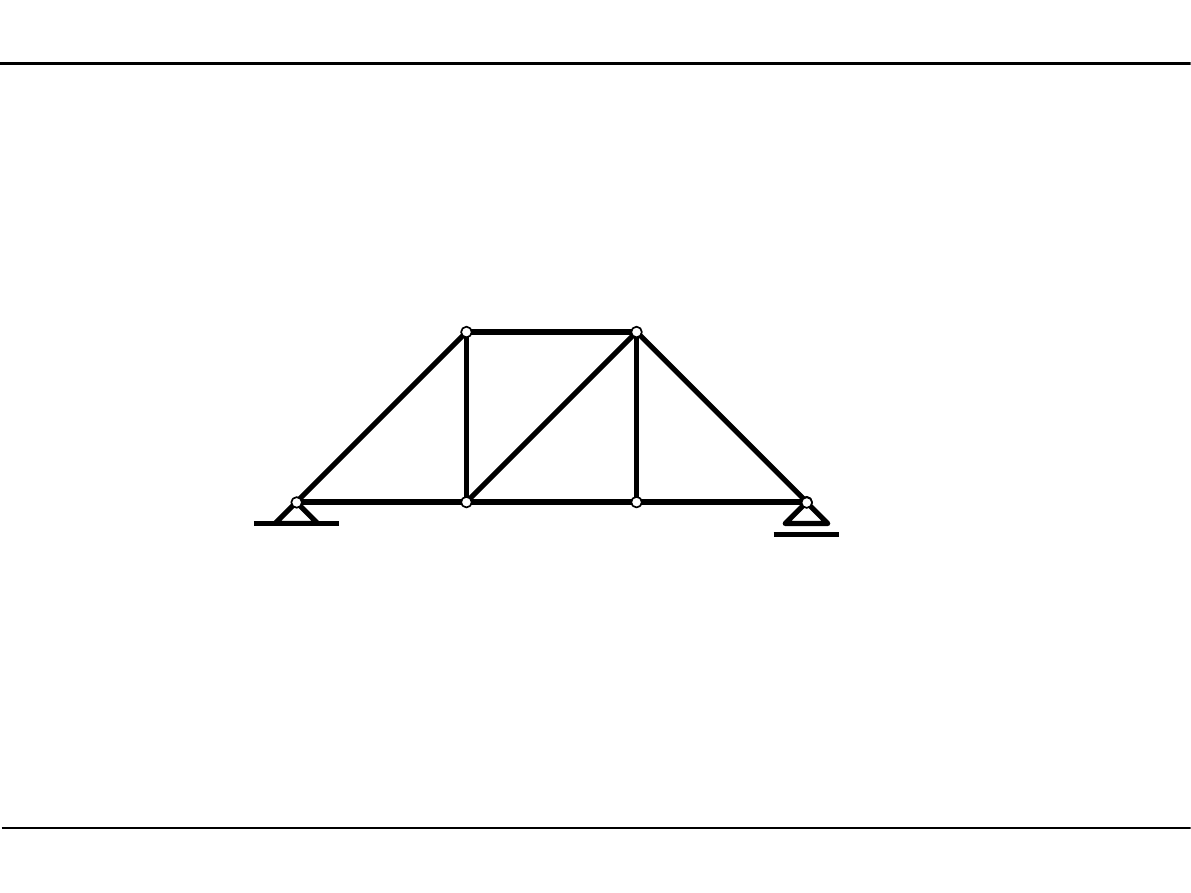
6.6. Zadanie 1

Metodą zrównoważenia węzłów wyznaczyć siły normalne we wszystkich prętach kratownicy

płaskiej.

Metodą Rittera wyznaczyć siły normalne w prętach numer 2, 4 i 8.

1

2

3

4

5

6

1

2

3

4

5

6

7

8

9

62,0 kN

[m]

4,0

4,0

4,0

3,

7

Dr inż. Janusz Dębiński

11

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.6. Zadanie 1

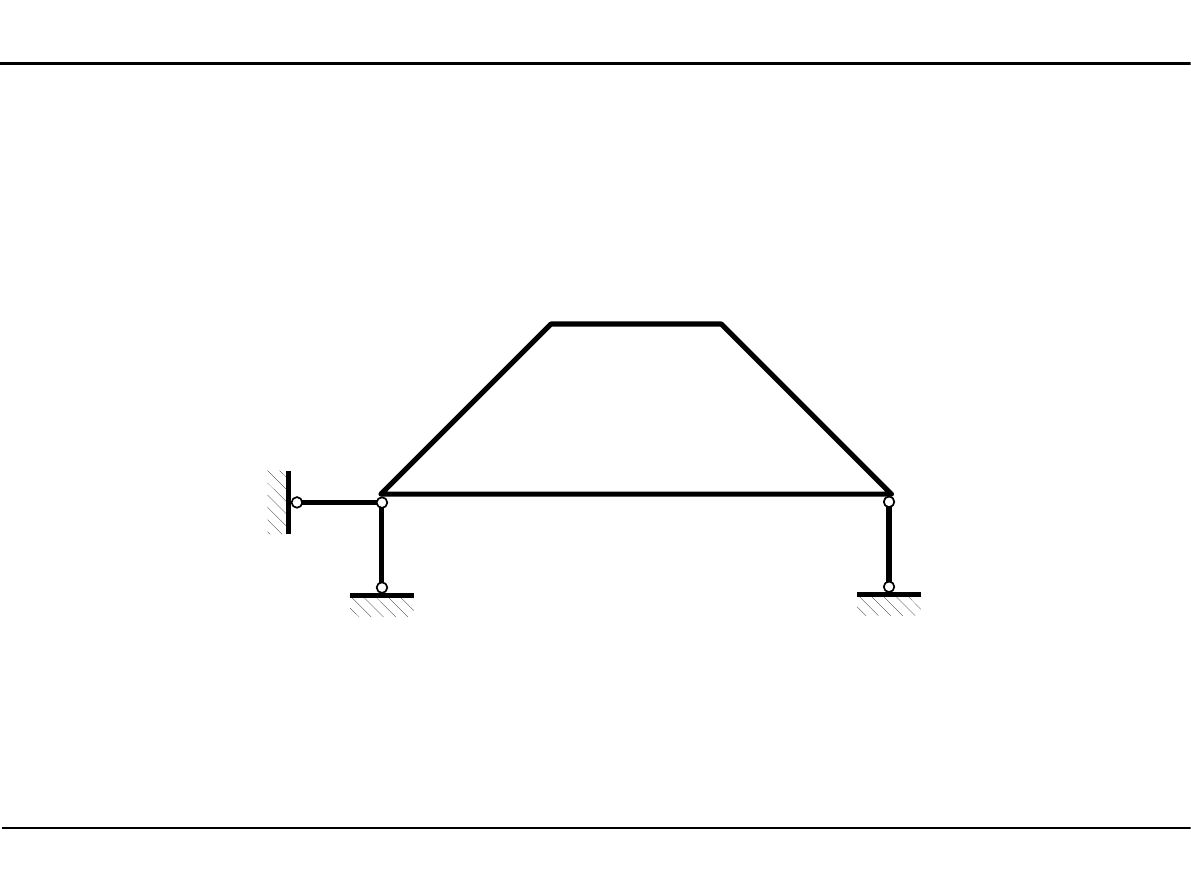
Analiza kinematyczna

Warunek konieczny geometrycznej niezmienności

1

2

3

4

5

6

1

2

3

4

5

6

7

8

9

w = 6

p = 9

r = 3

2∙6 = 9 + 3

Warunek konieczny geometrycznej niezmienności został spełniony.

Dr inż. Janusz Dębiński

12

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.6. Zadanie 1

Analiza kinematyczna

Warunek dostateczny geometrycznej niezmienności

I

1

2

3

Kierunki trzech prętów podporowych nie przecinają się w jednym punkcie.

Kratownica płaska - geometrycznie niezmienna.

Dr inż. Janusz Dębiński

13

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.6. Zadanie 1

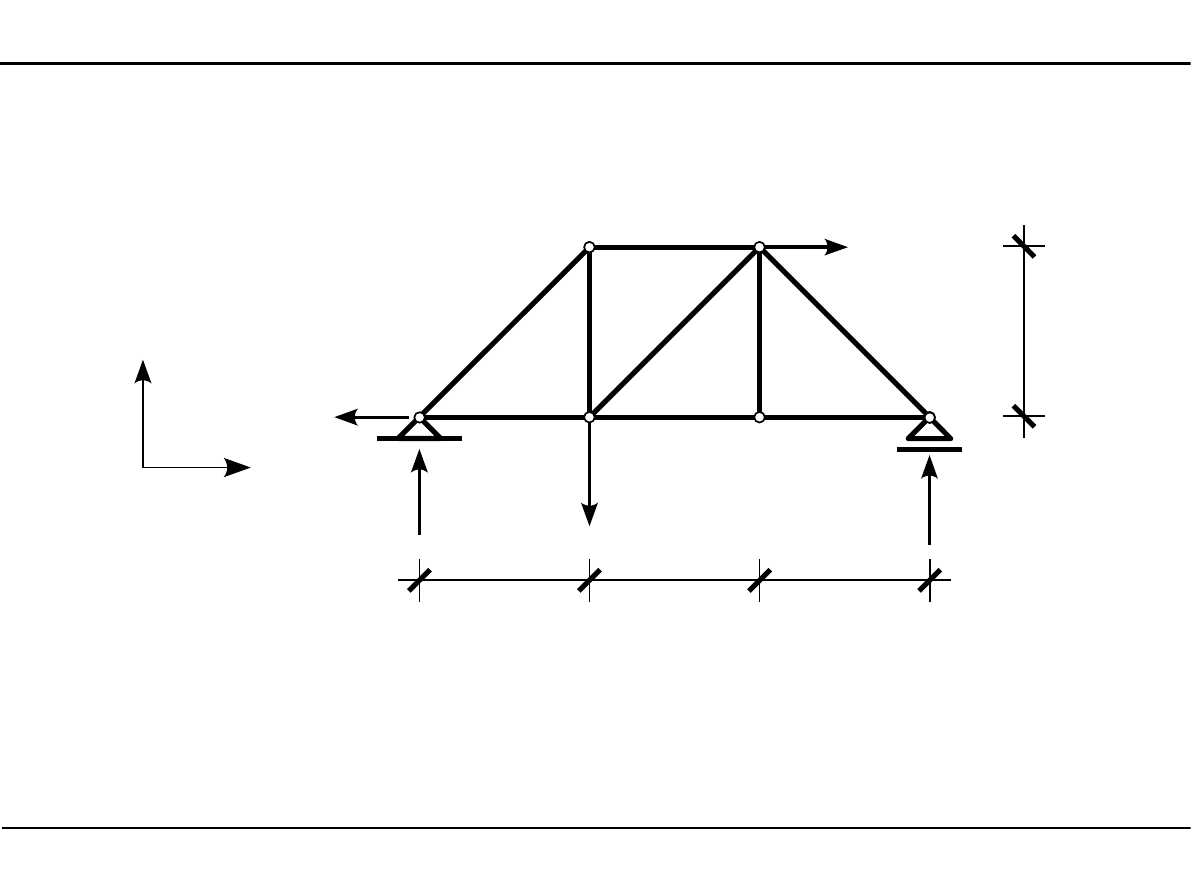
Wyznaczenie reakcji

1

2

3

4

5

6

1

2

3

4

5

6

7

8

9

4,0

4,0

4,0

[m]

3,

7

98,0 kN

62,0 kN

V

1

H

1

V

6

X

Y



X =0

−

H

1



62,0=0

H

1

=

62,0 kN

Dr inż. Janusz Dębiński

14

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.6. Zadanie 1

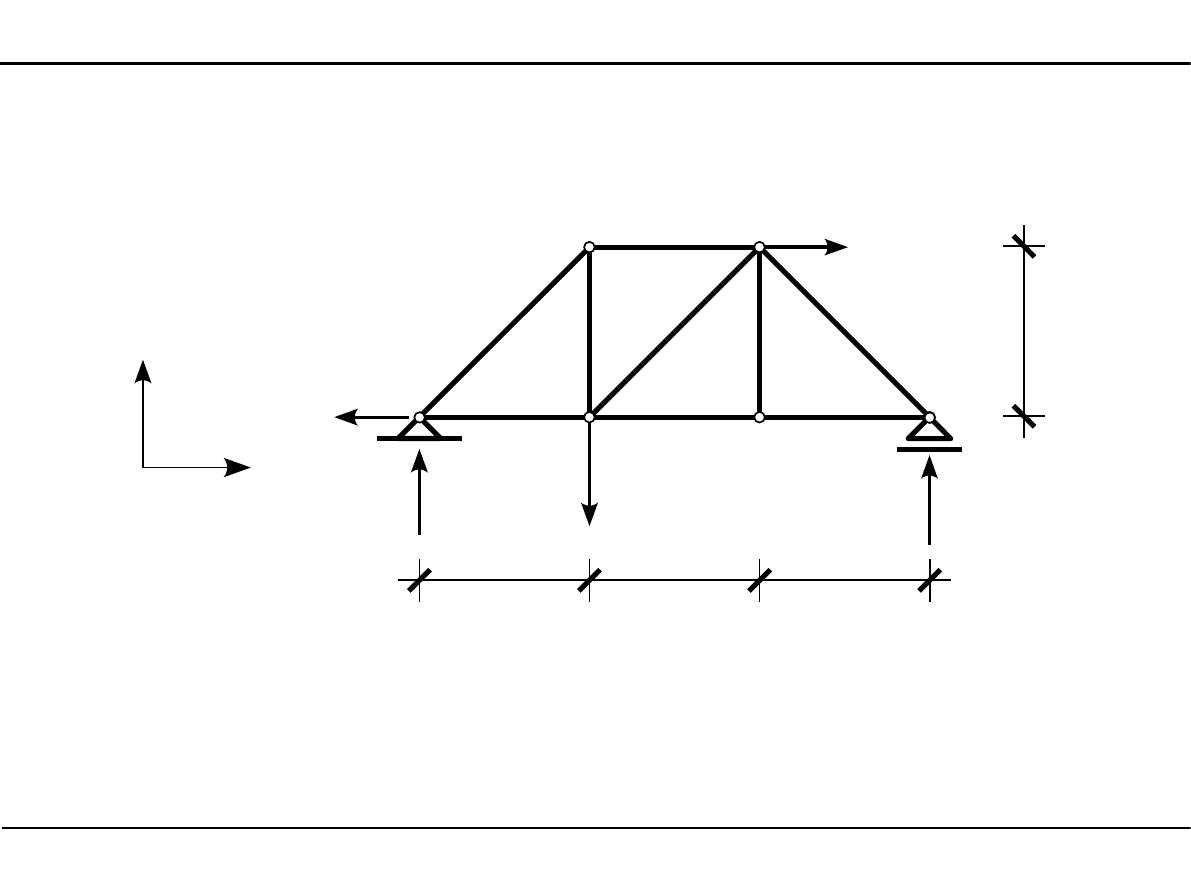
Wyznaczenie reakcji

1

2

3

4

5

6

X

Y

1

2

3

4

5

6

7

8

9

4,0

4,0

4,0

[m]

3,

7

98,0 kN

62,0 kN

V

1

H

1

V

6



M

6

=

0

V

1

⋅

12,0−98,0⋅8,062,0⋅3,7=0

V

1

=

46,22 kN

Dr inż. Janusz Dębiński

15

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.6. Zadanie 1

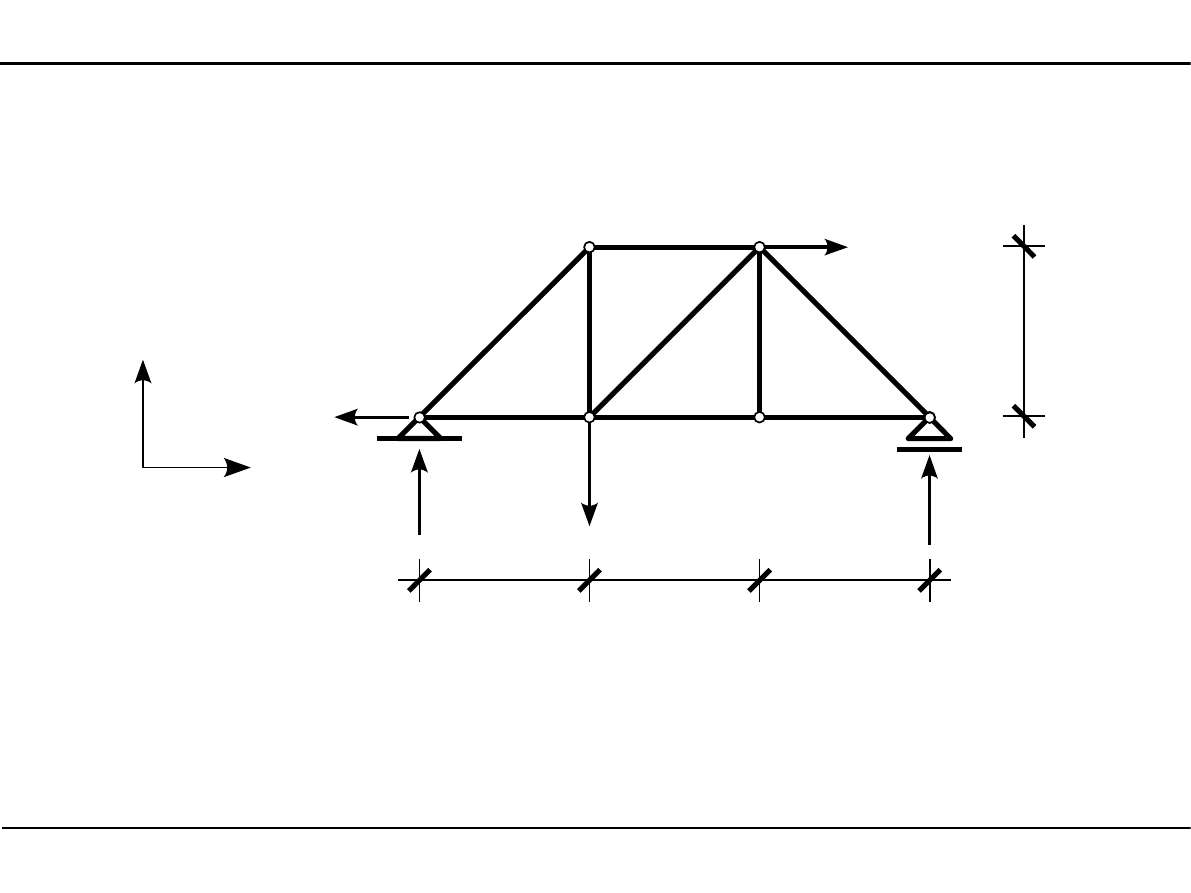
Wyznaczenie reakcji

1

2

3

4

5

6

X

Y

1

2

3

4

5

6

7

8

9

4,0

4,0

4,0

[m]

3,

7

98,0 kN

62,0 kN

V

1

H

1

V

6



M

1

=

0

−

V

6

⋅

12,098,0⋅4,062,0⋅3,7=0

V

6

=

51,78 kN

Dr inż. Janusz Dębiński

16

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.6. Zadanie 1

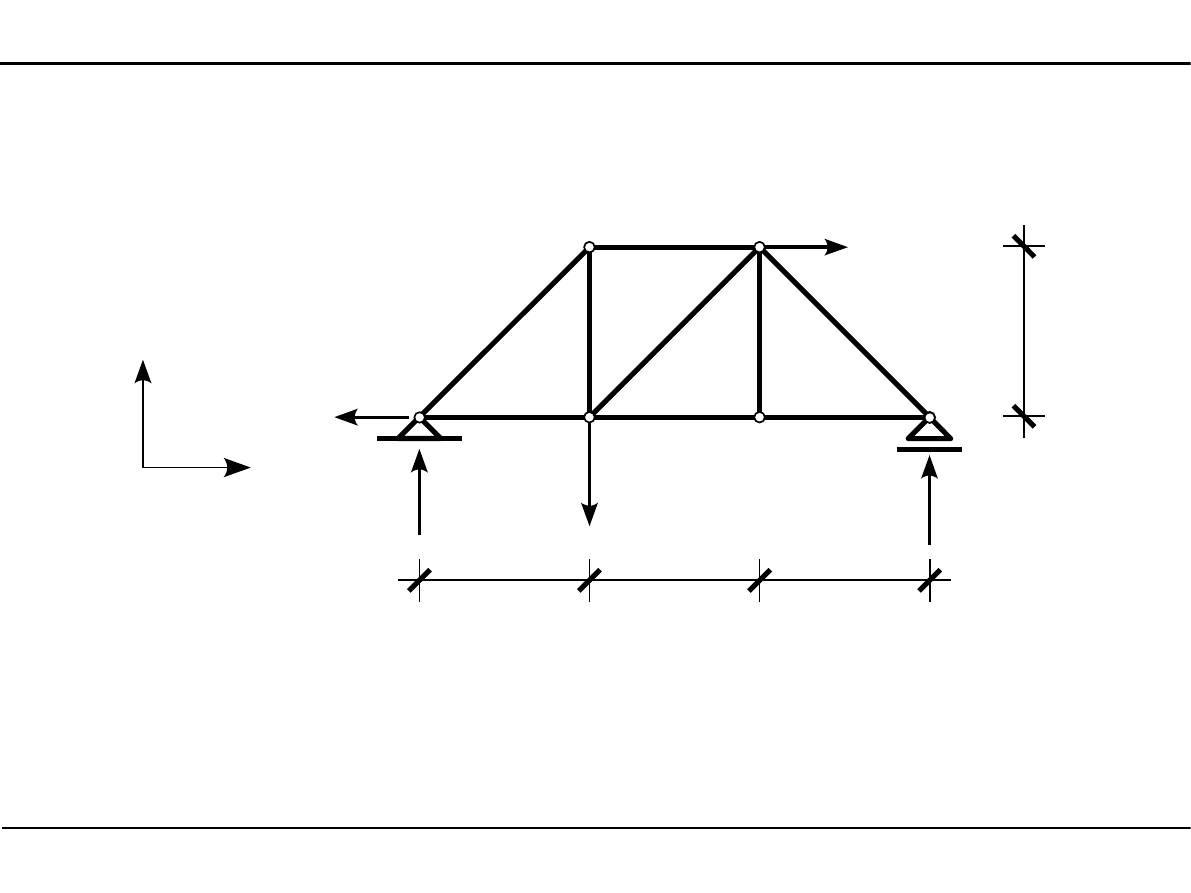
Wyznaczenie reakcji

1

2

3

4

5

6

X

Y

1

2

3

4

5

6

7

8

9

4,0

4,0

4,0

[m]

3,

7

98,0 kN

62,0 kN

V

1

H

1

V

6



Y =0

V

1



V

6

−

98,0=46,2251,78−98,0=0

Dr inż. Janusz Dębiński

17

6. Wyznaczanie sił normalnych w kratownicach płaskich

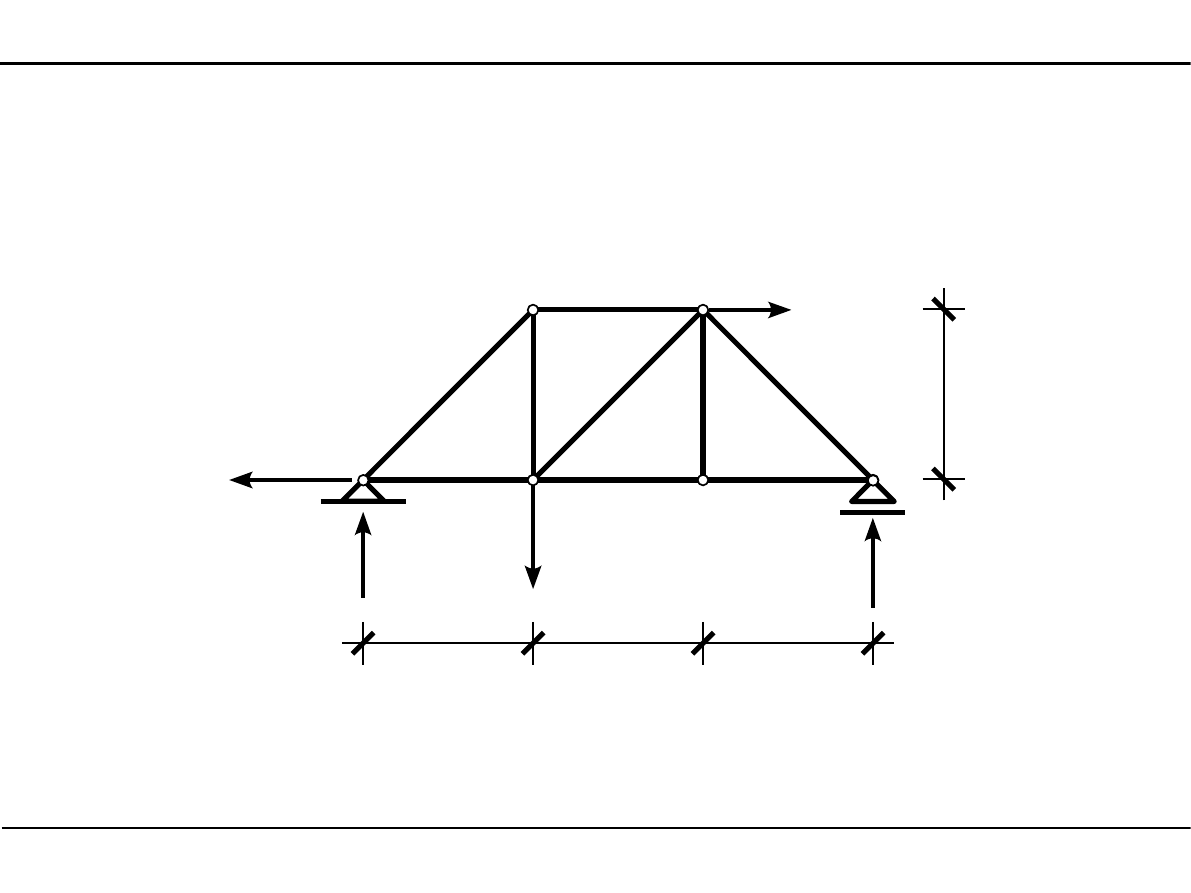
6.6. Zadanie 1

Wyznaczenie reakcji

1

2

3

4

5

6

1

2

3

4

5

6

7

8

9

4,0

4,0

4,0

[m]

3,

7

98,0 kN

62,0 kN

62,0 kN

46,22 kN

51,78 kN

Dr inż. Janusz Dębiński

18

6. Wyznaczanie sił normalnych w kratownicach płaskich

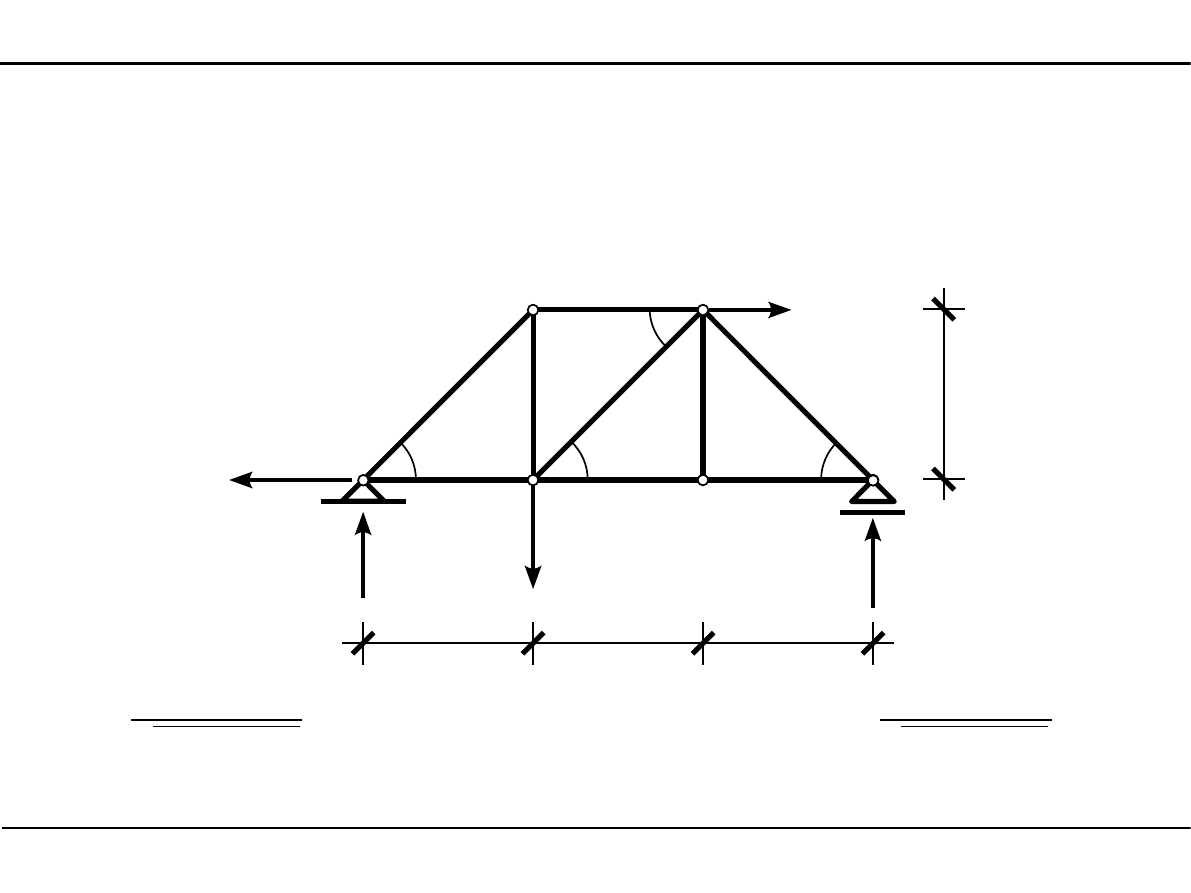
6.6. Zadanie 1

Kąty nachylenia krzyżulców

α

α

α

α

sin







=

3,7



3,7

2



4,0

2

=

0,6790

cos







=

4,0



3,7

2



4,0

2

=

0,7341

0,6790

2



0,7341

2

=

1

1

2

3

4

5

6

1

2

3

4

5

6

7

8

9

4,0

4,0

4,0

[m]

3,

7

98,0 kN

62,0 kN

46,22 kN

62,0 kN

51,78 kN

Dr inż. Janusz Dębiński

19

6. Wyznaczanie sił normalnych w kratownicach płaskich

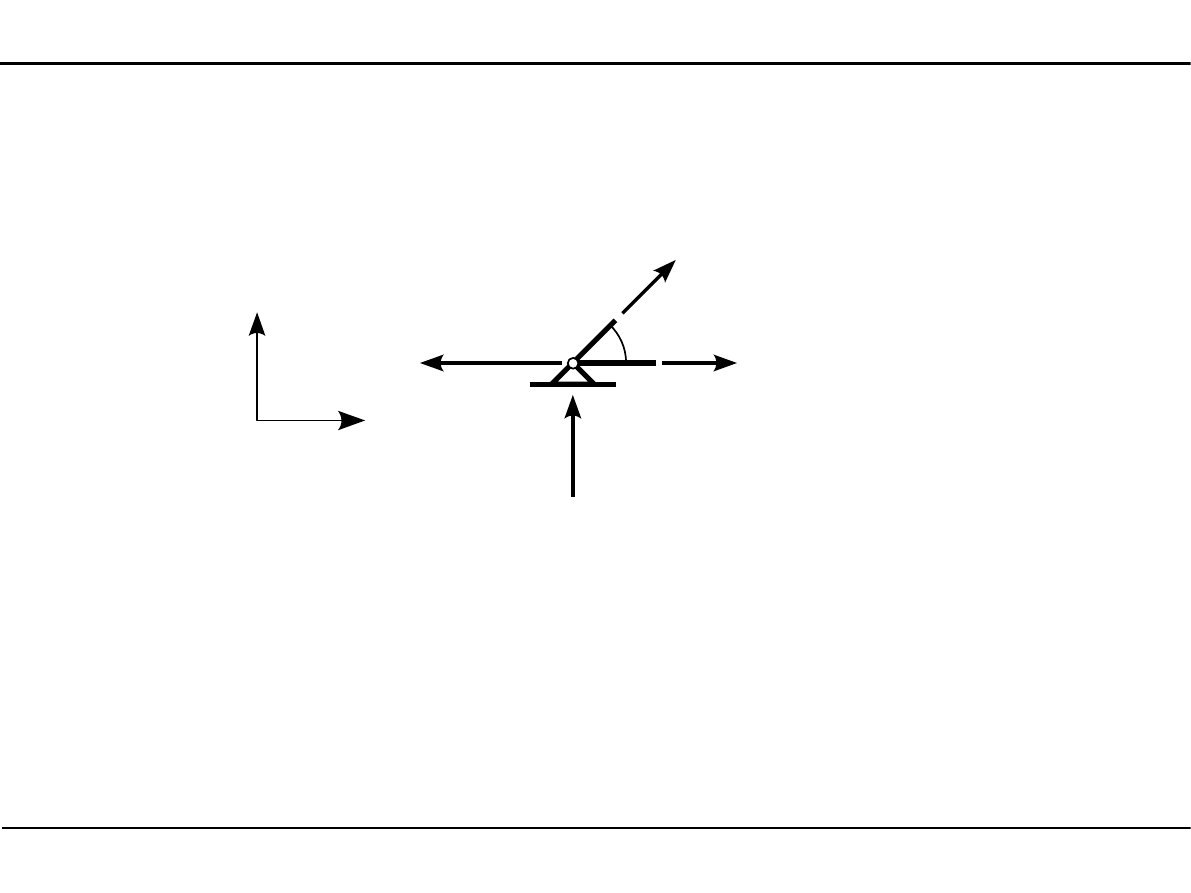
6.6. Zadanie 1

Węzeł numer 1

1

α

46,22 kN

62,0 kN

N

1

N

7



Y =0

N

7

⋅

sin









46,22=0

N

7

⋅

0,679046,22=0

N

7

=−

68,07 kN



X =0

N

1



N

7

⋅

cos







−

62,0=0

N

1



N

7

⋅

0,7341−62,0=0

N

1

−

68,07⋅0,7341−62,0=0

N

1

=

112,0 kN

X

Y

Dr inż. Janusz Dębiński

20

6. Wyznaczanie sił normalnych w kratownicach płaskich

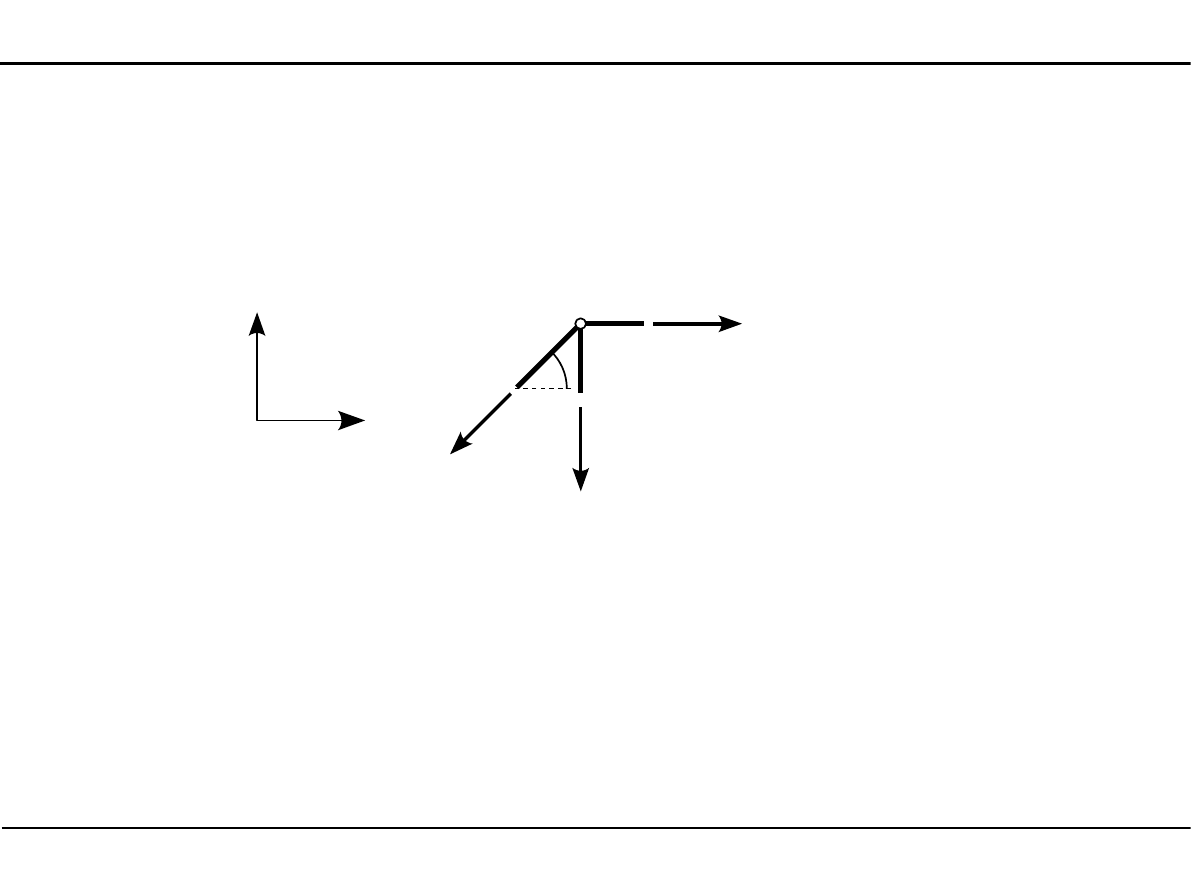
6.6. Zadanie 1

Węzeł numer 2

2

α

N

7

N

4

N

5



X =0

−

N

7

⋅

cos









N

4

=

0

−

N

7

⋅

0,7341N

4

=

0



Y =0

−

N

7

⋅

sin







−

N

5

=

0

−

N

7

⋅

0,6790− N

5

=

0

−



−

68,07



⋅

0,7341 N

4

=

0

N

4

=−

49,97 kN

−



−

68,07



⋅

0,6790−N

5

=

0

N

5

=

46,22 kN

X

Y

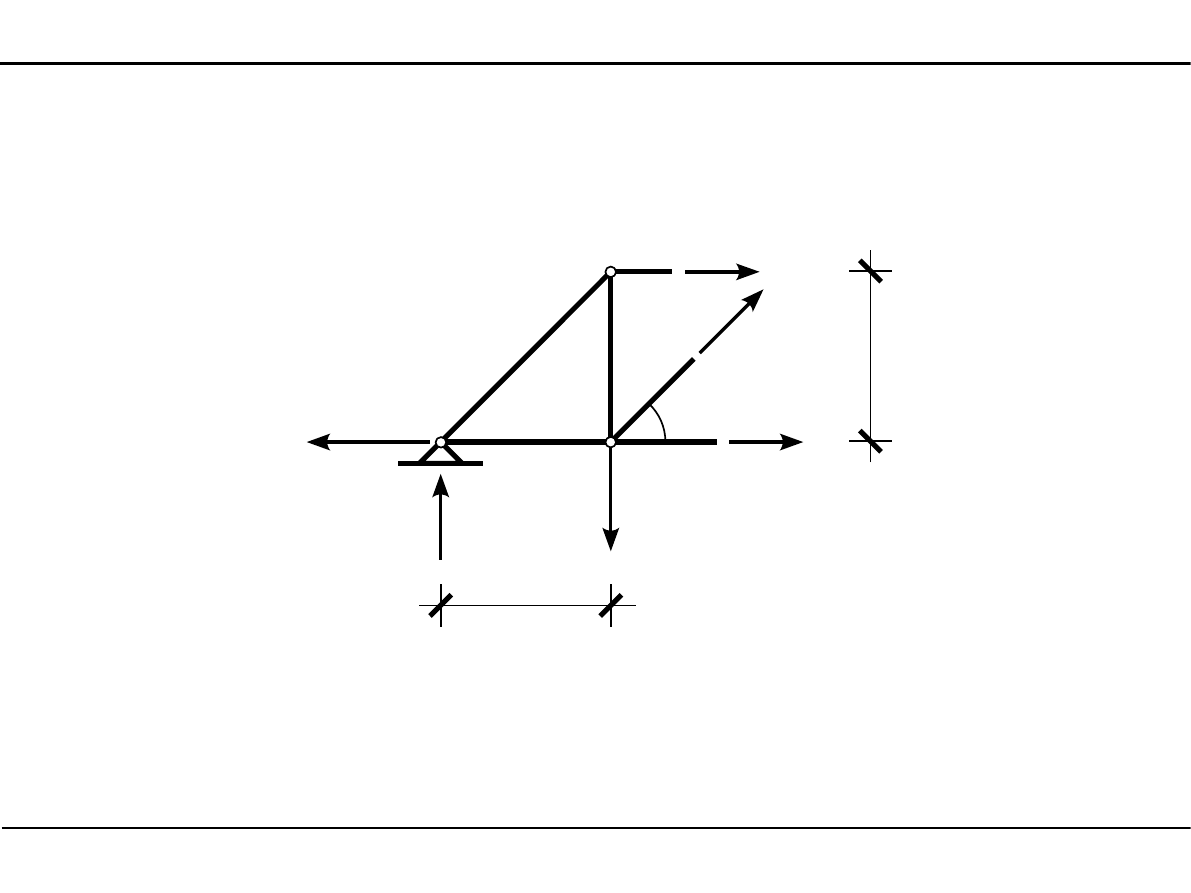
Dr inż. Janusz Dębiński

21

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.6. Zadanie 1

Pręt numer 4 - metoda Rittera

N

4

N

8

N

2

1

2

3

1

2

4

5

7

8

4,0

[m]

3,

7

98,0 kN

46,22 kN

62,0 kN

α



M

3

=

0

N

4

⋅

3,746,22⋅4,0=0

N

4

=−

49,97 kN

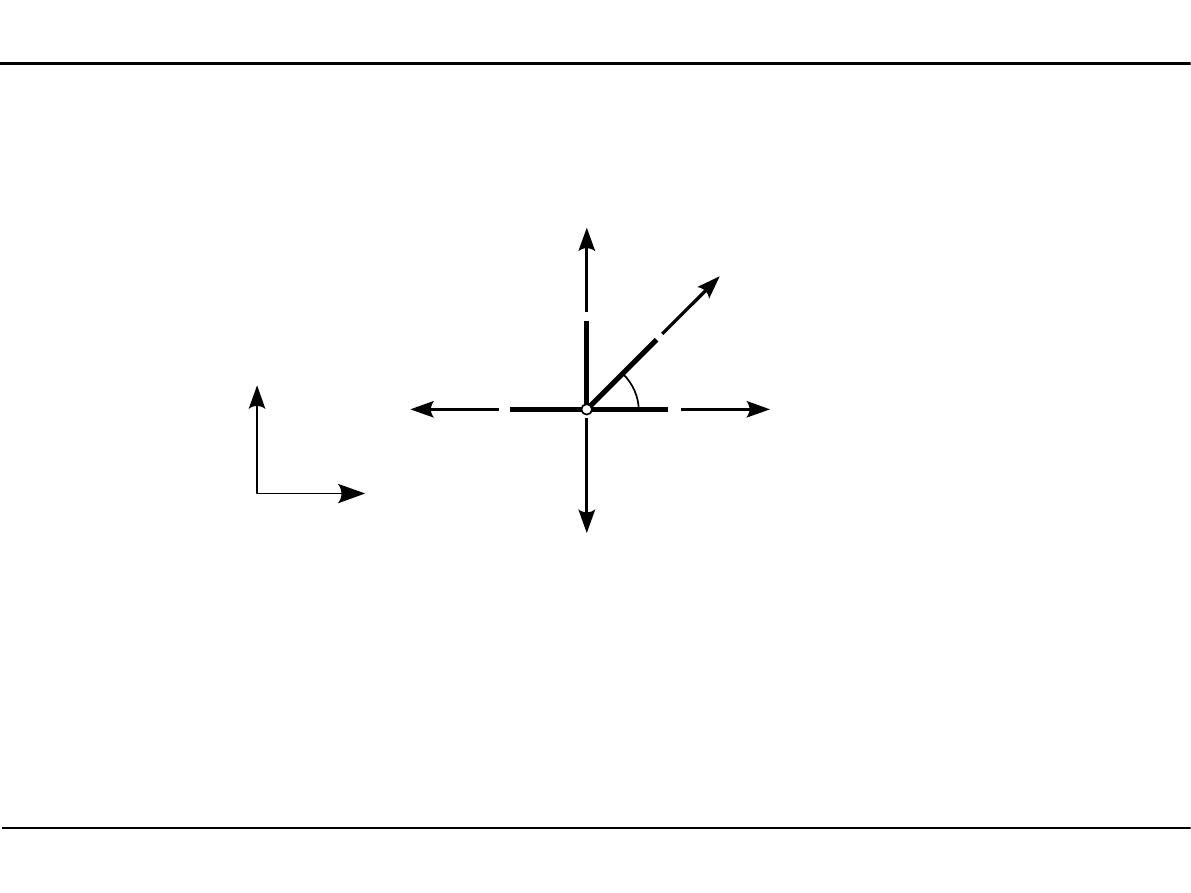
Dr inż. Janusz Dębiński

22

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.6. Zadanie 1

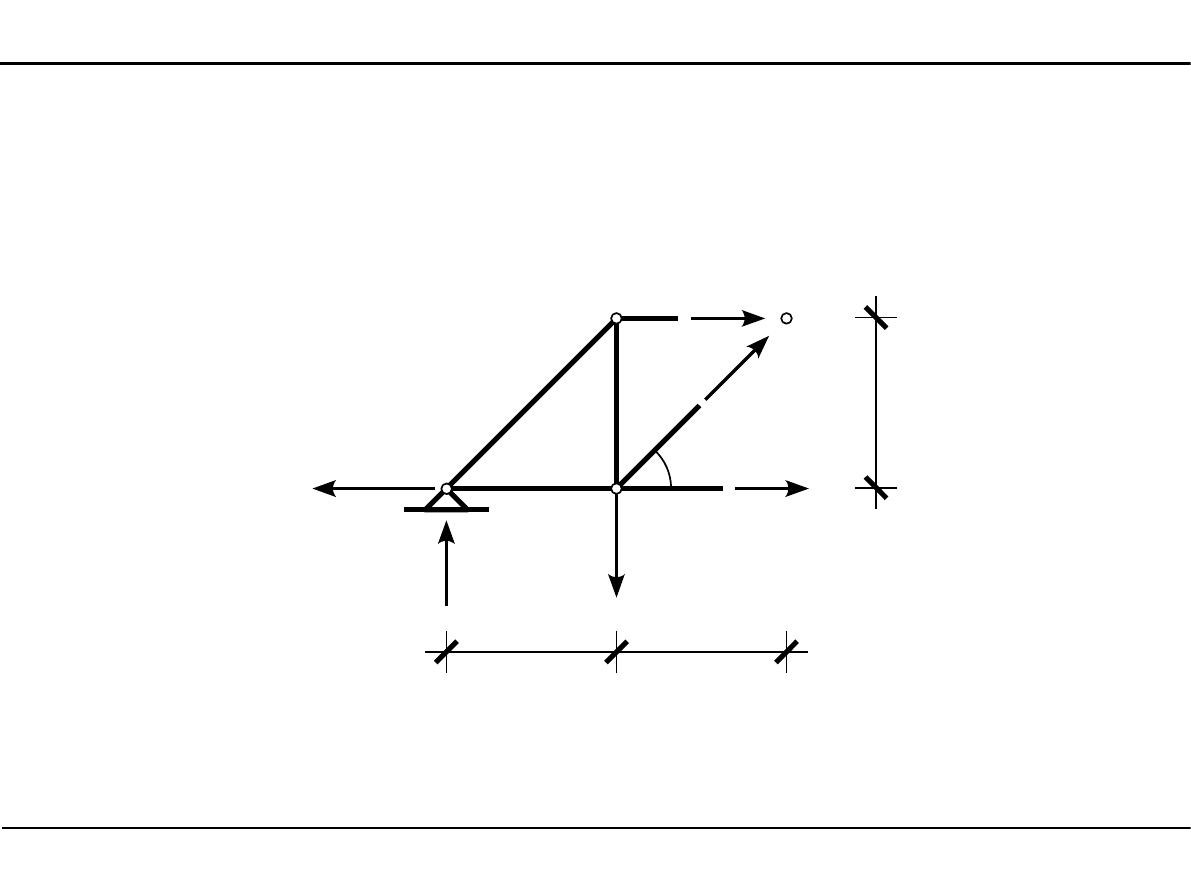
Węzeł numer 3

3

α

98,0 kN

N

1

N

5

N

8

N

2



X =0

N

8

⋅

cos









N

2

−

N

1

=

0

N

8

⋅

0,7341N

2

−

N

1

=

0



Y =0

N

8

⋅

sin









N

5

−

98,0=0

N

8

⋅

0,6790 N

5

−

98,0=0

46,22 N

8

⋅

0,6790−98,0=0

N

8

=

76,26 kN

−

112,0 N

2



76,26⋅0,7341=0

N

2

=

56,02 kN

X

Y

Dr inż. Janusz Dębiński

23

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.6. Zadanie 1

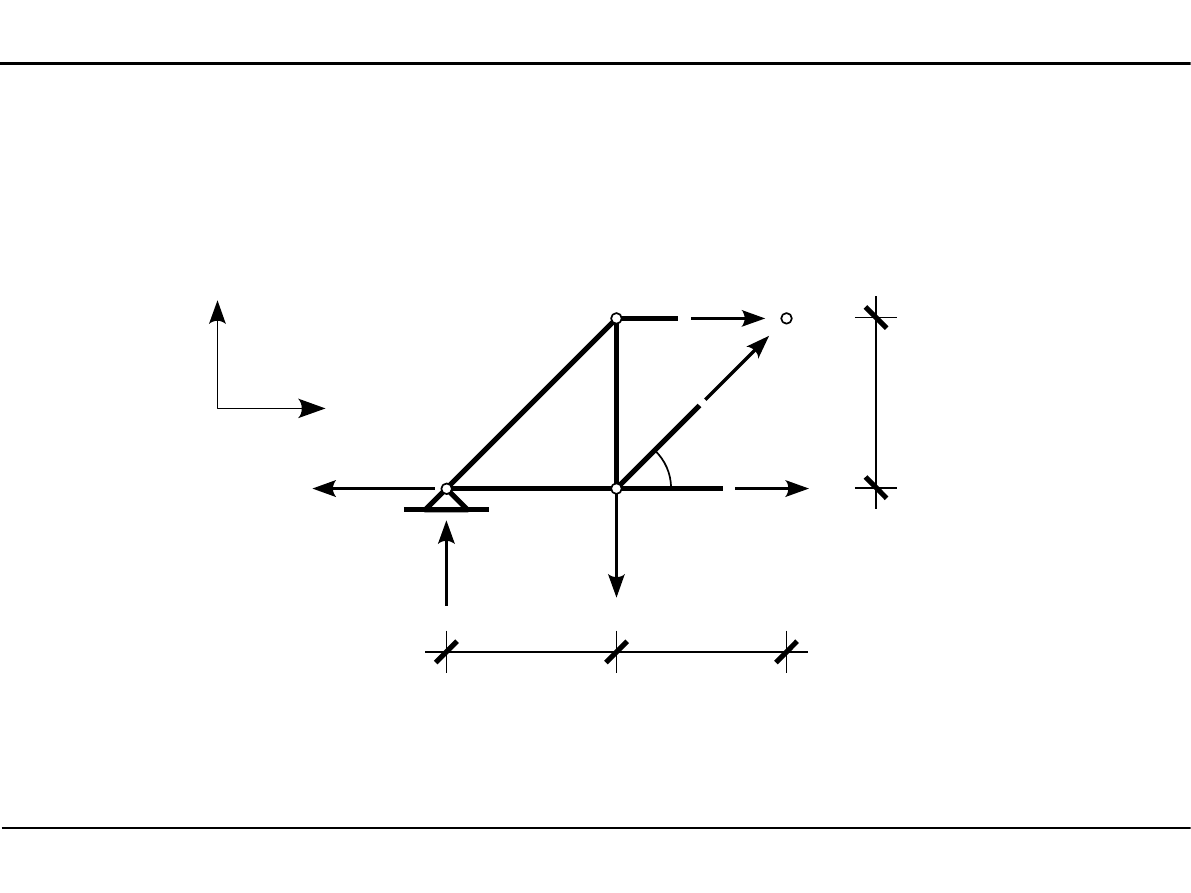
Pręty numer 2 i 8 - metoda Rittera

1

2

3

1

2

4

5

7

8

4,0

4,0

[m]

3,

7

98,0 kN

46,22 kN

62,0 kN

α

N

4

N

8

N

2

4



M

4

=

0

−

N

2

⋅

3,7−98,0⋅4,046,22⋅8,062,0⋅3,7=0

N

2

=

55,99 kN

Dr inż. Janusz Dębiński

24

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.6. Zadanie 1

Pręty numer 2 i 8 - metoda Rittera

X

Y

1

2

3

4

1

2

4

5

7

8

4,0

4,0

[m]

3,

7

98,0 kN

46,22 kN

62,0 kN

α

N

2

N

8

N

4



Y =0

N

8

⋅

sin







−

98,046,22=0

N

8

=

76,26 kN

Dr inż. Janusz Dębiński

25

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.6. Zadanie 1

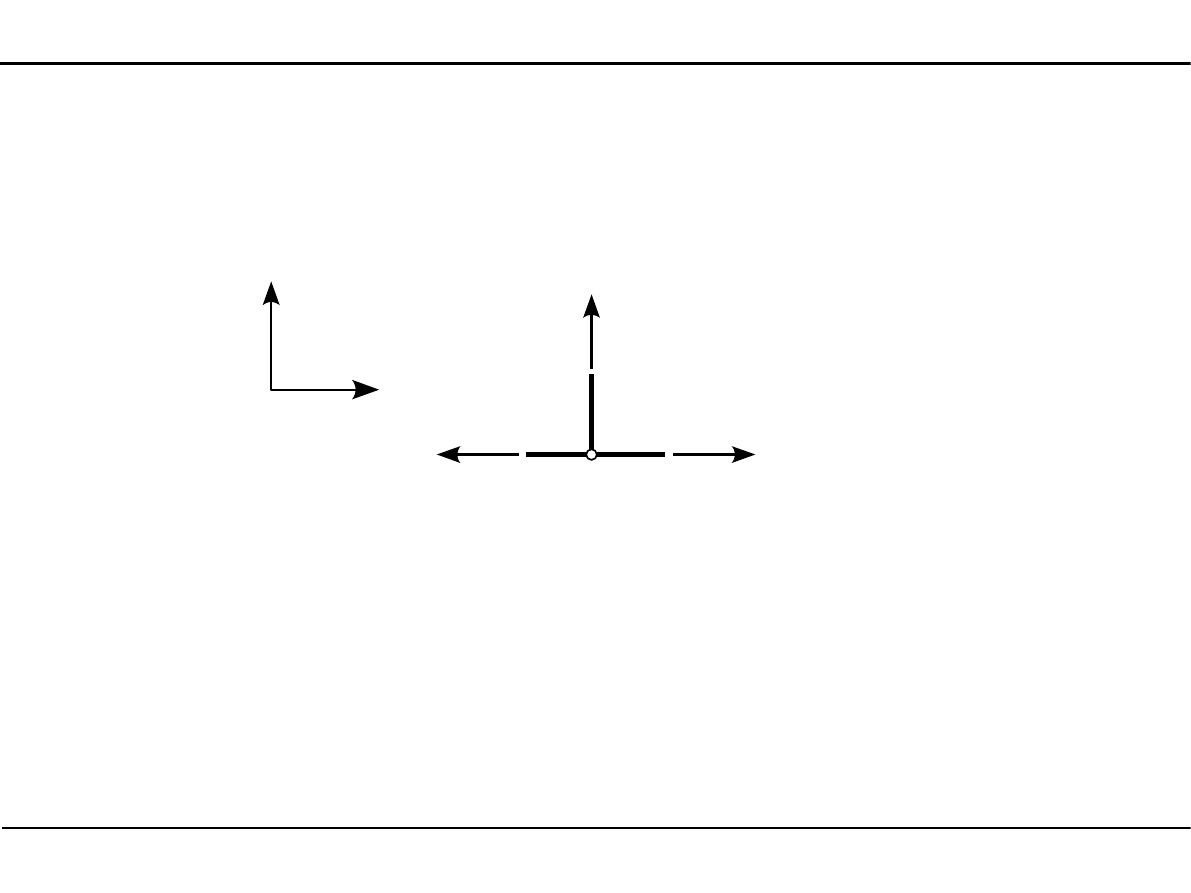
Węzeł numer 5

5

N

2

N

6

N

3



X =0

−

N

2



N

3

=

0



Y =0

N

6

=

0,0 kN

−

56,02 N

3

=

0

N

3

=

56,02 kN

X

Y

Dr inż. Janusz Dębiński

26

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.6. Zadanie 1

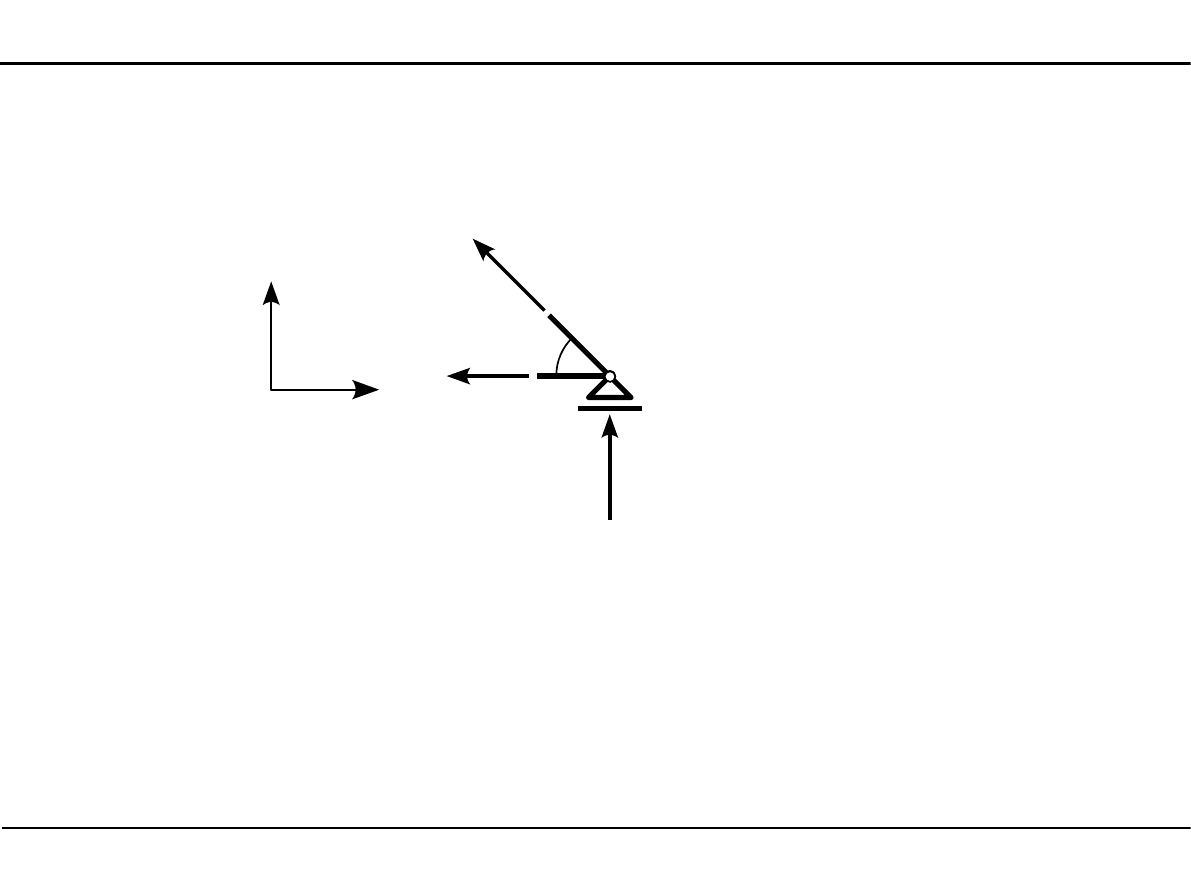
Węzeł numer 6

6

α

51,78 kN

N

3

N

9



X =0

−

N

9

⋅

cos







−

N

3

=

0

−

N

9

⋅

0,7341−N

3

=

0



Y =0

N

9

⋅

sin









51,78=0

N

9

⋅

0,679051,78=0

N

9

=−

76,26 kN

−

56,02−



−

76,26



⋅

0,7341=−0,003753 kN≈0

X

Y

Dr inż. Janusz Dębiński

27

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.6. Zadanie 1

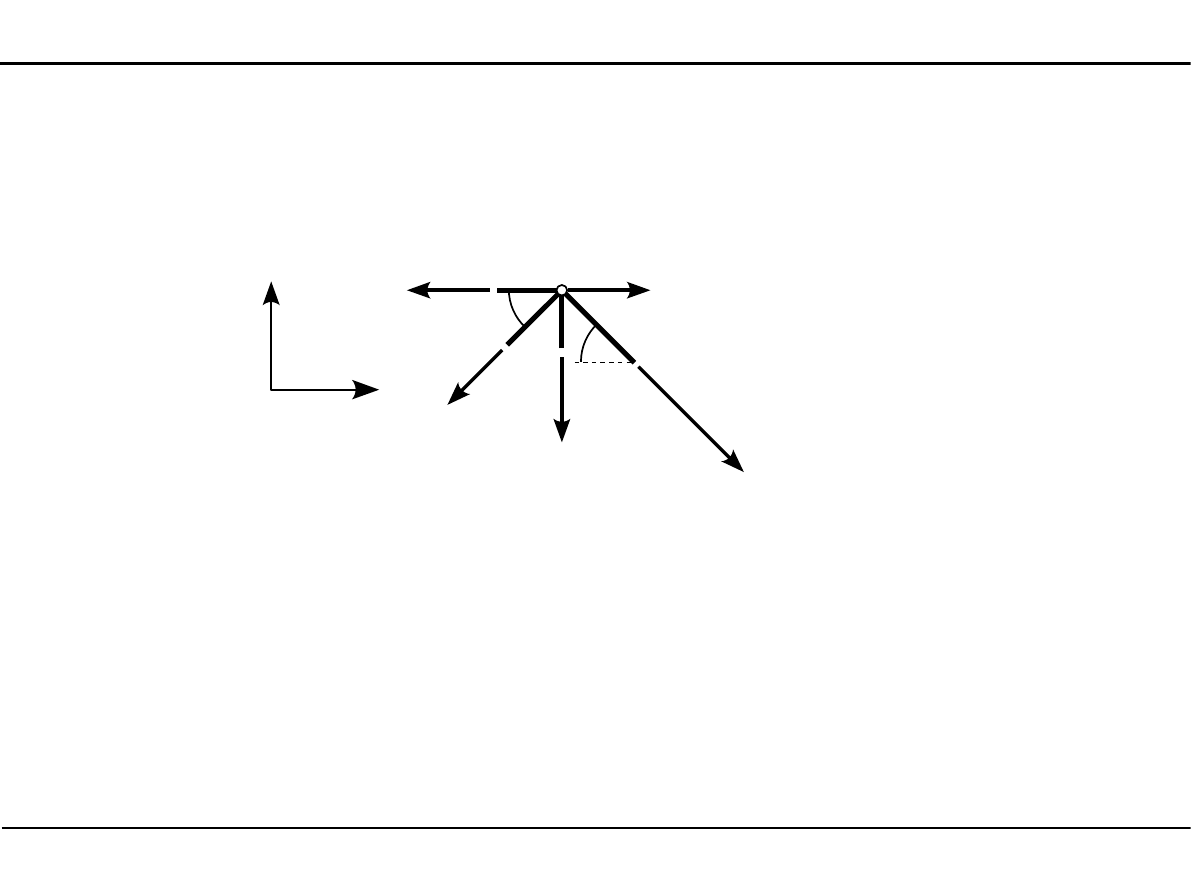
Węzeł numer 4

4

α

α

62,0 kN

N

4

N

8

N

6

N

9



X =0

−

N

4

−

N

8

⋅

cos









N

9

⋅

cos









62,0=−



−

49,97



−

76,26⋅0,7341−

−

76,26⋅0,734162,0=0,005068 kN≈0



Y =0

−

N

8

⋅

sin







−

N

6

−

N

9

⋅

sin







=−

76,26⋅0,6790−0,0−



−

76,26



⋅

0,6790=0

X

Y

Dr inż. Janusz Dębiński

28

6. Wyznaczanie sił normalnych w kratownicach płaskich

98,0 kN

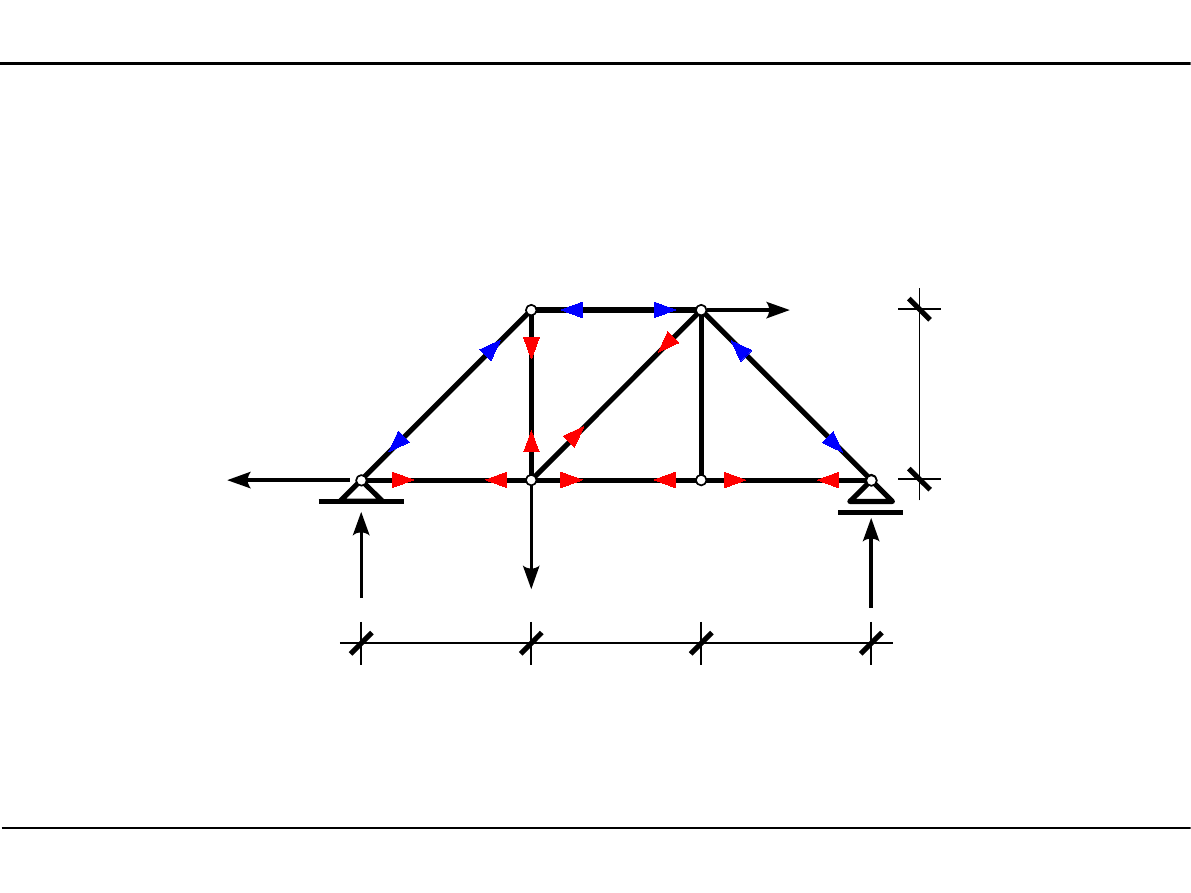
6.6. Zadanie 1

Rysunek zestawieniowy

4,0

4,0

4,0

[m]

3,

7

62,0 kN

62,0 kN

46,22 kN

51,78 kN

112,0 kN

56,02 kN

56,02 kN

49,97 kN

46

,2

2

kN

0

68

,0

7

kN

76

,2

6

kN

76

,26

kN

Dr inż. Janusz Dębiński

29

6. Wyznaczanie sił normalnych w kratownicach płaskich

6.7. Zadanie 2

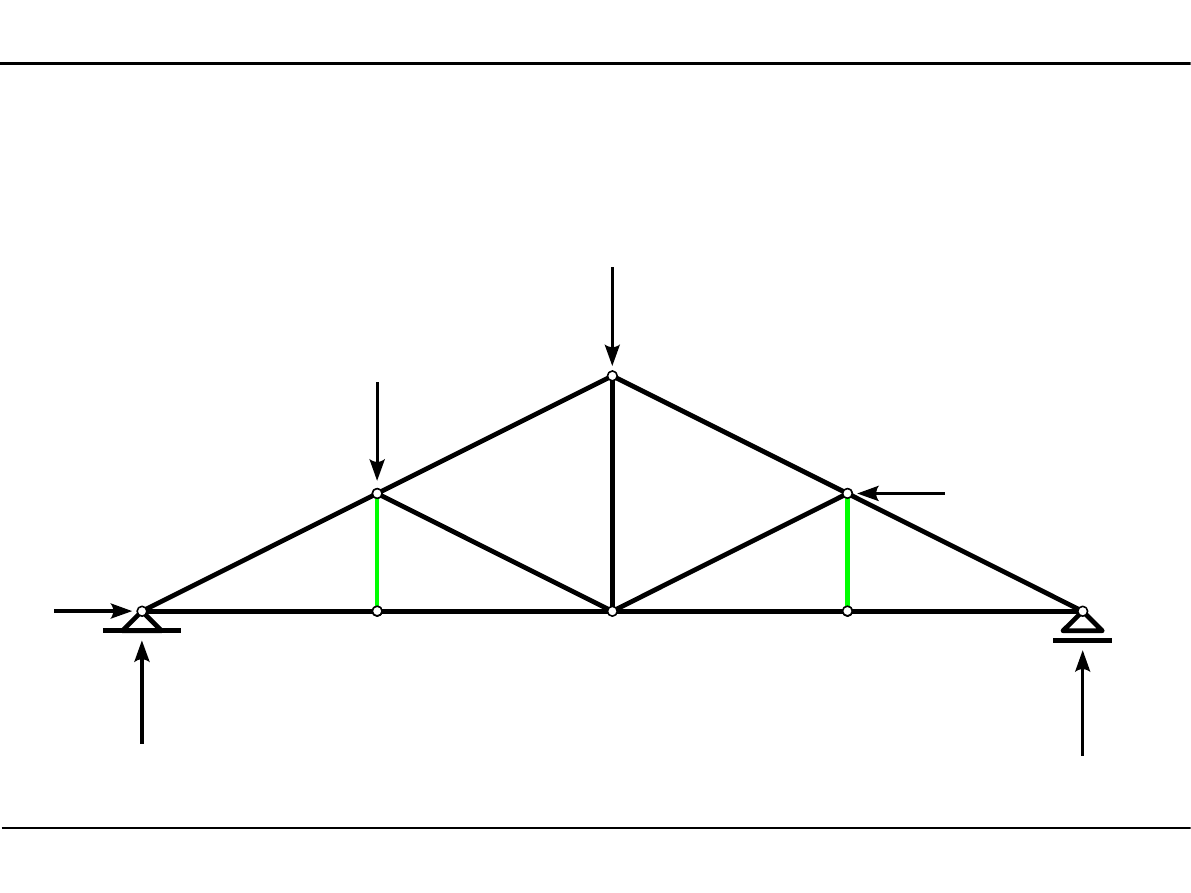
Wyznaczyć pręty zerowe w kratownicy płaskiej.

1

2

3

4

6

5

7

8

1

2

3

4

5

6

7

8

9

10

11

12

13

P

1

P

2

P

3

H

1

V

1

V

8

Dr inż. Janusz Dębiński

30

6. Wyznaczanie sił normalnych w kratownicach płaskich

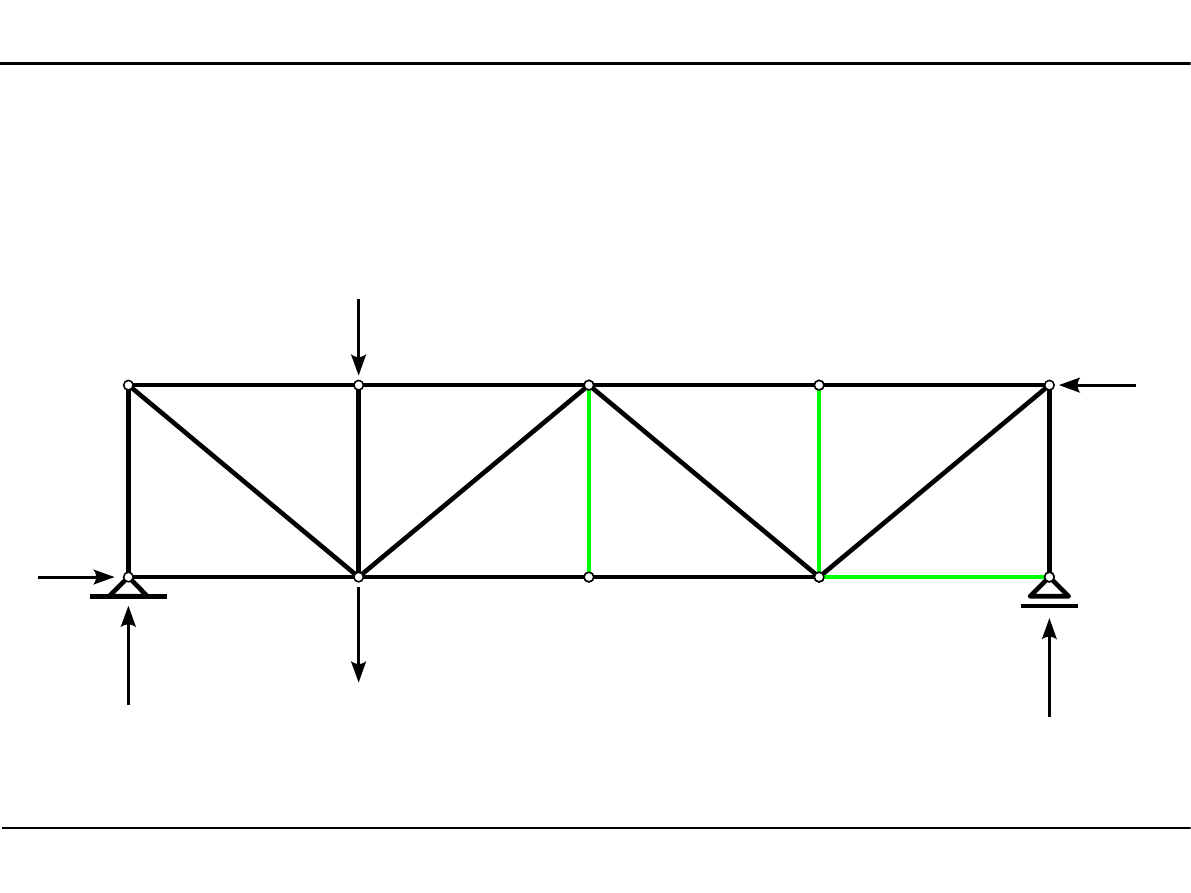
6.8. Zadanie 3

Wyznaczyć pręty zerowe w kratownicy płaskiej.

1

2

4

6

8

10

3

5

7

9

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

P

1

P

2

P

3

H

1

V

1

V

9

Dr inż. Janusz Dębiński

31

6. Wyznaczanie sił normalnych w kratownicach płaskich

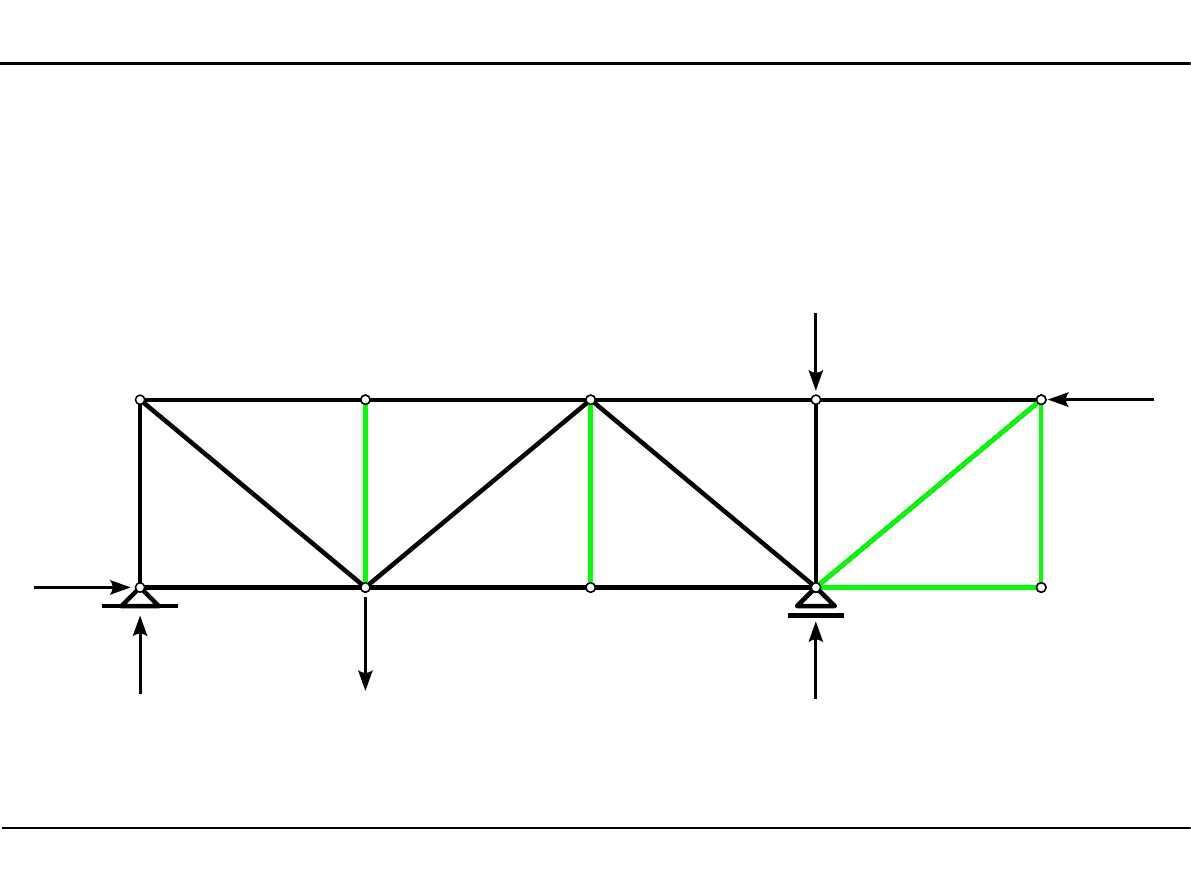
6.9. Zadanie 4

Wyznaczyć pręty zerowe w kratownicy płaskiej.

1

2

4

6

8

10

3

5

7

9

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

P

1

P

2

P

3

H

1

V

1

V

7

Dr inż. Janusz Dębiński

32

6. Wyznaczanie sił normalnych w kratownicach płaskich

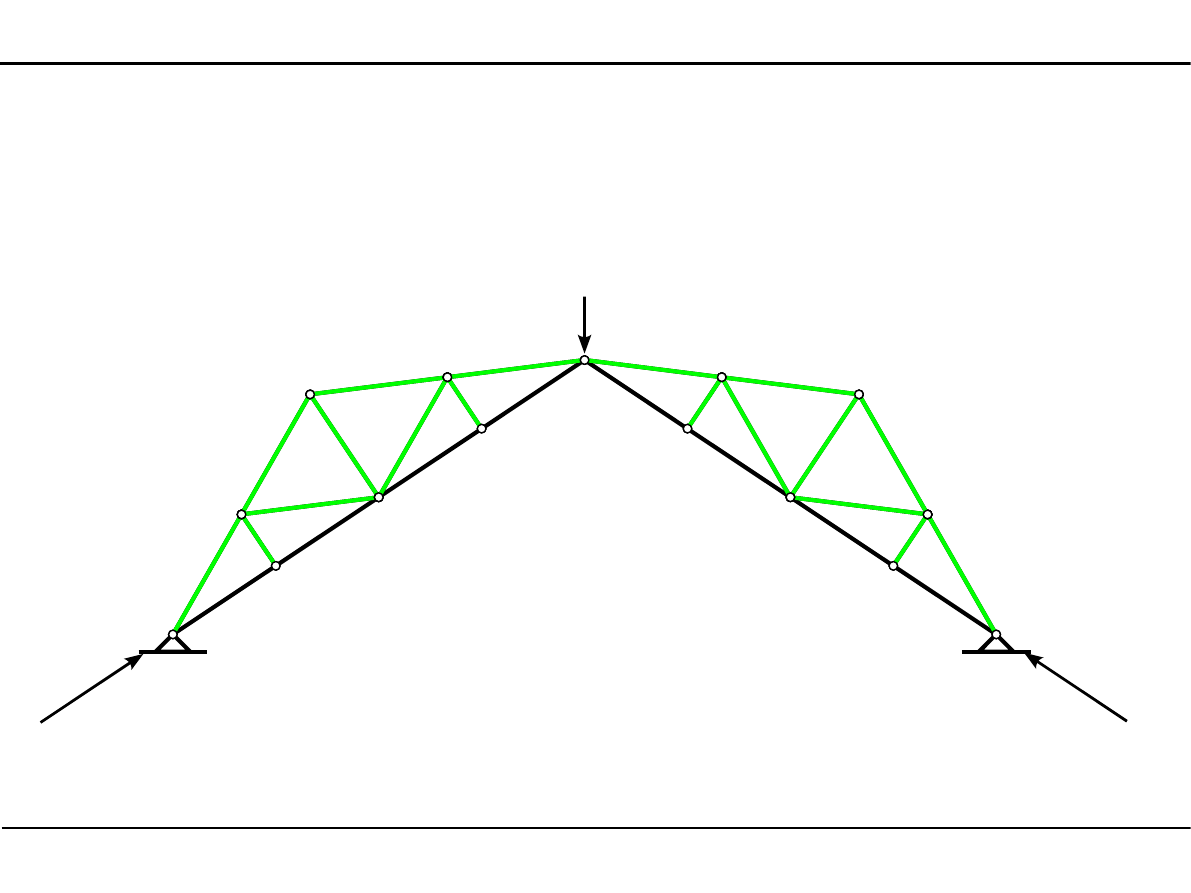
6.10. Zadanie 5

Wyznaczyć pręty zerowe w kratownicy płaskiej.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

1

2

3

4

5

6

7

8

9

10

11

12 13

14

15

16

17

18

19

20

21

22

23

24

25

26

P

R

1

R

15