5. Badanie funkcji
5.1. Asymptoty
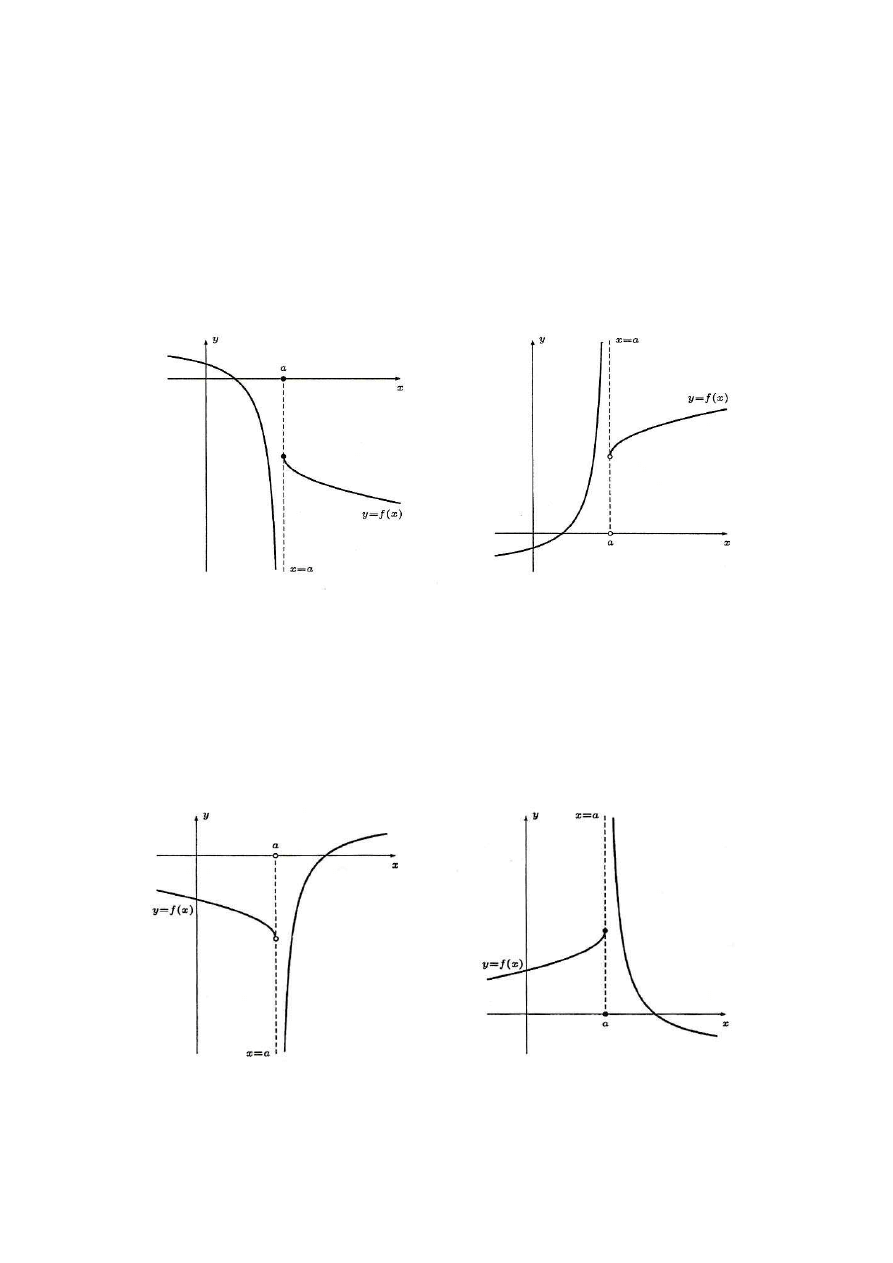
Asymptota pionowa lewostronna (rys. 5.1)
Prosta x = a jest asymptotą pionową lewostronną funkcji f(x), jeżeli
−∞
=
−
→
)
(
lim
x
f
a
x
lub
∞
=
−
→
)
(
lim
x
f
a
x
Rys. 5.1. Asymptoty pionowe lewostronne funkcji f(x)
Asymptota pionowa prawostronna (rys. 5.2)
Prosta x = a jest asymptotą pionową prawostronną funkcji f(x), jeżeli
−∞
=
+
→
)
(
lim
x
f
a
x
lub
∞
=
+
→
)
(
lim
x
f
a
x
Rys. 5.2. Asymptoty pionowe prawostronne funkcji f(x)
2
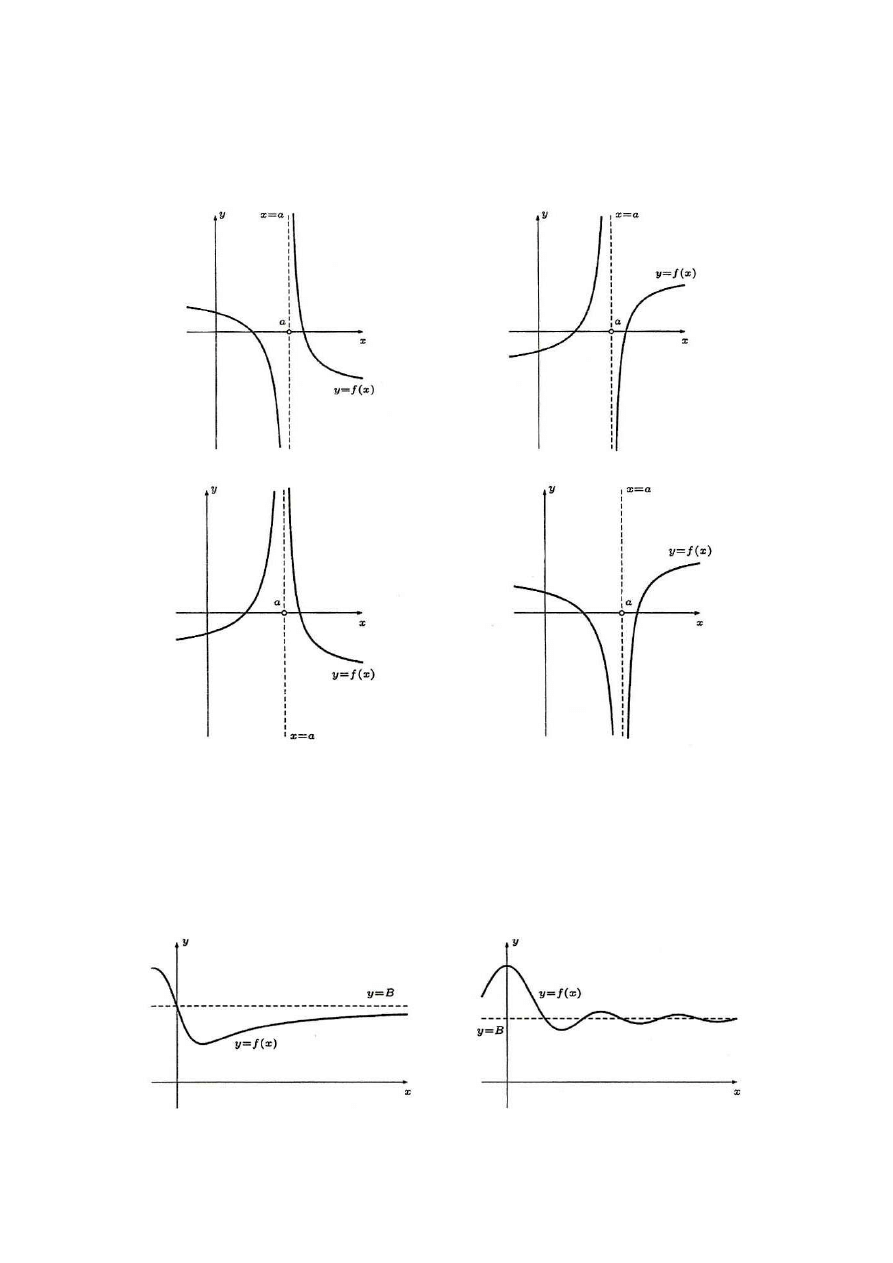
Asymptoty pionowe obustronne (rys. 5.3)
Prosta x = a jest asymptotą pionową obustronną funkcji f(x), jeżeli jest jednocześnie asympto-
tą lewostronną i prawostronną.
Rys. 5.3. Asymptoty pionowe obustronne funkcji f(x)
Asymptoty poziome (rys. 5.4)
Prosta y = B jest asymptotą pozioma funkcji f(x) w ∞ jeżeli
B
x
f
x
=
∞
→
)
(
lim
Rys. 5.4. Asymptoty poziome funkcji f(x) w ∞
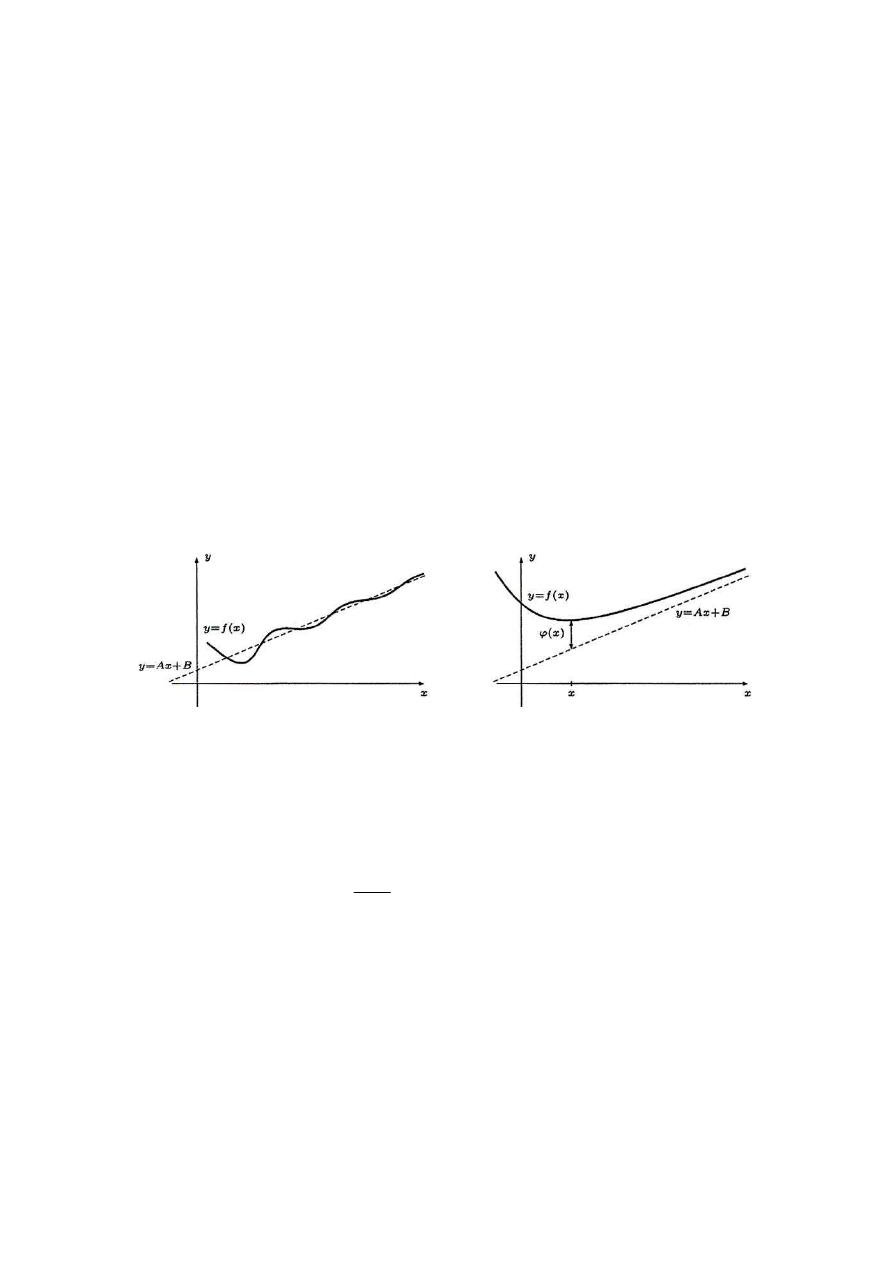
3
Prosta y = B jest asymptotą poziomą funkcji f(x) w –∞ jeżeli
B
x
f
x
=
−∞
→
)
(
lim
.
Asymptoty ukośne (rys. 5.5)
Prosta
B
Ax
y
+
=
jest asymptotą ukośną funkcji f(x) w ∞ jeżeli
[
]
0
)
(
)
(
lim
=
+
−
∞
→
B
Ax
x
f
x
. (5.1)
To znaczy, że prosta
B
Ax
y
+
=
jest asymptotą ukośną funkcji f(x) w ∞ jeżeli funkcję f(x)
można przedstawić w postaci
)
(
)
(
x
B
Ax
x
f
ϕ
+
+
=
, (5.2)
gdzie
0
)
(
lim
=
∞
→
x
x
ϕ
. Można zatem powiedzieć, że dla dostatecznie dużych argumentów x wy-
kres funkcji f(x) dowolnie mało różni się od wykresu linii prostej (rys. 5.5).
Rys. 5.5. Asymptoty ukośne funkcji f(x) w ∞
Asymptotę ukośną funkcji f(x) w –∞ definiuje się analogicznie zastępując we wzorach nie-
skończoność ∞ przez nieskończoność –∞.
Współczynniki A i B asymptoty można wyznaczyć z równań (5.1) i (5.2):
x
x
f
A
x
)
(
lim
∞
→
=
,
[
]
Ax
x
f
B
x
−
=
∞
→
)
(
lim
.
5.2. Punkty przegięcia
Funkcję f(x) nazywamy
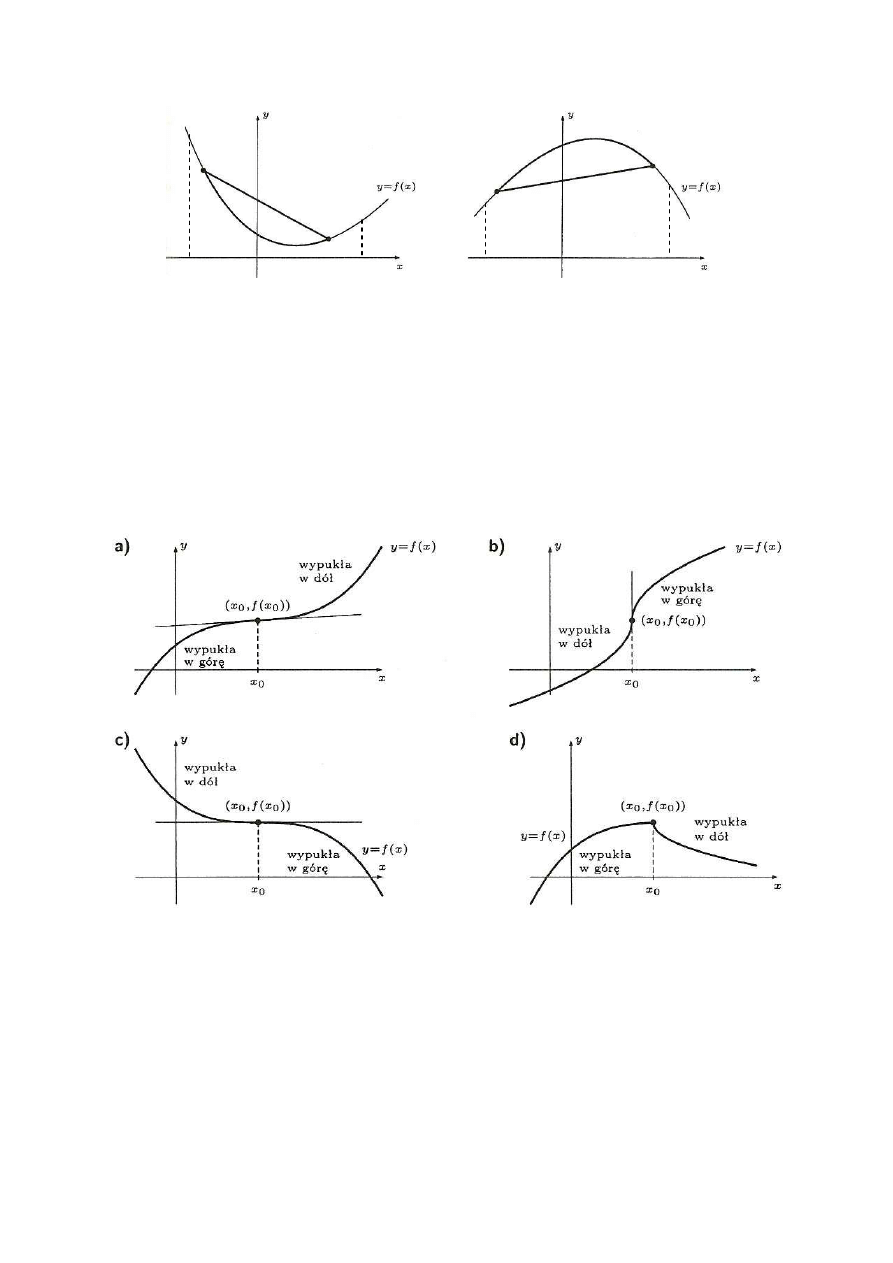
wypukłą w dół w przedziale (a, b), jeżeli każda sieczna w (a, b) leży
wyżej niż część wykresu między punktami, przez które przechodzi sieczna.
Funkcję f(x) nazywamy
wypukłą w górę w przedziale (a, b), jeżeli każda sieczna w (a, b)
leży niżej niż część wykresu między punktami, przez które przechodzi sieczna (rys. 5.6).
Niech
funkcja f(x) będzie określona i dwukrotnie różniczkowalna
w przedziale (a, b).
4
Funkcja wypukła w dół Funkcja wypukła w górę
Rys. 5.6. Funkcje wypukłe
Jeżeli w przedziale (a, b) funkcja spełnia warunek
)
(x
f
′′
> 0, to funkcja jest wypukła w dół.
Jeżeli w przedziale (a, b) funkcja spełnia warunek
)
(x
f
′′
< 0, to funkcja jest wypukła w górę.
Punkt x
0
wykresu funkcji nazywa się
punktem przegięcia, jeżeli w punkcie x
0
funkcja ma
styczną i zmienia w tym punkcie rodzaj wypukłości (rys. 5.7).
Rys. 5.7. Wykresy funkcji: a), b), c) z punktami przegięcia, d) bez punktu przegięcia
Jeżeli x
0
jest punktem przegięcia funkcji f(x), to f ′′(x) = 0.
Twierdzenie odwrotne nie jest prawdziwe.
a
a
b
b
5
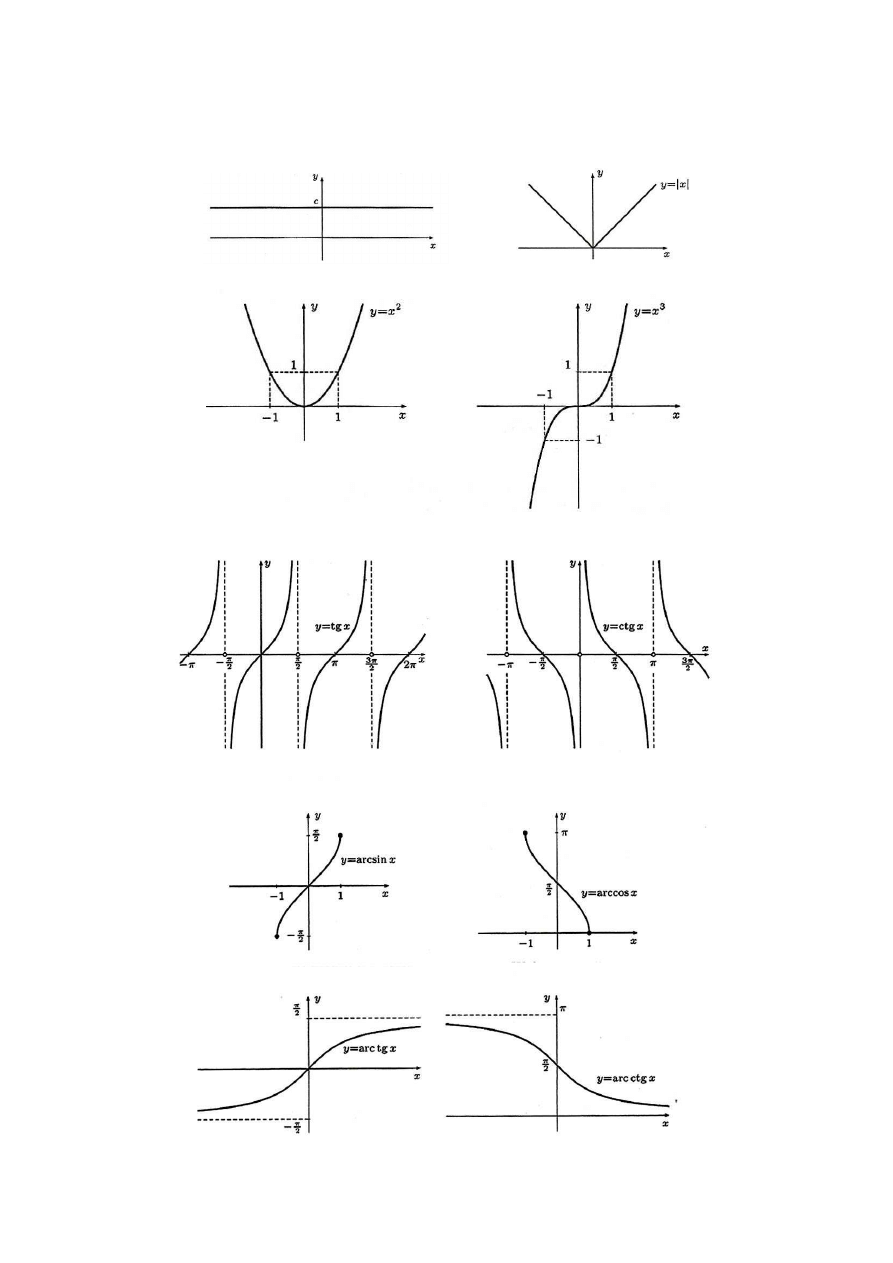
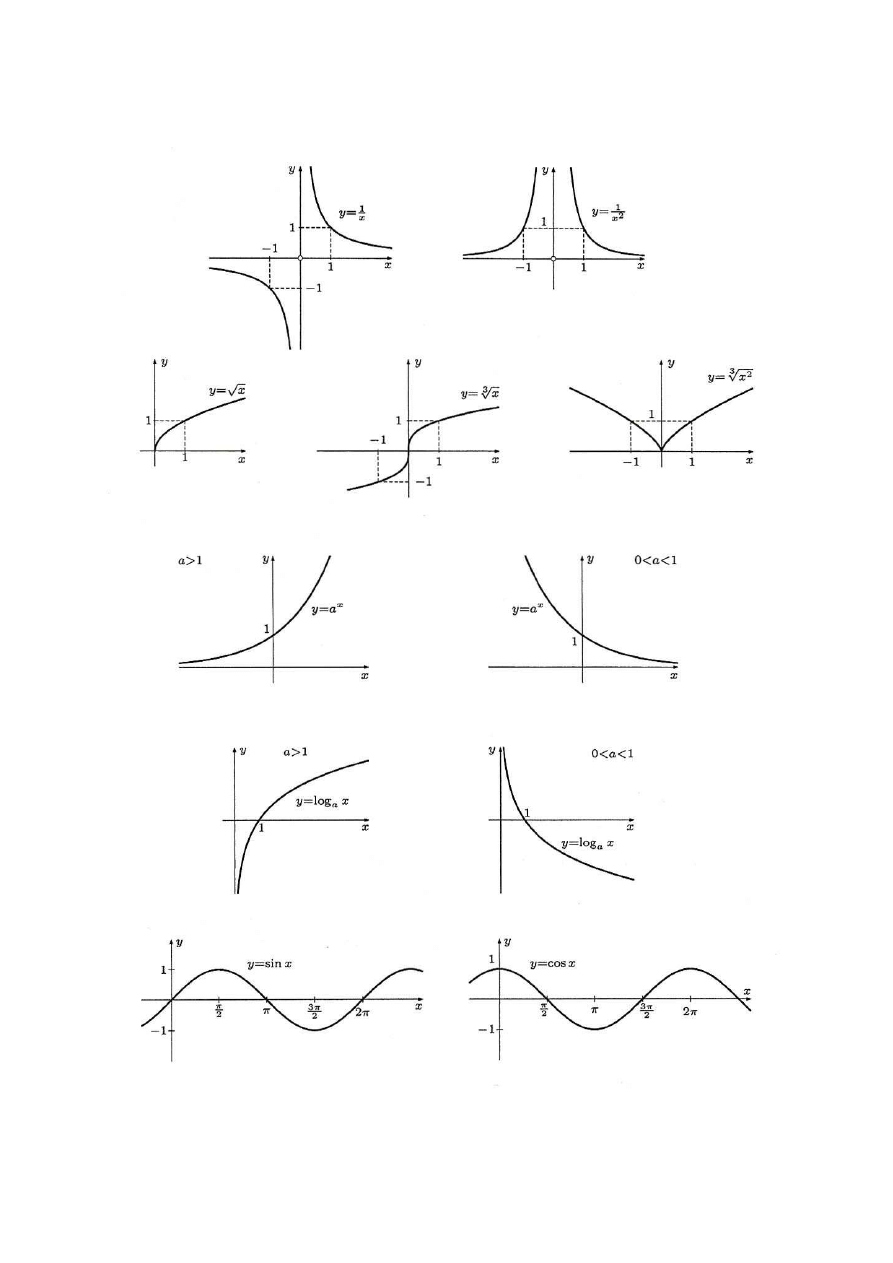
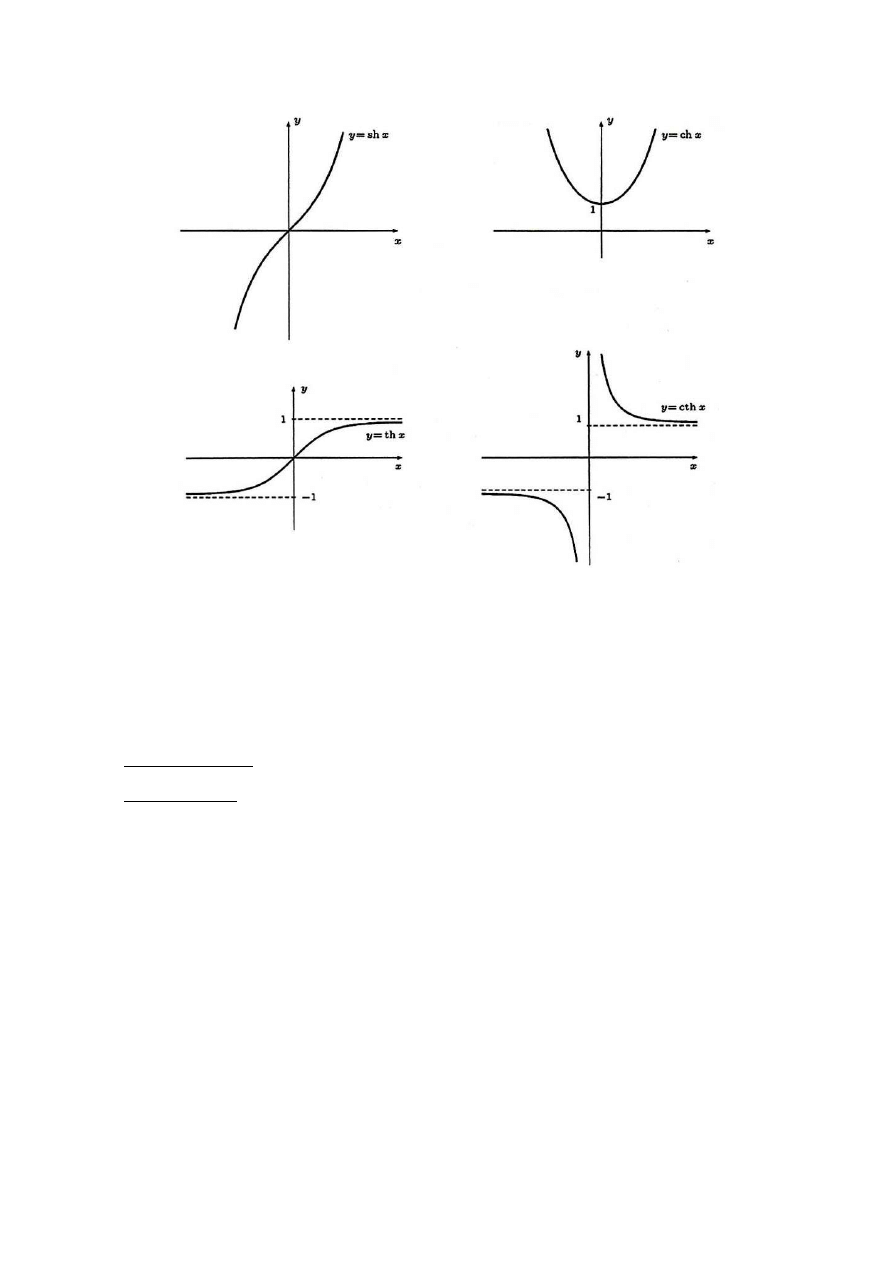
5.3. Wykresy funkcji elementarnych
6
7
5.4. Przykłady badania przebiegu zmienności funkcji
Przykład 1. Zbadać przebieg zmienności funkcji
2
9
3
)
(
2
3
−
−
+
=
x
x
x
x
f
.
Rozwiązanie
1. Dziedzina funkcji. Funkcja jest określona dla wszystkich wartości rzeczywistych
R
x
∈
.
2. Miejsca zerowe. Wyznaczamy punkty, w których spełnione jest równanie
0
2
9
3
)
(
2
3
=
−
−
+
=
x
x
x
x
f
.
Pierwiastków całkowitych wielomianu
2
9
3
)
(
2
3
−
−
+
=
x
x
x
x
f
szukamy wśród podzielni-
ków całkowitych wyrazu wolnego –2. Metodą prób znajdujemy pierwiastek x
1
= 2, gdyż
0
)
2
(
=
f
.
Aby znaleźć kolejne pierwiastki należy podzielić wielomian
2
9
3
)
(
2
3
−
−
+
=
x
x
x
x
f
przez
czynnik x – 2
1
5
)
2
(
:
)
2
9
3
(
2
2
3
+
+
=
−
−
−
+
x
x
x
x
x
x
.
Stąd
)
1
5
)(
2
(
)
2
9
3
(
2
2
3
+
+
−
=
−
−
+
x
x
x
x
x
x
.
Pozostałe pierwiastki obliczamy z równania
0
1
5
2
=
+
+
x
x
.

8
Rozwiązaniami równania
0
1
5
2
=
+
+
x
x
są liczby:
8
,
4
2
21
5
2
−
≈
−
−
=
x
oraz
2
,
0
2
21
5
3
−
≈
+
−
=
x
.
Wielomian
2
9
3
)
(
2
3
−
−
+
=
x
x
x
x
f
można zatem rozłożyć na czynniki:
)
2
,
0
)(
8
,
4
)(
2
(
)
)(
)(
(
2
9
3
)
(
3
2
1
2
3
+
+
−
≈
−
−
−
=
−
−
+
=
x
x
x
x
x
x
x
x
x
x
x
x
x
f
.
3. Ekstrema lokalne. Obliczamy pochodną wielomianu
2
9
3
)
(
2
3
−
−
+
=
x
x
x
x
f
9
6
3
)
(
2
−
+
=
′
x
x
x
f
.
Ekstrema lokalne występują w punktach zerowych pochodnej
9
6
3
)
(
2
−
+
=
′
x
x
x
f
.
Po rozwiązaniu równania
0
9
6
3
2
=
−
+
x
x
otrzymuje się
3
01
−
=
x
oraz
1
02
=
x
.
Pochodną
9
6
3
)
(
2
−
+
=
′
x
x
x
f
można rozłożyć na czynniki
)
1
)(
3
(
)
)(
(
9
6
3
)
(
02
01
2
−
+
=
−
−
=
−
+
=
′
x
x
x
x
x
x
x
x
x
f
W punkcie
3
01
−
=
x
występuje maksimum lokalne, gdyż z lewej strony punktu
3
01
−
=
x
po-
chodna jest dodatnia, a z prawej strony jest ujemna.
W punkcie
1
02
=
x
występuje maksimum lokalne, gdyż z lewej strony punktu
1
02
=
x
pochod-
na jest ujemna, a z prawej strony jest dodatnia.
To samo można wywnioskować badając znak drugiej pochodnej
6
6
)
(
+
=
′′
x
x
f
.
W punkcie
3
01
−
=
x
mamy
12
)
3
(
−
=
−
′′
f
< 0, zatem w punkcie
3
01
−
=
x
jest maksimum lo-
kalne, a w punkcie
1
02
=
x
mamy
12
)
1
(
=
′′
f
> 0, zatem w punkcie
1
02
=
x
jest minimum lo-
kalne.
Maksimum lokalne jest równe
25
2
)
3
(
9
)
3
(
3
)
3
(
)
3
(
2
3
max
=
−
−
−
−
+
−
=
−
=
f
f
.
Minimum lokalne jest równe
7
2
)
1
(
9
)
1
(
3
)
1
(
)
1
(
2
3
min
−
=
−
−
+
=
=
f
f
4. Punkty przegięcia. Punkt przegięcia może wystąpić w miejscu zerowania się drugiej po-
chodnej
0
6
6
)
(
03
03
=
+
=
′′
x
x
f
, tj. w punkcie x
03
= –1.
Wartość funkcji w punkcie x
03
= –1 jest równa
9
2
)
1
(
9
)
1
(
3
)
1
(
)
1
(
2
3
=
−
−
−
−
+
−
=
f
5. Asymptoty – nie występują
9
Tabela przebiegu zmienności funkcji
2
9
3
)
(
2
3
−
−
+
=
x
x
x
x
f
x
–∞ ... –3 ... –1 ...
1
... +∞
)
(x
f
′′
–∞ –
–
–
0
+
+
+ +∞
)
(x
f
′
+∞ +
0
–
–
–
0
+ +∞
)
(x
f
–∞ ↑ 25 ↓
9
↓
–7 ↑ +∞
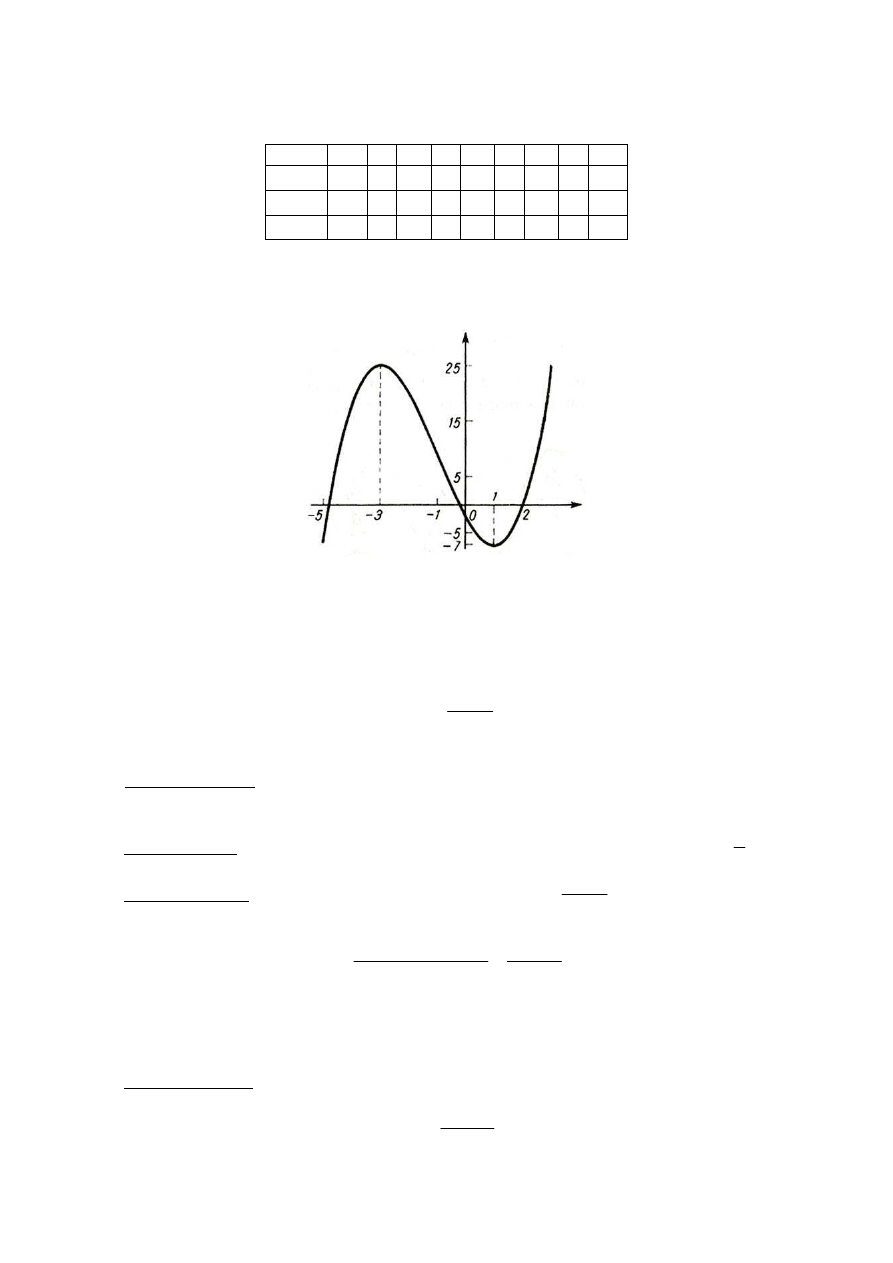
Na podstawie tabeli można sporządzić wykres funkcji
2
9
3
)
(
2
3
−
−
+
=
x
x
x
x
f
, który jest
przedstawiony na rysunku poniżej.
Wykres funkcji
2
9
3
)
(
2
3
−
−
+
=
x
x
x
x
f
Przykład 2. Zbadać przebieg zmienności funkcji homograficznej (iloraz dwóch funkcji li-
niowych)
1
3
2
)
(
+
−
=
x
x
x
f
.
Rozwiązanie
1. Dziedzina funkcji. Funkcja jest określona dla wszystkich wartości rzeczywistych
R
x
∈
z
wyjątkiem wartości x = –1.
2. Miejsca zerowe. Wyznaczamy punkt, w którym zeruje się licznik
0
3
2
=
−
x
, tj. x =
2
3
.
3. Ekstrema lokalne. Obliczamy pochodną wielomianu
1
3
2
)
(
+
−
=
x
x
x
f
2
2
)
1
(
5
)
1
(
)
3
2
(
1
)
1
(
2
)
(
+
=
+
−
−
+
=
′
x
x
x
x
x
f
> 0.
Ponieważ pochodna jest większa od zera dla wszystkich x, zatem nie występują ekstrema lo-
kalne. Funkcja jest rosnąca dla wszystkich x, w których jest określona.
4. Punkty przegięcia. Druga pochodna funkcji jest równa
3
)
1
(
10
)
(
+
−
=
′′
x
x
f
< 0,
f(x)
x
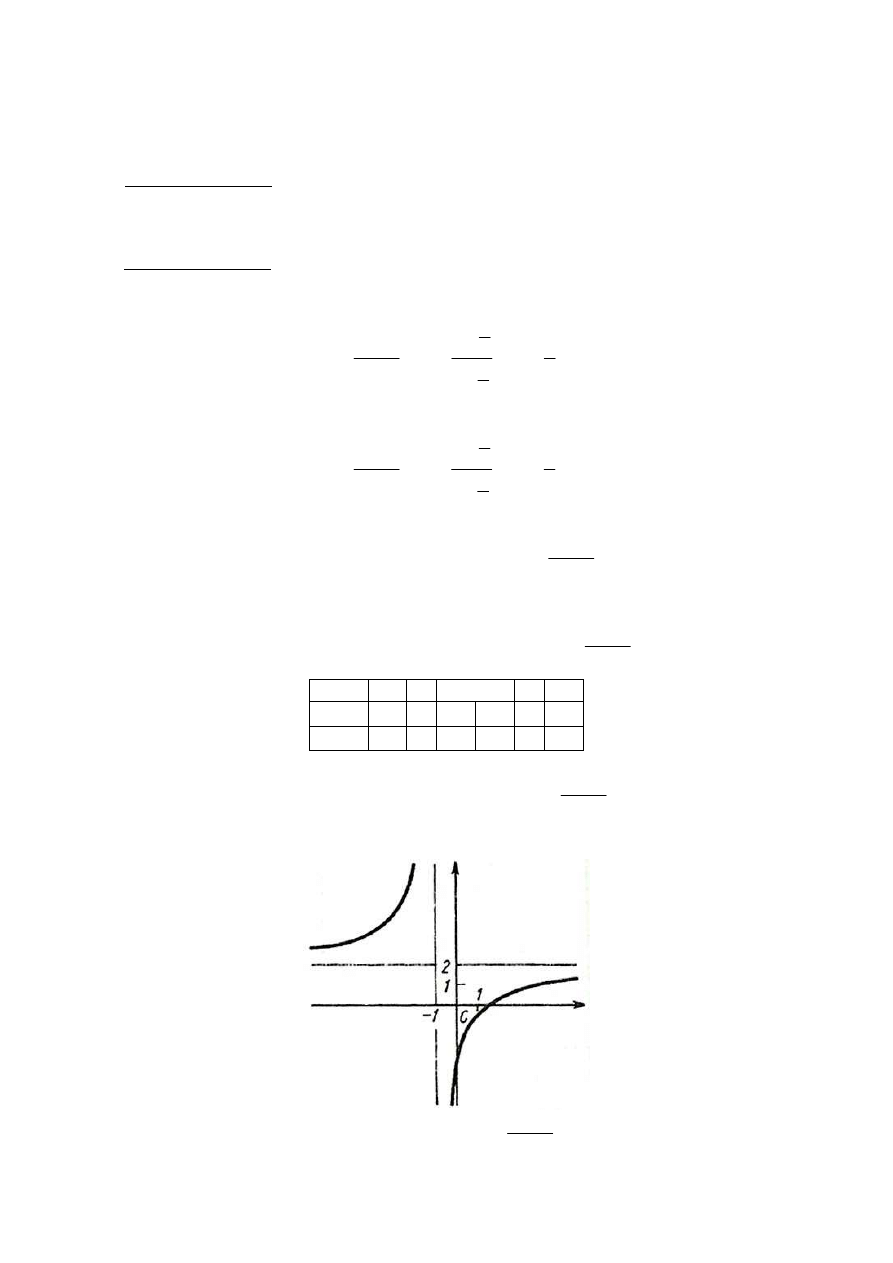
10
zatem jest mniejsza od zera we wszystkich punktach określoności. Punkty przegięcia nie wy-
stępują.
5. Asymptoty pionowe. Punkt x = 1 jest punktem nieciągłości funkcji. W tym punkcie warto-
ś
ci funkcji dążą do +∞ z lewej strony oraz do –∞ z prawej strony, zatem w punkcie
x = 1 występuje asymptota pionowa obustronna.
6. Asymptoty poziome.
Obliczamy granice
2
1
2
lim
1
1
3
2
lim
1
3
2
lim
=
=
+
−
=
+
−
=
−∞
→
−∞
→
−∞
→
x
x
x
x
x
x
x
,
2
1
2
lim
1
1
3
2
lim
1
3
2
lim
=
=
+
−
=
+
−
=
+∞
→
+∞
→
+∞
→
x
x
x
x
x
x
x
,
zatem prosta y(x) = 2 jest asymptotą poziomą funkcji
1
3
2
)
(
+
−
=
x
x
x
f
.
Tabela przebiegu zmienności funkcji
1
3
2
)
(
+
−
=
x
x
x
f
x
–∞ ...
–1
... +∞
)
(x
f
′
0
+ +∞ +∞ + +∞
)
(x
f
2
↑
+∞ –∞ ↑
2
Na podstawie tabeli można sporządzić wykres funkcji
1
3
2
)
(
+
−
=
x
x
x
f
, który jest przedstawio-
ny na rysunku poniżej.
Wykres funkcji
1
3
2
)
(
+
−
=
x
x
x
f
f(x)
x

11
Przykład 3. Zbadać przebieg zmienności funkcji
2
4
)
(
x
x
x
f
−
=
.
Rozwiązanie
1. Dziedzina funkcji. Funkcja jest określona dla wszystkich wartości rzeczywistych
R
x
∈
z
wyjątkiem wartości
x = 0.
2. Miejsca zerowe. Ponieważ
2
3
2
4
4
)
(
x
x
x
x
x
f
−
=
−
=
,
zatem wyznaczamy punkt, w którym zeruje się licznik
x
3
– 4 = 0, tj.
3
4
=
x
.
3. Ekstrema lokalne. Obliczamy pochodną funkcji
2
4
)
(
x
x
x
f
−
=
3
3
3
8
8
1
)
(
x
x
x
x
f
+
=
+
=
′
.
Pochodna jest równa zeru dla
x = –2.
Druga pochodna funkcji jest równa
4
24
)
(
x
x
f
−
=
′′
oraz
16
24
)
2
(
24
)
2
(
4
−
=
−
−
=
−
′′
f
< 0,
zatem w punkcie
x = –2 występuje maksimum lokalne równe
3
)
2
(
−
=
−
f
.
4. Asymptoty pionowe. Obliczamy granice jednostronne funkcji w punkcie nieciągłości x = 0
−∞
=
−
−
→
2
0
4
lim
x
x
x
oraz
−∞
=
−
+
→
2
0
4
lim
x
x
x
,
zatem funkcja
2
4
)
(
x
x
x
f
−
=
ma w punkcie x = 0 asymptotę pionową obustronną pokrywają-
cą się z pionową osią układu współrzędnych .
5. Asymptoty poziome. Ponieważ
−∞
=
−∞
→
)
(
lim
x
f
x
oraz
+∞
=
+∞
→
)
(
lim
x
f
x
, funkcja
)
(x
f
nie ma
asymptot poziomych.
6. Asymptoty ukośne. Obliczamy granice
1
4
1
lim
)
(
lim
3
=
−
=
−∞
→
−∞
→
x
x
x
f
x
x
oraz
1
4
1
lim
)
(
lim
3
=
−
=
−∞
→
+∞
→
x
x
x
f
x
x
,
zatem
1
)
(
lim
=
=
∞
→
x
x
f
A
x
.
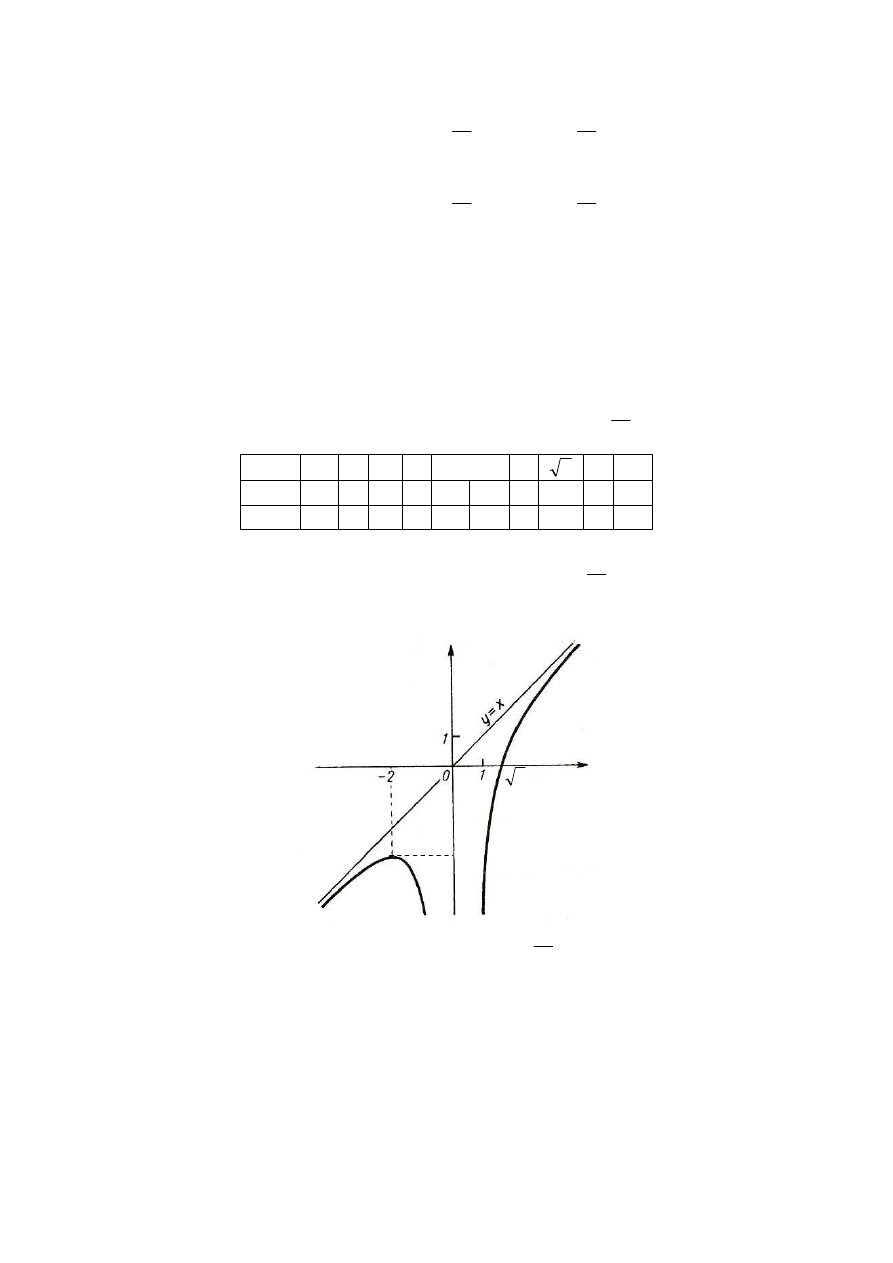
12
[
]
0
4
lim
4
lim
)
(
lim
2
2
=
−
=
−
−
=
−
−∞
→
−∞
→
−∞
→
x
x
x
x
Ax
x
f
x
x
x
,
[
]
0
4
lim
4
lim
)
(
lim
2
2
=
−
=
−
−
=
−
+∞
→
+∞
→
+∞
→
x
x
x
x
Ax
x
f
x
x
x
,
Zatem
[
]
Ax
x
f
B
x
−
=
∞
→
)
(
lim
= 0.
Stąd wynika, że prosta
B
Ax
y
+
=
=
x jest wspólną asymptotą ukośną w –∞ oraz +∞.
Tabela przebiegu zmienności funkcji
2
4
)
(
x
x
x
f
−
=
x
–∞ ... –2 ...
0
...
3
4
... +∞
)
(
x
f
′
+
+
0
– –∞ +∞ +
+
+
+
)
(
x
f
–∞ ↑ –3 ↓ –∞ –∞ ↑
0
↑
+∞
Na podstawie tabeli można sporządzić wykres funkcji
2
4
)
(
x
x
x
f
−
=
, który jest przedstawio-
ny na rysunku poniżej.
Wykres funkcji
2
4
)
(
x
x
x
f
−
=
Opracowano na podstawie:
1. M. Gewert, Z. Skoczylas: Analiza matematyczna 1. Definicje, twierdzenia, wzory. Oficyna
Wyd. GiS. Wrocław 2011.
2. W. Krysicki, L. Włodarski: Analiza matematyczna w zadaniach 1. PWN 2011.
f(x)
x
3
4
–3
Wyszukiwarka
Podobne podstrony:
badania operacyjne 3 id 76767 Nieznany (2)
24 Badanie czwornikow id 30562 Nieznany
5 ekstrema funkcji id 40709 Nieznany (2)
badania spoleczne id 76697 Nieznany
Badania Marketingowe id 76354 Nieznany
7 Funkcjonalizm id 44874 Nieznany (2)
Badania laboratoryjne id 76309 Nieznany
Funkcje 5 id 181902 Nieznany
Funkcje 6 id 181903 Nieznany
analiza i badanie rynku id 6045 Nieznany (2)
AMI 14 Funkcje c d id 59050 Nieznany (2)
badania operacyjne 1 id 76766 Nieznany
Badanie gleby id 77148 Nieznany
Badanie przedmiotowe id 77693 Nieznany (2)
generator funkcji (1) id 187188 Nieznany
Pochdne funkcji id 364356 Nieznany
Granice funkcji 4 id 195392 Nieznany
badania operacyjne 9 id 76768 Nieznany
C Typy Funkcje id 96656 Nieznany
więcej podobnych podstron