Elektrotechnika i elektronika (konspekt)
Franciszek Gołek
(golek@ifd.uni.wroc.pl)
www.pe.ifd.uni.wroc.pl
Wykład 7 i 8.
Maszyny elektryczne prądu zmiennego
Elektrotechnika i elektronika (konspekt)
Franciszek Gołek
(golek@ifd.uni.wroc.pl)
www.pe.ifd.uni.wroc.pl
Wykład 7 i 8.
Maszyny elektryczne prądu zmiennego
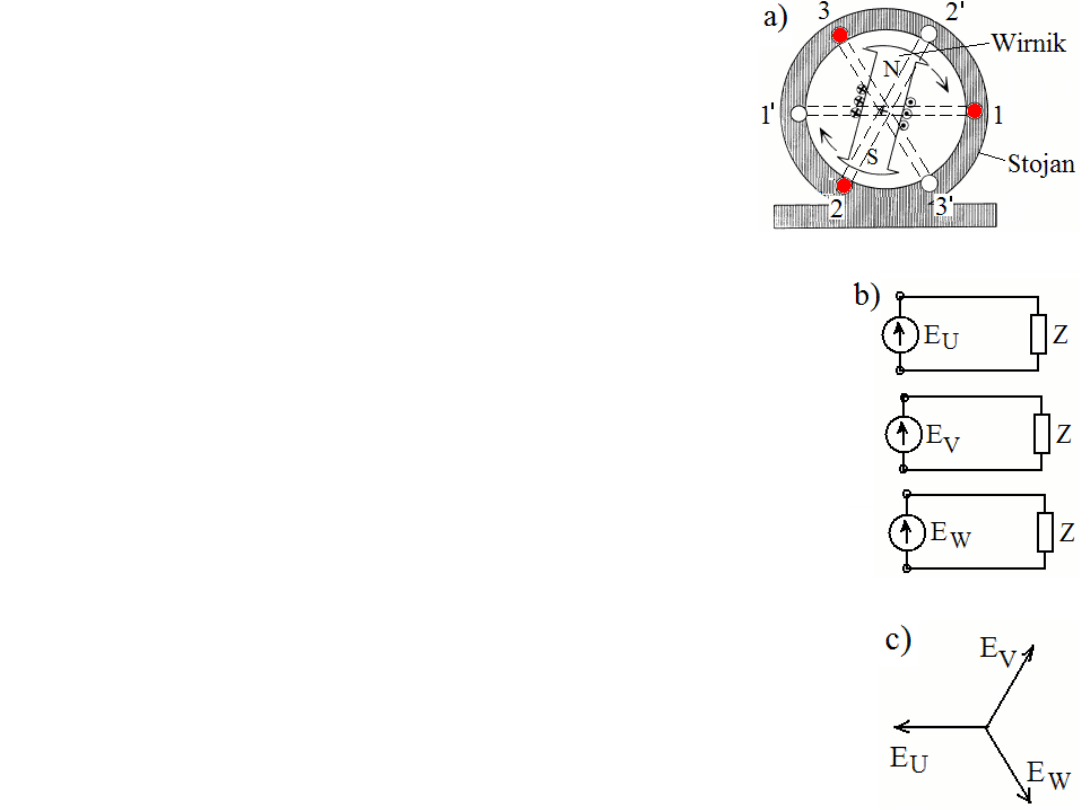
Układy trójfazowe
Gdy umieścimy trzy uzwojenia 1-1’, 2-2’
i 3-3’ tak jak na rys. (a), kąt między
kolejnymi ramkami wynosi tu 120° to
wirujący magnes w ich środku wygeneruje
siły elektromotoryczne SEM, które będą
się różnić między sobą fazą o 120° i można je
zapisać jako I) e
U
= E
Um
sin(
ω
t), II) e
V
= E
Vm
sin(
ω
t -
2
π
/3), III) e
W
= E
Wm
sin(
ω
t - 4
π
/3) = E
Wm
sin(
ω
t +
2
π
/3). Dopóki obwody te nie są ze sobą połączone
nazywamy je nieskojarzonymi (rys. b). Łącząc taki
układ w gwiazdę lub w trójkąt uzyskujemy
trójfazowy układ skojarzony (powszechnie zwany
układem trójfazowym, rys. c). Układy trójfazowe są
powszechnie stosowane w elektroenergetyce.
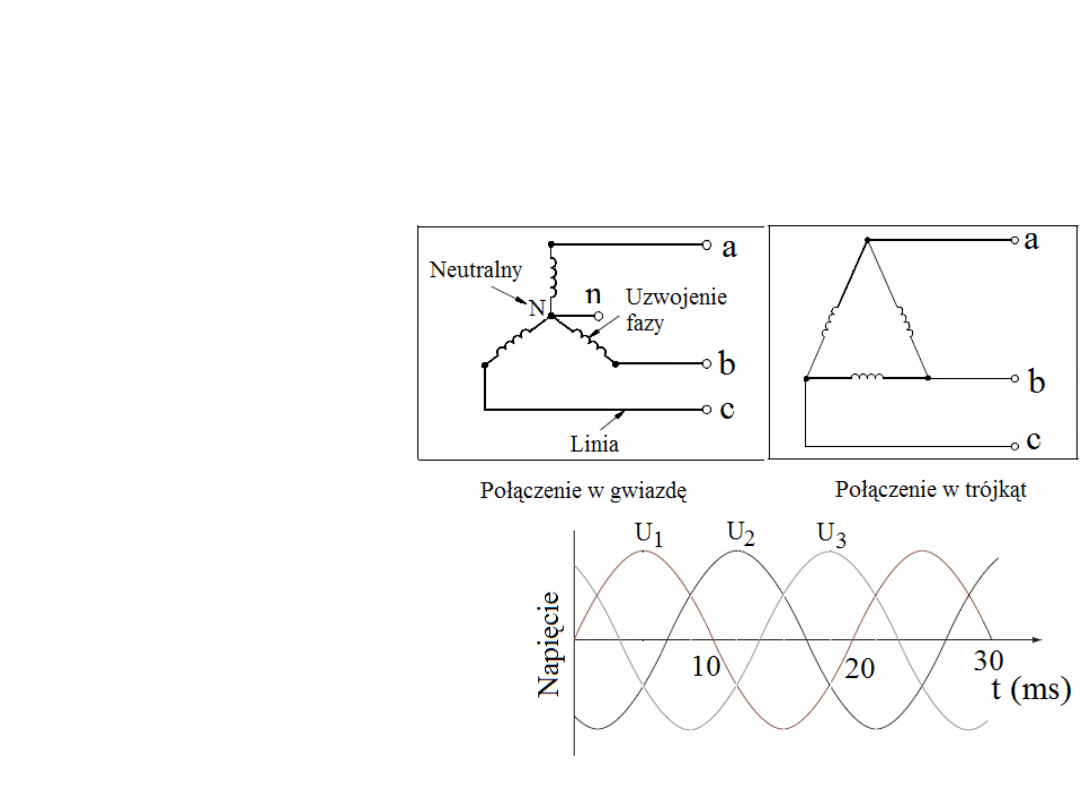
Układy trójfazowe skojarzone możemy łączyć na dwa sposoby:
połączenie w trójkąt (deltę
∆
) i w gwiazdę (Y). Przy połączeniu w
gwiazdę mamy dwie możliwości: trójprzewodowa (a b i c) lub
czteroprzewodowa – z przewodem neutralnym.
Warto zauważyć, że
przy symetrycznym
obciążeniu wszystkich
faz suma wektorowa
napięć podobnie jak
suma wektorowa
prądów wyniesie zero
w każdej chwili.
U
an
= U
an
∠
0°,
U
bn
= U
bn
∠
-120°,
U
cn
= U
cn
∠
-240° = U
cn
∠
120°,
Często operujemy wartościami: U
an
= U
bn
= U
cn
= U
skuteczne
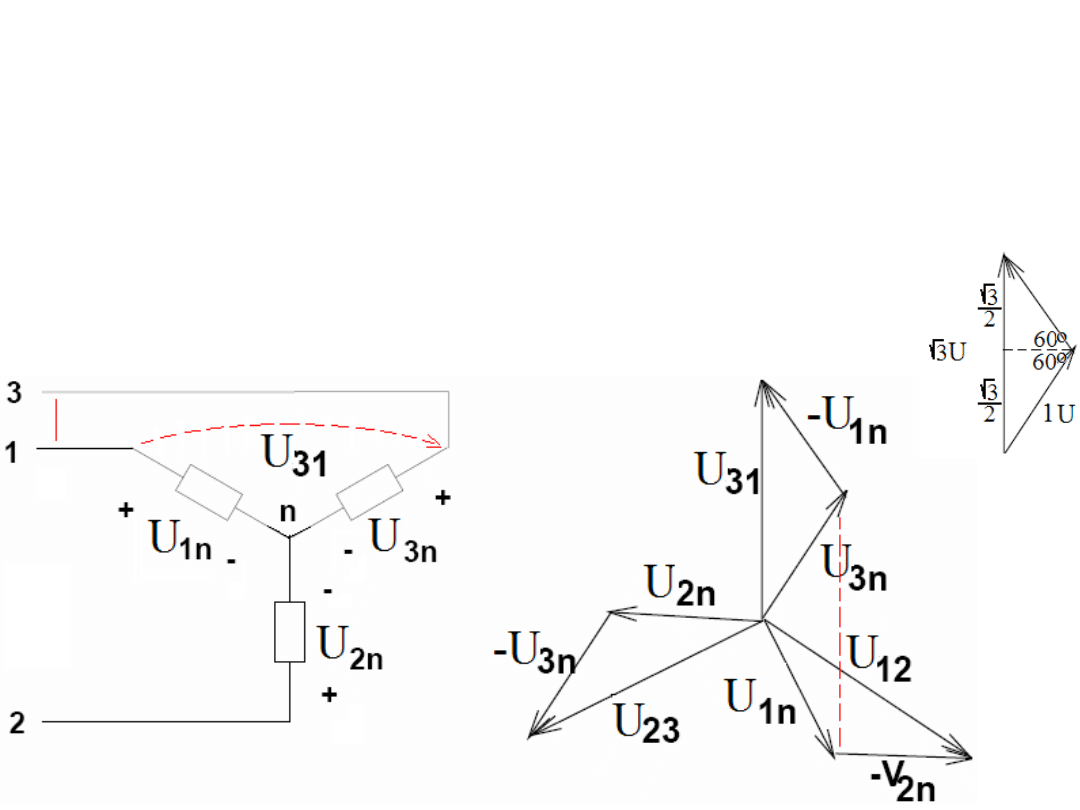
Relacje między napięciami fazowymi i międzyfazowymi.
Gdy obciążenie w układzie trójfazowym jest symetryczne to moduły prądów są
identyczne a same prądy są względem siebie przesunięte o 120° ich suma w
przewodzie neutralnym zeruje się. Gdy obciążenie jest niesymetryczne to w
przewodzie neutralnym (przy połączeniu w gwiazdę) płynie prąd niezerowy
będący niezerową sumą prądów fazowych.
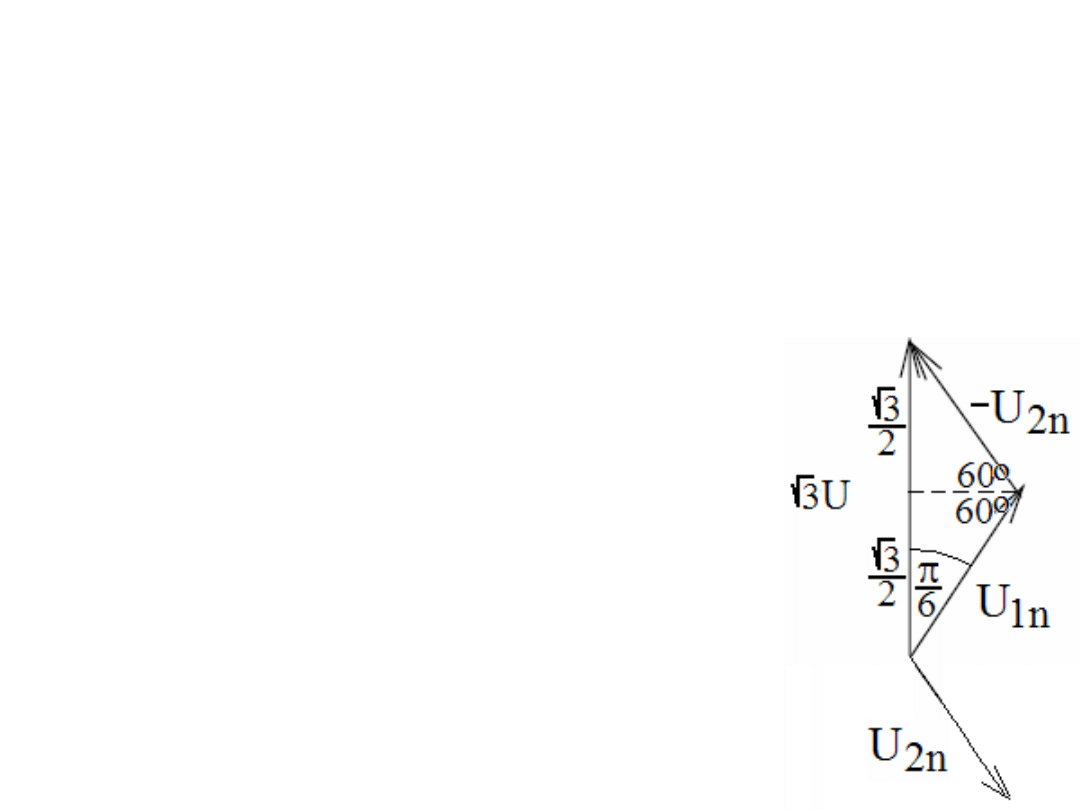
Gdy obciążenie w układzie trójfazowym połączonym w Y
(gwiazdę) jest symetryczne to moduły napięć
międzyfazowych są
√
3 razy większe od modłów napięć
fazowych. To samo dotyczy operowania wartościami
skutecznymi.
Przykładowo U
1n
= U
∠
Φ, U
2n
= U
∠
(Φ - 2
π
/3),
U
3n
= U
∠
(Φ + 2
π
/3),
U
12
= U
1n
– U
2n
= U
∠
Φ – U
∠
(Φ - 2
π
/3)
= U
∠
Φ + U
∠
(Φ +
π
- 2
π
/3)
= U
∠
Φ + U
∠
(Φ +
π
/3),
=
√
3U
∠
(Φ +
π
/6),
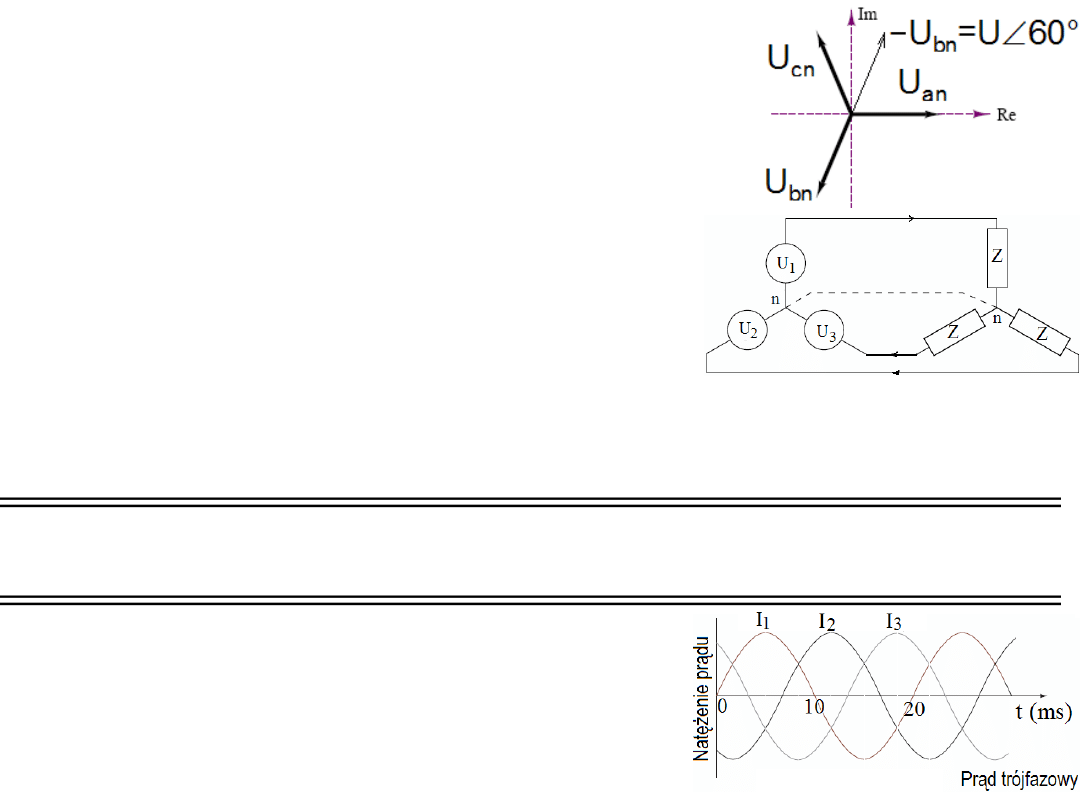
U
ab
= U
an
– U
bn
= U
∠
0°- U
∠
-120°
= U
∠
0°+ U
∠
60° =
√
3U
∠
30°
U
bc
= U
∠
-120°- U
∠
120° =
√
3U
∠
-90°
U
ca
= U
∠
120°- U
∠
0° =
√
3U
∠
150°
U
an
+ U
bn
+ U
cn
= 0 podobnie:
I
n
= I
a
+ I
b
+ I
c
= (U
an
+ U
bn
+ U
cn
)/Z
= 0
Moc: dla uproszczenia niech Z = R
p
a
(t) = (U
a
cos
ω
t)
2
/R = (U
a
2
/R)(cos
ω
t)
2
= (U
a
2
/R)(1/2)(1 + cos2
ω
t) = (U
skutecz
2
/R)(1 + cos2
ω
t)
= (U
2
/R)(1 + cos2
ω
t),
p
b
(t) = (U
b
cos(
ω
t – 120°)
2
/R = (U
2
/R)[1 + cos(2
ω
t - 240°)]
= (U
2
/R)[1 + cos(2
ω
t +120°)],
p
c
(t) = (U
c
cos(
ω
t – 240°)
2
/R = (U
2
/R)[1 + cos(2
ω
t - 120°)].
p(t) = p
a
(t) + p
b
(t)+ p
c
(t) = 3U
2
/R + (U
2
/R)[cos(2
ω
t) + cos(2
ω
t - 120°) + cos(2
ω
t + 120°)] =
= 3U
2
/R = stała wartość! Cała moc chwilowa nie pulsuje! Gdy jest symetria!
Jeżeli Z
a
= Z
b
= Z
c
=
Z
Y
∠ϕ
to mamy moc zespoloną:
dla każdej fazy S = UI* = P + jQ = UI*cos
ϕ
+ jUI*sin
ϕ
gdzie U i I* - wartości skuteczne. Razem: S
Total
= S
T
=
= 3P + j3Q =
√
[(3P)
2
+ (3Q)
2
]
∠ϕ
. Moc pozorna:
S
T
= 3
√
[(UIcos
ϕ
)
2
+ (UIsin
ϕ
)
2
] = 3UI, P
T
=
S
T
cos
ϕ
.
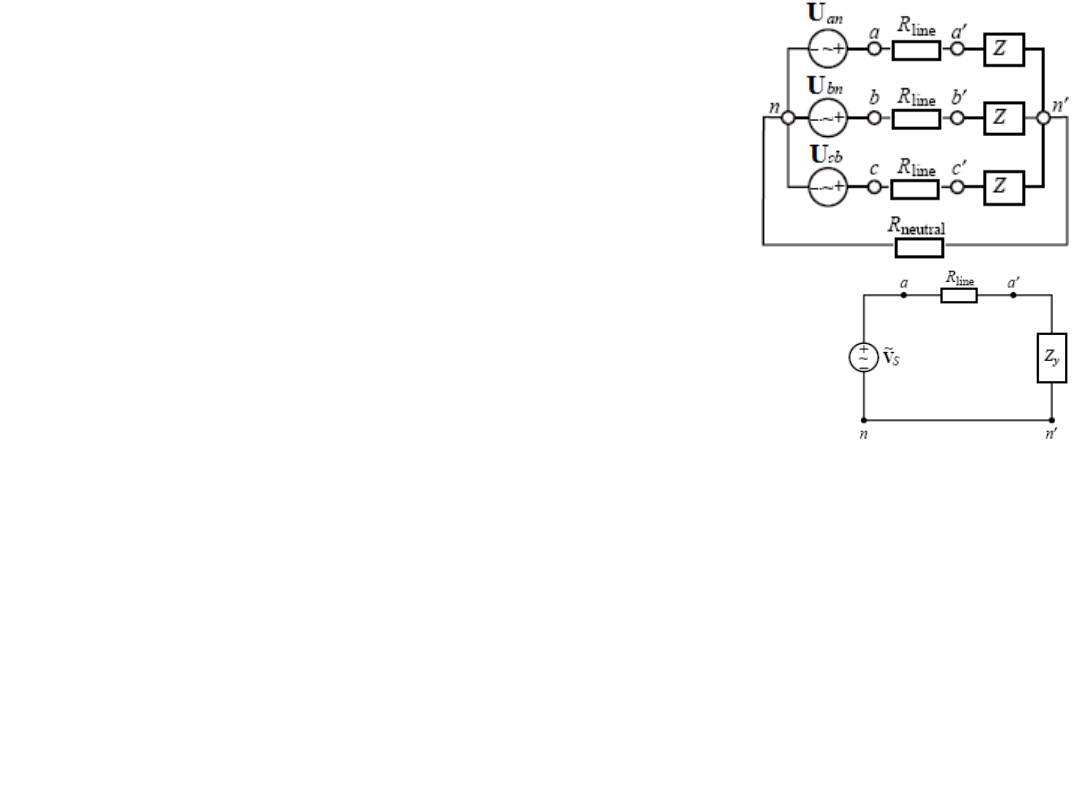
Przykład. Obliczyć moc P
o
dostarczaną
z generatora trójfazowego do obciążenia
w układzie jak na rysunku mając dane:
U
an
= 480
∠
0° V, U
bn
= 480
∠
-2
π
/3 V,
U
cn
= 480
∠
2
π
/3 V, Z = 2 + j4 = 4,47
∠
(1,107)
Ω
,
R
line
= 2
Ω
, R
neutral
= 10
Ω
.
(stosować wartości skuteczne napięć).
Rozw. Ponieważ układ jest zrównoważony
(tj. symetrycznie obciążony) możemy stosować
obliczenia dla jednej fazy. Prąd w linii „neutral” jest równy 0
oraz U
nn’
= 0.
P
a
= I
2
R
o
I =
U
an
/(Z + R
line
)
=
(480
∠
0)/(2 + j4 + 2)
=
(480
∠
0)/(5,657
∠π
/4)
= 84,85 A !
P
a
= I
2
R
o
= (84,85)
2
×
2 = 14,4 kW.
Komentarz: warto odnotować, że przy symetrycznym obciążeniu w przewodzie
neutralnym jednak prąd wynosi 0 A, nie ma tam spadku napięcia, dzieje się tak
dzięki zerowej sumie prądów z wszystkich trzech faz. Dlatego pomijamy R
neutral
.
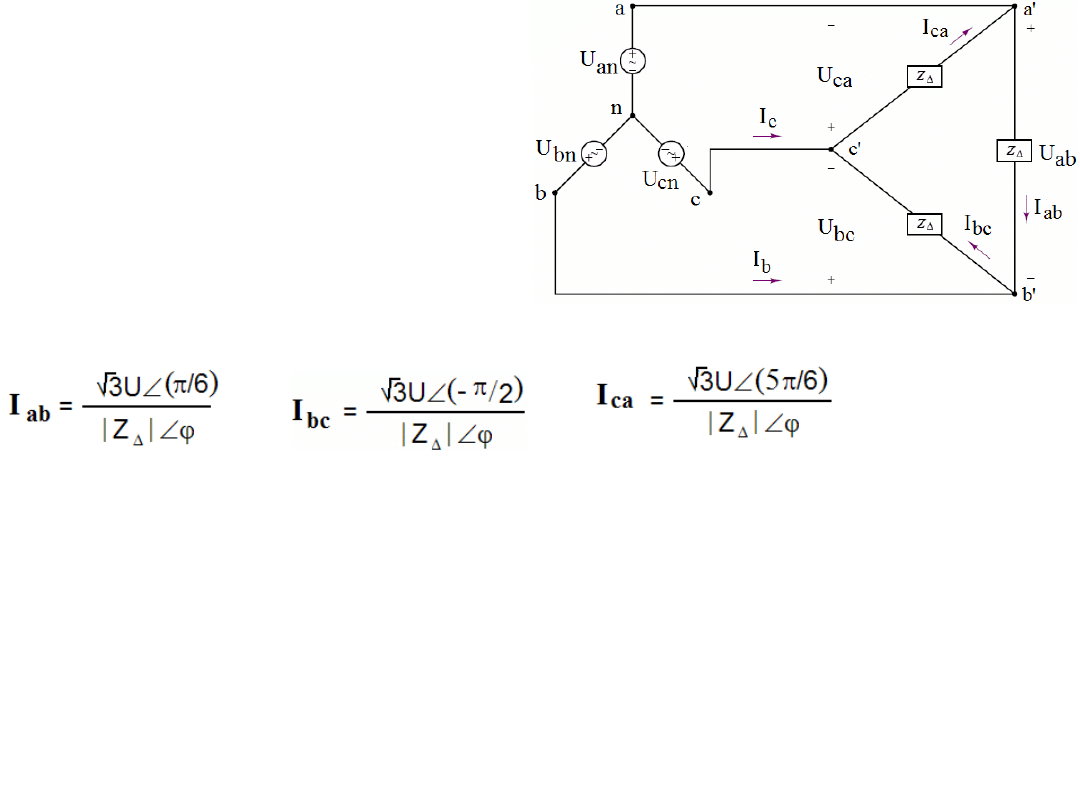
Zdarza się, że generator trójfazowy
w układzie gwiazdy jest obciążony
odbiornikiem mocy w układzie delta
(trójkąta) jak na rysunku.
W tej sytuacji prądy w obciążeniach Z
∆
będą wynosić (zobacz na stronie 6
dlaczego U
międzyfazowe
=
√
3U
fazowe
):
Zatem prąd w Z
Δ
jest
√
3 razy większy niż płynełoby przez Z
Y
. Okazuje się, że
prądy w liniach czyli I
a
, I
b
i I
c
będą aż 3-krotnie większe niż w sytuacji, gdy
obciążenia były połączone w gwiazdę:
(I
a
)
∆
= U
ab
/Z – U
ca
/Z = (1/Z)(U
an
– U
bn
– U
cn
+ U
an
) = (1/Z)[2U
an
– (U
bn
+ U
cn
)] =
= 3U
an
/Z
Zatem i pobierana moc będzie tu 3-krotnie większa:
Linie przesyłowe niskiego napięcia do około 1 kV oraz napięć średnich (1 – 30
kV) budowane są jako kablowe w sieci miejskiej i napowietrzne jako rejonowe
(poza miastem i na terenach wiejskich).
Linie wysokiego napięcia, 110 kV i wyższe (220, 400 i 750 kV), są przeważnie
budowane jako napowietrzne sporadycznie budowane są jako kablowe (na
terenach o znacznej gęstości zabudowy) wynika to z faktu, iż linie kablowe są
kilkukrotnie droższe od napowietrznych.
Podstawowymi elementami linii napowietrznych są: przewody fazowe,
przewody odgromowe, słupy (konstrukcje wsporcze), izolatory, osprzęt
(przewodowy i izolatorowy) oraz uziomy słupów.
W liniach średniego napięcia słupy są wykonane z żelbetonu lub rur stalowych.
W liniach wysokiego napięcia stosowane są słupy stalowe kratowe lub rurowe.
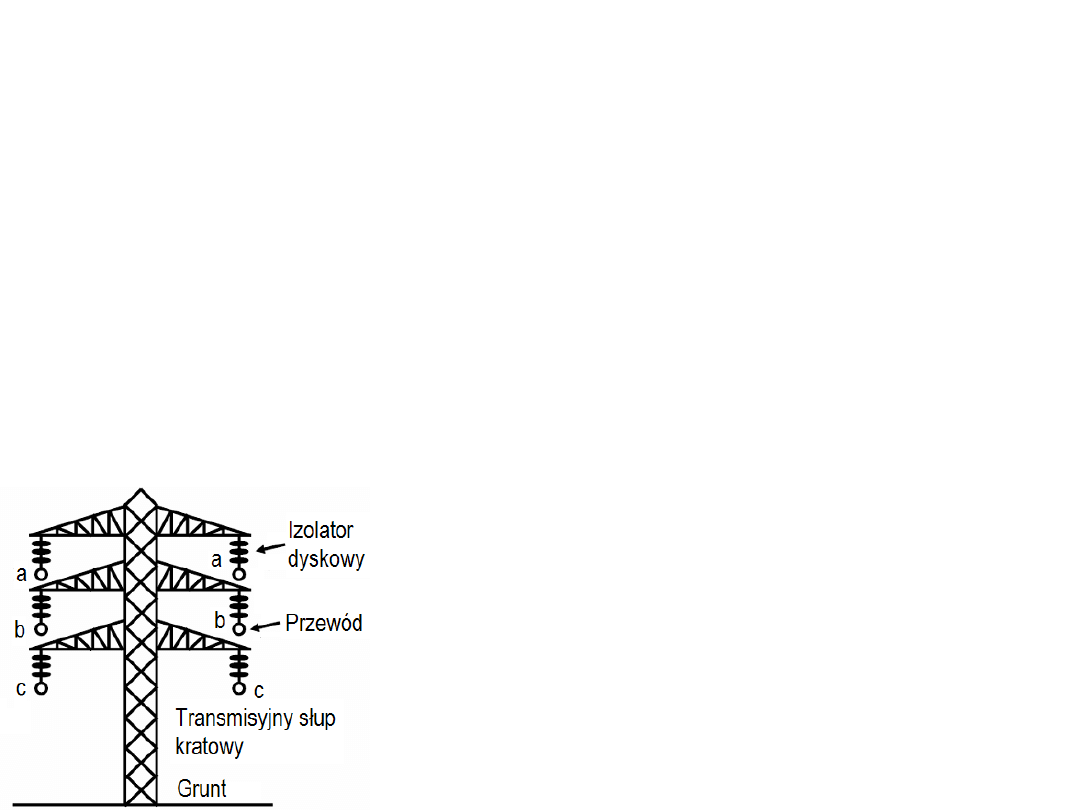
Słupy transmisyjne
(wynik projektowania
słupów o małej masie – czyli oszczędnych
i dużej wytrzymałości nie zawsze jest pozytywny: w wyniku
oblodzenia przewodów zniszczenia mogą przeważyć nad
oszczędnościami!)
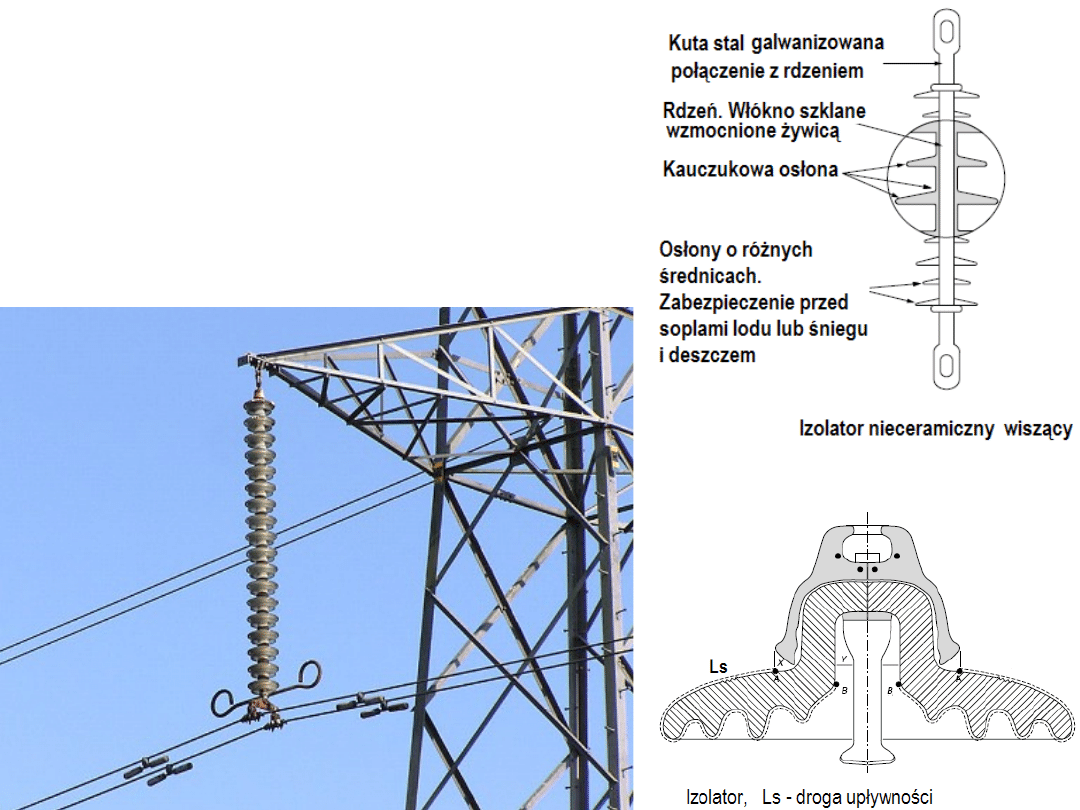
Zadaniem izolatorów jest nie
tylko podtrzymywać przewody
ale też eliminować prądy
upływności!
Linie wysokiego napięcia od linii niskiego
napięcia oddzielają transformatory (zanurzone w
oleju!).
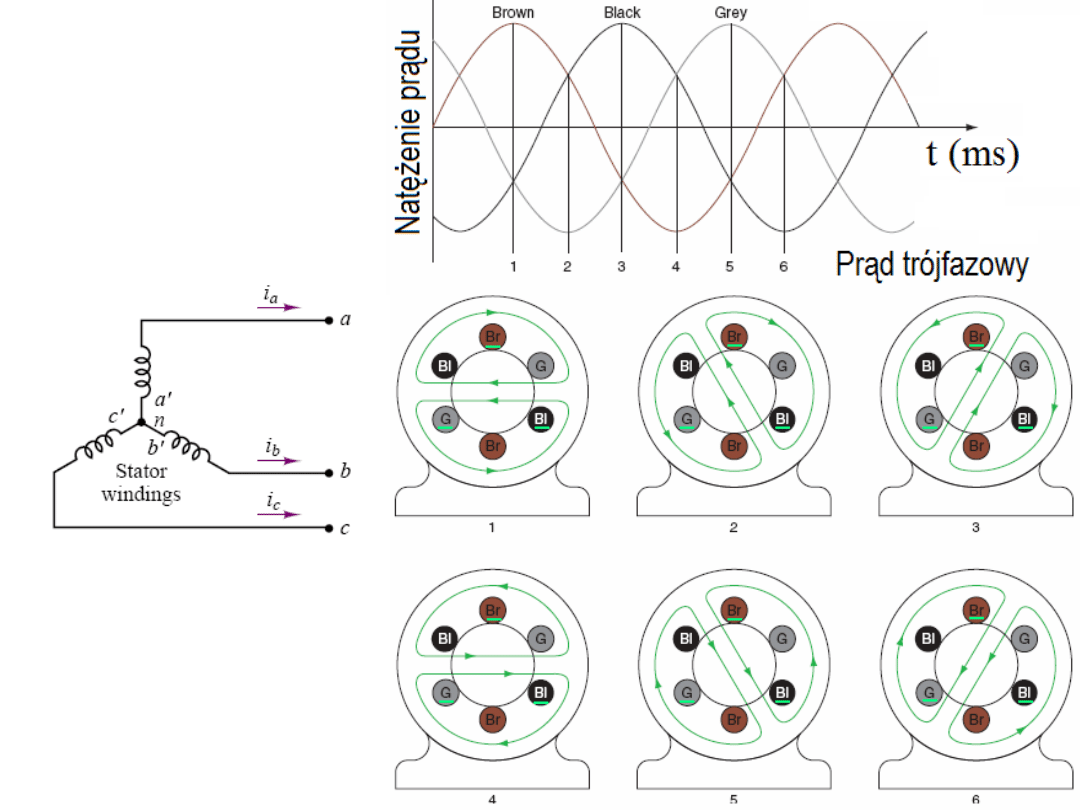
Wytwarzanie
wirującego pola
magnetycznego
Fundamentalną zasadą działania maszyn prądu przemiennego
jest wytwarzanie wirującego pola magnetycznego, które wymusza
obroty wirnika z prędkością zależną od prędkości wirowania pola
magnetycznego.
Prądnice (generatory) prądu przemiennego (zmiennego) są
produkowane jako jednofazowe lub jako wielofazowe. W śród
wielofazowych mamy do czynienia niemal wyłącznie z
trójfazowymi.
Maszyny synchroniczne
Maszyny synchroniczne budowane są zarówno jako prądnice i jako silniki.
Obecnie większość energii elektrycznej jest produkowana przez generatory
synchroniczne trójfazowe, które stosowane są przede wszystkim w
elektrowniach, w Polsce instalowane są jednostki o mocy nawet 500 MW.
Silniki synchroniczne stosowane są do napędu maszyn a zwłaszcza tam gdzie
wymagana jest stała prędkość obrotowa. Silniki synchroniczne trójfazowe są
budowane na duży zakres mocy; aż do 50 000 KM.
Jednofazowe silniki synchroniczne stosowane są w zakresie małych mocy
(poniżej 0,1 KM). Brak komutatorów w maszynach prądu zmiennego oznacza
bark problemów związanych z komutatorami (ścieranie szczotek itp.).
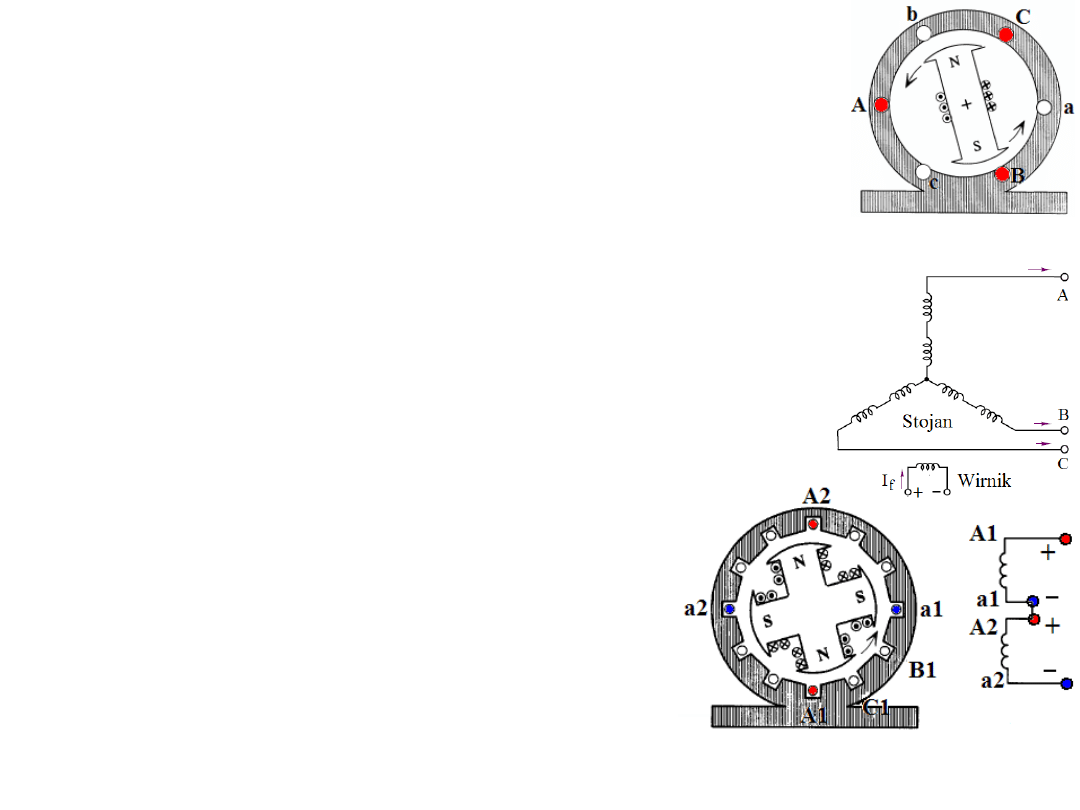
Maszyny synchroniczne podobnie jak maszyny prądu stałego
składają się z twornika i wzbudzenia (czasem nazywanego
magneśnicą). W przypadku maszyn synchronicznych jednak
magneśnicą zwykle jest wirnik a twornikiem stojan (przeciwnie do
maszyn prądu stałego). Gdy w układzie przedstawionym obok
dwubiegunowy wirnik wiruje z prędkością 3000 obr/min (czyli 50
obr/s) to w 3 uzwojeniach stojana generowane będą trzy siły
elektromotoryczne o częstotliwości 50 Hz i przesunięte
względem siebie o +/-120°. Będzie to napięcie trójfazowe!
Prędkość wirowania przy większej ilości par biegunów p
i częstotliwości napięcia f = 50 Hz jest
mniejsza i wynosi: n = f/p obr/s
Przykładowo przy czterech biegunach mamy ich
dwie pary: n = 50/2 = 25 obr/s = 1500 obr/min
bo przy jednym obrocie mamy 2 cykle zmian pola.
W praktyce liczbę par biegunów w generatorach
dyktuje napęd: gdy mamy szybkie turbiny parowe
wystarczy 1 lub 2 pary, dla powolnych hydroturbin trzeba więcej! Dolny rysunek
pokazuje ideę ułożenia uzwojeń.
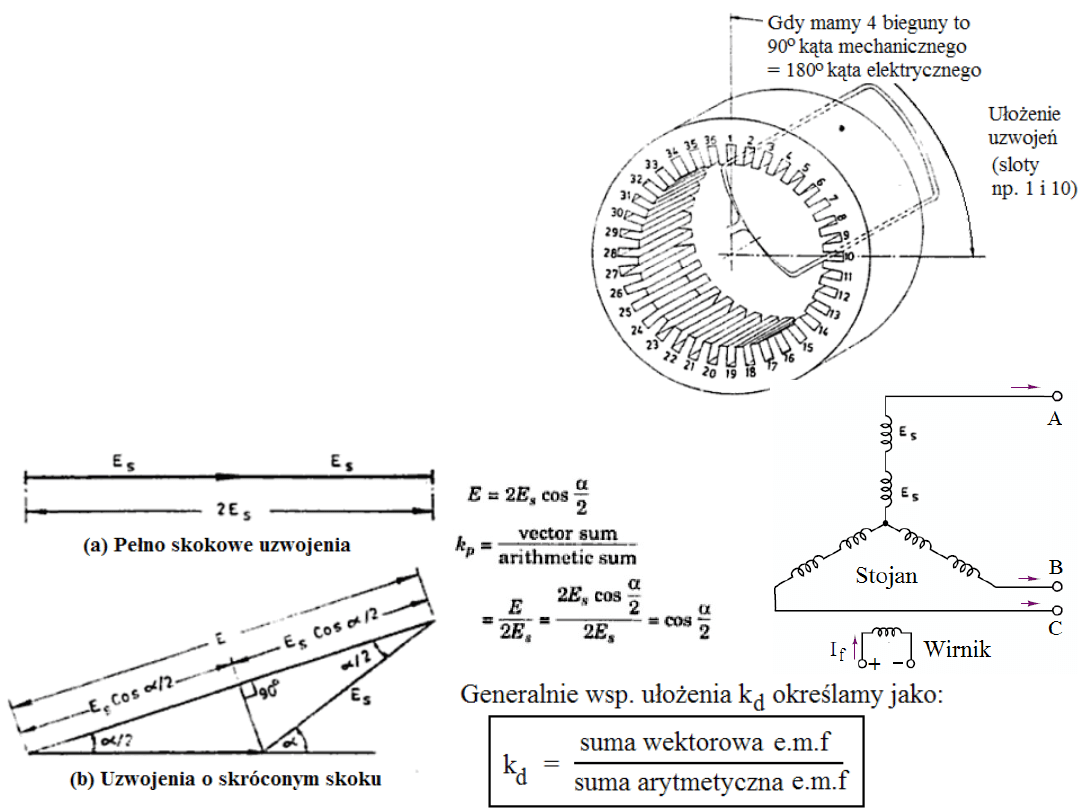
Odnośnie skoku uzwojeń stojana należy
dodać, że połączone szeregowo
składniki (części uzwojeń) prowadzą
do sumowania nie zawsze idealnie
zgodnych w fazie części SEM.
Mówimy wtedy, że tzw. „pitch factor”
k
p
= cos(α/2) < 1 jest mniejszy od jedności.
Dla wyższych harmonicznych
k
pn
= cos(nα/2) i przy nα/2 = 90º mamy
cenne wyeliminowanie n-tej harmonicznej.
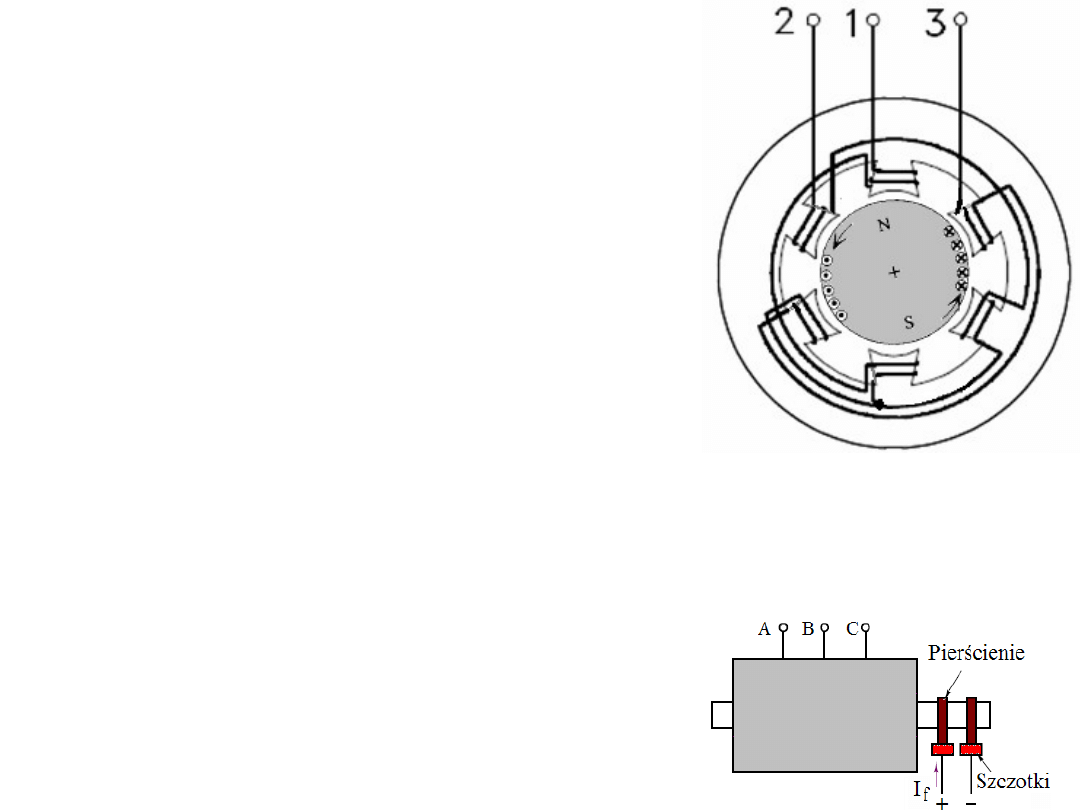
Rotor może mieć geometrię wystających
nabiegunników (bieguny jawne) albo geometrię
walca (bieguny utajone) z zanurzonymi w slotach
uzwojeniami.
Geometria cylindryczna jest łatwiejsza w analizie,
gdyż taki rotor praktycznie nie zmienia pola
stojana w czasie wirowania. Takie maszyny mogą
pracować z dużymi prędkościami do 3000 obr/min.
Maszyny z rdzeniami jawnymi budowane są do
małych prędkości, do 750 obr/min.
Dodać należy, że chociaż nie ma w tych
maszynach komutatorów to jednak, dla
wymuszenia prądu stałego wzbudzenia
(namagnesowania) w wirniku, konieczne są
kontakty ślizgowe czyli szczotki ślizgające się po
wirujących pierścieniach.
Moment obrotowy T
maszyny z cylindrycznym wirnikiem możemy wyrazić
przy pomocy natężenia stałego prądu wirnika I
f
oraz natężenia zmiennego
prądu stojana I
s
:
T = k I
s
(t) I
f
sin(
γ
),
γ
- kąt między polami stojana a wirnika, k – stała maszyny. Albo:
T = k√2I
ss
sin(ω
e
t) I
f
sin(
γ
),
I
ss
– wartość skuteczna I
s
, ω
e
– pulsacja prądu (częstość elektryczna).
Uwzględniając zależność czasową
γ
=
γ
0
+ ω
m
t, gdzie
γ
0
– kąt początkowy, ω
m
– prędkość kątowa (mechaniczna) wirnika, można napisać, że:
T = k√2I
ss
I
f
sin(ω
e
t) sin(ω
m
t +
γ
0
)
= k(√2/2)I
ss
I
f
cos[(ω
m
− ω
e
)t − γ
0
] − cos[(ω
m
+ ω
e
)t + γ
0
]
Widać, że średnia wartość będzie niezerowa tylko wtedy gdy (ω
m
− ω
e
) = 0
tzn. gdy silnik obraca się synchronicznie z wirującym polem (ma prędkość
synchroniczną) i wtedy T jest sumą wartości stałej i pulsującej z częstością
2ω
e
. Ta pulsacja wzięła się z powodu rozważań tylko jednej fazy, zastosowanie
wielu faz redukuje ten efekt do zera i zapewnia stały moment obrotowy. Mamy
zatem:
〈
T
〉
= k√2I
ss
I
f
cos(
γ
0
)
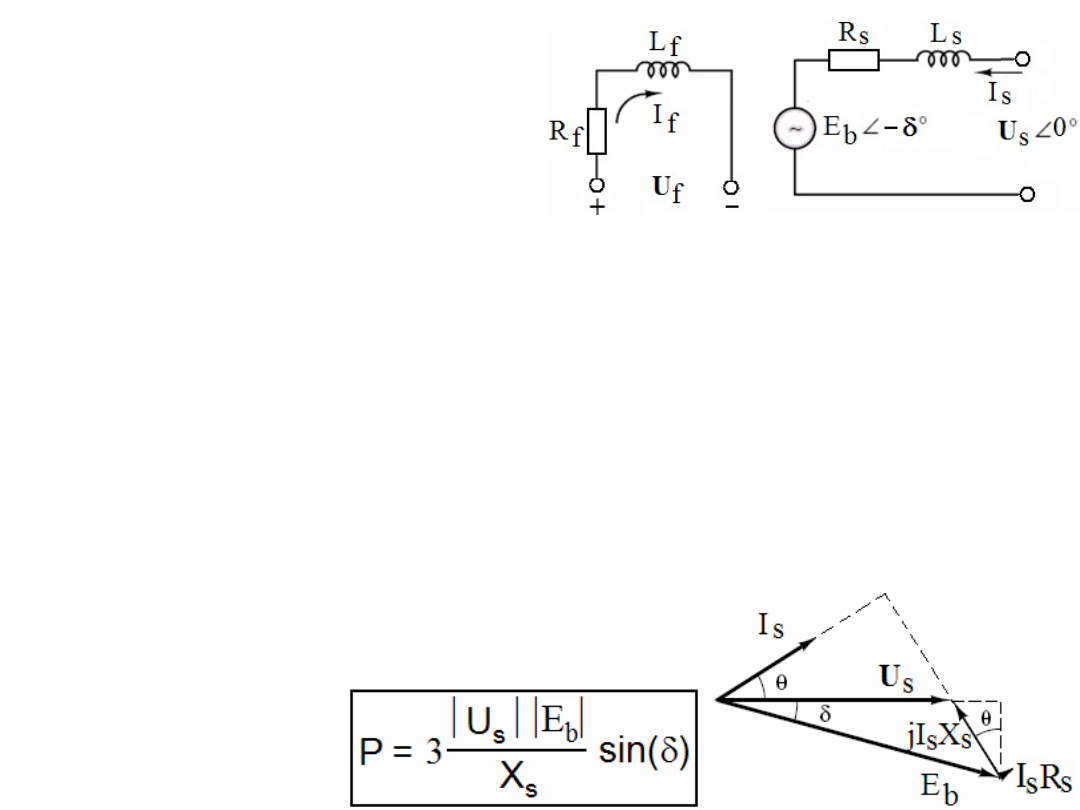
Model jednej fazy silnika synchronicznego
pokazuje rys obok. Uzwojenie wirnika
reprezentuje rezystancja R
f
i indukcyjność
L
f
. Jedno uzwojenie stojana reprezentuje
rezystancja R
s
, indukcyjność L
s
oraz
Indukowana (wsteczna) SEM E
b
. Bilans napięć stojana możemy zapisać jako:
U
s
= E
b
+ I
s
(R
s
+ jX
s
)
gdzie X
s
reprezentuje efektywną reaktancję stojana (z uwzględnieniem magnetyzacji).
Moc silnika pochodzącą od jednej fazy możemy wyrazić jako:
P
wy
=
ω
s
T =
U
s
I
s
cos(
Θ
)
gdzie
Θ
- różnica faz między U
s
i I
s
. Zakładając, że R
s
≈
0 możemy wnosić, że moc
tracona jest do zaniedbania i moc wejściowa jest równa mocy wyjściowej:
P
1Φ
= P
we
= P
wy
=
ω
s
T =
U
s
I
s
cos(
Θ
),
z wykresu:
E
b
sin(
δ
) =
I
s
X
s
cos(
Θ
), mnożąc przez U
s
:
E
b
U
s
sin(
δ
) =
U
s
I
s
X
s
cos(
Θ
) = P
1Φ
X
s
,
Zatem cała moc maszyny
trójfazowej wyniesie:
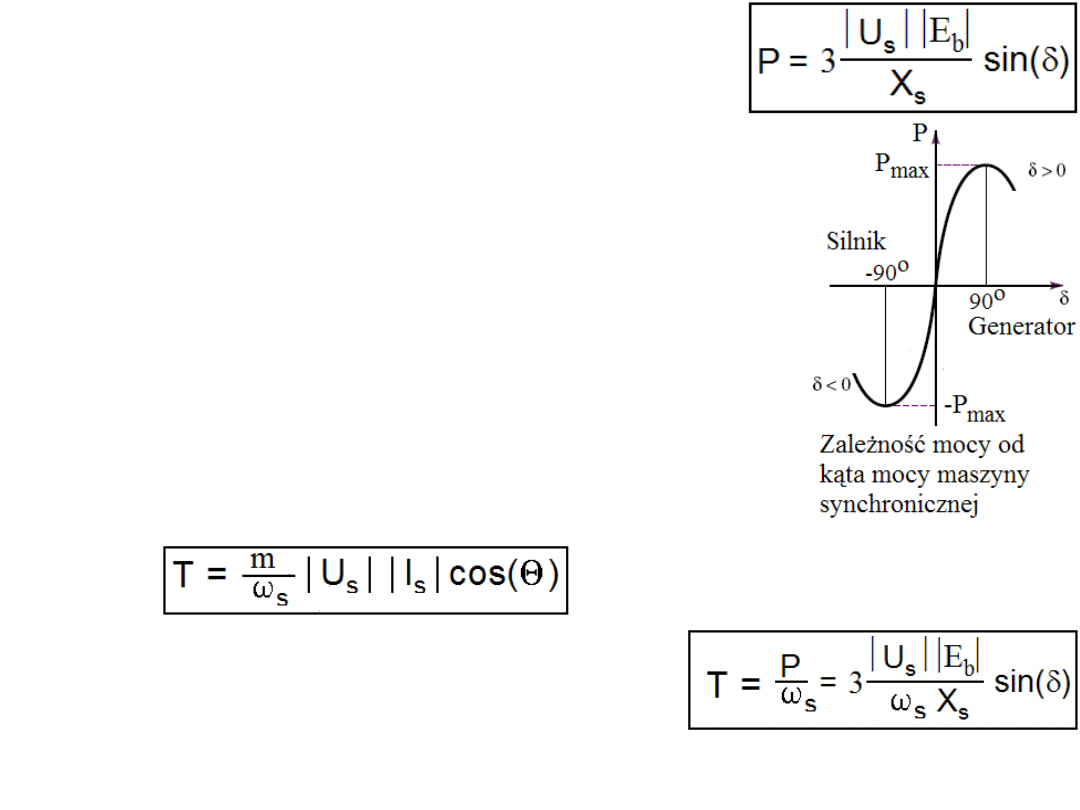
Ponieważ, jak widać, kąt
δ
ma wpływ na
moc maszyny nazywamy go kątem mocy.
Prądnice (generatory) synchroniczne zwykle
pracują przy kącie mocy w przedziale 15° do 25°.
Silniki natomiast pracują niemal w całym zakresie
0° - 90°. Po osiągnięciu
δ
= 90° silnik jednak
zwalnia i wypada z biegu synchronicznego, wtedy
odpowiednie zabezpieczenie wyłącza silnik.
Maksymalny moment obrotowy (nazywany
momentem zrównania Pull-out) jest ważnym
parametrem silnika synchronicznego.
Całkowity moment obrotowy możemy wyrazić jako:
gdzie m – jest liczbą faz. Dla 3 faz otrzymamy:
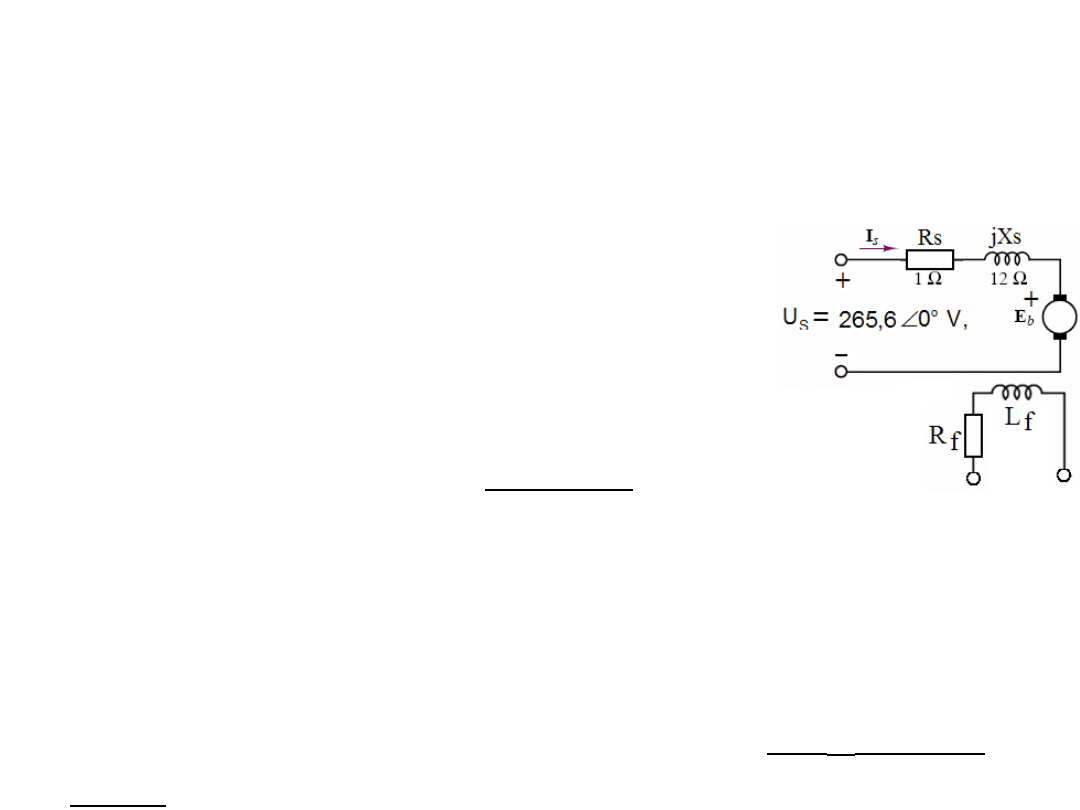
Przykład. Obliczyć wartość nominalną S [kVA]; indukowane
napięcie E
b
i kąt mocy wirnika
δ
dla pełnego obciążenia silnika
synchronicznego. Dane: nominalne napięcie międzyfazowe: 460
V; 3 Φ (3 fazy); pf (power factor) = 0,707 opóźnienie; prąd stojana
przy pełnym obciążeniu 12,5 A, Z
s
= 1 + j12
Ω
.
Rozwiązanie.
Na jedną fazę w połączeniu
gwiazdowym przypada prąd i napięcie:
I
S
= 12,5 A,
U
S
= 460/
√
3 = 265,6 V,
S = 3 U
s
I
s
= 3
×
12,5
×
265,6 = 9959 VA.
Ze schematu zastępczego mamy:
E
b
= U
s
– I
s
(R
s
+ iX
s
)
= 265,6 V – (12,5
∠
-45° A)
×
(1 + j12
Ω
) = 265,6 V – (12,5
∠
-45°
A)
×
(12,04
∠
85,23°
Ω
) = 265,6 V – 150,52
∠
40,23°=
265,6 V – (115,3 + j96,8) V = 150,3 – j96,8 V = 179
∠
-32,8° V
δ
= -32,8°
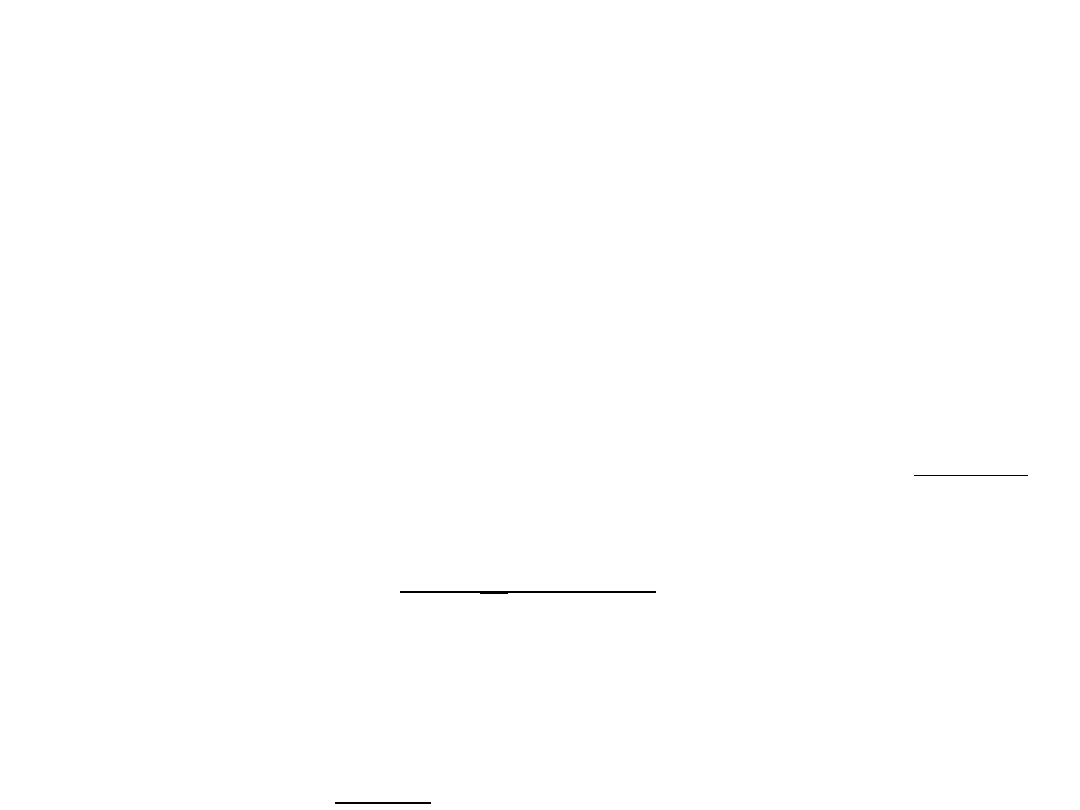
Przykład. Obliczyć prąd stojana I
s
, prąd linii I
Lin
(połączenie
∆
)
oraz indukowane napięcie silnika synchronicznego 3-fazowego.
Dane: 208 V; 45 kVA, 50 Hz, 3 Φ; pf 0,8 wyprzedzający; Z
s
= 0 +
j2,5
Ω
. Straty (tarcie) P
str
=1,5 kW, straty w rdzeniu P
core
= 1 kW;
obciążenie P
o
= 15 KM (1 KM = 0,746 kW).
Rozw.
Moc wyjściowa wynosi: P
out
= 15 KM
×
0,746 kW/KM = 11,19 kW
Moc wejściowa (elektryczna) P
in
= P
out
+ P
mech
+ P
core
+ P
el i inne
= 11,19 + 1,5 + 1
+ 0 = 13,69 kW.
Prąd I
Lin
= P
in
/(
√
3 U
s
cos
Θ
) = 13690 W/(
√
3
×
208 V
×
0,8) = 47,5 A.
Przy połączeniu w trójkąt
∆
, prąd twornika I
s
= I
Lin
/
√
3 =
47,5 A/
√
3
∠
arccos0,8 = 27,4
∠
36,87° A.
SEM E
b
obliczymy z bilansu napięć (II prawo Kirchhoffa):
E
b
= U
s
– jX
s
I
s
= 208
∠
0° V – j2,5
Ω
(27,4
∠
36,87° A) = 208
∠
0° +
68,5
∠
-53,13 = 208 + 41,1 – j54,8 V= 249,1 – j54,8 V =
255
∠
-12,4°
δ
= -12,4°
Silniki synchroniczne nie należą do najbardziej rozpowszechnionych z wielu powodów.
Jednym z nich jest wymóg stałej szybkości, który można obejść tylko gdy zbuduje się
zasilanie o zmiennej częstotliwości. Ponadto konieczne jest oddzielne zasilanie prądem
stałym i prądem zmiennym.
Silniki indukcyjne obchodzą te przeszkody i są najszerzej stosowanymi
dzięki ich konstrukcyjnej prostocie.
Jako prądnice nie mają zbyt wielu zalet i zastosowań.
Maszyny indukcyjne (asynchroniczne)
Maszyny indukcyjne są maszynami na prąd przemienny i mogą być używane jako
prądnice, silniki a nawet jako hamulce. Maszyny indukcyjne są koncepcyjnie podobne do
maszyn synchronicznych z tą tylko różnicą, że ich wirniki mają prostsze obwody
elektryczne, są to przewodzące pręty zagłębione w materiale wirnika i zwarte na
końcach. Są silniki trójfazowe – stosowane w przemyśle (silniki wiatraków, pomp,
obrabiarek itp., komercyjnie dostępne od 1 do 10 000 KM), są jednofazowe – stosowane
w gospodarstwach domowych i usługach i są też dwufazowe – stosowane w napędach
specjalnych i automatyce. Dzięki sensorom i mikroprocesorowym sterownikom silniki
indukcyjne mogą być stosowane nawet w precyzyjnych układach sterowania,
serwomechanizmach. Regulację prędkości silników indukcyjnych można dokonywać
poprzez regulację napięcia lub regulację napięcia i częstotliwości, przez zmianę ilości
biegunów, przez zastosowanie rheostau w wirniku. Ze względu na konstrukcję wirnika
silniki indukcyjne dzielą się na pierścieniowe i klatkowe. W obu przypadkach zasada
działania polega na indukowaniu prądów w wirniku polem magnetycznym stojana
.
Oddziaływanie wirującego pola stojana z polem wyindukowanych prądów wirnika
wytwarza moment obrotowy. Ponieważ indukcja może tu zachodzić tylko przy różnych
prędkościach wirnika i pola stojana (konieczny jest niezerowy ruch względny prętów i
pola magnetycznego) dlatego funkcjonuje też nazwa: „maszyny asynchroniczne”.
Wirujące pole magnetyczne uzyskuje się wówczas, gdy co najmniej dwa uzwojenia
stojana są geometrycznie przesunięte względem siebie a prądy w nich występujące są
przesunięte w fazie. Przez odpowiednią geometrię wykonania uzwojeń stojana i wirnika
realizowane jest pole stojana
Φ
(n
s
) wirujące z prędkością synchroniczną n
s
oraz pole
wirnika (rotora)
Φ
(n) wirujące z prędkością asynchroniczną n. Prędkość synchroniczna
n
s
zależy od częstotliwości f prądu stojana i geometrii uzwojeń – czyli ilości par
biegunów p, które tworzą uzwojenia.
Oddziaływanie tych pół wymusza obroty wirnika w kierunku obrotów wirującego pola
stojana. Wirnik obraca się z prędkością mniejszą niż prędkość synchroniczna tj. niż
wirujące pole stojana bo pole musi przecinać przewody by w nich indukował się prąd.
Brak kontaktów elektrycznych rotora (brak szczotek itp.) w silnikach indukcyjnych
zapewnia ich prostotę wykonania. Gdy do wirnika przyłożymy zewnętrzny napęd
wymuszający obroty to otrzymamy generator, który (dzięki prostocie – brak oddzielnego
obwodu wzbudzenia i dzięki elastyczności w odniesieniu do szybkości obrotów) ma
zastosowanie w wiatrakowych elektrowniach. Ich wadą jest duża indukcyjność i przez to
trzeba stosować kompensację pojemnościową aby zmniejszyć przesunięcie fazowe
między prądem a napięciem.
Załóżmy, że wirnik w postaci klatki metalowej
(rys. obok) zostanie umieszczony w stojanie
gdzie wytwarzane jest wirujące pole magnetyczne.
To wirujące pole będzie indukowało w metalowych
prętach wirnika prądy elektryczne zależne od
indukowanej SEM i impedancji wirnika.
W pierwszej chwili gdy po włączeniu prądów w stojanie wirnik
jeszcze spoczywa to pole magnetyczne pochodzące od jego
indukowanych prądów jest synchroniczne z polem stojana (pola
stojana i wirnika są wtedy przez chwilę w stałej względem siebie
konfiguracji). Wtedy właśnie generowany jest startowy moment
obrotowy. Gdy ten moment obrotowy jest wystarczający
wirnik zaczyna się obracać i przyspieszać aż do osiągnięcia
prędkości pracy. Prędkość pracy jest oczywiście niższa od
prędkości synchronicznej n
s
(bo przy synchronicznej prędkości nie
było by indukowanych SEM i prądów w wirniku – zero mocy!).
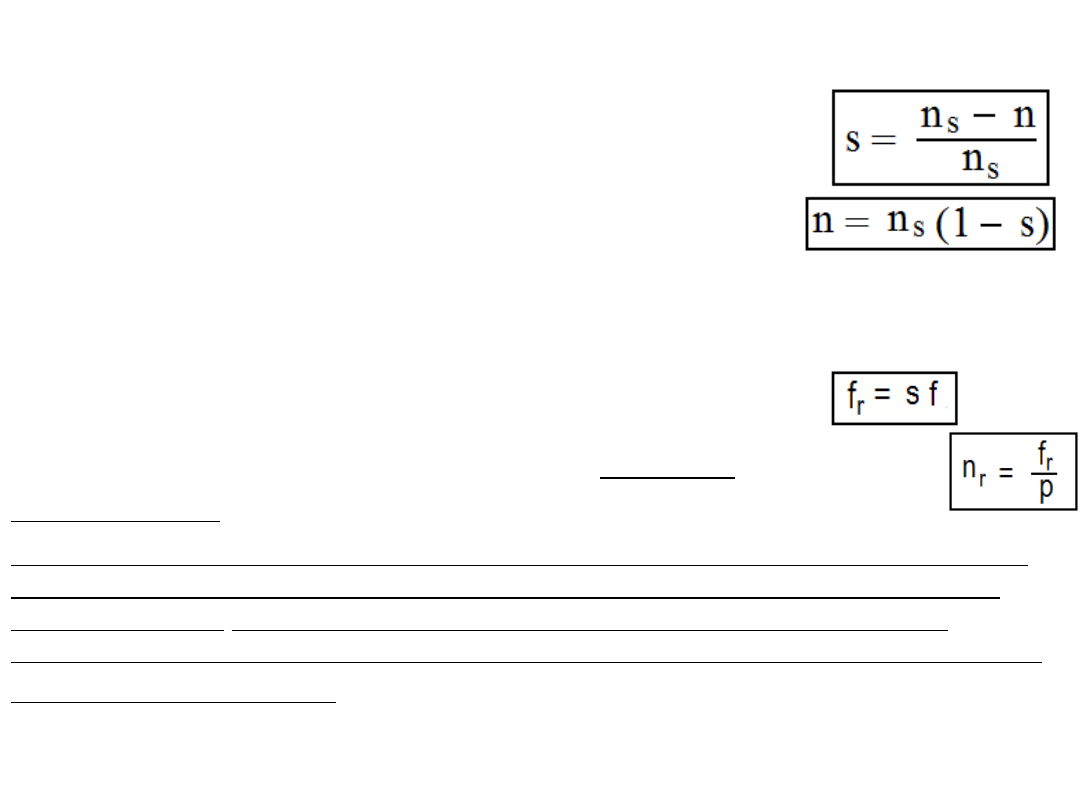
Załóżmy, że ta prędkość wirnika wynosi n wtedy prędkość wirującego pola
stojana względem obracającego się wirnika wyniesie: (n
s
– n). Względna
różnica tych prędkości nazywa się poślizgiem s:
Wartość znamionowa s
N
zawiera się zwykle
w przedziale 2 – 4% (0,02 – 0,04).
Prędkość wirnika n to prędkość mechaniczna:
Poślizg oczywiście zależy od obciążenia i konstrukcji silnika
(klatkowy, pierścieniowy, dużej lub małej mocy).
Częstotliwość prądu w uzwojeniach wirnika f
r
jest
znacznie niższa od częstotliwości synchronicznej f
s
i wynosi:
Stąd prędkość pola magnetycznego wirnika względem
samego wirnika n
r
jest też mała, przy p = liczba par biegunów wynosi:
Podkreślmy raz jeszcze, że dzięki istnieniu pewnej prędkości względnej między
strumieniem stojana i wirnikiem będą indukowane napięcia i w konsekwencji
prądy w wirniku. Ale prądy wirnika jak i strumienie przez nie generowane
podążają za wirującym strumieniem stojana - mają tę samą prędkość n
s
= n
r
+ n –
prędkość synchroniczną!
Strumień wirnika (sprzężony z, i podążający za
strumieniem stojana) możemy traktować jako synchroniczny strumień wsteczny
(reakcyjny) „pokonywany” przez moc dostarczaną do stojana. Przy stałym obciążeniu
oba pola
Φ
s
i
Φ
r
są względem siebie nieruchome, tworzą stały kąt.
Przykład. Obliczyć poślizg s wirnika przy pełnym obciążeniu oraz
częstotliwość indukowanego napięcia f
R
przy prędkości
nominalnej w czterobiegunowym (p = 2) silniku indukcyjnym.
Wiadomo, że nominalne napięcie wynosi 230 V, 60 Hz i prędkość
przy pełnym obciążeniu: n = 1725 obr/min.
Rozwiązanie.
Prędkość synchroniczna silnika wynosi n
s
= f/(p) obr/s = f
×
60/(p) obr/min =
60
×
60/2 = 1800 obr/min.
Poślizg wynosi s = (n
s
– n)/n
s
= (1800 – 1725)/1800 = 0,0417.
Częstotliwość indukowanego napięcia w wirniku wynosi:
f
R
= sf = 0,0417
×
60 = 2,5 Hz.
Silnik indukcyjny podobnie jak transformator ma dwa zestawy
uzwojeń, uzwojenia stojana i uzwojenia wirnika, sprzężonych
magnetycznie. Zatem silnik indukcyjny można opisać z pomocą
układu zastępczego - wirującego transformatora. Z racji symetrii
układu faz wystarcza analiza jednej fazy, której schemat
zastępczy ilustruje rysunek na następnej stronie.
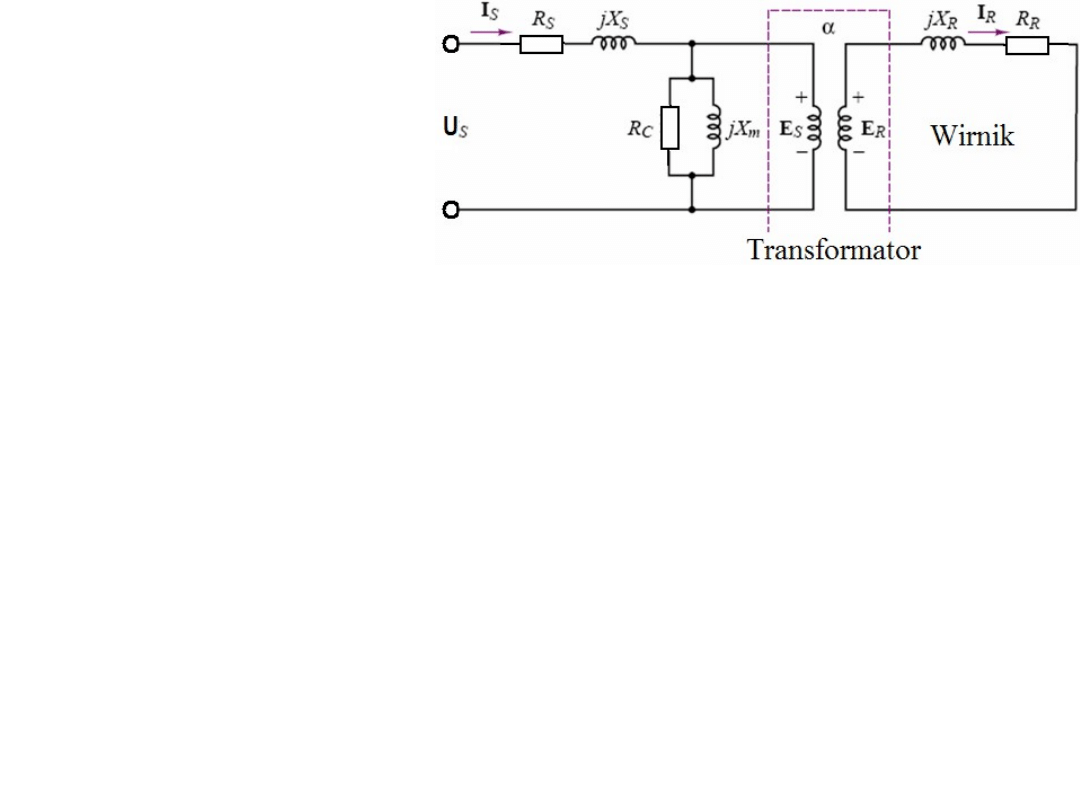
R
s
– rezystancja stojana
przypadająca na jedną
fazę. R
R
– rezystancja
wirnika (rotora) przypadająca
na jedną fazę. X
s
– reaktancja
stojana X
R
– reaktancja wirnika
na 1f. X
m
– reaktancja wzajemna (mutual) magnetyzacji. R
c
– rezystancja
„równoważna” stratom w rdzeniu (core-loss equivalent resistance).
E
s
= k
s
n
s
Φ
w szczelinie
– indukowana SEM na 1f w stojanie. E
R
– indukowana SEM
na 1f w wirniku (rotorze), E
R
jest proporcjonalna do poślizgu s (E
R
= sE
R0
) gdzie
E
R0
jest wielkością SEM gdy wirnik stoi.
E
s
w uzwojeniu pierwotnym (stojana) jest sprzężone z E
R
w uzwojeniu wtórnym
(wirnika) z efektywnym stosunkiem ilości zwoi N
s
/N
R
. Uwzględniając poślizg s,
możemy zapisać, że indukowana w wirniku SEM:
E
R
= sE
R0
, również X
R
=
ω
R
L
R
= 2
π
f
R
L
R
= 2
π
sfL
R
= sX
R0
, gdzie X
R0
= 2
π
fL
R
jest
reaktancją wirnika przed rozpoczęciem ruchu (maksymalna wartość f
R max
= f).
Prąd wirnika wyniesie zatem:
I
R
= E
R
/(R
R
+jX
R
) = sE
R0
/(R
R
+jsX
R0
) = E
R0
/(R
R
/s + jX
R0
)
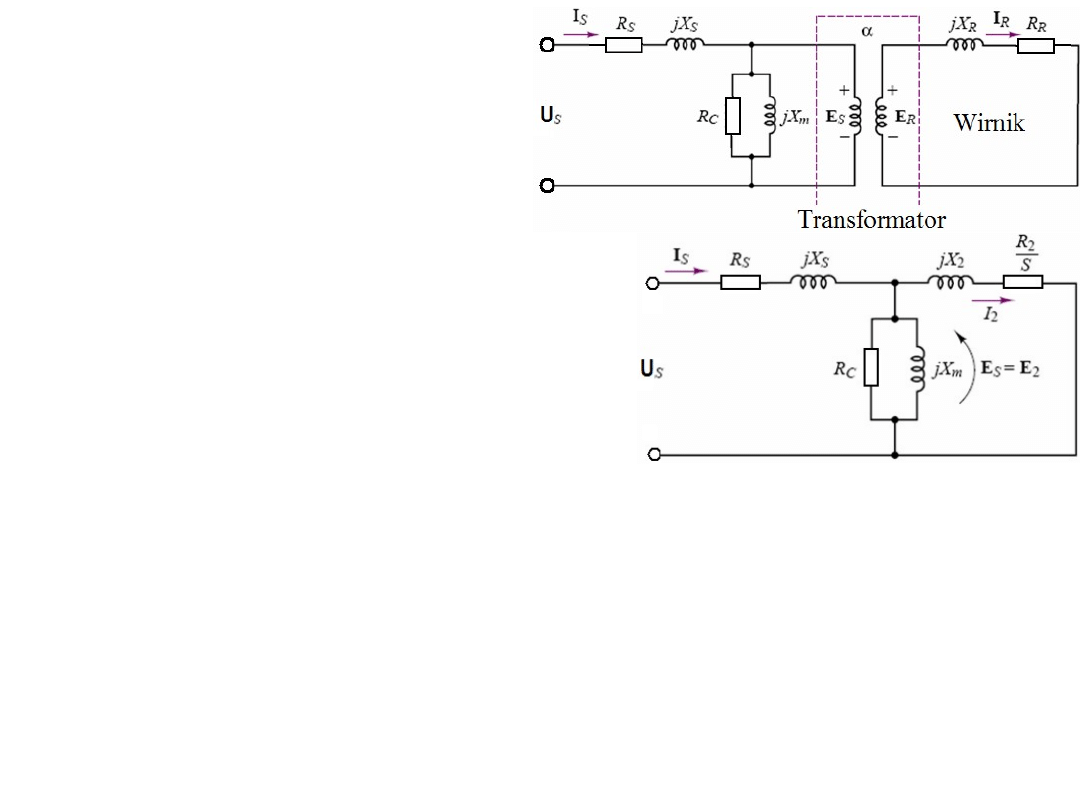
Prąd, napięcie i impedancja
z obwodu wtórnego
(z obwodu wirnika)
mogą być „transformowane”
do obwodu pierwotnego
(obwodu stojana) przez
odpowiednie przekładnie uzwojeń.
Przetransformowana SEM wyniesie:
E
2
= (N
s
/N
R
)E
R
, Prąd: I
2
= I
R
/(N
s
/N
R
),
rezystancja:
R
2
= (N
s
/N
R
)
2
R
R
- ale odczuwana w stojanie
wartość zależy od s i wynosi: R
2
/s = R
2 (straty w Cu)
+ R
2
(1-s)/s
(mechaniczne obciążenie)
,
reaktancja przetransformowana: X
2
= (N
s
/N
R
)
2
X
R0
.
Analiza przykładowego silnika indukcyjnego
o parametrach: 460 V, 60 Hz, 4-bieguny, s = 0,022, P = 14 KM,
R
s
= 0,641
Ω
, R
2
= 0,332
Ω
, X
s
= 1,106
Ω
, X
2
=0,464
Ω
, X
m
= 26,3
Ω
,
Zakładamy symetryczne obciążenia czyli analizujemy co przypada na jedną fazę oraz
pomijamy straty w rdzeniu R
c
= 0. Wyliczmy n;
ω
m
; I
s
; pf; T.
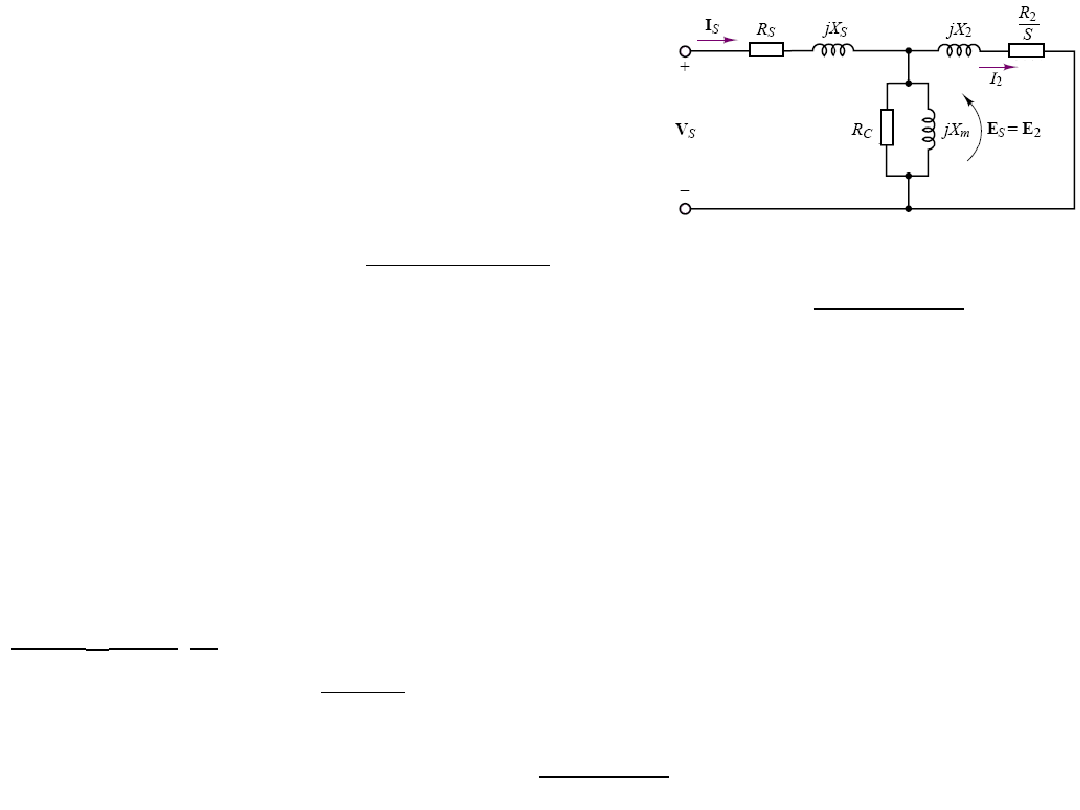
Wyliczamy n: Prędkość synchroniczna wynosi
N
s
= (f/p)
×
(60s/min) =
((60 Hz)/(2 pary biegunów))
×
(60s/min) =
1800 obr/min.
Mechaniczna prędkość wirnika n = (1 – s)n
s
=
(1 – 0,022)1800 obr/min = 1760 obr/min.
ω
m
= (1 – 0,022)
ω
s
= 0,978
×
2
×
3,14
×
60/(2 pary biegunów) = 184,4 rad/s
Obliczamy I
s
; U
s
/Z
total
Z
2
= R
2
/s + jX
2
= 0,332/0,022 + j0,464
Ω
= 15,09 + j0,464
Ω
= 15,1
∠
1,76° ,
Impedancje rotora i magnetyzacji możemy zastąpić przez : Z = 1/(1/jX
m
+ 1/Z
2
)
= 1/(1/j26,3 + 1/(15,1
∠
1,76°)) = 1/(-j0,038 + 0,0662
∠
-1,76°) = 1/(-j0,038 +
0,06617 – j0.002) = 1/(0,06617 – j0,04) = 1/(0,0773
∠
31,2°) = 12,93
∠
31,2°,
Z
total
= Z
s
+ Z = 0,641 + j1,106 + 12,93
∠
31,2° = 0,641 + j1,106 + 11,06 + j6,69
= 11,71 + j7,79 = 14,06
∠
33,6°, zatem I
s
= U
s
/Z
total
= (460/
√
3
∠
0°)/14,06
∠
33,6° =
18,89
∠
-33,6° A
pf = cos
ϕ
= cos33,6° = 0,883, Przeliczamy P
out
= 14KM = 14
×
746 kW =
10,444kW, z tego mamy:
T = P
out
/
ω
m
= (10444 W)/(184,4 rad/s) = 56,64 Nm
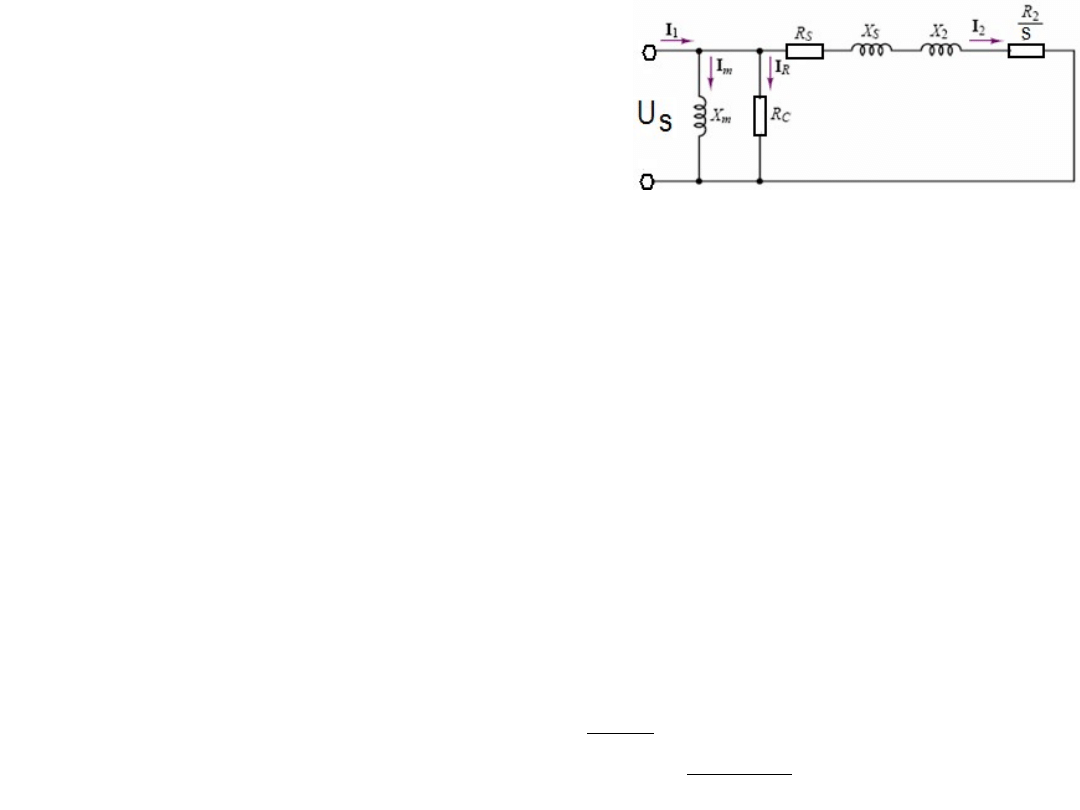
Przykład: Parametry silnika: 500 V, 3 Φ, 50 Hz,
p = 4 pary, s = 0,05, P = 14 kM, i jego uzwojeń:
R
s
= 0,13
Ω
, R’
R
=0,32
Ω
, X
s
= 0,6
Ω
,
X’
R
= 1,48
Ω
, admitancja opisująca straty
w rdzeniu i induktancję wzajemną
Y
m
= G
C
+ jB
m
= 0,004 – j0,05
Ω
-1
,
Stosunek uzwojeń (przekładnia) stojana do wirnika: 1/
α
= 1/1,57.
Obliczyć: I
S
, pf i T. Obliczenia: na jedną faze. Zaniedbać straty mechaniczne.
R
2
= R’
R
×
(1/
α
)
2
= 0,32
×
(1/1,57)
2
= 0,13
Ω
,
X
2
= X’
R
×
(1/
α
)
2
= 1,48
×
(1/1,57)
2
= 0,6
Ω
, Z = R
s
+ R
2
/s + j(X
s
+ X
2
) =
= 0,13 + 0,13/0,05 + j(0,6 + 0,6) = 2,73 + j1,2
Ω
.
Zgodnie z uproszczonym schematem:
I
2
= U
s
/Z = (500/
√
3
∠
0)/(2,73 + j1,2) = (288,7
∠
0)/(2,98
∠
23,73°) = 88,7 – j39 A =
96,9
∠
-23,73°.
I
R
= U
s
G
s
= 288,7 V
×
0,004
Ω
-1
= 1,15 A, I
m
= jU
s
B
m
= -j288,7 V
×
0,005
Ω
-1
=
= -j14,4 A, I
1
= I
2
+ I
R
+ I
m
= 88,7 – j39 +1,15 – j14,4 A = 89,85 – j 53,4 A.
Wejściowy pf = Re(I
1
)/
I
1
= 89,85/104,5 = 0,86. Moment obrotowy T = 3P/
ω
s
= (3I
2
2
R
2
/s)/(2
π
f/p) = (3
×
96,9
2
×
0,13/0,05)/(314/4) = 933 Nm
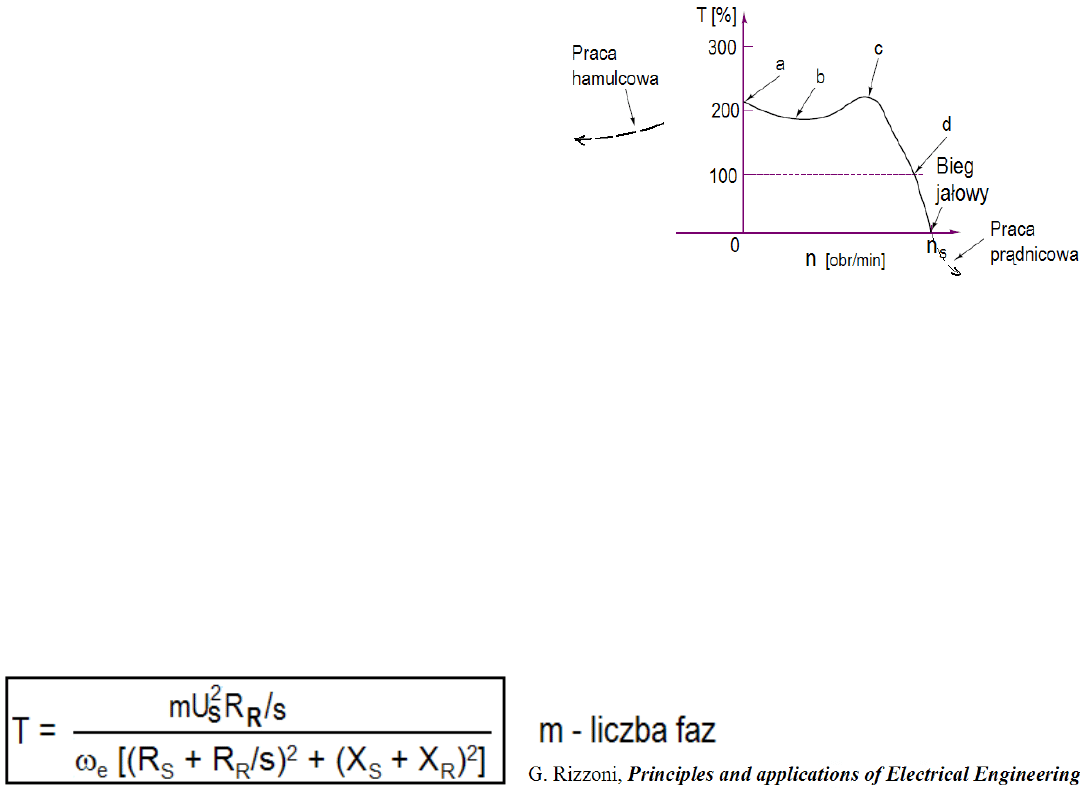
Zależność momentu obrotowego
od szybkości wirnika przedstawia
rys obok. Punkt „a” określa
startowy moment obrotowy.
Punkt „b” ilustruje minimalny moment
rozruchowy. Ze wzrostem prędkości
kątowej wirnika jego reaktancja maleje
ponieważ maleje częstotliwość indukowanego napięcia - zdeterminowana
różnicą między prędkością kątową wirnika i wirującego pola stojana. Moment
obrotowy jest maksymalny gdy indukcyjna reaktancja wirnika zrówna się z jego
rezystancja. Ta maksymalna wartość momentu jest też nazywana momentem
krytycznym - punkt „c”. Powyżej tej prędkości moment spada do wartości
zerowej przy zrównaniu prędkości rotora z prędkością synchroniczną n
s
(
ω
e
).
Punkt „d” ilustruje nominalną wartość momentu obrotowego. Ogólna formuła
dla wyznaczania stacjonarnej charakterystyki moment - prędkość (poślizg s)
jest podana poniżej.
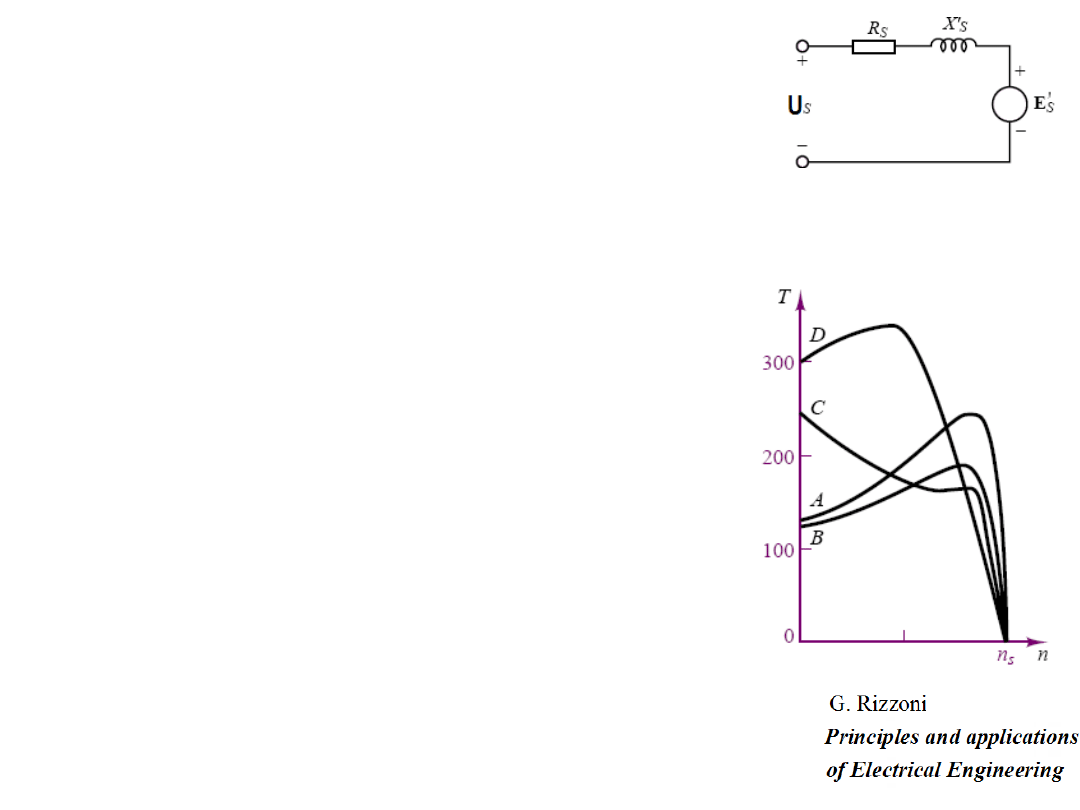
Złożoność tej formuły oraz występujące
efekty nieliniowe powodują, że układy
z silnikami indukcyjnymi muszą być analizowane
z pomocą programów symulacyjnych.
Gdy jednak precyzyjna analiza nie jest
konieczna można korzystać z bardzo
uproszczonych schematów zastępczych
przykładowo biorąc pod uwagę tylko R
s
–
rezystancję stojana, X’
r
– reaktancję przejściową,
i napięcie wsteczne E’s za reaktancją przejściową.
W praktyce zasadniczym problemem bywa
dobór odpowiedniego silnika do danego zadania.
W przypadku silników indukcyjnych zależnie
od konstrukcji ich charakterystyki mogą różnić
się kształtem pozwalając na dobór odpowiedniego
wariantu.
Charakterystyki czterech podstawowych klas
silników A, B, C i D ilustruje rysunek obok.
Silniki indukcyjne po procesie rozruchu pracują z prawie stałą prędkością (choć
zależną od obciążenia). Gdyż zachodzi konieczność zmiany prędkości to
pewną możliwość daje zmiana ilości biegunów uzwojenia stojana:
Przy przełączaniu i manipulowaniu uzwojeń istnieje jednak ryzyko pomyłki i
zniszczenia silnika.
Inna możliwość to regulacja poślizgu można ją uzyskać
zmieniając napięcie zasilania. Daje to jednak mały zakres zmian,
zmiany są dopuszczalne w zakresie powyżej punktu c.
Innym rozwiązaniem w silnikach z wirnikiem z uzwojeniem
jest dodanie do obwodu wirnika regulowanej rezystancji.
Tu choć zmienia się nieco charakterystyka silnika to
zmiany są również w małym zakresie – powyżej punktu c.
Obie powyższe metody mają wspólną wadę: wnoszą
dodatkowe straty. Pod tym względem znacznie lepszym rozwiązaniem jest
jednoczesna regulacja częstotliwości i napięcia zasilania.
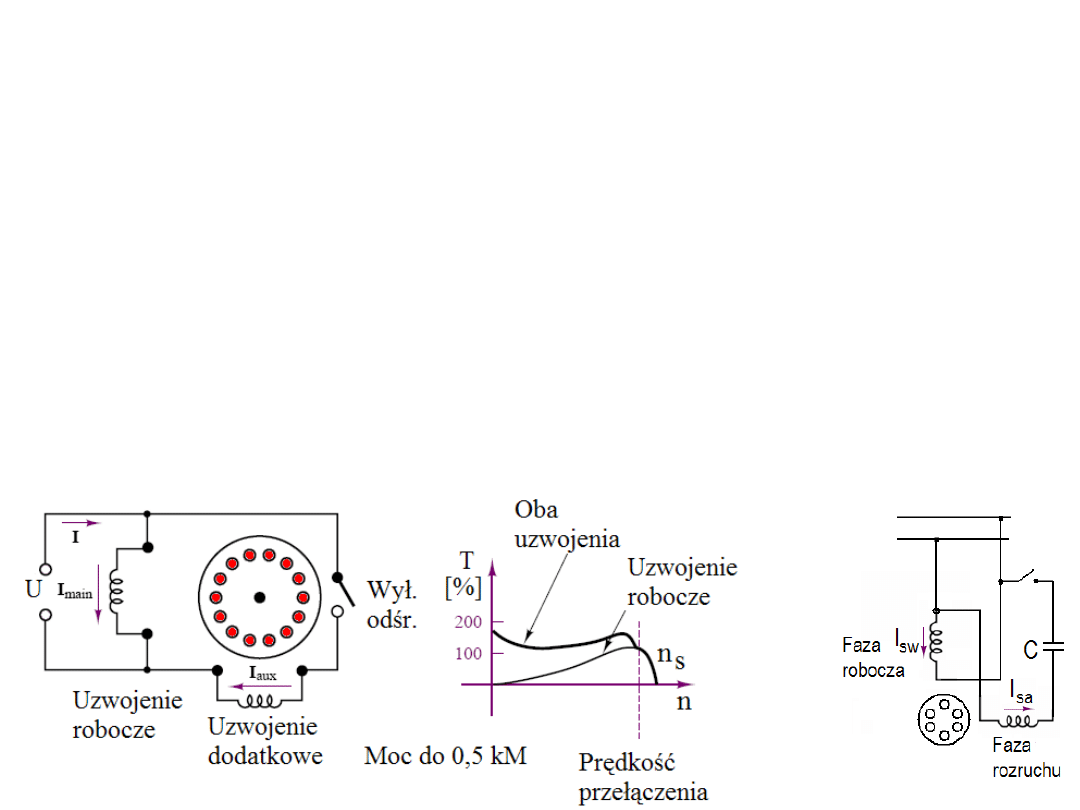
Silniki indukcyjne jednofazowe.
Ich zaletą jest zasilanie z sieci jednofazowej (gospodarstwa domowe); ich moc jest
niewielka, do 5 kW. Budowane są głównie z wirnikami klatkowymi. Ponieważ jedno
uzwojenie wytwarza pole pulsujące (nie wirujące, które nie może rozruszać wirnika)
stojany tych silników zawierają dwa uzwojenia: robocze i pomocnicze - rozruchowe.
Uzwojenie robocze zajmuje około 2/3 obwodu stojana a pomocnicze około 1/3 tego
obwodu. Osie uzwojeń są przesunięte o kąt 90°. Przez uzwojenie pomocnicze prąd
płynie tylko w czasie rozruchu do momentu uzyskania prędkości n
≈
0,8 n
s
, poczym
zostaje ono odłączone od źródła napięcia (np. wyłącznikiem odśrodkowym)
aby
zmniejszyć straty na zbędne grzanie.
Przesunięcie fazowe strumieni równe
przesunięciu fazowemu prądów w tych uzwojeniach uzyskuje się przez szeregowe
włączenie kondensatora lub rezystora do uzwojenia pomocniczego (lub użycie uzwojenia
z większą rezystancją).
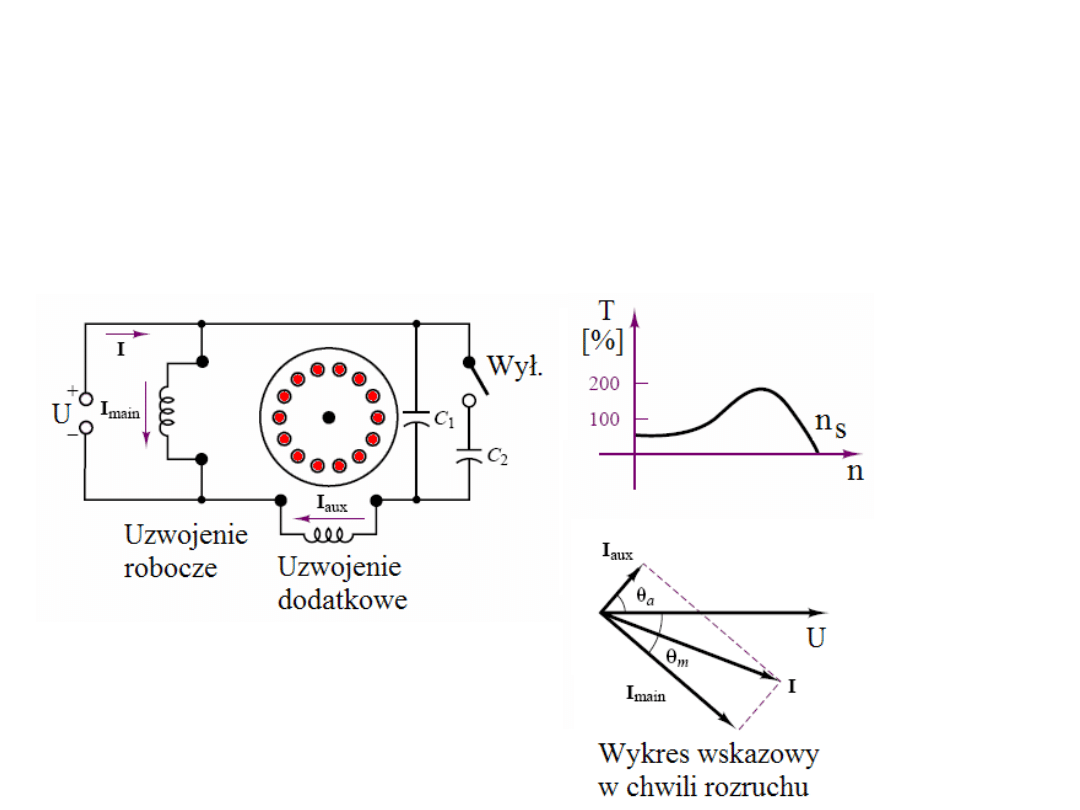
Są też silniki indukcyjne jednofazowe z nieodłączanym kondensatorem po
rozruchu – mają one prostszą konstrukcję i oferują pewien kompromis
pomiędzy charakterystykami rozruchu i pracy.
Lepszy kompromis można jednak osiągnąć stosując dwa kondensatory: jeden
o małej pojemności dla uzyskania stałego przesunięcia faz i poprawienia
charakterystyki pracy, oraz drugi o znacznie większej pojemności dla
poprawienia charakterystyki rozruchowej.
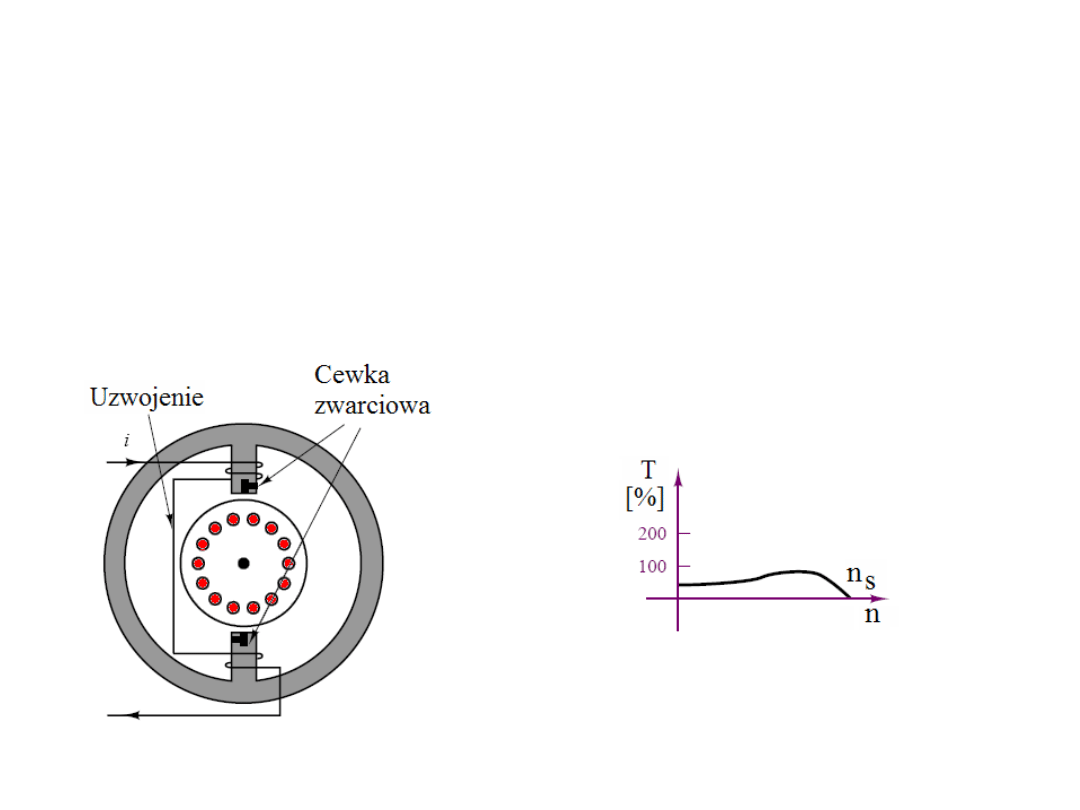
Silnik zwartobiegunowy.
Ten typ silnika, o mocy do 0,05 kM, pracuje na nieco innej zasadzie. Stojan w
tym silniku ma wystające bieguny, które zawierają zwarciowe cewki w postaci
uzwojenia otaczającego część każdego bieguna. Strumień w części bieguna
otoczonej takim zwojem opóźnia się w stosunku do strumienia w pozostałej
części tego samego bieguna. Daje to efekt wirowania pola w kierunku części
otoczonej zwojem i w konsekwencji zapewnia rozruchowy moment obrotowy.
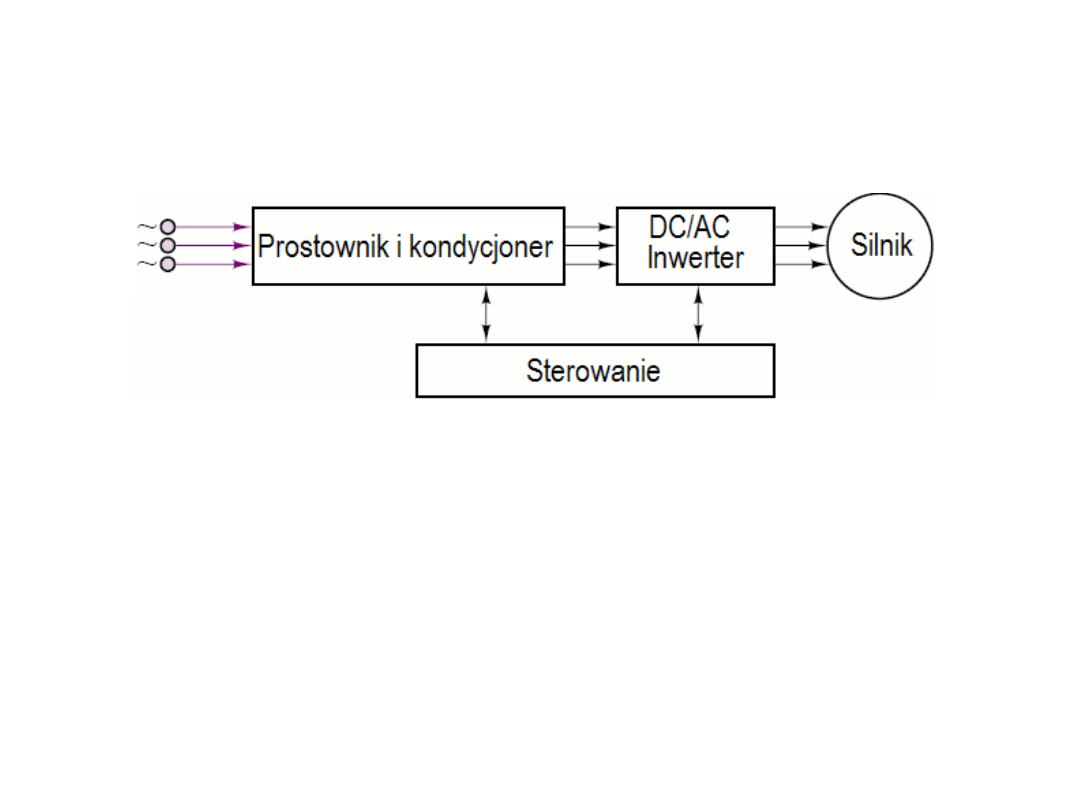
Silniki z jednoczesną regulacją częstotliwości i napięcia zasilania.
Utrzymując stały stosunek U
s
/f
s
można zmieniać prędkość wirnika utrzymując
stały moment obrotowy. Schemat blokowy takiego rozwiązania przedstawia
poniższy rysunek.
Takie rozwiązanie jest coraz szerzej stosowane dzięki szybkiemu rozwojowi
możliwości elektroniki.
Ponadto to rozwiązanie można zaliczać do tzw. specjalnych maszyn
elektrycznych stosowanych w nowoczesnych dziedzinach inżynierii jak
robotyka, sprzęt kosmiczny, automatyka itp.
Innymi tego typu rozwiązaniami są np.: silniki bezszczotkowe, silniki o zmiennej
reluktancji lub silniki krokowe, gdzie ma miejsce naturalne sprzężenie
pomiędzy elektromechanicznymi urządzeniami i układami logiki cyfrowej.
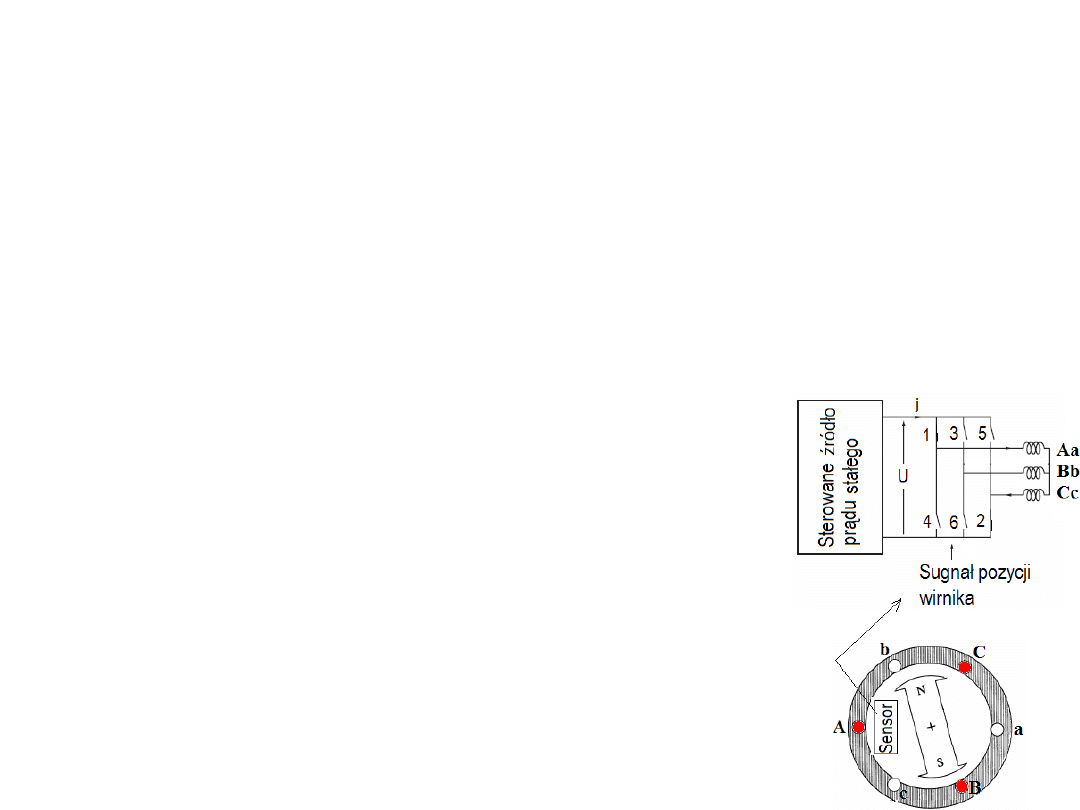
Silniki bezszczotkowe.
Chociaż często nazywane są silnikami
prądu stałego to w rzeczywistości nie są to silniki prądu stałego lecz zwykle
maszynami synchronicznymi ze stałym magnesem. Nazwę uzasadnia nie
konstrukcja lecz fakt, że ich charakterystyka pracy przypomina charakterystykę
silnika bocznikowego (ze stałym prądem wytwarzającym pole). Taką
charakterystykę uzyskuje się dzięki zasilaniu, którego częstotliwość jest
zawsze identyczna z częstotliwością obrotów wirnika.
Uzyskuję się to w falowniku (ang. inverter) DC-AC zawierającym tranzystory
przełączane z częstotliwością odpowiadającą prędkości wirnika. Falownik zatem czerpie
energię ze źródła prądu stałego i generuje prąd zmienny o zmiennej
częstotliwości. Tak więc użytkownik podłącza silnik do źródła
prądu stałego ale prąd w uzwojeniach jest prądem zmiennym.
W efekcie silnik bezszczotkowy prądu stałego jest silnikiem
synchronicznym, w którym kąt momentu obrotowego
δ
jest
utrzymywany stałym dzięki odpowiedniemu prądowi wzbudzenia.
Silnik taki zawiera czujnik obrotów optyczny lub halotronowy
zapewniający formowanie zasilania o odpowiedniej, zgodnej
częstotliwości. Warto podkreślić, iż zamiana komutacji
szczotkowej na elektroniczną stwarza szerokie możliwości
konstrukcyjne dla silników bezszczotkowych.
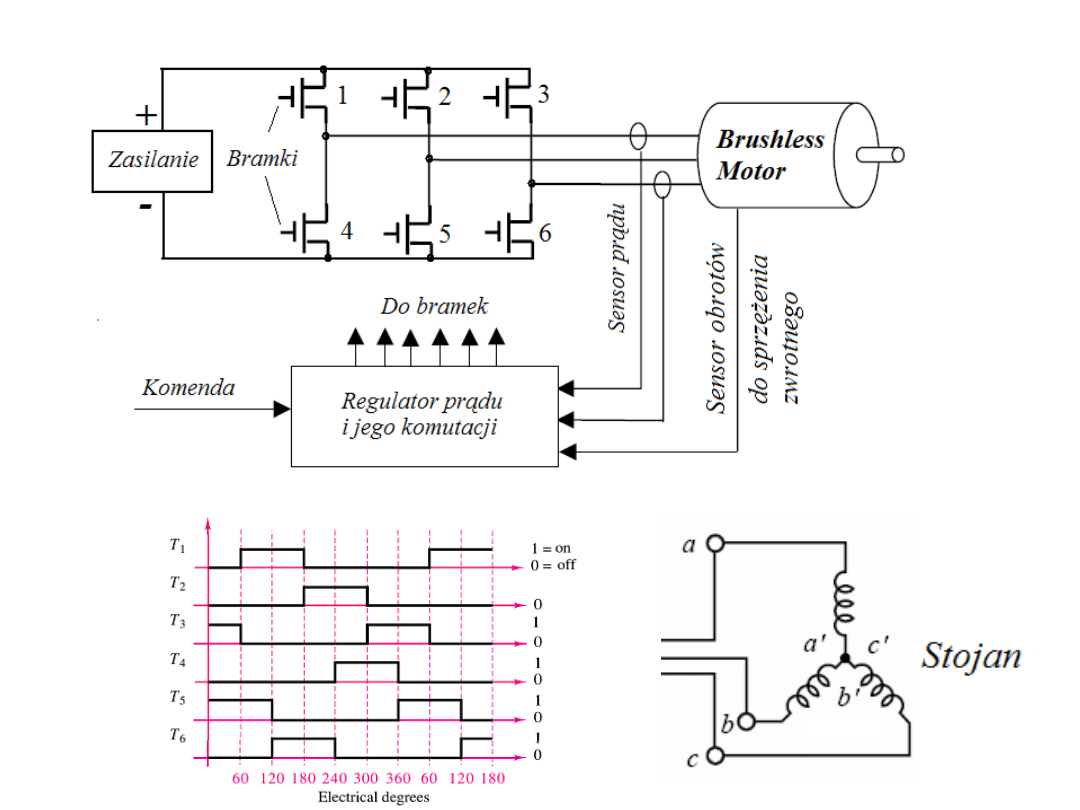
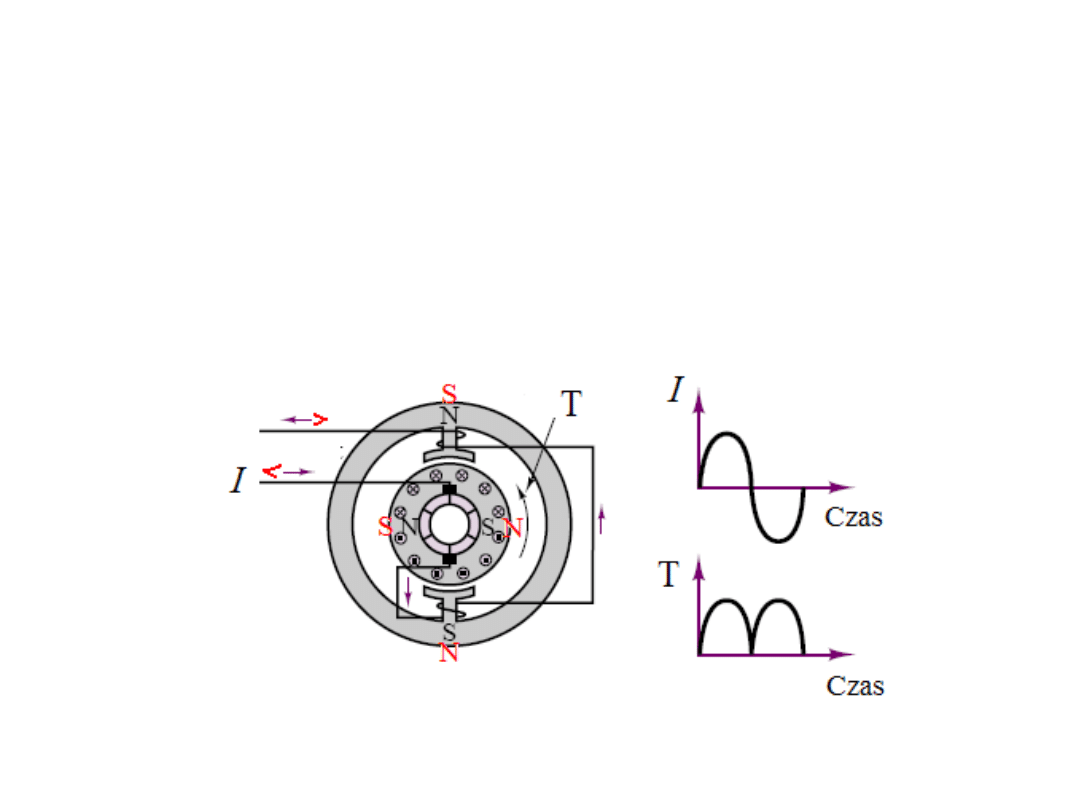
Idea działania silników bezszczotkowych.
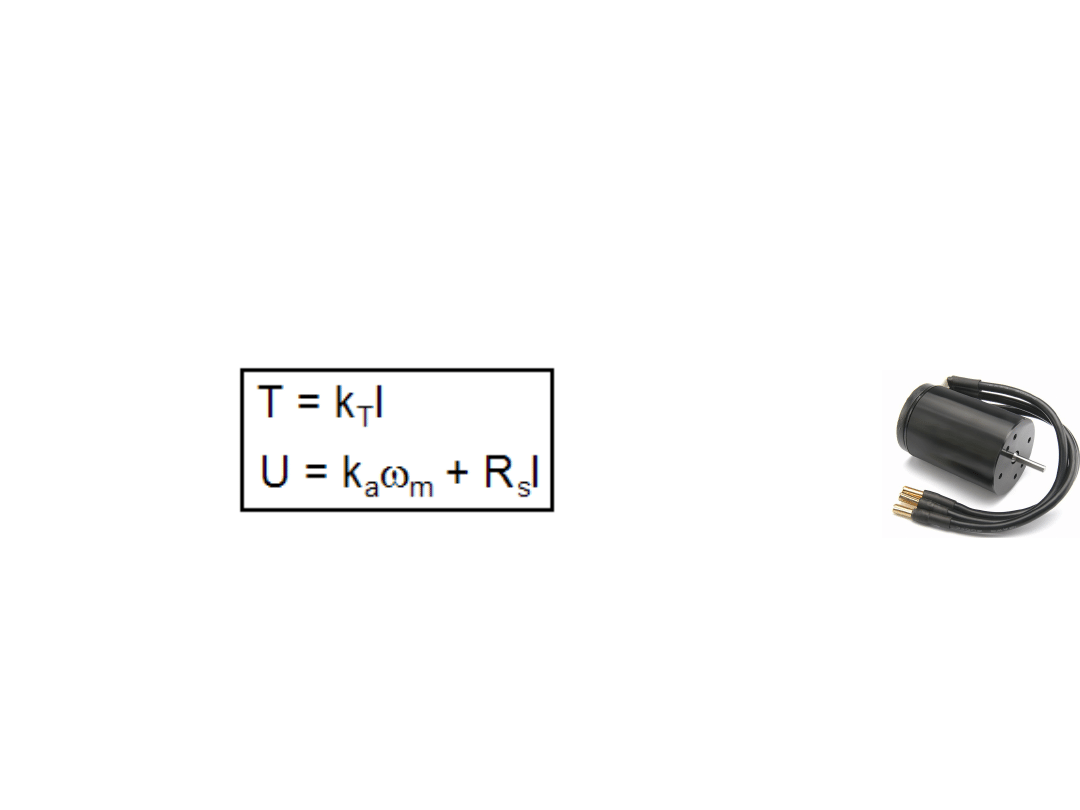
W silnikach bezszczotkowych
prądu stałego ciepło wydziela się w
stojanie (tam jest uzwojenie) a nie w wirniku (jak w innych silnikach prądu
stałego) dlatego są one łatwiejsze do chłodzenia. Silniki te mogą z łatwością
być budowane jako wodoszczelne. Magnes wirnika jest wykonywany z takich
materiałów jak Sm-Co lub ceramiczne magnesy - ferryty. Silniki tego typu mogą
być budowane na moce do 250 kW i prędkości 50 000 obr/min. Sensor będąc
zainstalowanym wewnątrz silnika musi być odporny na wibracje i odpowiedni
zakres temperatur. Silnik bezszczotkowy jest podobny do standardowego
silnika na prąd stały z magnesem trwałym i można go opisywać prostymi
wyrażeniami:
U – przyłożone napięcie, k
a
– stała armatury = k
T
– stała momentu obrotowego,
ω
m
– prędkość mechaniczna (wirnika), R
s
= rezystancja uzwojenia, T – moment
obrotowy, I – prąd silnika (armatury). Silniki bezszczotkowe mają większy
moment obrotowy i mniejszą bezwładność od zwykłych silników prądu stałego.
Zastosowanie między innymi w układach sterujących, napędach dysków
komputerowych i pojazdach elektrycznych.
Uwagi o falownikach
Gdy w falowniku zastosuje się modulację szerokości impulsu (MSI = ang. PWM - Pulse
Width Modulation), to równocześnie ze zmianą częstotliwości można regulować wartość
skuteczną napięcia wyjściowego a zatem też wartość mocy. Falowniki pozwalają nie
tylko regulować obroty silników ale również umożliwiają ich łagodny start. Są więc
stosowane w rozmaitych urządzeniach np. do zmiany prędkości obrotowej bębna pralki,
w nowoczesnych tramwajach, stanowią element składowy niektórych zasilaczy
impulsowych.
Dawniej stosowane były falowniki tyrystorowe, obecnie pracują one na tranzystorach
polowych lub IGBT (tranzystory bipolarne z izolowaną bramką).
Wyróżnia się:
Falowniki napięcia – zasilane źródłem napięciowym (z kondensatorem o dużej
pojemności).
Falowniki prądu – zasilane ze źródła prądowego (z dławikiem o znacznej indukcyjności).
Falowniki przemysłowe tzw. przemienniki częstotliwości (stosowane przy regulacji
prędkości obrotowej silników elektrycznych).
falowniki zasilane 1-fazowo z wyjściem 3-fazowym
falowniki zasilane 3-fazowo z wyjściem 3-fazowym
Falowniki z charakterystyką liniową.
Falowniki z charakterystyką nieliniową.
Silnik uniwersalny.
Okazuje się, że w odpowiednim silniku prądu stałego można połączyć
szeregowo uzwojenie stojana oraz (poprzez komutator) uzwojenie wirnika.
Przy takim połączeniu silnik prądu stałego może być zasilany ze źródła prądu
przemiennego i też będzie działał!
Silniki krokowe –
zamieniają informację cyfrową na ruch i poruszają się
„krocząc” (wykonując określone ułamki obrotu). Chociaż
zasada działania była znana od
lat 1920-tych ich znaczące zastosowania pojawiły się dopiero w erze komputeryzacji –
wszędzie tam, gdzie konieczne jest pozycjonowanie. Silniki krokowe dzielą się na trzy
kategorie:
1) Silniki krokowe z magnesem trwałym w wirniku, PM (permanent magnet). Siła
występuje między magnesem trwałym wirnika a impulsowo sterowanymi
elektromagnesami stojana. Dzięki obecności magnesu trwałego bez zasilania
występuje tu pewien opór przy zewnętrznej próbie ruszenia osi wirnika.
Dostępne
wykonują 4 do 200 kroków na jeden obrót.
2) Silniki krokowe ze zmienną reluktancją VR (variable reluctance). Są to silniki
bez magnesu trwałego, czyli z wirnikiem magnetycznie miękkim (wąska histereza,
o znikomej pozostałości magnetycznej) zawierającym liczne zęby (występy).
Podczas sterowania siła wynika z dążenia wirnika do minimalizacji reluktancji
(oporu magnetycznego przez redukcję szczelin tam gdzie aktualnie wymuszany
jest strumień magnetyczny prądem uzwojeń stojana). Ten silnik nie wykazuje
oporu osi wirnika po wyłączeniu sterowania elektrycznego.
Typowo dostępne
wykonują 24 do 200 kroków na jeden obrót.
3) Silniki hybrydowe HB są kombinacją silników PM i VR. Silnik HB zawierają dwa
sektory miękkiej magnetycznie stali na obwodzie wirnika oraz osiowo usytuowany
(osiowo namagnesowany) magnes wewnątrz wirnika. Dostępne wykonują 72 do 800
kroków na jeden obrót.
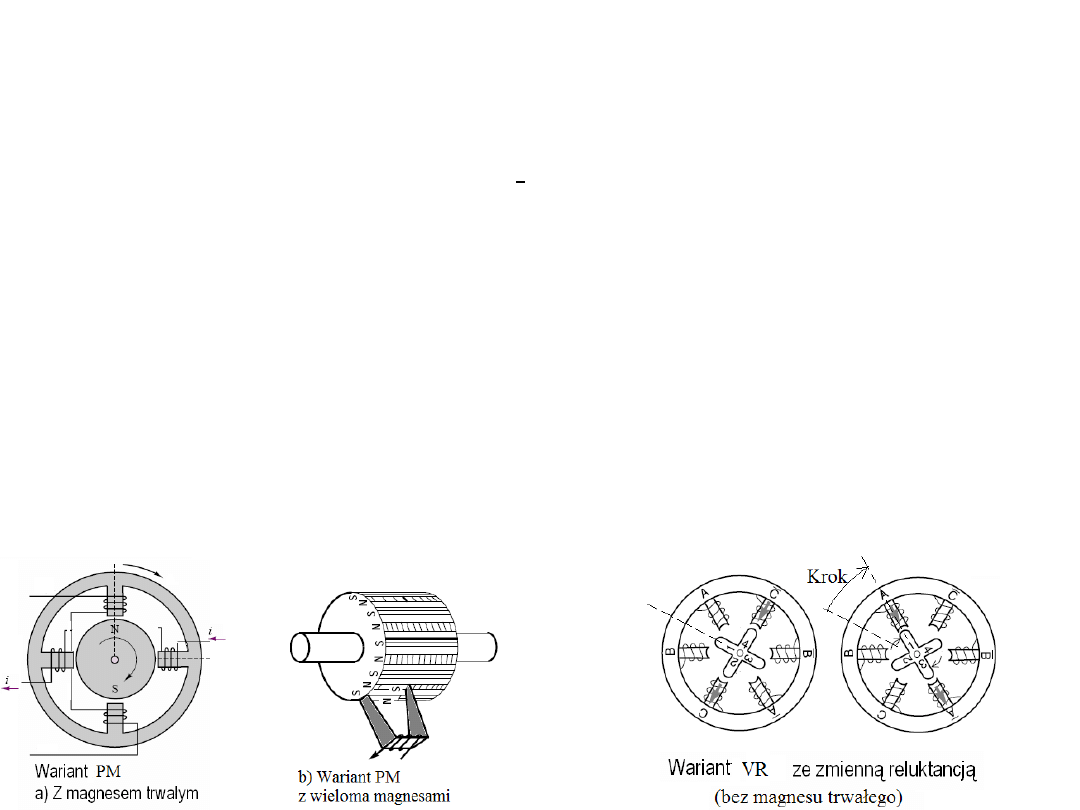
U podstaw zasady działania wszystkich silników krokowych jest siła z jaką
wirnik układa się do aktualnego pola magnetycznego stojana tak aby uzyskać
minimum energetyczne. Pole stojan jest sterowane (zmieniane) sekwencją
impulsów elektrycznych. Ta sekwencja decyduje o kolejnych pozycjach wirnika
czyli o kierunku kroczenia i szybkości.
Najważniejszą cechą tych silników jest to, że kąt obrotu wirnika jest
proporcjonalny do ilości impulsów wejściowych oraz błąd tego kąta jest mały i
nie kumuluje się z ilością impulsów (i wielkością obrotu). Ponadto trwale
utrzymuje swoją aktualną pozycję bez potrzeby stosowania hamulca!
Wariant z magnesem trwałym, realizuje kroki o długości zależnie od ilości biegunów.
Typowymi są: 7,5, 11,25, 15, 18, 45 lub 90
°
. Wariant VR zawiera ząbkowany żelazny
wirnik a moment obrotowy pojawia się jako skutek oddziaływania zębów wirnika z
elektromagnetycznie wzbudzanymi zębami stojana, tu krok zwykle wynosi 15
°
. Wariant
hybrydowy zawiera wielo-zębowy wirnik z trwałym polem osiowym i stojan i jest
mieszaniną dwóch poprzednich wariantów.
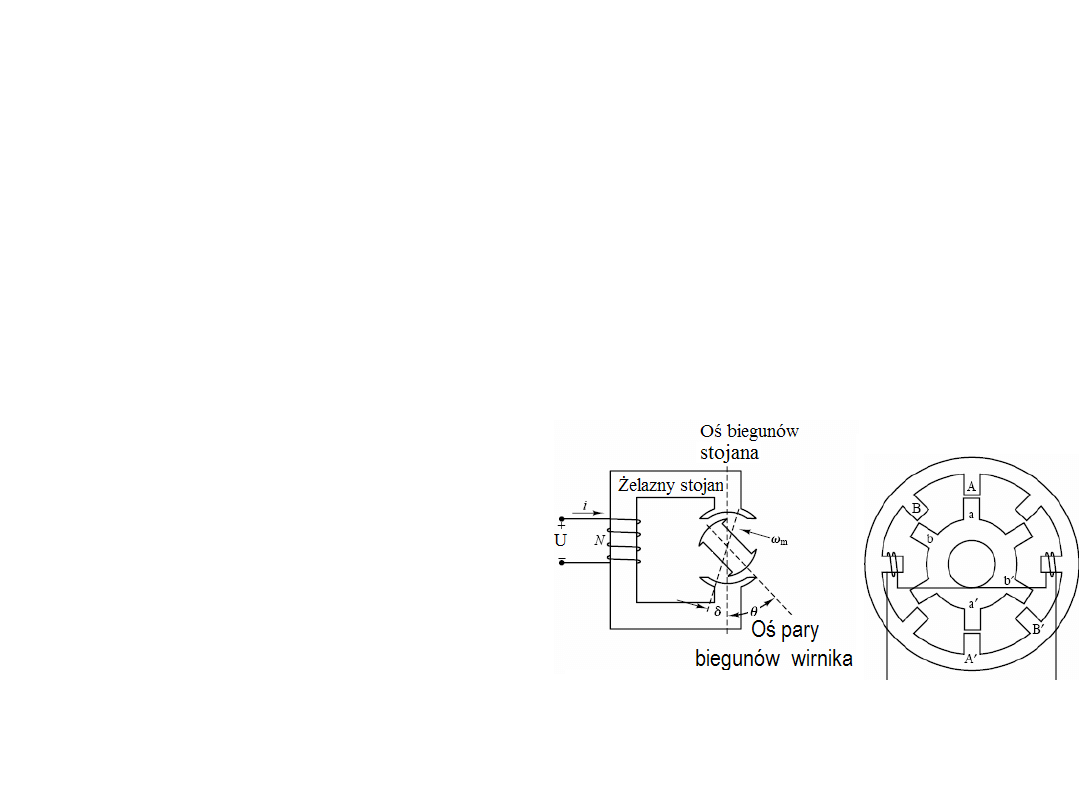
Silniki z przełączaną reluktancją VR
Panuje przekonanie, że ten typ silnika ze względu na niską cenę stanowi bazę dla
napędów elektrycznych i hybrydowo-elektrycznych pojazdów, wyciągów itp.. Dzięki
możliwości pracy z różnymi prędkościami znajduje coraz szersze zastosowanie w
przemyśle (i napędach motoryzacyjnych). Obwód magnetyczny w tych silnikach stanowi
tylko żelazo i powietrze - magnes trwały jest zbędny. Wirnik ma wystające żelazne
bieguny i gdy popłynie prąd przez uzwojenie pojawia się moment obrotowy wymuszający
zgodność osi biegunów wirnika z osią namagnesowanych w danym momencie biegunów
stojana. Gdy
θ
= 0 moment obrotowy znika bo osiągnięte jest minimum reluktancji a
przez to minimum magazynowanej energii. Uzwojenia takiego silnika są wzbudzane
impulsami prądu w synchronizacji z bieżącą pozycją wirnika. Szybkość wirnika jest
zatem zdeterminowana częstotliwością prądów w uzwojeniach stojana.
Zakładając, że induktancja uzwojenia jest
sinusoidalną funkcją pozycji wirnika możemy
zapisać: L(
θ
) = L’’ + L’cos2
θ
(2 bo para biegunów)
. Niech prąd
w uzwojeniu wyraża się przez:
i(t) = I
m
sin(
ω
t), Zmagazynowana energia
magnetyczna wynosi: W
m
= (1/2)L(
θ
)i
2
(t),
Strumień skojarzony:
ψ
(
θ
) = L(
θ
)i(t)
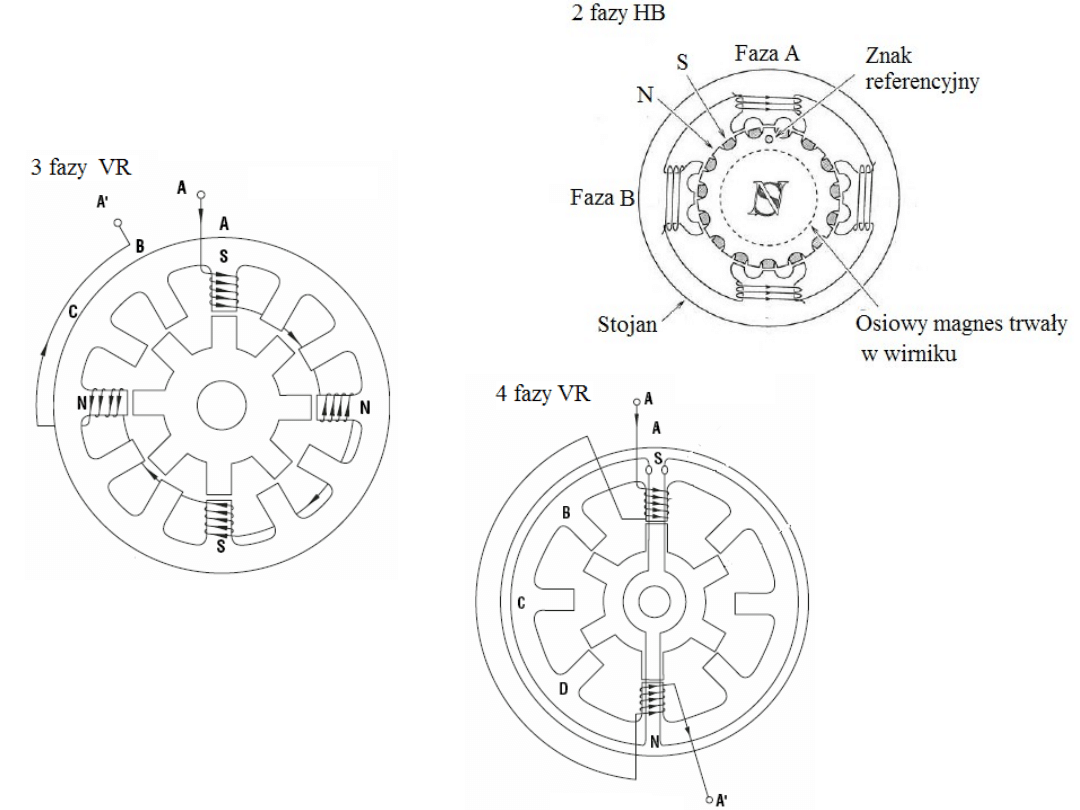
Przykłady silników
o różnej ilości faz
Silniki HB
Łączą zalety silników PM i VR,
są jednak droższe i bardziej złożone.
Krok wynosi: Δθ = 360º/Nt,
N – liczba faz (par uzwojeń),
t – liczba zębów wirnika.
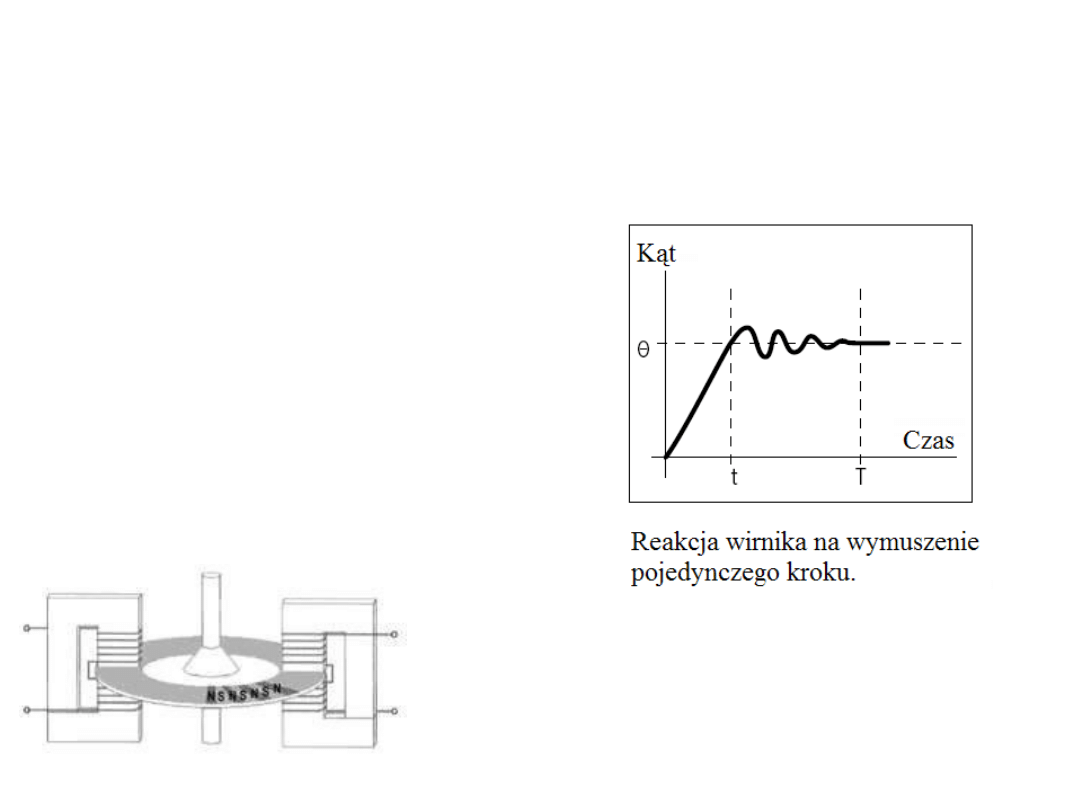
Silniki krokowe mogą wykazywać wpadanie w rezonans przy
pewnych szybkościach sterowania (wymuszania kroków).
Zjawisko to można wyeliminować przez stosowanie mikro-kroków
lub przez zmianę tempa wykonywania kroków.
Silnik krokowy tarczowy PM
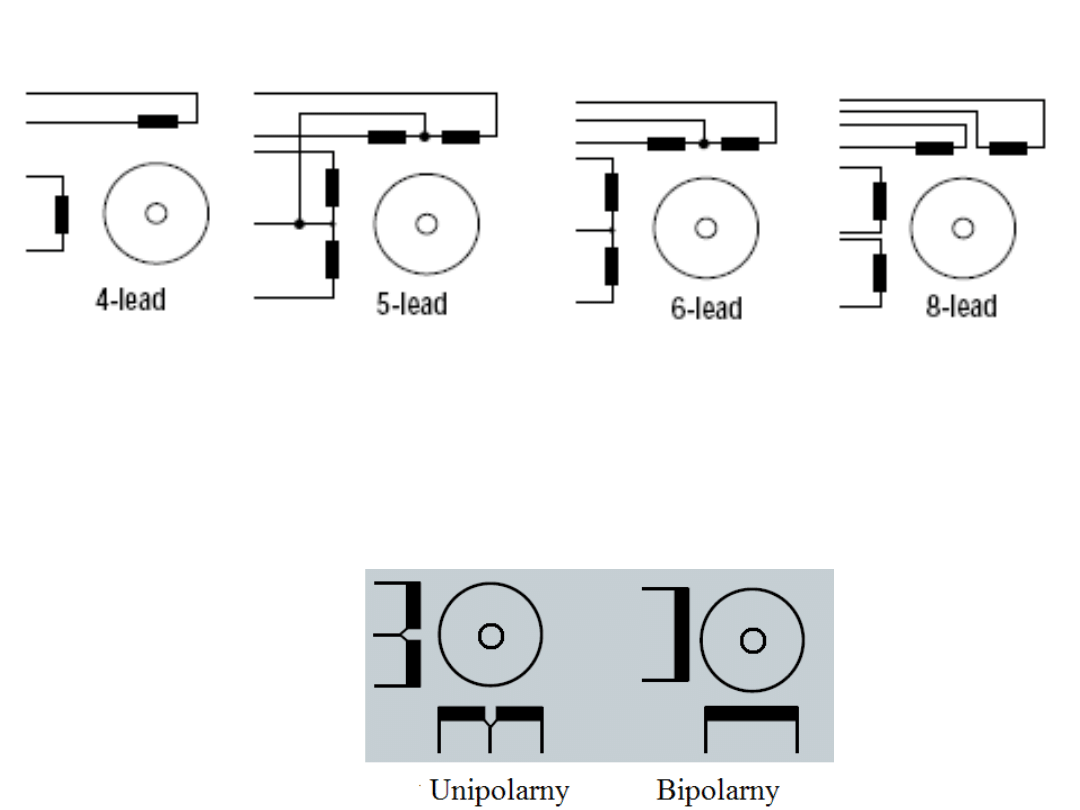
Mnogość konfiguracji wyprowadzeń
Mody pracy uzwojeń.
1) Unipolarny – proste sterowanie ale mniejszy moment obrotowy bo tylko
połowy uzwojeń są jednocześnie aktywne. 2) Bipolarny – bardziej złożone
sterowanie ale większy moment obrotowy bo całe uzwojenia są lepiej
wykorzystywane.
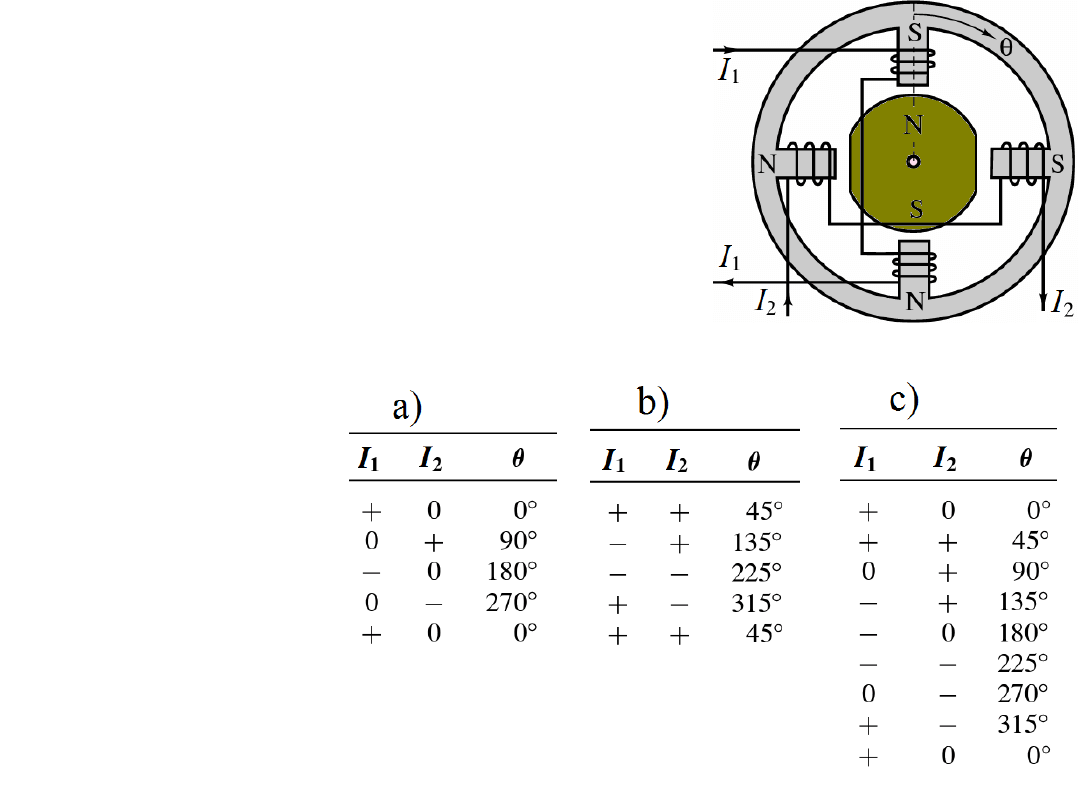
Przykład.
Przedstaw sekwencje prądów I
1
i I
2
dla silnika krokowego jak na rysunku obok, aby uzyskać
scenariusze obrotu: a) pełen krok i jedna faza,
b) pełen krok i obie fazy, c) kroki połówkowe.
Rozwiązanie
Widać, że obecność tylko jednego prądu ustawia wirnik
wzdłuż biegunów stojana, a obecność obu prądów I
1
i I
2
ustawia wirnik w pozycji między biegunami stojana łatwo
Odgadnąć następujące odpowiedzi:
Widać, że Δθ =
360º/(liczba faz)
⋅
(liczba biegunów)
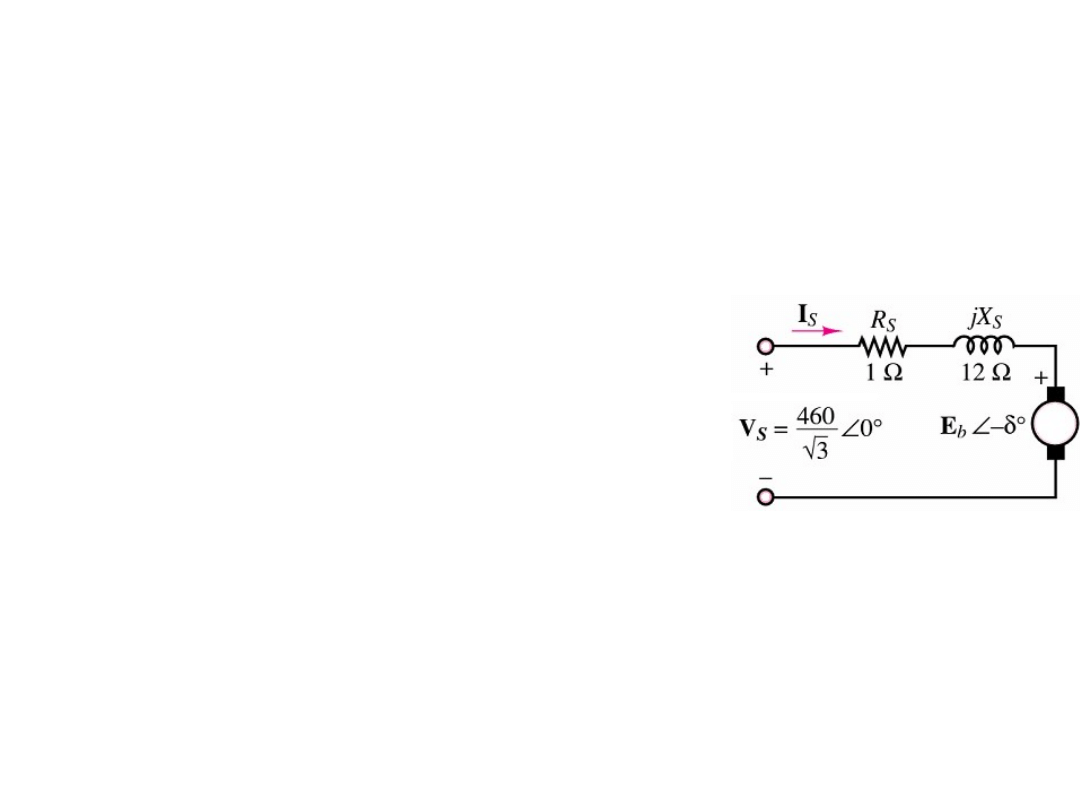
Elektrotechnika i elektronika Lista 07.
1. Oblicz moc dostarczaną do obciążenia w układzie trójfazowym przy połączeniu
gwiazda – gwiazda wiedząc, żę U
an
= 480
∠
0 V i symetrycznie U
bn
i U
cn
, Z
Y
= 2 + j4
Ω
, R
line
= 2
Ω
, R
neutral
= 10
Ω
.
2. Oblicz moc dostarczaną do obciążenia w układzie trójfazowym przy połączeniu
gwiazda – trójkąt wiedząc, żę U
an
= 480
∠
0 V i symetrycznie U
bn
i U
cn
, Z
∆
= 5 –j2
Ω
,
R
line
= 2
Ω
, R
neutral
= 10
Ω
.
3. Oblicz moc dostarczaną do obciążenia uzyskanego z połączenia równoległego
obciążeń z zadania 1 i 2 i przy identycznym źródle energii.
4. Oblicz wartość nominalną S [kVA]; indukowane
napięcie E
b
i kąt mocy wirnika
δ
dla pełnego
obciążenia silnika synchronicznego.
Dane: nominalne napięcie międzyfazowe: 460 V;
3 Φ (3 fazy); pf (power factor) = 0,707 opóźnienie;
prąd stojana przy pełnym obciążeniu I
s
= 12,5 A,
Z
s
= 1 + j12
Ω
. (Obliczać wg. schematu: ile na jedną fazę.)
5. Oblicz wartość nominalną S [kVA]; indukowane napięcie E
b
i kąt mocy wirnika
δ
dla
pełnego obciążenia silnika synchronicznego. Dane: nominalne napięcie
międzyfazowe: 380 V; 3 Φ (3 fazy); pf (power factor) = 0,707 a) wyprzedzanie, b)
opóźnienie; prąd stojana przy pełnym obciążeniu 10 A, Z
s
= 0 + j2
Ω
.
6. Obliczyć poślizg s wirnika przy pełnym obciążeniu oraz częstotliwość indukowanego
napięcia f
R
przy prędkości nominalnej w czterobiegunowym silniku indukcyjnym.
Wiadomo, że nominalne napięcie wynosi 200 V, 50 Hz i prędkość przy pełnym
obciążeniu: n = 1450 obr/min.
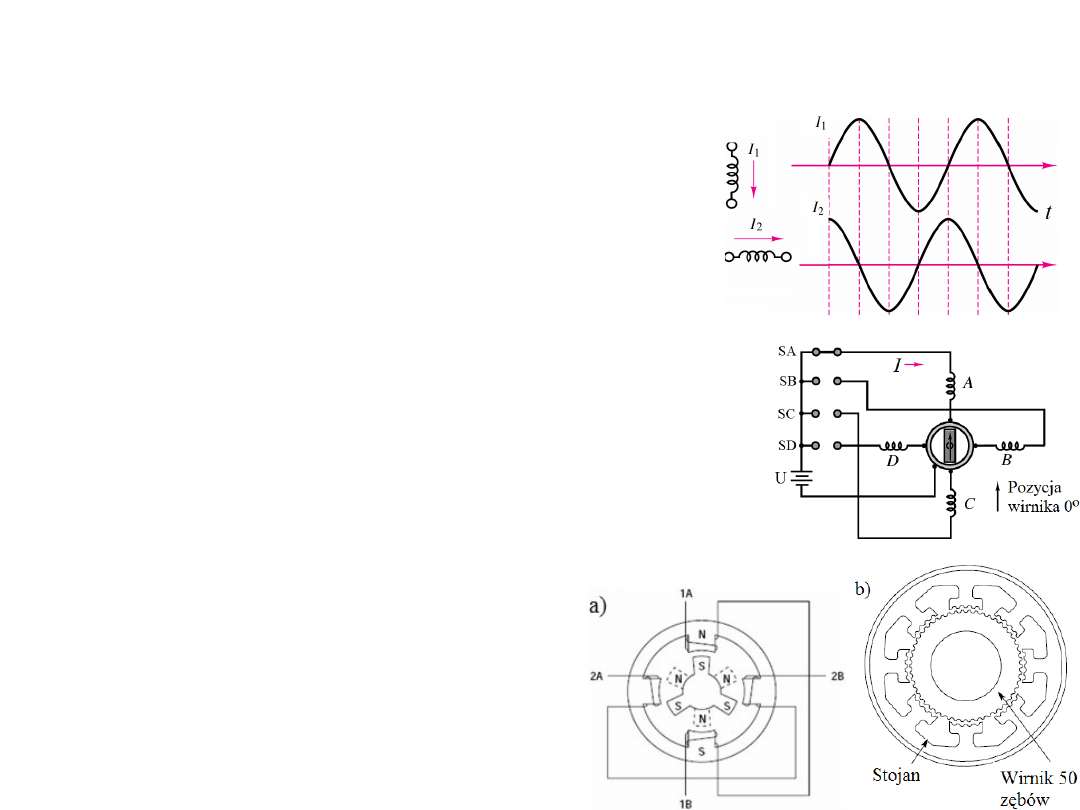
Elektrotechnika i elektronika Lista 08
.
1.
Wykazać, że w bezszczotkowym 2-fazowym silniku
zasilanym przebiegiem sinusoidalnym prądu, jak na rys. obok
I
1
= I
m
sin
ω
t I
2
= I
m
cos
ω
t może występować stały
(gładki – bez pulsacji) moment obrotowy.
2. Znajdź sekwencje włączeń wyłączników SA, SB, SC i SD
aby uzyskać kolejne kroki obroty po 45º.
3) Mając dane: Liczba zębów (występów) wirnika i stojana t = 4,
Liczba faz m = 3. Oblicz wielkość kroku Δθ.
4) Wyznacz najmniejszą wartość kroku w
krokowym silniku hybrydowym HB jak na
rys. a i b.
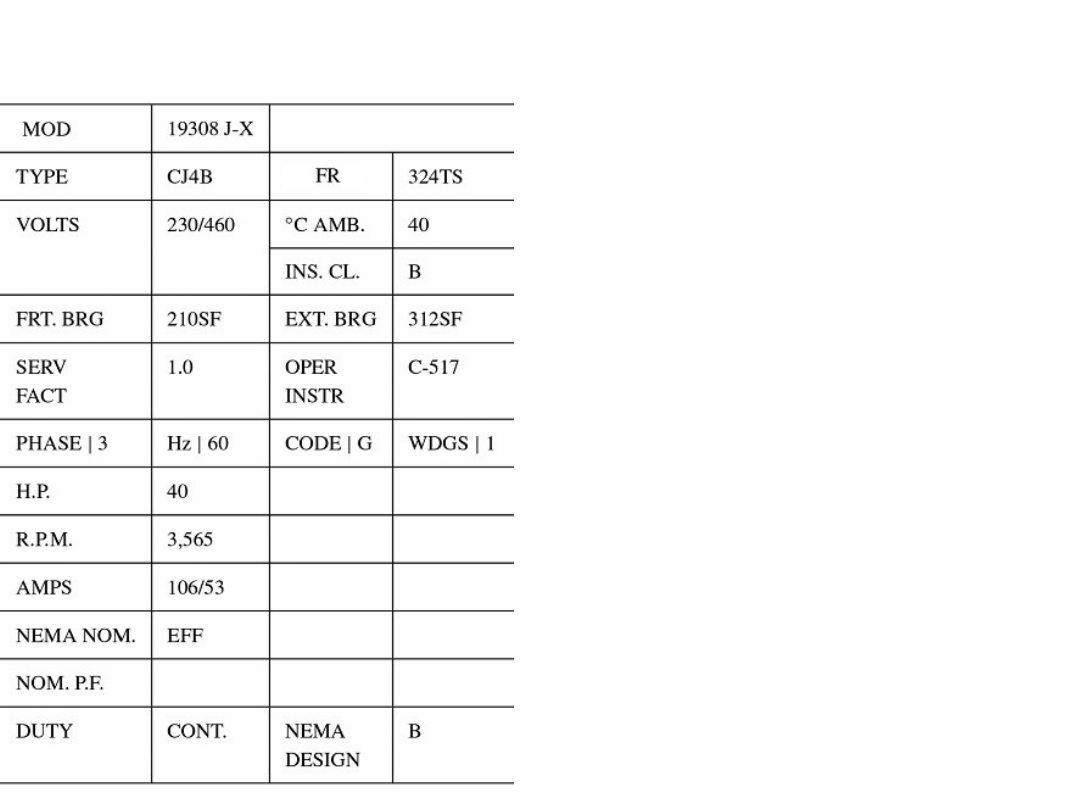
Przykładowa tabliczka na silniku Indukcyjnym
MOD – model (numer modelu
lub numer identyfikacyjny).
FR – (od „Frame”) specyfikuje
rozmiar i cechy konstrukcyjne.
AMB (lub MAX AMB) – określa
maksymalną dopuszczalna
temperaturę otoczenia.
INS. CL. – określa klasę
izolacji np. A (105
°
C), B (130
°
C) itd..
SERV FACT (service factor)
współczynnik określający
dopuszczalne przekroczenie
mocy nominalnej.
CODE – litera (od A do V z
pominięciem I, O i Q) oznacza
jeden z 19 granicznych
stosunków startowej mocy kVA
na kM.
DUTY – określa mod pracy
(np. CONT oznacza pracę
ciągłą)
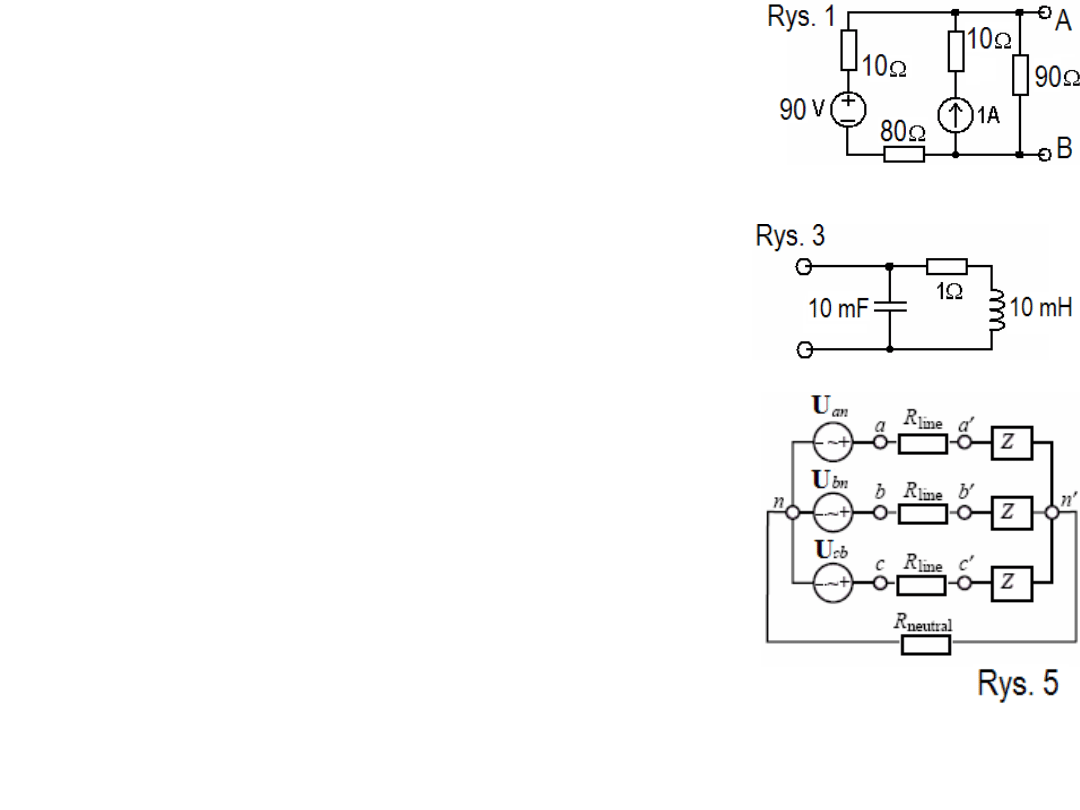
Elektrotechnika i elektronika kol-1.
1. Oblicz natężenie prądu w rezystorze 90
Ω
, rys. 1.
2. Dla układu z rys. 1 oblicz układy Thevenina i Nortona. Jaki prąd
pojawi się w odbiorniu o rezystancji 45
Ω
po podłączeniu do
zacisków AB.
3. Obliczyć zawadę odbiornika mocy z rys. 3 oraz przesunięcie
fazowe φ między przyłożonym napięciem U =100cos((100rad/s)t)V
a natężeniem prądu. Na ile Faradów zmienić pojemność w tym
układzie aby cosφ = 1. Oblicz moc wydzielaną przed i po korekcie.
4. Narysuj wykres wskazowy napięć i prądów w zadaniu 3.
5. Obliczyć moc P dostarczaną z generatora trójfazowego do
obciążenia w układzie jak na rys. 5 mając dane:
U
an(skuteczne)
= 141
∠
0° V, Z = 1 + j, R
line
= 0
Ω
, R
neutra
= √2
Ω
.
6. Generator 36 kW, 240 V, pracuje z obciążeniem równym połowie
nominalnego i sprawnością 90%. Oblicz moc pobieraną przez
generator oraz moc strat.
7. Silnik indukcyjny o parametrach 380 V, 50 Hz, P = 31,4 kW, 4
bieguny, pod pełnym obciążeniem jego wirnik obraca się z
prędkością n = 1200 obr/min. Oblicz: prędkość synchroniczną,
poślizg i moment obrotowy
.
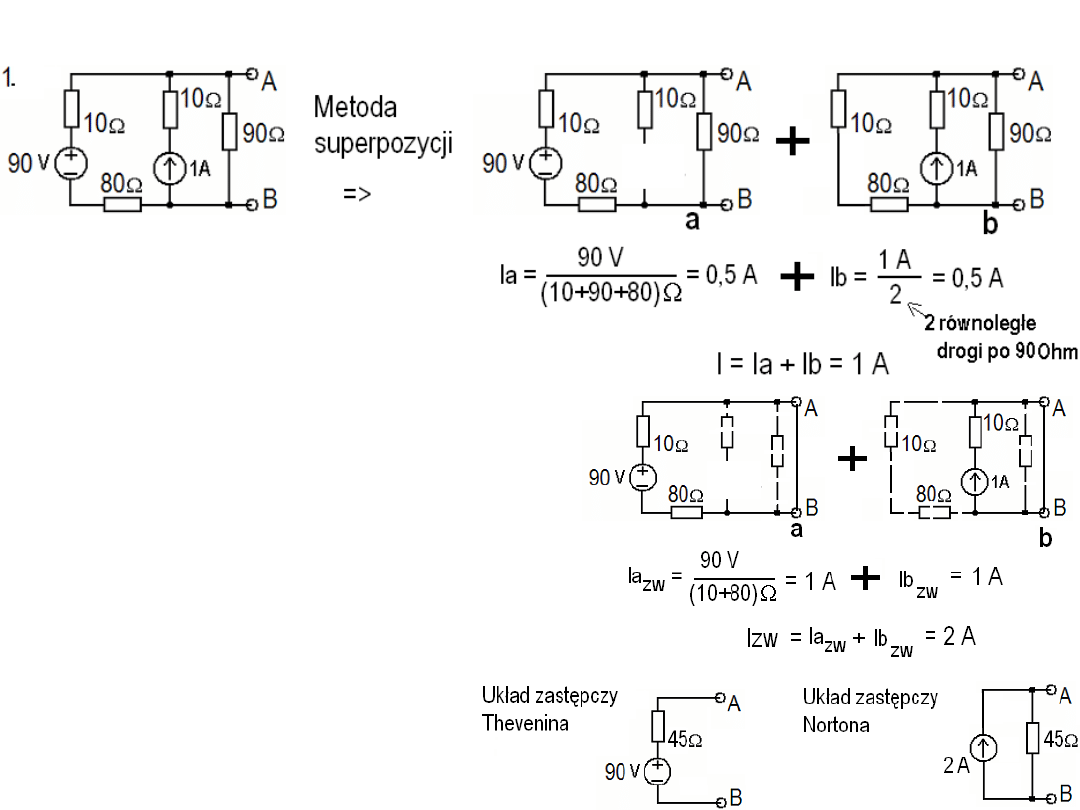
Elektrotechnika i elektronika kol-1, odpowiedzi i rozwiązania z przesadą.
2. U
T
= U
rozwarcia
= U
90 Ohm
= (90
Ω
)·(1 A) = 90 V
I
zwarcia
= 2 A jest to suma (superpozycja) prądów
z obu źródeł, jak na rysunku obok.
R
T
= R
N
= (U
rozwarcia
)/I
zwarcia
= 90/2 = 45
Ω
,
U
T
= U
rozwarcia
= 90V, I
N
=2A,
.
Elektrotechnika i elektronika kol-1, odpowiedzi.
3. Vs = 311cos(314t) V -> U
skuteczne
= 220 V -> U = 220
∠
0 V,
ω
= 100rad/s,
Z = (Z
RL
)(Z
c
)/(Z
RL
+ Z
C
) = (1 + j
ω
L)(1/j
ω
C)/(1 + j
ω
L + 1/j
ω
L) =
(1 + j100
⋅
0,01)(1/j100
⋅
0,01)/(1+j100
⋅
0,01 + 1/j100
⋅
0,01)
Ω
= (1+j)
⋅
(-j)/(1 + j - j)
Ω
=
(1-j)/1
Ω
= (√2
∠
-45°). W odbiorniku przeważa pojemność, kąt φ jest ujemny! Należy
zmniejszyć pojemność. Obliczymy jaka powinna być wypadkowa pojemność, zatem policzymy co
powinno być dołączone równolegle do gałęzi RL zamiast kondensatora 100 mF.
S = P + Q
L
= UI
*
= (220
∠
0)[(220
∠
0)/(1 + j)]* = (220
∠
0)
2
/(1 – j) = (220
∠
0°)
2
/(
√
2
∠
-45°) =
(48400/
√
2)
∠
45° VA = (48400/
√
2)(
√
2/2)W + j(48400/
√
2)(
√
2/2) VAR.
= 24200 W + j 24200 VAR -> P = 14200 W, Q
L
= j(24200) VAR.
Q
C
= -j24200 VAR = U(U/Z
C
)* = U
2
/Z
C
* -> Z
c
* = U
2
/Q
C
= 220
2
/(-j24200) = j2
Ω
,
Z
c
= -j2 = -j/
ω
C -> -j2 = -j/100C -> C = 1/200 F = 5 mF. Wniosek: zmienić 10 mF na 5 mF!
Przed korektą P = 24200 W. Po korekcie S = UI* = (220
∠
0)[(220
∠
0)/Z
po korekcie
Z
po korekcie
= (1 + j100
⋅
0,01)(1/j100
⋅
0,005)/(1+j100
⋅
0,01 + 1/j100
⋅
0,005)
Ω
=
(1+j)
⋅
(-j2)/(1 + j – j2)
Ω
= (2– j2)/(1-j) = 2
Ω
(to normalne bo obw. równoległy ma największa
impedancje w rezonansie)
Zatem S = UI* = (220
∠
0)[(220
∠
0)/2 = 24200 W -> P
po korekcie
= 24200 W.
Komentarz: to po co ta korekta? Przed korekta prąd był większy i większe straty na niezerowej
oporności linii przesyłowej (pominiętej w tym zadaniu)!
I
przed
=220V/(
√
2
∠
-45°) =155,6
∠
45°A -> I
skutecz. Przed
= 155,6 A
I
po
= 220V/(2
∠
0) = 110
∠
0) A -> I
skuteczne po
= 110 A
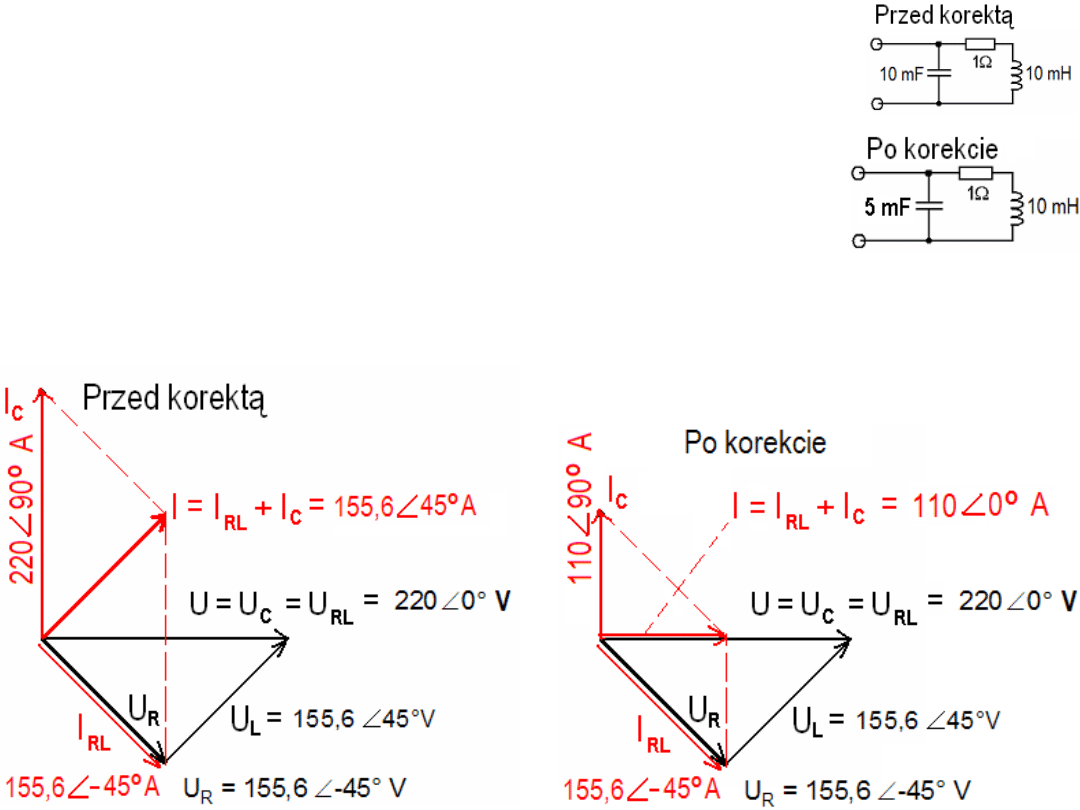
Elektrotechnika i elektronika kol-1, odpowiedzi.
4. Warto zacząć wykres od napięcia U = 220
∠
0 V, bo jest ono wspólne
dla kondensatora C i cewki z rezystancją LR. Przed korektą:
Prądy: I
C
= (220 V)/((1/j
ω
C)
Ω
) = 220/(-j1) A =j220 A = 220
∠
90 °A.
I
RL
= (220 V)/((1 + j
ω
L)
Ω
) =220/(1 + j) A = 220/ (√2
∠
45°) = 155,6
∠
-45°A
Napięcia: U
R
= I
RL
R = 155,6
∠
-45°A
⋅
1 Ω = 155,6
∠
-45° V
U
L
= I
RL
⋅
j
ω
L = 155,6
∠
-45°A
⋅
j1 Ω = 155,6
∠
-45°A
⋅
1
∠
90º Ω =
155,6
∠
45°V
Po korekcie: I
RL
= (220 V)/((1 + j
ω
L)
Ω
) =220/(1 + j) A = 220/ (√2
∠
45°) = 155,6
∠
-45°A bez zmian,
Podobnie U
R
i U
L
są bez zmian. Zmienił się kondensator zatem zmieniony jest I
C
:
I
C
= (220 V)/(Z
C
) = 220/(-j2) A = j220 A = 110
∠
90 °A. (zmniejszył się 2-krotnie)
5. Ponieważ układ jest zrównoważony (tj. symetrycznie obciążony) możemy stosować obliczenia
dla jednej fazy. Prąd w linii „neutral” jest równy 0 oraz U
nn’
= 0. Pa = I
2
Ro
I =
U
an
/(Z + R
line
)
=
(480
∠
0)/(1 + j + 0)
=
(141
∠
0)/(√2
∠π
/4)
= 100 A !
Pa = I
2
Ro = (100)
2
×
1 = 10 kW. Po = P
3 fazy
=3
⋅
Pa = 30 kW.
6. 36
×
0,5 = 18 kW to stanowi 90% -> P
in
= (18/0,9) = 20 kW, P
strat
= (20 – 18) kW = 2 kW.
7. Rozw:Prędkość synchoniczna ns = f/(2 pary biegunów)
×
(60s/min) = 1500 obr/min,
Poślizg s = (n
s
– n)/n
s
= (1500 – 1200)1500 = 0,2 => 20%,
T = P/
ω
m
= P/(2
π×
n/60) = 31,4
⋅
10
3
/(2
×
3,14
×
1200/60) = 250 Nm.