Opracowanie bimbałowego examu z 25 czerwca 2010. © by Kokosz

Zadanie 1
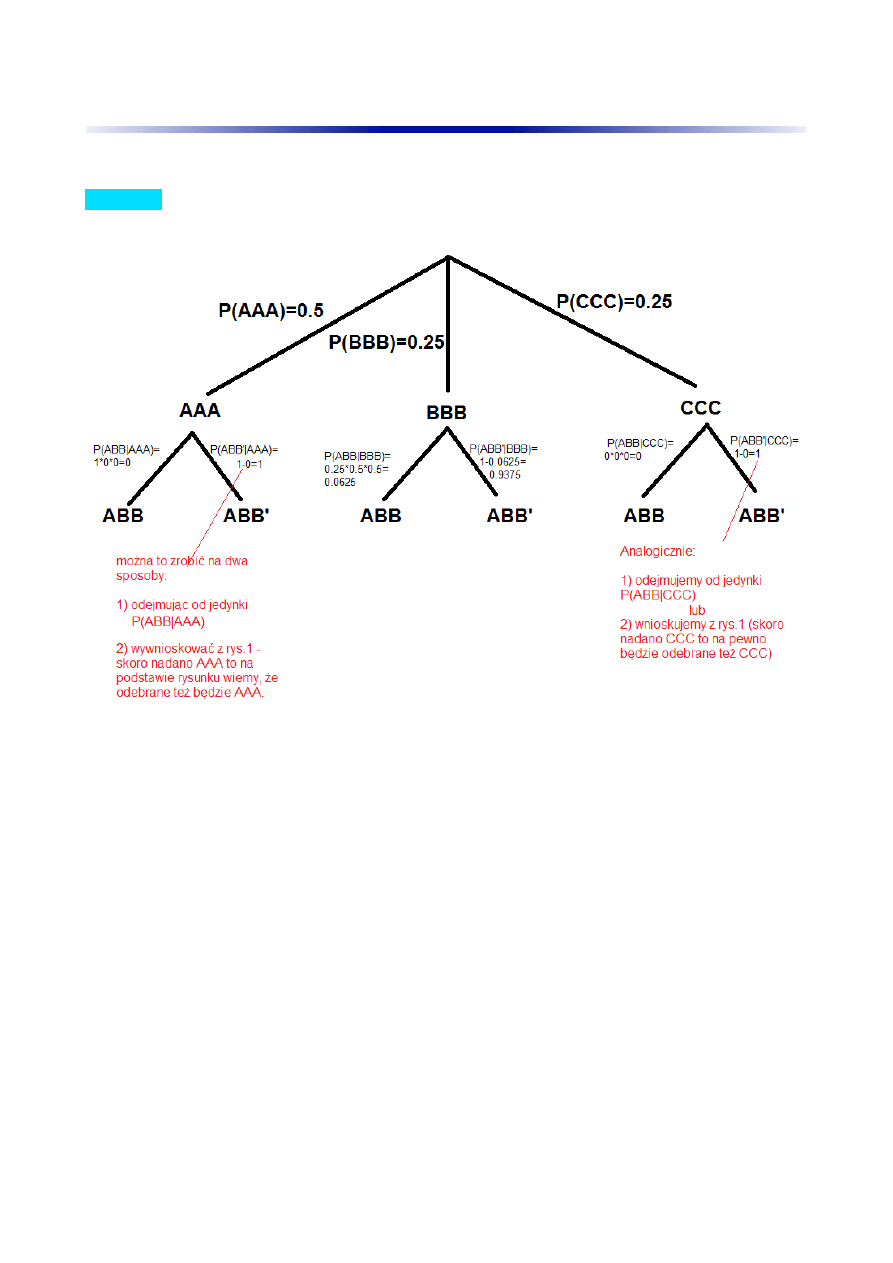
Aby dobrze zrozumieć to zadanie najlepiej je rozrysować w formie „drzewka”:

Oznaczenie ABB' oznacza tutaj zdarzenie polegające na odebraniu jakiegokolwiek sygnału różnego
od ABB, reszta oznaczeń jest raczej intuicyjna.

Prawdopodobieństwa „pierwszej części” drzewka odczytujemy bezpośrednio z treści, zaś „drugiej
części” wnioskujemy na podstawie danego rys.1

Przykładowo prawdopodobieństwo P(ABB|BBB) to prawdopodobieństwo odebrania sygnału ABB
gdy nadano BBB i tak:
-pierwsza litera: prawdopodobieństwo odebrania A gdy nadano B wynosi 0.25
-druga litera: prawdopodobieństwo odebrania B gdy nadano B wynosi 0.5
-trzecia litera: prawdopodobieństwo odebrania B gdy nadano B wynosi 0.5

Stąd prawdopodobieństwo P(ABB|BBB) wynosi 0.25*0.5*05=0.0625

Analogicznie dla reszty gałęzi.

1

Opracowanie bimbałowego examu z 25 czerwca 2010. © by Kokosz

a) Mamy obliczyć P(ABB), czyli prawdopodobieństwo odebrania sygnału ABB. Skorzystamy ze
wzoru na prawdopodobieństwo zupełne (inna nazwa: całkowite):

P  ABB = P  ABB∣AAA⋅P  AAAP  ABB∣BBB⋅P  BBB P  ABB∣CCC ⋅P CCC =

= 0⋅

1
2



1

16

⋅

1
4



0⋅

1
4

=

1

64

b) Mamy obliczyć P(AAA|ABB), czyli prawdopodobieństwo odebrania sygnału ABB gdy ktoś
nadał go jako AAA. Skorzystamy z twierdzenia Bayesa:

P  AAA∣ABB=

P  ABB∣AAA⋅P  AAA

P  ABB∣AAA⋅P  AAAP  ABB∣BBB ⋅P  BBB P  ABB∣CCC⋅P CCC 

=

=

0⋅

1
2

0⋅

1
2



1

16

⋅

1
4



0⋅

1
4

= 0

Zgadza się to z intuicją, ponieważ skoro ktoś nadałby sygnał AAA to z rys.1 widać, że odebrany on
też musi być jako AAA, zatem nie może być odebrany jako ABB (prawdopodobieństwo takiej
sytuacji wynosi 0, co wyżej pokazano).

Zadanie 2
a) Stałą C wyliczamy z tzw. warunku normalizacyjnego, tzn

∫

−∞

∞

p  x  dx=1

U nas:

∫

−

ᴫ
2

ᴫ

2

Ccosx dx=C

∫

−

ᴫ
2

ᴫ
2

cosx dx=C [ sinx]

− ᴫ

2

ᴫ
2

= C [sin

ᴫ
2

−

sin −

ᴫ
2

]

= C [sin

ᴫ
2



sin

ᴫ
2

]=

C [2sin

ᴫ
2

]=

2C

Zatem

2C=1  C =

1
2

b) Wartość przeciętna E  X  to inaczej wartość średnia, dla zmiennej losowej ciągłej
zdefiniowana jako:

E  X =

∫

−∞

∞

x⋅p x dx

2

Opracowanie bimbałowego examu z 25 czerwca 2010. © by Kokosz

U nas:

E  X  =

∫

−

ᴫ
2

ᴫ
2

x

1
2

⋅

cosx dx =

1
2

∫

−

ᴫ
2

ᴫ
2

x⋅cosx dx =

1
2

[

x⋅sinxcosx]

− ᴫ

2

ᴫ
2

=

1
2

[

ᴫ
2

⋅

sin

ᴫ
2



cos

ᴫ
2

−[−

ᴫ
2

⋅

sin −

ᴫ
2



cos−

ᴫ
2

]]

=

1
2

[

ᴫ

2



0−[

ᴫ
2

⋅

sin

ᴫ
2



cos

ᴫ
2

]]

=

1
2

[

ᴫ
2

−

ᴫ
2



0]= 0

Znowu można powiedzieć, że zgadza się to z intuicją, bo „na oko” widać, że wartość średnia
funkcji 1/2cosx (czyli tego p(x)) to 0.

c) Mediana dla zmiennej losowej o rozkładzie ciągłym to taka wartość

x

med

, że F  x

med

=

1
2

(dystrybuanta na argumencie x który jest medianą wynosi ½). To sprowadza się do spełnienia

równości

∫

−∞

x

med

p x  dx=

1
2

Dodatkowo mediana należy u nas do przedziału <−

ᴫ
2

;

ᴫ

2

> (treść zadania).

Zatem u nas:

∫

− ᴫ

2

x

med

1
2

cosx dx =

1
2

∫

− ᴫ

2

x

med

cosx dx =

1
2

[

sinx]

−

ᴫ
2

x

med

=

1
2

[

sin x

med

−

sin −

ᴫ
2

]

=

1
2

[

sin x

med



1]=

1
2

sin x

med



1
2

To jest lewa strona powyżej równości, prawa wynosi ½ stąd mamy, że

1
2

sin x

med

=

0

sin x

med

=

0

x

med

=

kᴫ gdzie k ∈ℤ ale jeszcze mamy, że x

med

∈

<−

ᴫ
2

;

ᴫ
2

>

Stąd x

med

=

0

d) Aby obliczyć wariancję skorzystamy ze wzoru obliczeniowego:

W  X =E  X

2

−[

E  X ]

2

3

Opracowanie bimbałowego examu z 25 czerwca 2010. © by Kokosz

E  X

2



=

∫

−

ᴫ
2

ᴫ
2

x

2

1
2

⋅

cosx dx =

1
2

∫

−

ᴫ
2

ᴫ
2

x

2

⋅

cosx dx =

1
2

[

x

2

sinx2xcosx−2sinx ]

−

ᴫ

2

ᴫ
2

=

1
2

[

ᴫ
2



2

sin

ᴫ
2



2

ᴫ
2

cos

ᴫ
2

−

2sin

ᴫ
2

−[ −

ᴫ
2



2

sin−

ᴫ

2



2−

ᴫ
2



cos −

ᴫ
2

−

2sin −

ᴫ
2

]]

=

1

2

[

ᴫ
2



2



0−2−[−

ᴫ
2



2

sin

ᴫ
2

−

2

ᴫ
2

cos

ᴫ
2



2sin

ᴫ
2

]]

=

1
2

[

ᴫ
2



2

−

2

ᴫ

2



2

−

2] =

ᴫ

2

−

8

4

już obliczyliśmy w punkcie b ), że E  X =0, zatem

W  X =

ᴫ

2

−

8

4

−

0

2

=

ᴫ

2

−

8

4

e) Między gęstością prawdopodobieństwa p(x) a dystrybuantą F(x) zachodzi dla zmiennej losowej
ciągłej związek:

F  x =

∫

−∞

x

p  x dx

U nas więc:

F  x =

∫

−

ᴫ
2

x

1
2

cosx dx =

1
2

∫

−

ᴫ
2

x

cosx dx =

1
2

[

sinx]

− ᴫ

2

x

=

1
2

[

sin x−sin −

ᴫ
2

]

=

1
2

[

sin x1]=

1
2

sin x 

1
2

przy okazji potwierdza się tutaj wyliczona przez nas wcześniej mediana, bo widać, że F 0=

1
2

f) Można tu skorzystać z definicji dystrybuanty: F  x =P  X x 
Widać więc, że szukane prawdopodobieństwo P  X 0 to po prostu wartość dystrybuanty w
punkcie 0, czyli

P  X 0=F 0=

1
2

Zadanie 3
a)
Przede wszystkim możemy od razu dopisać do naszej tabeli rozkłady brzegowe, tzn. np. P(X=-1),
sumujemy wówczas całą kolumnę gdzie X=-1, analogicznie dla reszty kolumn i wierszy.

Tak otrzymana tabelka jest poniżej:

4

Opracowanie bimbałowego examu z 25 czerwca 2010. © by Kokosz

P  X =i ;Y = j

X =i

-1

0

1

Y = j -1

1
3

0

0

P Y =−1 =

1
3

0

0

1
3

0

P Y =0 =

1
3

1

0

0

1
3

P Y =1=

1
3

P  X =−1 =

1
3

P  X =0 =

1
3

P  X =1=

1
3

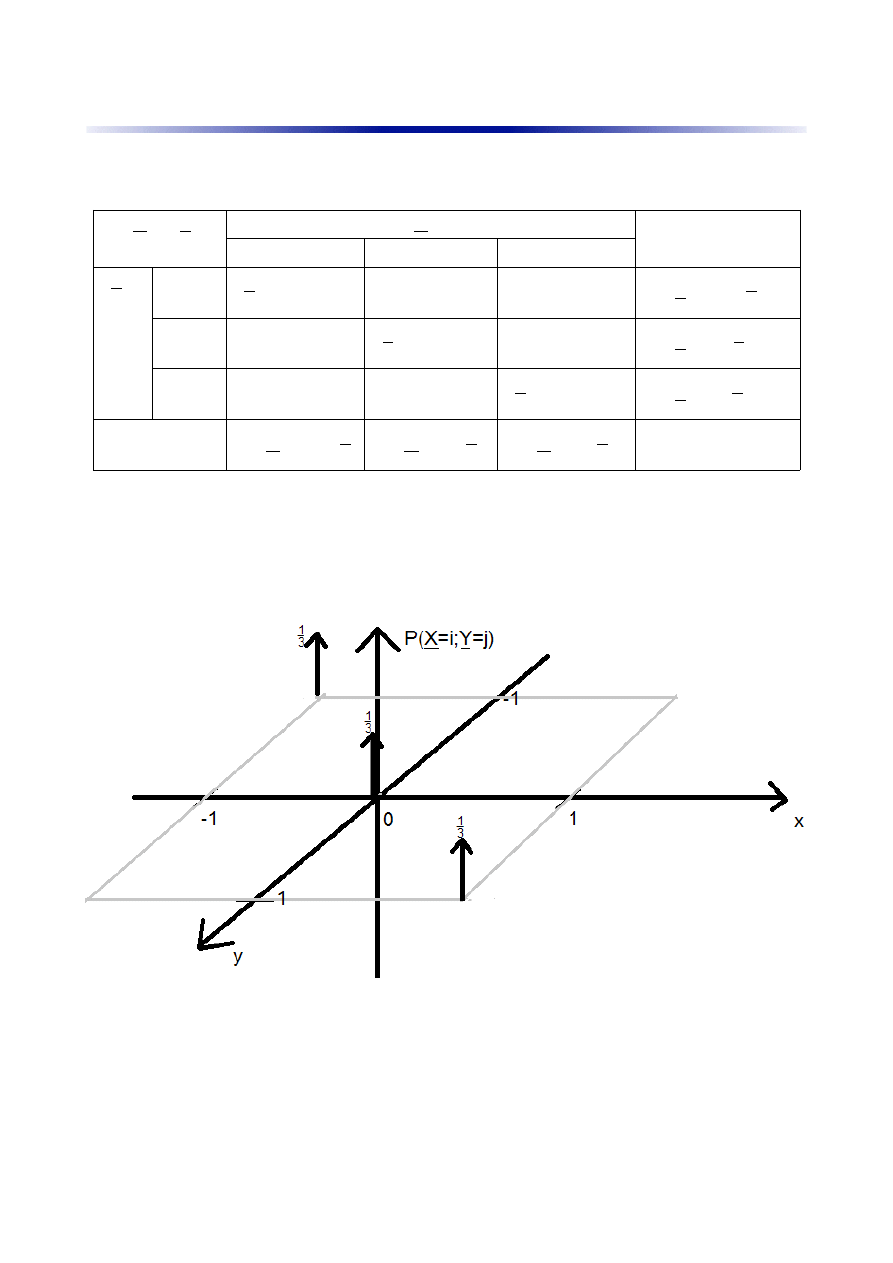
Aby dobrze zrozumieć jak oblicza się dystrybuantę najlepiej narysować wykres funkcji rozkładu
prawdopodobieństwa (szare linie są tylko pomocnicze):

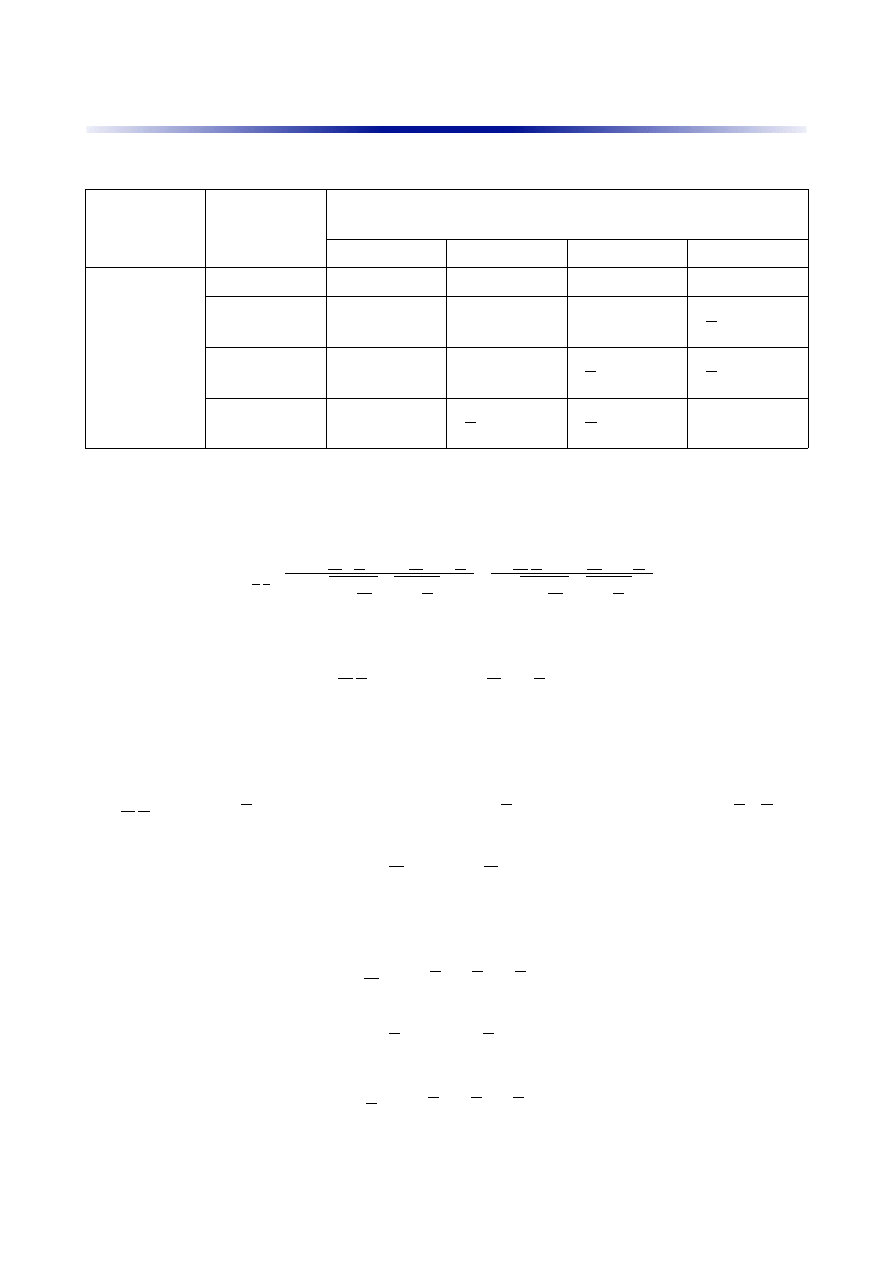
Teraz wpisujemy wartości do tabeli dystrybuanty, np. w pole gdzie X(0;1> i Y(-1;0> wpisujemy
sumę wysokości wszystkich strzałek z powyższego wykresu, których współrzędne są mniejsze niż
górne granice przedziałów, tzn. X są mniejsze od 1, a Y są mniejsze od 0.

5

Opracowanie bimbałowego examu z 25 czerwca 2010. © by Kokosz

F(x,y)

X

(−∞ ;−1 >

(−1 ;0 >

( 0 ;1 >

(1 ;∞ >

Y

(−∞ ;−1 >

0

0

0

0

(−1 ;0 >

0

0

0

1
3

( 0 ;1 >

0

0

1
3

2
3

(1 ;∞ >

0

1
3

2
3

1

I to już jest podana dystrybuanta łączna.

b)
Współczynnik korelacji (unormowany współczynnik kowariancji) jest dany wzorem:

ρ

X Y

=

corr  X , Y −E  X  E Y 



W  X ⋅



W Y 

=

E  X Y −E  X  E Y 



W  X ⋅



W Y 

Teraz musimy policzyć wszystkie występujące we wzorze wielkości.

E  X Y =

∑

∀

j

∑

∀

i

i⋅j⋅P  X =i ;Y = j

W praktyce liczymy to mnożąc współrzędne każdego pola w tabelce rozkładu przez wartość tego
pola:

E  X Y =−1⋅−1⋅

1
3

−

1⋅0⋅0−1⋅1⋅00⋅−1⋅00⋅0⋅

1
3



0⋅1⋅01⋅−1⋅01⋅0⋅01⋅1⋅

1
3

=

2
3

E  X =

∑

∀

i

i⋅P  X =i

W praktyce liczymy to mnożąc każdą możliwą wartość X przez prawdopodobieństwo, że ZL
przyjmie tą właśnie wartość X (te prawdopodobieństwa brzegowe dopisaliśmy w powyższej tabelce
nad wykresem). Stąd:

E  X =−1⋅

1
3



0⋅

1
3



1⋅

1
3

=

0

Analogcznie dla Y:

E Y =

∑

∀

j

j⋅P Y = j

E Y =−1⋅

1
3



0⋅

1
3



1⋅

1
3

=

0

6

Opracowanie bimbałowego examu z 25 czerwca 2010. © by Kokosz

Wariancje policzymy korzystając z podanego już we wcześniejszym zadaniu wzoru
obliczeniowego:

W  X =E  X

2

−[

E  X ]

2

i analogicznie W Y =E Y

2

−[

E Y ]

2

E  X

2

=

∑

∀

i

i

2

⋅

P  X =i Stąd:

E  X

2

=−

1

2

⋅

1
3



0

2

⋅

1
3



1

2

⋅

1
3

=

2
3

Analogicznie dla Y: E Y

2

=

∑

∀

j

j

2

⋅

P Y = j ; EY

2

=−

1

2

⋅

1
3



0

2

⋅

1
3



1

2

⋅

1
3

=

2
3

Zatem wariancje wynoszą (można zauważyć, że wszystkie wartości występujące we wzorze na
wariancję są takie same dla X i Y, więc wariancja X będzie równa wariancji Y):

W  X =W Y =

2
3

−

0

2

=

2
3

Mamy więc wszystko do współczynnika korelacji:

ρ

X Y

=

E  X Y −E  X  E Y 



W  X ⋅



W Y 

=

2
3

−

0⋅0



2
3

⋅



2
3

= 1

c)
ZL X i Y będą niezależne statystycznie, gdy będzie zachodzić

∑

∀

j

∑

∀

i

P  X =i ;Y = j=P  X =i⋅P Y = j

Sprawdźmy więc czy dla pierwszego pola z tabeli rozkładu prawdopodobieństwa zachodzi
powyższy warunek:

P  X =−1 ;Y =−1=P  X =−1⋅P Y =−1

1
3

=

1
3

⋅

1
3

1
3

≠

1
9

Widać więc, że podany warunek nie zachodzi dla każdego i oraz j, więc zmienne losowe X i Y nie
są niezależne statystycznie (są zależne).

7