1

Metody sztucznej inteligencji

Politechnika Śląska

Katedra Podstaw Konstrukcji Maszyn

Rok akademicki 2009/2010

Wykład 4

2

Użycie logiki pierwszego rzędu nie 

zapewnia powodzenia z powodu

• niedokładność - skompletowanie pełnej listy 

możliwych reguł wymaga za dużo pracy i za 
dużo czasu, 

• nieznajomości teorii - np. medycyna nie zna 

wytłumaczenia powodów wszystkich schorzeń,

• nieznajomości praktyki - nawet jeżeli znamy 

wszystkie reguły nie możemy być pewni czy w 
przypadku konkretnego pacjenta określone 
reguły są poprawne.

3

Teoria prawdopodobieństwa

• pozwala na sumowanie niepewności wynikającej 

z wielu przyczyn

• prawdopodobieństwo 0.8 oznacza 80% 

stopień

przekonania

o prawdziwości zdania 

(stwierdzenia)

• prawdopodobieństwo nie oznacza stopnia 

prawdziwości zdania (stwierdzenia) 

4

Podstawowe rodzaje 

prawdopodobieństwa

• Prawdopodobieństwo bezwarunkowe (a priori)

• Prawdopodobieństwo warunkowe (a posteriori)

• Prawdopodobieństwo łączne

5

Twierdzenie Bayesa

)

(

)

|

(

)

(

B

P

B

A

P

B

A

P

=

∧

)

(

)

|

(

)

(

A

P

A

B

P

B

A

P

=

∧

)

(

)

(

)

|

(

)

|

(

A

P

B

P

B

A

P

A

B

P

=

Reguła Bayesa

Reguła Bayesa umożliwia obliczenie 
nieznanych prawdopodobieństw na podstawie 
znanych prawdopodobieństw.

6

Sieć bayesowska (sieć

przekonań - belief network)

• Zbiór zmiennych losowych (

węzły sieci

)

• Zbiór zorientowanych krawędzi (

określają, 

która zmienna ma bezpośredni wpływ na 

inną

)

• Tablica prawdopodobieństw warunkowych 

(

określa wpływ „rodziców” na węzeł

)

Sieć przekonań to graf skierowany, acykliczny

Sieć przekonań reprezentuje łączny rozkład 
prawdopodobieństwa dla danej dziedziny

7

Rodzaje wnioskowania

w sieciach przekonań (1)

• Wnioskowanie diagnostyczne

(od efektów do 

przyczyn)

– Wiemy że JohnCalls
– wnioskujemy P(Burglary|JohnCalls) = 0.016

• Wnioskowanie przyczynowe

(od przyczyn do 

efektów)

– Wiemy, że Burglary
– wnioskujemy P(JohnCalls|Burglary) = 0.86,

P(MaryCalls|Burglary) = 0.67

Russel S., Norvig P.: Artificial Intelligence. A modern approach

8

Rodzaje wnioskowania

w sieciach przekonań (2)

• Wnioskowanie międzyprzyczynowe

(pomiędzy przyczynami wspólnego efektu)

– jeśli wiemy, że Alarm, P(Burglary|Alarm) = 0.376
– gdy wiemy dodatkowo, że Earthquake, to

P(Burglary|Alarm

∧ Earthquake) = 0.003

Russel S., Norvig P.: Artificial Intelligence. A modern approach

9

Rodzaje wnioskowania

w sieciach przekonań (3)

• Wnioskowanie mieszane

(łączy dwa lub więcej 

powyższych rodzajów wnioskowań):

– JohnCalls = True (efekt) oraz Eartquake = False

(przyczyna) daje:
P(Alarm|JohnCalls

∧¬ Eartquake) = 0.03

[jednoczesne zastosowanie wnioskowania diagnostycznego 
i przyczynowego]

P(Burglary|JohnCalls

∧¬ Eartquake) = 0.0017

[jednoczesne zastosowanie wnioskowania diagnostycznego 
i międzyprzyczynowego]

Russel S., Norvig P.: Artificial Intelligence. A modern approach

10

Rozumowanie rozmyte

„

Logika rozmyta nie jest logiką, która jest rozmyta, ale 
logiką, która jest używana do opisania rozmycia 
wiedzy.

„

Logika rozmyta jest oparta na tym, że zjawiska 
(zdarzenia, fakty – temperatura, wzrost, prędkość, 
odległość, wygląd) opisuje się zazwyczaj za pomocą
rozmytej skali pojęć (np. gorąco, bardzo wysoki).

„

Logika klasyczna oparta jest na ostrym rozróżnieniu 
między zbiorami (klasami).

„

Logika rozmyta odzwierciedla rozumowanie człowieka 
i jest próbą numerycznego modelowania rozumienia 
sensu pojęć.

11

Logika rozmyta (LR) jest zbiorem matematycznych 
zasad określających reprezentację wiedzy i stopień
przynależności do zbioru.

W odróżnieniu od dwuwartościowej logiki 
Boolowskiej, logika rozmyta jest wielowartościowa.

Zastosowanie LR polega na wyliczaniu stopni 
przynależności i stopni prawdziwości.  

Podobnie jak w logice Boolowskiej, w LR 0 oznacza 
fałsz, a 1 prawdę.

12

Reguła rozmyta

Reguła rozmyta jest definiowana jako zdanie 
warunkowe o postaci:

IF

x jest A

THEN y jest B

gdzie x i y są zmiennymi lingwistycznymi; a A i B są
wartościami lingwistycznymi określonymi przez 
zbiory rozmyte.

13

Różnica między regułą ostrą i rozmytą

W klasycznej regule stosuje się logikę binarną,

Reguła: 1
IF

prękość > 100

THEN  miejsce zatrzymania 

jest daleko

Regułą: 2
IF

prędkość < 40

THEN miejsce zatrzymania 

jest blisko

Zmienna prędkość może mieć wartości numeryczne np. od 
0 do 220 km/h, ale zmienna miejsce zatrzymania może 
przyjmować tylko wartości daleko lub blisko..  

Nengnevintsky M.: Artificial Intelligence

14

Wnioskowanie Mamdaniego

„

Metoda Mamdaniego polega na realizacji czterech 
kroków:

z

rozmywaniu zmiennych wejściowych, 

z

ocenie reguł

z

agregacji wyjść reguł

z

wyostrzaniu .

15

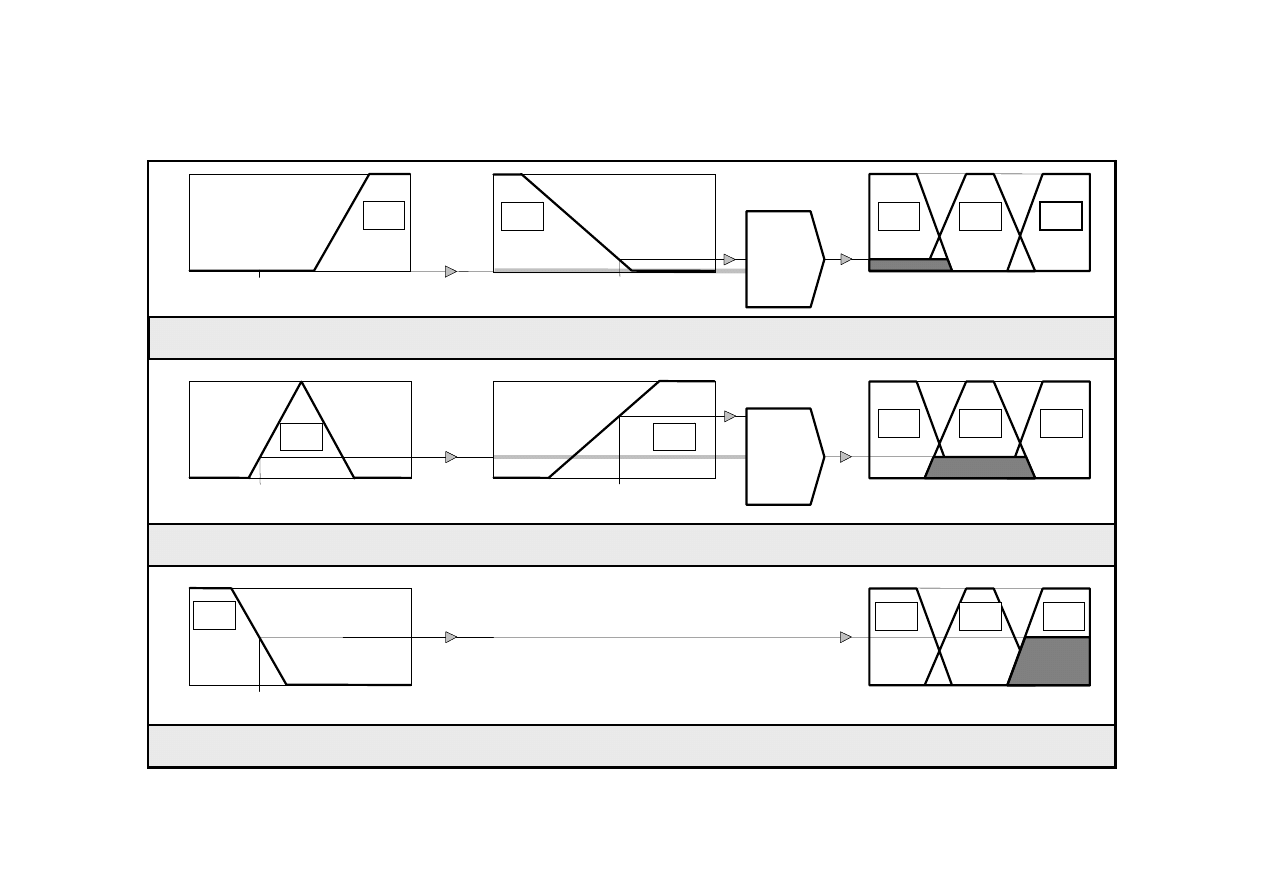
Ocena reguł metodą Mamdamiego

A3

1

0

X

1

y1

0

Y

0.0

x1

0

0.1

C1

1

C2

Z

1

0

X

0.2

0

0.2

C1

1

C2

Z

A2

x1

Rule 3:

A1

1

0

X

0

1

Z

x1

THEN

C1

C2

1

y1

B2

0

Y

0.7

B1

0.1

C3

C3

C3

0.5

0.5

OR

(max)

AND

(min)

OR

THEN

Rule 1:

AND

THEN

Rule 2:

IF x is A3 (0.0)

y is B1 (0.1)

z is C1 (0.1)

IF x is A2 (0.2)

y is B2 (0.7)

z is C2 (0.2)

IF x is A1 (0.5)

z is C3 (0.5)

Nengnevintsky M.: Artificial Intelligence

16

„

Metoda wnioskowania Mamdaniego polega na 
znajdowaniu środka ciężkości dwuwymiarowej 
figury. Procedura ta nie jest efektywna 
obliczeniowo.

„

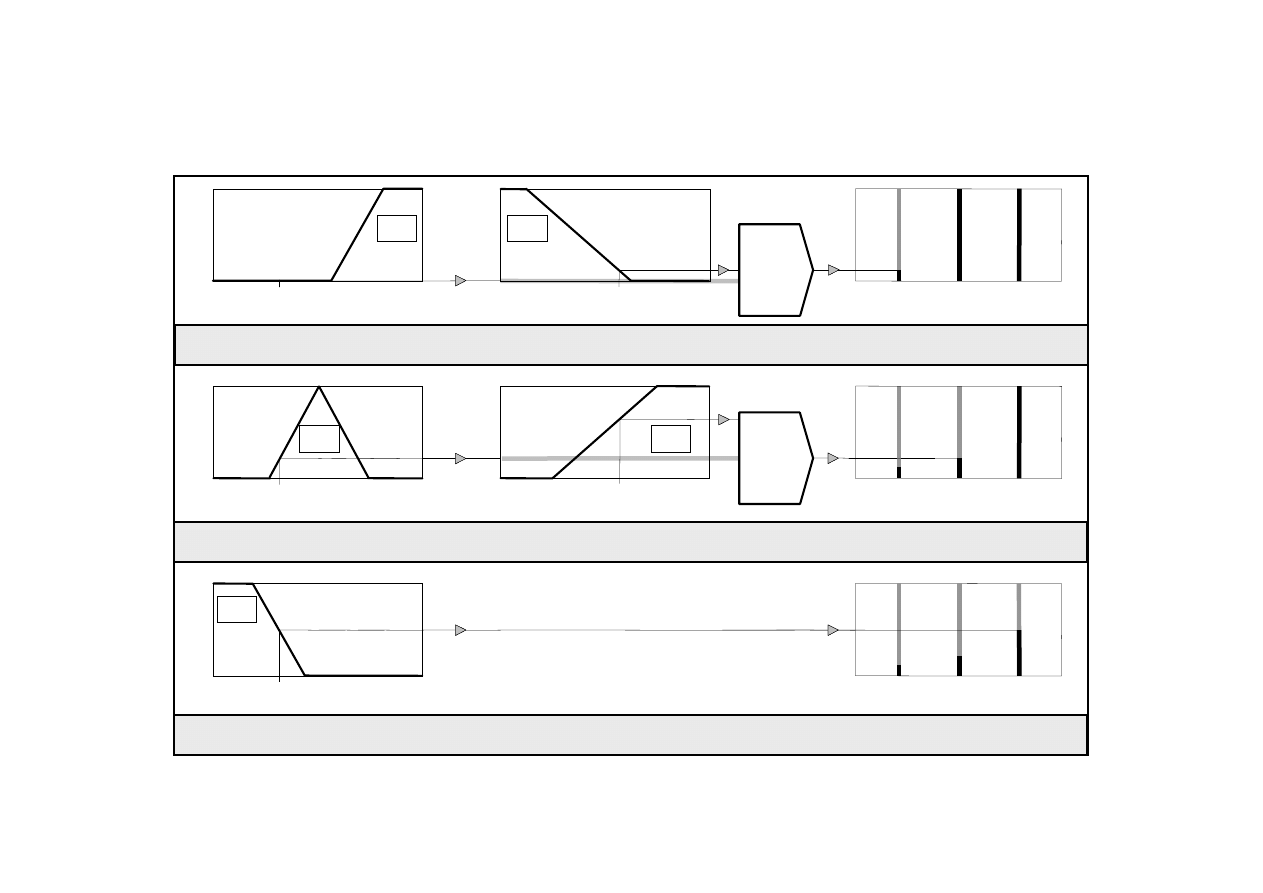
Michio Sugeno wprowadził singleton jako funkcję
przynależności konkluzji wynikających z reguł.

„

Singleton (rozmyty singleton) jest zbiorem 
rozmytym, którego funkcja przynależności 
przyjmuje wartość 1 w jednym punkcie, a poza nim 
przyjmuje wartość 0.

Wnioskowanie metodą Sugeno

17

A3

1

0

X

1

y1

0

Y

0.0

x1

0

0.1

1

Z

1

0

X

0.2

0

0.2

1

Z

A2

x1

IF x is A1 (0.5)

z is k3 (0.5)

Rule 3:

A1

1

0

X

0

1

Z

x1

THEN

1

y1

B2

0

Y

0.7

B1

0.1

0.5

0.5

OR

(max)

AND

(min)

OR y is B1 (0.1)

THEN

z is k1 (0.1)

Rule 1:

IF x is A2 (0.2) AND y is B2 (0.7)

THEN

z is k2 (0.2)

Rule 2:

k1

k2

k3

IF x is A3 (0.0)

Ocena reguł w metodzie Sugeno

Nengnevintsky M.: Artificial Intelligence