ELEMENTY TEORII ZBIORÓW ROZMYTYCH

OPRACOWAŁ: M. KWIESIELEWICZ

POJĘCIA NIEPRECYZYJNE

ODDZIAŁYWANIA CZŁOWIEK-OBIEKT TECHNICZNY
OTOCZENIE (Hoang 1990):
· człowieka na otoczenie, np.: ergonomiczna konstrukcja

otoczenia,

· otoczenia na człowieka, np.: temperatura, skład powietrza,
· człowieka na obiekt, np.: doświadczenie w obsłudze,
· obiektu na człowieka, np.: złożoność obiektu, wyposażenie

techniczne,

· otoczenia na obiekt, np.: warunki klimatyczne,
· obiektu na otoczenie, np.: chałas, emisja substancji

szkodliwych.

KATEGORIE SUBIEKTYWNE
Przykłady zmiennych lingwistycznych:

•

“niska temperatura”, “wysoka temperatura”,

•

“wysoki poziom chałasu”, “niski poziom chałasu”.

Czynnik ludzki

•

ryzyko, zmęczenie, poziom stresu, itd.

Podstawy teoretyczne modelowania człowiek - obiekt techniczny z
zastosowaniem teorii zbiorów rozmytych

Podstawowe pojęcia z zakresu teorii zbiorów rozmytych

Niech X będzie zbiorem obiektów, zwanym przestrzenią rozważań.

Dowolny element ze zbioru X oznaczmy przez x . Załóżmy ponadto
że przynależność elementu x do podzbioru A zbioru X określona jest
za pomocą funkcji przynależności

[ ]

µ

A

X

:

,

→

0 1

. Zbiór rozmyty A

zdefiniowany jest następująco (Zadeh 1965):

( )

(

)

{

}

A

x

x

x

X

A

=

∈

,

,

µ

Notacja:

( )

A

x

x

A

x X

=

∈

∑

µ

/

( )

A

x

x

A

i

i

i

n

=

=

∑

µ

/

1

Przykład:
Zbiór rozmyty “mała liczba naturalna” określony w przestrzeni
rozważań

{

}

X

=

1 2 3 4 5 6 7 8 9 10

, , , , , , , , ,

:

“mała liczba naturalna”

= 1 / 1 + 0.9 / 2 + 0.8 / 3 + 0.7 / 4 + 0.5 / 5 + 0.1 / 6

Interpretacja graficzna:

0

50

1

(x)

µ

niska

wysoka

Rys.2. Funkcje charakterystyczne

zbiorów "temperatura niska"

w sensie logiki klasycznej.

t [

°C]

temperatura temperatura

i "temperatura wysoka"

0

50

1

(x)

µ

niska

wysoka

Rys.3.Funkcje charakterystyczne

zbiorów "temperatura niska"

w sensie logiki rozmytej.

t [

°C]

temperatura temperatura

i "temperatura wysoka"

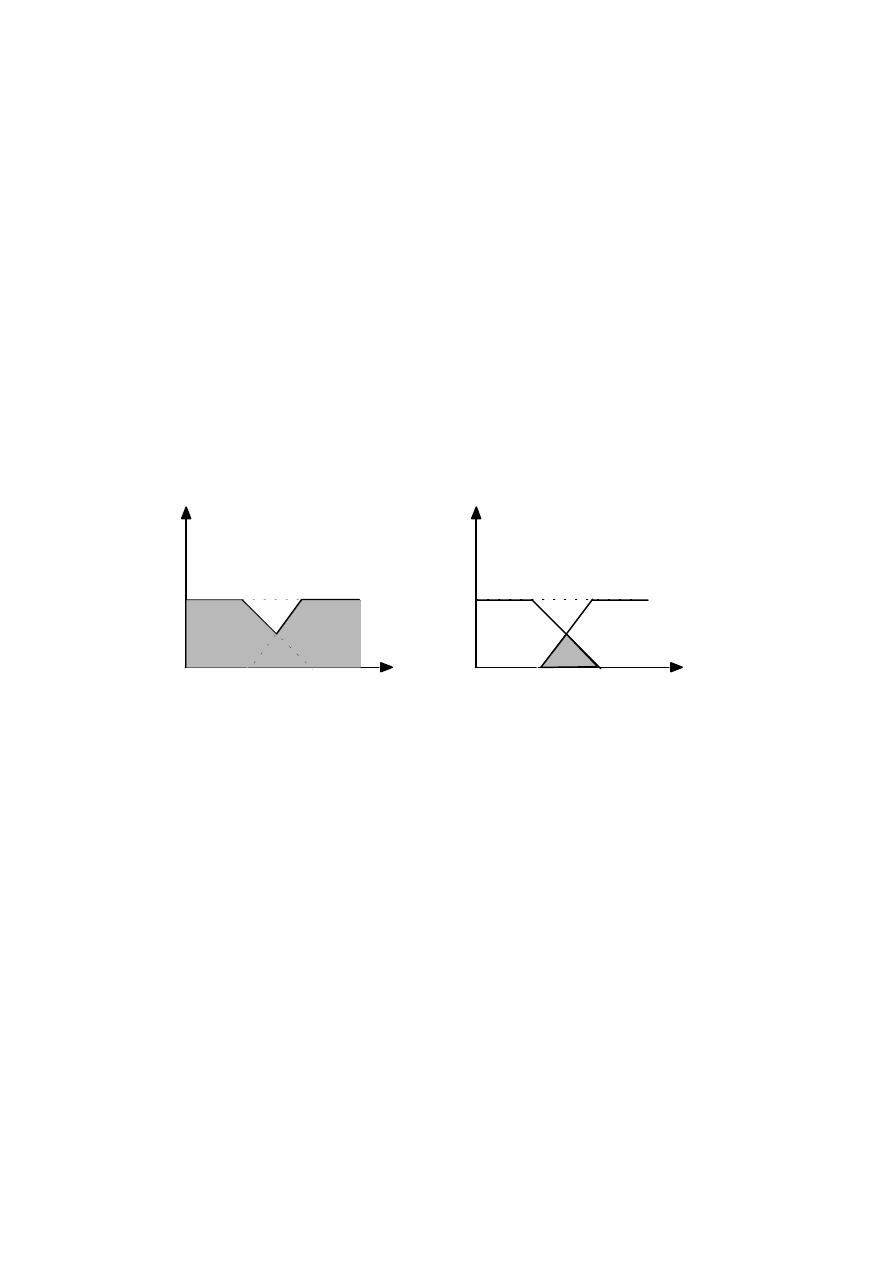
Podstawowe operacje na zbiorach rozmytych zdefiniowane są
następująco (Zadeh 1965, Kacprzyk 1986)
· suma zbiorów rozmytych A i B:

( )

( ) ( )

{

}

µ

µ

µ

A B

A

B

x

x

x

∪

=

max

,

,

· przecięcie zbiorów rozmytych A i B:

( )

( ) ( )

{

}

µ

µ

µ

A B

A

B

x

x

x

∩

=

min

,

· negacja zbioru rozmytego A:

( )

( )

µ

µ

¬

= −

A

A

x

x

1

,

· iloczyn kartezjański zbiorów rozmytych A i B (są one

zdefiniowane na różnych przestrzeniach rozważań):

(

)

( )

(

)

{

}

µ

µ

µ

C A B

A

B

x y

x

y

= ×

=

,

min

,

0

50

1

(x)

µ

niska

wysoka

Rys.4. Interpretacja graficzna

sumy zbiorów rozmytych

"temperatura niska"

t [

°C]

temperatura temperatura

lub "temperatura wysoka"

0

50

1

(x)

µ

niska

wysoka

Rys.5. Interpretacja graficzna

iloczynu zbiorów rozmytych

"temperatura niska"

t [

°C]

temperatura temperatura

i "temperatura wysoka"

Przykład:

A

=

+

+

+

+

+

0 6 1 0 4 2 0 3 3 0 8 4 0 5 5 1 6

. /

. /

. /

. /

. /

/

{

}

X

=

1 2 3 4 5 6

, , , , ,

B

=

+

+

+

+

+

0 8 1 0 3 2 1 3 1 4 0 4 5 0 9 6

. /

. /

/

/

. /

. /

{

}

Y

=

1 2 3 4 5 6

, , , , ,

.

Iloczyn kartezjański:

Y

A B

X

1

2

3

4

5

6

1
2

3
4
5
6

0 6 0 3 0 6 0 6 0 4

0 6

0 4 0 3 0 4 0 4 0 4

0 4

0 3 0 3 0 3 0 3 0 3

0 3

0 8 0 3 0 8 0 8 0 4

0 8

0 5 0 3 0 5 0 5 0 4 0 5
0 8 0 3

1

1

0 4

0 9

× =





































.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

/

.

.

.

.

Definicja.

α

- przekrojem zbioru rozmytego A

⊂

~

X, oznaczonym A

α

,

nazywamy następujący zbiór nierozmyty:

A

α

= { x

∈

X :

µ

A

( x )

≥

α

},

∀α

∈

[0, 1]

Interpretacja graficzna

α

- przekroju została przedstawiona na rysunku

4:

Rys.6. Interpretacja graficzna

α

- przekroju

Twierdzenie o dekompozycji Każdy zbiór rozmyty A

⊂

~

X, można

przedstawić w postaci:

A =

α ∈

∑

[ , ]

0 1

α

A

α

,

przy czym

α

A

α

oznacza zbiór rozmyty, którego elementom przypisano

następujące stopnie przynależności:

µ

α

α

A

(x) =

α

α

α

dla x

A

dla x

A

∈

∉







0

Definicja Nośnikiem zbioru rozmytego A

⊂

~

X, oznaczanym

S

A

nazywamy następujący zbiór nierozmyty:

S

A

= { x

∈

X :

µ

A

( x ) > 0 }

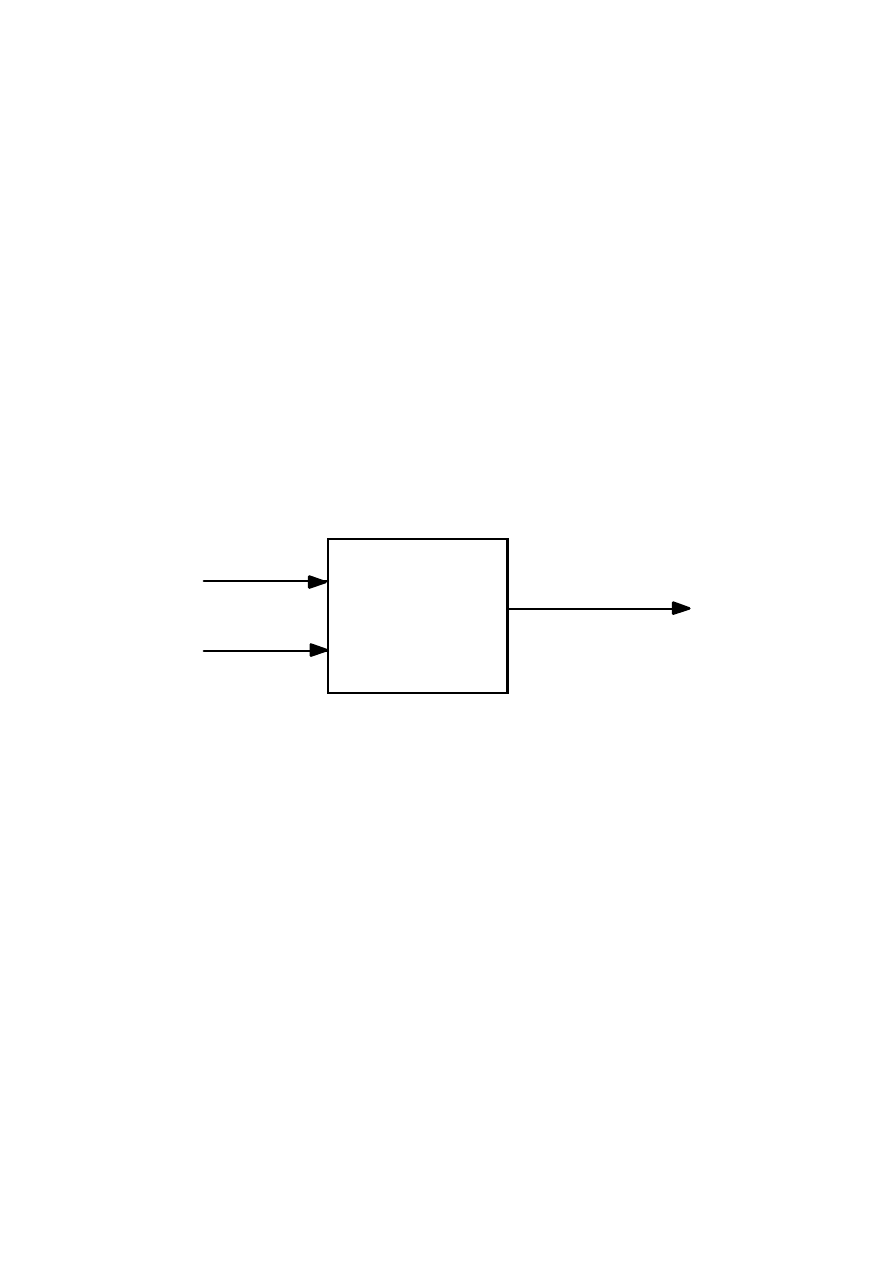
Rozmyty system ekspertowy

Uogólnioną rozmytą regułę wnioskowania modus ponens, można

przedstawić przy pomocy następującego schematu (Dubois and Prade
1988, Kacprzyk 1986):

(

)

I P

Q

P P

W P

P

Q

:

:

:

′ ⇒

− − − − − − − − −

′ ⇒

!

,

gdzie: "

!

" jest złożeniem typu max-min, I jest implikacją

lingwistyczną, P przesłanką lingwistyczną, W wnioskiem z
rozumowania rozmytego. Implikacja rozmyta może być zdefiniowana
na różne sposoby (Kacprzyk 1986, Mizumoto 1988). W niniejszej
pracy przyjęto iloczyn kartezjański (7) (metoda Zadeha i Mamdaniego
(Zadeh 1973,1992)).

Rozmyty

System

Ekspercki

u

1

u

2

y

Rys.7. Schemat blokowy systemu eksperckiego.

W trakcie syntezy systemu eksperckiego występują następujące

zadania do wykonania:

•

wybór wielkości wejściowych i wyjściowych systemu,

•

dyskretyzacja przestrzeni rozważań dla wielkości wejściowych i
wyjściowych,

•

ustalenie reguł wnioskowania,

•

wybór odpowiedniej metody wnioskowania,

•

zastosowanie odpowiedniej metody wyostrzania w przypadku,
kiedy oczekujemy zmiennej decyzyjnej rzeczywistej,

•

realizacja systemu eksperckiego w wybranym środowisku
programowym.

REGUŁY

1. If is

and is

then is

2. If is

and is

then is

If is

and is

then is

If is

and is

then is

u

low

u

low

y

low

u

low

u

high

y

low

u

high

u

low

y

high

u

high

u

high

y

high

1

2

1

2

1

2

1

2

3

4

.

.

,

DYSKRETYZACJA

low

high

0

10

u

1

1

µ

u

1

( )

low

high

0

10

u

2

1

µ

u

2

( )

low

high

0

10

1

µ

)

(y

y

Rys.8. Dyskretyzacja przestrzeni rozważań dla zmiennych

wejściowych i zmiennej wyjściowej.

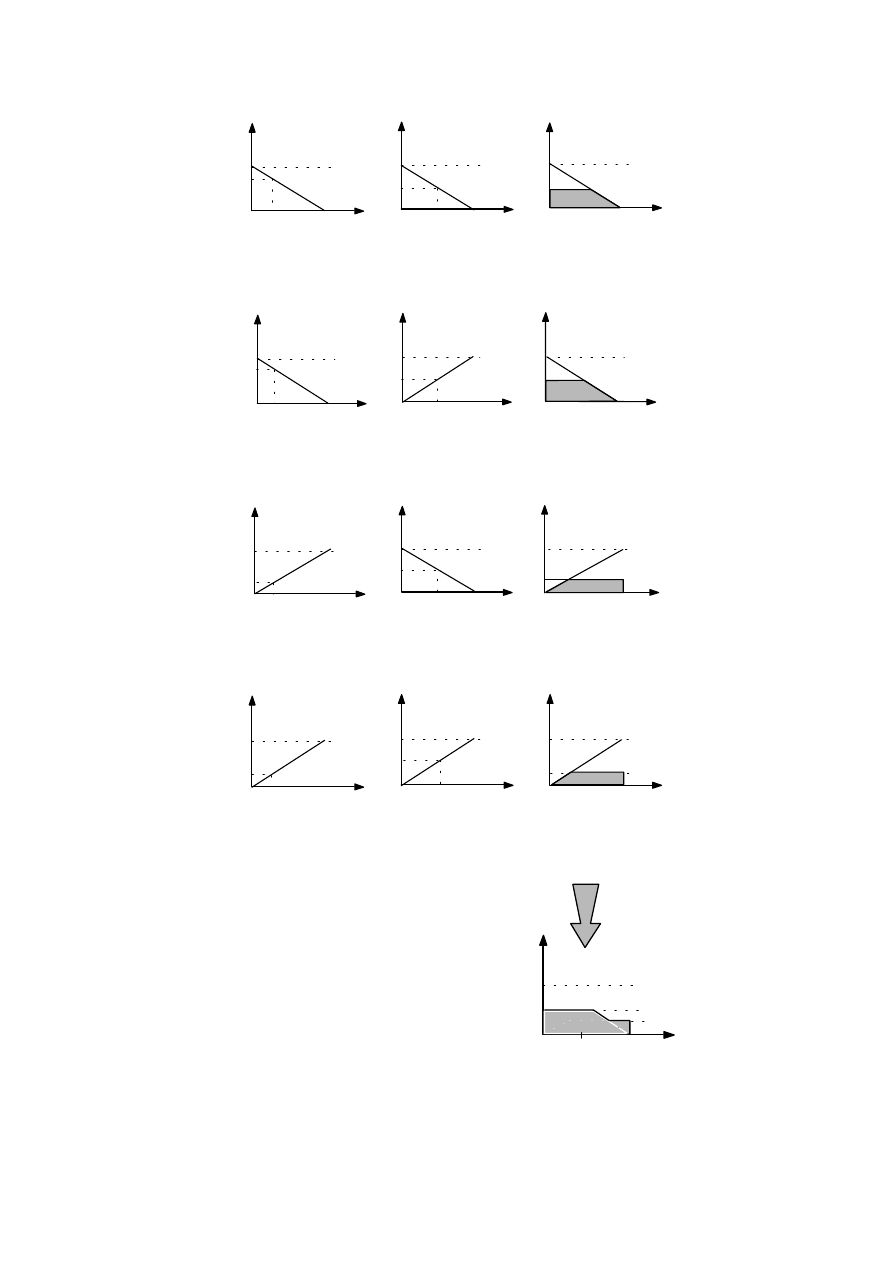
low

0

10

u

1

1

µ

u

1

( )

low

0

10

u

2

1

µ

u

2

( )

y

0.7

0.5

3

5

low

0

10

1

µ

)

(y

0.5

0.5=min(0.7,0.5)

Rys.9. Rozmyte wnioskowanie dla reguły 1.

low

0

10

u

1

1

µ

u

1

( )

high

0

10

u

2

1

µ

u

2

( )

low

0

10

1

µ

)

(y

y

0.7

3

0.5

5

0.5

0.5=min(0.7,0.5)

Rys.10. Rozmyte wnioskowanie dla reguły 2.

low

0

10

u

1

1

µ

u

1

( )

high

0

10

u

2

1

µ

u

2

( )

0

10

1

µ

)

(y

y

0.3

3

0.5

5

0.3

0.3=min(0.3,0.5)

high

Rys.11. Rozmyte wnioskowanie dla reguły 3.

high

0

10

u

1

1

µ

u

1

( )

high

0

10

u

2

1

µ

u

2

( )

0.3

3

0.5

5

high

0

10

1

µ

)

(y

y

0.3

0.3=min(0.3,0.5)

Rys.12. Rozmyte wnioskowanie dla reguły 4.

0

10

1

µ

)

(y

y

0.3

0.5

y

w

max

Rys.13. Składanie wyniku.

Operacje na liczbach rozmytych

Wprowadźmy definicję liczby rozmytej (Zadeh 1965).
Definicja. Liczbą rozmytą A nazywamy zbiór rozmyty określony na
zbiorze liczb rzeczywistych R co zapisujemy:

A

⊂

~

R.,

µ

A

: R

→

[0,1]

Podstawowe operacje na liczbach rozmytych można zdefiniować
stosując zasadę rozszerzania (Zadeh 1965):
Definicja. Niech dana będzie pewna operacja dwuargumentowa na
liczbach rzeczywistych:

*: R

×

R

→

R

Ponadto, niech A i B będą liczbami rozmytymi A, B

⊂

~

R, wtedy

operację ‘*‘ można rozszerzyć na argumenty rozmyte A i B w
następujący sposób:

( )

( ) ( )

{

}

=

min

µ

µ

µ

C

A

B

z

x

y

x y

z

sup

,

*

=

Dla operacji jednoargumentowych zasada rozszerzania sprowadza

się do postaci:

( )

( )

( )

µ

µ

C

A

z

x

z

f x

=

=

max

Dodawanie:

( )

( ) ( )

{

}

=

min

µ

µ

µ

C

A

B

z

x

y

x

y

z

sup

,

+ =

( ) (

)

{

}

=

−

sup

,

.

min

µ

µ

A

B

x

z x

x

Jest to szczególny przypadek splotu.

LICZBY ROZMYTE W REPREZENTACJI LR

Spłaszczona liczba rozmyta (ogólnienie przedziału rozmytego)

(

)

M

m m

LR

=

, , ,

α β

,

gdzie m i m są odpowiednio dolną i górną wartością modalną liczby
rozmytej M, natomiast

α

β

są odpowiednio jej dolnym i górnym

rozrzutem.
Funkcja przynależności zdefiniowana jest następująco:

( )

(

)

(

)

(

)

(

)

µ

α

α

β

β

M

x

L m x

dla x

m

dla m x

m

R x m

dla x

m

=

−

≤

>

< <

−

≥

>













,

,

0

1

0

0

w pozostałych przypadkach

Przypadki szczególne:

•

liczba rzeczywistą m jeśli

(

)

M

m m

LR

=

, , ,

0 0

,

•

przedział liczbowy [a,b] jeśli

(

)

M

a b

LR

=

, , ,

0 0

,

•

liczbę rozmytą

(

)

M

m m

LR

=

, , ,

α β

,

•

formę trapezoidalną i trójkątną liczbę rozmytą jeśli zastosujemy
następującą funkcję

( )

( )

(

)

L u

R u

u

=

=

−

max ,

0 1

odpowiednio dla

przedziału rozmytego M i dla liczby rozmytej M.

Podstawowe operacje algebraiczne dotyczące przedziałów rozmytych
opisane są w pracach (Dubois and Prade 1979a, 1979b, 1980, 1988):
Dodawanie

(

)

(

)

(

)

a b

c d

a c b d

LR

LR

LR

, , ,

, , ,

,

,

,

α β

γ δ

α γ β δ

⊕

=

+

+

+

+

.

Odejmowanie

(

)

a b

LR

, , ,

α β

(

)

(

)

c d

a d b c

RL

LR

, , ,

,

,

,

γ δ

α δ β γ

=

−

−

+

+

.

Mnożenie (dla dodatnich przedziałów rozmytych)

(

)

(

)

(

)

a b

c d

ac bd c

a d

b

LR

LR

LR

, , ,

, , ,

,

,

,

α β

γ δ

α

γ β

δ

⊗

=

+

+

.

Laarhoven and Pedrycz (1983) proponują inną notację dla trójkątnej
liczby rozmytej. Z powodzeniem można ją zastosować dla formy
trapezoidalnej:

(

)

M

l m m u

=

, , ,

gdzie m i m są odpowiednio dolną i górną wartośćią modalną formy
trapezoidalnej M, natomiast l oraz u są odpowiednio jej dolną i górną
wartością. Funkcja przynależności zdefiniowana jest następująco:

( )

µ

M

x

m l

x

l

m l

dla l

x

m

dla m x

m

m u

x

u

m u

dla m x u

=

−

−

−

≤ ≤

< <

−

−

−

≤ ≤

















1

1

1

0

w pozostałych przypadkach

,

Podstawowe opearcje algebraiczne będą zdefiniowane następująco:
Dodawanie

(

) (

) (

)

l m m u

l m m u

l

l m

m m

m u

u

a

a

a

a

b

b

b

b

a

b

a

b

a

b

a

b

,

,

,

,

,

,

,

,

,

⊕

=

+

+

+

+

.

Odejmowanie

(

)

l m m u

a

a

a

a

,

,

,

(

) (

)

l m m u

l

u m

m m

m u

l

a

a

a

a

a

b

a

b

a

b

a

b

,

,

,

,

,

,

=

−

−

−

−

.

Mnożenie (dla dodatnich form trapezoidalnych)

(

) (

) (

)

l m m u

l m m u

l l m m m m u u

a

a

a

a

b

b

b

b

a b

a

b

a

b

a b

,

,

,

,

,

,

,

,

,

⊗

=

Podstawowe operacje algebraiczne dla przedziałów liczbowych
zdefiniowane są następująco (Moore 1966):
Dodawanie

[

] [

] [

]

l u

l u

l

l u

u

a

a

b

b

a

b

a

b

,

,

,

⊕

=

+

+

.

Odejmowanie

[

]

l u

a

a

,

[

] [

]

l u

l

u u

l

a

a

a

b

a

b

,

,

=

−

−

.

Mnożenie (dla dodatnich przedziałów liczbowych)

[

] [

] [

]

l u

l u

l l u u

a

a

b

b

a b

a b

,

,

,

⊗

=

Nguyen (1978) udowodnił, że dla podstawowych operacji
algebraicznych na liczbach rozmytych tzn. dla dodawania,
odejmowania, mnożenia i dzielenia równoważnym z zasadą
rozszerzania jest następujący algorytm:

•

rozłożyć dane liczby rozmyte na skończoną liczbę

α

- przekrojów w

wyniku dla każdej liczby rozmytej otrzymamy taką samą skończoną
liczbę przedziałow liczbowych,

•

wykonać operacje algebraiczne dla każdego

α

- przekroju oddzielnie

korzystając z arytmetyki przedziałowej

•

złożyć wynik.

Twierdzenie Jeśli funkcja

f :R R

R

× →

jest ciągła, funkcje

charakterystyczne liczb rozmytych A i B są kawałkami ciągłe oraz ich
nośniki są zwarte, wówczas:

( )

[

]

(

)

f A B

f A B

,

,

α

α

α

=

.