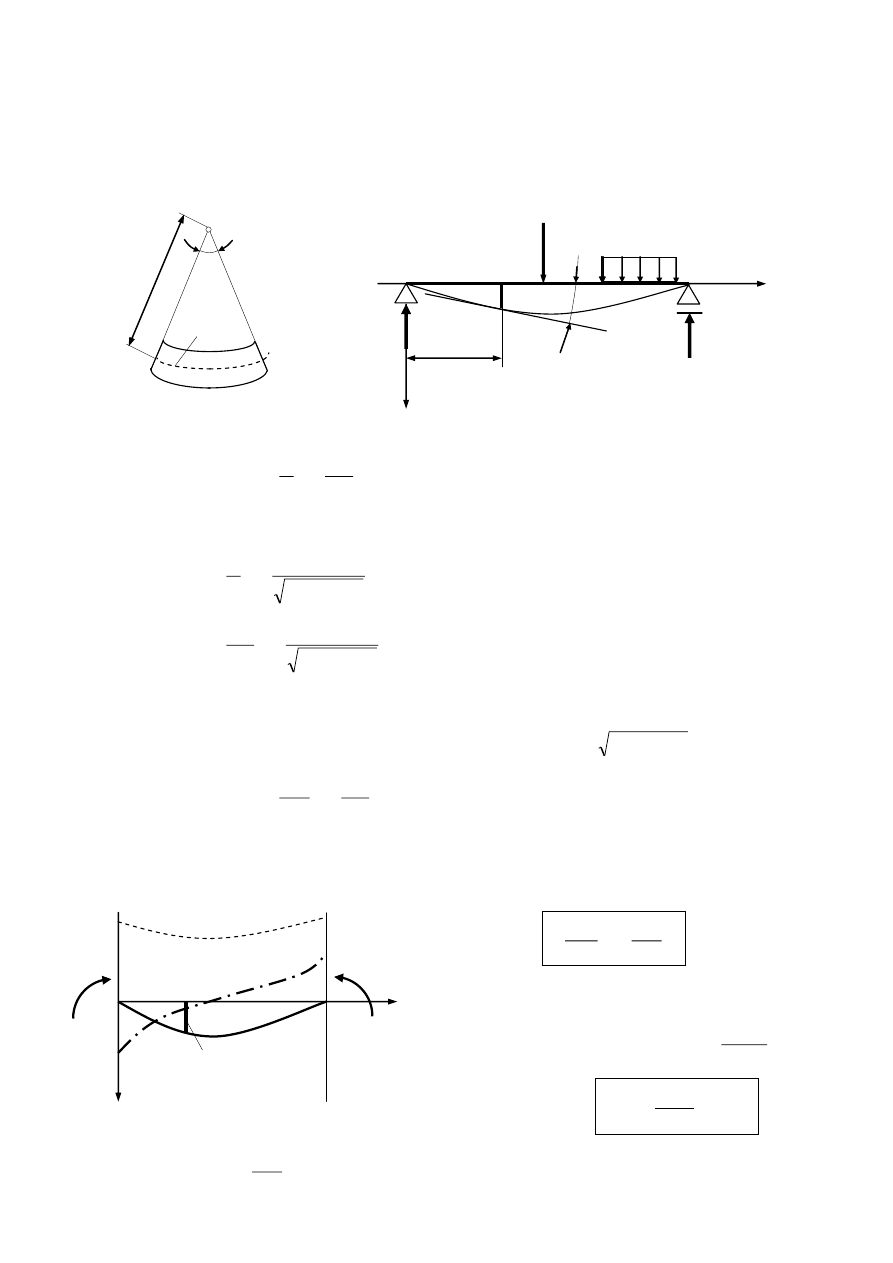
RÓWNANIE RÓŻNICZKOWE OSI UGIĘTEJ BELKI
W wyniku działania M
g
zachodzi wzajemny obrót względem osi obojętnej równoległych
uprzednio przekrojów. Odkształcenia te powodują ugięcie prostej osi pręta. W zginaniu
prostym oś ugięta jest krzywą płaską.
W
układzie osi x,y oś ugiętą określa równanie osi ugiętej y=f(x), a jej krzywiznę wyraża wzór:
EJ
M
g
1
(nie uwzględnia on minimalnego wpływu siły T).
Z geometrii różniczkowej wiadomo, że krzywiznę dowolnej krzywej płaskiej y=f(x) przedstawia
równanie
3
2
)
)
'
(
1
(
"
1
y
y
,
porównując oba równania otrzymamy:
3
2
)
)
'
(
1
(
"
y
y
EJ
M
g
-
równanie osi ugiętej w postaci różniczkowej.
Przy założeniu małych odkształceń (słuszne przy zwykle dużych sztywnościach prętów)
y - ugięcie,
-
kąt ugięcia,
1
)
)
'
(
1
(
1
)
'
(
'
3
2
2
y
i
y
tg
y
otrzymamy
EJ
M
dx
y
d
g
2
2
znaki zależą od ustalenia znaku M
g
i orientacji osi
Stosując układ:
równanie różniczkowe osi ugiętej
EJ
M
dx
y
d
g
2
2
przy EJ=const
. różniczkując równanie osi
dwukrotnie i uwzględniając
q
dx
M
d
g
2
2
mamy
q
dx
y
d
EJ
4
4
0
;
0
;
0
2
2
dx
y
d
y
M
g
-
równanie różniczkowe IV-rzędu.
d
ds=dx
R
1
y
R
2
x
P
q
x
y
υ
x
M
g
M
g
y
y’
y
y”
Całkując równanie różniczkowe dwukrotnie otrzymamy wyrażenia na kąt ugięcia i ugięcie:
D
Cx
dx
dx
M
EJ
y
C
dx
M
EJ
dx
dy
g
g
1
1
Stałe całkowania wyznaczymy z warunków brzegowych
1. Granica przedziałów: y
I
(x=a)=y
II
(x=a)
y’
I
(x=a)=y’
II
(x=a)
2. Przegub:
y
I
(x=b)=y
II
(x=b)
y’
I
(x=b)
y’
II
(x=b)
3. Podpora
y
I
(x=0)=0
4. Utwierdzenie
y
III
(x=l)=0
y’
III
(x=l)=0
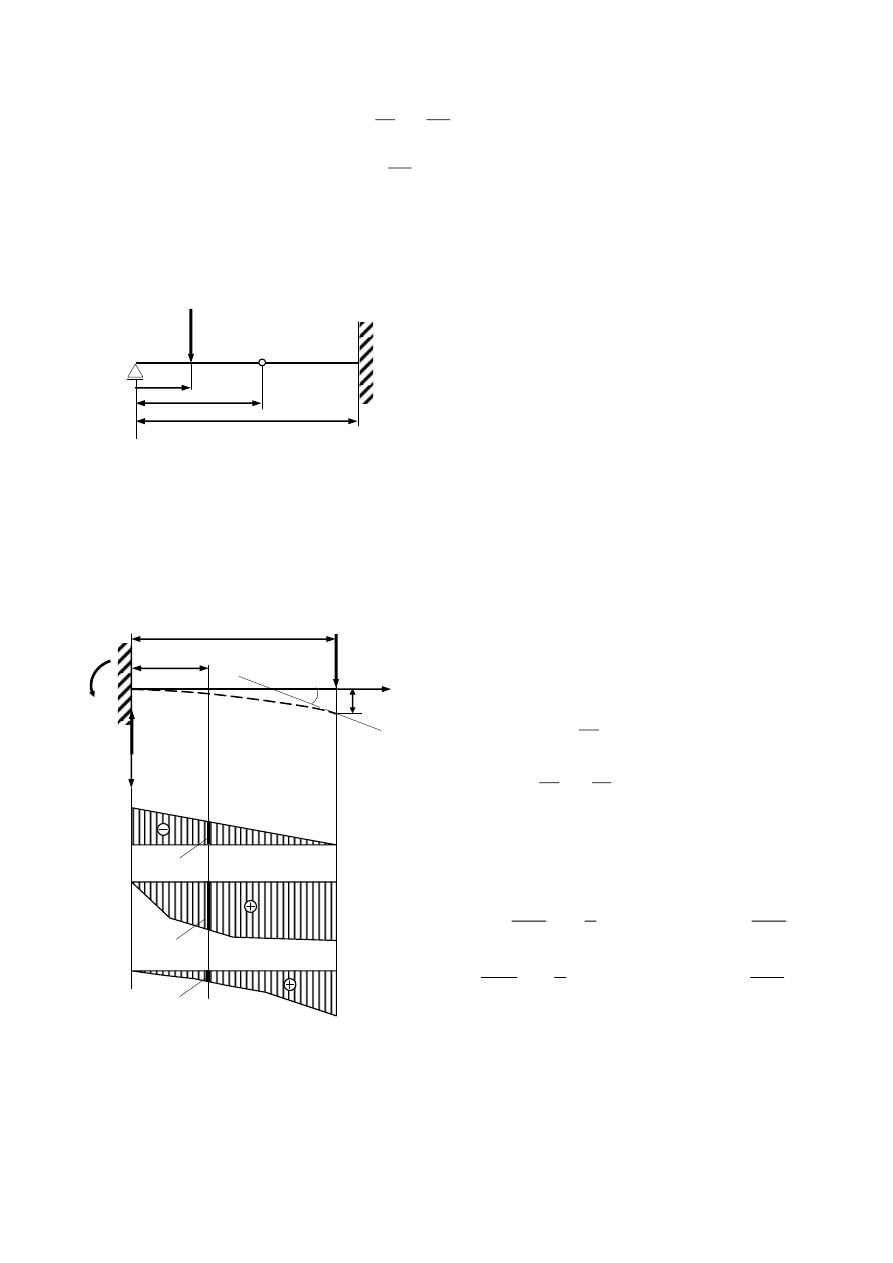
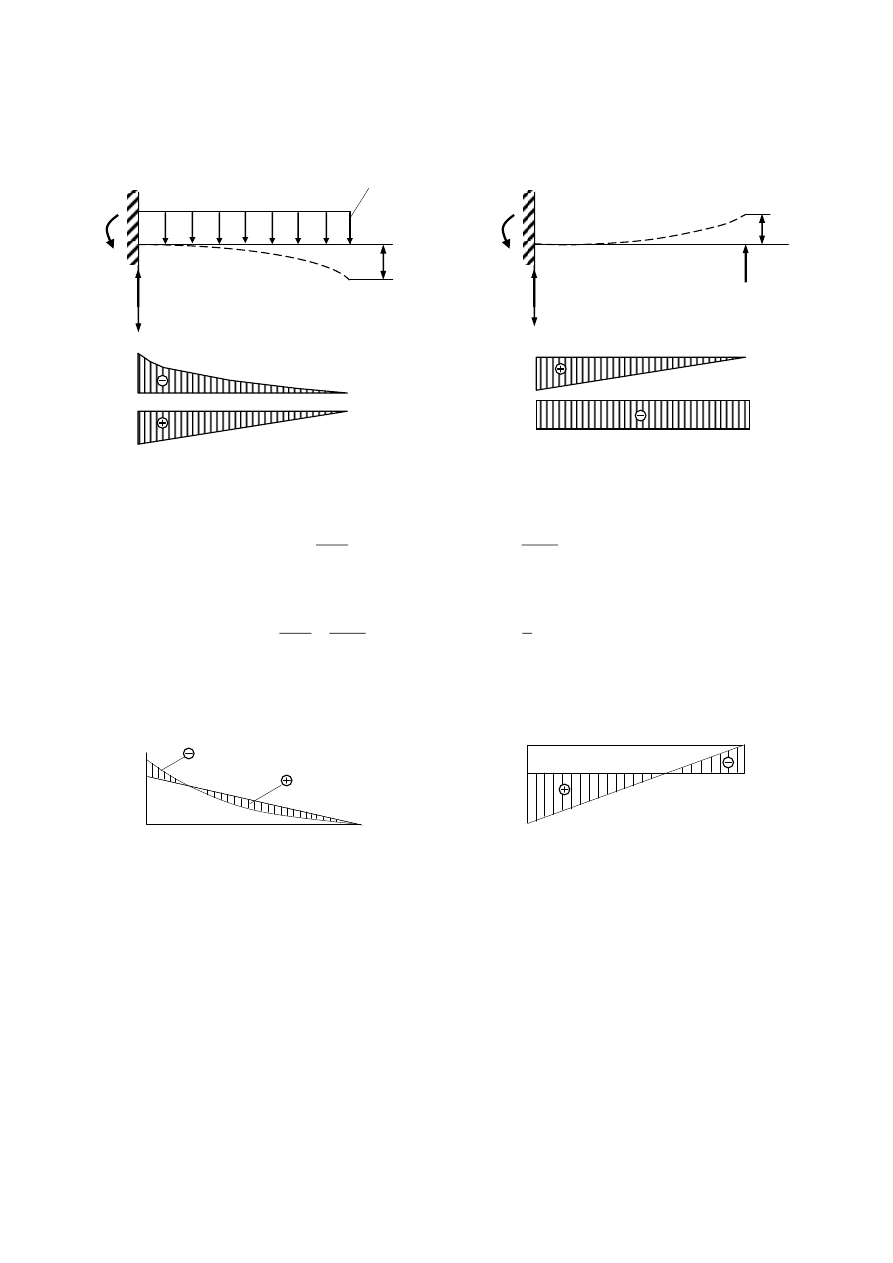
Przykład. Wyznaczyć przemieszczenia liniowe i kątowe w belce wspornikowej.
Dane: P, l, EJ=const.
EJ
Pl
y
l
x
dla
l
x
EJ
Plx
y
EJ
Pl
l
x
dla
l
x
EJ
Plx
y
D
y
x
C
y
x
brzegowych
warunków
z
D
Cx
x
P
x
Pl
EJy
C
x
P
Plx
EJy
Px
Pl
EJy
M
EJy
x
P
l
P
x
R
M
M
l
P
M
P
R
równowagi
warunków
Z
g
A
g
A
3
3
6
2
2
2
'
0
0
0
0
0
'
0
6
2
2
'
"
"
,
3
2
2
3
2
2
b
a
P
y
l
I
II
III
P
y
A
B
R
R
M
A
x
l
x
y
B
B
M
g
y
(x)
y(x)
M
g
(x)
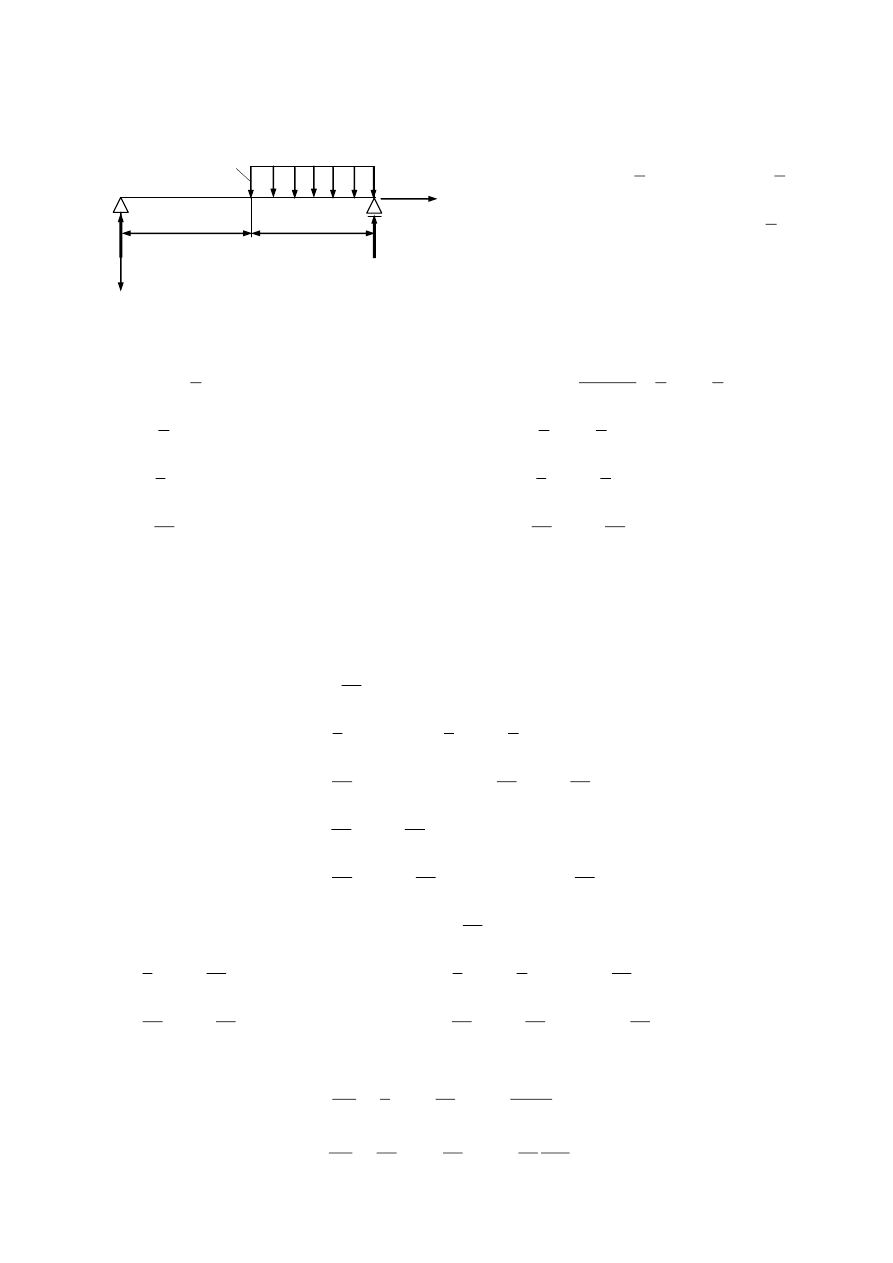
Przykład Metodą całkowania równania różniczkowego osi odkształconej wyznaczyć ugięcie
i kąt ugięcia w środku długości belki.
g
B
B
A
A
A
B
M
EJy
Równanie
qa
R
R
qa
R
Y
qa
R
a
qa
a
R
M
równowagi
równań
Z
"
4
3
0
4
1
0
2
1
2
:
EJ
qa
qa
qa
EJ
y
EJ
qa
qa
qa
EJ
y
a
x
dla
x
qa
a
x
q
qax
EJy
x
qa
qax
EJy
qa
a
x
q
qax
EJy
qa
qax
EJy
qa
C
A
aA
qa
a
A
qa
a
qa
x
A
a
x
q
qax
a
x
y
z
A
A
x
A
a
x
q
qax
C
x
C
qax
a
x
y
a
x
y
z
A
C
A
a
x
q
qax
C
qax
a
x
y
a
x
y
z
C
C
x
C
qax
x
y
z
y
y
a
x
y
a
x
y
y
a
x
y
x
brzegowe
Warunki
A
x
A
a
x
q
qax
EJy
C
x
C
qax
EJy
A
a
x
q
qax
EJy
C
qax
EJy
a
x
q
qax
EJy
qax
EJy
a
x
q
qax
a
x
q
x
R
M
qax
x
R
M
a
x
a
II
a
x
I
II
I
II
I
II
II
I
II
I
I
II
I
II
II
I
I
A
gII
A
gI
4
4
4
3
3
3
3
4
3
3
3
3
3
2
'
3
2
'
3
1
1
1
4
1
4
3
1
4
3
2
2
1
4
3
2
1
3
1
1
1
3
2
1
2
'
'
2
2
1
3
'
'
2
1
4
3
2
1
3
1
3
2
1
2
2
2
2
48
5
48
7
24
1
1
48
48
7
8
1
1
'
48
7
)
(
24
1
24
1
48
7
24
1
48
7
)
(
6
1
8
1
48
7
8
1
48
7
0
2
24
7
0
2
24
1
8
24
1
0
)
(
24
1
24
1
0
)
2
(
)
2
(
0
)
(
24
1
24
1
24
1
)
(
)
(
)
3
(
)
(
6
1
8
1
8
1
)
(
)
(
)
4
(
0
0
24
1
0
)
0
(
)
1
(
)
4
0
2
)
2
)
3
0
0
)
1
:
)
(
24
1
24
1
24
1
)
(
6
1
8
1
'
8
1
'
)
(
2
1
4
1
"
4
1
"
)
(
2
1
4
1
2
)
(
4
1
2
.
0
.
A
B
x
q
a
a
R
B
R
A
y
I
II
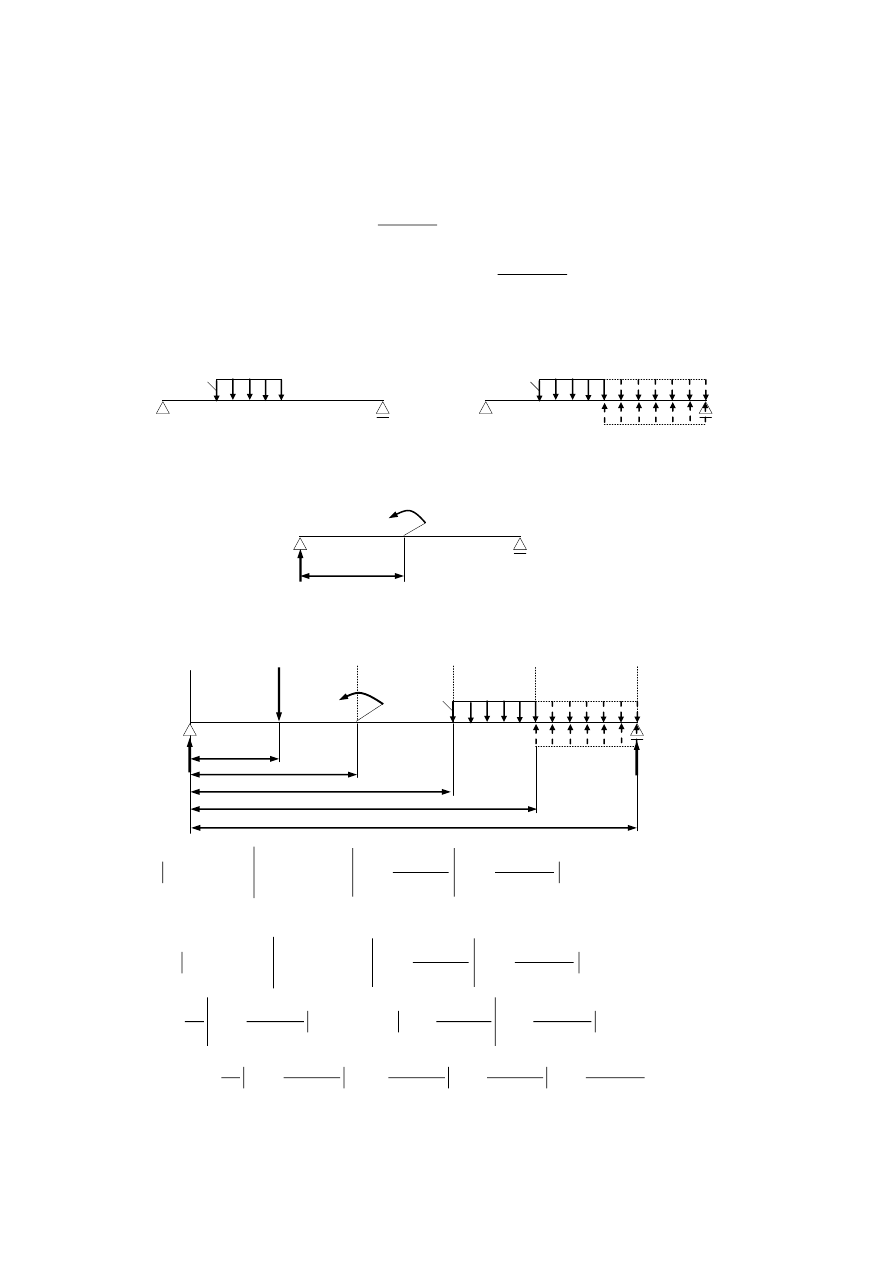
METODA CLEBSCHA CAŁKOWANIA RÓWNANIA RÓŻNICZKOWEGO
Dla belek ciągłych (bez przegubów), o stałej sztywności można uzyskać równość stałych
całkowania poprzez następujące postępowanie:
1)
Równanie Mg należy pisać tak, aby w równaniu dla każdego nowego przedziału
występowały wszystkie składniki równania dla przedziałów poprzednich.
2)
W wyrażeniach typu
2
)
(
);
(
2
a
x
q
a
x
P
nie należy rozwijać wyrażeń w nawiasach.
Całkuje się wg schematu:
C
n
a
x
dx
a
x
n
n
1
)
(
)
(
1
3)
W przypadku obciążenia ciągłego należy je tak przedstawić by każde zaczęte obciążenie
ciągłe przebiegało aż do końca belki.
4)
Moment skupiony zapisujemy z potęgą zerową np.
0
)
(
a
x
K
x
R
M
A
g
Przykład Wyznaczyć równanie linii ugięcia metoda Clebscha.
..........
0
0
0
0
:
24
)
(
24
)
(
2
)
(
6
)
(
6
6
)
(
6
)
(
)
(
2
)
(
2
'
2
)
(
2
)
(
)
(
)
(
"
"
2
)
(
2
)
(
)
(
)
(
4
4
4
3
2
2
3
1
3
0
5
3
4
3
3
2
2
1
2
0
5
2
4
2
3
0
2
1
0
5
2
4
2
3
0
2
1
0
C
y
l
x
D
y
x
brzegowych
warunków
Z
d
x
q
c
x
q
b
x
K
a
x
P
x
R
Cx
D
EJy
d
x
q
c
x
q
b
x
K
a
x
P
x
R
C
EJy
d
x
q
c
x
q
b
x
K
a
x
P
x
R
EJy
M
EJy
d
x
q
c
x
q
b
x
K
a
x
P
x
R
M
g
g
1
3
2
q
1
3
2
q
R
A
K
a
1
3
2
q
P
K
4
5
R
l
R
0
0
a
b
c
d
l
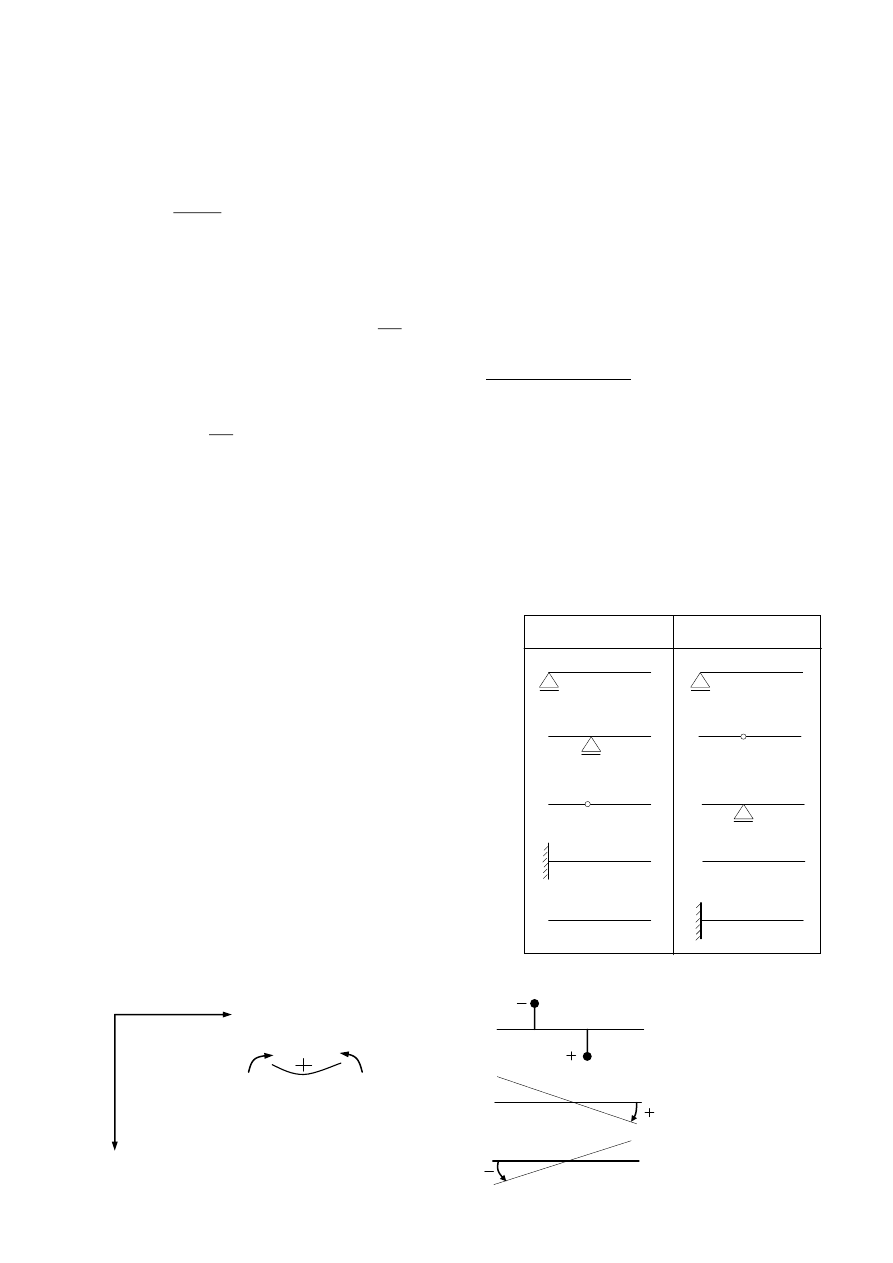
Metoda analityczno-wykre
ślna (Mohra lub momentów wtórnych)
całkowania równania różniczkowego osi ugiętej belki
Opiera się ona na podobieństwie zależności:
q
dx
M
d
g
2
2
( II tw. Schwedlera)
( ٭ )
i
EJy” = -M
g
( r. różniczkowe osi ugiętej)
( ٭٭ )
Zapisując je w postaci:
M
*
”= - q
*
i
EJ
M
y
"
M
*
, q
*
-
na razie wielkości fikcyjne, nie określone
Mamy do czynienia z analogia matematyczną, o ile warunki brzegowe obu równań będą
identyczne. Przyjmując równość prawych stron mamy:
*
*
q
EJ
M
q
zredukowany moment rzeczywisty
Wynika stąd równość:
y = M*
oraz
y’ = M*’= T* =
Chcąc wyznaczyć przemieszczenia konkretnej belki postępujemy następująco:
1) Rozw
iązujemy belkę rzeczywistą (pierwotną)
tzn. wyznaczamy reakcje i wykresy momentów.
2)
Budujemy belkę wtórną w taki sposób by były
spełnione warunki brzegowe.
3)
Obciążamy belkę wtórną obciążeniem ciągłym
równym polu momentów gnących belki
pierwotnej pomniejszonych EJ
– krotnie.
4)
Rozwiązujemy belkę wtórną tzn. wyznaczamy
reakcje, moment gnący i siłę tnącą w żądanych
przekrojach.
Przemieszczenie belki pierwotnej:
y = M*
= T*
Interpretacja znaków:
Belka I
Belka II
y=0
0
M*=0 T*
0
y=0
0
M*=0
T*
0
y
0
0
M*
0
T*
0
y
0
0
M*=0 T*=0
y=0
=0
M*
0 T*
0
y
x
M
g
EJy”=-M
g
y
x
x
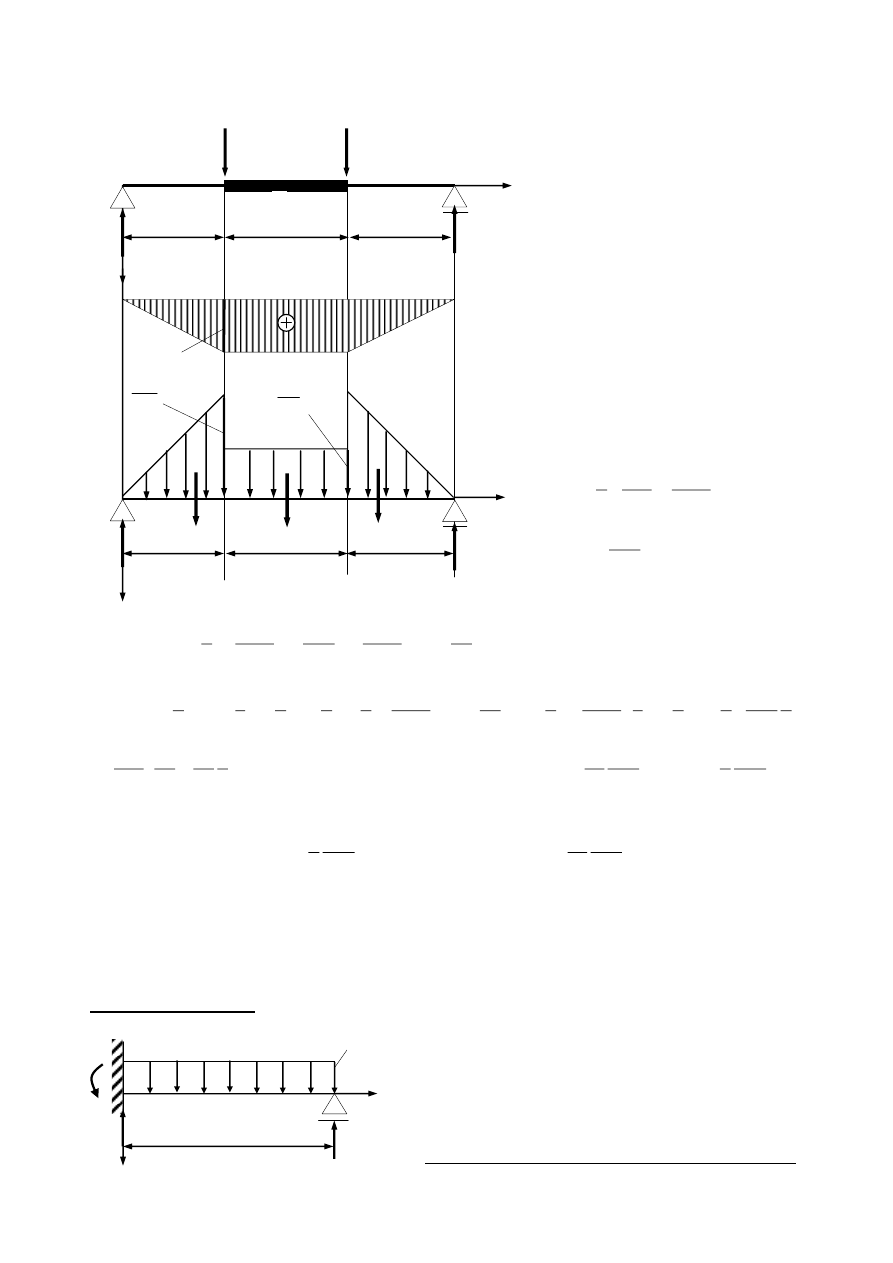
Przykład W belce o zmiennej skokowo sztywności obliczyć metodą analityczno-wykreślną kąt
obrotu na podporze i ugięcie w środku długości.
Belka I jest symetryczna, a więc
R
A
=R
B
=P
Maksymalny moment gnący:
Mg
max
=R
A
a=Pa
Belka wtórna jest również belką
symetryczną, więc reakcje
A*=B*=½(2
1
+
2
)
gdzie
1
2
1
1
2
2
1
EJ
Pa
EJ
Pa
a
2
2
EJ
Pa
b
2
1
1
2
1
2
2
2
2
2
1
*
J
J
b
a
EJ
Pa
EJ
Pa
b
EJ
Pa
A
1
3
*
1
2
*
1
2
1
3
*
1
2
2
1
2
1
*
2
1
2
2
1
1
2
1
*
48
31
4
3
*
4
3
*
,
48
31
)
4
(
8
3
4
1
2
1
2
1
3
1
2
2
2
4
2
1
)
2
1
3
1
(
)
2
(
*
EJ
Pa
M
y
EJ
Pa
A
T
EJ
Pa
A
EJ
Pa
M
a
b
i
J
J
dla
b
a
b
J
J
a
EJ
Pa
M
b
EJ
Pa
b
b
a
EJ
Pa
b
a
J
J
b
a
EJ
Pa
b
b
a
b
a
A
M
C
C
A
A
C
C
C
Belki statycznie niewyznaczalne
Do wyznaczenia reakcji nie
zbędne jest rozpatrzenie odkształceń. Istnieje wiele metod
rozwiązywania belek statycznie niewyznaczalnych. Pokażemy tu dwie z nich.
1 Metoda superpozycji
Wielkości podporowe:
M
A
, R
A
, R
B
.
Warunki równowagi:
Y=-R
A
+ql-R
B
=0
M
B
=M
A
-R
A
l+ql
2
/2=0
Układ jednokrotnie statycznie niewyznaczalny.
b
a
EJ
1
P
a
P
EJ
1
EJ
2
B
x
R
B
A
R
A
y
C
Pa
a
a
b
y
A*
B*
x
I
II
2
1
1
Pa
EJ
1
Pa
EJ
2
l
R
B
x
R
A
M
A
y
q
Warunki geometryczne narzucone przez podparcie układu:
y
A
=0, y
B
=0,
A
=0
Jako równanie dodatkowe obierzemy np. warunek y
B
=0
Reakcja R
B
jest reakcją hiperstatyczną (nadliczbową).
Układ podstawowy (usunięta r. Hiperstatyczna)
Układ obciążony tylko reakcją hiperstatyczną)
Obliczamy (lub znajdujemy z tablic) interesujące nas ugięcia – czyli f
0
i f
1
:
EJ
l
R
f
EJ
ql
f
B
3
8
3
1
4
0
Równanie dodatkowe:
y
B
= f
0
+ f
1
= 0
ql
R
EJ
l
R
EJ
ql
B
B
8
3
0
3
8
3
4
Z
równań równowagi wyznaczamy:
R
A
=
⅝
ql
i
M
A
=
⅛
ql
2
,
oraz budujemy wypadkowe wykresy M
g
i T:
Tok postępowania przy rozwiązywaniu belek statycznie niewyznaczalnych
1.
Zakładamy stosownie do konstrukcji podpór wielkości podporowe.
2.
Wypisujemy ogólne warunki równowagi.
3.
Obieramy wielkości statycznie niewyznaczalne.
4.
Rozkładamy układ statycznie niewyznaczalny na układy statycznie wyznaczalne:
a) obciążony obciążeniem zewnętrznym,
b) obciążony wyłącznie siłami przyjętymi za reakcje hiperstatyczne.
5. Ustalamy warunki geometryczne
– równanie dodatkowe.
6.
Wyznaczamy wielkości przemieszczeń.
7.
Wyznaczamy z równań dodatkowych wielkości hiperstatyczne.
8.
Z równań równowagi wyznaczamy pozostałe reakcje.
f
0
R
Ao
M
Ao
y
q
R
B
f
1
R
A1
M
A1
y
M
g
T
M
g
T
M
g
T
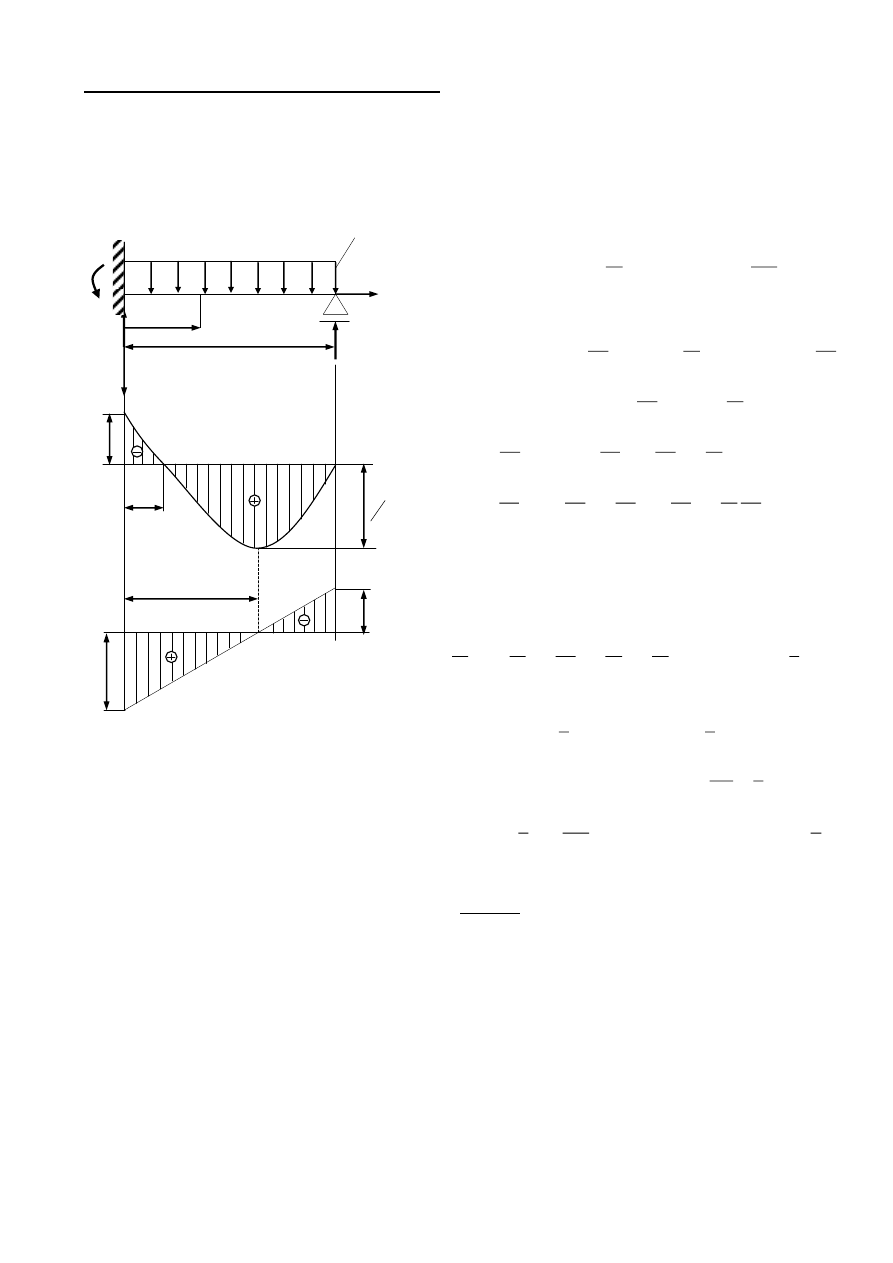
2.
Metoda całkowania równania różniczkowego
Wyznaczyć reakcje, narysować wykresy M
g
, T.
Układ 1-krotnie statycznie niewyznaczalny.
Wybieramy reakcję hiperstatyczną – R
B
.
Piszemy równania równowagi, wyrażając reakcje
przez obciążenie czynne i reakcję hiperstatyczną:
B
A
B
A
B
A
B
A
A
R
ql
R
R
ql
R
Y
l
R
ql
M
l
q
l
R
M
M
0
2
0
2
2
2
D
Cx
x
l
q
x
ql
x
q
x
l
R
x
R
EJy
C
x
l
q
x
ql
x
q
lx
R
x
R
EJy
l
q
qlx
x
q
l
R
x
R
M
EJy
x
q
x
R
qlx
l
q
l
R
x
q
x
R
M
M
B
B
B
B
B
B
g
B
B
A
A
g
2
2
6
24
2
6
2
2
6
2
'
2
2
"
2
2
2
2
2
3
4
2
3
2
2
3
2
2
2
2
2
2
z warunków brzegowych:
4
0
128
9
)
8
5
(
8
5
0
8
1
8
5
8
3
0
4
6
24
2
6
0
)
3
0
0
'
0
0
)
2
),
1
2
0
max
0
0
2
4
4
4
3
3
l
x
dla
M
ql
l
x
M
l
q
R
x
qx
R
T
ql
M
ql
R
równowagi
warunków
z
ql
R
l
q
l
q
l
q
l
R
l
R
R
y
l
x
D
C
y
i
y
x
g
g
A
A
A
A
B
B
B
B
Uwaga !
Wykres M
g
belek statycznie niewyznaczalnych zawsze
przecina oś zerowa.
l
R
B
x
R
A
M
A
y
q
x
T
M
g
⅛ ql
2
⅝ ql
⅜ ql
⅝ l
¼l
2
128
9
ql