AS 29/06/09 Część 1
1.
Odpowiedź impulsowa pewnego elementu ciągłego pierwszego rzędu przyjmuje wartości
t
0
+
10
20
30
g(t)
10
10e
-1
10 e
-2
10e
-3
Podaj transmitancję tego elementu, opisujące go równanie różniczkowe, naszkicuj jego odpowiedź
jednostkową, naszkicuj logarytmiczne charakterystyki częstotliwościowe połączenia szeregowego
tego elementu z idealnym integratorem o transmitancji
1
s
.
2.
Jaka jest transmitancja dyskretna tego układu? Dla jakich wartości a, b wystąpią dyskretne
przebiegi przejściowe zanikające po co najwyżej 2 okresach impulsowania? Naszkicuj odpowiedź
jednostkową układu w tym przypadku.
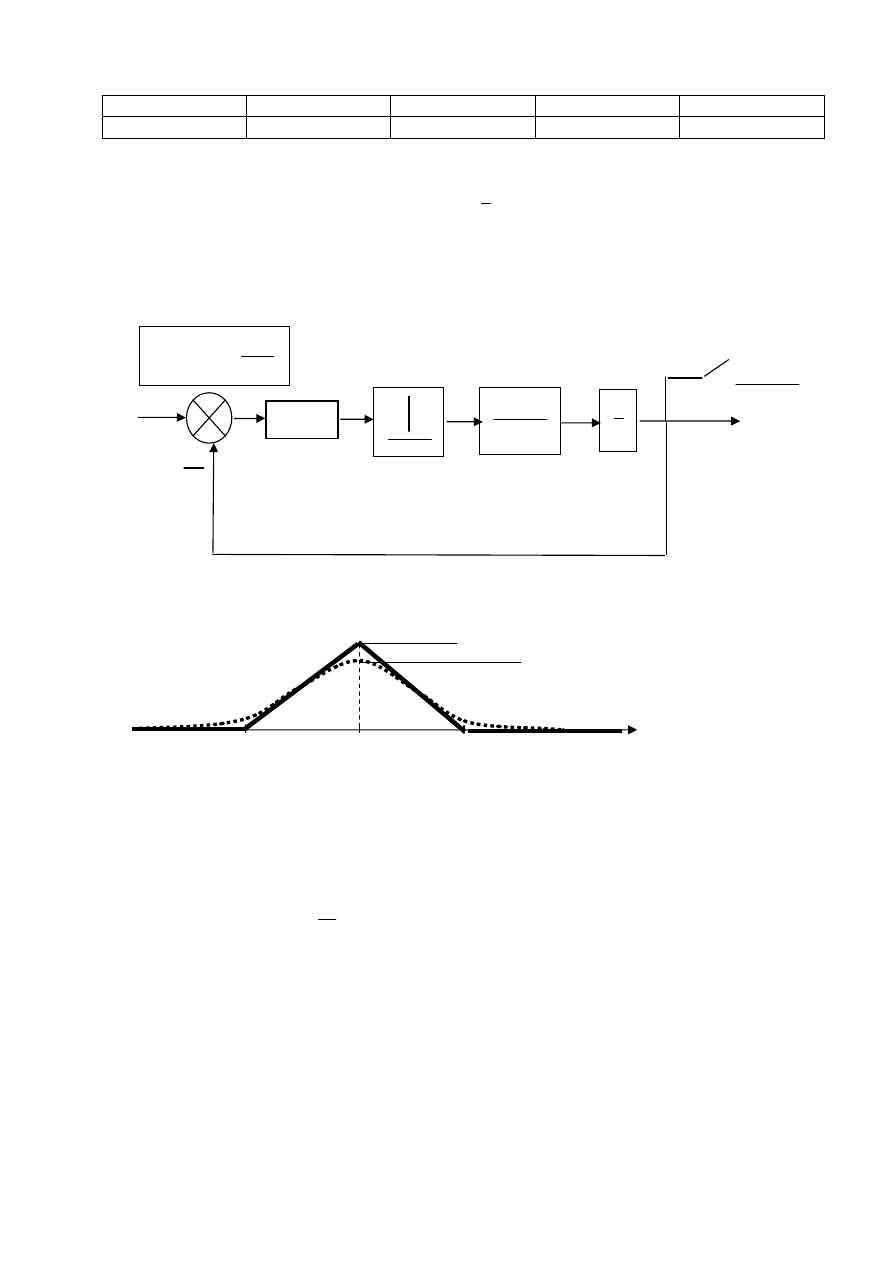
3.. Wyznacz transmitancję filtru o logarytmicznej charakterystyce modułowej zbliżonej do:
Narysuj asymptotyczne, logarytmiczne charakterystyki modułowe elementów filtru, ich
asymptotyczne logarytmiczne charakterystyki fazowe i wypadkową charakterystykę fazową filtru.
Naszkicuj charakterystykę amplitudowo-fazową filtru. Jaki sygnał ustali się na wyjściu filtru, jeśli na
wejście podamy sygnał
sin( t )
.
4. Wyznacz transmitancję układu
[
]
1
1
2
2
1
2
2
3
1
1 5
3 5
1
1 0
x ( t )
x ( t )
d
u( t )
x ( t )
x ( t )
.
.
dt
x ( t )
y( t )
x ( t )
−
=
+
−
−
=
. Co potrafisz
powiedzieć o sterowalności i obserwowalności tego układu: czy układ jest całkowicie
sterowalny/obserwowalny? Jeśli nie, to które mody są niesterowalne/nieobserwowalne? Jak wygląda
przestrzeń stanów sterowalnych (narysuj). Czy istnieje ograniczone sterowanie przeprowadzające wektor
stanu w skończonym czasie z punktu
1
1
do punktu
1
1
−
−
.
1
sT
e
s
−
−
1
s
y( t )
y( nT )
0 5
T
.
=
0
y ( t )
r
G ( z )
1
r
b
G ( z )
a
z
= +
−
0,1
1
10
ω
20 dB
14 dB
5 Wyznacz macierz K, tak by układ zamknięty miał podwójną wartość własną w zerze. Jaka będzie
wtedy transmitancja dyskretna układu zamkniętego i jego odpowiedź jednostkowa?
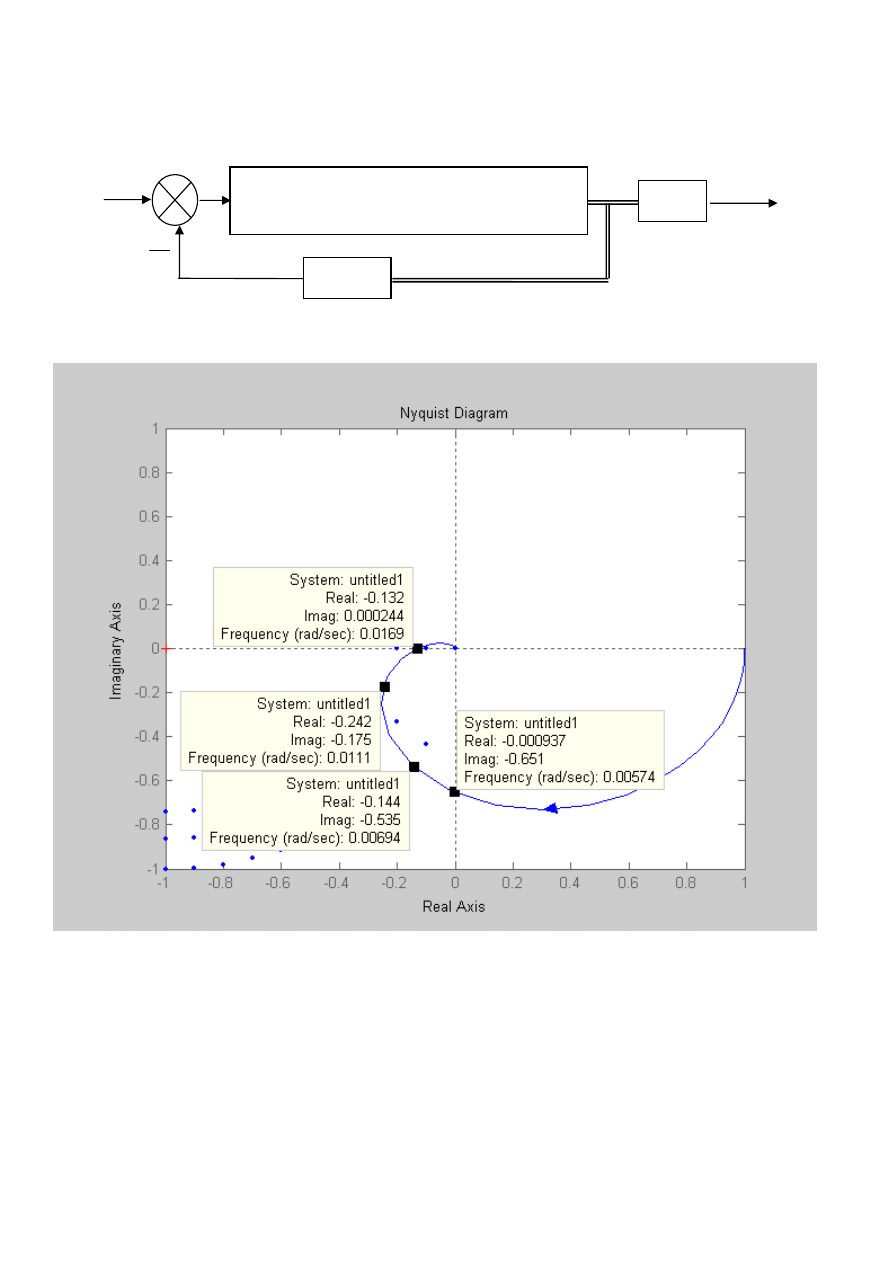
6. Na rysunku przedstawiono charakterystykę amplitudowo-fazową układu liniowego.
Czy transmitancja tego układu ma biegun w zerze (el. całkujący)?
Jaki sygnał ustali się na wyjściu tego układu jeśli na wejście podamy sinusoidę o amplitudzie 1 i
pulsacji 0.0057 rad/sek?
Czy po zamknięciu ujemnym sprzężeniem zwrotnym otrzymamy układ stabilny? Jaki jest zapas
modułu i fazy?
Czy układ zamknięty będzie astatyczny względem zakłócenia?
Jaki będzie współczynnik wzmocnienia układu zamkniętego?
Jaka jest pulsacja zakłóceń, które będą maksymalnie wzmacniane w układzie zamkniętym?
Jakie jest pasmo pulsacji zakłóceń, które będą tłumione w układzie zamkniętym?
1
1
2
2
1
0
1
0
1
0 81 1 8
1
x ( n
)
x ( n )
u( n )
x ( n
)
x ( n )
.
.
+
=
+
+
−
y( n )
0
y ( n )
[ ]
1 1
[
]
1
2
k
k
x( n )
u( n )

Część II.
1.
Co to znaczy, że układ dyskretny jest astatyczny drugiego rzędu względem sygnału zadającego?
Wyprowadź jaką postać powinna mieć transmitancja uchybowa w takim układzie.
2.
Wiedząc, że postać modalna rozwiązania równania stanu jest:
( )
0
1
1
0
i
i
t
n
n
s t
s t
T
T
i
i
i
i
i
i
x( t )
e v w x
e
v w Bu( )d
τ
τ τ
−
=
=
=
+
∑
∑
∫
nazwij wielkości występujące w tym wzorze i uzasadnij modalny warunek sterowalności. Podaj inny
znany ci warunek sterowalności układu. Jaki będzie stopień mianownika transmitancji układu o
czterech zmiennych stanu, jeśli dokładnie jeden mod tego układu jest niesterowalny, a wszystkie
mody są obserwowalne?
3.
Rozwiąż równania opisujące dyskretny układ liniowy w przestrzeni stanów. Podaj transformatę
macierzy tranzycyjnej układu. Jak można obliczyć macierz transmitancji dyskretnych tego układu.
Jaki jest związek miedzy wartościami własnymi macierzy stanu a biegunami transmitancji?
............................................................................................................................................................
Część II.
1
Co to znaczy, że układ dyskretny jest astatyczny drugiego rzędu względem sygnału zadającego?
Wyprowadź jaką postać powinna mieć transmitancja uchybowa w takim układzie.
2
Wiedząc, że postać modalna rozwiązania równania stanu jest:
( )
0
1
1
0
i
i
t
n
n
s t
s t
T
T
i
i
i
i
i
i
x( t )
e v w x
e
v w Bu( )d
τ
τ τ
−
=
=
=
+
∑
∑
∫
nazwij wielkości występujące w tym wzorze i uzasadnij modalny warunek sterowalności. Podaj inny
znany ci warunek sterowalności układu. Jaki będzie stopień mianownika transmitancji układu o
czterech zmiennych stanu, jeśli dokładnie jeden mod tego układu jest niesterowalny, a wszystkie
mody są obserwowalne?
3
Rozwiąż równania opisujące dyskretny układ liniowy w przestrzeni stanów. Podaj transformatę
macierzy tranzycyjnej układu. Jak można obliczyć macierz transmitancji dyskretnych tego układu.
Jaki jest związek miedzy wartościami własnymi macierzy stanu a biegunami transmitancji?
...................................................................................................................................................................
Część II.
1
Co to znaczy, że układ dyskretny jest astatyczny drugiego rzędu względem sygnału zadającego?
Wyprowadź jaką postać powinna mieć transmitancja uchybowa w takim układzie.
2
Wiedząc, że postać modalna rozwiązania równania stanu jest:
( )
0
1
1
0
i
i
t
n
n
s t
s t
T
T
i
i
i
i
i
i
x( t )
e v w x
e
v w Bu( )d
τ
τ τ
−
=
=
=
+
∑
∑
∫
nazwij wielkości występujące w tym wzorze i uzasadnij modalny warunek sterowalności. Podaj inny
znany ci warunek sterowalności układu. Jaki będzie stopień mianownika transmitancji układu o
czterech zmiennych stanu, jeśli dokładnie jeden mod tego układu jest niesterowalny, a wszystkie
mody są obserwowalne?
3
Rozwiąż równania opisujące dyskretny układ liniowy w przestrzeni stanów. Podaj transformatę
macierzy tranzycyjnej układu. Jak można obliczyć macierz transmitancji dyskretnych tego układu.
Jaki jest związek miedzy wartościami własnymi macierzy stanu a biegunami transmitancji?
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron