
Taylor’s Theorem
1. Introduction. Suppose f is a one-variable function that has n
+ 1 derivatives on an interval
about the point x
= a. Then recall from Ms. Turner’s class the single variable version of Taylor’s
Theorem tells us that there is exactly one polynomial p of degree
² n such that pÝaÞ = fÝaÞ,
p
v
ÝaÞ = f
v
ÝaÞ, p
vv
ÝaÞ = f
vv
ÝaÞ, u, p
ÝnÞ
ÝaÞ = f
ÝnÞ
ÝaÞ. This polynomial is given by
p
ÝxÞ = fÝaÞ + f
v
ÝaÞÝx ? aÞ +
f
vv
ÝaÞ
2!
Ýx ? aÞ
2
+ u + f
ÝnÞ
n!
Ýx ? aÞ
n
We also know the difference between f
ÝxÞ and pÝxÞ:
f
ÝxÞ ? pÝxÞ =
f
Ýn+1Þ
ÝYÞ
Ýn + 1Þ!
Ýx ? aÞ
n
+1
,
where
Y is somewhere between a and x.
The polynomial p is called the Taylor Polynomial of degree
² n for f at a.
Before we worry about what the Taylor polynomial might be in higher dimensions, we need to be
sure we understand what is a polynomial in more than one dimension. In two dimensions, a
polynomial p
Ýx, yÞ of degree ² n is a function of the form
p
Ýx, yÞ =
>
i,j
=0
i
+j=n
a
ij
x
i
y
j
.
Thus a polynomial of degree
² 2 (perhaps more commonly known as a quadratic) looks like
p
Ýx, yÞ = a
00
+ a
10
x
+ a
01
y
+ +a
11
xy
+ a
20
x
2
+ a
02
y
2
.
I hope it easy to guess what one means by a polynomial in three variables,
Ýx, y, zÞ, or indeed, in
any number of variables.
Now, how might we extend the idea of the Taylor polynomial of degree
² n for a function f at a
point a ? Simple enough. It’s a polynomial p
ÝxÞ of degree ² n so that
/
i
1
+u+i
q
f
ÝaÞ
/x
1
i
1
/x
2
i
2
u
/x
q
i
q
= /
i
1
+u+i
q
p
ÝaÞ
/x
1
i
1
/x
2
i
2
u
/x
q
i
q
,
for all i
1
, i
2
,
u, i
q
such that i
1
+ i
2
+ u + i
q
² n.
This looks pretty ferocious in general, so let’s see what it says for just two variables. In this case,
we have a
=Ýa, bÞ and the Taylor polynomial pÝx, yÞ at a becomes the polynomial such that
1
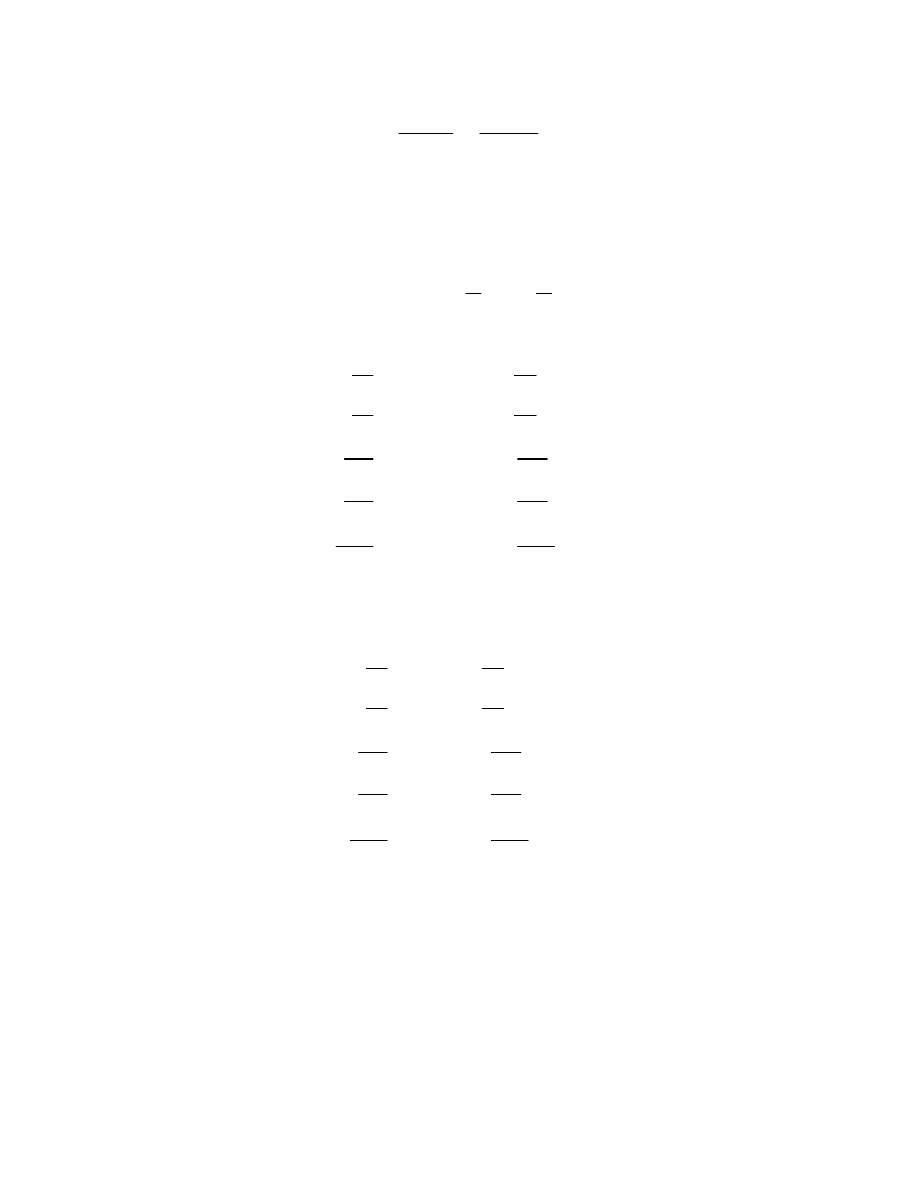
/
i
+j
f
ÝaÞ
/
i
x
/
j
y
= /
i
+j
p
ÝaÞ
/
i
x
/
j
y
,
for all i
+ j
² n.
Example
Let f
Ýx, yÞ = cosÝx + yÞ, and let pÝx, yÞ = 1 ?
x
2
2
? xy ?
y
2
2
. Let’s verify that p is the Taylor
polynomial of degree
² 2 for f at Ý0, 0Þ. He we go.
f
Ý0, 0Þ = 1, and pÝ0, 0Þ = 1;
/f
/x
=
?sinÝx + yÞ, and /
p
/x
=
?x ? y;
/f
/y
=
?sinÝx + yÞ, and /
p
/y
=
?x ? y;
/
2
f
/x
2
=
?cosÝx + yÞ, and /
2
p
/x
2
=
?1,
/
2
f
/y
2
=
?cosÝx + yÞ, and /
2
p
/y
2
=
?1,
/
2
f
/x/y
=
?cosÝx + yÞ, and /
2
p
/x/y
=
?1.
Now it’s easy to see that
f
Ý0, 0Þ = 0 = pÝ0, 0Þ;
/f
/x
Ý0, 0Þ = 0 = /
p
/x
Ý0, 0Þ;
/f
/y
Ý0, 0Þ = 0 = /
p
/y
Ý0, 0Þ;
/
2
f
/x
2
Ý0, 0Þ = ?1 = /
2
p
/x
2
Ý0, 0Þ;
/
2
f
/y
2
Ý0, 0Þ = ?1 = /
2
p
/y
2
Ý0, 0Þ; and
/
2
f
/x/y
Ý0, 0Þ = ?1 = /
2
p
/x/y
Ý0, 0Þ.
Exercises
1. Verify that the polynomial in the Example is also the Taylor polynomial for f at (0,0) of degree
² 3.
2. Let f
Ýx, yÞ = sinÝx + yÞ.Which Which of the following is the Taylor polynomial of degree ² 2 for
f at (0,0)? Explain.
a) p
Ýx, yÞ = 1 + x
2
+ y
2
b) p
Ýx, yÞ = xy
2
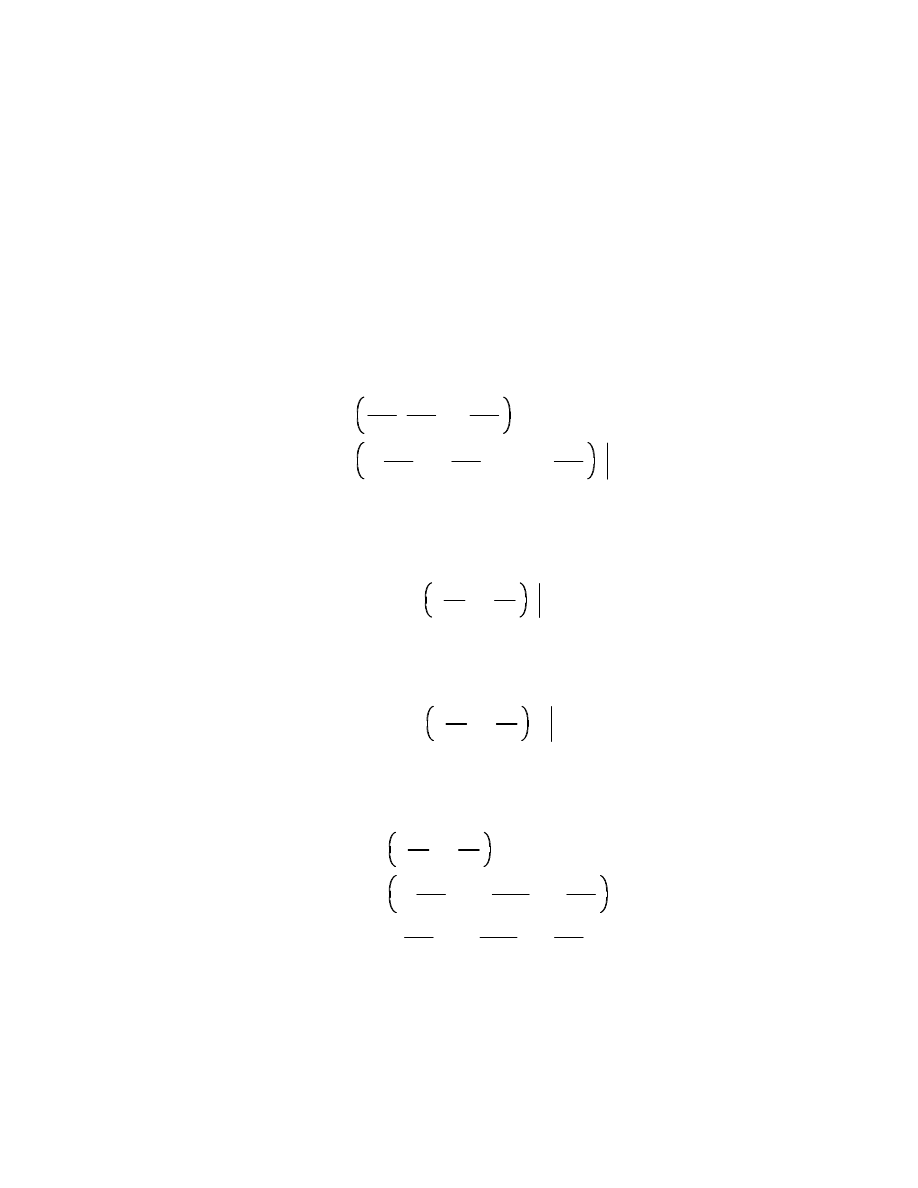
c) p
Ýx, yÞ = x
2
+ xy + 2y
d) p
Ýx, yÞ = x + y
2. Derivatives. Prior to finding a general recipe for the Taylor polynomial, we need look at finding
higher order derivatives of certain composite functions. Let f be a real-valued function defined on a
subset of R
q
. Suppose that in a neighborhood of the point x, the function f has a lot of continuous
partial derivatives. Define the function g by
g
ÝtÞ = fÝa + thÞ,
where a
= Ýa
1
, a
2
,
u, a
q
Þ and h = Ýh
1
, h
2
,
u, h
q
Þ. We know from the chain rule that g
v
ÝtÞ is
given by
g
v
ÝtÞ = 4fÝa + thÞ 6 h
=
/f
/x
1
, /f
/x
2
,
u, /f
/x
q
6 Ýh
1
, h
2
,
u, h
q
Þ
= h
1
/
/x
1
+ h
2
/
/x
2
+ u + h
q
/
/x
q
f
Ýa+thÞ
In keeping with our general practice of restricting ourselves to dimensions one, two, or three, let’s
look first at the case q
= 2. As usual, we’ll write x =Ýx, yÞ and h = Ýh, kÞ. The expression for g
v
ÝtÞ
now looks like:
g
v
ÝtÞ = h /
/x
+ k /
/y
f
Ýx+thÞ
We are now in business, for we have a nice recipe for higher order derivatives of g :
g
ÝmÞ
ÝtÞ = h /
/x
+ k /
/y
m
f
Ýx+thÞ
For example,
g
vv
ÝtÞ = h /
/x
+ k /
/y
2
f
= h
2
/
2
/x
2
+ 2hk /
2
/x/y
+ k
2
/
2
/y
2
f
= h
2
/
2
f
/x
2
+ 2hk /
2
f
/x/y
+ k
2
/
2
f
/y
2
Example
Suppose f
Ýx, yÞ = x
2
y
3
+ y
2
. Let’s find the second derivative of the function
g
ÝtÞ = fÝ1 + 3t, ?2 + tÞ
3

First,
g
vv
ÝtÞ = 3 /
/x
+ /
/y
2
f
= 9 /
2
f
/x
2
+ 6 /
2
f
/x/y
+ /
2
f
/y
2
Now,
/f
/x
= 2xy
3
, and
/f
/y
= 3x
2
y
2
+ 2y, and so
/
2
f
/x
2
= 2y
3
,
/
2
f
/y/x
= 6y
2
, and
/
2
f
/y
2
= 6x
2
y
+ 2.
Thus,
g
vv
ÝtÞ = 18Ý?2 + tÞ
3
+ 36Ý
?2 + tÞ
2
+ 6Ý1 + 3tÞ
2
Ý?2 + tÞ + 2
Exercises
3. Let f
Ýx, yÞ = xe
y
. Find the derivative of g
ÝtÞ = fÝ1 + t, 3 ? 4tÞ.
4. Find the second derivative of the function g defined in Problem 3.
5. Let F
Ýu, vÞ = u
3
v
+ v
2
. Find the second derivative of R
ÝzÞ = FÝz, 3zÞ.
6. Find g
vvv
ÝtÞ, where g is the function defined in the Example.
3. The Taylor polynomial. To find the Taylor polynomial for a function f of several variables at a
point a, we shall simply apply the one-dimensional results to the function
g
ÝtÞ = fÝa + thÞ.
Thus,
g
ÝtÞ =
>
m
=0
n
g
ÝmÞ
Ý0Þ
m!
t
m
+
g
Ýn+1Þ
ÝYÞ
Ýn + 1Þ!
t
n
+1
,
where
Y is a number between 0 and t. Next, substitute t = 1 into the above:
g
Ý1Þ = fÝaÞ =
>
m
=0
n
g
ÝmÞ
Ý0Þ
m!
+
g
Ýn+1Þ
ÝYÞ
Ýn + 1Þ!
We know the value of g
ÝkÞ
from Section 2:
f
Ýa + hÞ =
>
m
=0
n
1
m!
h
1
/
/x
1
+ h
2
/
/x
2
+ u + h
q
/
/x
q
m
f
ÝaÞ
4

+
1
Ýn + 1!
h
1
/
/x
1
+ h
2
/
/x
2
+ u + h
q
/
/x
q
n
+1
f
ÝcÞ
The point c lies somewhere on the line segment joining a and a
+ h.
The polynomial
p
ÝhÞ =pÝh
1
, h
2
,
u, h
q
Þ =
>
m
=0
n
1
m!
h
1
/
/x
1
+ h
2
/
/x
2
+ u + h
q
/
/x
q
m
f
ÝaÞ
is the Taylor polynomial of degree
² n for f at a; the last term is traditionally called the error term
or sometimes, the remainder term. Actually, if we let h
= x
? a, then qÝxÞ =pÝx ? aÞ is the thing
we called the Taylor polynomial in the first section.
This is pretty fierce looking. Let’s look at the two variable case:
f
Ýa
1
+ h, a
2
+ kÞ =
>
m
=0
n
1
m!
h /
/x
+ k /
/y
m
f
Ýa
1
, a
2
Þ
+
1
Ýn + 1!Þ
h /
/x
+ k /
/y
n
+1
f
Ýc
1
, c
2
Þ
where
Ýc
1
, c
2
Þ is on the line joining Ýa
1
, a
2
Þ and Ýa
1
+ h, a
2
+ kÞ.
Example
Let f
Ýx, yÞ = sinxsiny. For n = 2 and a = Ý0, 0Þ, Taylor’s polynomial becomes
p
Ýh, kÞ = fÝ0, 0Þ + h /f
/x
Ý0, 0Þ + k /f
/y
Ý0, 0Þ + h
2
2
/
2
f
/x
2
Ý0, 0Þ + hk /
2
f
/x/y
Ý0, 0Þ + k
2
2
/
2
f
/y
2
Ý0, 0Þ
We have
/f
/x
= cos x sin y;
/f
/y
= sin x cos y;
/
2
f
/x
2
=
?sinxsiny;
/
2
f
/x/y
= cos xcosy;
/
2
f
/y
2
=
?sinxsiny.
Thus,
p
Ýh, kÞ = hk.
Let’s get an estimate for how well this approximates sin x sin y near
Ý0, 0Þ. We know that
|sin x sin y
? xy| = 1
3!
x /
/x
+ y /
/y
3
f
ÝY, WÞ
where
ÝY, WÞ is one the segment joining Ýx, yÞ and the origin. Now,
5

x /
/x
+ y /
/y
3
f
= x
3
/
3
f
/x
3
+ 3x
2
y /
3
f
/x
2
/y
+ 3xy
2
/
3
f
/x/y
2
+ y
3
/
3
f
/x
3
.
Next, let’s suppose that |x|
² c and |y| ² c for some constant c. Noting that all the partial
derivatives in the above expression are simply products of sine and cosines, we can estimate
x /
/x
+ y /
/y
3
f
² 8c
3
,
and so, at last,
|sin x sin y
? xy| ² 8c
3
6
= 4
3
c
3
Exercises
7. Find the Taylor polynomial of degree
² 1 for fÝx,yÞ = e
xy
at
Ý0, 0Þ.
8. Find the Taylor polynomial of degree
² 2 for fÝx,yÞ = e
xy
at
Ý0, 0Þ.
9. Find the Taylor polynomial of degree
² 3 for fÝx,yÞ = e
xy
at
Ý0, 0Þ.
10. Find the Taylor polynomial of degree
² 1 for fÝx,yÞ = e
x
cos y at
Ý0, 0Þ.
11. Use Taylor’s Theorem to find a quadratic approximation of e
x
cos y at the origin.
12. Estimate the error in the approximation found in Problem 11 if |x|
² 0.1 and |y| ² 0.1.
6
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron