Opracowanie: Tomasz Trawka

S p i s t r e ś c i

Podstawowe definicje...................................................................................................................2

Cecha statystyczna..............................................................................................................................................2

Cecha statystyczna, wariant cechy.................................................................................................................2
Podział cech statystycznych...........................................................................................................................2
Rozpoznawanie cech w opisie badania..........................................................................................................3

Szereg statystyczny.............................................................................................................................................3

Definicje i podział..........................................................................................................................................3
Szereg szczegółowy.......................................................................................................................................4
Szereg rozdzielczy punktowy........................................................................................................................4
Szereg rozdzielczy przedziałowy...................................................................................................................5

Definiowanie przedziałów w szeregu rozdzielczym przedziałowym (na przykładzie)..........6

1 / 8

Materiały do zajęć, wersja bardzo skrócona, 1.0

Podstaw ow e definicje

C e c h a s t a t y s t y c z n a

C e c h a s t a t y s t y c z n a , w a r i a n t c e c h y

Cecha statystyczna to właściwość populacji będącej przedmiotem badania

statystycznego, w ramach którego zbierane są wartości określonej cechy statystycznej
(nazywane także wartościami zaobserwowanymi lub danymi statystycznymi). Cechą
statystyczną dla populacji pracowników fabryki jest na przykład staż pracy, wiek, płeć,
wzrost, data zatrudnienia, itp.

Wariant cechy statystycznej to pojedyncza, unikalna wartość cechy. Na przykład, w

pewnym badaniu cecha statystyczna kolor oczu składa się z czterech różnych wartości
(zielone, niebieskie, szare, brązowe), więc cecha ta posiada 4 warianty.

Liczba wariantów cechy może być skończona lub nieskończona. Jeżeli cecha ma tylko

dwa warianty to nazywamy ją dychotomiczną (dwudzielną, binarną). Jeśli ma więcej niż
dwa warianty to jest cechą politomiczną (wielodzielną).
P o d z i a ł c e c h s t a t y s t y c z n y c h

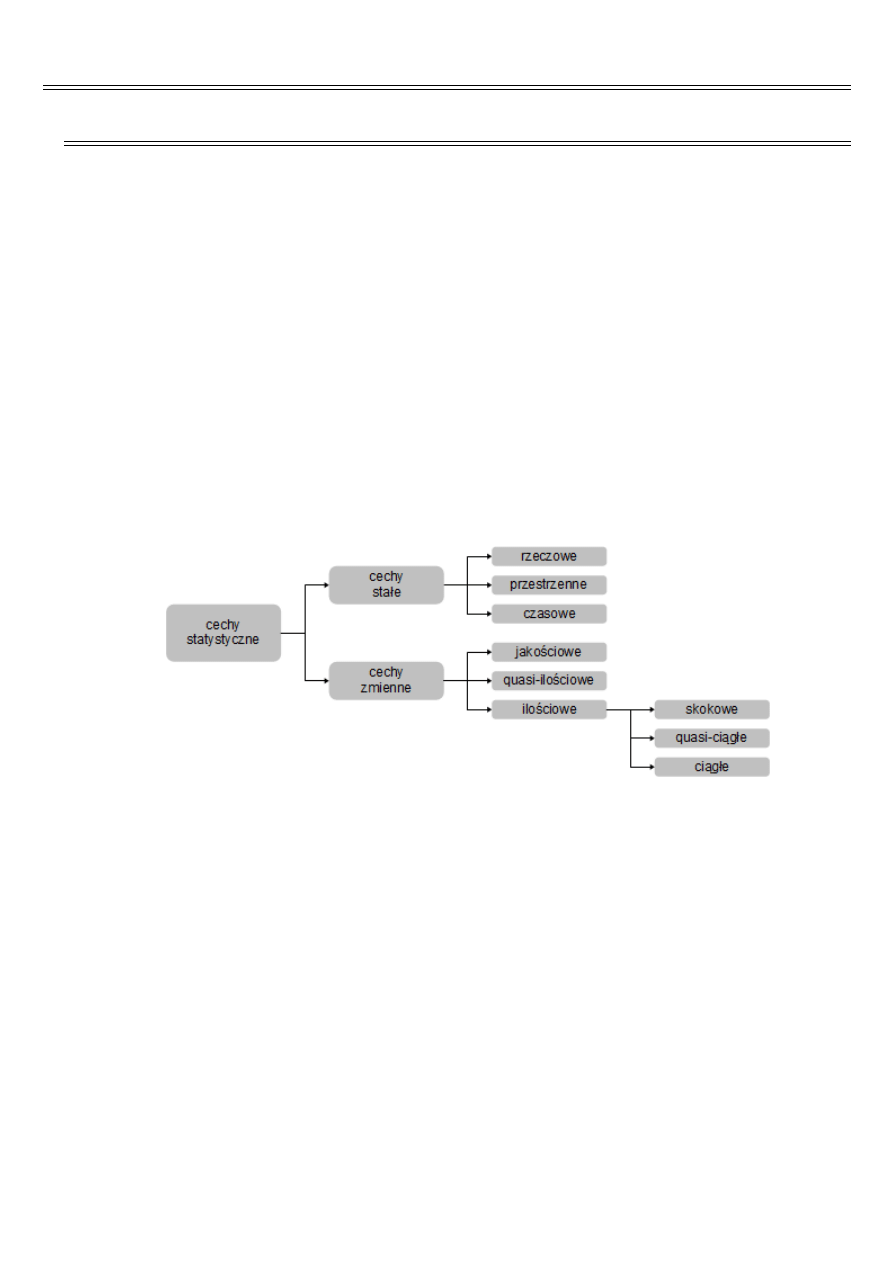
Podział cech statystycznych przedstawia ilustracja poniżej.

Podział cech statystycznych

cechy zmienne – to cechy różnicujące poszczególne jednostki z badanej populacji
cechy zmienne jakościowe - to cechy niemierzalne, które można jedynie określić przez

opis i nie da się ich w żaden sposób uszeregować. Taką cechą jest na przykład kolor oczu:
poszczególne warianty są przedstawione przez opis (niebieskie, szare, zielone) i nie można
ich ułożyć, bo nie ma żadnej reguły mówiącej, że kolor oczu niebieski powinien być przed
zielonym

cechy zmienne quasi-jakościowe (inaczej porządkowe) - to cechy niemierzalne, które

można jedynie określić przez opis, ale które da się w jakiś sposób uszeregować.
Przykładem takiej cechy jest wzrost określony słownie: niski, średnio niski, średni, średnio
wysoki, wysoki. Określenia cechy są niemierzalne, ale można je uszeregować w pewnej
kolejności, bo niski jest niższy od średniego, a średni z kolei niższy od wysokiego

cechy zmienne ilościowe (mierzalne) - to cechy dające się wyrazić liczbami
cechy zmienne ilościowe skokowe - to cechy określane za pomocą przeliczalnego

zbioru liczb, do którego nie możemy dodawać nowych wariantów cechy w
nieskończoność. Przykładowa cecha skokowa to ilość dzieci w rodzinie - może być dwóje,

2 / 8

Opracowanie: Tomasz Trawka

może być troje, ale nie może być dwoje i pół

cechy zmienne ilościowe quasi-ciągłe - to odmiana cech skokowych, ale z dużą ilością

wariantów powodujących postrzeganie jej jako cechy ciągłej

cechy zmienne ilościowe ciągłe - to cechy określane najczęściej za pomocą liczb

rzeczywistych i mające tę właściwość, że pomiędzy dwoma przyległymi wariantami cechy
zawsze można wprowadzić kolejny wariant tej cechy (np. między 2,345 a 2,346 można
wprowadzić 2,3455)

cechy stałe – to właściwości stałe dla całej badanej populacji, nie powodujące

różnicowania jednostek. Stanowią one najczęściej tylko kryterium przynależności
jednostki do określonej zbiorowości statystycznej, np. w badaniu statystycznym mężczyzn
czterdziestoletnich cechami stałymi są płeć oraz wiek, gdyż nie zmieniają się one w całej
badanej grupie

cechy stałe rzeczowe - określają co jest przedmiotem badania
cechy stałe przestrzenne - określają gdzie (miejsce lub obszar) jest ulokowana badana

jednostka statystyczna

cechy stałe czasowe - określają moment lub okres badanej cechy

R o z p o z n a w a n i e c e c h w o p i s i e b a d a n i a

Mamy opis pewnego badania statystycznego. W nawiasach dodano do niego

klasyfikację występujących w nim cech statystycznych.

Wśród kobiet (cecha stała rzeczowa) z województwa podlaskiego (cecha stała

przestrzenna) przeprowadzono ankietę pytając o: miejsce zamieszkania (cecha zmienna
jakościowa), wiek (cecha zmienna ilościowa skokowa), wykształcenie (cecha zmienna
quasi-ilościowa), długość stażu pracy w miesiącach (cecha zmienna ilościowa
skokowa/quasi-ciągła), stan cywilny (cecha zmienna jakościowa), ilość dzieci (cecha
zmienna ilościowa skokowa) i zarobki (cecha zmienna ilościowa quasi-ciągła).

S z e r e g s t a t y s t y c z n y

D e f i n i c j e i p o d z i a ł

Szereg statystyczny - to zbiór jednostek statystycznych zawierających wartości badanej

cechy uporządkowany według określonych kryteriów. Ilustracja poniżej przedstawia
klasyfikację szeregów statystycznych.

Podział szeregów statystycznych

Szereg szczegółowy zawiera wszystkie dane ze zbioru danych posortowane rosnąco lub

3 / 8

Materiały do zajęć, wersja bardzo skrócona, 1.0

malejąco.

Szereg rozdzielczy zawiera wszystkie dane zebrane w grupy według wartości cech.
Szereg rozdzielczy (z cech mierzalnych) przedziałowy zawiera dane zebrane w grupy,

a każda grupa jest określona przez zakres wartości „od-do”. Najczęściej wchodzą do niego
cechy zmienne ilościowe ciągłe

Szereg rozdzielczy (z cech mierzalnych) punktowy zawiera dane zebrane w grupy, a

każda grupa jest określona przez jedną wartość. Grupy są posortowane. Najczęściej
wchodzą do niego cechy zmienne ilościowe skokowe i quasi-ciągłe

Szereg rozdzielczy (z cech niemierzalnych) zawiera dane zebrane w grupy, a każda

grupa jest określona przez jedną wartość. Najczęściej wchodzą do niego cechy zmienne
jakościowe

Szereg przestrzenny zawiera dane statystyczne wraz z informacjami o ich

przestrzennym rozłożeniu na terenie kraju lub świata.

Szereg dynamiczny zawiera dane statystyczne przedstawiające zmiany danych

statystycznych w czasie.

W zadaniach będziemy głównie korzystali tylko z trzech rodzajów szeregów

statystycznych. Zostały one szerzej opisane poniżej.
S z e r e g s z c z e g ó ł o w y

Szereg szczegółowy to po prostu dane uporządkowane rosnąco lub - rzadziej -

malejąco. Ilustracja poniżej przedstawia zestaw danych oraz utworzony z niego (przez
posortowanie) szereg szczegółowy.

Surowe dane oraz stworzony z nich szereg szczegółowy

S z e r e g r o z d z i e l c z y p u n k t o w y

Przy dużej ilości danych w szeregach szczegółowych, gdy utrudnione jest prowadzenie

na nich obliczeń, można łączyć dane tego samego typu w grupy. Szeregi rozdzielcze
punktowe opierają się na wszystkich cechach zmiennych poza ilościowymi ciągłymi i
quasi-ciągłymi. Ilość grup odpowiada ilości wariantów cechy. Dane w szeregu przedstawia
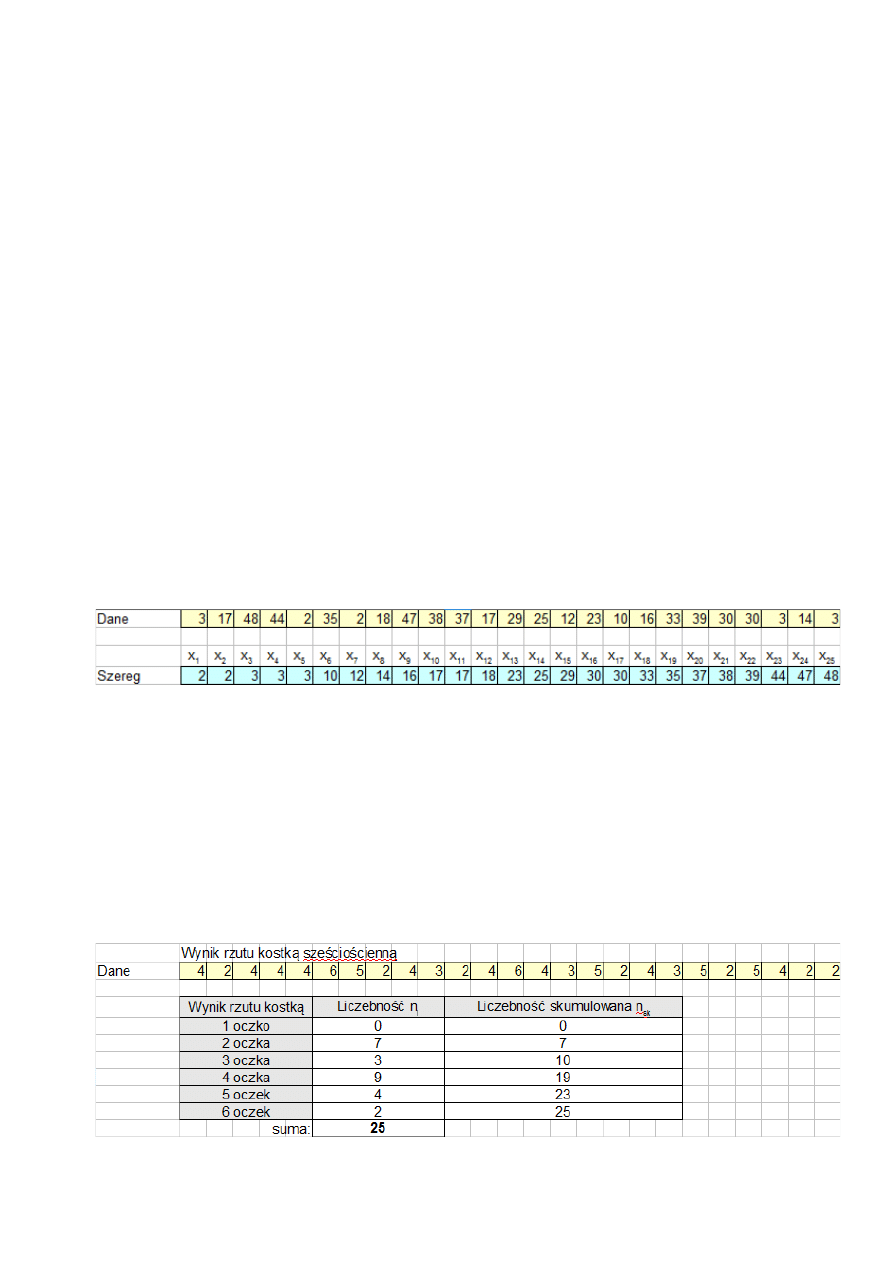
podając liczebność, czyli ilość danych w grupie, dla każdej grupy. Dodatkowo liczy się
liczebność skumulowaną, czyli sumę wszystkich wyników od pierwszej do wskazanej
grupy włącznie (w przykładzie poniżej liczebność skumulowana dla 3 oczek wynosi
0+7+3=10).

Surowe dane oraz stworzony z nich szereg rozdzielczy punktowy

4 / 8

Opracowanie: Tomasz Trawka

S z e r e g r o z d z i e l c z y p r z e d z i a ł o w y

Szeregi rozdzielcze przedziałowe opierają się na cechach zmiennych ilościowych

ciągłych i quasi-ciągłych. Dane grupowane są w wyznaczonych przedziałach, a ilość
przedziałów oraz ich wielkość oblicza się z wzorów (patrz następny rozdział). W celu
przedstawienia wyników zliczamy dla każdego przedziału liczebność, czyli ilość danych
statystycznych znajdujących się w przedziale. Podaj się także liczebność skumulowaną
(opis w poprzednim szeregu).

Surowe dane oraz stworzony z nich szereg rozdzielczy przedziałowy

5 / 8

Materiały do zajęć, wersja bardzo skrócona, 1.0

Definiow anie przedziałów w szeregu rozdzielcz ym
przedziałow ym (na prz ykładzie)

Z przeprowadzonej ankiety uzyskaliśmy dane jak na ilustracji poniżej. Są one

nieuporządkowane, zebrane w tabeli w kolejności wynikającej z terminu wypełniania
ankiet. Wykres pokazuje rozłożenie tych danych na osi X. Aby uzyskać szereg
szczegółowy sortujemy dane.

Dane zebrane z ankiet

Rozłożenie danych z ankiet na osi

Szereg szczegółowy utworzony z danych

Wzorów i reguł opisujących prawidłowy podział danych na przedziały jest kilka. Ich

zadaniem jest raczej pomóc określić ilość przedziałów w przybliżeniu. Ogólne zasady
mówią, że przedziałów nie powinno być mniej niż 6 i nie więcej niż 30. Poniżej wzory
pozwalające określić ilość przedziałów klasowych.

k =

[

5⋅log n

]

lub

k =[



n]

lub

k =

[

13,222⋅logn

]

Korzystając z wzoru określamy ilość przedziałów, na które podzielimy dane z szeregu

szczegółowego. Ilość przedziałów musi być liczbą całkowitą, więc dobieramy ją na
podstawie uzyskanego wyniku. W poniższym zadaniu przyjęto podział na 6 przedziałów.

k =

[

13,222⋅log n 

]

(w przykładzie

k =

[

13,222⋅log 30

]

=

[

5,76

]

=

6

)

Na podstawie wzorów określamy teraz parametry przedziałów: szerokość oraz początek

i koniec każdego przedziału. Początek przedziału określany jest jako jego granica dolna, a
koniec przedziału jako jego granica górna.

Parametry opisujące przedziały

Rozstęp to odległość między wartością minimalną a maksymalną w zbiorze danych.

R= x

max

−

x

min

(w przykładzie

R=95−5=90

)

Szerokość przedziału jest taka sama dla wszystkich przedziałów zdefiniowanych w

zbiorze i wynika z rozstępu i obliczonej ilości przedziałów.

h=

R

k −1

(w przykładzie

h=

90

6−1

=

18

)

Granice przedziałów zaczynamy obliczać od przedziału pierwszego. Dolna granica jest

oznaczona jako x

1D

(1 bo pierwszy przedział, D bo granica dolna), a górna jako x

1G

.

x

1D

=

x

min

−

1

2

h

(w przykładzie

x

1D

=

5−

1
2

18=−4

)

6 / 8

Opracowanie: Tomasz Trawka

x

1G

=

x

1D



h

(w przykładzie

x

1G

=−

418=14

)

Dolna granica przedziału drugiego zaczyna się w miejscu, w którym kończy się

przedział 1. Górną granicę przedziału drugiego liczymy analogicznie jak w pierwszym.

x

2D

=

x

1G

(w przykładzie

x

2D

=

14

)

x

2G

=

x

2D



h

(w przykładzie

x

2G

=

1418=32

)

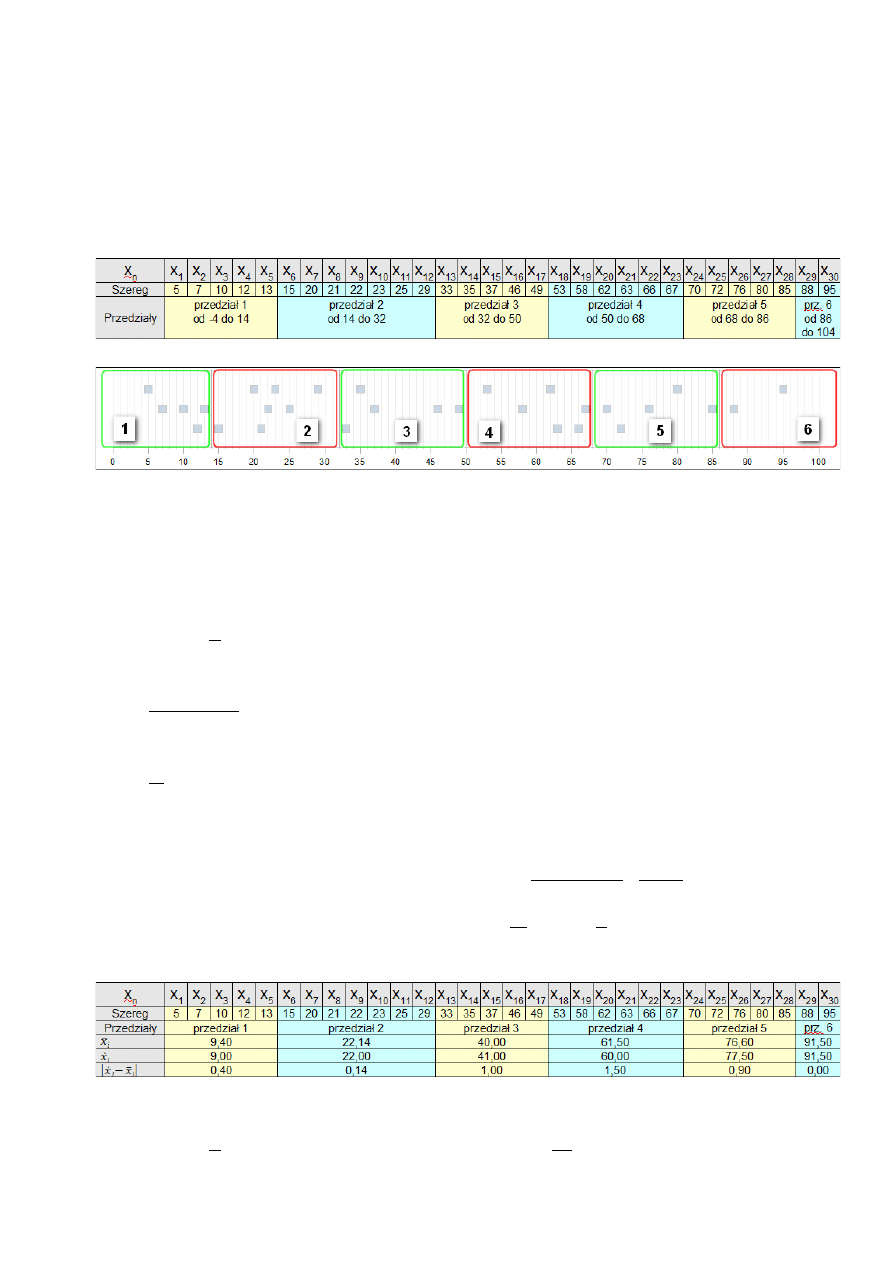
Podobnie liczymy granice pozostałych przedziałów. Uzyskany podział przedstawiają

ilustracje poniżej.

Szereg szczegółowy z podziałem na sześć przedziałów

Graficzna reprezentacja przedziałów

Podział został dokonany, ale konieczne jest jeszcze sprawdzenie, czy taka forma

przedstawienia danych nie spowodowała zbytniej utraty własności statystycznych. Określa
się to sprawdzając, czy suma wartości bezwzględnych z różnic między wartością
środkową a średnią z każdego przedziału jest mniejsza lub równa połowie szerokości
przedziału (tego zdania lepiej nie czytać, poniższy wzór wyjaśnia to zdecydowanie lepiej).

∑

i=1

k

∣ ˙x

i

− 

x

i

∣

h
2

gdzie:

˙x

i

=

x

max , i



x

min ,i

2

- środek przedziału o numerze i, obliczany na podstawie największej i

najmniejszej liczby w przedziale



x

i

=

1

n

i

∑

j =1

n

i

x

j , i

- średnia z liczb w przedziale numer i

Wartości środkowe oraz średnie z poszczególnych przedziałów przedstawia ilustracja

poniżej. Dla przedziału pierwszego obliczenia wyglądają następująco:

•

wartość środkowa przedziału 1 wynosi

˙

x

1

=

x

max ,1



x

min,1

2

=

135

2

=

9

•

wartość średnia przedziału 1 wynosi



x

1

=

1

n

1

∑

j=1

n

1

x

j ,1

=

1
5



57101213=9,40

•

wartość bezwzględna z różnicy dla przedziału 1 wynosi

∣ ˙x

1

− x

1

∣=∣

9−9,40∣=0,40

Obliczenia konieczna do sprawdzenia poprawności podziału na przedziały

Ostatecznie uzyskujemy

∑

i=1

k

∣ ˙x

i

− 

x

i

∣

h
2

⇒ 

0,400,141,001,500,900,00

18

2

⇒

3,949

7 / 8

Materiały do zajęć, wersja bardzo skrócona, 1.0

co oznacza, że uzyskany podział jest odpowiedni i spełnia wymagania.

8 / 8