PRODUKCJA ENTROPII I SPRZĘŻENIA PROCESÓW

Entropia jest jedną z funkcji stanu, „miarą molekularnego i energetycznego nieporządku

układu”. Jest definiowana (w termodynamice) przez swoją różniczkę zupełną i związana z energią
przekazywaną na sposób ciepła, ulegającą tym samym rozproszeniu i zwiększąjącą chaotyczność
układu. Różniczka entropii jest równa ilorazowi ciepła elementarnego wymienionego między
układem a otoczeniem w elementarnym procesie odwracalnym oraz temperatury układu.

Z tej definicji wynika m.in. to, że dopływ ciepła wywoła większy skutek w układzie o niższej

temperaturze. Żeby obliczyć różnicę entropii między dwoma stanami, trzeba wymyśleć proces
odwracalny łączący je, a następnie scałkować wymienione na całej drodze ciepło podzielone przez
T. Entropia przyjmuje wartości nieujemne, natomiast przyrost entropii może być tak dodatni, jak
ujemny (np. kiedy układ oddaje ciepło).

Natomiast w elementarnym procesie nieodwracalnym przyrost entropii jest większy od tej

różniczki związanej z wymienionym ciepłem.

Jako że entropia jest funkcją stanu, jej różnica jest tu taka sama jak gdyby to był proces

odwracalny, ale wymieniona zostaje inna – mniejsza - ilość ciepła. Prostym przykładem niech
będzie izotermiczne [298K] rozprężanie [1000 moli] gazu doskonałego [od 1dm3 do 10dm3]. Za
proces odwracalny posłuży rozprężanie quasi-statyczne. Zmiana entropii wynosi Q/T =
nRT·ln(V2/V1)/T = 19150. W procesie nieodwracalnym – rozprężaniu pod ciśnieniem np. 100kPa
całkowita zmiana entropii jest taka sama, ale wymienione ciepło wynosi p(V2-V1) = 900000, a Q/T =
3020.

Różnica pomiędzy całkowitym przyrostem entropii a różniczką dQ/T to właśnie produkcja

entropii. Wynika ona z nieodwracalnych zmian m.in. strukturalnych wewnątrz układu takich jak
przepływ ciepła czy masy. Część cieplna nazywa się „transportem entropii”. Tutaj analizujemy
proces elementarny, stąd różniczki. Produkcja entropii oraz ciepło wymienione są zależne od
procesu – drogi pomiędzy danymi stanami, natomiast ich suma, czyli całkowity przyrost entropii
zależy tylko od stanu początkowego i końcowego. Największa wymiana ciepła zachodzi dla
procesu odwracalnego. Produkcję entropii oblicza w ten sposób właśnie, odejmując od przyrostu
entropii obliczonej dla procesu odwracalnego iloraz ciepła i T.

Z nierówności Clausiusa (dS >= dQ/T) wynika, że produkcja entropii nie może być mniejsza

niż 0. Jako że według II zasady termodynamiki w przyrodzie zachodzą samorzutnie wyłącznie
procesy nieodwracalne, dla wszystkich samorzutnych procesów produkcja entropii jest dodatnia.
Jeśli całkowity przyrost entropii jest równy wymienionemu ciepłu przez temperaturę (ΔS = Q/T) to
proces nie przebiegnie, nie przebiegnie też proces odwrotny do niego – układ jest w stanie
równowagi względem danego procesu.

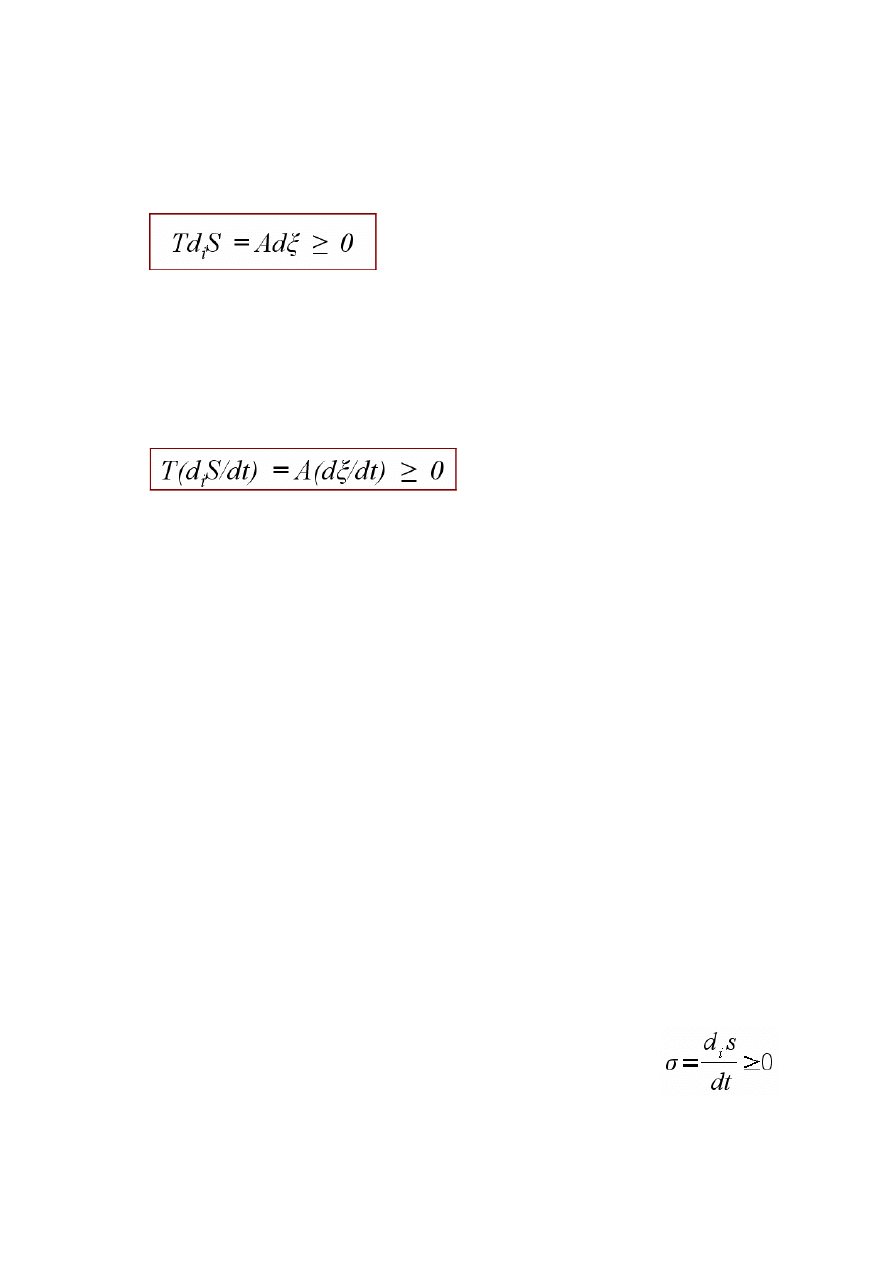
Jeśli w układzie zachodzi reakcja chemiczna, produkacja entropii z nią związana jest

proporcjonalna do zmiany liczby postępu reakcji (dξ). Współczynnikiem proporcjonalności dla
iloczynu T i diS jest chwilowe powinowactwo chemiczne reakcji.

Jest ono funkcją temperatury, ciśnienia i stężeń składników, czyli również liczby postępu (ξ).

Z tego równania wynika, że jeśli A > 0, to dξ również ≥ 0, a jeśli A < 0, to dξ ≤ 0, natomiast gdy A = 0,
to dξ = 0. Oznacza to, że dla dodatniego powinowactwa reakcji postęp wzrasta z czasem zgodnie z
zapisem równania reakcji. Ujemne powinowactwo natomiast oznacza przebieg reakcji „od prawej
do lewej”, a zerowe – brak reakcji. Oczywiście po podstawieniu i przekształceniu pewnych wielkości
i wzorów wyjdzie, że powinowactwo jest równe ujemnej różnicy entalpii swobodnej (A = -ΔG).
Zarówno produkcja entropii, jak i postęp reakcji są funkcjami czasu, można więc to równanie
zapisać w ten sposób:

Dla układów nie wymieniających ciepła z otoczeniem (czyli izolowanych lub adiabatycznie

izolowanych) przyrost entropii wynika jedynie z jej produkcji wewnątrz układu, która musi być
dodatnia dla procesów nieodwracalnych. Tak więc w układzie izolowanym mogą przebiegać
samorzutnie tylko procesy zwiększające jego entropię. Za taki układ możemy uważać wszechświat,
dlatego przyrost entropii w całym wszechświecie jest ogólnym kryterium samorzutności procesów.
Entropie sumują się. Przyrost entropii systemu izolowanego jest równy sumie przyrostów entropii
dla poszczególnych części systemu.

Na przykład dla interesującego nas układu i jego otoczenia, razem tworzących izolowany

wszechświat, suma zmian entropii układu i otoczenia musi być większa od zera, jeśli to ma być
spontaniczny proces zachodzący w realnym wszechświecie. Z tego wynika, że zmiana entropii
układu będzie większa niż zmiana entropii otoczenia z przeciwnym znakiem (bądź na odwrót). W
układzie nieizolowanym mogą przebiegać samorzutnie procesy zmniejszające jego entropię,
jednak tylko jeśli jednocześnie rośnie (i to bardziej) entropia otoczenia, tak że wciąż suma jest
dodatnia, przy czym obie zmiany entropii muszą być wynikiem procesów sprzężonych.

Za kryterium samorzutności procesu w danych, narzuconych warunkach służy przyrost

odpowiedniego potencjału termodynamicznego. Potencjał termodynamiczny to funkcja, której
wartość w wyniku spontanicznej przemiany maleje przy narzuconych więzach, aby w stanie
równowagi osiągnąć kres dolny. Zatem dla procesów samorzutnych przyrost takiej funkcji zawsze
jest ujemny.

Tak więc bezpośrednim kryterium samorzutności procesów w warunkach izotermiczno-

izobarycznych jest entalpia swobodna. Jej ujemny przyrost może być spowodowany bądź silnie
ujemnym składnikiem entalpowym – energetycznym, bądź silnie dodatnim składnikiem
entropowym. Np. we wnętrzu gwiazd przy ogromnej temperaturze mogą zachodzić procesy
endotermiczne bądź zmniejszające entropię.

Pochodną produkcji entropii po czasie oznacza się symbolem σ i nazywa

źródłem entropii. Parametr ten jest miarą tworzenia entropii w procesie
nieodwracalnym w danej komórce przestrzeni i w jednostce czasu. Zwykle
przy jego obliczeniach używa się wielkości molowych. Najpowszechniejsze
procesy, wskutek których tworzy się entropia to: przepływ ciepła, dyfuzyjny
przepływ masy oraz reakcja chemiczna. Tak wyglądałoby wyrażenie na zmianę energii
wewnętrznej w małej komórce przestrzeni:

a przy założeniu stałej jej objętości i wyciągnięciu przyrostu entropii otrzymamy:

Pierwszy wyraz odpowiada przepływowi energii, drugi – dyfuzji masy, trzeci – przebiegowi

reakcji. Pierwsze dwa są wektorami, trzeci jest skalarem. W przypadku przepływów bezpośrednią
przyczyną wzrostu entropii jest kontakt z otoczeniem (czyli z sąsiednimi komórkami) i różniące się
wartości ich temperatur i potencjałów chemicznych. Można więc zapisać równanie w ten sposób:

Posługując się strumieniami przepływów, czyli ilościami wielkości skalarnej jaka przepływa w

jednostce czasu przez jednostkową powierzchnię prostopadłą do rozważanego elementu objętości
oraz zamieniając różnice na wartości graniczne otrzymamy następujące wyrażenie:

gdzie symbol

oznacza operator nabla. Mnożąc wektor jednostkowy przez wektor

strumienia otrzymamy skalar, więc ostatecznie źródło entropii będzie również skalarem. W postaci
ogólnej równanie to wygląda następująco:

Symbole J to strumienie przepływów gęstościowych wielkości ekstensywnych, a parametry

X, których występowanie jest przyczyną tych przepływów, noszą nazwę sił termodynamicznych.
Środkowa suma dotyczy strumieni dyfuzyjnych, które nie są od siebie niezależne. Można wykazać,
że dla układu nieruchomego suma strumieni dyfuzyjnych jest równa zero... co sprawia, że dla
układu n-składnikowego, tylko n-1 przepływów jest niezależnych. Przepływ zależny, umownie
przypisany rozpuszczalnikowi (indeks s), będzie równy:

Umożliwia to przedstawienie naszego równania w następującej postaci:

Ta tabela podaje zestawienie wybranych strumieni i skoniugowanych z nimi sił

termodynamicznych. W ostatniej kolumnie wymienione są tzw. bodźce termodynamiczne, czyli
pierwotne przyczyny inicjujące proces nieodwracalny. A oznacza powierzchnię, iA jest wektorem
jednostkowym prostopadłym do tej powierzchni. Pojawienie się niezerowego bodźca
termodynamicznego, a następnie skoniugowanej siły termodynamicznej generuje przepływ w
układzie.

Jednak często dany przepływ uzależniony jest również od pozostałych sił

termodynamicznych, za pomocą których może być wywołany jako przepływ sprzężony. Przyjmuje
się (w termodynamice nierównowagowej liniowej), że funkcje te są liniowe, czyli zachodzi coś
takiego:

Równań takich jest n – po jednym dla każdego przepływu, nazywa się je równaniami

fenomenologicznymi. Współczynniki Lik zwane współczynnikami fenomenologicznymi
charakteryzują przebieg procesu. Zasada Onsagera, zwana relacją wzajemności Onsagera lub też IV
zasadą termodynamiki mówi, że macierz tych współczynników jest symetryczna, to znaczy, że Lik =
Lki. Np. dwa przepływy są charakteryzowane przez trzy, a nie cztery współczynniki.

Przepływy te są źródłem entropii. Źródło entropii jako wielkość jest także funkcją wszystkich

bodźców. Można wykazać następującą zależność:

W tej sytuacji istnieje możliwość, że obok przepływów odbywających się w kierunku

działania bodźców, którym są przyporządkowane, mogą istnieć przepływy „wymuszone” tworzące
nowe bodźce, byle by był spełniony ten warunek:

Współczynniki Lik są miarą sprzęgania procesów, opisują tzw. efekty krzyżowe.

Podstawiając przepływ do wzoru na źródło entropii otrzymamy:

Jak widać, źródło entropii jest kwadratową funkcją sił termodynamicznych. Wymóg

nieujemności tej wielkości nakłada pewien wymóg na współczynniki, np. współczynnik
skoniugowany musi być nieujemny (Lii ≥ 0), a także iloczyn dwóch współczynników
skoniugowanych musi być większy niż iloczyn odpowiednich wiążących współczyników (Lii Ljj ≥ Lij
Lji). Dodatkowe ułatwienie wynika z zasady Curie, która nakazuje, aby współczynniki wiążące siły i
przepływy o różnym typie wektorowym były równe zero, np. te wiążące przebieg reakcji
chemicznej i przepływ ciepła czy dyfuzję.

σ =

∑

i

∑

j

L

ij

X

i

X

j

PRZYKŁADY PROCESÓW SPRZĘŻONYCH

Przyjrzyjmy się bliżej procesowi termodyfuzji. W mieszaninie gazów wytwarzamy gradient

temperatury. Konsekwencją tego jest nieodwracalny proces wymiany energii na sposób ciepła. Ale
przepływ energii realizowany jest poprzez ruch cząsteczek. Jeśli cząsteczki są różne (układ jest co
najmniej dwuskładnikowy), wkład poszczególnych cząsteczek do przekazywanej w ten sposób
energii kinetycznej jest różny (np. z powodu grawitacji). Powoduje to powstanie gradientu stężeń (i
potencjałów chemicznych), a więc swego rodzaju dyfuzję. Proces tej tzw. termodyfuzji jest wtórny
wobec pierwotnego (czyli wyrównywania energii) i charakteryzuje się zmniejszeniem entropii.
Oczywiście sumaryczne źródło entropii musi spełniać warunek nieujemności, ale byłoby większe,
gdyby termodyfuzja nie wystąpiła. Oznacza to, że nieodwracalny przepływ energii wymuszony
przez gradient temperatury produkuje entropię, ale kosztem zaniku jej części odbywa się
wymuszony proces termodyfuzji. Proces termodyfuzji jest zatem sprzężony z procesem przepływu
energii. Można powiedzieć, że przepływ skoniugowany generuje przepływ sprzężony, który
hamuje proces pierwotny. Ten wzajemny wpływ sięga dalej, ponieważ bezpośrednim efektem
zróżnicowania stężeń wskutek termodyfuzji jest uruchomienie zwykłego procesu dyfuzji.

W konsekwencji otrzymamy nieskończony ciąg wzajemnie sprzęgających się i wzajemnie

hamujących się procesów, które doprowadzą układ do wyzerowania bodźców i do stanu
równowagi, kiedy wszystkie przepływy znikną. Jeśli natomiast przynajmniej jeden bodziec
termodynamiczny nie zniknie, będąc utrzymywanym na stałym poziomie, to wzajemny wpływ
przepływu skoniugowanego i sprzężonego sprawi, że nastąpi ustalenie przepływów i układ
osiągnie stan stacjonarny. Procesy sprzężone, charakteryzujące się zanikaniem, a nie tworzeniem
entropii są regułą, a nie wyjątkiem. Są niezwykle istotną częścią biologii.

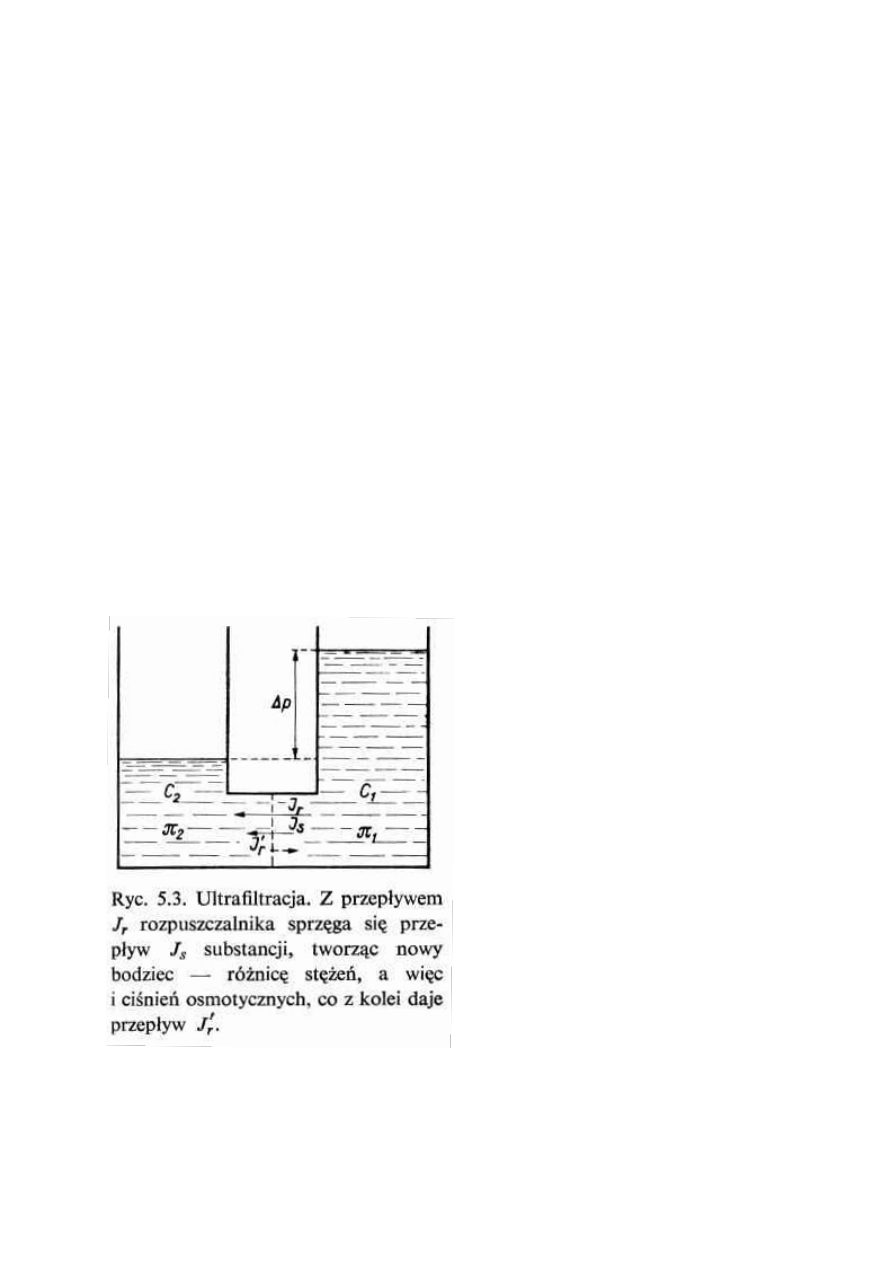
Przyjrzyjmy się teraz procesowi osmozy

w przypadku błony biologicznej
przepuszczalnej dla rozpuszczalnika, a z
trudem przepuszczającej substancję
rozpuszczoną. Bodziec różnicy ciśnień Δp
powoduje przepływ rozpuszczalnika Jr, a ten
pociąga za sobą sprzężony przepływ
substancji Js. To opóźnienie powoduje
powstanie różnicy stężeń c1 > c2. Podczas gdy
przepływ rozpuszczalnika Jr zmniejsza
bodziec w postaci Δp, z czym wiąże się wzrost
entropii, przepływ substancji Js powoduje
powstawanie nowych bodźców, czyli
zmniejsza entropię. Bodźce te można
sprowadzić do różnicy ciśnień osmotycznych
Δπ = π1 – π2, która daje wtórny przepływ
rozpuszczalnika Jr’ w kierunku odwrotnym do
początkowego, a więc podtrzymującym
bodziec początkowy Δp. Układ w końcu
znalazłby się w stanie równowagi. Mimo to
procesy sprzężone przedłużają nieco jego
życie. Gdyby udało się utrzymać różnicę
ciśnień Δp na stałym poziomie, układ

znalazłby się w stanie stacjonarnym. Jego entropia byłaby stała i mniejsza niż w stanie wyjściowym
z powodu nowopowstających bodźców. Układ by „żył” – istniałyby przepływy tworzące entropię,
co kompensowałaby wymiana energii i substancji z otoczeniem.

Przykładem sprzężenia jest także powiązanie reakcji redoks z fosforylacją ADP. Reakcje

redoks zwiększają entropię, czyli mogą zachodzić samorzutnie, fosforylacja ADP oczywiście nie.
Schemat takiego sprzężenia przedstawia się następująco... Bodźcem termodynamicznym jest
różnica potencjałów redoks, procesem skoniugowanym jest reakcja redoks, procesem sprzężonym
– reakcja fosforylacji ATP, a bodźcem wtórnym - potencjał chemiczny ATP.

Podobnie jest z biosyntezą makrocząsteczek, która jako zmniejszająca entropię jest

sprzężona z procesem hydrolizy ATP...

I podobnie transport jonów przez błony wbrew gradientowi stężeń dzięki pompom

wykorzystującym energię z hydrolizy ATP.

W zasadzie cały metabolizm organizmów polega na sprzężeniu procesów zwiększających

entropię oraz lokalnie ją obniżających. Oczywiście jej zwiększenie w procesach katabolicznych
znacznie przewyższa owe lokalne jej zmniejszenia w procesach anabolicznych. Organizm
otrzymuje od otoczenia entropię dS’ > 0 wraz z produktami pokarmowymi, natomiast oddaje
entropię dS’’ < 0 wraz ze zdegradowanymi produktami przemiany materii i zdegradowaną energią
w postaci ciepła. |dS’’| > |dS’|, więc transport entropii netto jest ujemny. W organizmie zachodzą
oczywiście nieodwracalne procesy produkujące entropię. W dojrzałym organiźmie, nie
zmieniającym swej biomasy szybkość tworzenia entropii jest równa szybkości jej oddawania.
Entropia organizmu nie zmienia się więc w czasie, a organizm jest w stanie stacjonarnym. Z kolei w
organiźmie rosnącym, zwiększającym biomasę szybsze tworzenie entropii prowokuje - poprzez
procesy sprzężone - jeszcze szybsze wydalanie entropii. Entropia w przeliczeniu na jednostkę masy
maleje. Jest to stan przejściowy. Szybkość produkcji oraz wydalania entropii maleje, aż do
osiągniecia minimum i stanu stacjonarnego.