
ZADANIA Z ALGEBRY
Wielomiany
1. Rozłożyć wielomiany na czynniki liniowe względem C:
f (z) = z
2
+ z + 1,
f (z) = iz
2
− z + 2i,
f (z) =
i
2
z
2
+ z − i,
f (z) = z
4
− 1,
f (z) = z
4
− 2z
2
− 3,
f (z) = z
6
+ 1.
2. Rozłożyć wielomiany na czynniki względem R:
f (x) = x
4
+ 1,
f (x) = x
4
− 4x
3
+ 6x
2
− 4x,
f (x) = x
6
+ 1,
f (x) = x
8
− 1,
f (x) = x
6
− 1.
3. Wykazać, że każdy wielomian o współczynnikach rzeczywistych, stopnia
nieparzystego ma co najmniej jeden pierwiastek rzeczywisty.
4. Jaką krotność ma pierwiastek x
0
wielomianu f (x):
f (x) = x
5
− 5x
4
+ 7x
3
− 2x
2
+ 4x − 8, x
0
= 2,
f (x) = 3x
5
− 6x
4
+ 2x
3
+ 36x
2
− 27x − 54, x
0
= 3.
5. Dla jakich a, b wielomian x
n+1
+ ax
n
+ b, jest podzielny przez (x − 1)
2
?
6. Znaleźć wszystkie wartości parametru a, dla których wielomian x
4
−4x+a
ma pierwiastki wielokrotne.
7. Rozłożyć wielomian x
4
− 2x
3
+ 3x
2
− 2x + 2 na czynniki nad R i nad C
jeśli wiadomo, że liczba 1 + i jest pierwiastkiem tego wielomianu.
8. Niech z
0
, z
1
, . . . , z
n−1
będą wszystkimi n-tymi pierwiastkami z 1 (to znaczy
z
n
k
= 1). Udowodnić, że:
z
0
+ z
1
+ · · · + z
n−1
= 0,
z
0
· z
1
· · · z
n−1
= (−1)
n+1
.
1
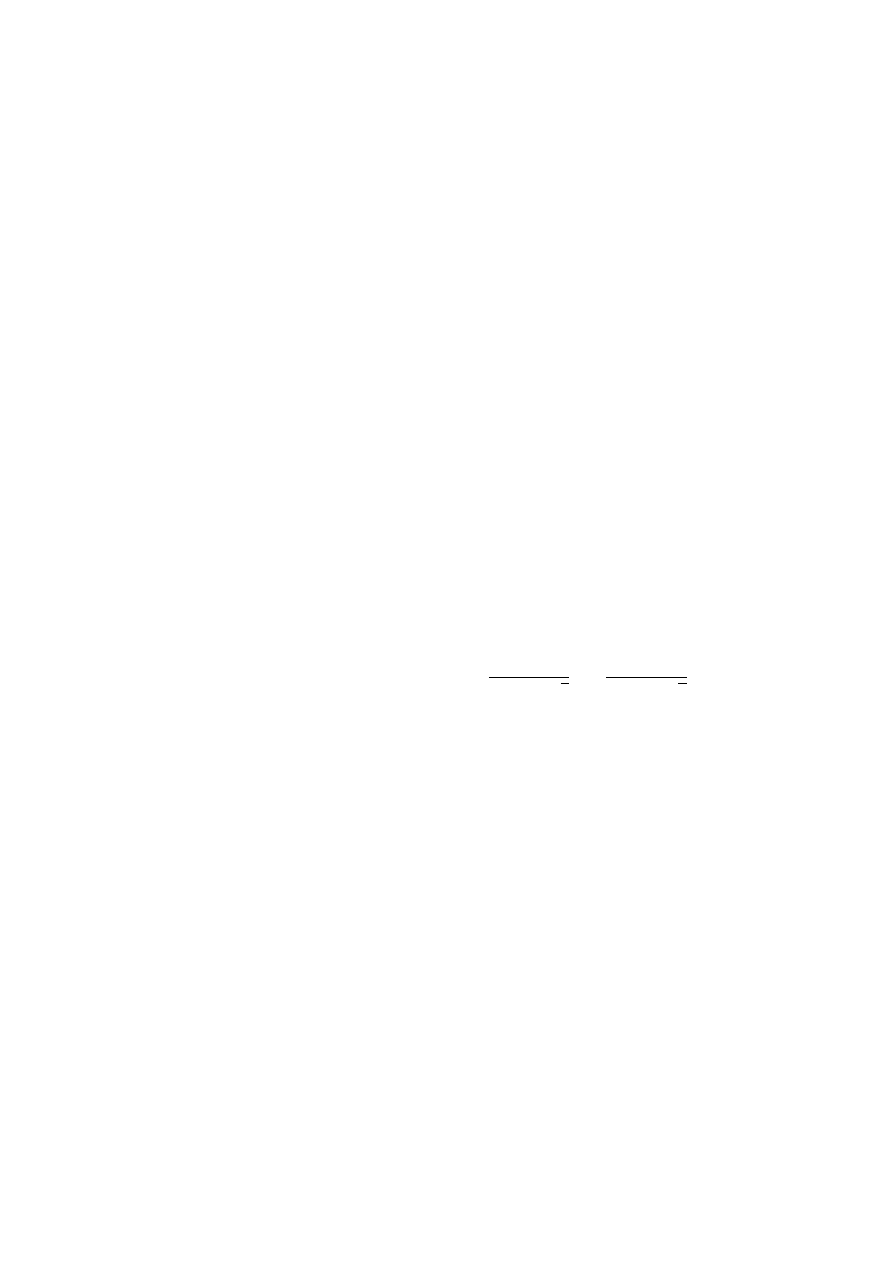
9. Skonstruować wielomian najmniejszego stopnia o współczynnikach rze-
czywistych, który ma dwukrotny pierwiastek i oraz jednokrotny pierwiastek
−1 − i.
10. Udowodnić, że jeśli K jest ciałem skończonym to istnieje wielomian,
który nie ma pierwiastka w ciele K.
11. Wyznaczyć wielomian o współczynnikach z ciała Z
5
, który nie ma pier-
wiastków w Z
5
.
12. Wyznaczyć liczby a, b, c jeśli są one pierwiastkami równania
x
3
− ax
2
+ bx − c = 0.
13. Liczby a, b, c są pierwiastkami równania x
3
− 6x
2
+ 11x − 6 = 0. Napisać
równanie stopnia trzeciego, którego pierwiastkami są liczby ab, ac, bc.
14. Wyznaczyć sumę współczynników wielomianu
(x
3
− x + 1)
50
+ (2x
2
− 2x + 1)
30
.
15. Wykazać, że prawdziwa jest równość
3
q
20 + 14
√
2 +
3
q
20 − 14
√
2 = 4.
2
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron