
Metoda Sił
w ujęciu macierzowym
Belka statycznie
niewyznaczalna
Więzy sprężyste
Wykonanie w programie Matlab

Układy z więzami sprężystymi
J. Ledziński „Mechanika budowli cz.2”
W rzeczywistych układach statycznych często
występują więzy ograniczające swobodę obrotów
i przesuwów w sposób sprężysty, proporcjonalnie do ich
sztywności.
Sprężyste więzy przeciwobrotowe nakładają na układ
dodatkowe ograniczenia.
Każde ograniczenie swobody
podwyższa stopień statycznej niewyznaczalności.
Zasadnicza różnica między więzami sprężystymi
(podatnymi) a więzami niepodatnymi polega ntym, że na
przykład w utwierdzeniu niepodatnym kąt obrotu jest
równy zero a w utwierdzeniu sprężystym =M·k
-1
.

Układy z więzami sprężystymi
J. Ledziński „Mechanika budowli cz.2”
Układy
statyczne
z
więzami
sprężystymi
rozwiązujemy metodą sił w omówiony dotychczas
sposób, jedynie przemieszczenia obliczamy ze wzoru:
gdzie:
k
j
– sztywność kolejnego więzu przeciwobrotowego
k
s
– sztywność kolejnego więzu przeciprzesuwnego
s
s
sp
si
j
j
jp
ji
p
i
ip
s
s
sk
si
j
j
jk
ji
k
i
ik
ds
ds
k
R
R
k
M
M
EI
M
M
k
R
R
k
M
M
EI
M
M
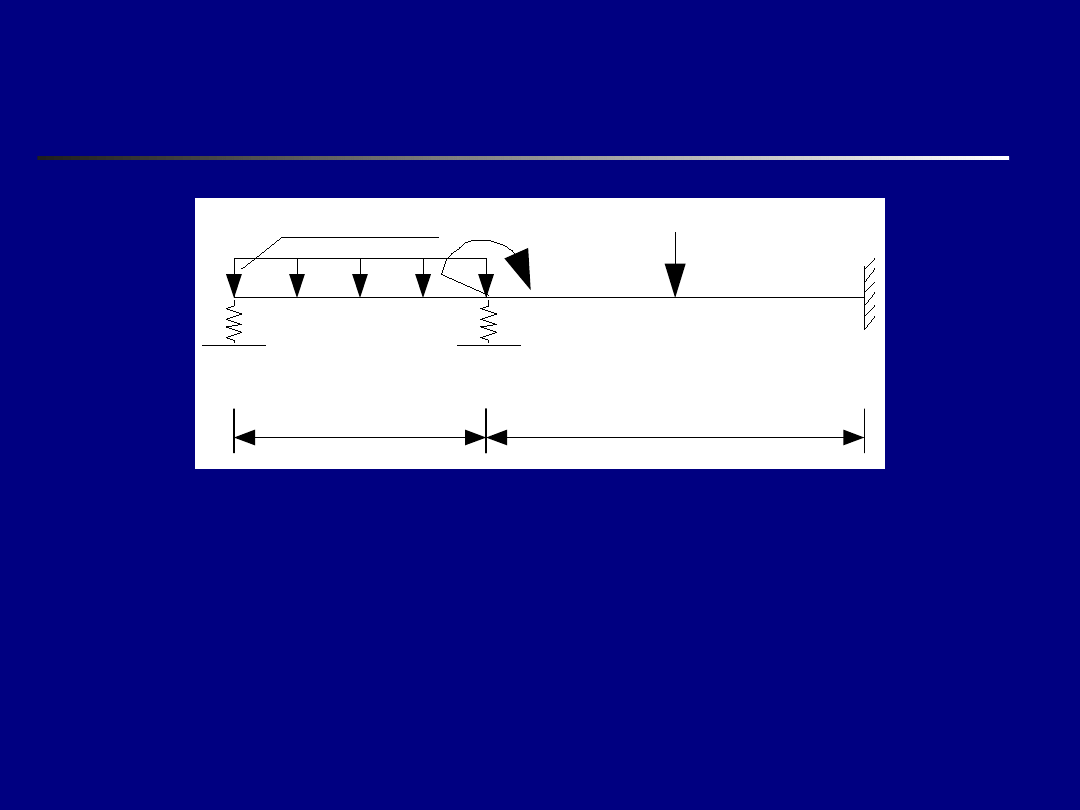
Rozważana belka
Ze względu na to, że macierz podatności dla układu z
więzami sprężystymi jest różna od macierzy podatności
dla układu z więzami niepodatnymi, poprzednio
uzyskane rozwiązanie dla belki poddanej obciążeniu
statycznemu nie jest właściwe.
q=1,0 kN/m
4,0 m
6,0 m
EI
2EI
M=4 kNm
P=2 kN
k
s
=1000
kN
/
m
k
s

Obliczenie elementów macierzy
Obecnie rozważamy belkę z więzami sprężystymi –
tylko przeciwprzesuwnymi. W takim przypadku nie
nastąpiło
ograniczenie
swobody
układu
czyli
uwzględnienie sprężystości podpór nie podwyższa stopnia
statycznej niewyznaczalności. Jeśli tak, to SNS układu nie
ulega
zmianie
i
możemy
dalej
korzystać
z
dotychczasowego układu podstawowego.
Stąd elementy macierzy podatności mogą być
wyliczane ze wzoru:
s
s
sk
si
ik
ik
k
R
R
*
gdzie:
ik
– macierz podatności dla belki o więzach niepodatnych

Obliczenie elementów wektora
p
Elementy wektora wyrazów wolnych mogą być
wyliczane ze wzoru:
s
s
sp
si
ip
ip
k
R
R
*
gdzie:
ip
– wektor wyrazów wolnych dla belki o więzach niepodatnych
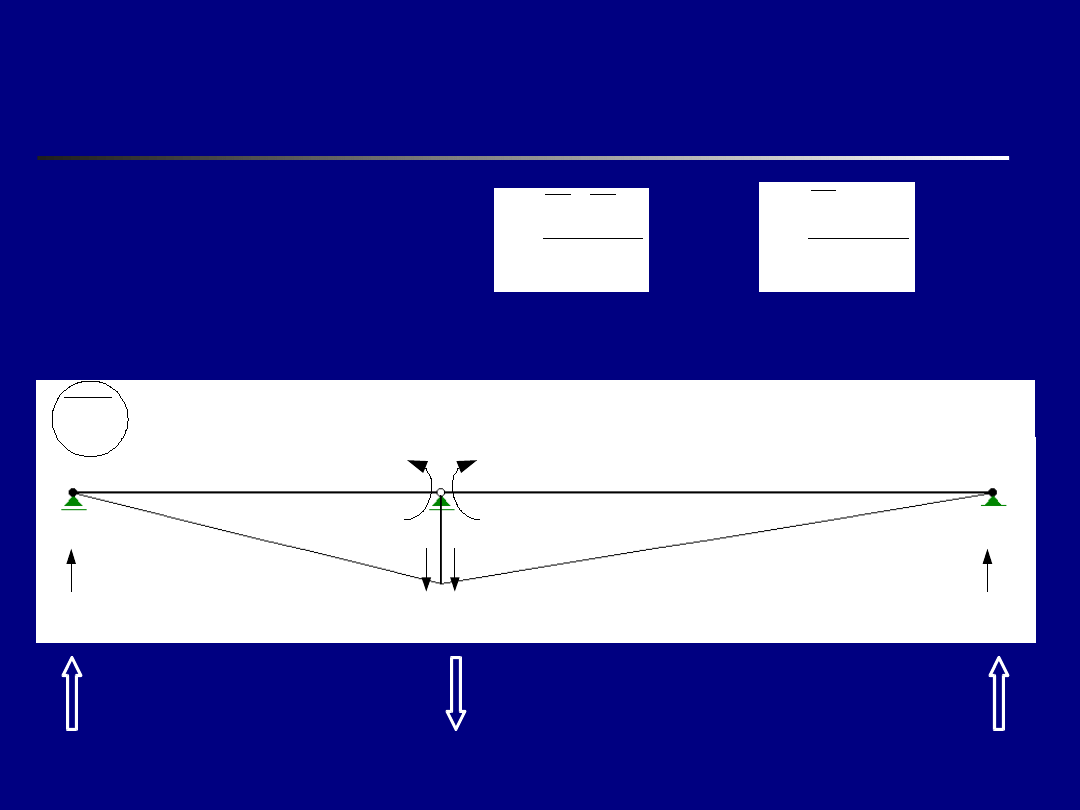
Aby wyliczyć człony:
oraz
Obliczenie elementów
i
p
1,0
1
/
4
1
/
6
l =
4,0
l =
6,0
1
/
6
M
1
1
/
4
1,0
1,0
#1
#2
#3
R
21
=1/4+1/6=10/24
R
31
=1/6
R
11
=1/4
potrzebne są reakcje w poszczególnych podporach od
obciążeń jednostkowych oraz obciążenia zewnętrznego.
s
s
sp
si
k
R
R
s
s
sk
si
k
R
R
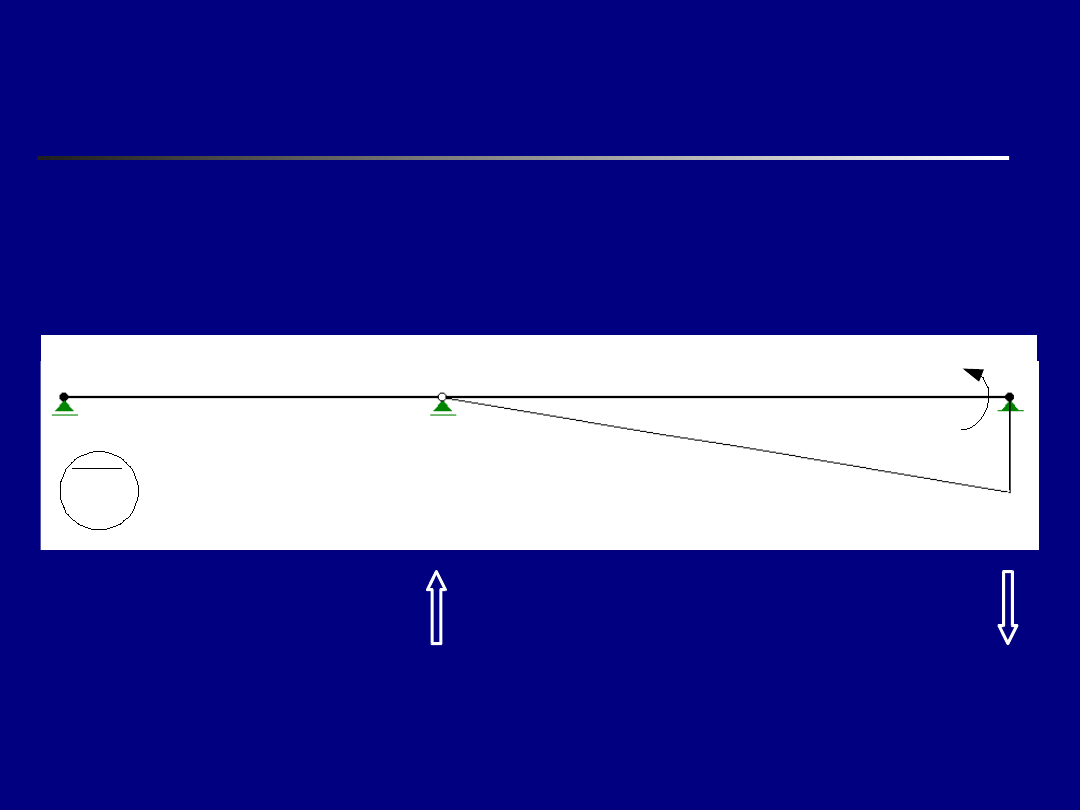
Obliczenie elementów
i
p
– c.d.
R
22
=1/6
R
32
=1/6
1,0
M
2
1,0
#1
#3
#2
R
12
=0
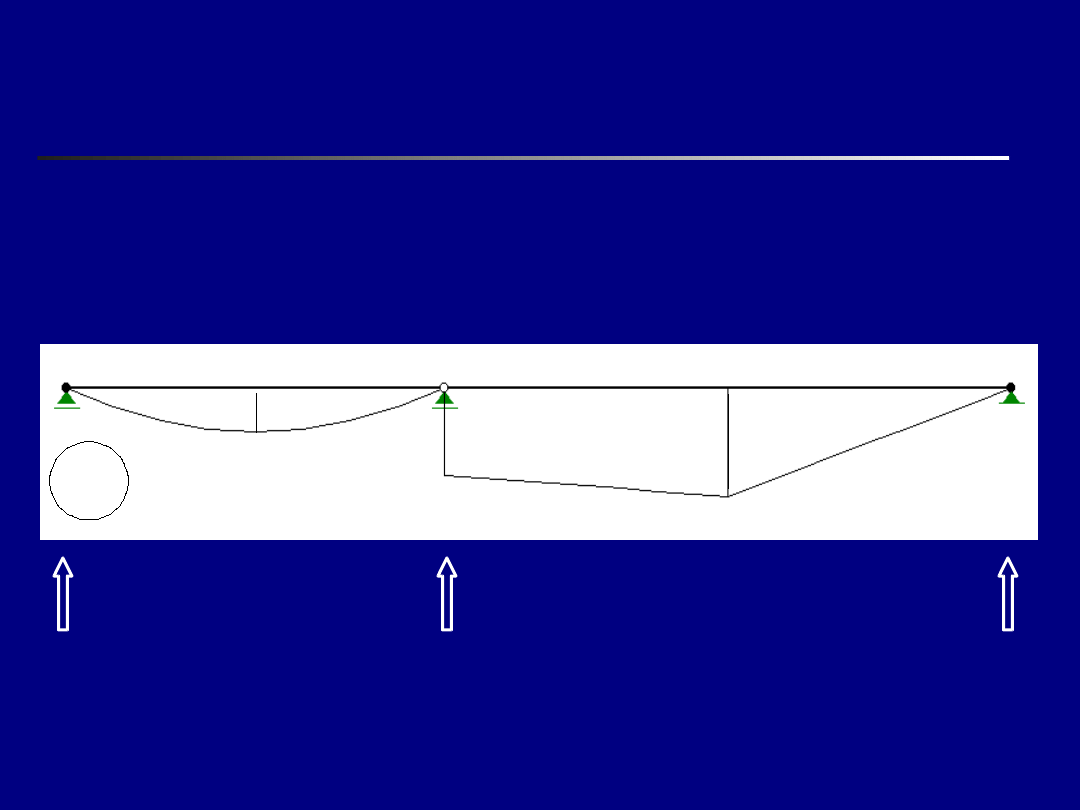
Obliczenie elementów
i
p
– c.d.
2,0
5,0
4,0
M
p
#1
#3
#2
R
2p
=2.333
R
3p
=1.667
R
1p
=2.0

Obliczenie elementów
i
p
– c.d.
Po rozpisaniu względem indeksów, otrzymujemy, że
dodatkowe człony dla poszczególnych elementów
wynoszą:
11
(R
1
1
·R
1
1
+ R
2
1
·R
2
1
)/k
Uwaga:
uwzględniamy tylko podpory
#1
i
#2
, gdyż
tylko tam są więzy sprężyste
21
12
(R
1
1
·R
1
2
+ R
2
1
·R
2
2
)/k
22
(R
1
2
·R
1
2
+ R
2
2
·R
2
2
)/k
1p
(R
1
1
·R
1
p +
R
2
1
·R
2
p
)/k
2p
(R
1
2
·R
1
p +
R
2
2
·R
2
p
)/k

Obliczenie elementów
i
p
– c.d.
Podstawiając i uwzględniając zwroty reakcji (
jako
+
)
otrzymujemy dodatkowe człony dla:
11
(
1
/
4
·
1
/
4
+ (-
10
/
24
) · (-
10
/
24
)) /k
21
12
(0 + (-
10
/
24
)
·
1
/
6
) /k
22
( 0 +
1
/
6
·
1
/
6
) /k
1p
(
1
/
4
· 2.0+ (-
10
/
24
)
· 2.333) /k
2p
(0 +
1
/
6
· 2.333) /k
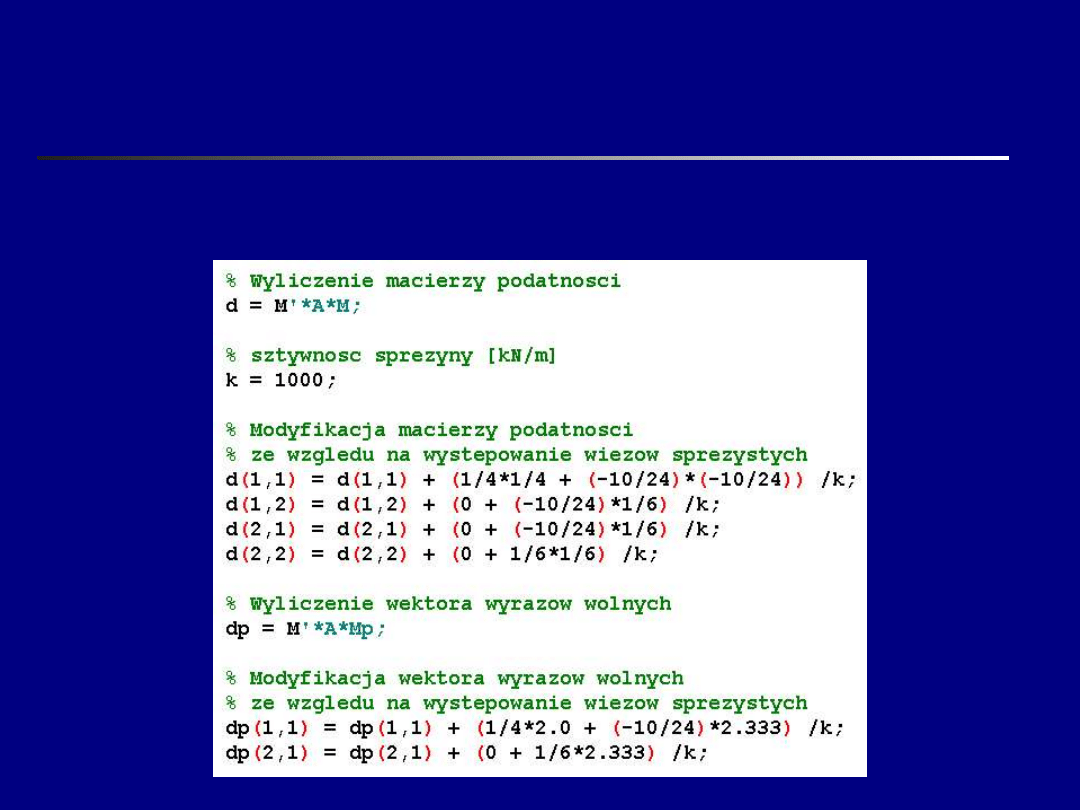
Zmiany w skrypcie
W skrypcie dopisujemy linie modyfikujące
dotychczasowe elementy macierzy i wektora
p
:

Zmiany w skrypcie – c.d.
Aby wyniki przedstawionych na poprzednim slajdzie
obliczeń były prawidłowe należy zmodyfikować fragment
skryptu kluczowy dla wyliczenia macierzy A, a co za tym
idzie macierzy i wektora
p
.
Należy pamiętać o podaniu wartości modułu Young’a
i wartości momentu bezwładności przekroju oraz
uwzględnieniu ich w podmacierzach macierzy A
używanej do całkowania metodą Simpsona.
s
s
sp
si
p
i
ip
s
s
sk
si
k
i
ik
ds
ds
k
R
R
EI
M
M
k
R
R
EI
M
M
Zmiany w skrypcie – c.d.
Do tej pory nie było konieczne podawanie wartości
iloczynu EI (uwzględniano jedynie stosunek sztywności
poszczególnych przęseł belki), gdyż ten jako stały
mnożnik upraszczał się przy wyliczaniu X= -
·
p
.
Obecnie to uproszczenie nie może nastąpić, gdyż EI
nie występuje w członach wzoru Maxwella-Mohra
wykorzystywanych do wyliczenia przemieszczeń układu
wynikających z istnienia więzów sprężystych.
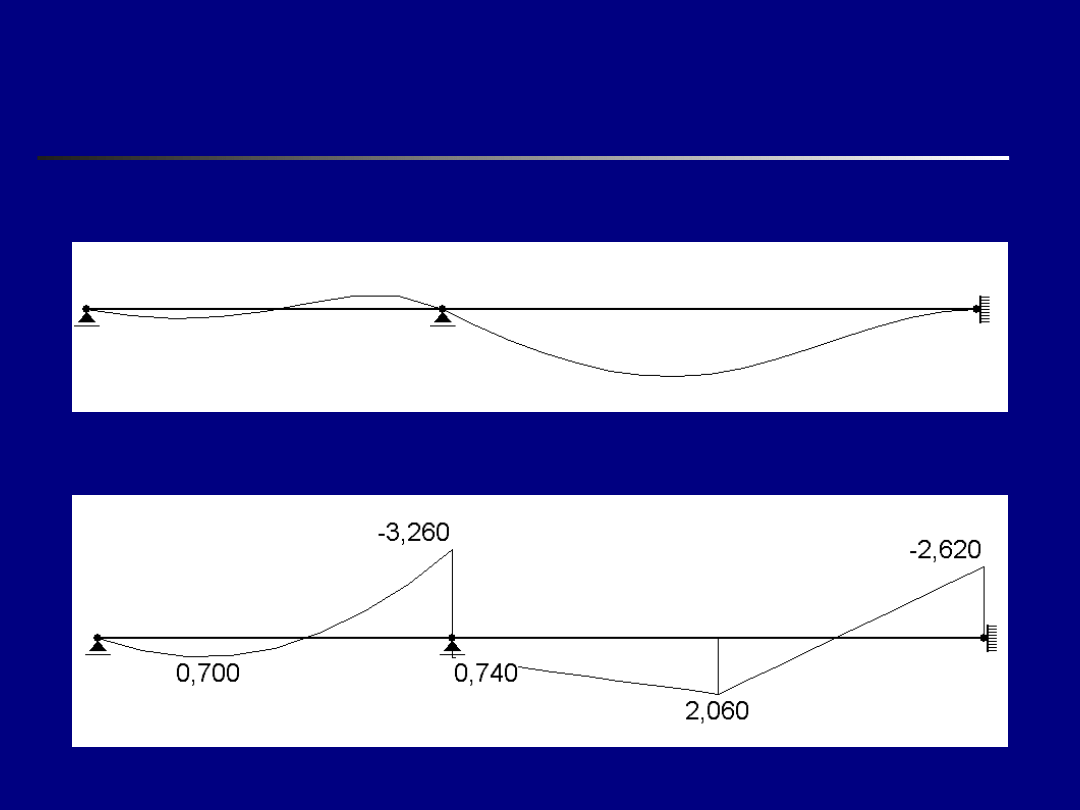
Wyniki dla obciążenia statycznego – układ o
więzach niepodatnych
Przemieszczenia
Momenty zginające [kNm]
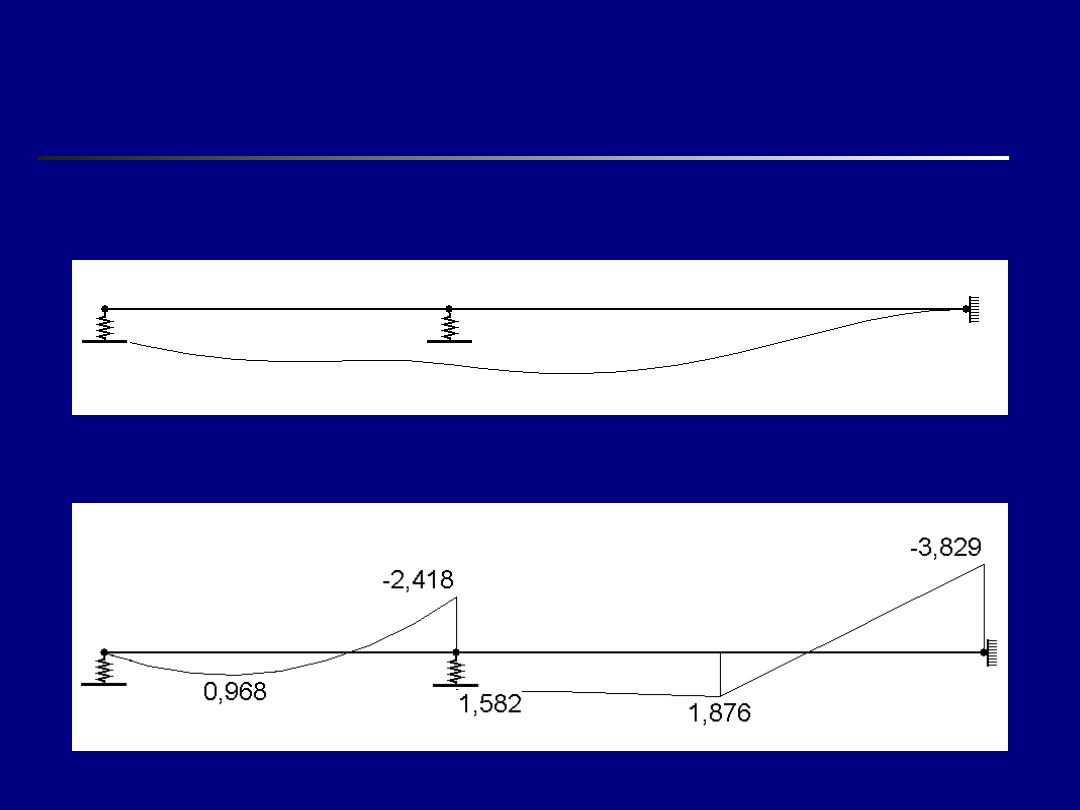
Wyniki dla obciążenia statycznego – układ o
więzach sprężystych
Przemieszczenia
Momenty zginające [kNm]
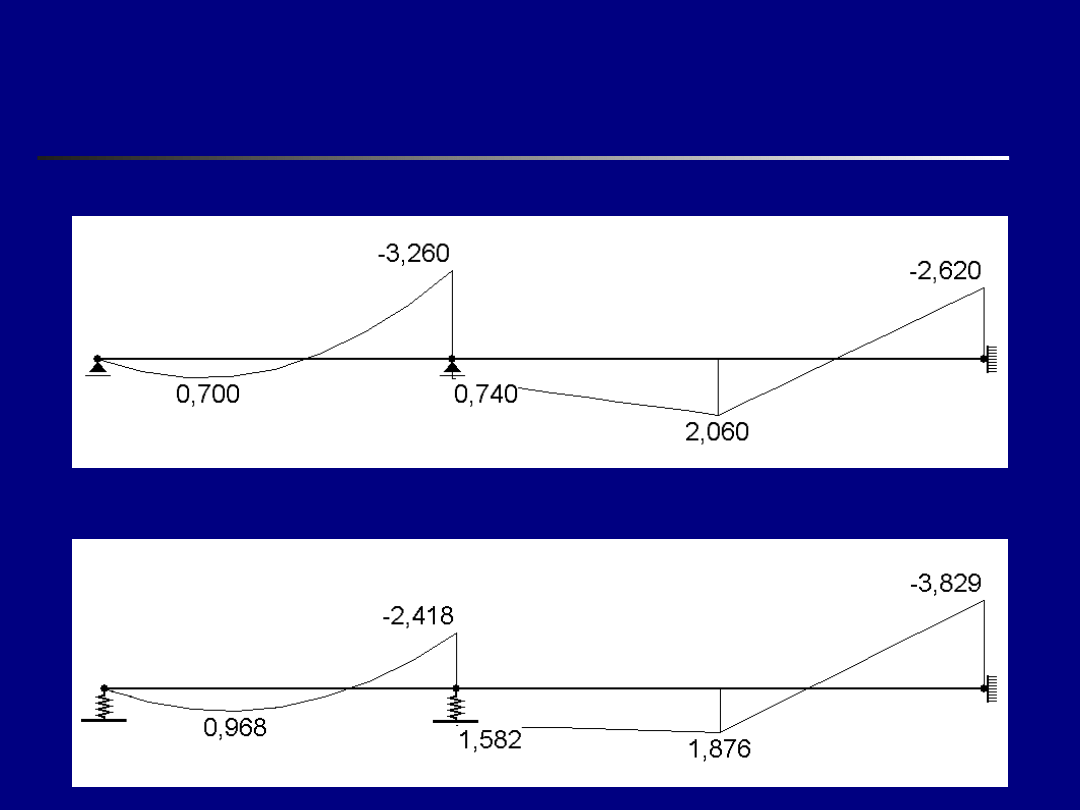
Porównanie wykresów
Momenty zginające [kNm] – belka z podporami
sprężystymi
Momenty zginające [kNm]

Wnioski
Przy
rozwiązywaniu
układów
statycznie
niewyznaczalnych
o
więzach
niepodatnych,
poddanych
obciążeniu
statycznemu
wystarczy
uwzględnić
stosunki
sztywności
pomiędzy
poszczególnymi elementami.
W przypadku układów o więzach sprężystych należy
pamiętać o tym, że otrzymane rozwiązanie jest
zależne od iloczynu EI, tj. materiału, z którego
wykonana
jest
konstrukcja,
charakterystyk
geometrycznych elementów oraz sztywności więzów
podporowych.
Sztywność,
podatność
więzów
podporowych
(podłoża, konstrukcji wsporczej) przyjmuje się
zgodnie z odpowiednimi normami lub oblicza.
Uwzględnienie sprężystości więzów podporowych
prowadzi do znaczących różnic w rozwiązaniu
zadania statyki konstrukcji.

Sprawozdanie
Sprawozdanie z tej części projektu powinno zawierać:
1)
schemat belki z uwzględnieniem podpór sprężystych
2)
rozpisane dodatkowe człony dla elementów macierzy
podatności tak, jak pokazano to na stronie 11.
3)
wyrażenia na obliczanie elementów wektora
p
tak,
jak to pokazano na stronie 8.
4)
wykres momentów zginających od obciążenia
statycznego dla belki o podporach niepodatnych –
przerysować z części pierwszej projektu
5)
wykres momentów zginających od obciążenia
statycznego dla belki o podporach sprężystych
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron