Belki na podłożu sprężystym

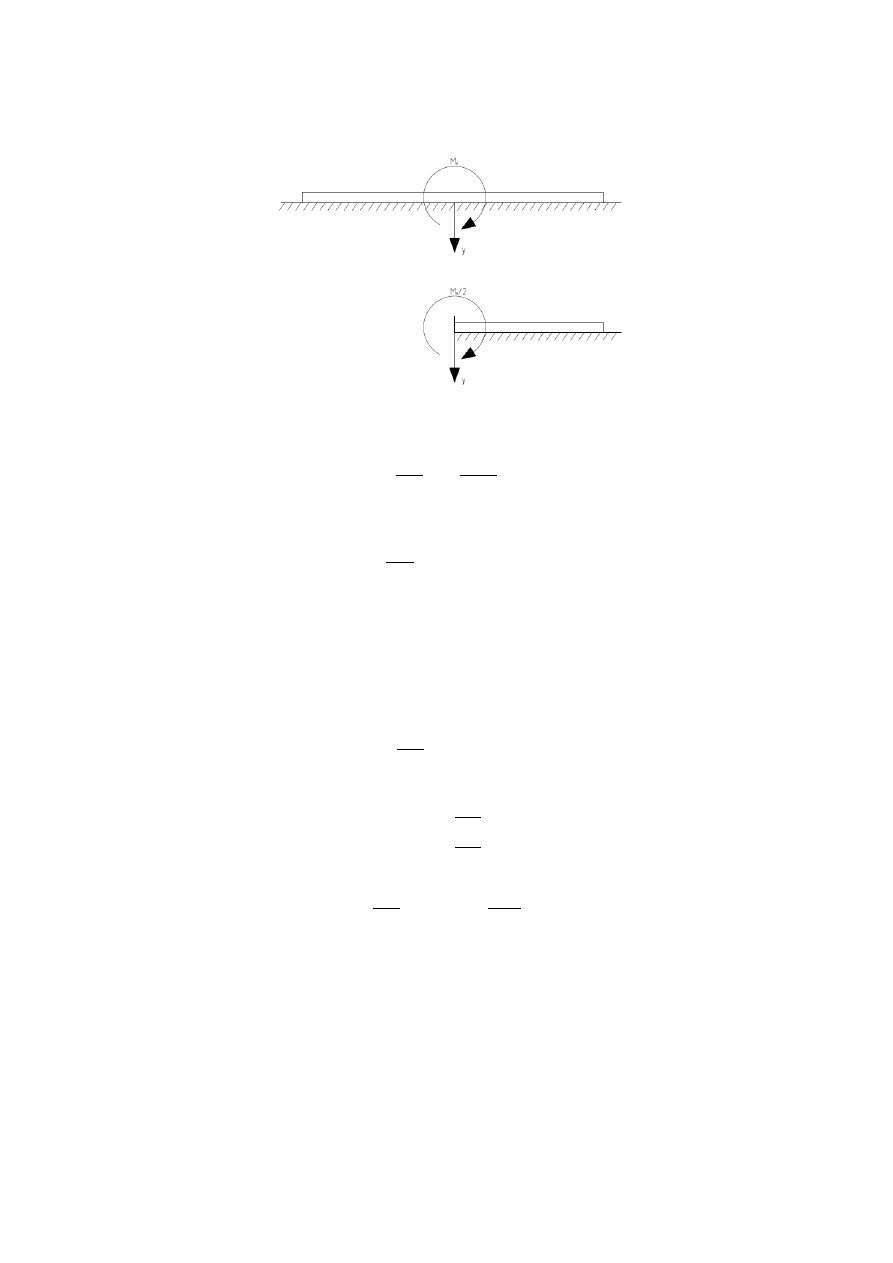
1. Nieskończenie długą belkę o stałej sztywności na zginanie, spoczywającą na podłożu sprężystym, obciążono

parą sił o momencie M

0

. Wyznaczyć równanie ugiętej osi belki i zapisać warunki brzegowe. Dane: EI, M

0

, k

Zapiszmy równanie różniczkowe osi ugiętej belki:

Dwukrotnie różniczkując i mnożąc przez EI, otrzymamy:

Gdzie:

k- moduł podłoża sprężystego

Podstawiając:

Podstawmy:

√

Otrzymaliśmy R.R linii ugięcia belki na podłożu sprężystym

Rozwiązanie tego R.R będzie typu:

Zakładamy że:

1) Jeżeli x dąży do nieskończoności, to C

1

=C

2

=0 (warunek skończoności ugięcia belki, w przeciwnym wypadku

wyrażenie w nieskończoności osiągnęło by wartość nieskończoną, co nie ma sensu)

2) Z racji iż w nieskończoności ugięcie belki y=0, całka szczególna powyższego równania równa się 0

Uwzględniając powyższe założenia, otrzymujemy rozwiązanie R.R o postaci:

Zapiszmy warunki brzegowe:

{

Co wynika bezpośrednio z rysunku. Podstawiając pierwszy W.B do równania:

Aby podstawić wartość momentu gnącego, zróżniczkujemy dwukrotnie równanie ugięcia belki

I drugi raz, po przekształceniach:

Podstawiamy do równania z uwzględnieniem 2 W.B:

Ostatecznie:

Podstawiając stałe całkowania, otrzymujemy równanie linii ugięcia belki:

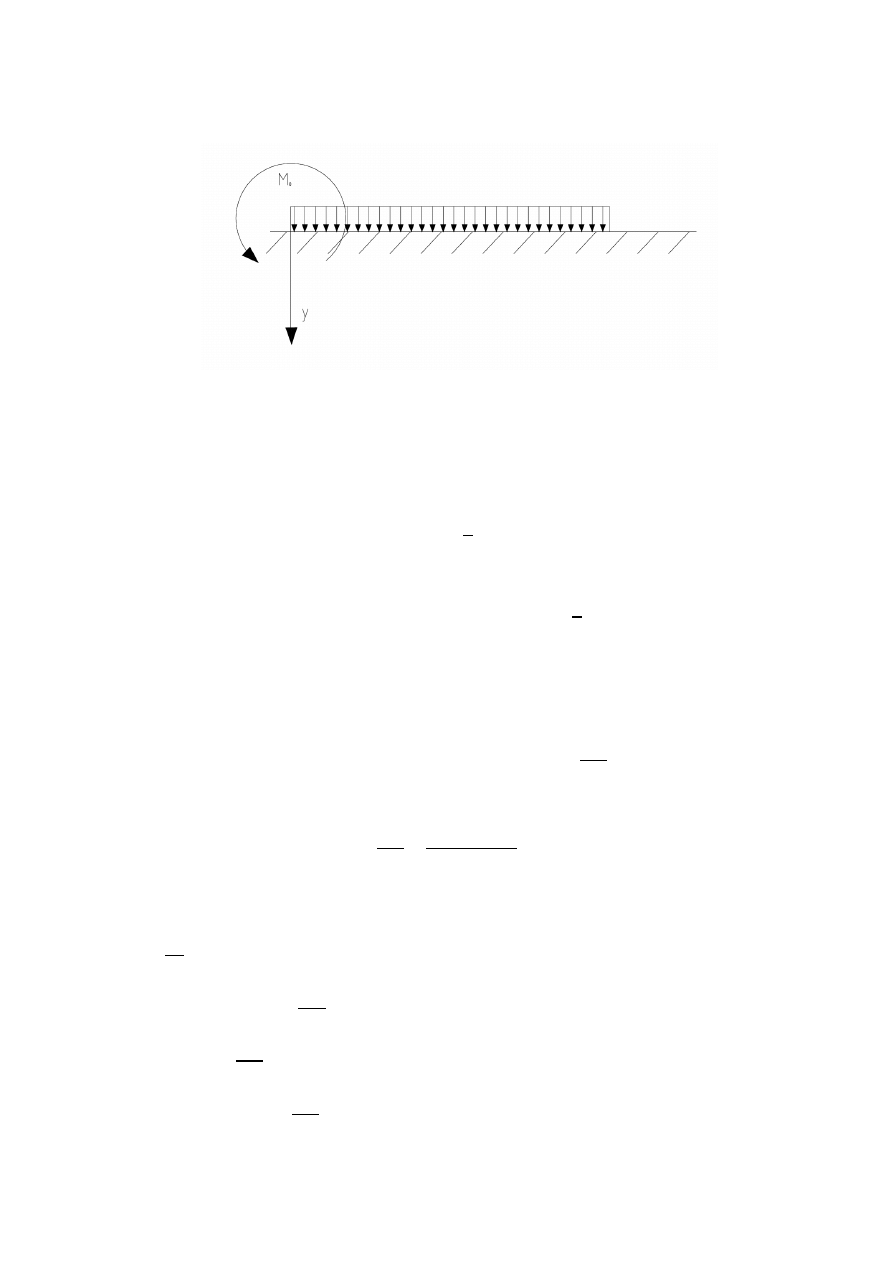
2. Nieskończenie długą belkę o stałej sztywności na zginanie, spoczywającą na podłożuy sprężystym, obciążono

obciążeniem ciągłym q

0

i momentem M

0

. Wyznaczyć równanie ugiętej osi belki i zapisać warunki brzegowe.

Analogicznie, jak w przypadku zadania poprzedniego rozwiązanie R.R, będące równaniem osi ugięcia, będzie postaci:

Z tą różnicą, że całka szczególna, z racji iż belka obciążona jest obciążeniem ciągłym, będzie równa:

Więc, rozwiązanie będzie postaci:

Warunki brzegowe:

{

⇒ ⇒

Drugi warunek brzegowy wynika z zależności

Aby podstawić powyższe warunki brzegowe należy przeprowadzić czterokrotne różniczkowanie równania ugięcia osi
belki:

Podstawiając warunki brzegowe, otrzymujemy:

{

(

)

{

Ostatecznie, równanie ugięcia osi belki przyjmie postać:

(

)