1
MACIERZE I WYZNACZNIKI
Def. 3.1
Macierzą rzeczywistą (zespoloną) wymiaru m
n, gdzie m, n
N, to prostokątna tablica złożona z mn liczb
rzeczywistych (zespolonych) ustawionych w m wierszach i n kolumnach.
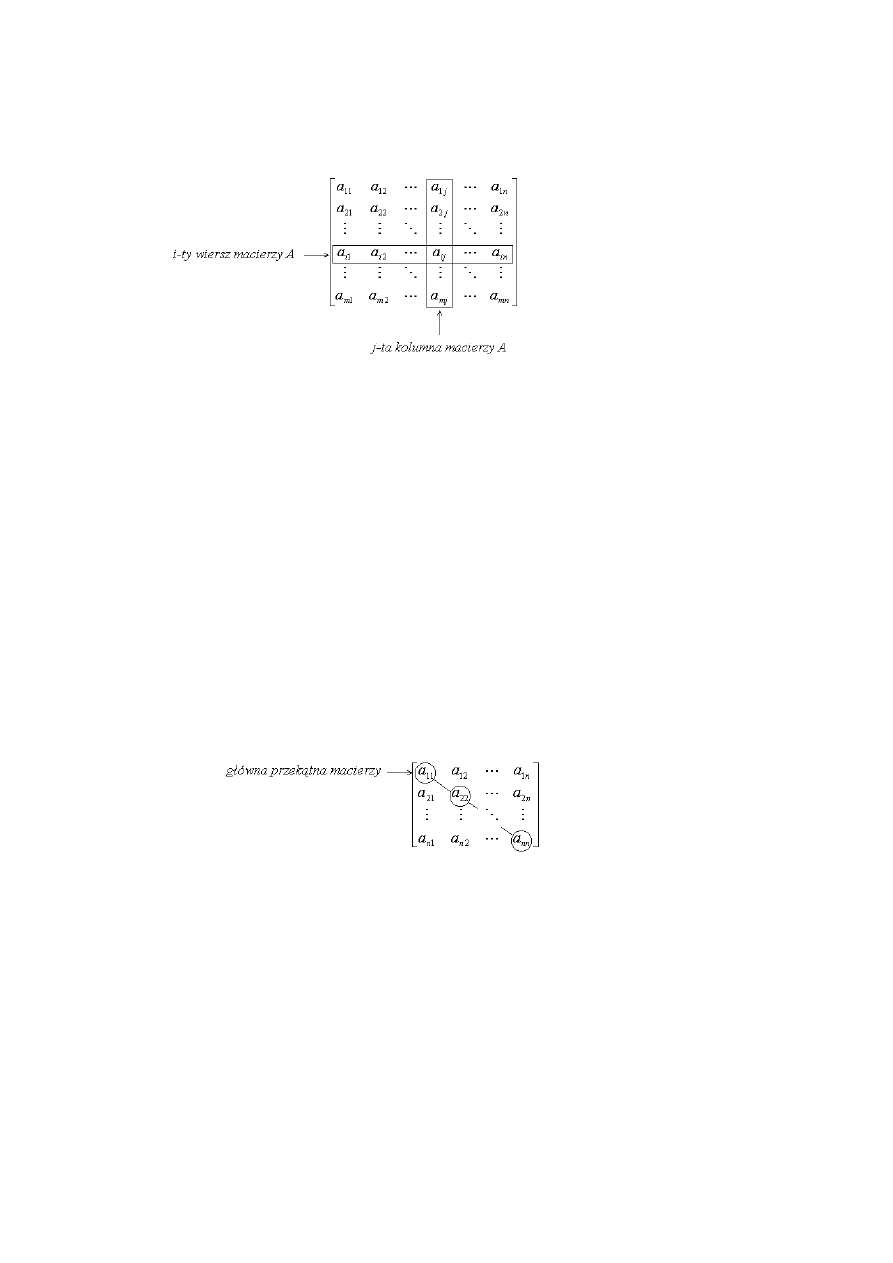
a
ij
- element macierzy A stojący w i–tym wierszu oraz w j–tej kolumnie
Wymiar macierzy - liczba określająca ilość wierszy i ilość kolumn, co zapisujemy jako m
n.
Macierze oznaczamy dużymi literami alfabetu np. A, B, X itp., lub w postaci
n
m
ij
a
]
[
, [a
ij
], gdy znany jest jej
wymiar.
Def. 3.2
Macierze A i B są równe, gdy mają te same wymiary m
n oraz a
ij
= b
ij
dla każdego 1
i
m, 1
j
n.
Def. 3.3
1. Macierz zerowa - macierz wymiaru m
n, której wszystkie elementy są równe 0. Oznaczamy ją
n
m
0
lub przez 0, gdy znamy jej wymiar.
0
0
0
0
0
0
0
0
0
2. Macierz kwadratowa - macierz, której liczba wierszy równa się liczbie kolumn m = n. Liczbę wierszy
(kolumn) nazywamy stopniem macierzy kwadratowej. Elementy macierzy, które mają ten sam numer
wiersza co kolumny, tworzą główną przekątną macierzy.
3. Macierz trójkątna dolna - macierz kwadratowa stopnia n
2, w której wszystkie elementy stojące nad
główną przekątną są równe 0.
nn
n
n
n
a
a
a
a
a
a
a
a
a
a
3
2
1
33
32
31
22
21
11
0
0
0
0
0
0
Macierz trójkątna górna
nn
n
n
n
a
a
a
a
a
a
a
a
a
a
0
0
0
0
0
0
3
33
2
23
22
1
13
12
11

2
4. Macierz diagonalna lub przekątniowa - macierz kwadratowa stopnia n, w której wszystkie elementy,
oprócz tych na głównej przekątnej są równe 0.
nn
a
a
a
a
0
0
0
0
0
0
0
0
0
0
0
0
33
22
11
5. Macierz jednostkowa - macierz diagonalna stopnia n, w której wszystkie elementy głównej przekątnej są
równe 1. Oznaczamy ją przez I
n
lub przez I, gdy znany jest jej stopień.
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
6. Niech A = [a
ij
] będzie macierzą wymiaru m
n. Macierzą transponowaną do macierzy A nazywamy
macierz B = [b
ij
] wymiaru n
m określoną wzorem:
ij
ji
b
a
dla 1
i
m oraz 1
j
n.
Macierz transponowaną do macierzy A oznaczamy A
T
.
Przy transponowaniu, kolejne wiersze macierzy wyjściowej stają się kolejnymi kolumnami macierzy
transponowanej.
7. Niech A będzie macierzą kwadratową. Macierz A jest symetryczna wtedy i tylko wtedy, gdy
A
A
T
.
Macierz jest symetryczna, gdy jej elementy położone symetrycznie względem głównej przekątnej są sobie
równe.
8. Niech A będzie macierzą kwadratową. Macierz A jest antysymetryczna wtedy i tylko wtedy, gdy
A
A
T
.
Macierz jest antysymetryczna, gdy jej elementy położone symetrycznie względem głównej przekątnej
różnią się tylko znakiem, a elementy głównej przekątnej są równe 0.
Działania na macierzach
Def. 3.4
Niech A = [a
ij
]
m
n
i B = [b
ij
]
m
n
.
Sumą (różnicą) macierzy A i B nazywamy macierz C = [c
ij
], której elementy określone są wzorem:
C = A + B
ij
ij
ij
c
a
b
, 1
i
m, 1
j
n,
C = A – B
ij
ij
ij
c
a
b
, 1
i
m, 1
j
n.
Def. 3.5
Niech A = [a
ij
]
m
n
oraz niech
R
C
.
Iloczynem macierzy A przez liczbę
nazywamy macierz B = [b
ij
], której elementy są określone wzorem:
B =
A
ij
ij
b
a
, 1
i
m, 1
j
n.

3
Własności działań na macierzach
Niech A, B, C będą dowolnymi macierzami tego samego wymiaru rzeczywistymi lub zespolonymi oraz niech
,
będą odpowiednio liczbami rzeczywistymi lub zespolonymi. Wtedy
1. A + B = B + A
5.
(A + B) =
A +
B
2. A + (B + C) = (A + B) + C
6. (
+
)A =
A +
A
3. A + 0 = 0 + A = A
7. 1
A = A
4. A + (–A) = 0
8. (
) A =
(
A)
Def. 3.6
Niech A = [a
ij
]
m
n
, B = [b
ij
]
n
k
.
Iloczynem macierzy A i B nazywamy macierz C = [c
ij
], wymiaru m
k, której elementy określone są wzorem:
C = AB
1 1
2 2
...
ij
i
j
i
j
in nj
c
a b
a b
a b
, 1
i
m, 1
j
k.
A
n
czynników
n
A
AA...
Iloczyn macierzy A i B można obliczyć tylko wtedy, gdy liczba kolumn macierzy A równa się liczbie wierszy
macierzy B.
Mnożenie macierzy kwadratowych nie jest przemienne, na ogół AB
BA.
Własności iloczynu macierzy
1. Niech A
m
n
, B
n
k
i C
n
k
. Wtedy
AC
AB
C
B
A
)
(
.
2. Niech A
m
n
, B
m
n
, C
n
k
. Wtedy
BC
AC
C
B
A
)
(
.
3. Niech A
m
n
, B
n
k
oraz niech
R
C
. Wtedy
)
(
)
(
)
(
AB
B
A
B
A
.
4. Niech A
m
n
, B
n
k
, C
k
l
. Wtedy
)
(
)
(
BC
A
C
AB
.
5. Niech A
m
n
. Wtedy
A
A
I
AI
m
n
.
Własności transpozycji macierzy
1. Niech A
m
n
, B
m
n
. Wtedy
T
T
T
B
A
B
A
)
(
.
2. Niech A
m
n
oraz niech
R
C
.. Wtedy
A
A
T
T
oraz
T
T
A
A
.
3. Niech A
m
n
, B
n
k
. Wtedy
T
T
T
A
B
AB
)
(
.
4. Niech A
n
n
oraz niech r
N. Wtedy
r
T
T
r
A
A
)
(
)
(
.
Wyznacznik macierzy
Def. 3.7
Wyznacznikiem macierzy kwadratowej
i j
n n
A
a
(macierzy stopnia n ) nazywamy liczbę rzeczywistą
(zespoloną): det lub
A
A określoną następująco:
1) dla
1
n
11
11
det
det
A
a
a
2) dla
2
n
11
12
1
1 1
1 2
1
21
22
2
11
11
12
12
1
1
1
2
det
det
1
1
...
1
n
n
n
n
n
n
n
nn
a
a
a
a
a
a
A
a
M
a
M
a
M
a
a
a
ij
M - wyznacznik macierzy stopnia
1
n
powstały ze skreślenia w macierzy A i – tego wiersza oraz j – tej
kolumny. Wyznacznik taki nazywamy minorem.
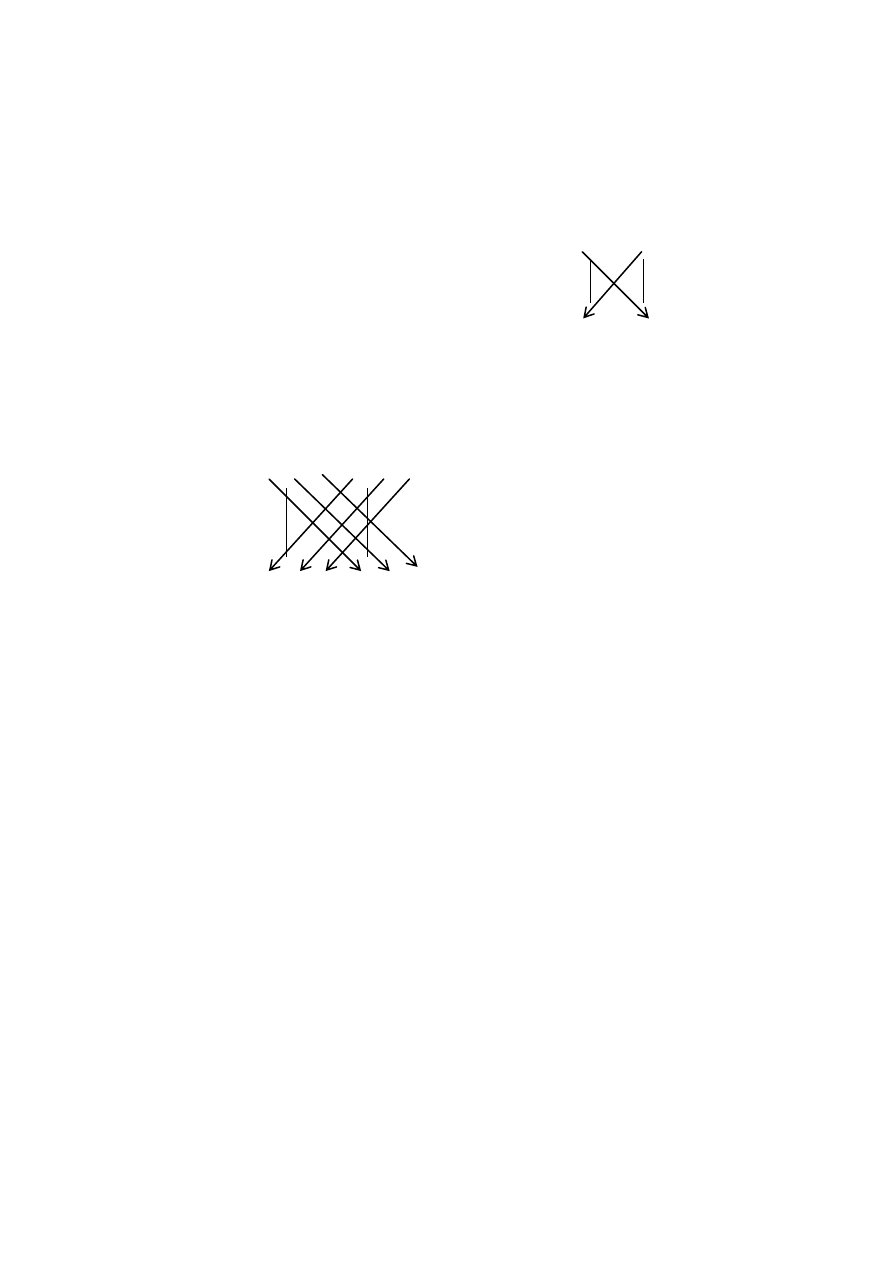
4
Def. 3.8
Niech będzie dana macierz
,
2
n n
A
n
.
Dopełnieniem algebraicznym elementu
i j
a macierzy A nazywamy liczbę
i j
D określoną następująco:
1
i j
i j
i j
D
M
Reguły obliczania wyznaczników stopnia 2 – go
Jeśli
2 2
, gdzie
, , ,
; ( , , ,
)
a
b
A
a b c d
a b c d
c
d
R
C
, to det
a
b
A
ad
cb
c
d
Reguły obliczania wyznaczników stopnia 3 – go (metoda Sarrusa)
Jeśli
3 3
, , , , ,
, , ,
,
, gdzie
( , , , , ,
, , ,
);
a
b
c
a b c d e f g h i
A
d
e
f
a b c d e f g h i
g
h
i
R
C
, to
det
a
b
c
a
b
A
d
e
f
d
e
aei
bfg
cdh
ceg
afh bdi
g
h
i
g
h
Reguły obliczania wyznaczników stopnia wyższego niż trzeci
Tw.3.1 (Twierdzenie Laplace’a)
Wyznacznik macierzy kwadratowej
,(
2)
n n
A
n
jest równy sumie iloczynów elementów dowolnego wiersza
(kolumny) i odpowiadających tym elementom dopełnień algebraicznych.
Niech A będzie macierzą kwadratową stopnia n
2 oraz niech liczby 1
i, j
n.
Wyznacznik macierzy A można obliczyć ze wzorów:
1. Rozwinięcie Laplace’a względem i – tego wiersza przedstawia się następująco:
1
1
2
2
det
...
i
i
i
i
i n
i n
A
a D
a D
a D
.
2. Rozwinięcie Laplace’a względem j – tej kolumny przedstawia się następująco:
1
1
2
2
det
...
j
j
j
j
n j
n j
A
a D
a
D
a
D
.
Własności wyznaczników
1. Wyznacznik macierzy kwadratowej mającej kolumnę (wiersz) złożoną z samych zer jest równy 0.
2. Wyznacznik macierzy kwadratowej zmieni znak jeżeli między sobą przestawimy dwie kolumny (wiersze).
3. Wyznacznik macierzy kwadratowej mającej dwie jednakowe kolumny (wiersze) jest równy 0.
4. Jeżeli wszystkie elementy pewnej kolumny (wiersza) macierzy kwadratowej zawierają wspólny czynnik, to
czynnik ten można wyłączyć przed wyznacznik tej macierzy.
+
-
+ + +
- - -
5
11
12
1
1
11
12
1
1
21
22
2
2
21
22
2
2
1
2
1
2
i
n
i
n
i
n
i
n
n
n
ni
nn
n
n
ni
nn
a
a
ca
a
a
a
a
a
a
a
ca
a
a
a
a
a
c
a
a
ca
a
a
a
a
a
.
Ponadto
11
12
1
1
11
12
1
1
21
22
2
2
21
22
2
2
1
2
1
2
i
n
i
n
i
n
i
n
n
n
n
ni
nn
n
n
ni
nn
ca
ca
ca
ca
a
a
a
a
ca
ca
ca
ca
a
a
a
a
c
ca
ca
ca
ca
a
a
a
a
.
5. Wyznacznik macierzy nie zmieni się, jeżeli do elementów dowolnej kolumny (wiersza) dodamy odpowiadające
im elementy innej kolumny (innego wiersza) tej macierzy pomnożone przez dowolną liczbę.
6. Wyznacznik macierzy trójkątnej górnej lub dolnej jest równy iloczynowi elementów stojących na głównej
przekątnej.
11
11
12
13
1
21
22
22
23
2
11
22
1
2
3
0
0
0
0
0
0
...
0
0
0
n
n
nn
n
n
n
nn
nn
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
7. Wyznaczniki macierzy kwadratowej i jej transpozycji są równe: det
det
T
A
A
Tw.3.2 (Twierdzenie Cauchy’ego)
Niech będą dane macierze:
n
n
n
n
B
A
,
. Wówczas wyznacznik iloczynu macierzy jest równy iloczynowi
wyznaczników tych macierzy, tzn.
det
det
det
A B
A
B
.
Macierz odwrotna
Def. 3.9
Niech A będzie macierzą stopnia n.
Macierzą odwrotną do macierzy A nazywamy macierz
1
A
spełniającą warunek:
1
1
n
A A
A
A
I ,
I
n
- macierz jednostkowa stopnia n.
Def. 3.10
Macierz kwadratową A nazywamy macierzą:
osobliwą, gdy det
0
A
,
nieosobliwą, gdy det
0
A
.
Tw.3.3 Warunek odwracalności macierzy
Macierz kwadratowa jest odwracalna wtedy i tylko wtedy, gdy jest nieosobliwa.
Tw.3.4 (o postaci macierzy odwrotnej)
Niech macierz A = [a
ij
] stopnia n będzie nieosobliwa. Wtedy
1
1
det
T
D
A
A
A
,
D
A - macierz dopełnień algebraicznych elementów a
ij
macierzy A.
Własności macierzy odwrotnych
Niech będą dane macierze odwracalne:
,
n n
n n
A
B
,liczby:
R
, (
C
),
N
n
.

6
Wówczas macierze
1
,
,
,
,
T
n
A
A
AB
A A
są również odwracalne i zachodzą następujące równości:
1.
1
1
det
det
A
A
2.
1
1
A
A
3.
1
1
T
T
A
A
4.
1
1
1
A
A
5.
1
1
1
AB
B A
6.
1
1
n
n
A
A
Równania macierzowe
Trzy podstawowe typy równań macierzowych:
1. Równanie: A X
B
,
n n
A
- macierz odwracalna ( det
0
A
),
B - macierz odpowiedniego wymiaru
X - niewiadoma macierz.
Wówczas rozwiązując to równanie postępujemy następująco:
A X
B
1
1
A
A X
A
B
1
X
A
B
I
1
X
A
B
2. Równanie: X A B
Wówczas macierz X znajdujemy wykorzystując wzór:
1
X
B A
3. Równanie: A X B C
Wówczas macierz X znajdujemy wykorzystując wzór:
1
1
X
A
C B
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron