
Minimalizacja funkcji (część 2)
1
Przedmioty prowadzone w ramach
Programu Rozwoju WSFiZ w Białymstoku realizowane są w ramach
Programu Operacyjnego Kapitał Ludzki, Priorytet IV Szkolnictwo wyższe i nauka, Poddziałanie 4.1.1
Wzmocnienie potencjału dydaktycznego uczelni, współfinansowanego ze środków
Europejskiego Funduszu Społecznego (POKL.04.01.01-00-030/08)
5. Minimalizacja funkcji
(część 2)
Spis treści
5.3
Realizacja funkcji z elementów I, LUB i NIE
Ostatnią faza realizacji projektu układu przełączającego jest jego implementacja fizyczna, która
zazwyczaj realizowana jest na podstawie schematu przedstawiającego układ za pomocą
dostępnych na rynku elementów. W rozdziale tym założymy, że są nimi elementy I, LUB i NIE.
Od razu zaznaczmy, że znaczenie praktyczne takich realizacji jest bardzo ograniczone, gdyż
rynek zdominowany jest przez elementy NAND i NOR. Są jednak co najmniej dwie przesłanki,
dzięki którym zaproponowane założenie ma sens:
1. Uzyskanie schematów z elementy I, LUB i NIE na podstawie kanonicznych i
niekanonicznych postaci normalnych funkcji przełączających jest naturalne i
natychmiastowe;
2. Istnieją proste procedury pozwalające na mechaniczne przekształcenie układów
zbudowanych z elementów I, LUB i NIE na równoważne im układy złożone z elementów
NAND albo NOR (problematyce tej poświęcony jest kolejny rozdział).
Zaczniemy od przedstawienia symboli elementów I, LUB i NIE używanych w tego rodzaju
projektach. Z kilku powszechnie akceptowanych standardów na rysunku 5.7 pokazano ten, który
będzie używany w dalszej części tego wykładu. Rysunek 5.7a) i 5.7b) prezentuje symbole dla
dwu-argumentowych funkcji iloczynu i sumy. Przy większej liczbie argumentów należy
stosować zasadę, że każda kreska z lewej strony symbolu odpowiada jednej zmiennej
wejściowej. Symbolem negacji jest w zasadzie kropka, ale przyjęło się przedstawiać ją tak, jak na
rysunku.
a)
b)
c)
a
a
y = a∙b
y = a+b
a
y = a
b
b
Rysunek 5.7. Symbole oznaczające elementy I, LUB i NIE .
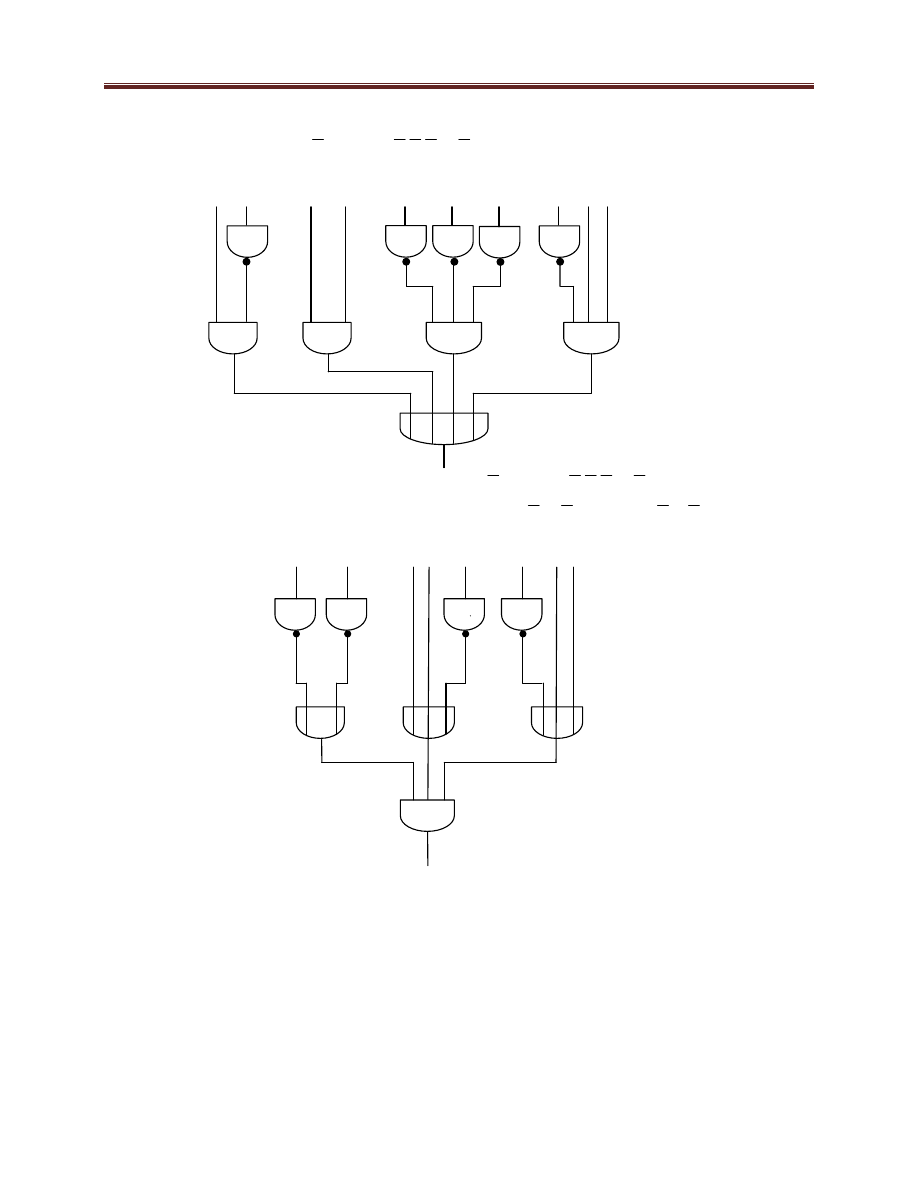
Minimalizacja funkcji (część 2)
2
Na rysuneku 5.8 (patrz niżej) pokazana została realizacja funkcji
y = x
1
x
4
+ x
1
x
3
+ x
1
x
3
x
4
+ x
2
x
3
x
4
.
x
1
x
4
x
1
x
3
x
1
x
2
x
3
x
2
x
3
x
4
III
-----------------------------------------------------------------------------------------------
II
-----------------------------------------------------------------------------------------------
I
Rysunek 5.8. Układ realizujący funkcję
y = x
1
x
4
+ x
1
x
3
+ x
1
x
3
x
4
+ x
2
x
3
x
4
.
A na rysunku 5.9 pokazana została realizacja funkcji y = (x
3
+ x
4
)(x
1
+ x
2
+ x
4
)( x
1
+ x
2
+ x
4
).
x
3
x
4
x
1
x
2
x
4
x
1
x
1
x
2
III
-----------------------------------------------------------------------------------------------
II
-----------------------------------------------------------------------------------------------
I
Rysunek 5.9. Układ realizujący funkcję (2).
Na obu rysunkach (5.8 i 5.9) zaznaczono przerywanymi liniami poziomymi umowną granicę
pomiędzy trzema dobrze wyróżnionymi grupami elementów I, LUB i NIE realizujących nie tylko
te, ale dowolne funkcje przełączające. Poziom trzeci zbudowany jest z elementów NIE. Realizują
one negacje zmiennych zanegowanych we wzorach funkcji. Jest ich tyle, ile negacji. Poziom
drugi tworzą: dla funkcji o normalnej postaci alternatywnej elementy AND, a dla funkcji o
normalnej postaci koniunkcyjnej elementy OR. Jest ich tyle, ile odpowiednio iloczynów i sum
występuje we wzorze. Poziom pierwszy tworzy jeden element – jest to OR dla funkcji o
normalnej postaci alternatywnej, a AND dla funkcji o normalnej postaci koniunkcyjnej.
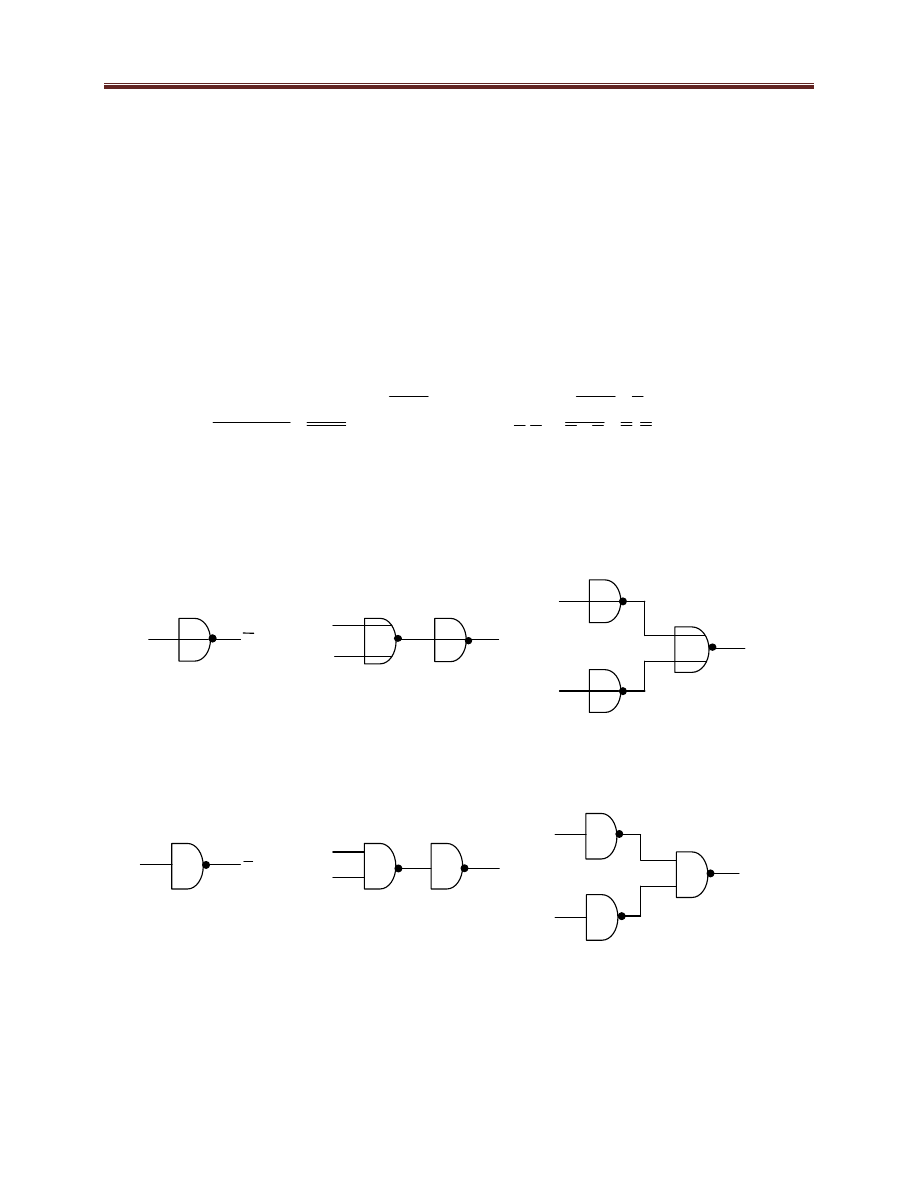
Minimalizacja funkcji (część 2)
3
5.4 Realizacja funkcj
i z elementów NAND i NOR
W praktyce inżynierskiej znakomita większość układów przełączających zrealizowana jest
przy użyciu elementów NAND i NOR. Powody takiego stanu rzeczy są liczne, a te najistotniejsze
to niższa (w porównaniu z elementami AND i OR) cena tych elementów wynikająca z ich
mniejszej wewnętrznej złożoności oraz to, że każdy z nich jest układem funkcjonalnie pełnym, co
istotnie upraszcza produkcję układów (zamiast trzech typów elementów potrzebny jest jeden).
Teoretycznie całość rozumowania dotyczącego realizacji funkcji przełączających można od
początku przeprowadzić przy założeniu, że dysponujemy wyłącznie elementami NAND i NOR.
Byłoby to jednak zbędna komplikacja, zwłaszcza (jak to za chwilę pokażemy) że przejście
(nazywane transformacją) z układów zrealizowanych na elementach AND, OR i NOT na układy
zrealizowane z elementów NAND i NOR jest trywialnie proste.
Przypomnijmy, że układ NOR (inaczej funkcja Peirce’a) spełnia następujące zależności.
fPe(a, b) = NOR(a, b) = a + b
NOR(a, 0) = a + 0 = a
NOR(a, b) = a + b = a + b
fPa(a, b) = a + b = a ∙ b = a ∙ b
Wnioski z tych wzorów są następujące:
1. Jeżeli sygnał 0 traktować jako brak sygnału, to negację realizuje 1-wejściowy układ NOR.
2. Sumę argumentów realizuje układ NOR z zanegowanym wyjściem.
3. Iloczyn argumentów realizuje układ NOR z zanegowanymi wejściami.
Rysunek 5.10 jest graficzną ilustracją wymienionych wniosków.
a
a
a
a
a+b
a∙b
b
b
Rysunek 5.10. Realizacja negacji, sumy i iloczynu z elementów NOR.
Analogicznych zależności można dowieść dla elementu NAND. Efekt tych dociekań pokazano
na rysunku 5.11.
a
a
a
a
a∙b
a+b
b
b
Rysunek 5.11. Realizacja negacji, iloczynu i sumy z elementów NAND.
Wnioski 1 – 3 można stosować wprost do schematów złożonych z elementów I, LUB i NIE
zamieniając te elementy na elementy NOR albo NAND. Na zakończenie takiego procesu należy
przeprowadzić pewne dodatkowe operacje, polegające np. na usunięciu zdwojonych negacji
(negacja negacji daje w rezultacie pierwotny sygnał). Metoda taka nosi nazwę transformacji
Minimalizacja funkcji (część 2)
4
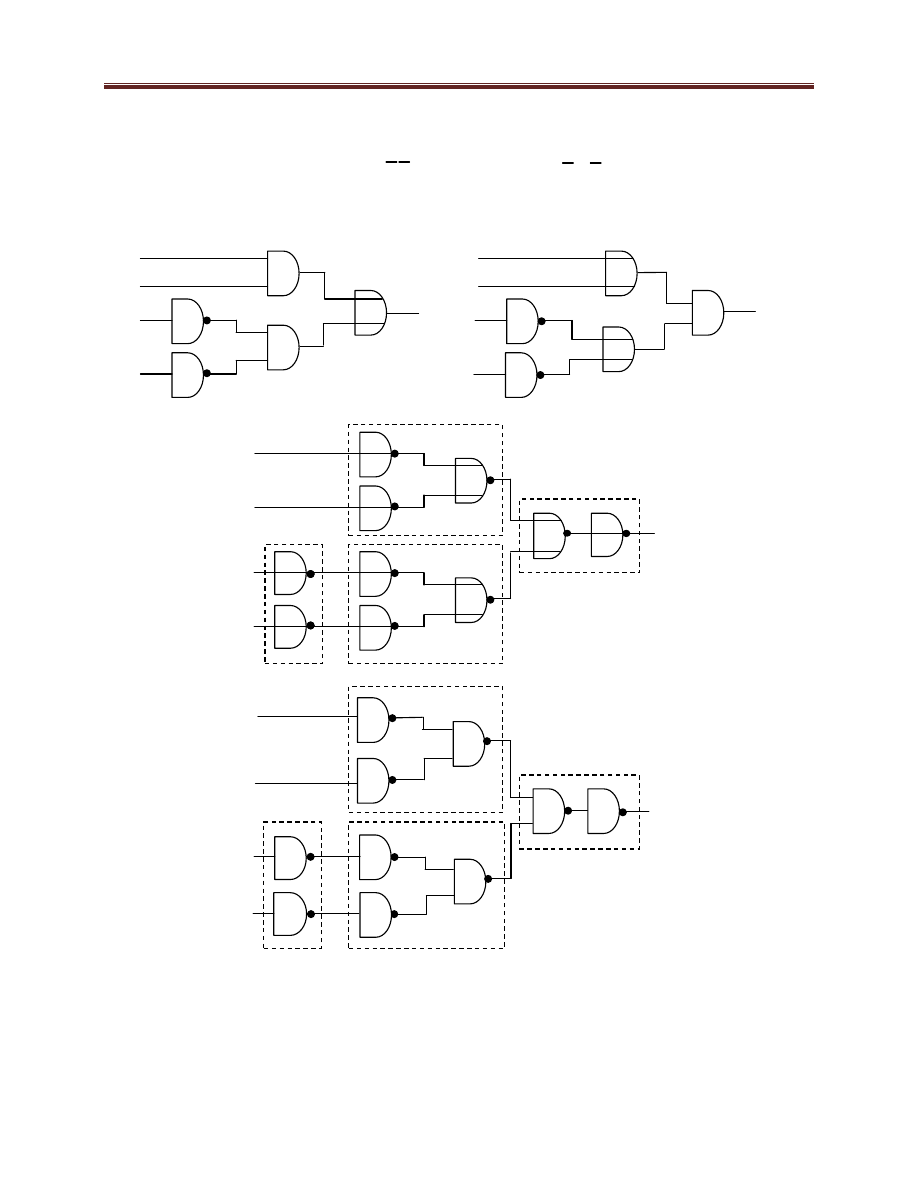
układów. Ilustruje ją rysunek 5.12, na którym transformacji poddano funkcję równoważności
będącą negacją poznanej wcześniej funkcji XOR. Funkcja ta dana jest wzorem:
y = a∙b + a∙b albo y = (a + b)(a + b)
a)
b)
a
a
b
b
a
a
b
b
c)
a
b
b
a
d)
a
b
a
b
Rysunek 5.12 a) - d) Transformacje funkcji XOR.
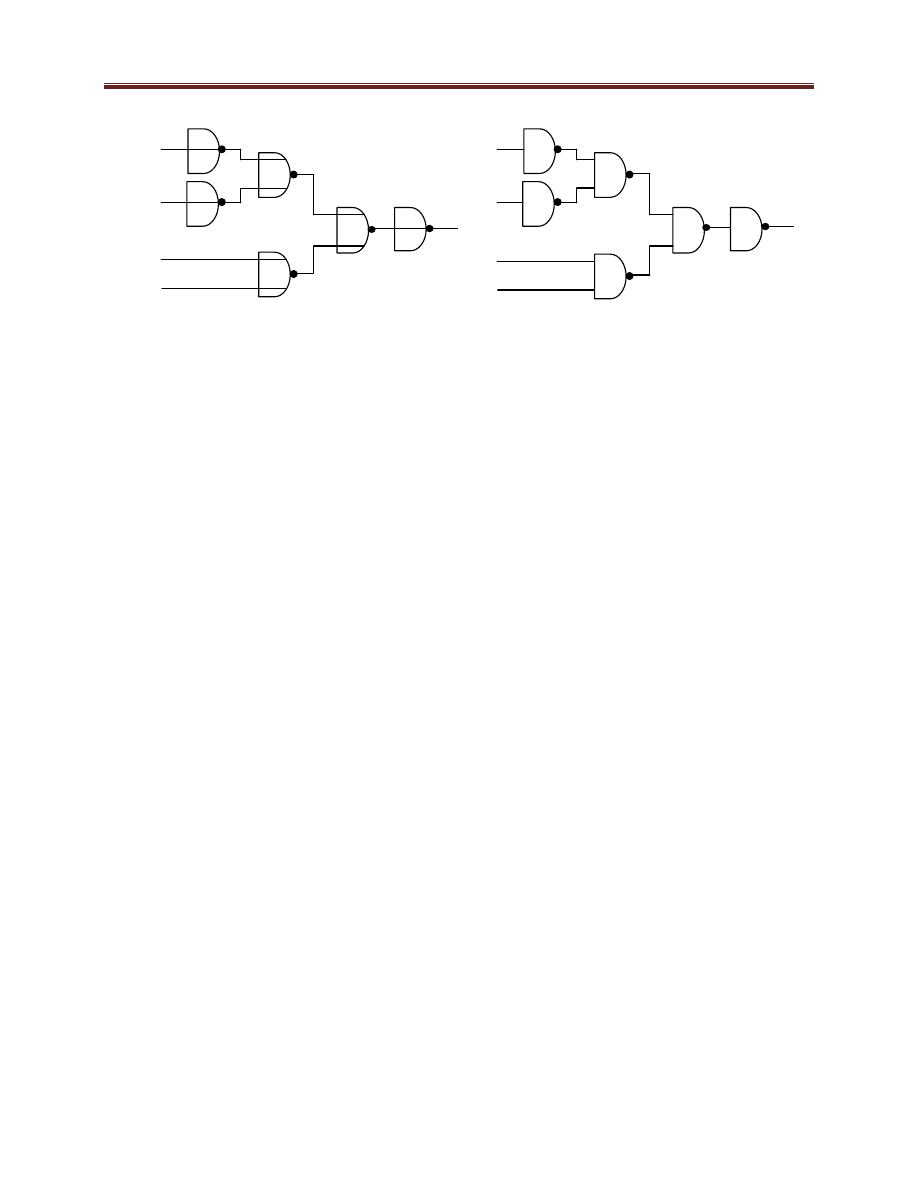
Minimalizacja funkcji (część 2)
5
e)
f)
a
a
b
b
a
a
b
b
Rysunek 5.12 e) - f) Transformacje funkcji XOR.
Na rysunku 5.12 (patrz wyżej) pokazane są kolejne kroki transformacji funkcji XOR od postaci
kanonicznej sumy (rysunek 5.12a) oraz postaci kanonicznej iloczynu (rysunek 5.12b) poprzez
fazę przejściową (rysunek 5.12c i 5.12d), w której elementy I oraz LUB zastępowane są przez
swoje odpowiedniki złożone z elementów NAND i NOR tak jak to było podane na rysunkach
5.10 (wyżej) i 5.11 (wyżej). Elementy, które zostały zamienione zostały na tych rysunkach
obwiedzione linią przerywaną. Rysunki 5.12e i f pokazują ostateczną postać funkcji XOR po
transformacji.
Powyższy przykład pokazuje, że prowadzona w taki sposób transformacja jest zajęciem
żmudnym, co dało asumpt do opracowania alternatywnej, prostszej (bo mechanicznej) metody
przejścia na elementy NAND i NOR. Metoda ta bazuje na podziale elementów I, LUB i NIE, z
których zrealizowany jest transformowany układ na trzy grupy nazywane poziomami, tak jak to
było pokazane na rysunku 5.8 (wyżej) i 5.9 (wyżej). Polega ona na wykonaniu kolejno
następujących kroków:
1. Jeżeli transformowany jest wzór typu ‘suma iloczynów’ to:
- poziom I buduje sie z dwóch elementów NOR albo jednego elementu NAND;
- poziom II zawiera tyle elementów NOR albo NAND, ile elementarnych iloczynów
występuje we wzorze;
- poziom trzeci w przypadku elementów NOR wytwarza negacje zmiennych, które we wzorze
nie były zanegowane, a w przypadku elementów NAND – negacje tych zmiennych, które we
wzorze były zanegowane.
2. Jeżeli transformowany jest wzór typu ‘iloczyn sum’ to:
- poziom I buduje sie z dwóch elementów NAND albo jednego elementu NOR;
- poziom II zawiera tyle elementów NOR albo NAND, ile elementarnych sum występuje we
wzorze;
- poziom trzeci w przypadku elementów NAND wytwarza negacje zmiennych, które we
wzorze nie były zanegowane, a w przypadku elementów NOR – negacje tych zmiennych,
które we wzorze były zanegowane.
Powyższe zasady pozwalają na rysowanie schematu układu wprost ze wzoru, o ile tylko ma on
jedną z postaci normalnych. Warto sprawdzić ich skuteczność chociażby na przykładzie funkcji
XOR.
Próba oszacowania liczby użytych do realizacji funkcji elementów NAND i NOR na podstawie
wzoru nie jest trudna. Z całą pewnością można powiedzieć, że liczba ta silnie zależy od liczby
zanegowanych zmiennych. Ponadto, układ typu ‘suma iloczynów’ jest prostszy do realizacji na
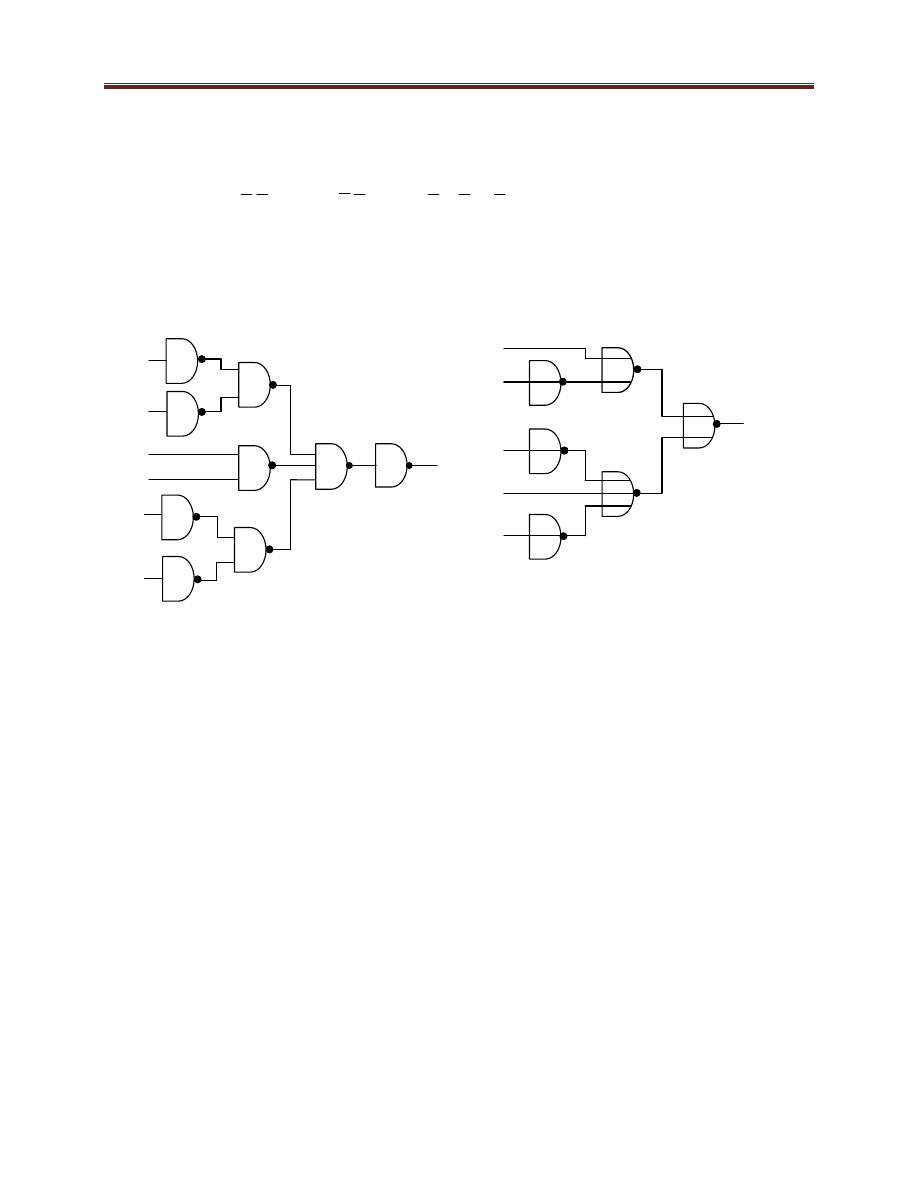
Minimalizacja funkcji (część 2)
6
elementach NAND, a układ typu ‘iloczyn sum’ – prostszy do realizacji na elementach NOR. Ta
ostatnia uwaga wynika wprost z ilości elementów niezbędnych do realizacji poziomu I.
Weźmy funkcję:
y = x
2
x
3
+ x
1
x
3
+ x
1
x
3
= (x
1
+ x
3
)( x
1
+ x
2
+ x
3
)
7 NOR, 9 NAND 6 NOR , 6 NAND
Wyliczone na podstawie podanych reguł liczby elementów NOR i NAND wypisane są pod
odpowiadającymi im postaciami funkcji, a uzyskane na tej samej podstawie schematy pokazane
są na rysunku 5.13.
x
2
x
1
x
3
x
3
x
1
x
3
x
1
x
1
x
3
x
2
x
3
Rysunek 5.13. Efekt zastosowania zasad tworzenia schematów funkcji wprost z zasad transformacji
Document Outline
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron