
Międzyszkolne Zawody Matematyczne
Klasa I LO i I Technikum- zakres podstawowy
Etap wojewódzki – 04.03.2006 rok
Czas rozwiązywania zadań 150 minut
Zad 1 ( 6 pkt)
Dany jest kwadrat ABCD o boku długości 8 cm. Wewnątrz tego kwadratu wybrano punkty M
i K tak, by trójkąty ABM i CDK były równoboczne. Oblicz pole części wspólnej trójkątów
ABM i CDK.
Zad.2 ( 6 pkt)
Wiadomo, że
c
c
b
a
b
c
b
a
a
c
b
a
−
+
=
+
−
=
+
+
−
.
Oblicz wartość wyrażenia
abc
a
c
c
b
b
a
)
)(
)(
(
+
+
+
Zad. 3 (6 pkt)
Cenę przejazdu taksówką firmy A opisuje funkcja
5
5
,
2
)
(
+
=
x
x
f
gdzie x oznacza liczbę
przejechanych kilometrów. Na trasie dłuższej niż 25 kilometrów firma ta udziela rabatu w
wysokości 10% ceny całego przejazdu. Firma B cenę przejazdu swoimi taksówkami oblicza
według wzoru
8
2
)
(
+
=
x
x
g
na trasie o dowolnej długości.
a)
Z usług której firmy należy skorzystać, jeżeli chcemy się przemieścić na odległość 30
kilometrów i zapłacić niższą kwotę za przejazd,
b)
Wyznacz długość trasy na której kwota zapłacona za przejazd taksówką obu firm jest
taka sama.
Zad 4 ( 6 pkt)
W trapezie ABCD łączymy środek E boku AD z końcami ramienia BC. Oblicz pole
powstałego trójkąta BEC, wiedząc, że pole trapezu równa się 16cm
2
.
Czy zauważasz jakiś związek pomiędzy polem trójkąta i polem trapezu? Zbadaj, czy jest on
spełniony dla każdego trapezu i tak powstałego trójkąta.
Zad 5 ( 6 pkt)
Jeżeli liczbę dwucyfrową podzielimy przez sumę jej cyfr, to otrzymamy 6 i resztę 3. Jeśli zaś
podzielimy tę liczbę przez sumę cyfr powiększoną o 2 to otrzymamy 5 i resztę 5.
Znajdź tę liczbę.
śyczymy powodzenia

Kryteria oceniania dla klasy I LO i I Technikum– zakres podstawowy
Nr
zad
Wykonana czynno
ść
Pkt
1
Analiza zadania, rysunek. Niech L i N będą wierzchołkami otrzymanego
czworokąta
0,5
Zauważenie, że czworokąt KLMN jest rombem
0,5
Obliczenie odległości wierzchołka M rombu od boku AB:
3
4
1
Obliczenie odległości wierzchołka K od boku AB:
)
3
2
(
4
3
4
8
−
=
−
1
Obliczenie długości przekątnej KM rombu:
)
3
2
(
4
3
4
−
−
=
)
1
3
(
8
−
1
Obliczenie długości drugiej przekątnej rombu :
3
)
3
3
(
8
−
1
Obliczenie pola rombu :
)
(
3
3
2
3
64
−
1
2
Zapisanie ułamków w postaci :
c
b
a
c
c
b
a
b
c
a
b
c
b
a
a
c
b
a
c
b
a
+
+
−
=
−
+
+
+
−
=
+
−
+
+
−
=
+
+
−
1
,
1
,
1
1
Zapisanie równości ułamków wynikającej z poprzedniego zapisu:
c
b
a
b
c
a
a
c
b
+
=
+
=
+
1
Zapisanie sum występujących w licznikach ułamków w postaci iloczynów:
ℜ
∈
=
+
=
+
=
+
k
gdzie
kc
b
a
kb
c
a
ka
c
b
,
,
,
1
Dodanie stronami równań i zapisanie równania :
)
(
)
(
2
c
b
a
k
c
b
a
+
+
=
+
+
0,5
Rozpatrzenie dwóch przypadków:
(
)
0
lub
2
=
+
+
=
c
b
a
k
0,5
Obliczenie wartości wyrażenia dla pierwszego przypadku: 8
1
Obliczenie wartości wyrażenia dla drugiego przypadku: -1
1
3
Obliczenie f(30) i g(30); 72 złote i 68 złotych
1
Wybór firmy z której usług należy skorzystać
0,5
Rozpatrzenie dwóch przypadków: x>25 km lub x
≤
25 km
0,5
Zapisanie równania dla I przypadku ;
8
2
)
5
5
,
2
(
1
,
0
)
5
5
,
2
(
+
=
+
−
+
x
x
x
1
Rozwiązanie równania i udzielenie odpowiedzi : x = 14, nie spełnia założenia
1
Zapisanie równania dla II przypadku;
8
2
5
5
,
2
+
=
+
x
x
1
Rozwiązanie równania i udzielenie odpowiedzi: x =6, spełnia założenie
1
4
Analiza zadania, rysunek. Niech a i b to długości podstaw, a h to długość
wysokości
0,5
Uzasadnienie, że długości wysokości poprowadzone w trójkątach ABE i DCE z
wierzchołka E stanowią połowę długości wysokości trapezu
2
Zapisanie pola trapezu jako sumy pól powstałych trójkątów:
P
ABCD
=
BEC
P
h
b
h
a
+
+
2
2
1
2
2
1
1
Przekształcenie równania do postaci:
16
)
(
4
1
=
+
+
BEC
P
h
b
a
, czyli
16
16
2
1
=
+
⋅
BEC
P
1
Obliczenie pola trójkąta BEC; 8cm
2
0,5

Zapisanie końcowego wniosku i jego uzasadnienie
1
5
Zapisanie założenia:
}
{
}
{
9
,
8
,
7
,
6
,
5
,
4
,
3
,
2
,
1
,
0
,
9
,
8
,
7
,
6
,
5
,
4
,
3
,
2
,
1
∈
∈
y
x
0,5
Zapisanie układu równań:
+
+
+
=
+
+
+
=
+
5
)
2
(
5
10
3
)
(
6
10
y
x
y
x
y
x
y
x
2
Rozwiązanie układu równań: x=7, y = 5
2
Sprawdzenie, że otrzymane liczby spełniają warunki zadania
1
Udzielenie odpowiedzi: Liczbą dwucyfrową spełniająca warunki zadania jest
liczba 75
0,5
Za poprawne rozwiązanie zadania metodą inną aniżeli opisana w schemacie punktowania,
należy przyznać maksymalną liczbę punktów. Jeżeli uczeń rozwiązał zadanie metodą inną
i popełnił błędy to należy określić i ocenić czynności równoważnie do wymienionych w
schemacie. Można przyznawać połówki punktów.

Międzyszkolne Zawody Matematyczne
Klasa II LO i II, III Technikum- zakres podstawowy
Etap wojewódzki – 04.03.2006 rok
Czas rozwiązywania zadań 150 minut
Zad.1 ( 6 pkt)
Udowodnij, że
3
2
cos
sin
1
cos
sin
1
6
6
4
4
=
−
−
−
−
α
α
α
α
Zad. 2 (6 pkt)
Wykaż, że dla pierwiastków
3
2
1
,
x
x
x
równania
0
,
0
2
3
≠
=
+
+
+
a
d
cx
bx
ax
prawdziwe są
wzory:
a
b
x
x
x
−
=
+
+
3
2
1
oraz
a
d
x
x
x
−
=
3
2
1
Zad 3 (6 pkt)
Reszta z dzielenia wielomianu W(x) przez dwumian (x - 1) jest równa 2, a reszta z dzielenia
wielomianu W(x) przez dwumian (x - 3) jest równa 5. Podaj wielomian R(x), który jest resztą
z dzielenia wielomianu W(x) przez wielomian ( x
2
- 4x + 3).
Zad. 4 (6 pkt)
Trójkąt o bokach a ,b ,c został rozcięty na romb i dwa trójkąty. Oblicz długości boków tych
figur.
Zad.5 ( 6 pkt)
Na kole o promieniu r =1 został opisany trójkąt prostokątny o przyprostokątnych x , y.
Napisz wzór funkcji opisującej zależność y od x i narysuj wykres otrzymanej funkcji.
śyczymy powodzenia
Kryteria oceniania dla klasy I I LO i II , III Technikum – zakres podstawowy
Nr
zad
Wykonana czynno
ść
Pkt
1
Zapisanie ułamka w postaci
α
α
α
α
α
α
α
α
6
6
2
2
4
4
2
2
cos
sin
cos
sin
cos
sin
cos
sin
−
−
+
−
−
+
0,5
Zapisanie ułamka w postaci
)
cos
1
(
cos
)
sin
1
(
sin
)
cos
1
(
cos
)
sin
1
(
sin
4
2
4
2
2
2
2
2
α
α
α
α
α
α
α
α
−
+
−
−
+
−
2
Zapisanie licznika ułamka w postaci
α
α
2
2
cos
sin
2
⋅
1
Zapisanie mianownika ułamka w postaci
α
α
2
2
cos
sin
3
⋅
2
Obliczenie ilorazu:
3
2
0,5
2
Zapisanie lewej strony równania w postaci
)
)(
)(
(
3
2
1
x
x
x
x
x
x
a
−
−
−
1
Przekształcenie postaci iloczynowej do postaci
[
]
)
(
)
(
)
(
3
2
1
3
2
3
1
2
1
2
3
2
1
3
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
a
−
+
+
+
+
+
−
2
Zapisanie równań :
b
x
x
x
a
=
+
+
−
)
(
3
2
1
oraz
d
x
x
ax
=
−
3
2
1
2
Przekształcenie równań do postaci :
a
d
x
x
x
i
a
b
x
x
x
−
=
−
=
+
+
3
2
1
3
2
1
1
3
Znajomość twierdzenia o reszcie i zapisanie układu równań W(1) = 2 i W(3) = 5
1,5
Zapisanie wielomianu
3
4
2
+
−
x
x
w postaci iloczynowej
)
1
)(
3
(
−
−
x
x
1
Zapisanie wielomianu W(x) w postaci
)
(
)
(
)
1
)(
3
(
)
(
b
ax
x
Q
x
x
x
W
+
+
−
−
=
1
Zapisanie układu równań
=
+
=
+
2
5
3
b
a
b
a
1
Rozwiązanie układu równań :
2
1
,
2
1
1
=
=
b
a
0,5
Zapisanie reszty R(x) =
2
1
2
1
1
+
x
1
4
Analiza zadania, rysunek.
0,5
Zauważenie i uzasadnienie, że powstałe trójkąty są podobne
1
Zapisanie proporcji
DB
CD
m
m
b
m
c
m
=
−
=
−
, gdzie
m to długość boku rombu , a
D to wierzchołek rombu należący do boku BC
1
Wyznaczenie
m:
c
b
bc
m
+
=
1
Wyznaczenie długości boków (
c –m) i (b –m) :
c
b
b
c
b
c
+
+
2
2
,
1
Zapisanie układu równań
=
+
=
a
DB
CD
c
b
DB
CD
0,5
Rozwiązanie układu równań:
c
b
ac
DB
c
b
ab
CD
+
=
+
=
,
1
5
Analiza zadania, rysunek
0,5
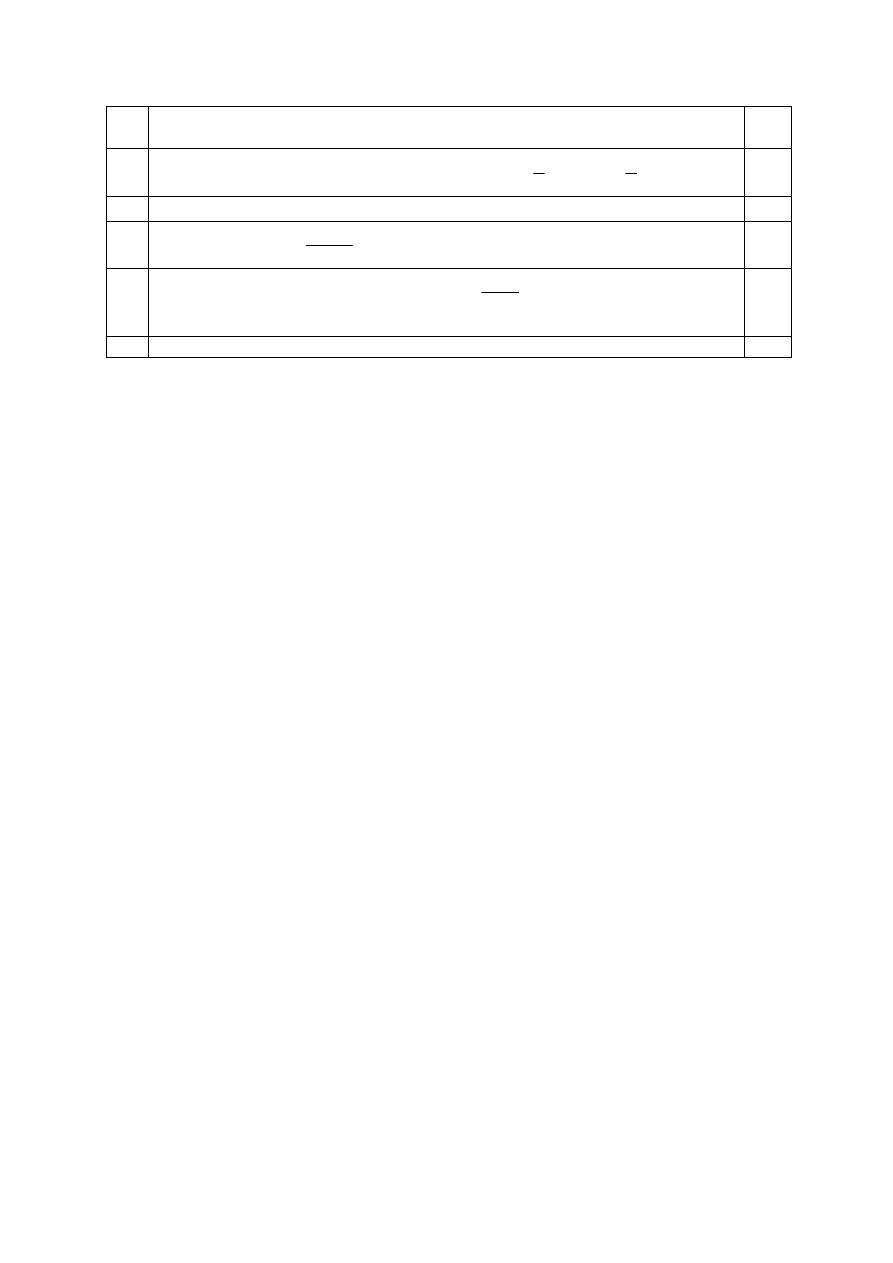
Zapisanie długości przeciwprostokątnej w postaci (
x - r + y - r) czyli
(
x + y – 2)
0,5
Zapisanie pola trójkąta w dwóch postaciach:
)
2
2
2
(
2
1
,
2
1
−
+
=
=
y
x
P
xy
P
ABC
ABC
1
Zapisanie równania
2
2
2
−
+
=
y
x
xy
0,5
Wyznaczenie
y:
2
2
2
2
≠
−
−
=
x
dla
x
x
y
1
Zapisanie przepisu funkcji w postaci
2
2
2
−
+
=
x
y
i wyznaczenie jej dziedziny
D
f
= (2,
∞
)
1,5
Sporządzenie wykresu funkcji
1
Za poprawne rozwiązanie zadania metodą inną aniżeli opisana w schemacie punktowania,
należy przyznać maksymalną liczbę punktów. Jeżeli uczeń rozwiązał zadanie metodą inną
i popełnił błędy to należy określić i ocenić czynności równoważnie do wymienionych w
schemacie. Można przyznawać połówki punktów.
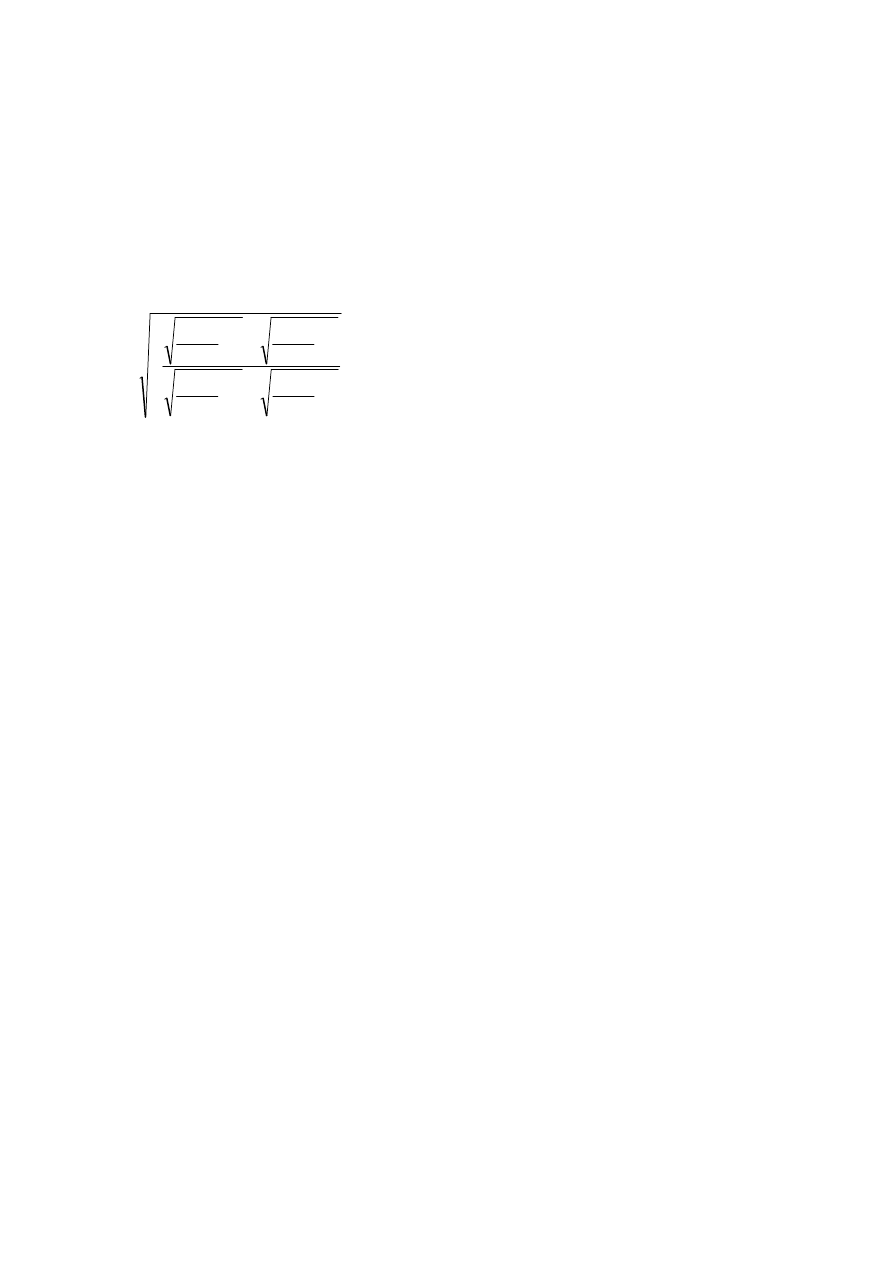
Międzyszkolne Zawody Matematyczne
Klasa IIILO i IV Technikum – zakres podstawowy
Etap wojewódzki – 04.03.2006 rok
Czas rozwiązywania zadań 150 minut
Zad 1 (6 pkt)
Sporządź wykres funkcji
1
2
1
1
2
1
1
2
1
1
2
1
2
2
2
2
−
+
+
+
+
−
+
−
+
+
=
x
x
x
x
x
x
x
x
x
y
Zad 2 ( 6 pkt)
Dla jakiej wartości parametru
m równanie
0
)
1
(
)
1
(
)
1
(
2
=
−
+
+
+
−
m
x
m
x
m
ma dwa różne
pierwiastki dodatnie?
Zad 3 (6 pkt)
W trójkącie prostokątnym długość wysokości i środkowej poprowadzonej z wierzchołka kąta
prostego oraz długość przeciwprostokątnej tworzą ciąg geometryczny, którego iloczyn
wyrazów jest równy 8.
Oblicz długość promienia okręgu wpisanego w trójkąt.
Zad 4 ( 6 pkt)
W ostrosłupie prawidłowym czworokątnym kąt między płaszczyznami sąsiednich ścian
bocznych wynosi
0
120 . Oblicz kąt nachylenia ściany bocznej do płaszczyzny podstawy.
Zad 5 ( 6 pkt)
W urnie znajduje się 8 kul białych i 4 czarne. Z urny wylosowano bez zwracania 5 kul.
Oblicz prawdopodobieństwo tego, że stosunek liczby kul czarnych do liczby kul białych w
urnie zwiększył się.
śyczymy powodzenia
Kryteria oceniania dla klasy III LO i IV Technikum – zakres podstawowy
Nr
zad
Wykonana czynno
ść
Pkt
1
Wyznaczenie dziedziny funkcji: D=(0,
∞
)
0,5
Przekształcenie wyrażeń do postaci :
x
x
x
x
i
x
x
x
x
2
1
1
2
1
2
1
1
2
1
2
2
−
=
−
+
+
=
+
+
2,5
Zapisanie przepisu funkcji w postaci:
≥
<
<
=
−
+
+
−
−
+
=
1
,
1
1
0
,
1
1
1
1
x
gdy
x
gdy
x
x
x
x
x
x
y
2
Wykonanie wykresu funkcji
1
2
Zapisanie układu warunków dla których równanie posiada dwa różne
pierwiastki:
>
−
−
+
≠
0
)
1
(
4
)
1
(
1
2
2
m
m
m
0,5
Rozwiązanie układu :
) (
)
3
,
1
1
,
3
1
∪
∈
m
2
Zapisanie układu warunków, dla których pierwiastki są dodatnie:
>
−
+
−
>
−
−
0
1
)
1
(
0
1
1
m
m
m
m
1
Rozwiązanie układu nierówności :
)
1
,
1
(
−
∈
m
2
Wyznaczenie m dla którego równanie posiada dwa różne pierwiastki:
)
1
,
3
1
(
∈
m
0,5
3
Analiza zadania, rysunek. Niech h- długość wysokości, d – długość środkowej,
a a, b- długości przyprostokątnych, c - długość przeciwprostokątnej
0,5
Zapisanie równania
8
2
=
⋅
⋅
hq
hq
h
gdzie q jest ilorazem ciągu i obliczenie
długości środkowej : d= 2
0,5
Zauważenie, że długość środkowej jest długością promienia okręgu opisanego
na trójkącie, a tym samym stanowi połowę długości przeciwprostokątnej
1
Obliczenie długości przeciwprostokątnej, długości wysokości oraz obliczenie q:
c
= 4, h = 1, q = 2
0,5
Zapisanie układu równań
=
+
=
⋅
16
4
2
2
b
a
b
a
1
Rozwiązanie układu równań :
3
4
8
,
3
4
8
+
=
−
=
b
a
1
Znajomość wzoru na długość promienia okręgu wpisanego w okrąg:
c
b
a
h
c
r
+
+
⋅
=
0,5
Obliczenie długości promienia okręgu wpisanego w trójkąt :
6
2
2
4
3
2
2
3
2
2
4
+
=
+
+
+
−
=
r
1
4
Analiza zadania, rysunek, niech np.
1
,
,
h
DE
BE
b
DW
BW
CW
AW
a
AB
=
=
=
=
=
=
=
gdzie E jest
punktem wspólnym wysokości ścian bocznych poprowadzonych od
0,5

wierzchołków B i D i
h
WF
=
( wysokość ściany bocznej),
0
120
=
∠
BED
Zapisanie h przy pomocy a i b :
4
2
2
a
b
h
−
=
0,5
Zapisanie
1
h
przy pomocy a :
3
6
1
a
h
=
0,5
Zauważenie, że trójkąty BCE i WFC są podobne i zapisanie proporcji:
b
h
a
h
=
1
1
Zapisanie równania :
b
a
b
4
3
6
2
2
−
=
0,5
Rozwiązanie równania ze względu na b:
2
3
a
b
=
1
Zapisanie h za pomocą a :
2
2
a
h
=
1
Obliczenie cosβ, gdzie β jest miarą kąta nachylenia ściany bocznej do
płaszczyzny podstawy:
2
2
cos
=
β
0,5
Podanie miary kąta :
0
45
0,5
5
Określenie przestrzeni zdarzeń elementarnych
0,5
Obliczenie stosunku liczby kul czarnych do liczby kul białych:
2
1
0,5
Zauważenie, że stosunek będzie większy gdy wylosujemy pięć kul białych lub
cztery kule białe i jedną czarną
2
Zapisanie prawdopodobieństwa:
+
5
12
1
4
4
8
5
8
2
Obliczenie prawdopodobieństwa:
33
14
1
Za poprawne rozwiązanie zadania metodą inną aniżeli opisana w schemacie punktowania,
należy przyznać maksymalną liczbę punktów. Jeżeli uczeń rozwiązał zadanie metodą inną
i popełnił błędy to należy określić i ocenić czynności równoważnie do wymienionych w
schemacie. Można przyznawać połówki punktów.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron