
Wykład 1
1
Hydraulika Stosowana
Studia magisterskie
Inżynieria Środowiska
Urządzenia Sanitarne
Semestr I
R. A. 2008/2009
Dr inż. Apoloniusz Kodura
Politechnika Warszawska
Wydział Inżynierii Środowiska

Wykład 1
2
Organizacja zajęć
• Wykłady + ćwiczenia audytoryjne – zajęcia łączone - 2
godziny tygodniowo, razem 30 h
• Ćwiczenia laboratoryjne – 15 h – (2 lub 3 spotkania)
• Kontakt –apoloniusz.kodura @is.pw.edu.pl,
www.is.pw.edu.pl/index.php?id=501, www.is.pw.edu.pl/
- Wydział – Pracownicy – Apoloniusz Kodura
• Zaliczenie:
– Wykład – egzamin
– Ćwiczenia audytoryjne – jedno kolokwium
– Laboratorium – 6 ćwiczeń, obecność obowiązkowa, sprawozdania,
dopuszczalne niezaliczenie jednego ćwiczenia

Wykład 1
3
Literatura
•
Marek Mitosek – „Mechanika Płynów w Inżynierii i
Ochronie Środowiska” OWPW, Warszawa 2000
• Marek Mitosek – „Mechanika Płynów w Inżynierii i
Ochronie Środowiska” PWN, Warszawa 2001
• Marek Mitosek, Mieczysław Matlak, Apoloniusz Kodura –
„Zbiór zadań z mechaniki płynów” OWPW, Warszawa
2008
• Mieczysław Matlak, Andrzej Szuster – „Ćwiczenia
laboratoryjne z mechaniki płynów” OWPW, Warszawa
2002

W y k
ład 1
4
Tematyka wykładów i ćwiczeń
1. Uderzenie hydrauliczne: układy przewodów, obliczanie zaworów
bezpieczeństwa i zbiorników wodno
-powietrznych.
Uderzenie
hydrauliczne.
2. Zawory bezpieczeństwa oraz zbiorniki wodno-powietrzne. Kawitacja.
Zmiany oporności przewodów w czasie eksploatacji.
3. Ustalony ruch wolnozmienny w korytach otwartych.
Metoda
Rűhlmanna i Tolkmitta obliczania przepływów wolnozmiennych.
4. Przelewy: Thomsona, proporcjonalne, o szerokiej koronie, boczne.
Obliczanie przelewów oraz kanałów zwężkowych.
5. Przepływy przez warstwy sypkie i porowate. Filtracja. Studnie
promieniste.
Ustalone
przepływy
wód
gruntowych.
Studnie
promieniste.
6. Opadanie swobodne., Sedymentacja. Fluidyzacja. Rozpylanie cieczy.
Sedymentacja. Fluidyzacja. Rozpylanie cieczy
7. Wznoszenie się pęcherzyków gazu w cieczy. Napowietrzanie
wgłębne.

Wykład 1
12
Uderzenie hydrauliczne: układy przewodów,
obliczanie zaworów bezpieczeństwa i zbiorników
wodno-powietrznych. Uderzenie hydrauliczne.
Wykład 1

Wykład 1
13
Ruch nieustalony (niestacjonarny)
•
Wielkości przepływu zależą od położenia i czasu
•
Zjawisko ruchu zależnego od czasu występuje bardzo często w
instalacjach (ruch turbulentny, zmienny pobór wody z sieci
wodociągowej)
•
W przypadku wydłużonych w czasie zmian natężeń przepływu - w
obliczeniach przyjmuje się schemat uproszczony ruchu ustalonego
•
Gwałtowne zmiany parametrów
– Wyłączenie\załączenie pompy
– Otwarcie\przymknięcie zaworu
– Systemy automatycznej regulacji
wymagają rozważenia zjawiska nieustalonego przepływu

Wykład 1
14
Ruch nieustalony - przypadki
•
Wahania w układzie
– Względnie wolne zmiany przepływu w przewodzie, wywołane zmianami
ciśnienia na jego końcach
– Założenie - zmiany prędkości występują jednocześnie w całej masie
cieczy
– Założenie - przyrosty ciśnienia są na tyle małe, że pomija się sprężystość
cieczy (ściśliwość) i przewodu
•
Uderzenie hydrauliczne
– Gwałtowne zmiany ciśnienia w przewodzie wywołane szybkimi zmianami
prędkości
– Zmiany ciśnienia rozprzestrzeniają się w postaci fali ciśnienia
– Wymagane jest uwzględnienie sprężystości cieczy (ściśliwości) i ścian
przewodu.

Wykład 1
15
Uderzenie hydrauliczne – założenia do wzoru
Żukowskiego - Allieviego
•
Gwałtowne zmiany ciśnienia w przewodzie pod ciśnieniem wywołane
szybkimi w czasie zmianami prędkości przepływu
•
Uderzenie dodatnie – przyrost ciśnienia w pierwszej fazie, wywołany
zmniejszeniem prędkości (np. przymykanie zaworu)
•
Uderzenie ujemne – spadek ciśnienia w pierwszej fazie, wywołany
wzrostem prędkości (np. otwarcie zaworu)
•
Zmiany wartości ciśnienia wywołane są siłami bezwładności
•
Analiza zjawiska na przykładzie uderzenia dodatniego
•
Dany przewód o długości L, średnicy D,
•
Przepływ w przewodzie z prędkością v
0
, ciśnienie początkowe p
0
•
Założenie
– Ruch odbywa się bez oporów hydraulicznych
– Rurociąg jest sprężysty

Wykład 1
16
Uderzenie hydrauliczne - schemat
v
0
0

Wykład 1
17
Uderzenie hydrauliczne – przymknięcie zaworu w
pewnej chwili t
0
•
Skokowe zmniejszenie prędkości w przekroju zasuwy o wartość
∆
v
•
Spowolnienie cieczy w przewodzie – powstają siły bezwładności
•
W obszarze cieczy wyhamowanej ciśnienie wzrasta o wartość
∆
p
•
Spowolnienie obejmuje kolejne porcje cieczy
•
Powstaje powierzchnia nieciągłości ciśnienia i prędkości rozdzielająca
ciecz o zmniejszonej prędkości i większym ciśnieniu od objętości
cieczy w której panują jeszcze niezmienione warunki ruchu ustalonego
– fala uderzeniowa, przemieszczająca się w przewodzie z prędkością
c
•
Dla opisu zjawiska, którego parametry hydrauliczne zmieniają się
zgodnie z warunkami rzeczywistymi w sposób ciągły należy
skorzystać z różniczkowych równań ruchu – np. Równania Eulera
Wykład 1
18
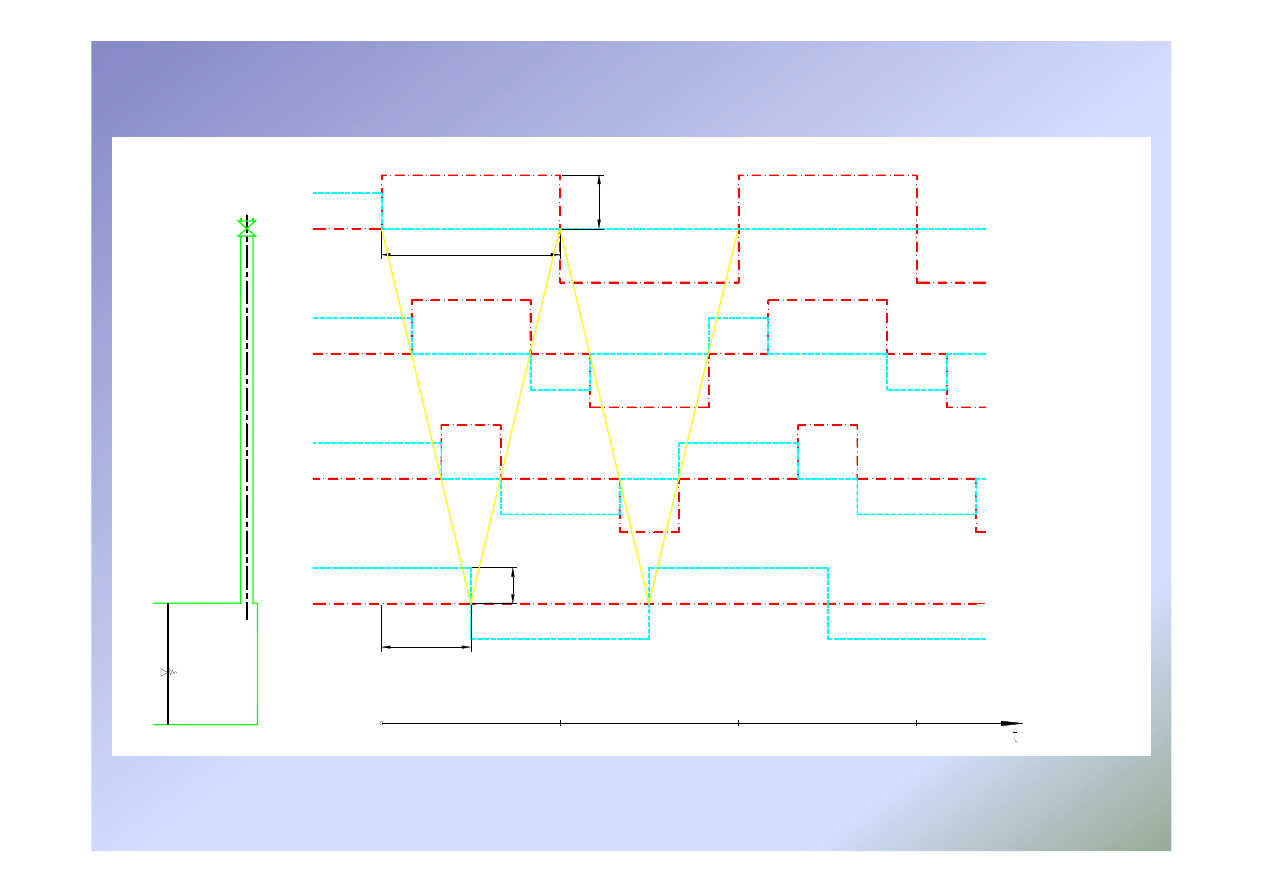
Uderzenie hydrauliczne – przebieg zjawiska
0
1
2
3
v
o
p
o
v = 0
v
o
-v
o
0 - Zbiornik
1
2
3 - Zawór
T
∆
p
T/2
v
o
0
v
o
p
o
p
o
v
o
v
o
p
o
T
2T
3T
Wykład 1
19
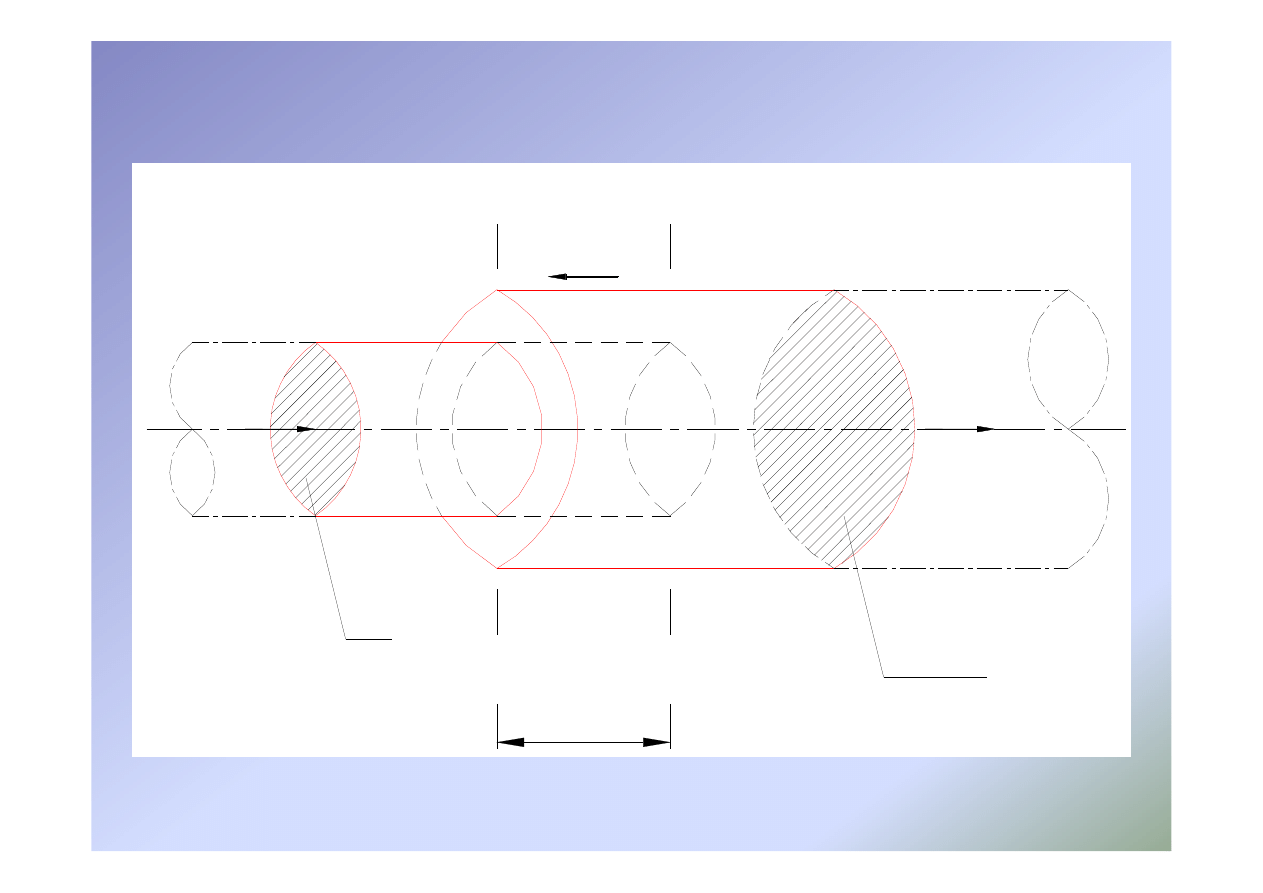
Uderzenie hydrauliczne – fala uderzeniowa
∆
L
c
2
1
2
1
v
0
p
0
A
0
A+
∆
A
0
v -
∆
v
0
p +
∆
p
0
Wykład 1
20
Uderzenie hydrauliczne – równanie ruchu
(pędu i popędu)
(
)
[
]
υ
ρ
∆
⋅
⋅
⋅
=
⋅
⋅
−
⋅
∆
+
L
A
t
A
p
A
p
p
d
d
0
0
0
0
A
A
≈
t
c
L
d
d
⋅
=
υ
ρ
∆
⋅
⋅
=
∆
c
p
Wzór Żukowskiego
0
υ
υ
=
∆
0
υ
ρ
⋅
⋅
=
∆
c
p
Wykład 1
21
Uderzenie hydrauliczne – równanie ciągłości
(
)
(
)
t
A
A
L
A
A
d
d
0
0
0
0
0
⋅
⋅
⋅
−
⋅
⋅
=
⋅
⋅
−
⋅
υ
ρ
υ
ρ
ρ
ρ
ρ
ρ
ρ
∆
+
=
0
A
∆
⋅
∆
ρ
Przyrost masy cieczy w odcinku przewodu jest równy różnicy dopływu i
odpływu masy cieczy do odcinka
A
A
A
∆
+
=
0
(
)
(
)
L
A
A
A
A
A
L
A
A
d
d
0
0
0
0
0
0
0
0
⋅
⋅
−
∆
⋅
∆
+
∆
⋅
+
⋅
∆
+
⋅
=
⋅
⋅
−
⋅
ρ
ρ
ρ
ρ
ρ
ρ
ρ
Pomijalnie mały
wyraz w
stosunku do
pozostałych
(
)
L
A
A
A
L
A
A
d
d
0
0
0
0
0
0
⋅
∆
+
∆
⋅
⋅
=
⋅
⋅
−
⋅
ρ
ρ
ρ
ρ
ρ
Wykład 1
22
Uderzenie hydrauliczne – równanie ciągłości
(
)
(
)
t
A
A
L
A
A
d
d
0
0
0
0
0
⋅
⋅
⋅
−
⋅
⋅
=
⋅
⋅
−
⋅
υ
ρ
υ
ρ
ρ
ρ
ρ
ρ
ρ
∆
+
=
0
A
∆
∆ ,
ρ
Przyrost masy cieczy w odcinku przewodu jest równy różnicy dopływu i
odpływu masy cieczy do odcinka
A
A
A
∆
+
=
0
Pomijalnie mały
wyraz w
stosunku do
pozostałych
(
) (
) (
)
[
]
(
)
t
A
A
t
A
A
A
d
d
0
0
0
0
0
0
0
0
0
⋅
⋅
⋅
−
⋅
⋅
=
⋅
∆
−
⋅
∆
+
⋅
∆
+
−
⋅
⋅
υ
ρ
υ
ρ
υ
υ
ρ
ρ
υ
ρ
(
)
t
A
A
t
A
d
d
0
0
0
0
0
⋅
⋅
⋅
−
⋅
⋅
=
⋅
∆
⋅
⋅
υ
ρ
υ
ρ
υ
ρ
Wykład 1
23
Uderzenie hydrauliczne – równanie ciągłości
Zestawienie obu stron równania
t
A
L
A
A
A
d
d
0
0
0
0
0
0
⋅
∆
⋅
⋅
=
⋅
∆
+
∆
⋅
⋅
υ
ρ
ρ
ρ
ρ
t
c
L
d
d
⋅
=
t
A
t
c
A
A
A
d
d
0
0
0
0
0
0
⋅
∆
⋅
⋅
=
⋅
⋅
∆
+
∆
⋅
⋅
υ
ρ
ρ
ρ
ρ
0
0
A
A
c
∆
+
∆
∆
=
ρ
ρ
υ
Wykład 1
24
Uderzenie hydrauliczne – prędkość fali c
K
ρ
ρ
ρ
∆
=
∆
0
Ciecz
Ścianka – prawo Hooke’a
D
D
E
l
l
E
∆
⋅
=
∆
⋅
=
∆
σ
D
l
⋅
=
π
Wzrost ciśnienie generuje
wzrost naprężeń w
ściance przewodu
L
e
L
D
p
∆
⋅
⋅
∆
=
∆
⋅
⋅
∆
2
σ
E
e
D
p
D
D
⋅
⋅
⋅
∆
=
∆
2
D
D
A
A
D
D
D
D
A
A
∆
⋅
=
∆
⇒
=
=
2
d
2
d
d
0
2
2
E
e
D
p
A
A
⋅
⋅
∆
=
∆
0
⋅
+
⋅
∆
∆
=
E
e
D
K
p
c
1
υ
Wykład 1
25
Uderzenie hydrauliczne – prędkość fali c
⋅
+
⋅
∆
∆
=
E
e
D
K
p
c
1
υ
0
υ
ρ
⋅
⋅
=
∆
c
p
E
K
e
D
K
c
⋅
+
=
1
ρ
∞
→
E
ρ
K
a
c
=
=
Wpływ
odkształcenia
przewodu
Wykład 1
26
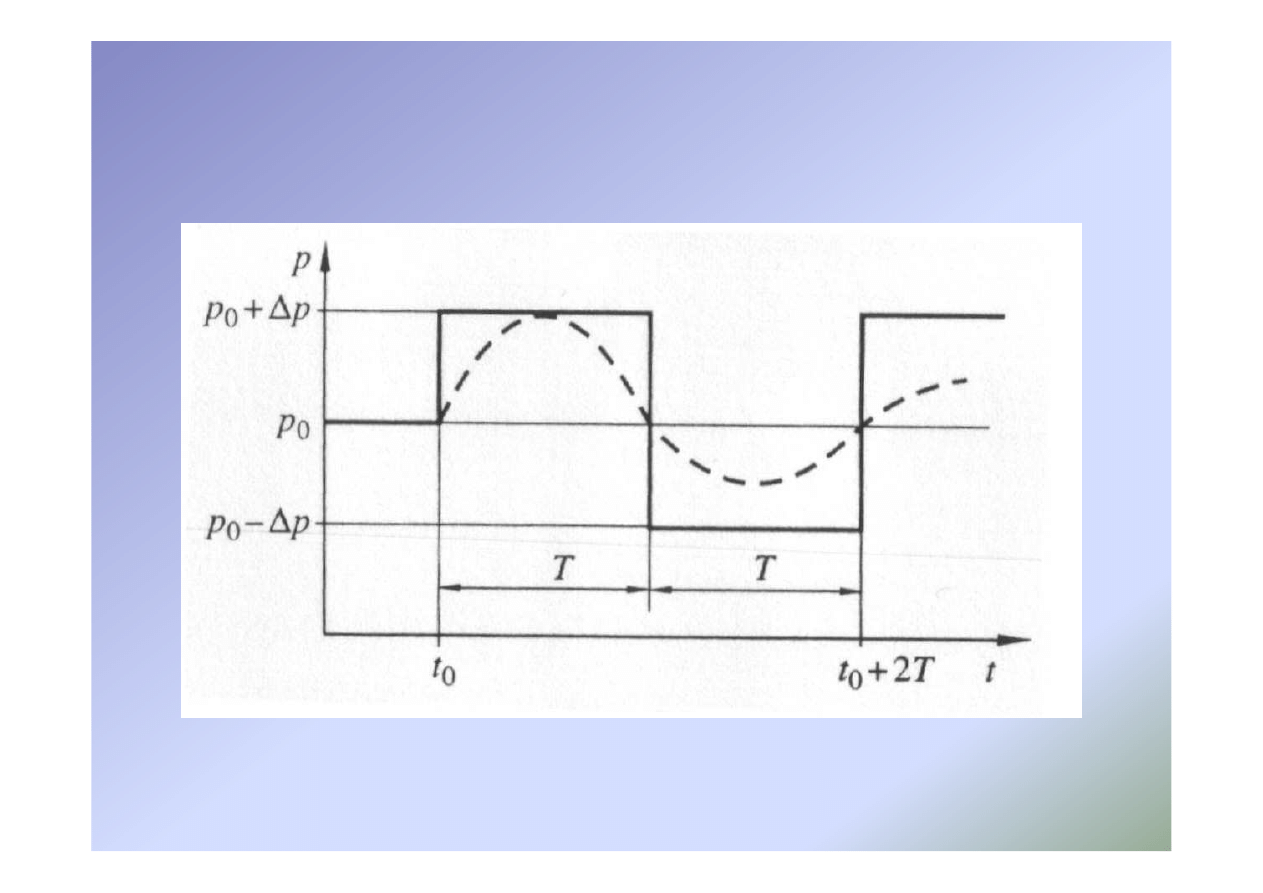
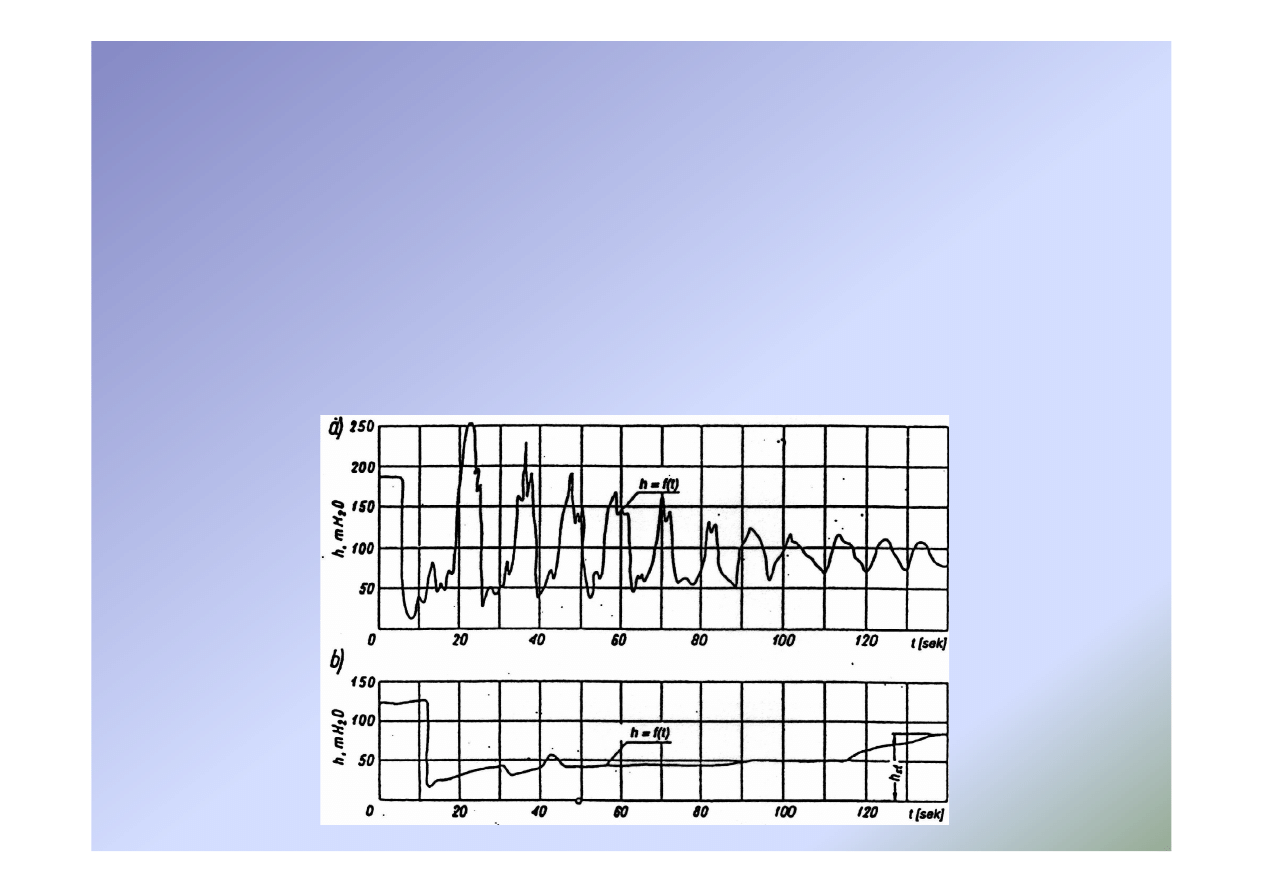
Uderzenie hydrauliczne – przebieg zjawiska

Wykład 1
27
Uderzenie hydrauliczne - okres
•
Okres fali T jest czasem, w którym fala wychodząca od zasuwy,
powróciła do niej w postaci fali odbitej
•
Uderzenie proste
•
Uderzenie nieproste (złożone)
•
Wzór Michaud’a
c
L
T
2
=
T
t
z
≤
T
t
z
≥
z
t
T
p
p =
∆
∆
max
z
t
L
p
⋅
⋅
⋅
=
∆
0
2
υ
ρ
0
2
,
2
p
p
⋅
≤
∆
Wykład 1
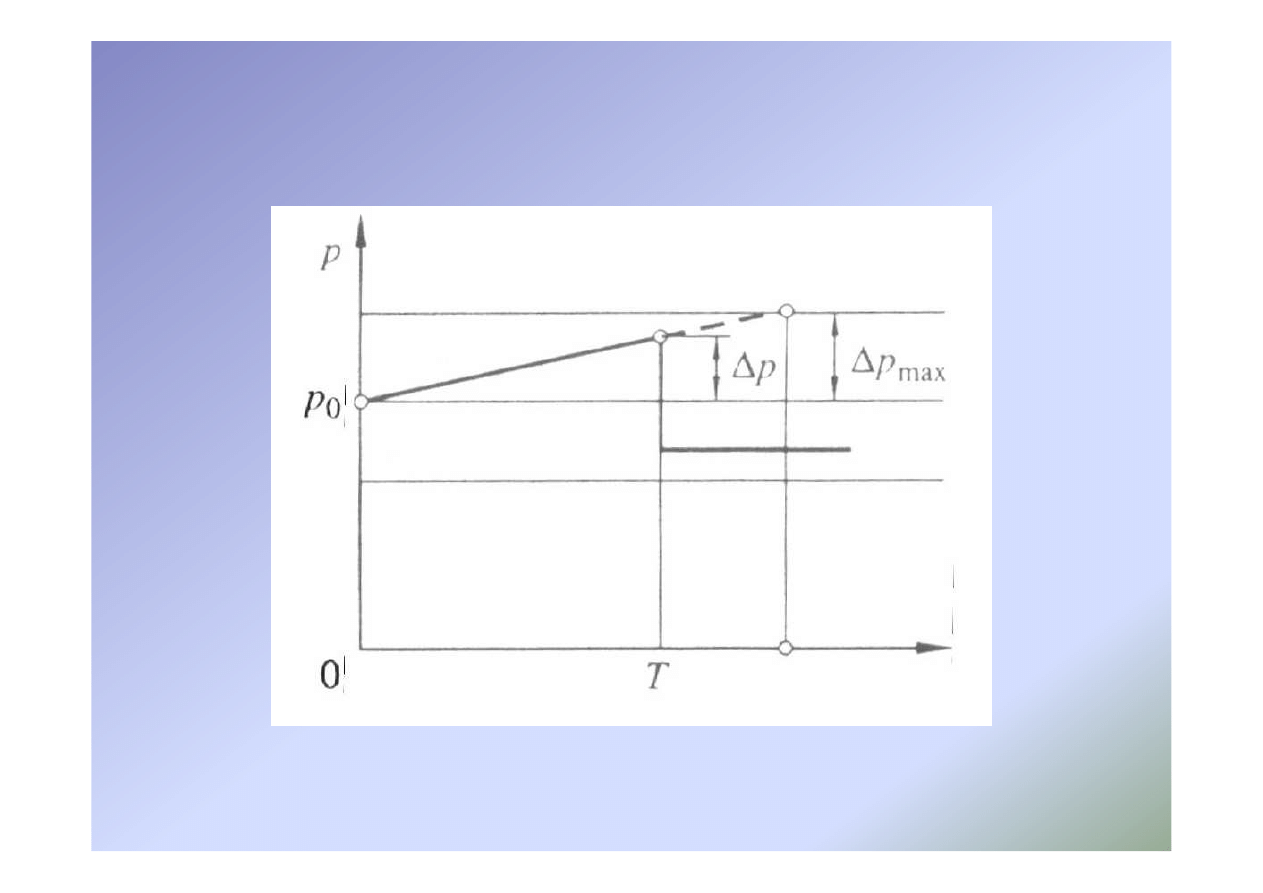
28
Złożone uderzenie hydrauliczne
Wykład 1
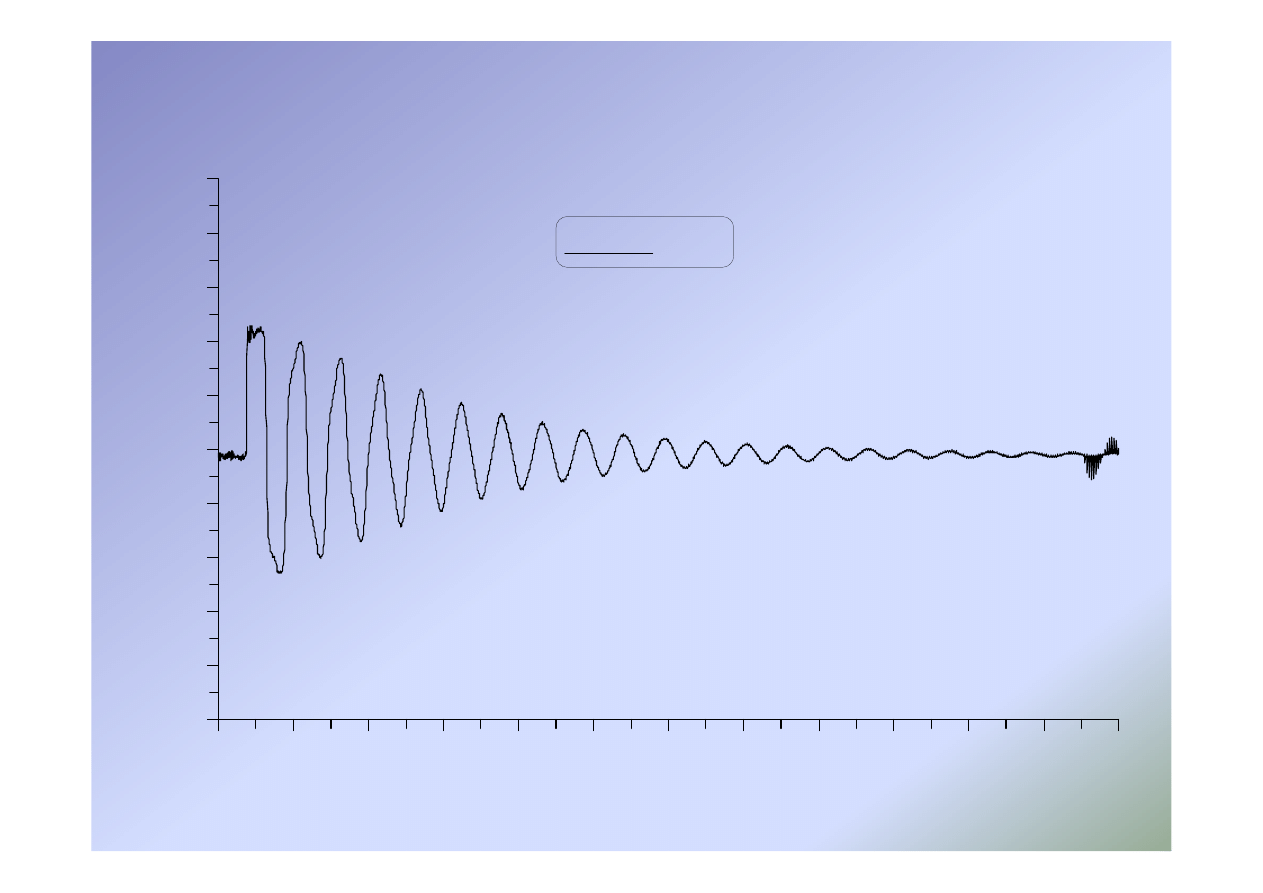
29
Uderzenie hydrauliczne – przebieg rzeczywisty
0
1
2
3
4
5
6
7
8
9
10
11
12
t
[s]
-10
0
10
20
30
40
50
60
70
80
90
p
[m
s
l
w
]
Legenda
Czujnik 1
Charakterystyka ciśnienia w funkcji czasu - Pomiar Z1 - czujnik Cz 1

Wykład 1
30
Uderzenie hydrauliczne w cieczy lepkiej
•
Punktem wyjścia jest układ równań różniczkowych: ruchu (np.
równanie Eulera) i ciągłości dla przepływu jednowymiarowego.
•
Uzupełnienie równania Eulera o człon tarcia (uwzględniający zmiany
kierunku ruchu)
•
Równanie ciągłości
X
D
x
p
x
t
=
+
∂
∂
+
∂
∂
+
∂
∂
2
1
υ
λ
ρ
υ
υ
υ
υ
Składowa
jednostkowej siły
masowej wzdłuż
osi x przewodu
0
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
x
Q
t
A
x
Q
t
A
ρ
ρ
ρ
ρ
0
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
x
A
t
A
A
x
x
t
υ
ρ
υ
ρ
ρ
υ
ρ
A
Q
υ
=
0
1
1
=
∂
∂
+
+
x
dt
dA
A
dt
dp
υ
ρ
Wykład 1
31
Uderzenie hydrauliczne w cieczy lepkiej
•
Wykorzystując zależności na względną zmianę gęstości i
odkształcalność ścianki
•
Podstawiając wzór Kortewega
0
1
1
=
∂
∂
+
+
x
dt
dp
E
e
K
D
K
υ
0
2
1
=
∂
∂
+
x
dt
dp
c
υ
ρ
0
1
=
∂
∂
+
∂
∂
+
∂
∂
x
c
x
p
t
p
c
υ
υ
ρ
Wykład 1
32
Uderzenie hydrauliczne w cieczy lepkiej
•
Układ równań dla metody charakterystyk
(
)
(
)
X
D
t
x
c
t
p
x
p
c
c
=
+
∂
∂
+
∂
∂
+
+
∂
∂
+
∂
∂
+
2
1
υ
λ
υ
υ
υ
υ
ρ
υ
(
)
(
)
X
D
t
x
c
t
p
x
p
c
c
=
+
∂
∂
+
∂
∂
−
+
∂
∂
+
∂
∂
−
−
2
1
υ
λ
υ
υ
υ
υ
ρ
υ
X
D
dt
d
dt
dp
c
=
+
+
2
1
υ
λ
υ
ρ
υ
X
D
dt
d
dt
dp
c
=
+
+
−
2
1
υ
λ
υ
ρ
υ
Dla
Dla
c
dt
dx
+
=
υ
c
dt
dx
−
=
υ
Wykład 1
33
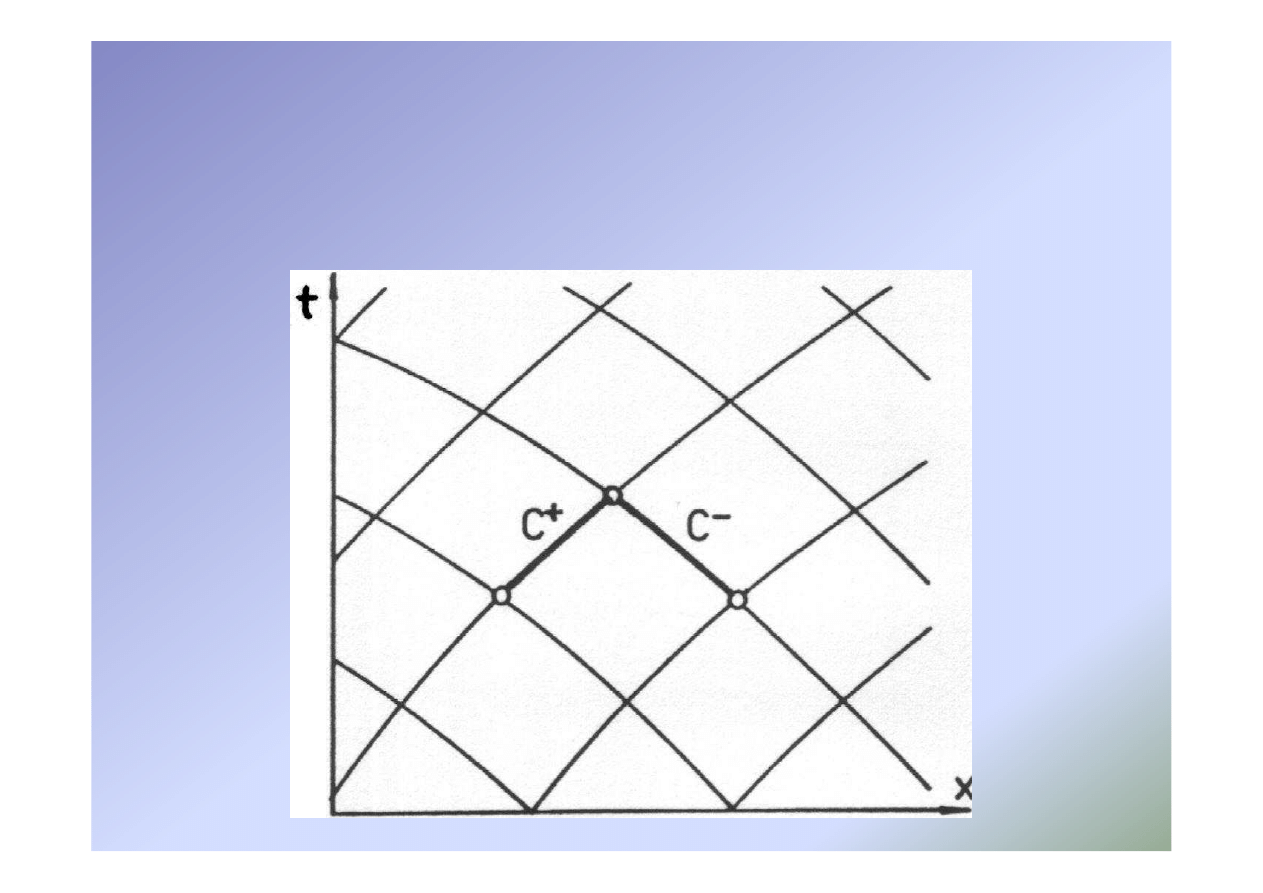
Uderzenie hydrauliczne w cieczy lepkiej
•
Metoda charakterystyk
Wykład 1
34
Uderzenie hydrauliczne w cieczy lepkiej - sieć
Wykład 1
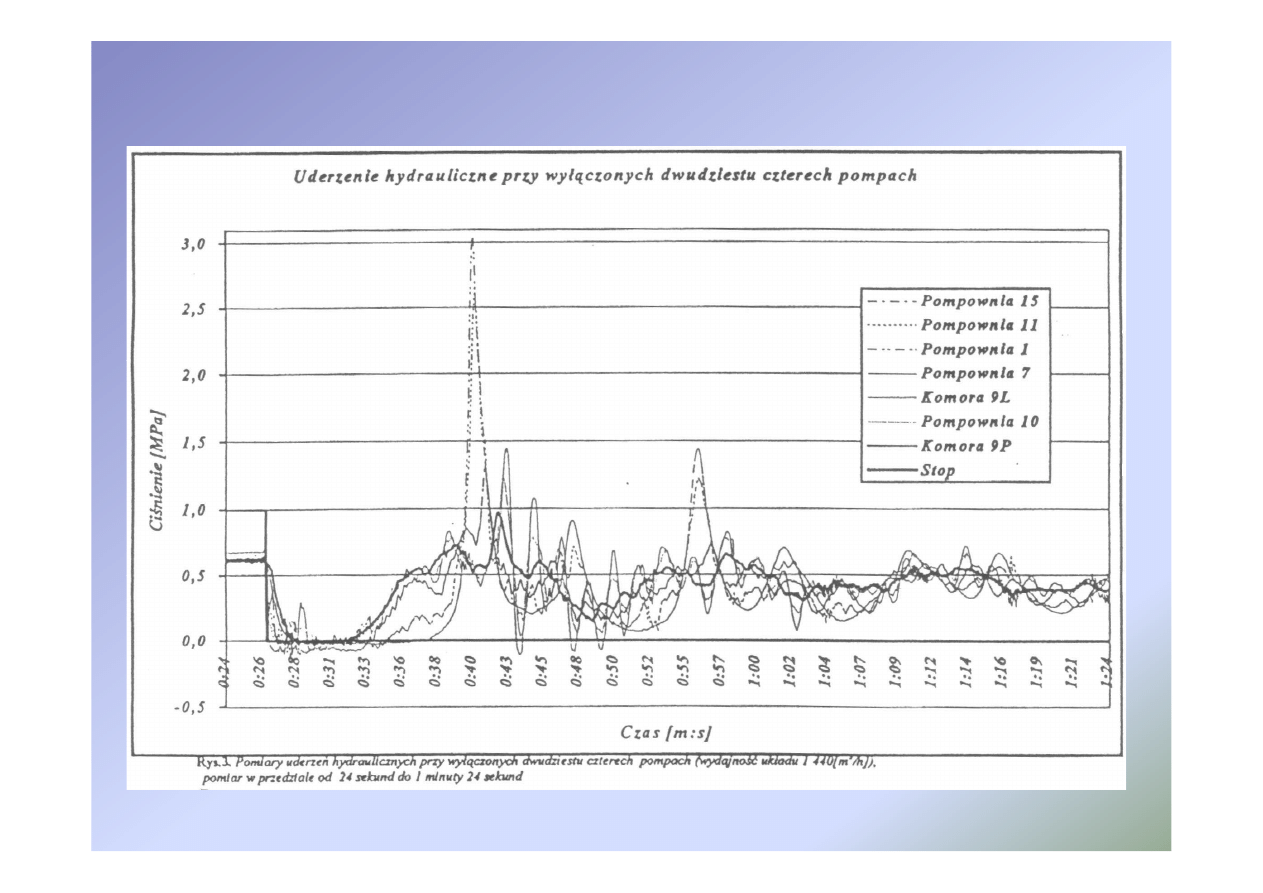
35
Uderzenie hydrauliczne w cieczy lepkiej - sieć
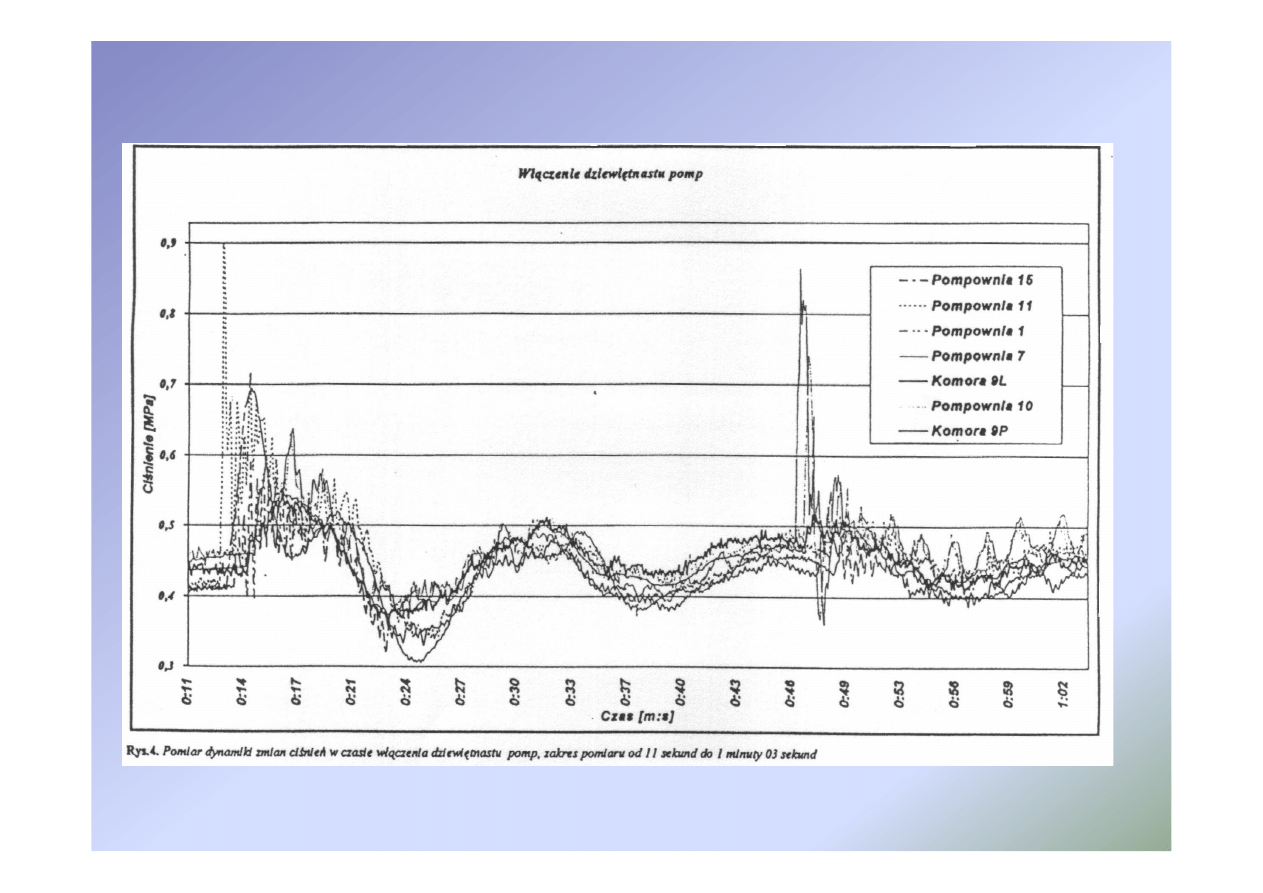
Wykład 1
36
Uderzenie hydrauliczne w cieczy lepkiej - sieć

Wykład 1
37
Metoda odbić i transformacji
•
Fala ciśnienia ulega odbiciu i transformacji (przenikaniu), w
miejscach, w których następują zmiany prędkości przepływu.
•
Dla cieczy nielepkiej zjawisko może być opisane przy użyciu
współczynnika odbicia r oraz współczynnika przenikania s
– A = pole przekroju poprzecznego przewodu,
–
ρ
= gęstość cieczy,
– c = prędkość fali ciśnienia
i
c
i
A
i
B
ρ
=
Wykład 1
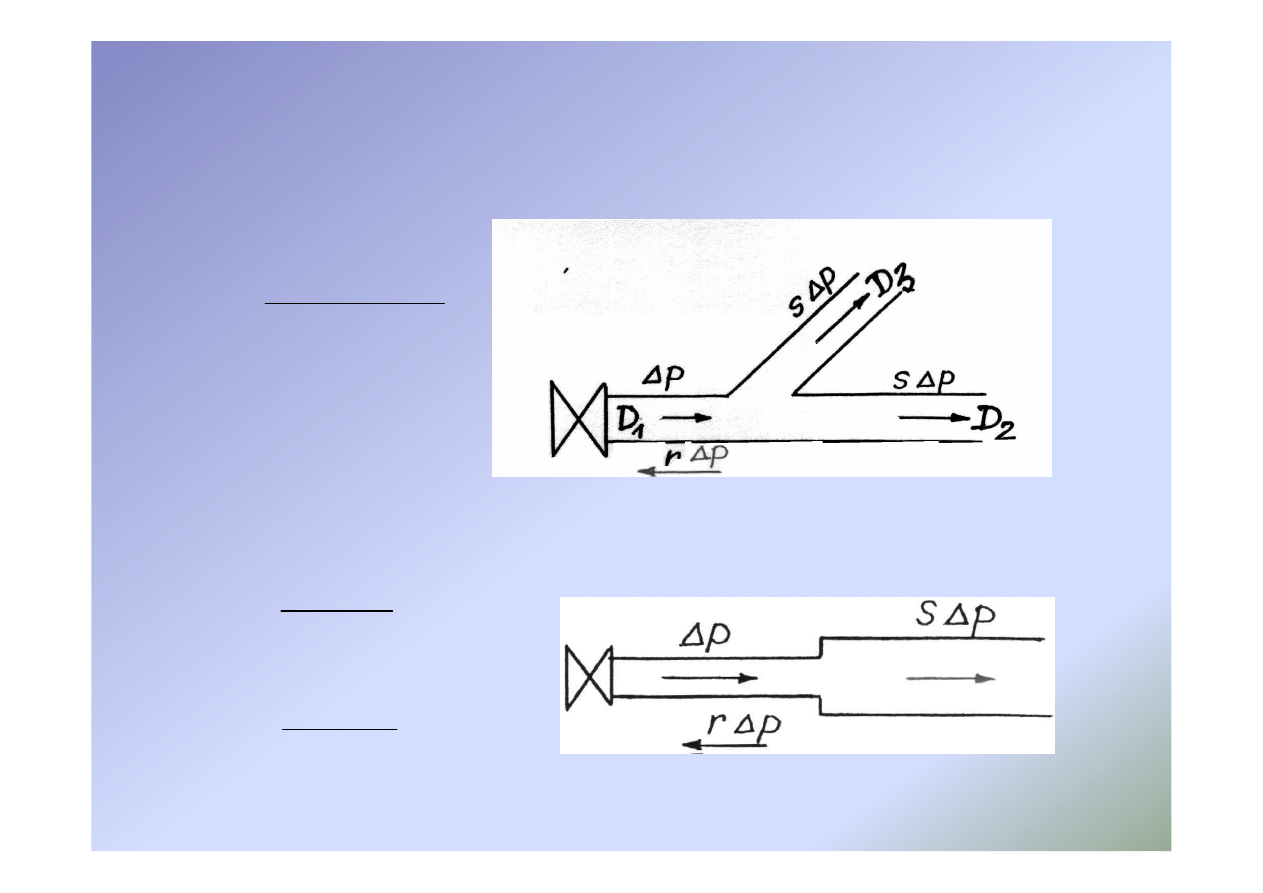
38
Metoda odbić i transformacji
•
Trójnik
•
Połączenie dwóch przewodów
3
2
1
1
2
B
B
B
B
s
+
+
=
1
−
= s
r
2
1
1
2
B
B
B
s
+
=
2
1
2
1
B
B
B
B
r
+
−
=
Wykład 1
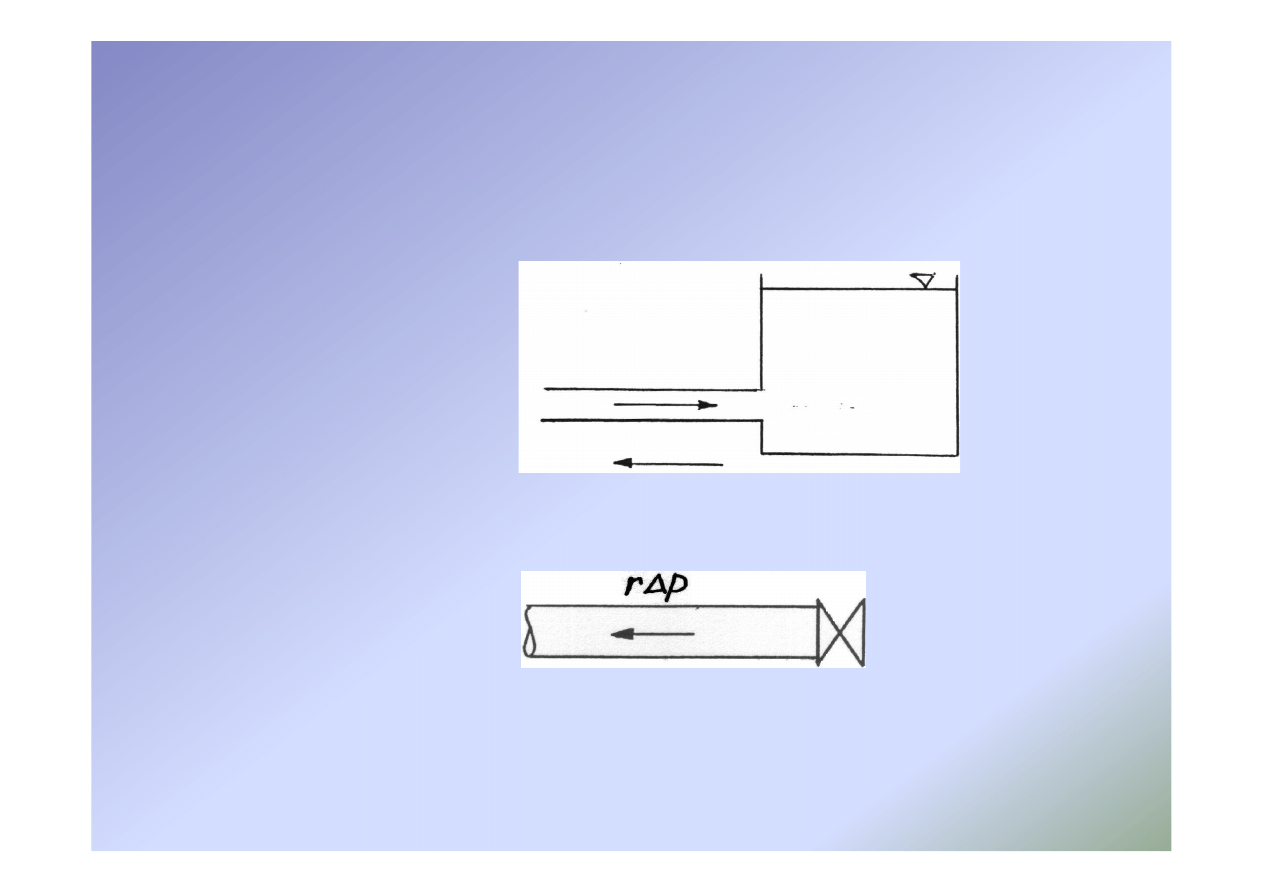
39
Metoda odbić i transformacji
•
Połączenie przewodu ze zbiornikiem
•
Odbicie od zamkniętej zasuwy
0
=
s
1
−
=
r
0
=
s
1
=
r
Wykład 1
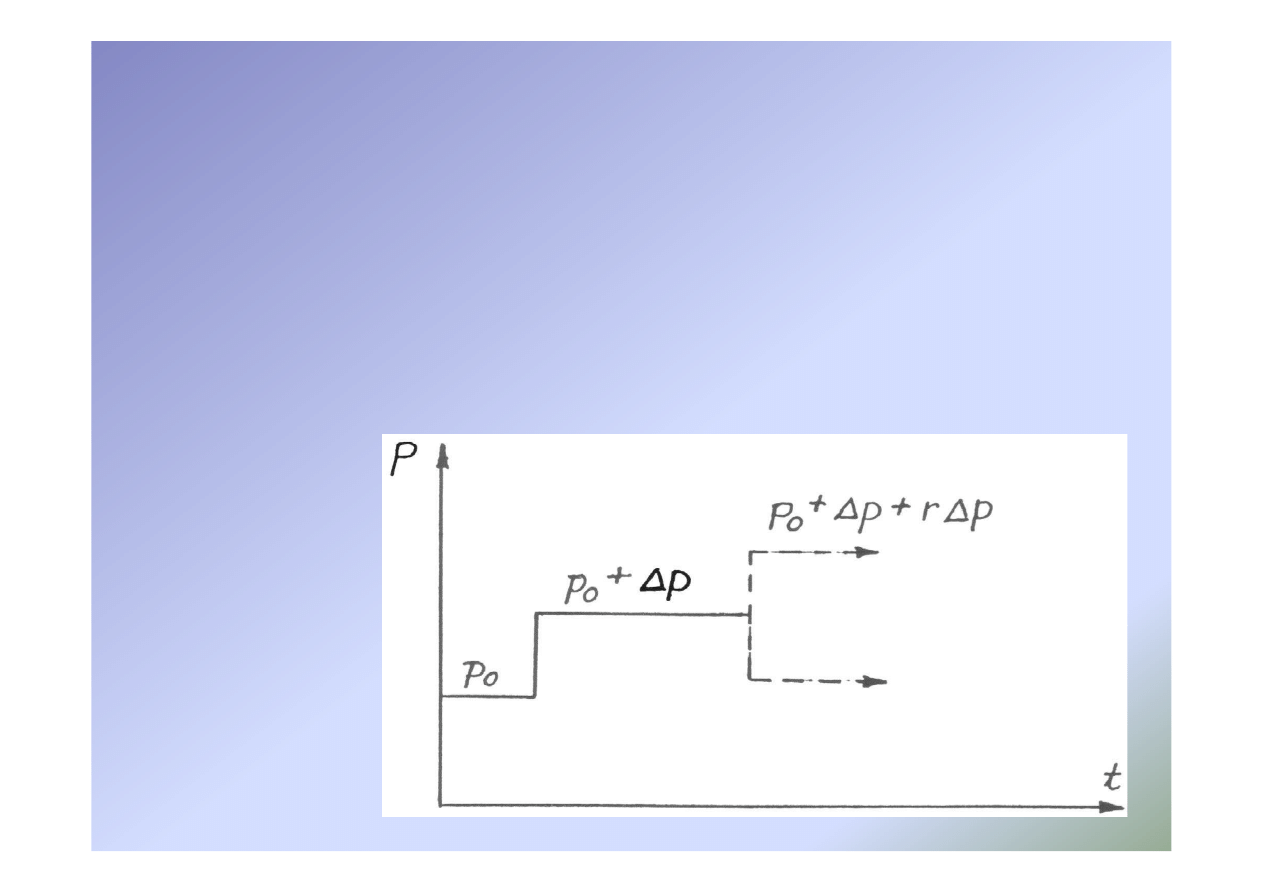
40
Metoda odbić i transformacji
•
Wartość ciśnienia przy zaworze w chwili powrotu fali odbitej
•
Ciśnienie za przekrojem
p
r
p
p
p
∆
+
∆
+
=
0
p
s
p
p
∆
+
=
0
Wykład 1
41
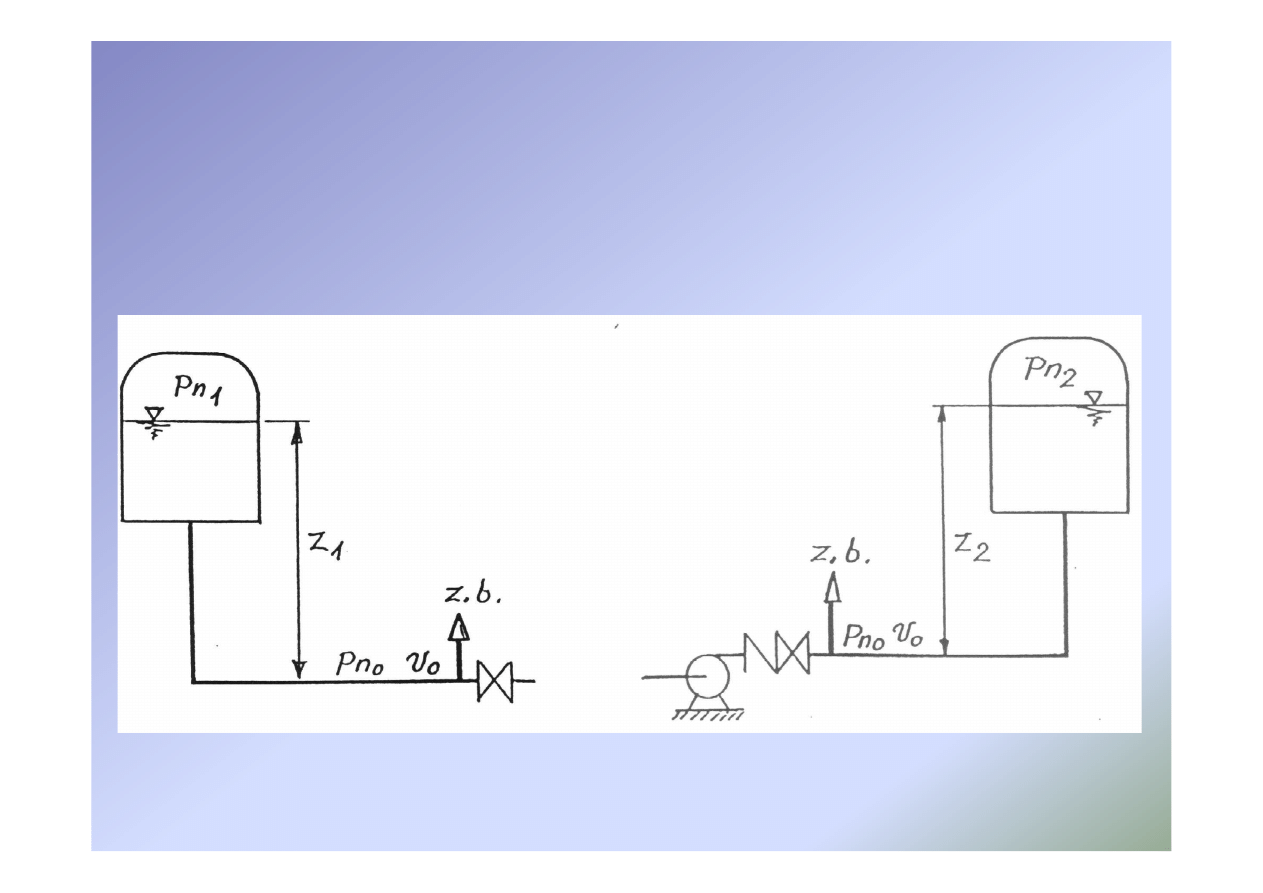
Zawory bezpieczeństwa
Połączenie zaworu bezpieczeństwa
a)
Przed zaworem odcinającym
b)
Za zaworem zwrotnym
a
b
Wykład 1
42
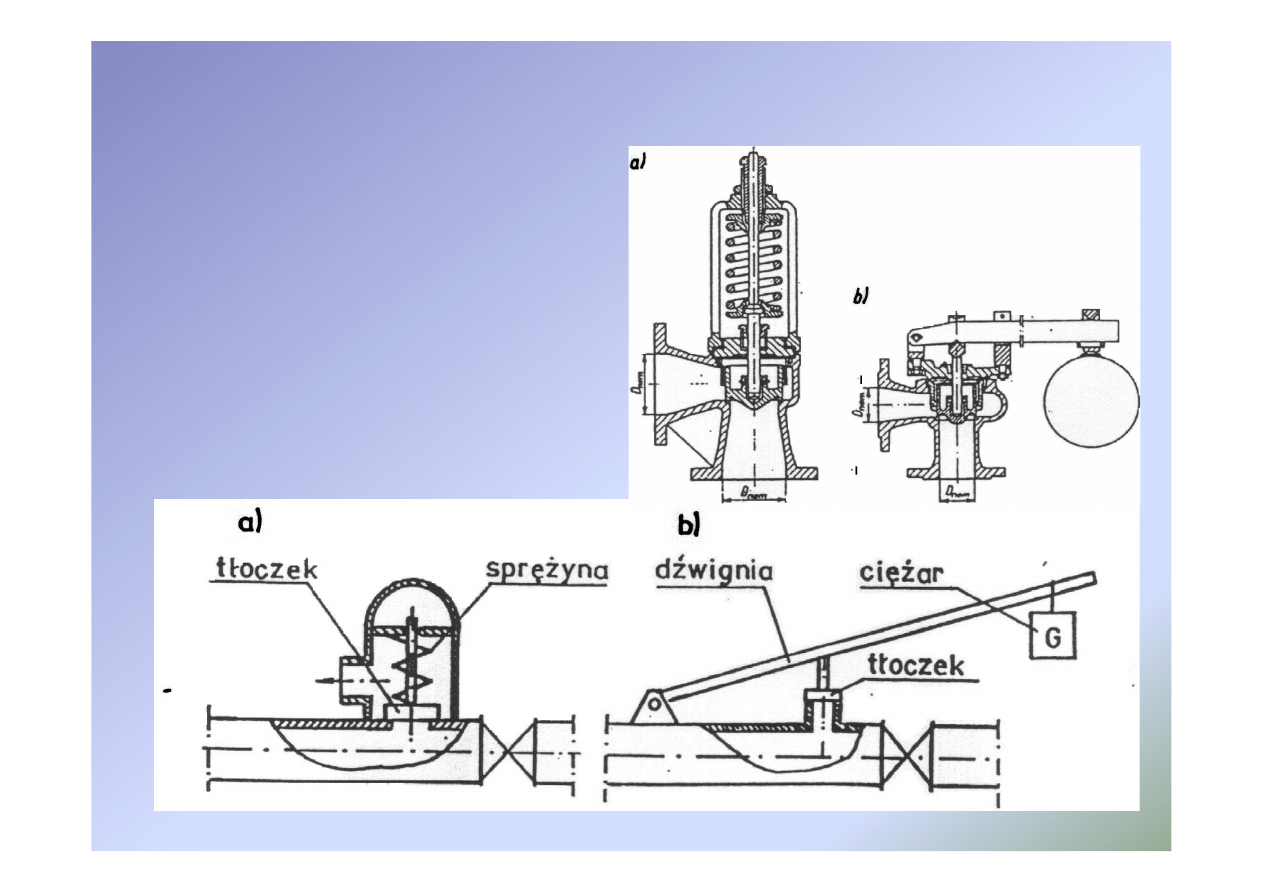
Zawory bezpieczeństwa
Zawory wysokociśnieniowe
a)
Sprężynowy
b)
dźwigniowy

Wykład 1
43
Obliczanie zaworów bezpieczeństwa
•
Zawór dźwigniowy:
– średnica gniazda d=?,
– masa obciążnika m=?.
•
Zawór sprężynowy:
– średnica gniazda d=?,
– parametry sprężyny dociskającej ?
•
Dane:
– dopuszczalne nadciśnienie dla danej instalacji - p
ndop
– nadciśnienie przy zaworze w warunkach statycznych - p
nst
– nadciśnienia cieczy przy zaworze w ruchu ustalonym - p
n0
– straty ciśnienia w ruchu ustalonym na długości rurociągu -
∆
p
f
– przyrost ciśnienia wywołanego uderzeniem hydraulicznym -
∆
p - dla
końcowej wartości prędkości w rurociągu
Wykład 1
44
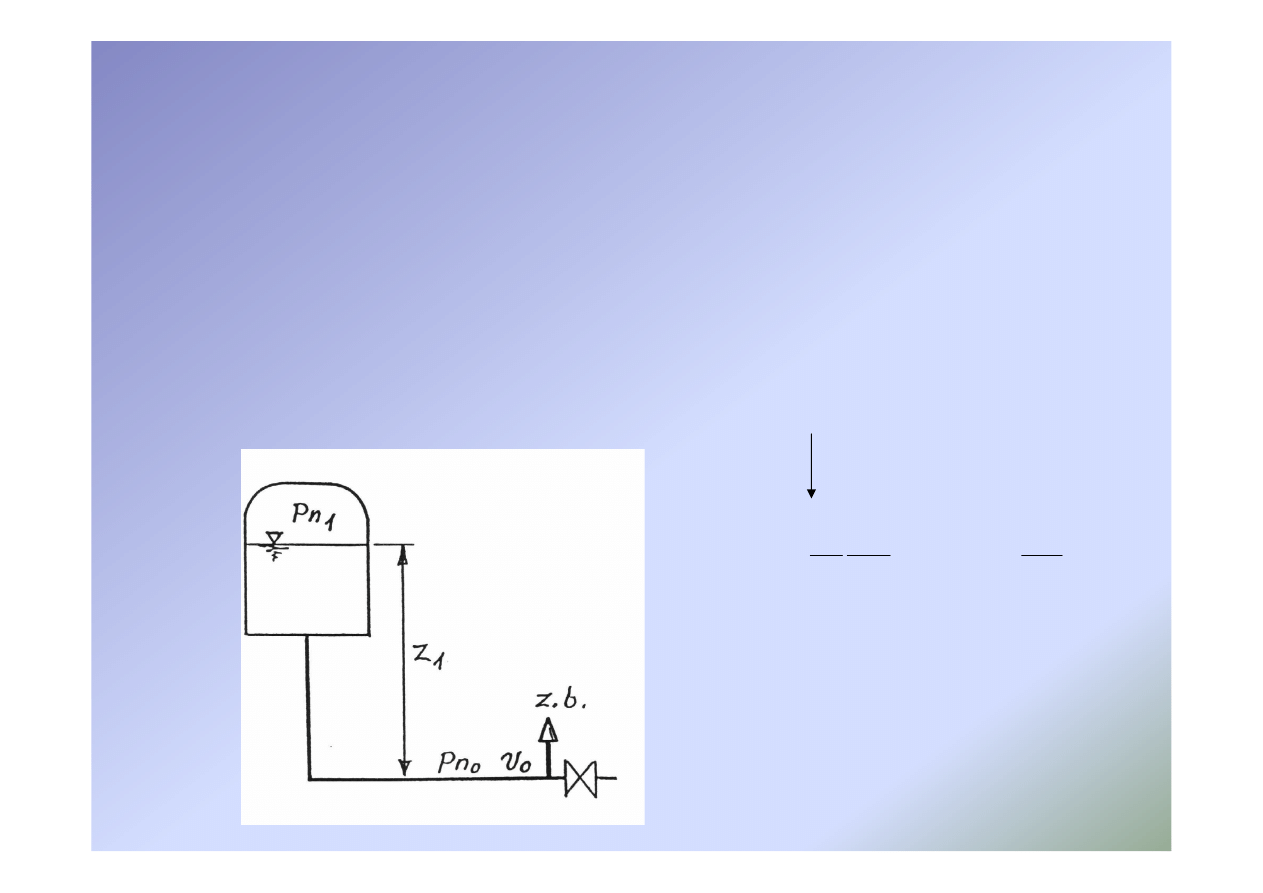
Obliczanie zaworów bezpieczeństwa
•
Nadciśnienie przy zaworze w warunkach statycznych – p
nst
•
Dopuszczalne nadciśnienie
f
n
n
nst
p
p
p
z
p
∆
+
=
+
=
0
1
1
γ
p
p
p
p
p
z
p
f
n
n
ndop
∆
+
∆
+
=
∆
+
+
=
0
1
1
γ
ρ
ζ
ρ
υ
λ
υ
∑
+
=
∆
=
n
i
f
i
D
L
p
1
2
0
2
0
2
2
Wykład 1
45
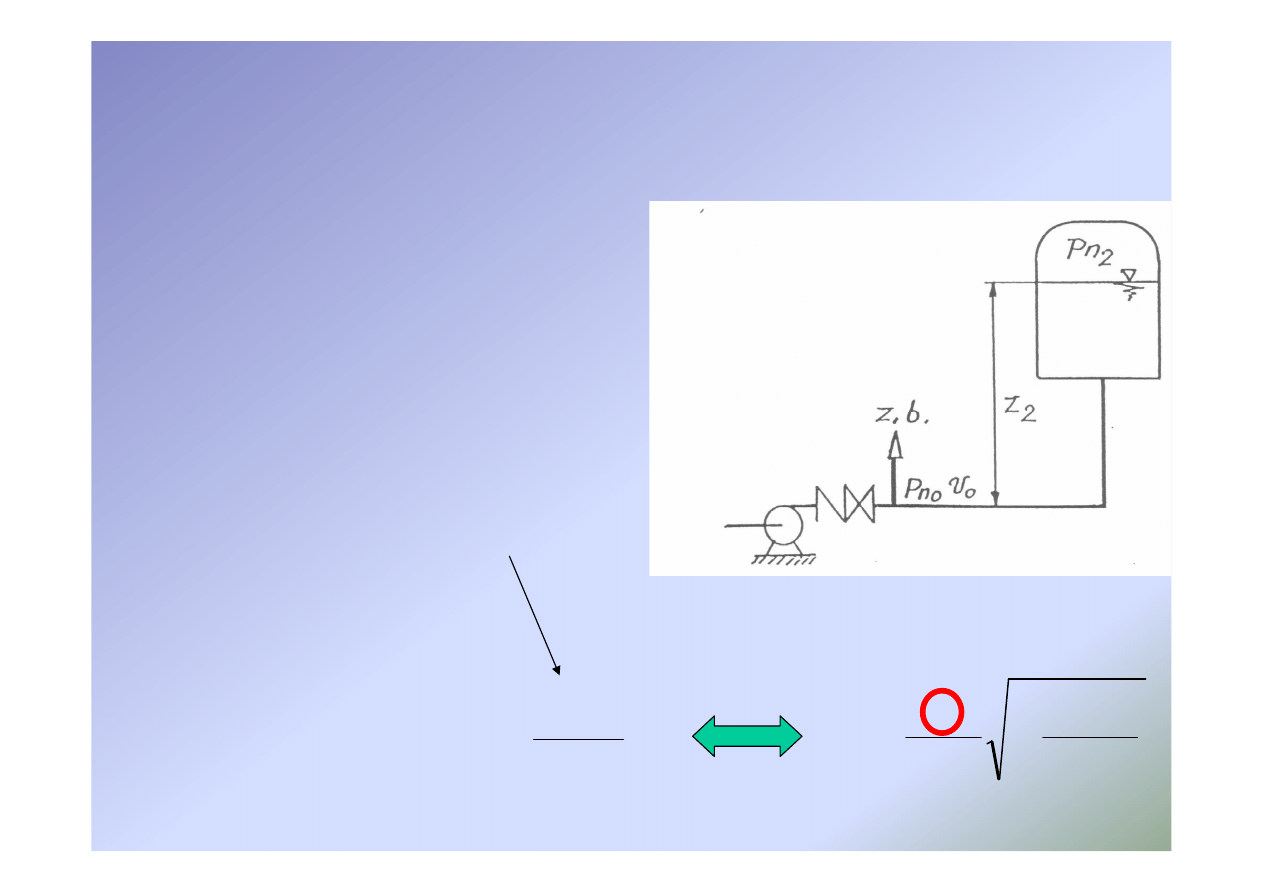
Obliczanie zaworów bezpieczeństwa
•
Dopuszczalne nadciśnienie
•
Przyrost ciśnienia wywołanego
uderzeniem
p
p
z
p
p
p
n
nst
ndop
∆
+
+
=
∆
+
=
2
2
γ
(
)
c
p
k
υ
υ
ρ
−
=
∆
0
v
k
- Minimalna prędkość, aby nie
przekroczyć dopuszczalnego
nadciśnienia p
n dop
k
D
Q
υ
π
4
2
=
ρ
π
µ
ndop
p
d
Q
2
4
2
=
4
.
0
≈
µ
Wykład 1
46
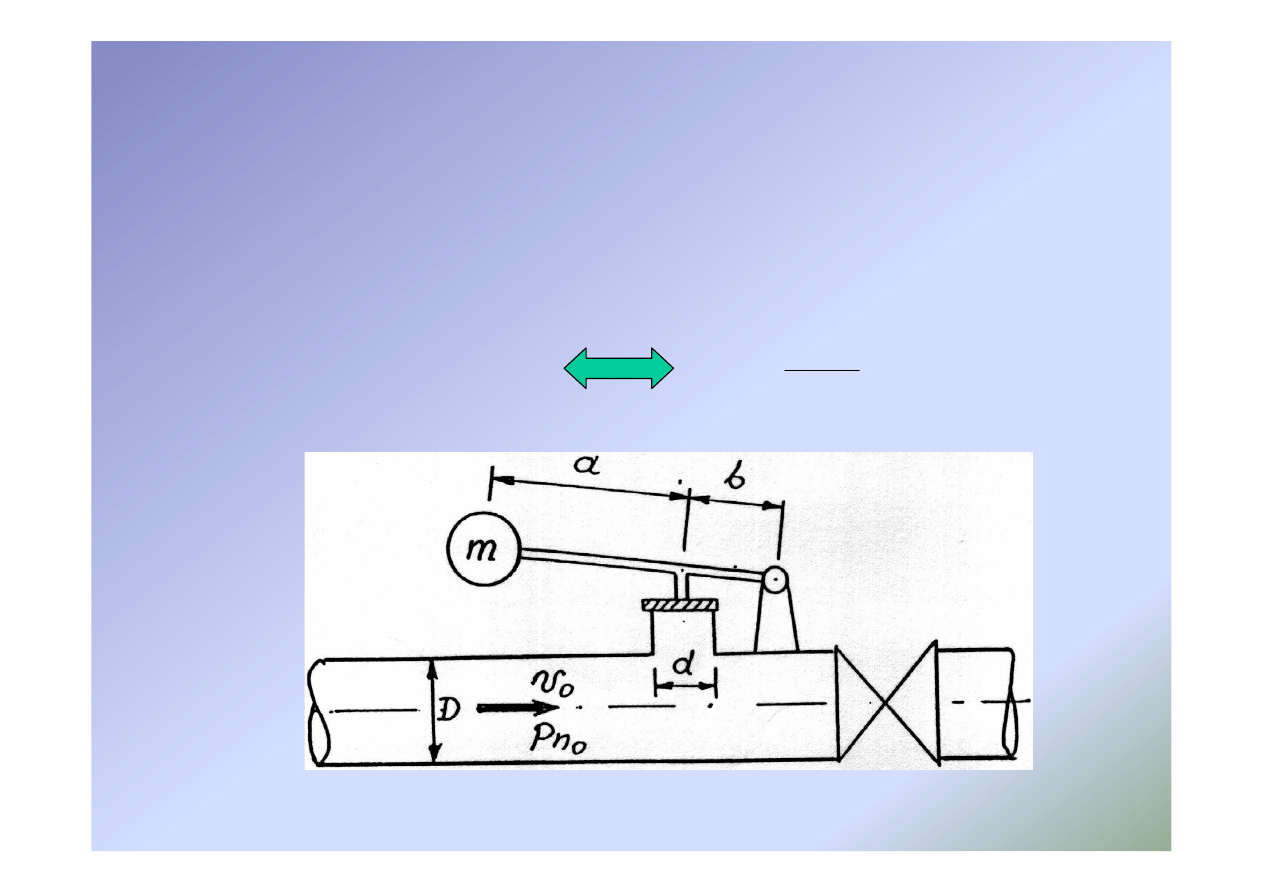
Obliczanie zaworów bezpieczeństwa
•
Określenie masy obciążnika
– Siła F działająca na grzybek zaworu bezpieczeństwa jest równa sile parcia
od nadciśnienia p
n dop
b
F
b
a
g
m
=
+ )
(
ndop
p
d
F
4
2
π
=

Wykład 1
47
Obliczanie zaworów bezpieczeństwa
•
Określenie parametrów sprężyny
– Warunkiem pracy jest równowaga sił: siły ściśnięcia\ sprężyny F
s
i siły
parcia od nadciśnienia p
n dop
– C
s
= stała sprężyny
– s
0
= normalne ściśnięcie sprężyny
0
s
C
F
s
s
=
ndop
p
d
F
4
2
π
=
Wykład 1
48
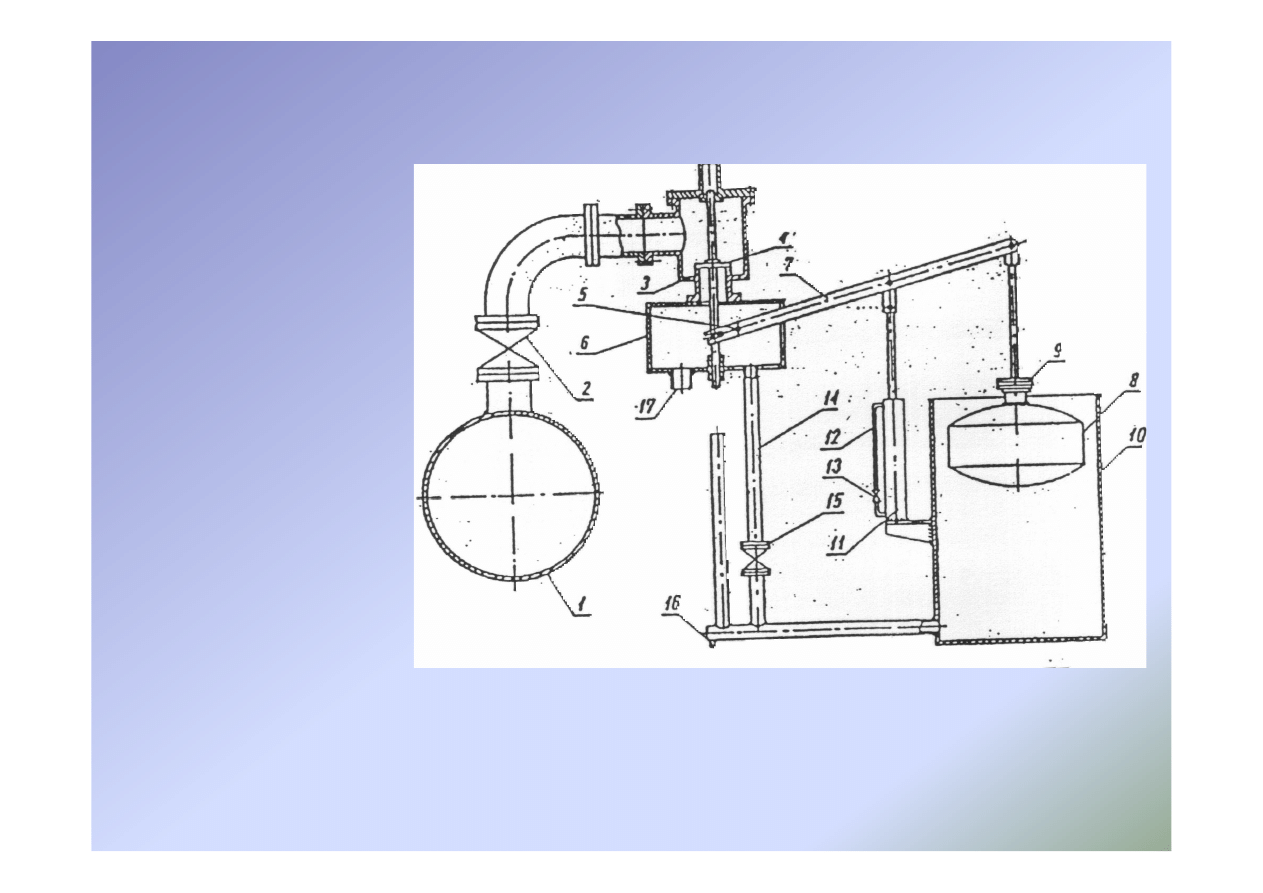
Zawory niskociśnieniowe
•
Celem jest spowalnianie szybkości otwarcia
•
Lokalizacja - na rurociągu tłocznym za zaworem zwrotnym w
pompowni
•
Skomplikowana budowa
•
Konieczność starannej konserwacji
Wykład 1
49
Zawory niskociśnieniowe
Schemat zaworu
niskociśnieniowego Chramca:
1. Przewód tłoczny
2. Zawór zasuwowy
3. Korpus zaworu
4. Grzybek
5. Oś obrotu dźwigni
6. Garnek odpływowy
7. Dźwignia
8. Pływak
9. Obciążniki
10. Zbiornik, 11. Hamulec olejowy, 12. Przewód obiegowy, 13. Zawór regulacyjny
14. Przewód odprowadzający wodę do zbiornika, 15. Zawór regulacyjny, 16. Odpływ ze
zbiornika, 17. Odpływ z zaworu
Wykład 1
50
Dobór zaworów bezpieczeństwa
1
2
1
1
2
2 – 3
3 – 4
125 - 150
125 – 150
150 – 200
200
200
200
200
300
400
500
600
900
1000
1200
Liczba zaworów
Średnica zaworu
bezpieczeństwa
[mm]
Średnica rurociągu
[mm]

Wykład 1
51
Obliczanie zaworów bezpieczeństwa – Przykład 1
•
Określić średnicę gniazda d oraz masę obciążnika m dźwigniowego
zaworu bezpieczeństwa (a = 500 mm, b = 100 mm), jeżeli: długość
rurociągu L = 2 km, średnica D = 400 mm, chropowatość ścianki k =
0.4 mm,
Σ
ξ
= 20, prędkość w ruchu ustalonym v
0
= 2.0 m/s, p
n0
= 4
bar, p
n dop
= 300% p
n0
, prędkość fali c = 1200 m/s,
ρ
= 10
3
kg/m
3
,
ν
=
1.3
⋅10
-6
m
2
/s.
Pa
bar
p
p
p
p
p
z
p
f
n
n
ndop
5
10
12
12
4
3
0
1
1
⋅
=
=
⋅
=
∆
+
∆
+
=
∆
+
+
=
γ
Pa
D
L
p
f
5
10
4
.
2
2
2
2
0
2
0
⋅
=
∑
+
=
∆
ρ
ζ
ρ
υ
λ
υ
Z wykresu C-W:
λ(Re =
6
⋅10
5
,
ε=1⋅10
-3
) = 0.02.
Pa
bar
p
p
p
p
f
n
ndop
5
10
6
.
5
6
.
5
4
.
2
4
12
0
⋅
=
=
−
−
=
∆
−
−
=
∆
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron