1
Podstawy Konstrukcji Maszyn
Wykład 3
Obciążenia zmienne
Dr inż. Jacek Czarnigowski
Zmienność obciążeń
Klasyfikacja obciążeń:
Obciążenia stałe
Obciążenia zmienne
Wartość, kierunek i zwrot
nie ulegają zmianie w czasie
Wartość, kierunek lub zwrot
(jedna lub wiele z
powyższych) ulega zmianie
w czasie
O zmienności ustalonej
O zmienności nieustalonej
2
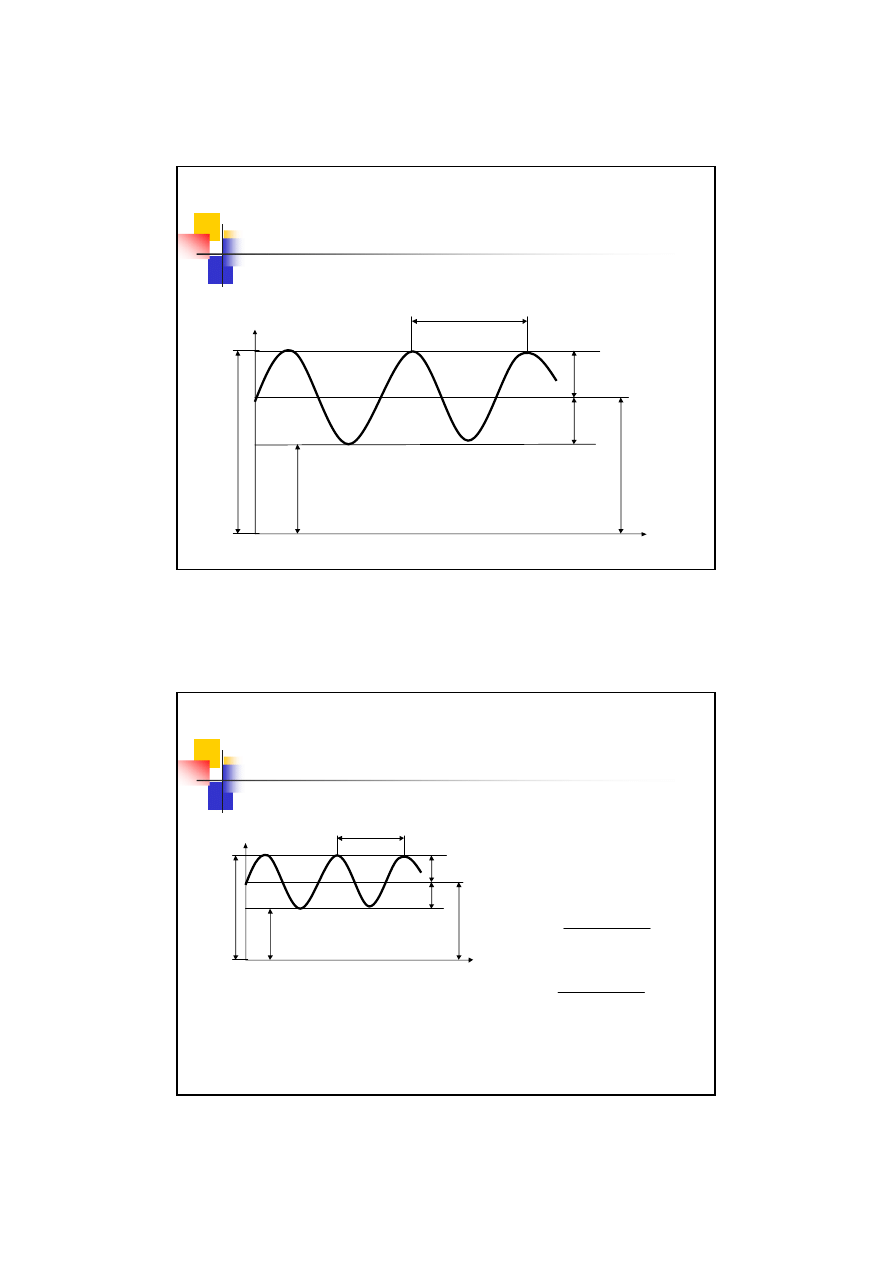
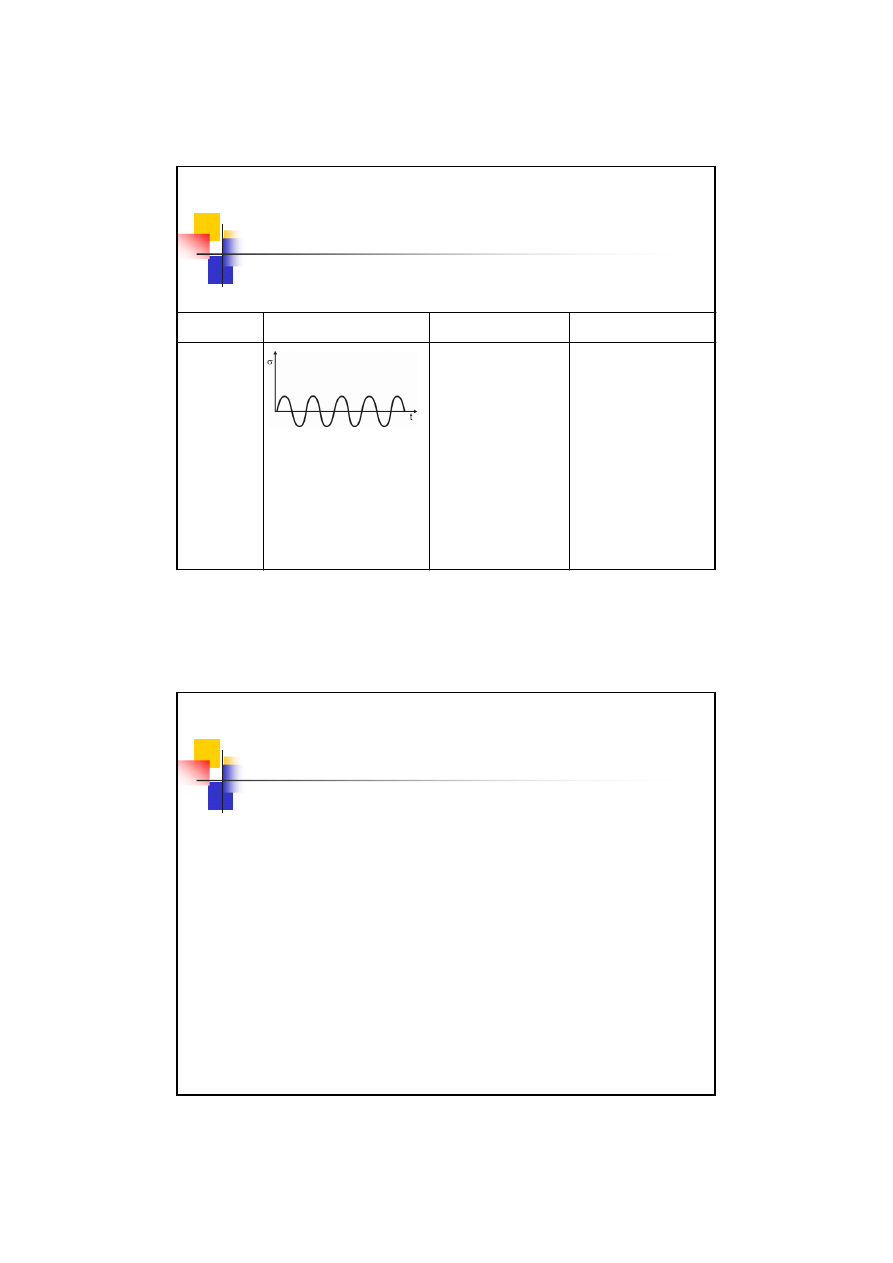
Zmienność obciążenia
Przebieg zmienności obciążenia
Czas
Naprężenie
σ
σ
min
σ
max
σ
a
σ
a
σ
m
Naprężenie maksymalne
Naprężenie minimalne
Naprężenie
amplitudowe
Naprężenie
średnie
T
– okres zmian
Zmienność obciążenia
Przebieg zmienności obciążenia
Czas
t
Naprężenie
σ
σ
min
σ
max
σ
a
σ
a
σ
m
T
– okres zmian
( )
( )
t
t
a
m
⋅
⋅
+
=
ϖ
σ
σ
σ
sin
2
min
max
σ
σ
σ
+
=
m
2
min
max
σ
σ
σ
−
=
a
a
m
σ
σ
σ
+
=
max
a
m
σ
σ
σ
−
=
min
3
Współczynniki charakteryzujące
zmienność cyklu
Do opisu zmienności cyklu (jego asymetrii) stosuje
się zamiennie dwa współczynniki
Współczynnik amplitudy cyklu
max
min
σ
σ
=
R
Współczynnik stałości obciążenia
a
m
σ
σ
κ
=
Współczynniki charakteryzujące
zmienność cyklu
Współczynniki te są względem siebie przekształcalne
Współczynnik amplitudy cyklu
max
min
σ
σ
=
R
Współczynnik stałości obciążenia
a
m
σ
σ
κ
=
max
min
σ
σ
=
R
a
m
a
m
σ
σ
σ
σ
+
−
=
1
1
+
−
=
a
m
a
m
σ
σ
σ
σ
1
1
+
−
=
κ
κ
a
m
σ
σ
κ
=
min
max
min
max
σ
σ
σ
σ
−
+
=
max
min
max
min
1
1
σ
σ
σ
σ
−
+
=
R
R
−
+
=
1
1
4
Współczynniki charakteryzujące
zmienność cyklu
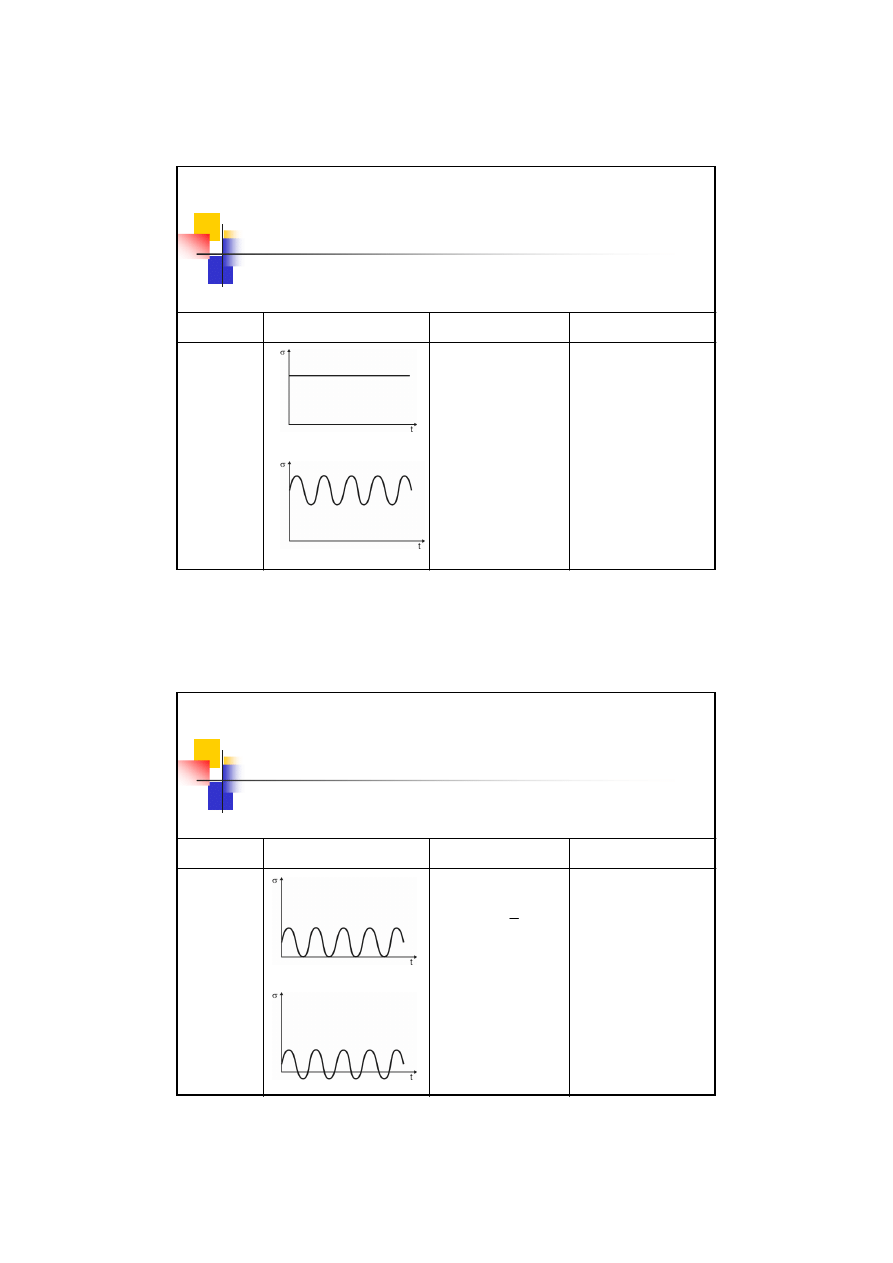
Wartości współczynników dla różnych zmienności obciążenia
Rodzaj
cyklu
Schemat
Naprężenia
Współczynniki
Stały
0
min
max
>
=
=
m
σ
σ
σ
0
=
a
σ
+∞
=
+
=
κ
1
R
Jednostronny
0
,
,
min
max
>
m
σ
σ
σ
0
>
a
σ
+∞
<
<
<
<
κ
1
1
0
R
Współczynniki charakteryzujące
zmienność cyklu
Wartości współczynników dla różnych zmienności obciążenia
Rodzaj
cyklu
Schemat
Naprężenia
Współczynniki
Odzerowo-
tętniący
0
0
min
max
=
>
σ
σ
max
2
1
σ
σ
σ
=
=
m
a
1
0
=
=
κ
R
Dwustronny
0
0
min
max
<
>
σ
σ
0
0
>
>
m
a
σ
σ
1
0
0
1
<
<
<
<
−
κ
R
5
Współczynniki charakteryzujące
zmienność cyklu
Wartości współczynników dla różnych zmienności obciążenia
Rodzaj
cyklu
Schemat
Naprężenia
Współczynniki
Wahadłowy
min
max
σ
σ
−
=
max
0
σ
σ
σ
=
=
a
m
0
1
=
−
=
κ
R
Wytrzymałość zmęczeniowa
Wytrzymałość materiału obciążonego w sposób zmienny
jest niższa niż w przypadku obciążenia stałego.
Jako „wytrzymałość” należy rozumieć graniczne
obciążenie jakie element jest w stanie przenieść
6
Wytrzymałość zmęczeniowa
Czynniki wpływające na wytrzymałość zmęczeniową
elementu:
2. Zmienność obciążenia
3. Kształt przedmiotu
4. Stan powierzchni
5. Wielkość przedmiotu
6. Agresywne działanie środowiska
7. Temperatura pracy
1. Materiał elementu
Wytrzymałość zmęczeniowa
Czynniki wpływające na wytrzymałość zmęczeniową
elementu:
2. Zmienność obciążenia
1. Materiał elementu
Badania nad wytrzymałością przy obciążeniach zmiennych przeprowadził
Wöhler (druga połowa XIX wieku)
7
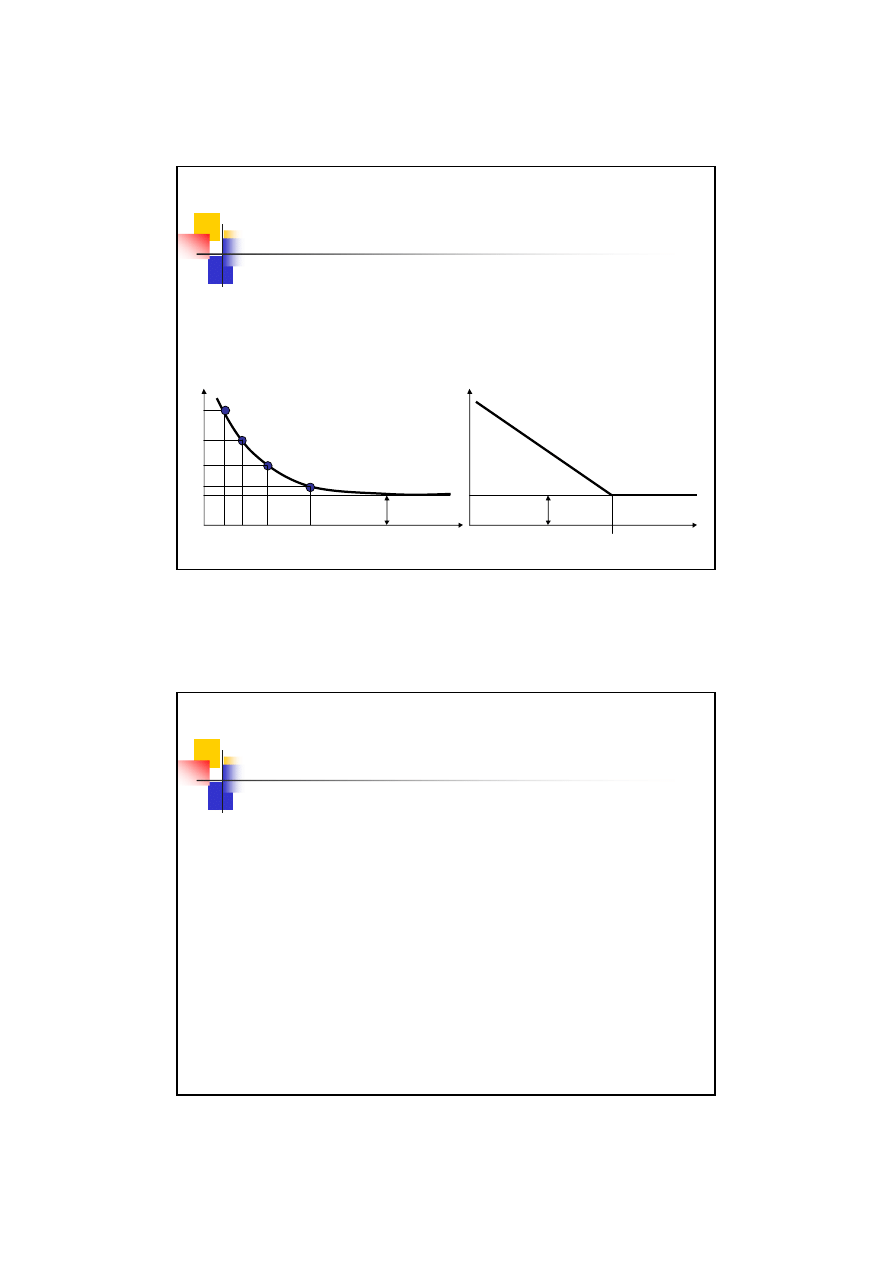
Wytrzymałość zmęczeniowa –
wykres Wöhlera
Przeprowadził badania dla próbki wzorcowej przy danym typie
obciążenia, przy zmiennej amplitudzie a stałym współczynniku
amplitudy cyklu
R. Celem badań było określenie ilości cykli
obciążenia jakie wytrzyma próbka przy danym obciążeniu
Liczba cykli N
σ
σ
1
N
1
σ
2
N
2
σ
3
N
3
σ
4
N
4
Z – granica zmęczenia
log N
σ
N=10 10
6
Granica zmęczenia
Granica zmęczenia (wytrzymałość zmęczeniowa)
Z –
największe naprężenie, przy którym próbka nie ulegnie zniszczeniu
po osiągnięciu umownej granicy liczby cykli
N (bazowa liczba cykli)
Bazowa liczba cykli wynosi:
– dla stali
N
= 10 ·10
6
– dla stopów metali nieżelaznych
N
= 100 ·10
6
– w badaniach porównawczych
N
= 2 ·10
6
, 5 ·10
6
, 20 ·10
6
Badania prowadzi się najczęściej dla dwóch charakterystycznych cykli:
- odzerowo-tętniącego
- wahadłowego.
8
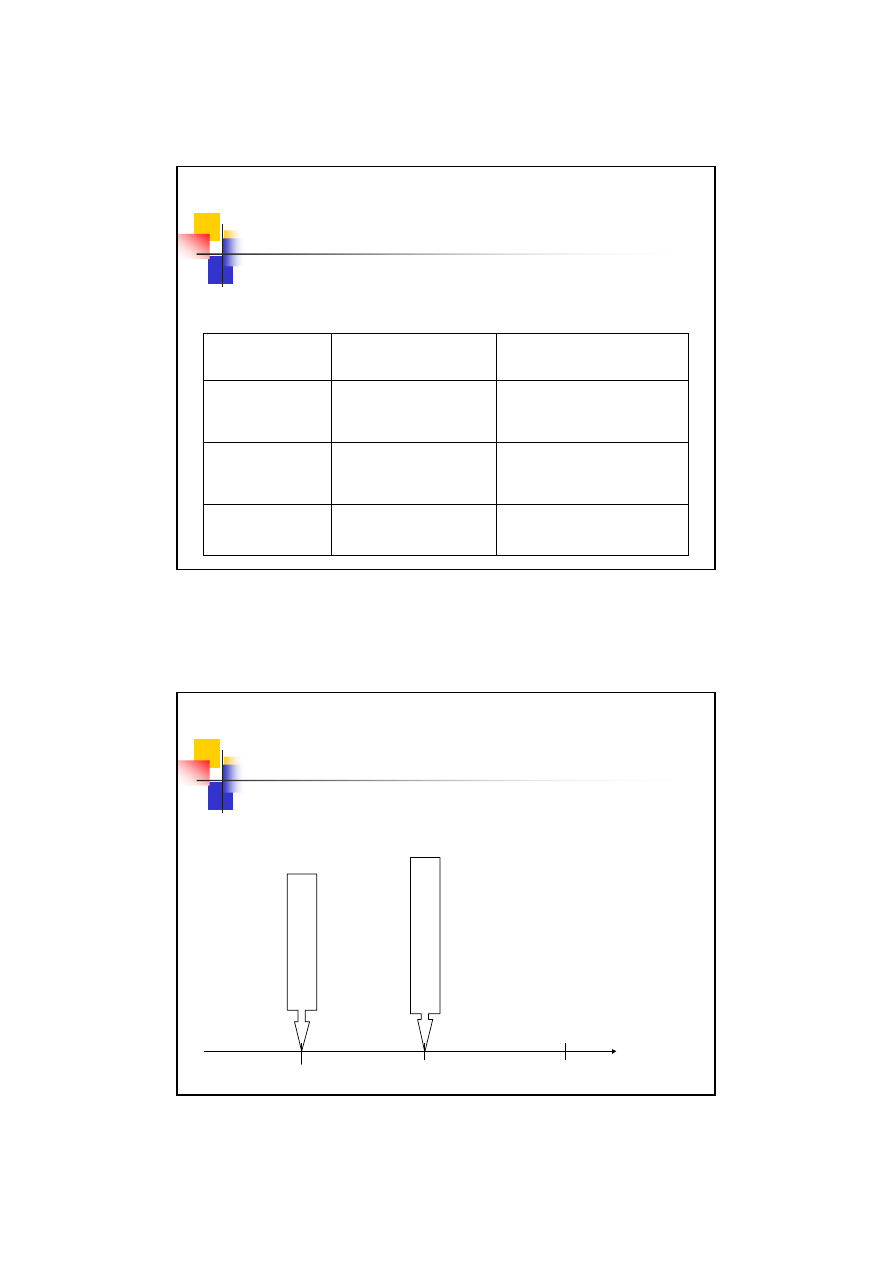
Granica zmęczenia
Granica zmęczenia
Z
dla stali wartości orientacyjne
Cykl wahadłowy
Cykl odzerowo-
tętniący
Skręcanie
Zginanie
Rozciąganie i
ściskanie
Obciążenie
(
)
m
rj
R
Z
⋅
÷
=
63
,
0
55
,
0
m
rc
R
Z
⋅
=
33
,
0
m
gj
R
Z
⋅
=
7
,
0
m
go
R
Z
⋅
=
45
,
0
(
)
m
sj
R
Z
⋅
÷
=
5
,
0
45
,
0
m
so
R
Z
⋅
=
25
,
0
Granica zmęczenia
Granica zmęczenia
Z określana jest dla 2 rodzajów cykli:
odzerowo-tętniącego i wahadłowego. Dla każdego materiału i
rodzaju obciążenia określane są te dwie wielkości.
-1
0
+1
Zmienność amplitudy
cyklu R
Z
rj
Z
gj
Z
sj
Z
tj
Z
cj
Z
rc
Z
go
Z
so
Z
to
?
?
9
Wykresy zmęczeniowe
Wykresy zmęczeniowe – na podstawie dalszych badań opartych
na badaniach Wöhlera opracowano zależności granicy zmęczenia od
cyklu obciążenia. Zauważono, że zależności te są identyczne dla
wszystkich badanych materiałów. Zależności te przedstawiono za
pomocą wykresów:
W układzie współrzędnych:
σ
max
σ
min
(
σ
m
)
W układzie współrzędnych:
σ
a
(
σ
m
)
Wykres Smitha
Wykres Haigha
σ
max
σ
min
σ
m
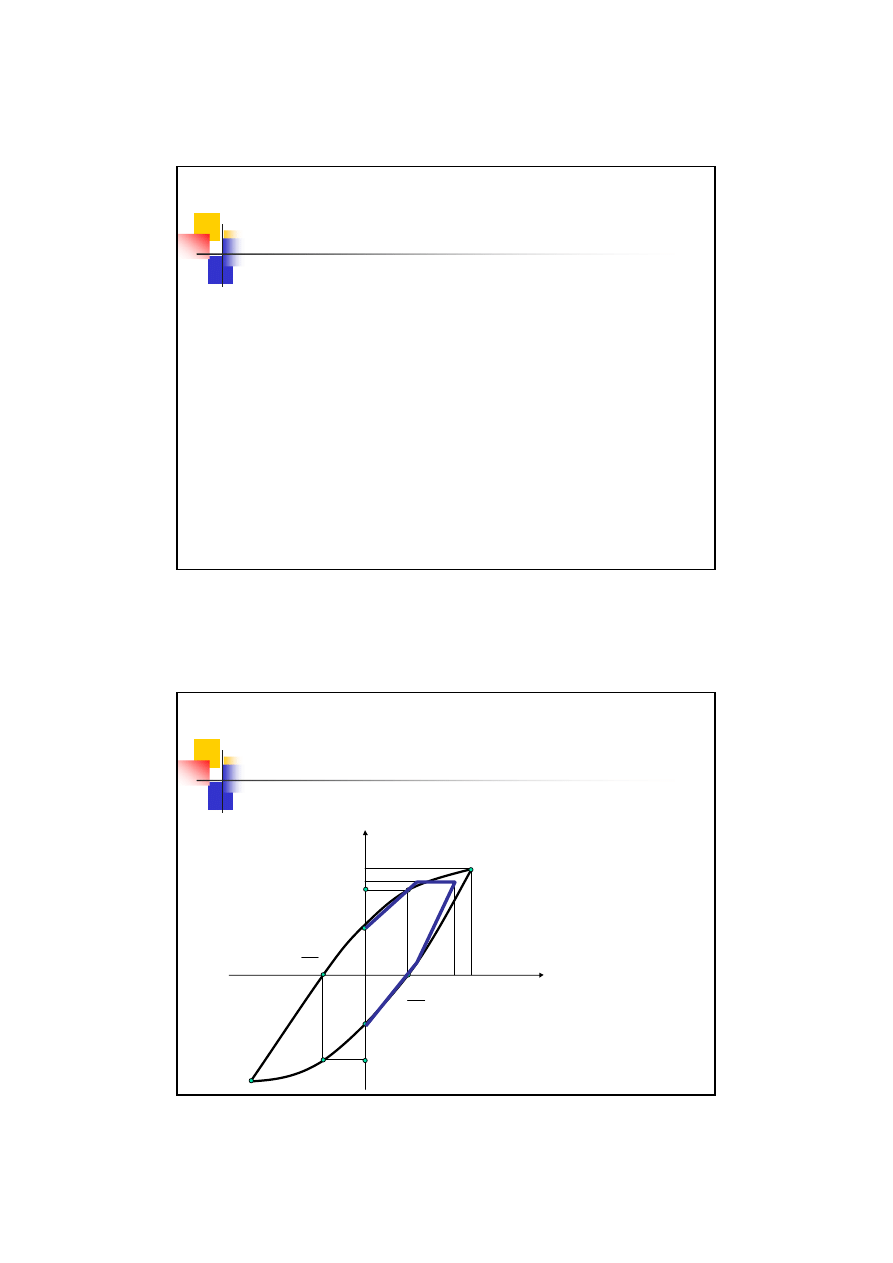
Wykresy zmęczeniowe – wykres
Smitha
W układzie współrzędnych:
σ
max
σ
min
(
σ
m
)
Z
rj
-Z
rc
Z
rc
Z
rj
2
-Z
rj
-Z
rj
2
R
m
R
m
R
e
R
e
10
σ
max
σ
min
σ
m
Wykresy zmęczeniowe – wykres
Smitha
Wykres uproszczony
Z
rj
-Z
rc
Z
rc
Z
rj
2
R
e
R
e
1
2
3
4
4’
5
6
7
7’
Wykres zawsze łączy punkty
1, 7, 6, 7’, 2
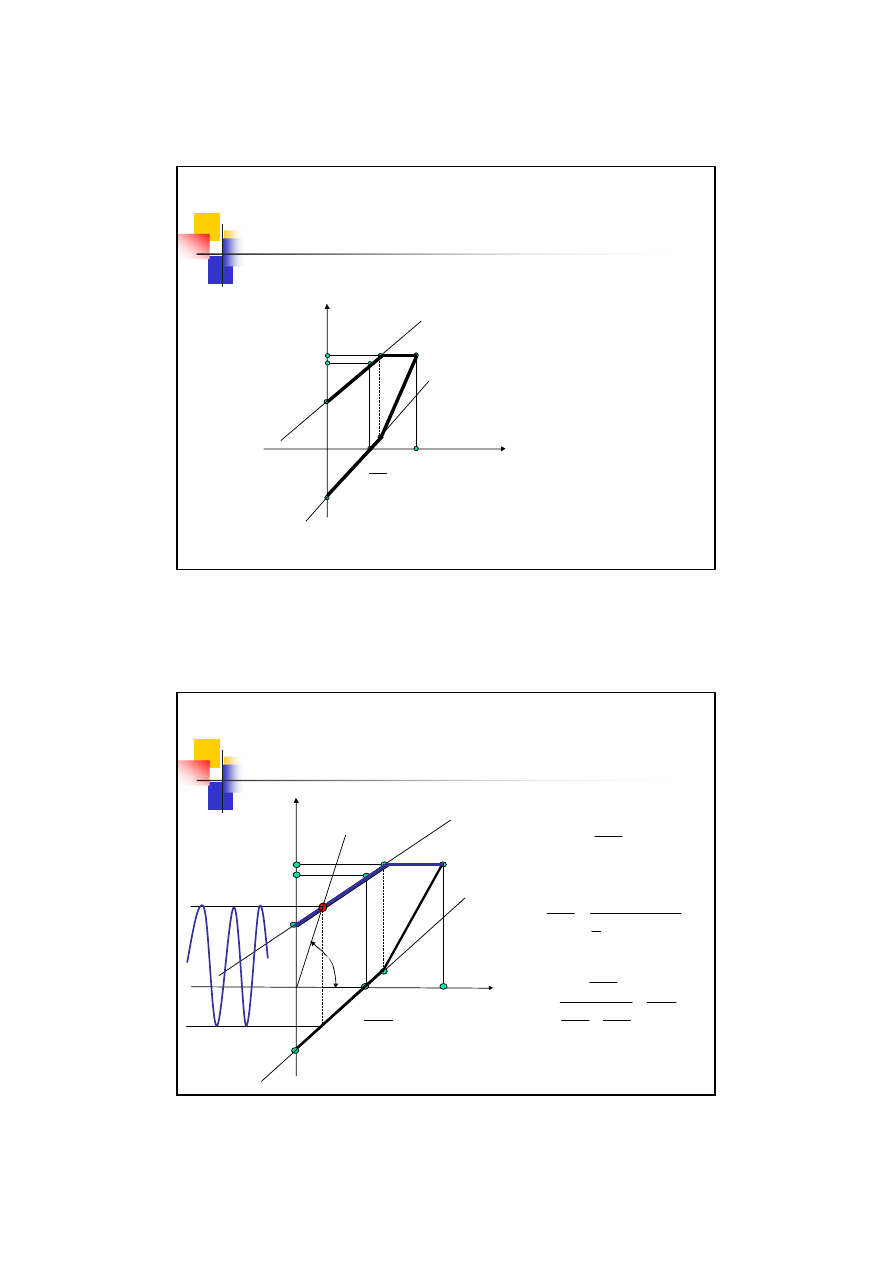
Wykresy zmęczeniowe – wykres
Smitha
Odczyt z wykresu
σ
max
σ
min
σ
m
Z
rj
-Z
rc
Z
rc
Z
rj
2
R
e
R
e
1
2
3
4
4’
5
6
7
7’
Z
r
κ
Widmo cyklu
β
m
tg
σ
σ
β
max
=
Współczynnik amplitudy cyklu
(
)
min
max
max
max
2
1
σ
σ
σ
σ
σ
β
+
⋅
=
=
m
tg
R
tg
+
=
+
⋅
=
1
2
2
max
min
max
max
max
max
σ
σ
σ
σ
σ
σ
β
11
Wykresy zmęczeniowe – wykres
Smitha
Odczyt z wykresu
σ
max
σ
min
σ
m
Z
rj
-Z
rc
Z
rc
Z
rj
2
R
e
R
e
1
2
3
4
4’
5
6
7
7’
Z
r
κ
Widmo cyklu
β
m
tg
σ
σ
β
max
=
Współczynnik stałości obciążenia
m
a
m
m
tg
σ
σ
σ
σ
σ
β
+
=
=
max
κ
σ
σ
β
1
1
1
+
=
+
=
m
a
tg
σ
a
σ
m
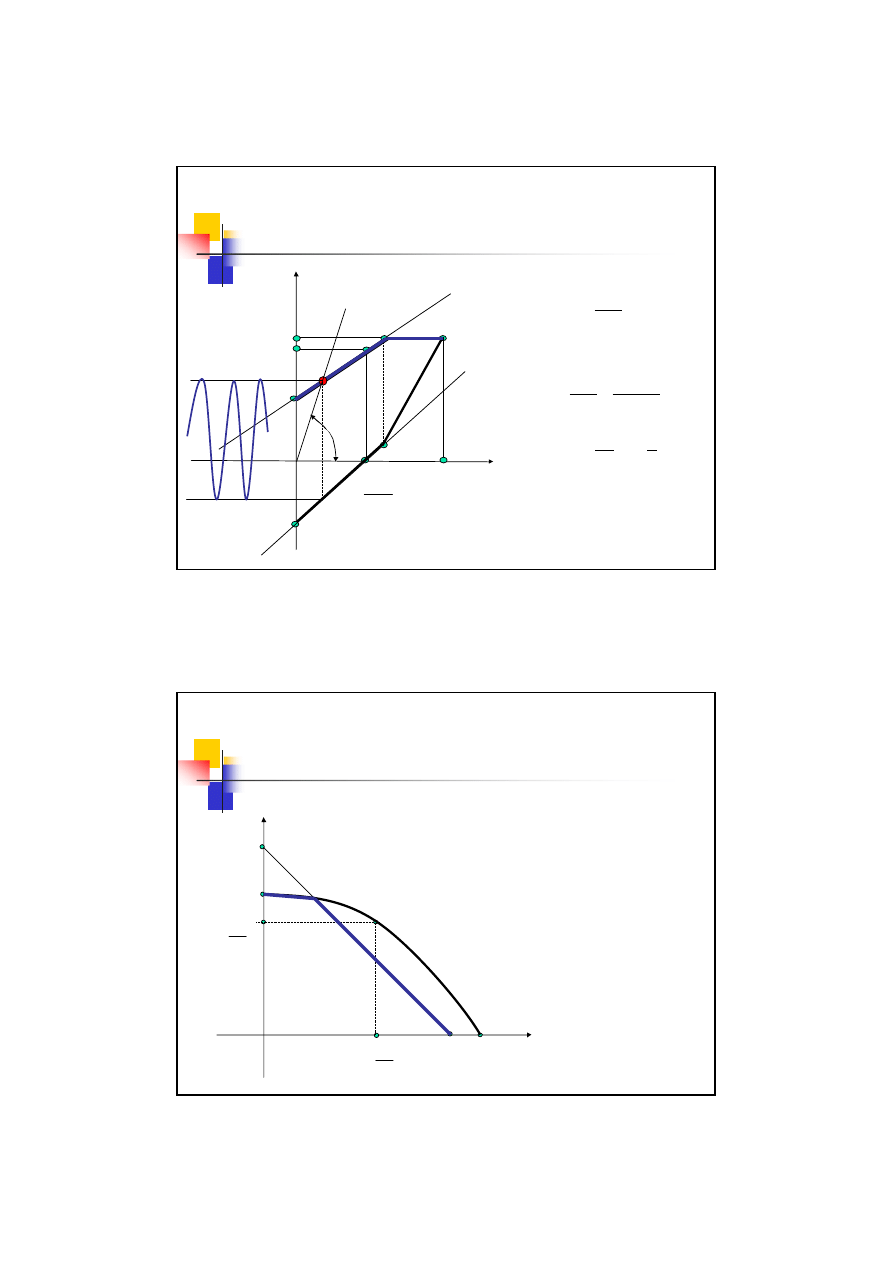
Wykresy zmęczeniowe – wykres
Haigha
W układzie współrzędnych:
σ
a
(
σ
m
)
Z
rc
Z
rj
2
Z
rj
2
R
m
R
e
R
e
12
σ
a
σ
m
Wykresy zmęczeniowe – wykres
Haigha
Wykres uproszczony
Z
rc
Z
rj
2
Z
rj
2
R
e
R
e
1
2
3
4
5
σ
a
σ
m
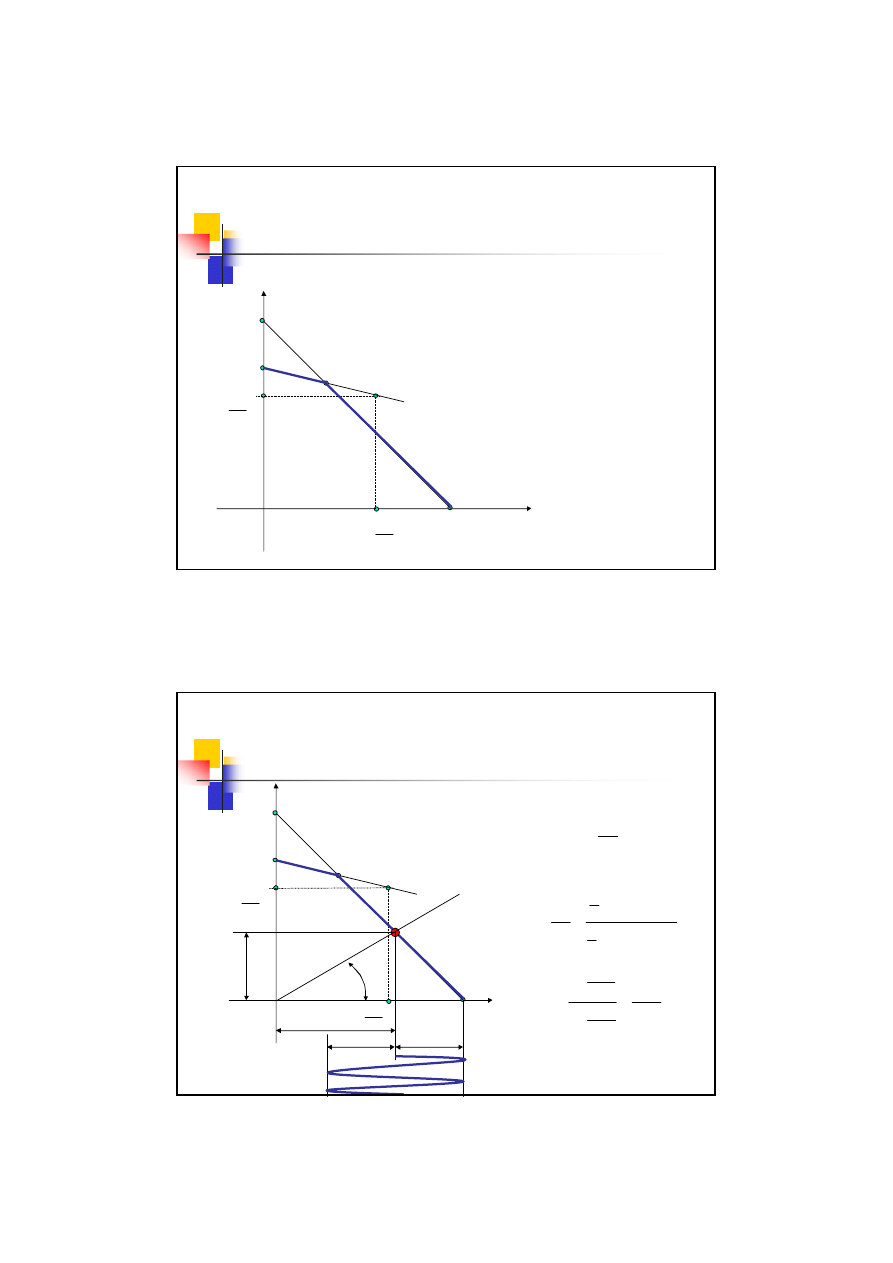
Wykresy zmęczeniowe – wykres
Haigha
Odczyt z wykresu
Z
rc
Z
rj
2
Z
rj
2
R
e
R
e
1
2
3
4
5
σ
a
κ
σ
m
κ
κ
κ
κ
σ
σ
a
m
r
Z
+
=
σ
a
κ
σ
a
κ
Widmo cyklu
β
m
a
tg
σ
σ
β
=
Współczynnik amplitudy cyklu
(
)
(
)
min
max
min
max
2
1
2
1
σ
σ
σ
σ
σ
σ
β
+
⋅
−
=
=
m
a
tg
R
R
tg
+
−
=
+
−
=
1
1
1
1
max
min
max
min
σ
σ
σ
σ
β
13
σ
a
σ
m
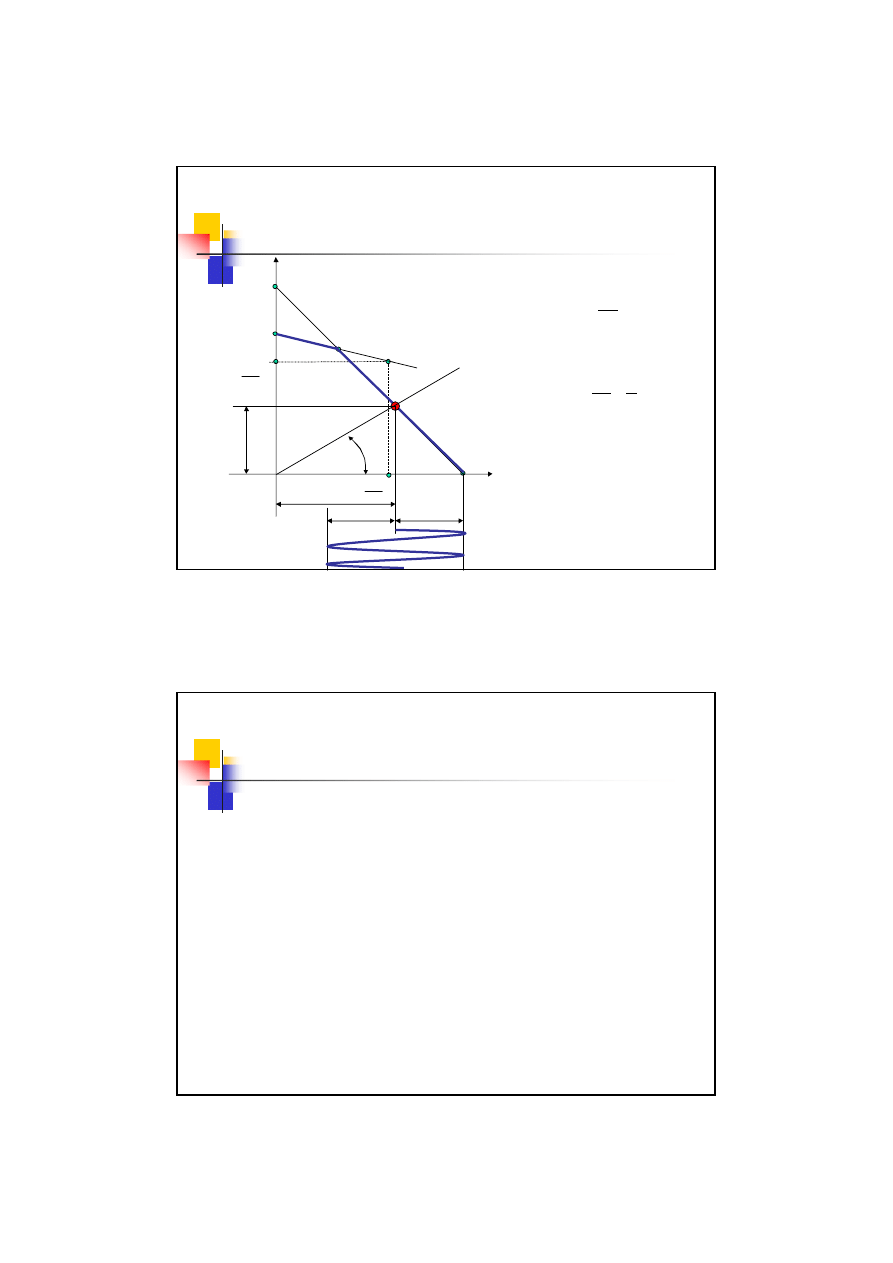
Wykresy zmęczeniowe – wykres
Haigha
Odczyt z wykresu
Z
rc
Z
rj
2
Z
rj
2
R
e
R
e
1
2
3
4
5
σ
a
κ
σ
m
κ
κ
κ
κ
σ
σ
a
m
r
Z
+
=
σ
a
κ
σ
a
κ
Widmo cyklu
β
m
a
tg
σ
σ
β
=
Współczynnik stałości obciążenia
κ
σ
σ
β
1
=
=
m
a
tg
Przykład 03.1
Określić granicę wytrzymałości dla cyklu zginania o
współczynniku amplitudy cyklu
R
= 0,5. Właściwości
materiału:
Z
go
= 200 MPa
Z
gj
= 300 MPa
R
e
= 350 MPa
14
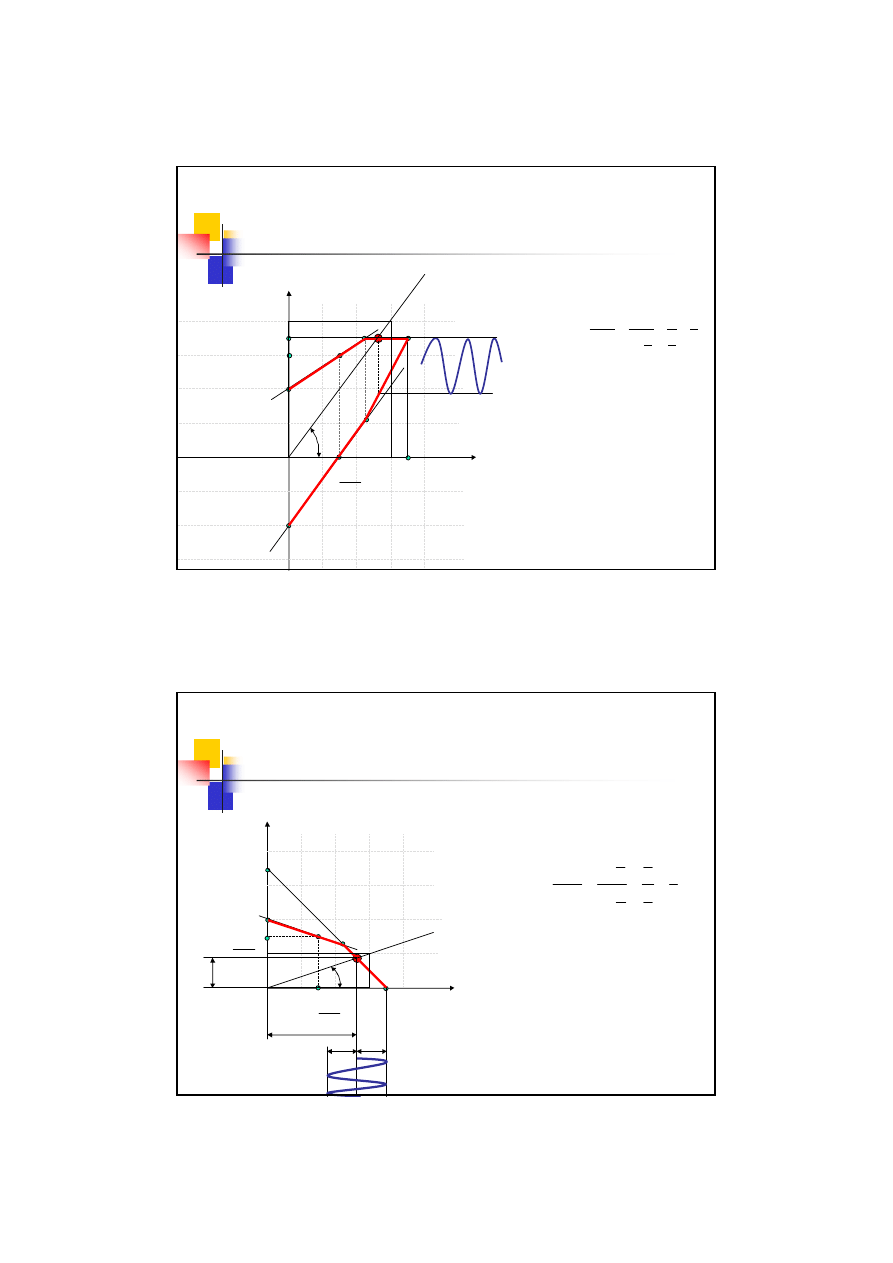
Przykład 03.1
Wykres Smitha
100
200
300
400
-100
-200
-300
100
200
300
400
Zgo
= 200 MPa
Zgj
= 300 MPa
Re
= 350 MPa
σ
max
σ
min
σ
m
Z
go
1
Z
g
κ
=
R
e
= 350 MPa
Widmo cyklu
β
Z
go
2
Z
gj
3
Z
gj
2
4’
4
R
e
5
R
e
6
7
7’
3
4
2
3
2
2
1
1
2
1
2
=
=
+
=
+
=
R
tg
β
Z
g
κ
=
R
e
= 350 MPa
Przykład 03.1
3
1
2
3
2
1
2
1
1
2
1
1
1
1
=
=
+
−
=
+
−
=
R
R
tg
β
Wykres Haigha
Zgo
= 200 MPa
Zgj
= 300 MPa
Re
= 350 MPa
100
200
300
400
100
200
300
σ
a
σ
m
400
Z
go
1
Z
gj
2
Z
gj
2
2
R
e
R
e
3
β
σ
m
κ
= 275 MPa
σ
a
κ
= 75 MPa
MPa
350
75
275
=
+
=
+
=
κ
κ
κ
σ
σ
a
m
g
Z
Widmo cyklu
Z
g
κ
=
R
e
= 350 MPa
15
Wytrzymałość zmęczeniowa
Czynniki wpływające na wytrzymałość zmęczeniową
elementu:
2. Zmienność obciążenia
3. Kształt przedmiotu
4. Stan powierzchni
5. Wielkość przedmiotu
6. Agresywne działanie środowiska
7. Temperatura pracy
1. Materiał elementu
Karb
Karb – miejsce zmian poprzecznych przekrojów elementów
lub zmian krzywizny powierzchni ograniczających przedmiot:
– odsadzenia
– rowki
– wycięcia
– gwinty
– otwory
–
itp...
16
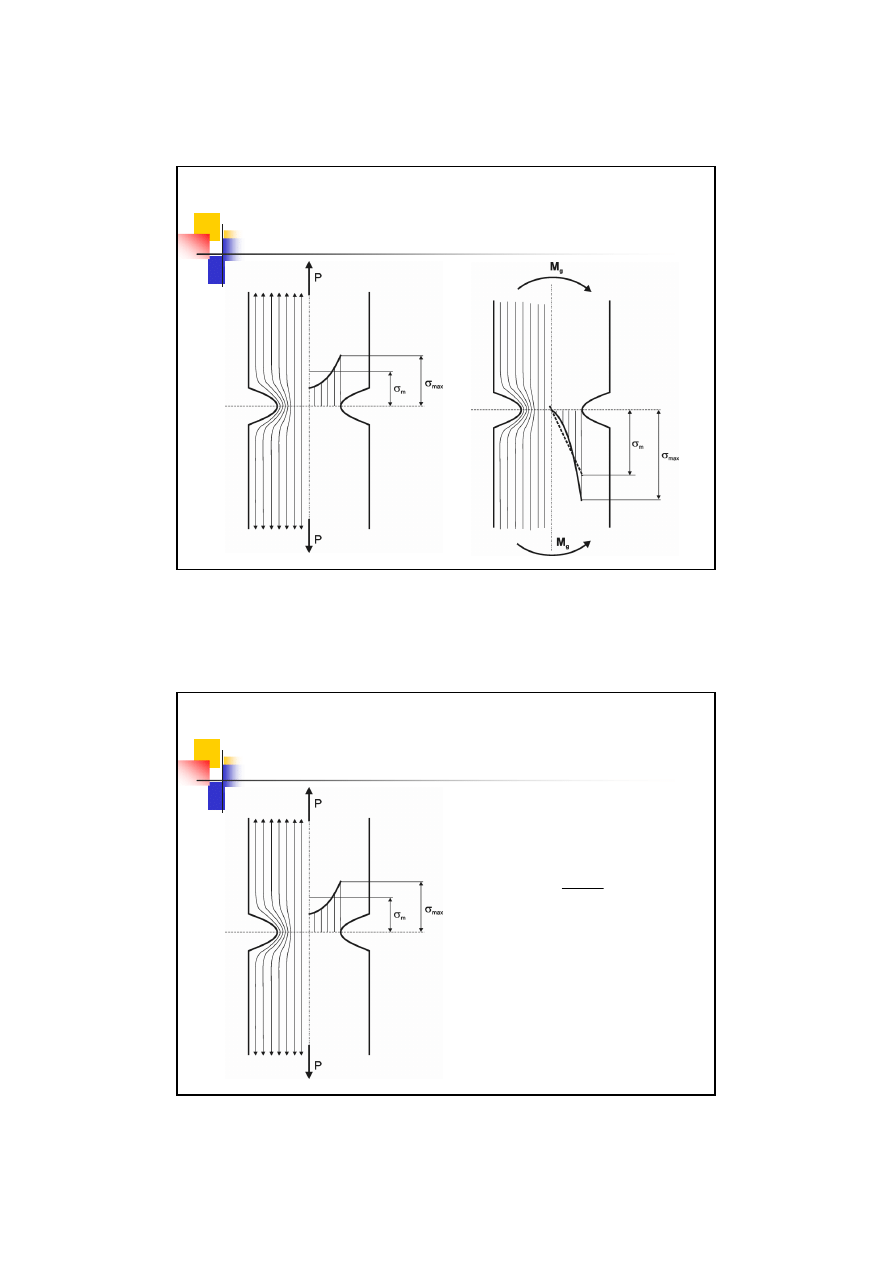
Karb
Karb – współczynnik kształtu
Karb powoduje lokalne
spiętrzenie naprężeń
m
k
σ
σ
α
max
=
α
αα
α
k
– współczynnik kształtu
17
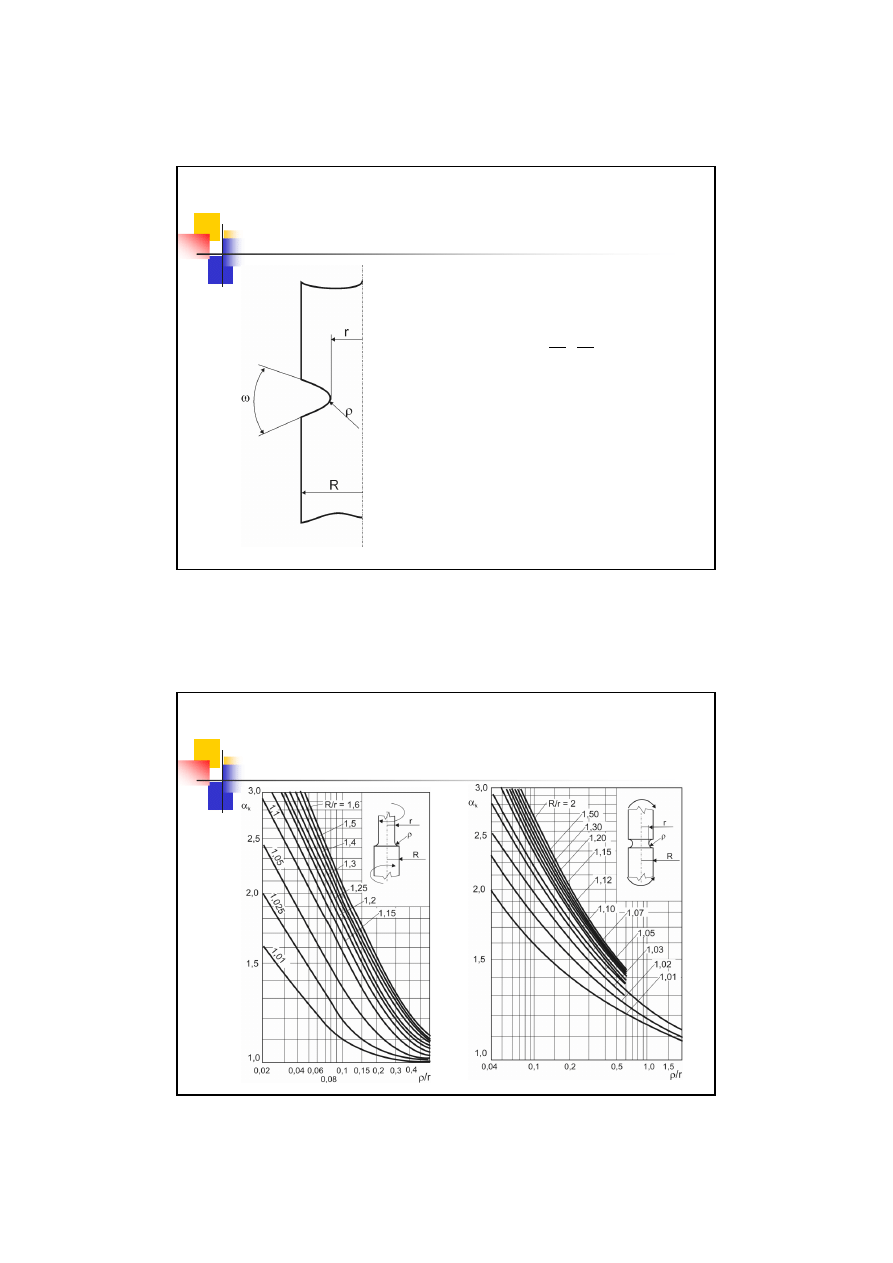
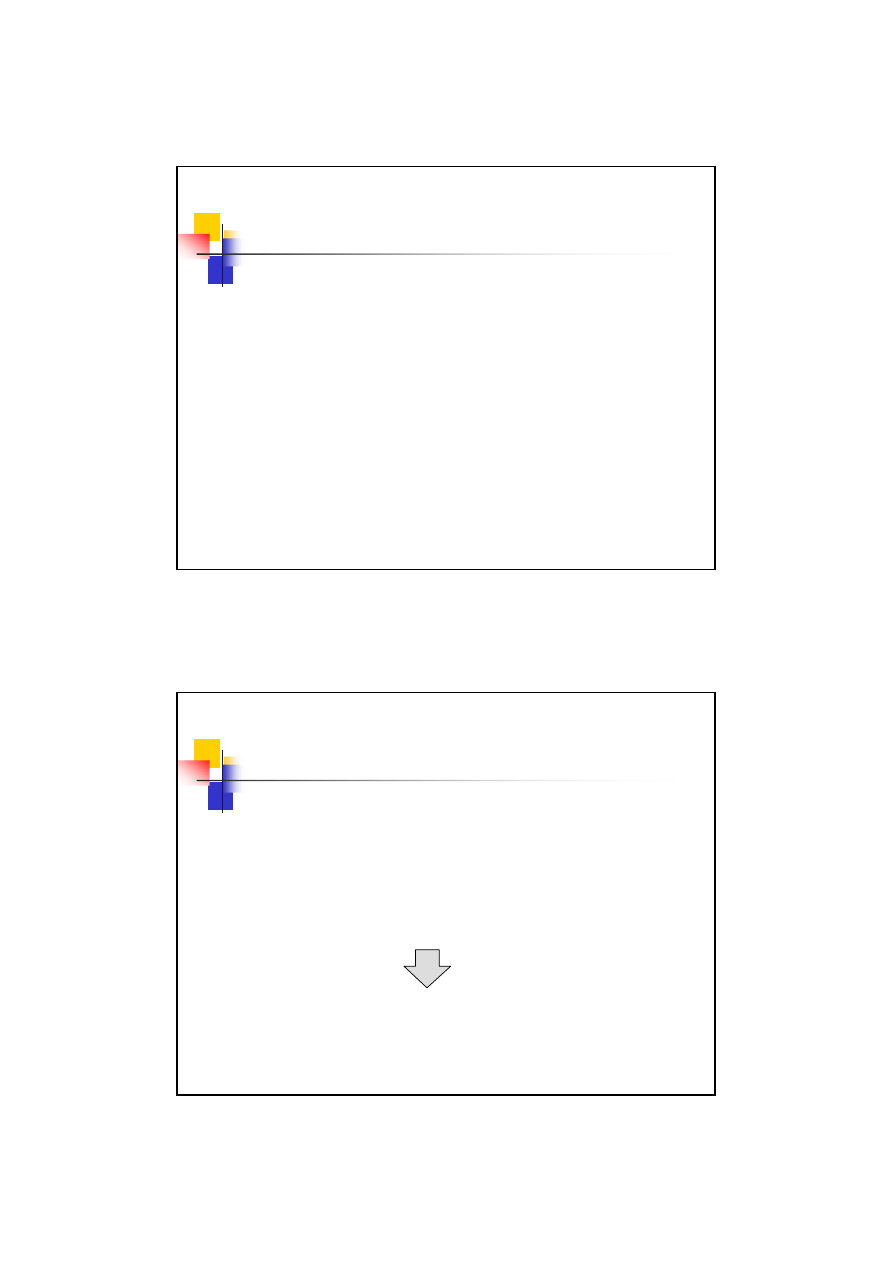
Karb – współczynnik kształtu
Współczynnik kształtu
=
ω
ρ
α
,
,
r
r
R
f
k
W przypadku karbów
współdziałających (np. wałek z
odsadzeniem i rowkiem) działania
karbu się nakładają i wyraża się to
we współczynniku jako:
1
1
)
(
+
−
=
∑
=
=
n
n
i
i
i
k
k
α
α
Karb – współczynnik kształtu
18
Karb – współczynnik kształtu
W przypadku karbów współdziałających (np.
wałek z odsadzeniem i rowkiem) działania karbu
się nakładają i wyraża się to we współczynniku
jako:
1
1
)
(
+
−
=
∑
=
=
n
n
i
i
i
k
k
α
α
Karb – współczynnik działania karbu
Współczynnik kształty zakłada idealnie liniowy model
sprężystości materiału.
Rzeczywiste materiały w różnym stopniu odbiegają od
ciał idealnie sprężystych.
Współczynnik działania karbu
β
k
19
Karb – współczynnik działania karbu
Opisany jest jako różnica wytrzymałości próbki gładkiej
z identyczną próbką z karbem.
K
gł
k
Z
Z
=
β
Z
gł
– granica zmęczenia próbki gładkiej
Z
K
– granica zmęczenia próbki z karbem
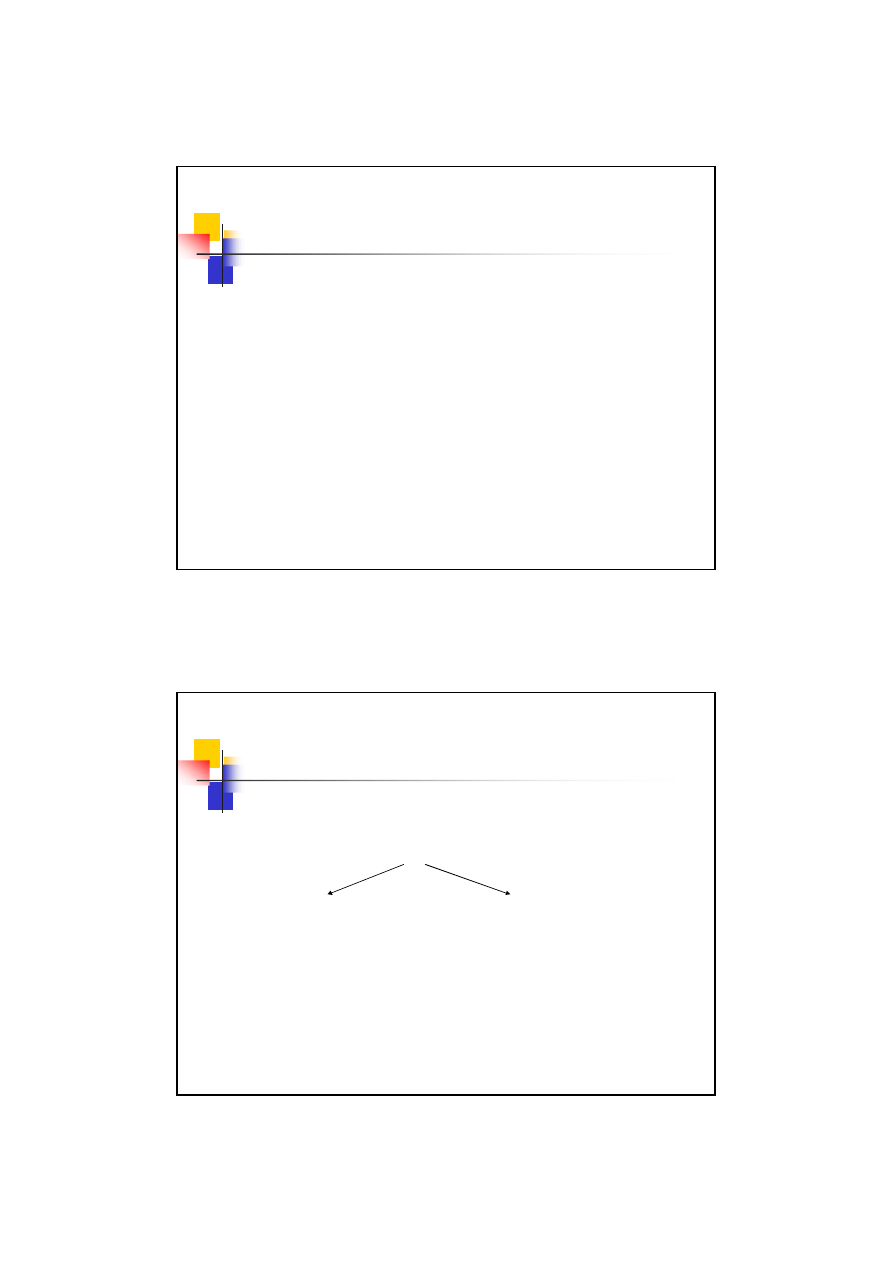
Karb – współczynnik działania karbu
(
)
m
k
k
R
f
,
,
ρ
α
β
=
20
Wytrzymałość zmęczeniowa
Czynniki wpływające na wytrzymałość zmęczeniową
elementu:
2. Zmienność obciążenia
3. Kształt przedmiotu
4. Stan powierzchni
5. Wielkość przedmiotu
6. Agresywne działanie środowiska
7. Temperatura pracy
1. Materiał elementu
Współczynnik stanu powierzchni
Każdy rodzaj obróbki powierzchni wpływa na
wytrzymałość zmęczeniową elementu. Wynika to z:
Geometrii powierzchni
Nieciągłości parametrów
wytrzymałościowych
przekroju
21
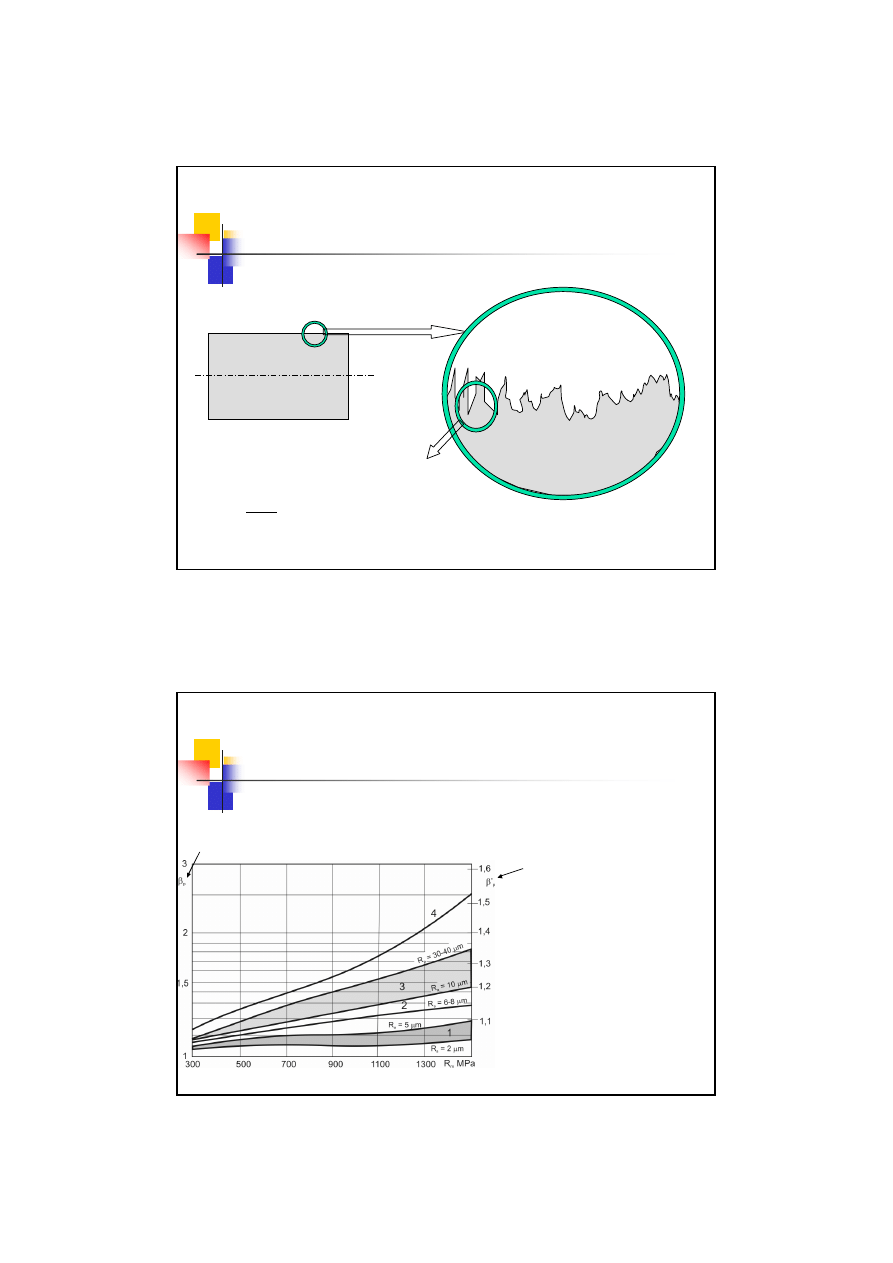
Współczynnik stanu powierzchni
Geometria powierzchni
Chropowatość
Małe karby na powierzchni
obr
pol
p
Z
Z
=
β
Z
obr
– granica zmęczenia próbki poddanej innej obróbce
Z
pol
– granica zmęczenia próbki polerowanej
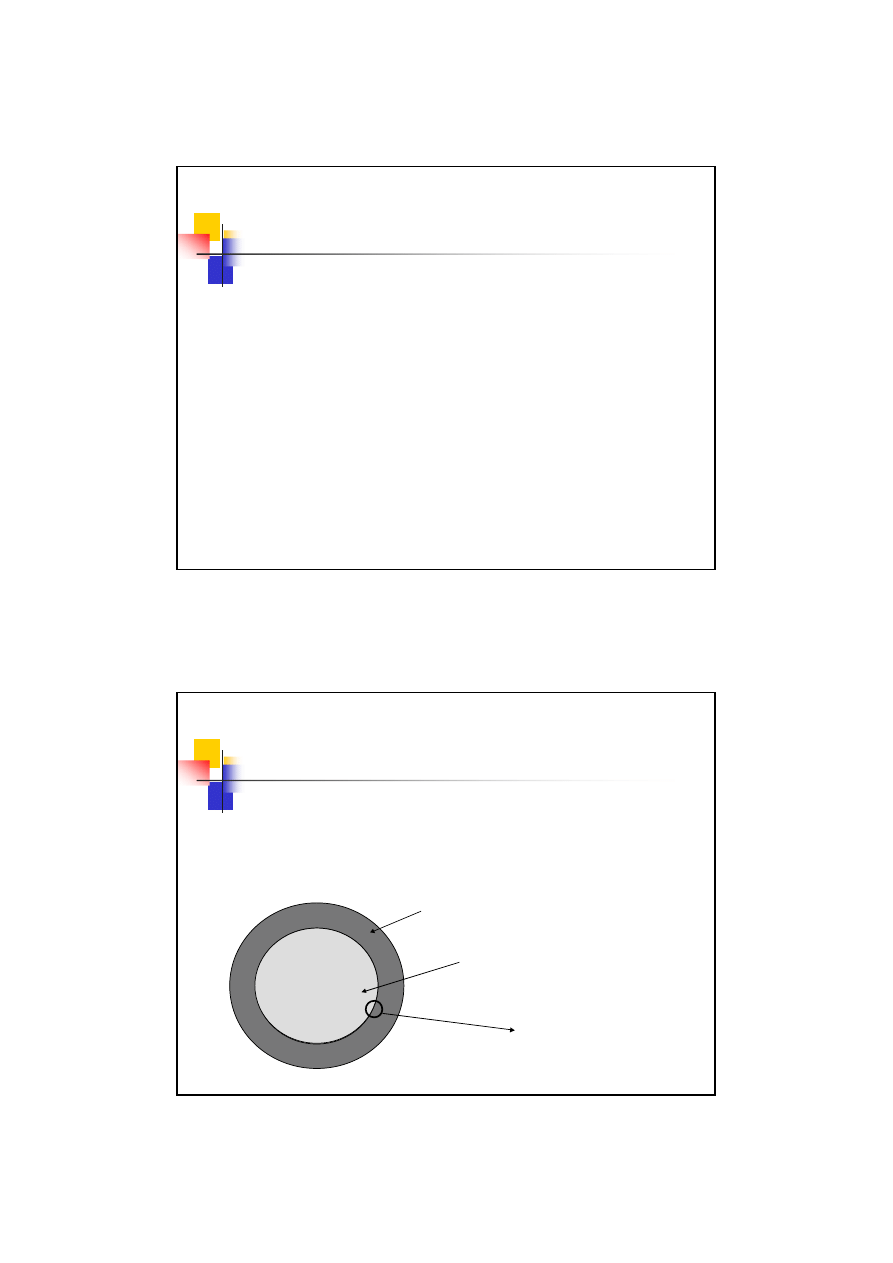
Współczynnik stanu powierzchni
Geometria powierzchni
(
)
obróbki
rodzaj
R
f
m
p
,
=
β
1 – szlifowanie
2 – toczenie, frezowanie dokładne
3 – toczenie, frezowanie zgrubne
4 – odlewanie, kucie …
Rozciąganie i zginanie
Skręcanie i ścinanie
22
Współczynnik stanu powierzchni
Nieciągłości parametrów wytrzymałościowych przekroju
wynikająca z:
Utwardzania powierzchniowego (młotkowanie itp.)
Obróbki chemicznej powierzchniowej:
- nawęglanie,
- azotowanie …
Obróbki cieplnej powierzchniowej:
- hartowanie powierzchniowe,
- …
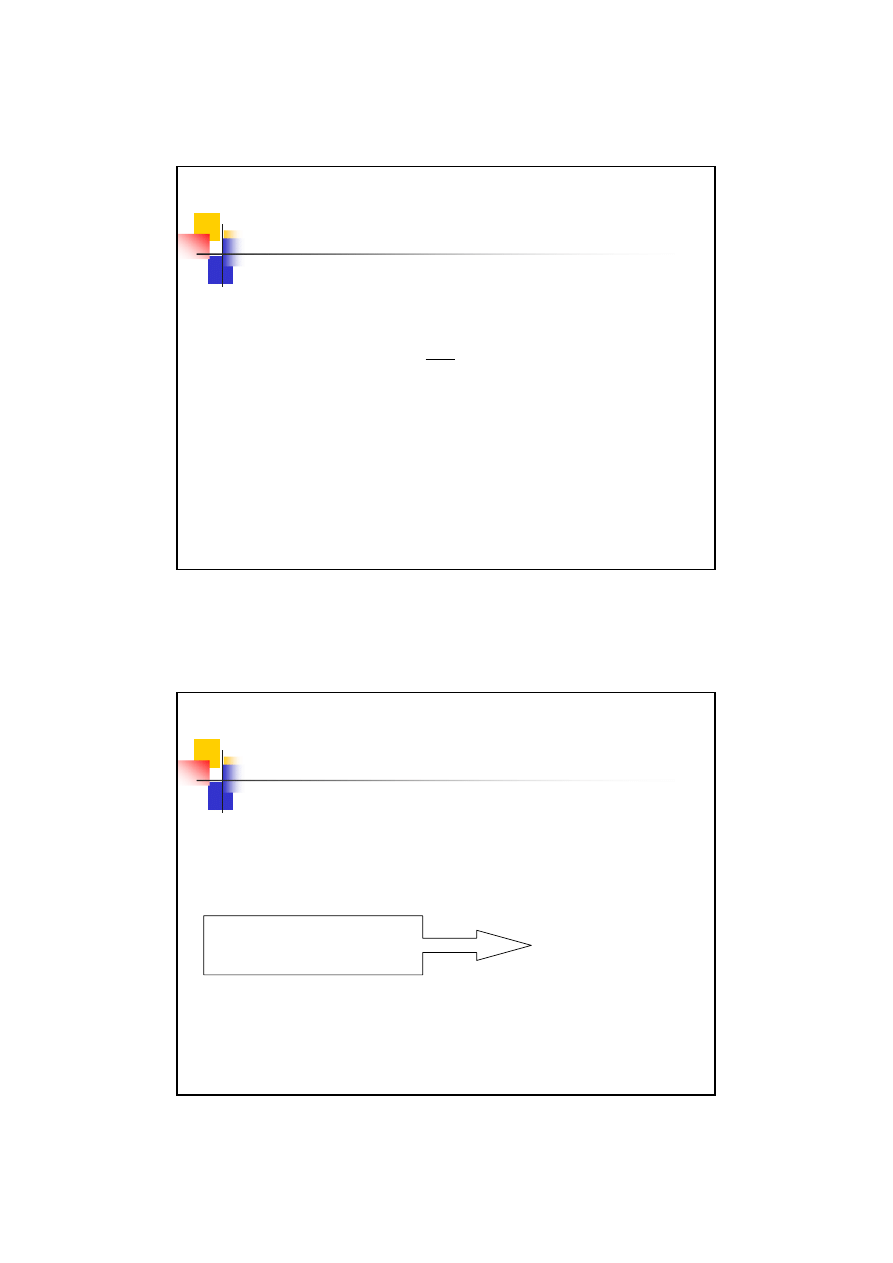
Współczynnik stanu powierzchni
Nieciągłości parametrów wytrzymałościowych przekroju
Warstwa o wzmocniona
Rdzeń
Obszar zmiany parametrów
takich jak:
- twardość,
- wytrzymałość,
- odkształcalność,
23
Współczynnik stanu powierzchni
Nieciągłości parametrów wytrzymałościowych przekroju
op
jed
pr
Z
Z
=
β
Z
op
– granica zmęczenia próbki poddanej obróbce powierzchniowej
Z
jed
– granica zmęczenia próbki o jednolitych własnościach przekroju
Wytrzymałość zmęczeniowa
Czynniki wpływające na wytrzymałość zmęczeniową
elementu:
2. Zmienność obciążenia
3. Kształt przedmiotu
4. Stan powierzchni
5. Wielkość przedmiotu
6. Agresywne działanie środowiska
7. Temperatura pracy
1. Materiał elementu
Współczynnik spiętrzenia
naprężeń
β
24
Współczynnik spiętrzenia naprężeń
Przy normalnej obróbce
1
−
+
=
p
k
β
β
β
Przy obróbce powierzchniowej
pr
k
β
β
β
⋅
=
Wytrzymałość zmęczeniowa
Czynniki wpływające na wytrzymałość zmęczeniową
elementu:
2. Zmienność obciążenia
3. Kształt przedmiotu
4. Stan powierzchni
5. Wielkość przedmiotu
6. Agresywne działanie środowiska
7. Temperatura pracy
1. Materiał elementu
25
Współczynnik wielkości przedmiotu
Brak jest
jednoznacznych
teoretycznych uzasadnień.
Najczęściej wpływ wielkości przedmiotu opisuje się
probabilistycznie
tzn. Wraz z powiększaniem się
objętości materiału
wzrasta prawdopodobieństwo
wystąpienia takich wad materiałowych
, które są
ogniskami zmęczeniowego pękania.
Wytrzymałość zmęczeniowa zwykle zmniejsza się
wraz ze wzrostem wymiarów elementu.
Współczynnik wielkości przedmiotu
d
wz
Z
Z
=
=
ε
γ
1
Z
d
– granica zmęczenia próbki o danej wielkości
Z
wz
– granica zmęczenia próbki wzorcowej (średnica 7 mm)
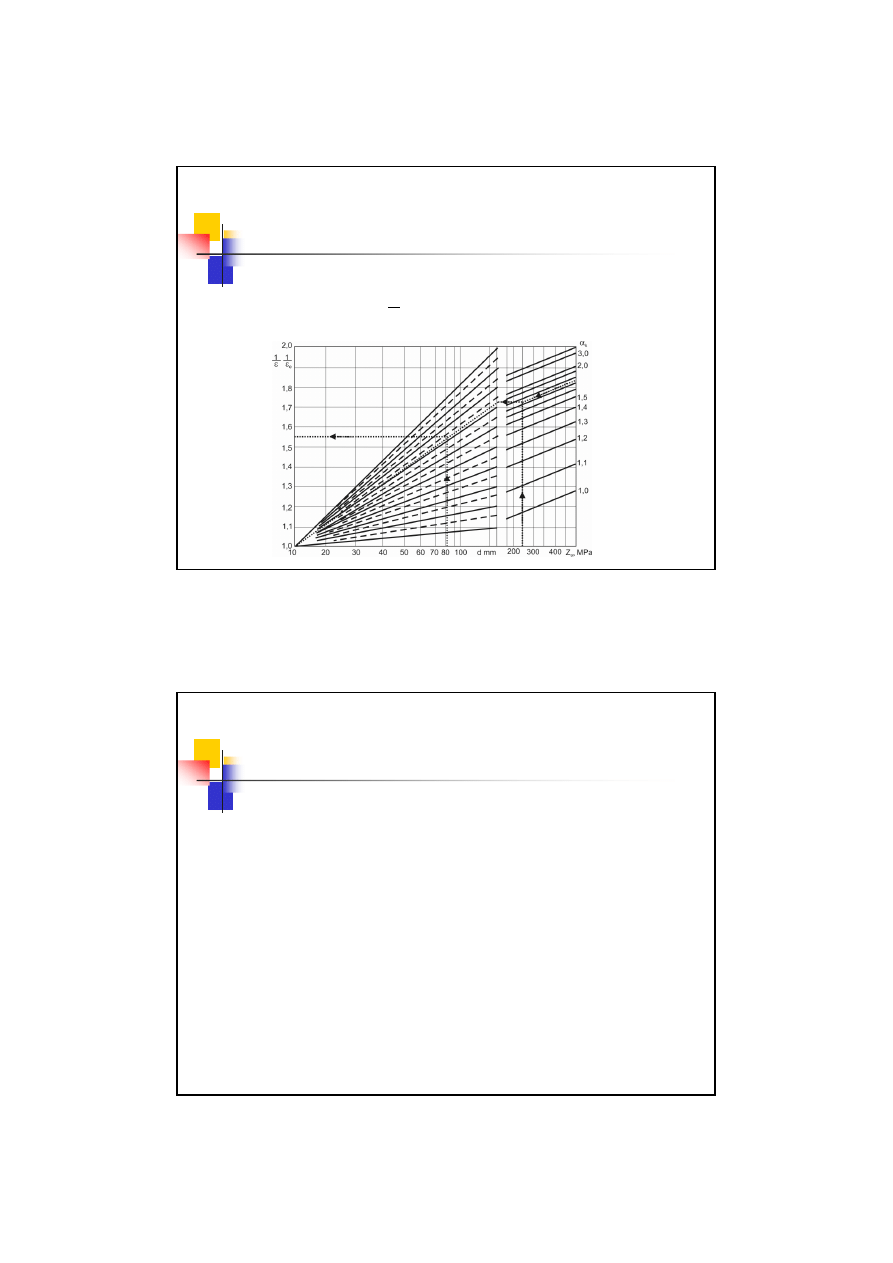
26
Współczynnik wielkości przedmiotu
(
)
A
Z
f
go
k
,
,
1
α
ε
γ
=
=
Wytrzymałość zmęczeniowa
Czynniki wpływające na wytrzymałość zmęczeniową
elementu:
2. Zmienność obciążenia
3. Kształt przedmiotu
4. Stan powierzchni
5. Wielkość przedmiotu
6. Agresywne działanie środowiska
7. Temperatura pracy
1. Materiał elementu
27
Współczynniki warunków pracy
k or
wn
k or
Z
Z
=
β
Obejmują one wpływ:
Wilgoci
Substancji korozyjnych
Temperatury
Światła
Z
kor
– granica zmęczenia próbki w badanych warunkach
Z
wn
– granica zmęczenia próbki w warunkach normalnych
kor
nor
β
β
β
⋅
=
Bezpieczeństwo
Wszystkie wcześniej przedstawione elementy pozwalają
na określenie
rzeczywistej granicy zmęczenia
dla danego
elementu.
γ
β
κ
⋅
=
Z
Z
Pojawia się jednak niepewność
28
Bezpieczeństwo
Niepewność
1. Zmienność parametrów materiału wynikająca z:
- niepowtarzalności procesu wytwarzania,
- różnic miedzy dostawcami,
- nierównomiernego rozłożenia składników w materiale,
- starzenie się materiału,
- …
Bezpieczeństwo
2. Zmienność parametrów obciążenia:
- niepełna wiedza o działaniu mechanizmu,
- możliwe chwilowe przeciążenia,
- błędna obsługa,
- zmienne warunki eksploatacji
- …
Niepewność
29
Bezpieczeństwo
3. Niedokładność wykonania:
- rozrzut statystyczny wymiarów,
- tępienie się narzędzi w czasie pracy,
- błędna obsługa maszyn,
- błędy technologiczne,
- …
Niepewność
Bezpieczeństwo
Dbanie o szczegóły:
-
Dokładna kontrola jakości,
-
Pilnowanie technologii,
- Testy i dokładniejsze ustalenie
obciążeń,
-
Wzrost dokładności wykonania,
-
…
Zapobieganie niepewności:
Zapewnienie zapasu
bezpieczeństwa
30
Współczynnik bezpieczeństwa
Obniża się naprężenia dopuszczalne o krotność
współczynnika bezpieczeństwa
δ
2,0 – 2,5
: przy orientacyjnym określeniu obciążeń i naprężeń, dla
nieznanych dokładnie warunków pracy
Wartości
δ
:
1,3 – 1,5
: znany rozkład naprężeń, wysoka technologia wykonania i przy
stosowaniu dobrych metod defektoskopowych
1,5 – 1,7
: zwykła dokładność obliczeń, dobra technologia wykonania i
czynności kontrolne
1,7 – 2,0
: elementy o większych wymiarach, średnia dokładność
obliczeń i wykonania
Naprężenie dopuszczalne
Uwzględnienie wszystkich czynników prowadzi do
wartości
naprężeń dopuszczalnych
k
będących
maksymalnymi naprężeniami jakie mogą
wystąpić w projektowanym elemencie maszyny
δ
γ
β
κ
⋅
⋅
=
Z
k
31
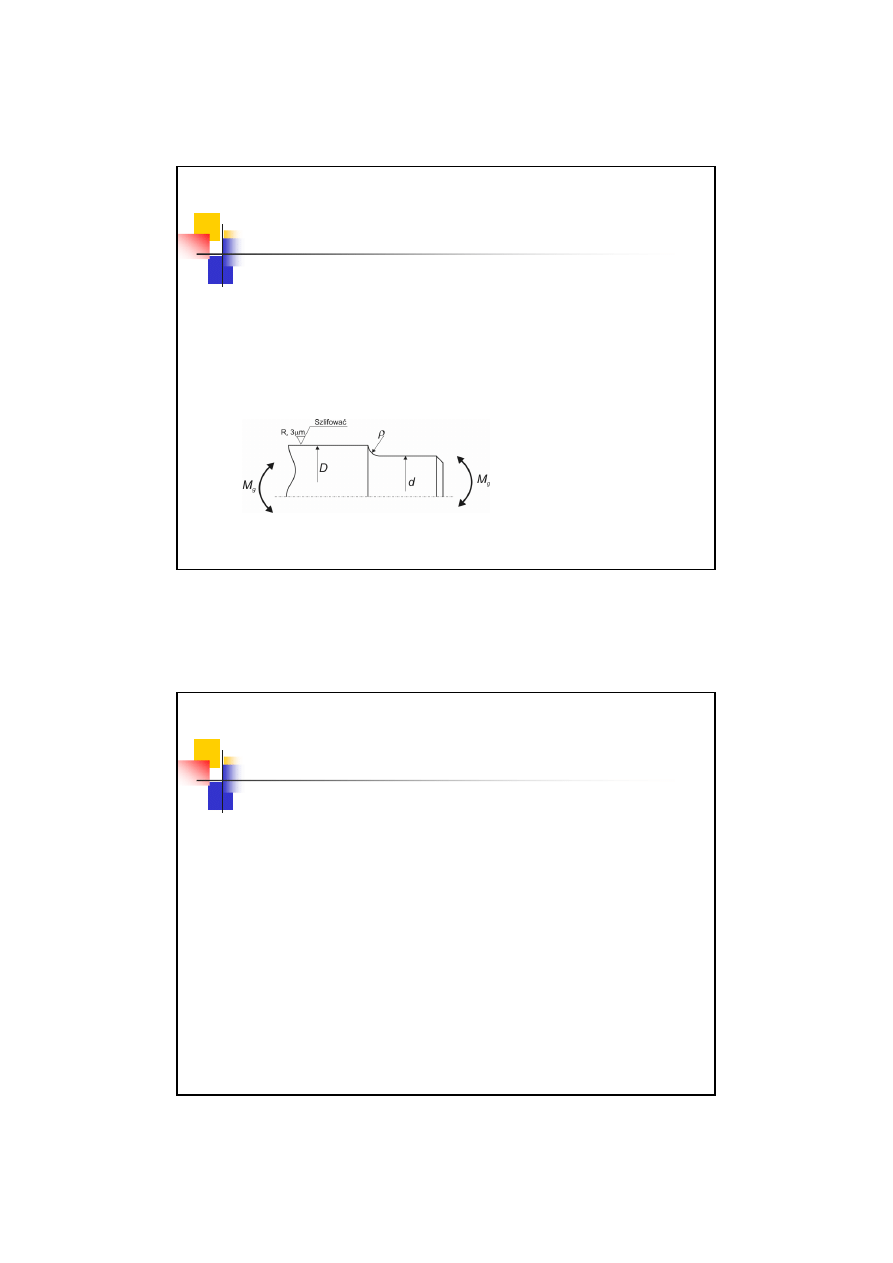
Przykład 03.2
Określić naprężenia dopuszczalne dla elementu przy cyklu
zginania o współczynniku amplitudy cyklu
R
= 0,5.
Właściwości materiału:
Z
go
= 200 MPa,
Z
gj
= 300 MPa,
R
e
= 350 MPa,
R
m
= 420 MPa
Wymiary:
D
= 30 mm
d
= 24 mm
ρ
= 2 mm
Przykład 03.2
Z przykładu 03.1
1. Określenie granicy zmęczenia dla danego materiału przy
danym cyklu obciążeń
Z
g
κκκκ
= 350 MPa
32
Przykład 03.2
2. Współczynnik kształtu
α
k
Wymiary:
D
= 30 mm
d
= 24 mm
ρ
= 2 mm
25
,
1
24
30
=
=
=
d
D
r
R
167
,
0
24
2
2
2
=
⋅
=
⋅
=
d
r
ρ
ρ
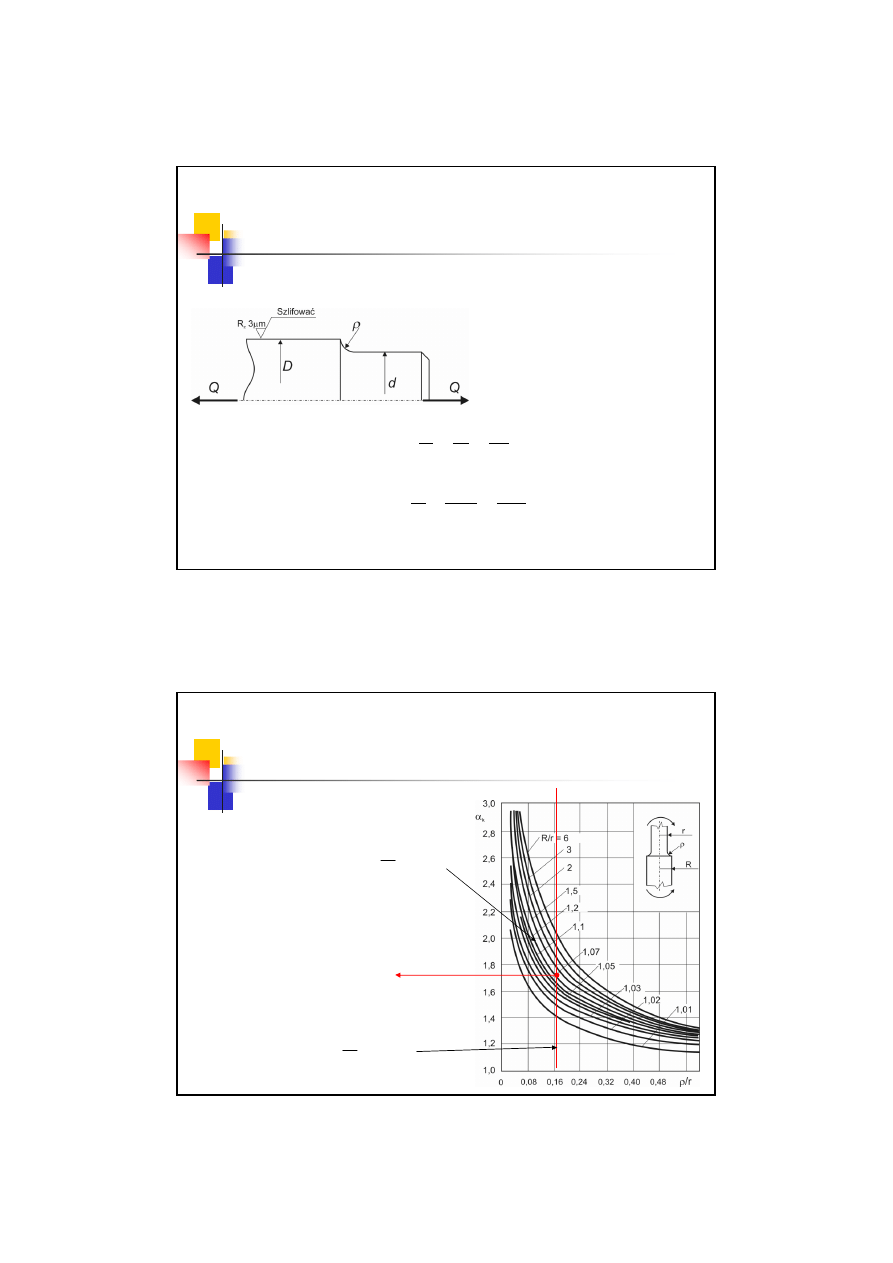
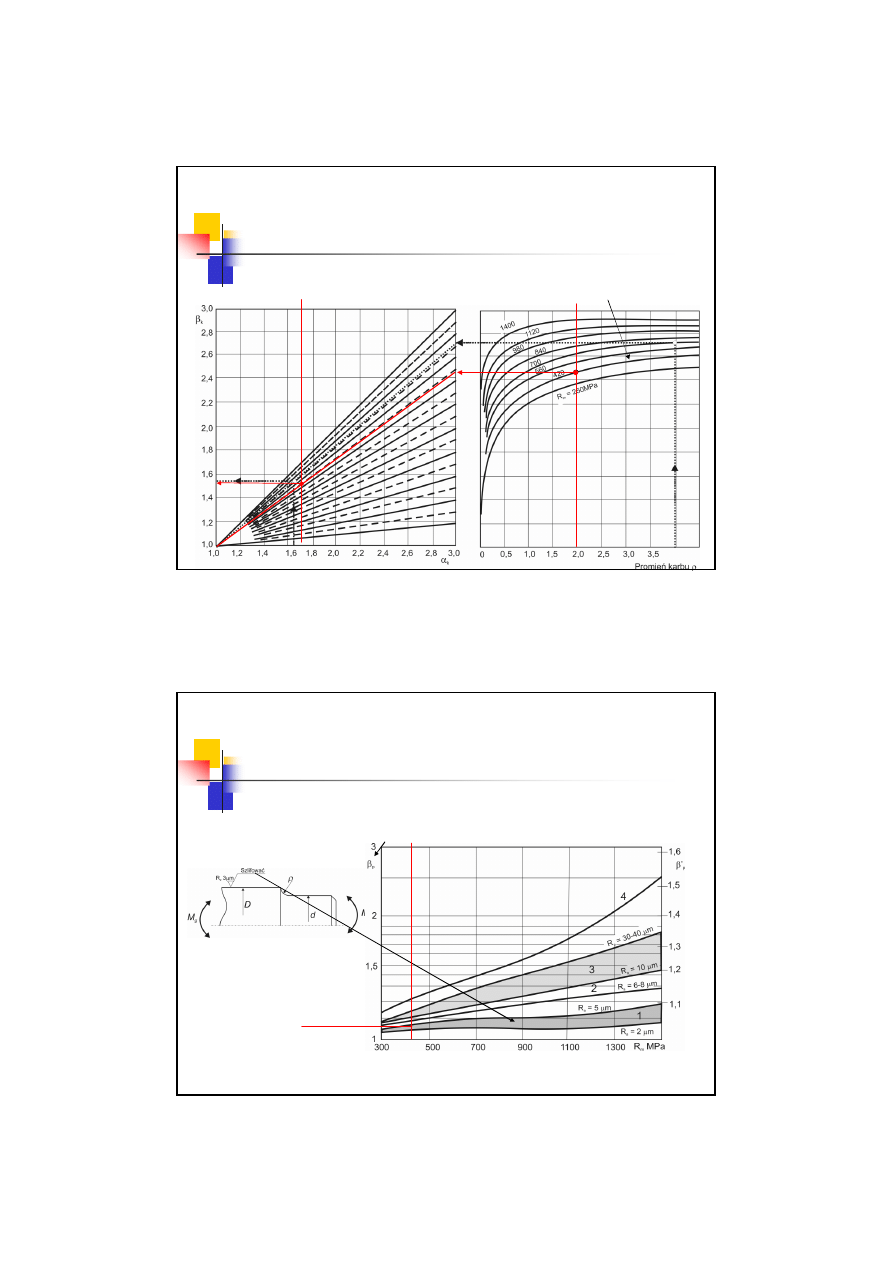
Przykład 03.2
2. Współczynnik kształtu
α
k
25
,
1
=
r
R
167
,
0
=
r
ρ
72
,
1
=
k
α
33
Przykład 03.2
3. Współczynnik działania karbu
β
k
R
m
= 420 MPa
ρ
= 2 mm
72
,
1
=
k
α
52
,
1
=
k
β
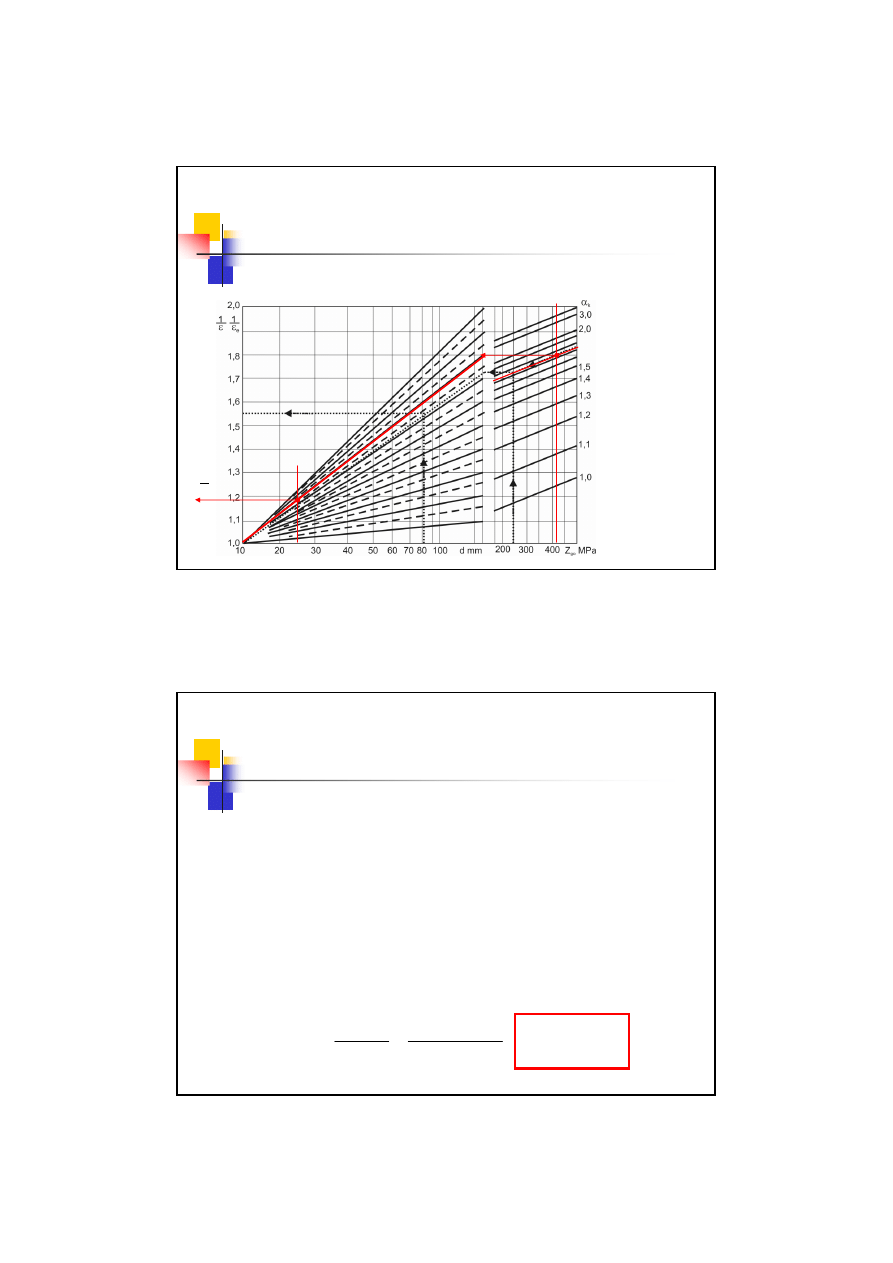
Przykład 03.2
4. Współczynnik stanu powierzchni
β
p
R
m
= 420 MPa
05
,
1
=
p
β
Rozciąganie i zginanie
34
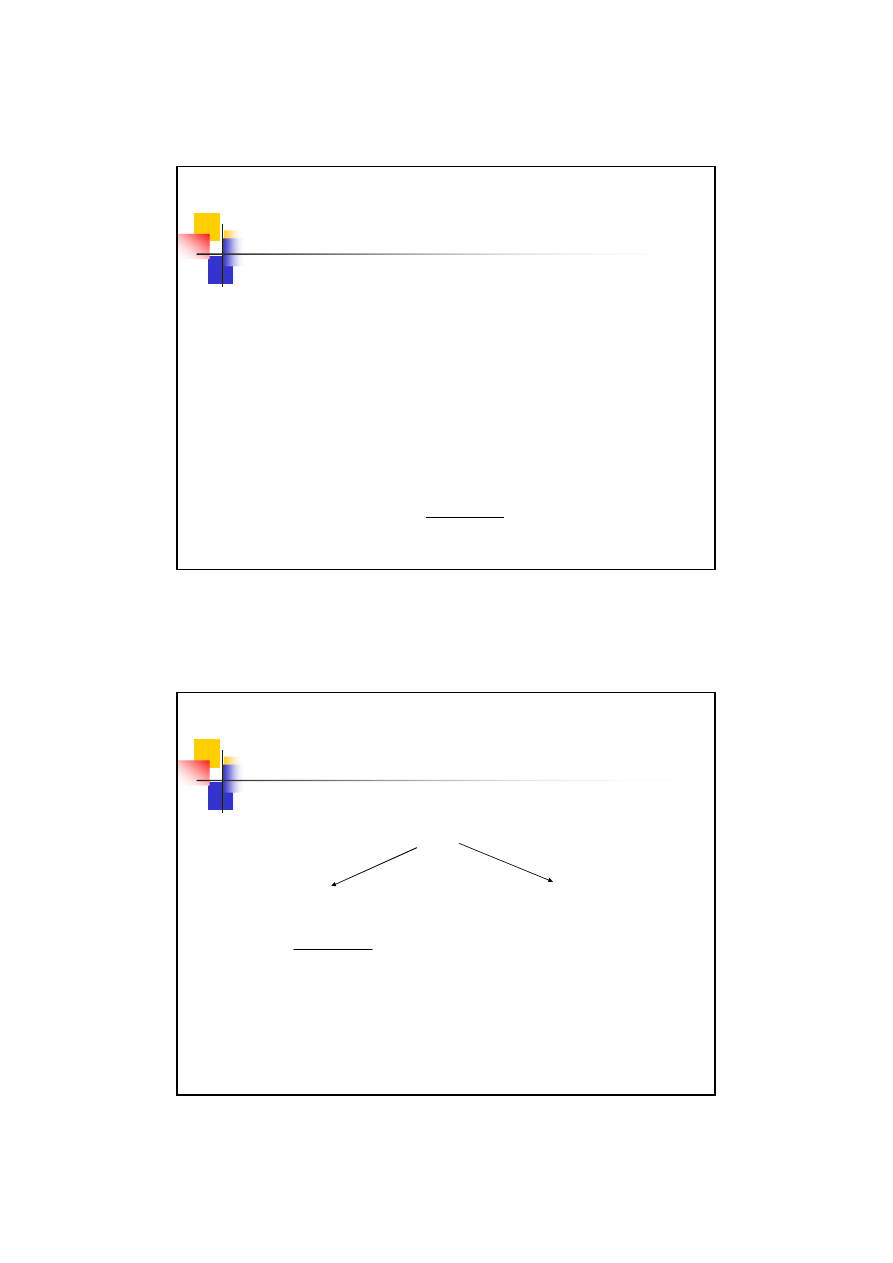
Przykład 03.2
4. Współczynnik wielkości przedmiotu
γ
Z
go
= 200 MPa
72
,
1
=
k
α
d
= 24 mm
18
,
1
1
=
=
ε
γ
Przykład 03.2
5. Współczynnik spiętrzenia naprężeń
β
5
,
1
=
δ
57
,
1
1
05
,
1
52
,
1
1
=
−
−
=
−
+
=
p
k
β
β
β
6. Współczynnik bezpieczeństwa
δ
Przyjmijmy średnią dokładność obliczeń i wykonania
7. Naprężenia dopuszczalne
k
g
κ
MPa
9
,
125
5
,
1
18
,
1
57
,
1
350
=
⋅
⋅
=
⋅
⋅
=
δ
γ
β
κ
κ
g
g
Z
k
35
Rzeczywisty współczynnik
bezpieczeństwa
Podejście odwrotne – znamy konstrukcję i jej
obciążenia a chcemy sprawdzić, czy ma
wystarczający zapas bezpieczeństwa
Zatem nadwyżka granicy zmęczenia dla danej konstrukcji
nad rzeczywistymi naprężeniami stanowi
–
rzeczywisty współczynnik bezpieczeństwa
max
σ
γ
β
δ
κ
⋅
⋅
=
Z
rz
Rzeczywisty współczynnik
bezpieczeństwa
Określanie rzeczywistego współczynnika
bezpieczeństwa
Metoda bezpośrednia
max
σ
γ
β
δ
κ
⋅
⋅
=
Z
rz
Metoda uproszczona
- Metoda Serensena
Nie wymaga ona znajomości
granicy zmęczenia
dla danego
materiału
36
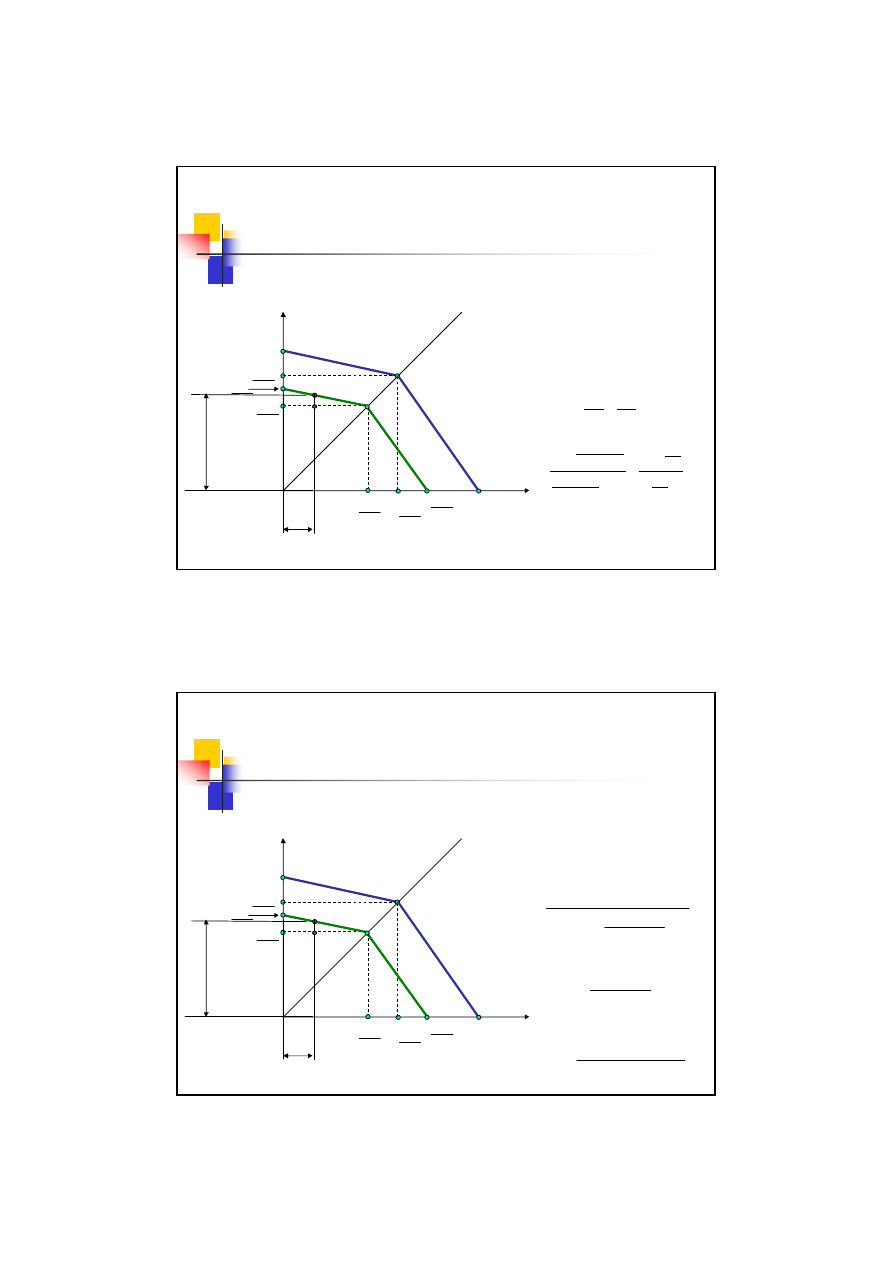
Metoda Serensena
Oparta jest na uproszczonym wykresie Haigha
σ
a
σ
m
Z
rj
2
Z
rj
2
R
m
Z
rc
A
B
C
D
E
A’
D’
B’
C’
E’
R
m
βγδ
Z
rj
2βγδ
Z
rj
2βγδ
Z
rc
βγδ
Dla cykli dwustronnych
-1 <
R
< 0
0 <
κ
< 1
σ
m
σ
a
F
G
Z podobieństwa trójkątów
ABE i FB’G
DB
AD
GB'
FG
=
2
2
2
2
rj
rj
rc
m
rj
rj
a
Z
Z
Z
Z
Z
−
=
−
⋅
⋅
⋅
⋅
⋅
⋅
−
σ
δ
γ
β
δ
γ
β
σ
Metoda Serensena
σ
a
σ
m
Z
rj
2
Z
rj
2
R
m
Z
rc
A
B
C
D
E
A’
D’
B’
C’
E’
R
m
βγδ
Z
rj
2βγδ
Z
rj
2βγδ
Z
rc
βγδ
Dla cykli dwustronnych
-1 <
R
< 0
0 <
κ
< 1
σ
m
σ
a
F
G
Co po przekształceniach daje:
m
rj
rj
rc
a
rc
Z
Z
Z
Z
σ
σ
γ
β
δ
⋅
−
⋅
+
⋅
⋅
=
2
Przyjmując:
rj
rj
rc
Z
Z
Z
−
⋅
=
2
ψ
Otrzymujemy:
m
a
rc
Z
σ
ψ
σ
γ
β
δ
⋅
+
⋅
⋅
=
37
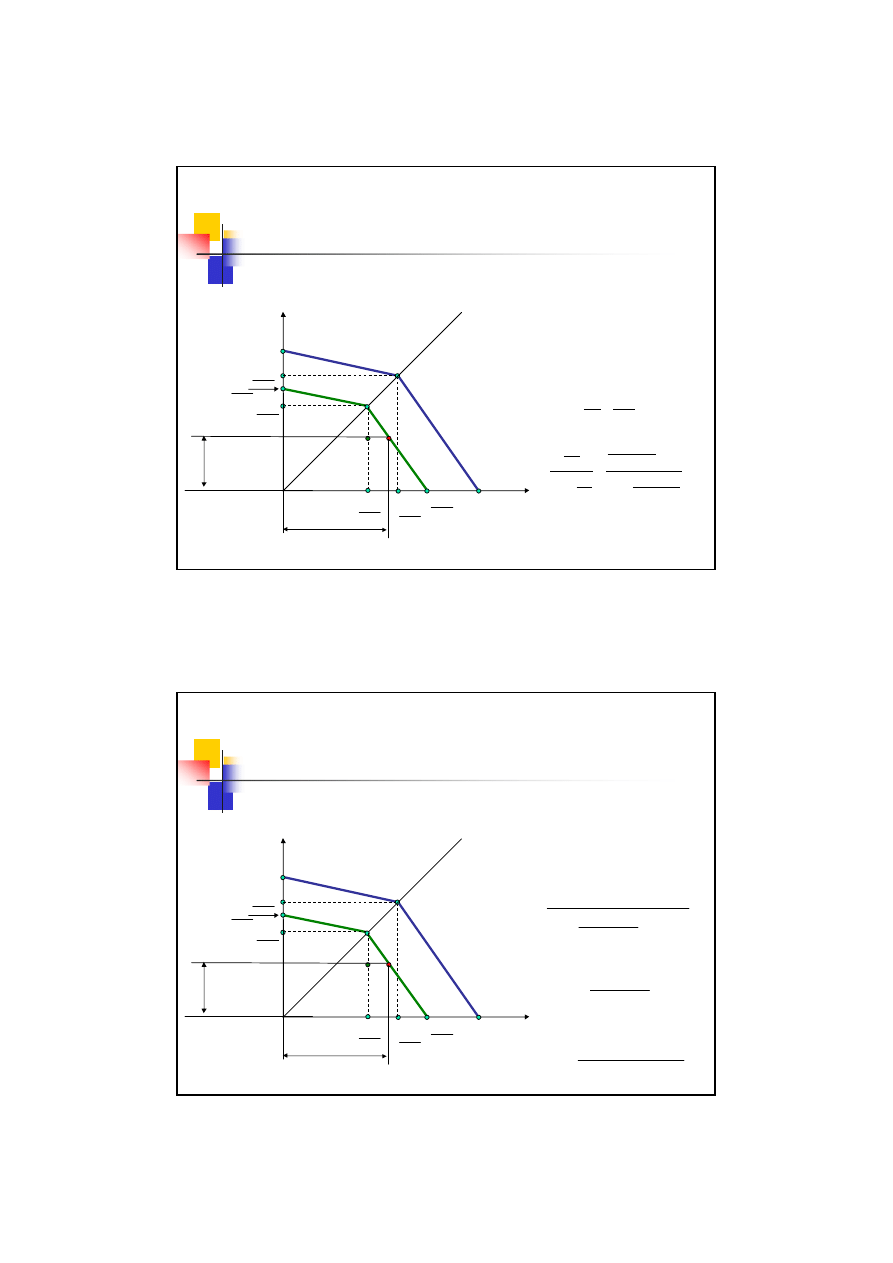
Metoda Serensena
σ
a
σ
m
Z
rj
2
Z
rj
2
R
m
Z
rc
A
B
C
D
E
A’
D’
B’
C’
E’
R
m
βγδ
Z
rj
2βγδ
Z
rj
2βγδ
Z
rc
βγδ
Dla cykli jednostronnych
0 <
R
< +1
1 <
κ
< +
∞
σ
m
σ
a
F
G
Z podobieństwa trójkątów
BEC i B’GF
GF
G
B'
EC
BE
=
δ
γ
β
σ
σ
δ
γ
β
⋅
⋅
⋅
−
−
⋅
⋅
⋅
=
−
2
2
2
2
rj
m
a
rj
rj
m
rj
Z
Z
Z
R
Z
Metoda Serensena
σ
a
σ
m
Z
rj
2
Z
rj
2
R
m
Z
rc
A
B
C
D
E
A’
D’
B’
C’
E’
R
m
βγδ
Z
rj
2βγδ
Z
rj
2βγδ
Z
rc
βγδ
Dla cykli jednostronnych
0 <
R
< +1
1 <
κ
< +
∞
σ
m
σ
a
F
G
Co po przekształceniach daje:
m
a
rj
rj
m
m
Z
Z
R
R
σ
σ
γ
β
δ
+
⋅
−
⋅
⋅
⋅
=
2
Przyjmując:
rj
rj
m
Z
Z
R
−
⋅
=
2
ξ
Otrzymujemy:
m
a
m
R
σ
σ
ξ
γ
β
δ
+
⋅
⋅
⋅
=
38
Metoda Serensena
Dla cykli jednostronnych
0 <
R
< +1
1 <
κ
< +
∞
rj
rj
m
Z
Z
R
−
⋅
=
2
ξ
m
a
m
R
σ
σ
ξ
γ
β
δ
+
⋅
⋅
⋅
=
Dla cykli dwustronnych
-1 <
R
< 0
0 <
κ
< 1
rj
rj
rc
Z
Z
Z
−
⋅
=
2
ψ
m
a
rc
Z
σ
ψ
σ
γ
β
δ
⋅
+
⋅
⋅
=
sj
sj
m
Z
Z
R
−
⋅
=
2
ξ
m
a
m
R
σ
σ
ξ
γ
β
δ
+
⋅
⋅
⋅
=
gj
gj
go
Z
Z
Z
−
⋅
=
2
ψ
m
a
go
Z
σ
ψ
σ
γ
β
δ
⋅
+
⋅
⋅
=
Złożony stan naprężeń
W przypadku złożonego stanu naprężeń
rzeczywisty współczynnik bezpieczeństwa oblicza
się z zasady superpozycji
2
2
2
1
2
1
δ
δ
δ
δ
δ
+
⋅
=
39
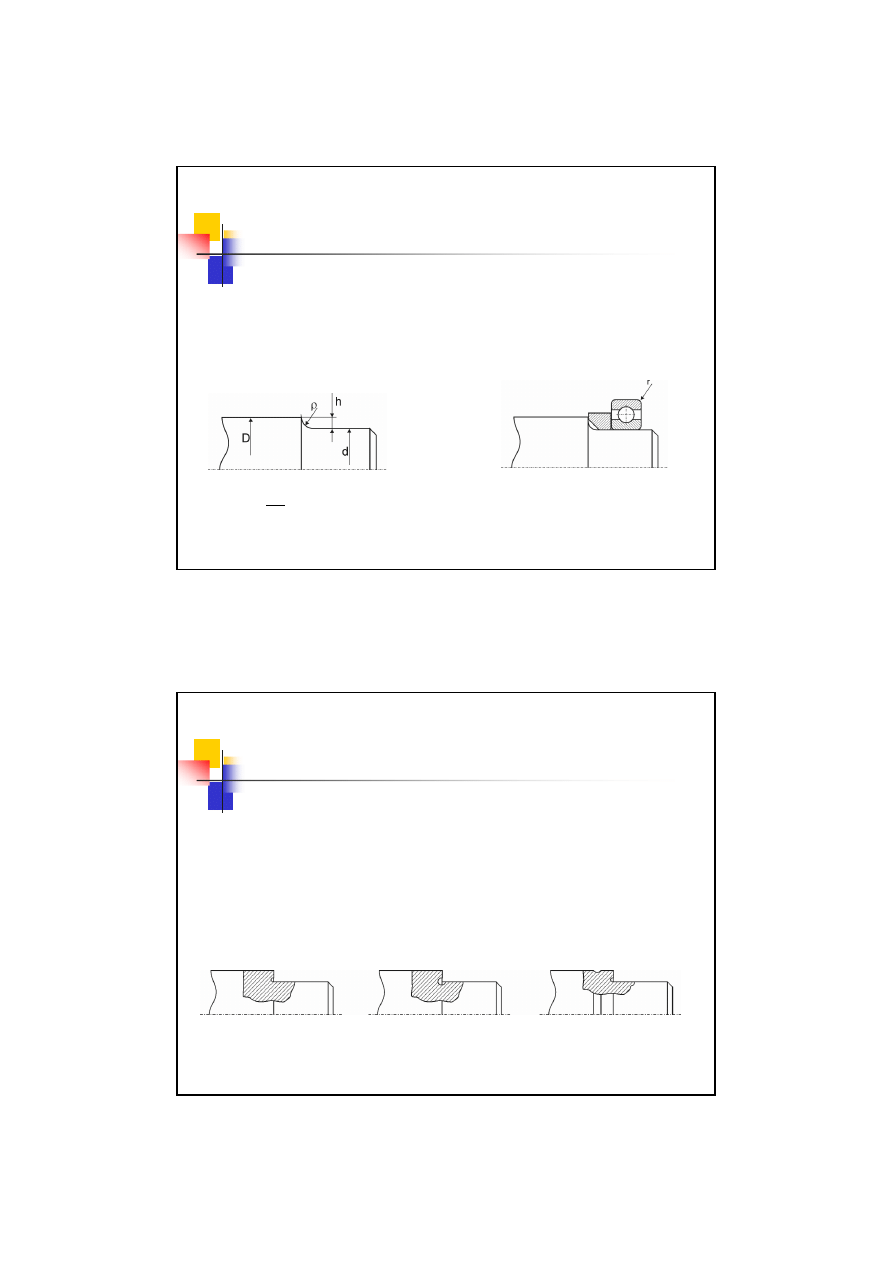
Zalecenia konstrukcyjne
Aby uniknąć nadmiernego osłabienia
wytrzymałości elementu w wyniku karbu należy:
Zmiany kształty prowadzić możliwe łagodnie
2
,
1
≤
d
D
Zalecenia konstrukcyjne
Aby uniknąć nadmiernego osłabienia
wytrzymałości elementu w wyniku karbu należy:
Jeżeli nie można uniknąć nagłych zmian kształtu to należy
wprowadzać karby konstrukcyjne
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron