1

Spektroskopia magnetycznego rezonansu jądrowego

gdy

I

≠ 0 to

jądro wykazuje właściwości magnetyczne

S =

√

I(I+1)

gdzie:

I – kwantowa liczba spinowa jądra

I = 0, ½, 1, 3/2, 2, 5/2, ... itd

h

2

π

12

C;

16

O;

32

S

0

parzysta

parzysta

2

H(1);

14

N(1);

30

B(13);

całkowita

nieparzysta

parzysta

13

C(1/2);

17

O(1/2);

29

Si(1/2);

połówkowa

parzysta

nieparzysta

1

H(1/2);

3

H(1/2);

15

N(1/2);

19

F(1/2);

31

P(1/2);

połówkowa

nieparzysta

nieparzysta

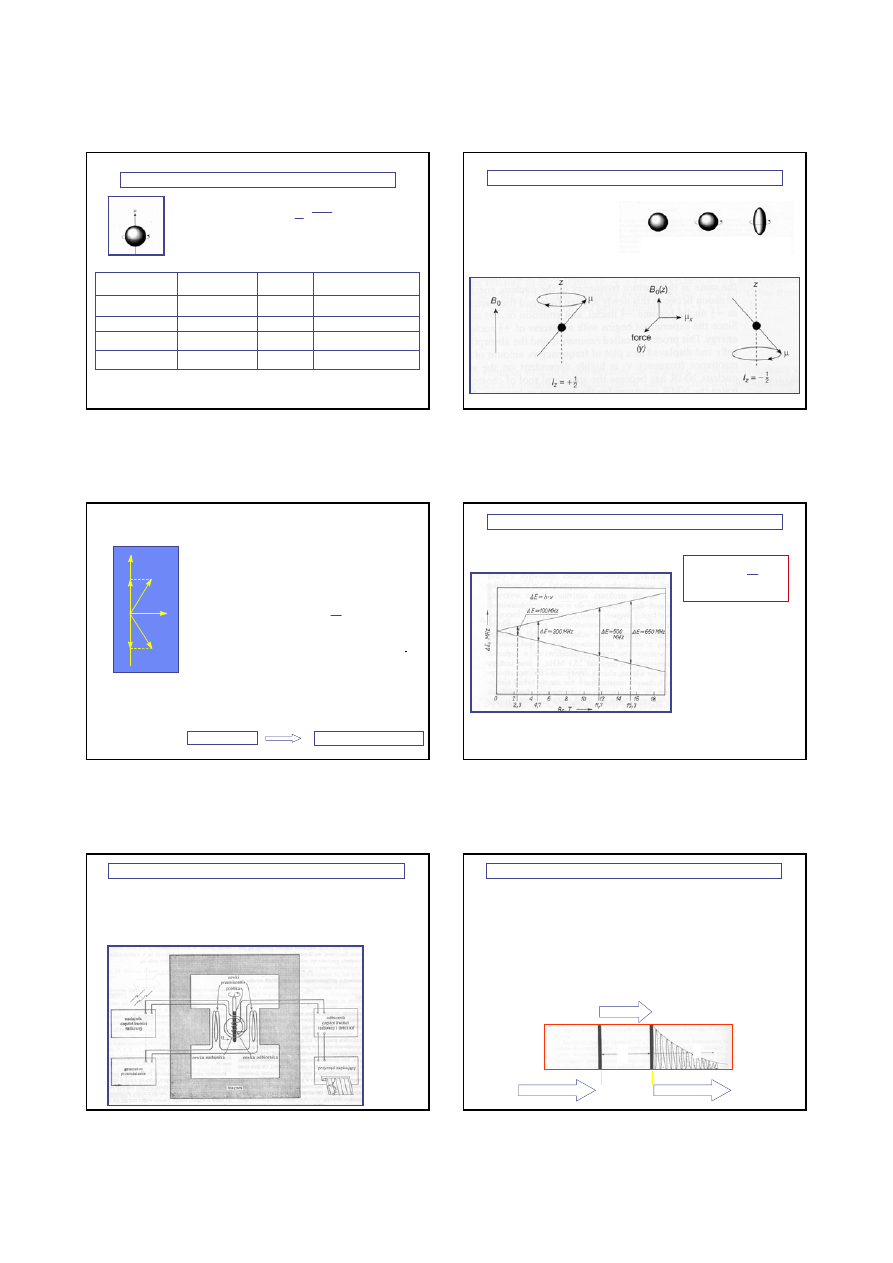
PRZYKŁADOWE JĄDRA

I

LICZBA ATOMOWA

(protony)

MASA ATOMOWA

(protony + neutrony)

µ

=

γ ×

S

gdzie:

γ – współczynnik żyromagnetyczny

µ

– moment magnetyczny

brak spinu

I = 0

spin sferyczny

I =

1
2

_

spin elipsoidalny

I = 1, , 2, ...

3
2

Spektroskopia magnetycznego rezonansu jądrowego

I = 1/2 m

I

=

±1/2

1

H

I = 1

m

I

= 1, 0, -1

14

N

µ

z

µ

z

z

µ

µ

y

N

= 2I + 1

STANY ENERGETYCZNE:

α i β

N

α

> N

β

∆

E = 2

µ

z

B

0

=

γ ×

B

0

h

2π

gdzie: h– stała Plancka;

γ

– współczynnik żyromagnetyczny; B

o

–

natężenie pola magnetycznego

h,

γ, π

– stałe

∆

E proporcjonalne do B

0

ν

1

=

γ×

B

0

1

2

π

WARUNEK REZONANSU

Spektroskopia magnetycznego rezonansu jądrowego

B

0

= 2.35T

v

1

dla protonu wynosi 100MHz

B

0

= 4.7T

v

1

dla protonu wynosi 200MHz

B

0

= 11.7T

v

1

dla protonu wynosi 500MHz

∆

E = h

ν

Spektroskopia magnetycznego rezonansu jądrowego

Energia o częstości radiowej

ν może być dostarczona do układu badanego:

™

metodą fali ciągłej ze stopniową zmianą zakresu częstości – w spektrometrach

CW próbka jest umieszczona w polu magnetycznym i naświetlana przy powolnej
zmianie częstości w określonym zakresie

Spektroskopia magnetycznego rezonansu jądrowego

Energia o częstości radiowej

ν może być dostarczona do układu badanego:

™

metodą impulsową poprzez wzbudzenie wszystkich częstości w wyniku

naświetlania jednym impulsem – próbkę umieszcza się w polu magnetycznym i
naświetla się impulsem RF wysokiej mocy, obejmującym cały zakres częstości
Taki impuls wzbudza w tym samym czasie wszystkie protony danej próbki .
Natychmiast po impulsie wzbudzone jądra zaczynają powracać do stanu
podstawowego i emitują zaabsorbowaną energię. Detektor rejestruje zmiany
energii w postaci swobodnego zaniku indukcji (FID), charakteryzującej
wszystkie jądra naświetlane w czasie trwania impulsu.

t

1

t

2

IMPULS RF

REJESTRACJA FID

CZAS MARTWY

2

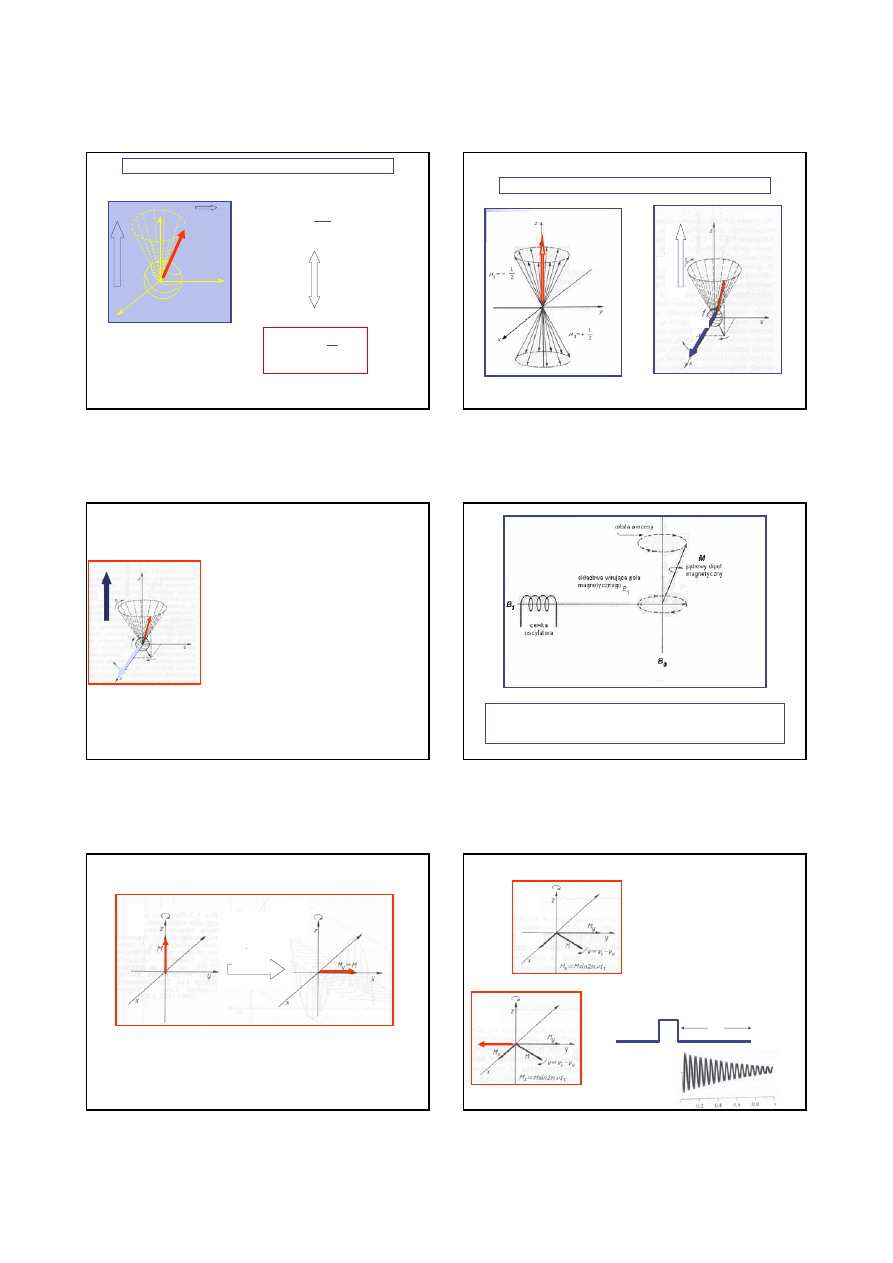
Częstość precesji, częstość Larmora

ν

L

=

γ

B

0

2

π

y

z

x

B

0

µ

Spektroskopia magnetycznego rezonansu jądrowego

ν

1

=

γ×

B

0

1

2

π

WARUNEK REZONANSU

µ

µ

M

M

B

0

B

1

Spektroskopia magnetycznego rezonansu jądrowego

B

0

>>

B

ef

brak rezonansu

częstość precesji

ν

L

znacznie różni się od częstości pola B

1

pole B

ef

zbliżone do pola B

0

wektor magnetyzacji M równoległy do kierunku pola B

0

B

0

≈

B

ef

spełniony war. rezonansu

Częstość precesji

ν

L

zbliżona do częstości pola B

1

B

ef

≈

B

1

precesja odbywa się wokół B

1

Wektor magnetyzacji M odchyla się od kierunku pola B

0

i podąża za wirującym polem B

1

M

B

0

B

1

• utrzymuje się stałą częstotliwość generatora drgań i dokonuje się zmian
natężenia pola w wąskim zakresie, tzw. przemiatanie polem
• zmienia się częstotliwość drgań generatora i utrzymuje się pole o stałym
natężeniu, tzw. przemiatanie częstotliwością

CW

IMPULS

( )

x

π
2

METODA IMPULSOWA

Po impulsie 90

° podanym z kierunku x – wektor namagnesowania znajdzie się na osi y;

tam też zlokalizowany jest nasz odbiornik – sygnał ma największą intensywność i
dodatnią fazę

METODA IMPULSOWA

M

x

= 0

Po pewnym czasie rotujący
wokół osi z wektor znajdzie
się na osi x- będzie
niewidoczny dla detektora
(na osi y) – sygnał równy
zero

Po chwili wektor znajdzie się na osi –y i
detektor zarejestruje sygnał o fazie
ujemnej.

t

⁄

3

Rozpuszczalniki stosowane w NMR

R-F + SbF

5

→ R

+

[SbF

6

]

-

Wzorzec do pomiarów NMR

• wzorzec wewnętrzny – wzorzec i próbka znajdują się w tym samym roztworze

wzorzec

wewnętrzny

mikroprobówka

wzorzec

zewnętrzny

• wzorzec zewnętrzny – wzorzec znajduje się w osobnej kapilarze,
należy skorygować przesunięcie chemiczne,

Wzorzec do pomiarów NMR

(CH

3

)

4

Si TMS

cykloheksan

C

6

H

6

1,4-dioksan

tert-butanol

np. dla pochodnych
cyklopropanu, związków
krzemoorganicznych

roztwory wodne

N

C

O

C

F

3

H

3

C

H

3

C

13

C

17

O

15

N

19

F

1

H

1

H

CH

3

COOCH

3

CDCl

3

CH

2

O

H

3

C

O

ν

0

= 60 MHz

ν

0

+ ∆ν

∆ν <

1kHz

B

lok

= B

0

(1-

σ)

gdzie:

σ

- stała przesłaniania

σ = σ

dia

+ σ

para

4

10

9

8

7

6

5

4

3

2

1

0

-1

wzrost częstotliwości

odsłanianie

przesłanianie

niskie natężenie pola

wysokie natężenie pola

Pomiar przesunięcia chemicznego

ν

sub

-

ν

wz

ν

0

δ

=

[ppm = 10

-6

]

gdzie:

ν

0

- częstość podstawowa aparatu

16 14 12 10 8 6 4 2 0 -2 -4 ppm,

δ

960

840 720 600 480 360 240 120 0 120 240 Hz,

(60 MHz)

1600 1400 1200 1000 800 600 400 200 0 200 400 Hz (

100 MHz)

-6 -4 -2 0 2 4 6 8 10 12

14

ppm,

τ

wzorzec TMS: Si(CH

3

)

4

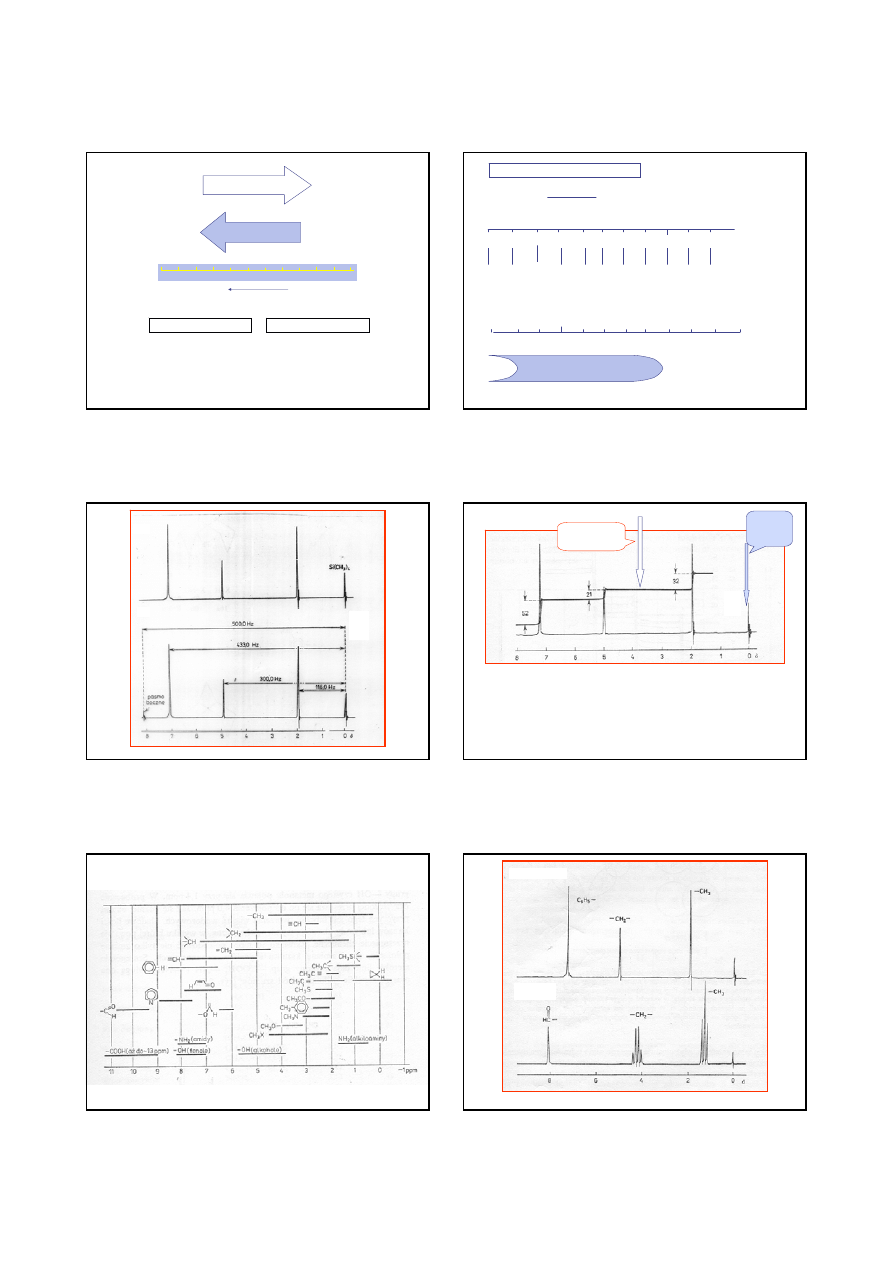
A

B

C

wzorzec

TMS

linia

integracyjana

A : B :

C

52

21

32

10.5 4.3

6.5

105 40

63

w przybliżeniu stosunek A : B : C = 5 : 2 : 3

Zależność między strukturą a przesunięciem chemicznym

dla protonów alifatycznych

δ: CH

3

- < -CH

2

- < =CH- wyjątek: cyklopropan

CH

3

COOCH

2

C

6

H

5

HCOOCH

2

CH

3

5

Sprzężenie spinowo-spinowe

polaryzacja magnetyczna powłoki elektronowej

X

A

X

A

B

0

spin jądrowy

δ

J

AX

[Hz]

Układ spinowy – zespół jąder między, którymi występuje sprzężenie spinowo-spinowe

stała sprzężenia – odległość między liniami dubletu

B

0

A

1

A

2

J

AX

= 0

A

1

A

2

J

AX

> 0

A

1

A

2

J

AX

X

1

X

2

J

AX

δ

A

x

δ

A

2

A

1

E

X

2

X

1

A

x

CH

2

CH

3

3

J

AX

3

J

AX

1

2

1

CH

2

1

3

3

1

CH

3

CH

2

CH

3

3

J

AX

3

J

AX

Multipletowość sygnału każdej
grupy jest większa o 1 od liczby
protonów w grupie sąsiedniej.

n + 1

gdzie n – liczba protonów w grupie sąsiedniej

przez 2 wiązania –

2

J stała sprzężenia geminalnego

przez 3 wiązania –

3

J stała sprzężenia vicynalnego

przez 4 wiązanie –

4

J stała sprzężenia dalekiego

zasięgu

Rodzaje sprzężeń:

jądra równocenne magnetycznie:

™

takie samo przesunięcie chemiczne

™

o takiej samej stałej sprzężenia z jądrami sąsiednimi

jądra równocenne chemicznie

-CH

3

-C(CH

3

)

3

jądra równocenne chemicznie

jądra równocenne magnetycznie:

F

HX

F

HA

J

13

≠

J

14

O

H

2

H

1

H

4

H

3

H

A

H

C

H

B

H

C

6

H

5

H

H

B

H

A

H

C

H

C

6

H

5

H

H

C

H

B

H

A

H

C

6

H

5

H

∆ν

ij

J

ij

> 6

widma pierwszego rodzaju (I – rzędu)

dla jąder o spinowej liczbie kwantowej I =1/2 multipletowość wynosi n + 1, gdzie n
– liczba jąder w sąsiedniej grupie

jeżeli w sąsiedztwie jest kilka grup, to należy je rozpatrywać oddzielnie – kolejność
rozpatrywania nie wpływa na wynik końcowy

odległość między liniami odpowiada stałej sprzężenia w [Hz]

względne natężenia linii w multiplecie są zgodne z wartościami trójkąta Pascala

n = 0

1

1 1 1

2 1 2 1

3 1 3 3 1

4 1 4 6 4 1

5 1 5 10 10 5 1

6 1 6 15 20 15 6 1

wartość stałej sprzężenia maleje wraz ze wzrostem odległości między jądrami

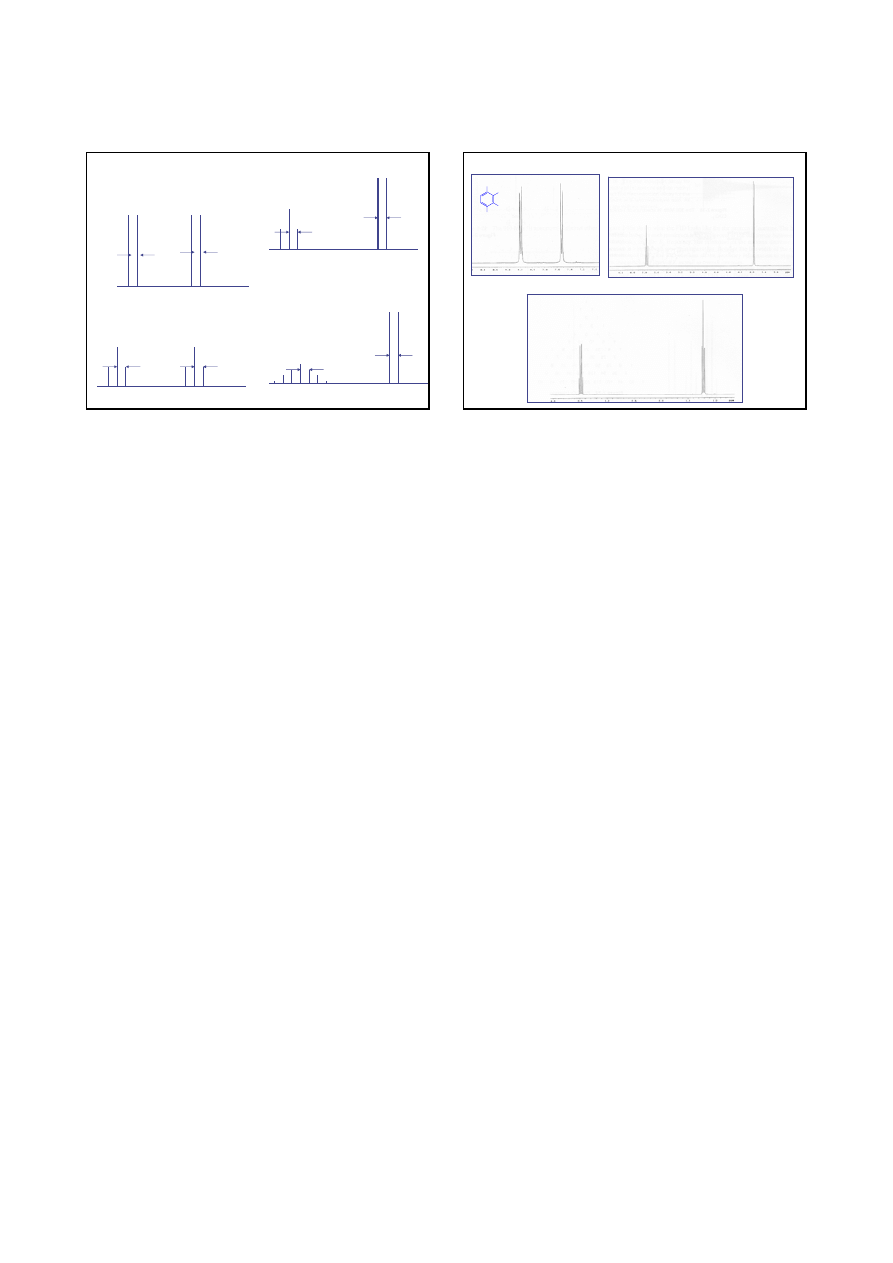
6

AX

CH-CH

J

AX

J

AX

AX

2

CH-CH

2

J

AX

J

AX

J

AX

J

AX

A

2

X

2

CH

2

-CH

2

J

AX

J

AX

AX

6

CH(CH

3

)

2

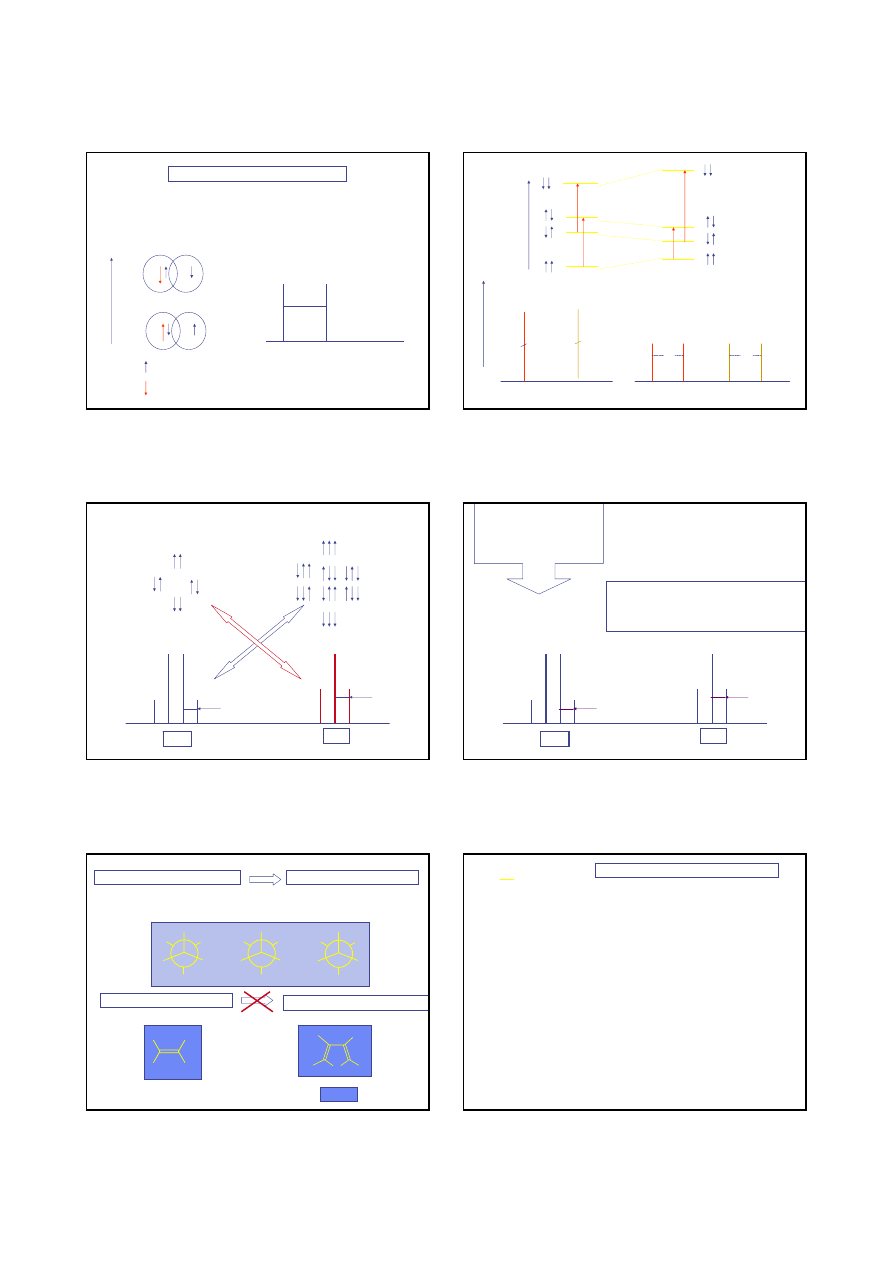
Przykładowe widma

1

H NMR [300 MHz]

Cl

H

NO

2

H

CH-CH

Cl

2

HC-CH

2

Cl

(CH

3

CH

2

)

2

O