1.
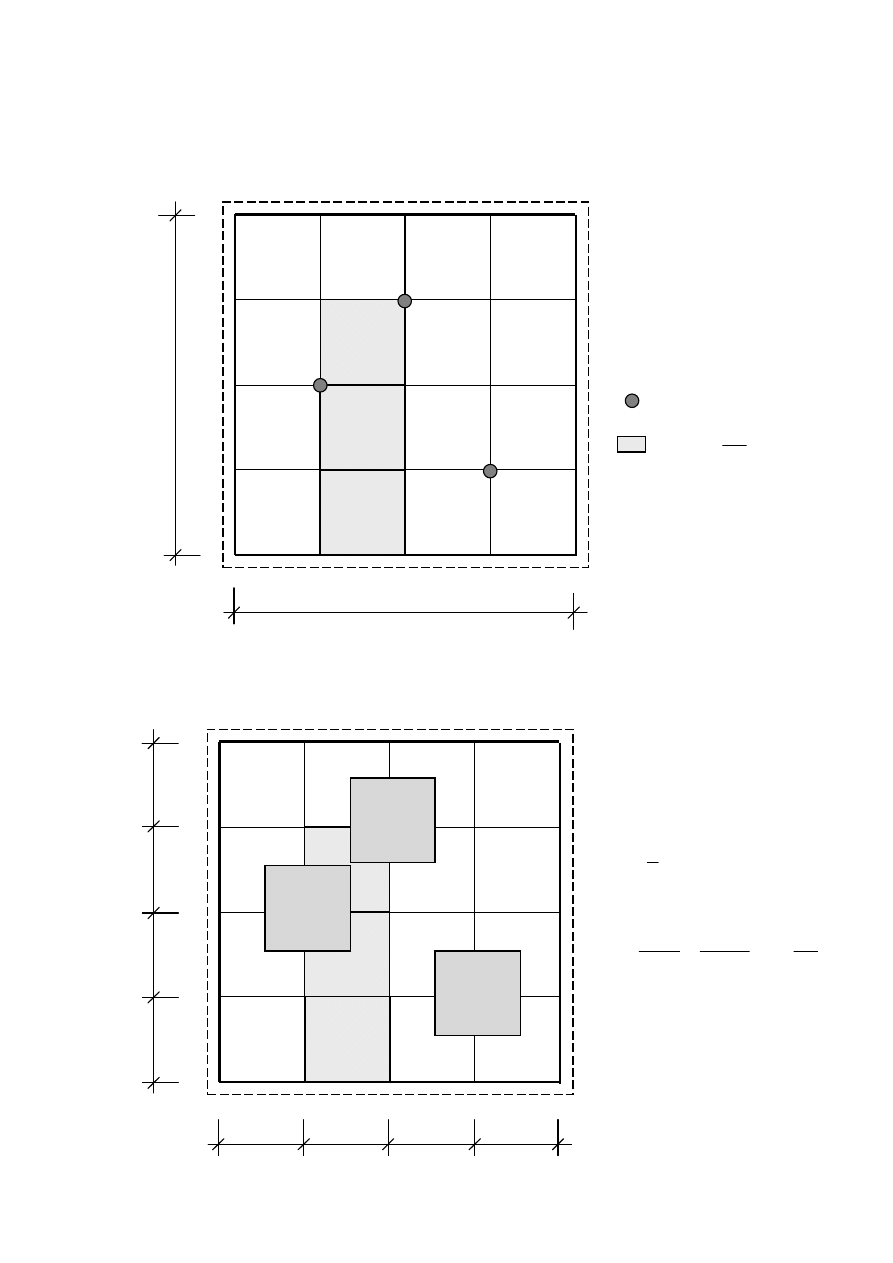
Obliczenie płyty swobodnie podpartej na obwodzie
Schemat podstawowy
Gdzie:
m
a
5
=
→
kN
P
15
=
→
2
2
m
kN
q
=
Dyskretyzacja układu wraz z obciążeniem zastępczym
m
x
25
,
1
4
5
=
=
∆
( ) ( )
2
2
2
6
,
9
25
,
1
15
~
m
kN
x
P
q
=
=
∆
=
∆
x
∆
x
∆
x
∆
x
∆
x
∆
x
∆
x
∆
x
24
33
44
11
13
12
14
15
21
23
22
25
31
32
34
35
51
53
52
54
55
41
43
42
45
q
~
q
~
q
~
a
a
11
13
12
14
15
21
23
22
24
25
31
33
32
34
35
51
53
52
54
55
41
43
42
44
45

Sformułowanie zagadnienia brzegowego
( )
( )
( ) ( )
=
=
=
=
=
=
=
∂
∂
+
∂
∂
∂
+
∂
∂
0
,
0
.
0
,
0
.
,
,
,
2
,
4
4
2
2
4
4
4
y
x
M
w
const
y
M
w
const
x
D
y
x
q
y
y
x
w
y
x
y
x
w
x
y
x
w
0
=
x
M
→
2
,
'
1
,
k
k
w
w
−
=
oraz
4
,
'
5
,
k
k
w
w
−
=
0
=
y
M
→
j
j
w
w
,
2
,'
1
−
=
oraz
j
j
w
w
,
4
,'
5
−
=
0
5
,
,
5
1
,
,
1
=
=
=
=
k
j
k
j
w
w
w
w
gdzie:
5
:
1
,
,
∈
∧
∈
j
k
N
j
k
(współrzędne punktu płyty)
Ilorazy różnicowe dla węzłów wewnętrznych i leżących w pobliżu krawędzi
Ilorazy różnicowe
( )
(
)
2
,
1
,
,
1
,
2
,
4
4
4
4
6
4
1
,
+
+
−
−
+
−
+
−
∆
≅
∂
∂
j
k
j
k
j
k
j
k
j
k
w
w
w
w
w
x
x
y
x
w
( )
(
)
1
,
1
,
1
1
,
1
1
,
,
1
,
1
,
1
,
1
1
,
1
4
2
2
4
2
2
4
2
2
2
,
2
+
+
+
−
+
+
−
+
−
−
−
−
+
−
+
−
+
−
+
−
∆
≅
∂
∂
∂
j
k
j
k
j
k
j
k
j
k
j
k
j
k
j
k
j
k
w
w
w
w
w
w
w
w
w
x
y
x
y
x
w
( )
(
)
j
k
j
k
j
k
j
k
j
k
w
w
w
w
w
x
y
y
x
w
,
2
,
1
,
,
1
,
2
4
4
4
4
6
4
1
,
+
+
−
−
+
−
+
−
∆
≅
∂
∂
Po zsumowaniu:
(
+
+
−
+
−
+
+
−
+
∆
+
+
−
−
+
−
−
−
−
−
2
,
1
,
,
1
,
2
,
1
,
1
,
1
1
,
1
,
2
4
8
20
8
2
8
2
1
j
k
j
k
j
k
j
k
j
k
j
k
j
k
j
k
j
k
w
w
w
w
w
w
w
w
w
x
( )
D
y
x
q
w
w
w
w
j
k
j
k
j
k
j
k
,
2
8
2
,
2
1
,
1
,
1
1
,
1
=
+
+
−
+
+
+
+
+
−
+
,
czyli:
(
) (
)
D
x
q
w
w
w
w
w
w
w
w
w
w
w
w
w
j
k
j
k
j
k
j
k
j
k
j
k
j
k
j
k
j
k
j
k
j
k
j
k
j
k
4
,
2
2
,
2
,
,
2
1
,
1
1
,
1
1
,
1
1
,
1
,
1
1
,
1
,
,
1
,
2
8
20
∆
⋅
=
+
+
+
+
+
+
+
+
+
+
+
+
−
+
+
−
−
+
+
−
+
+
−
−
−
+
+
−
−
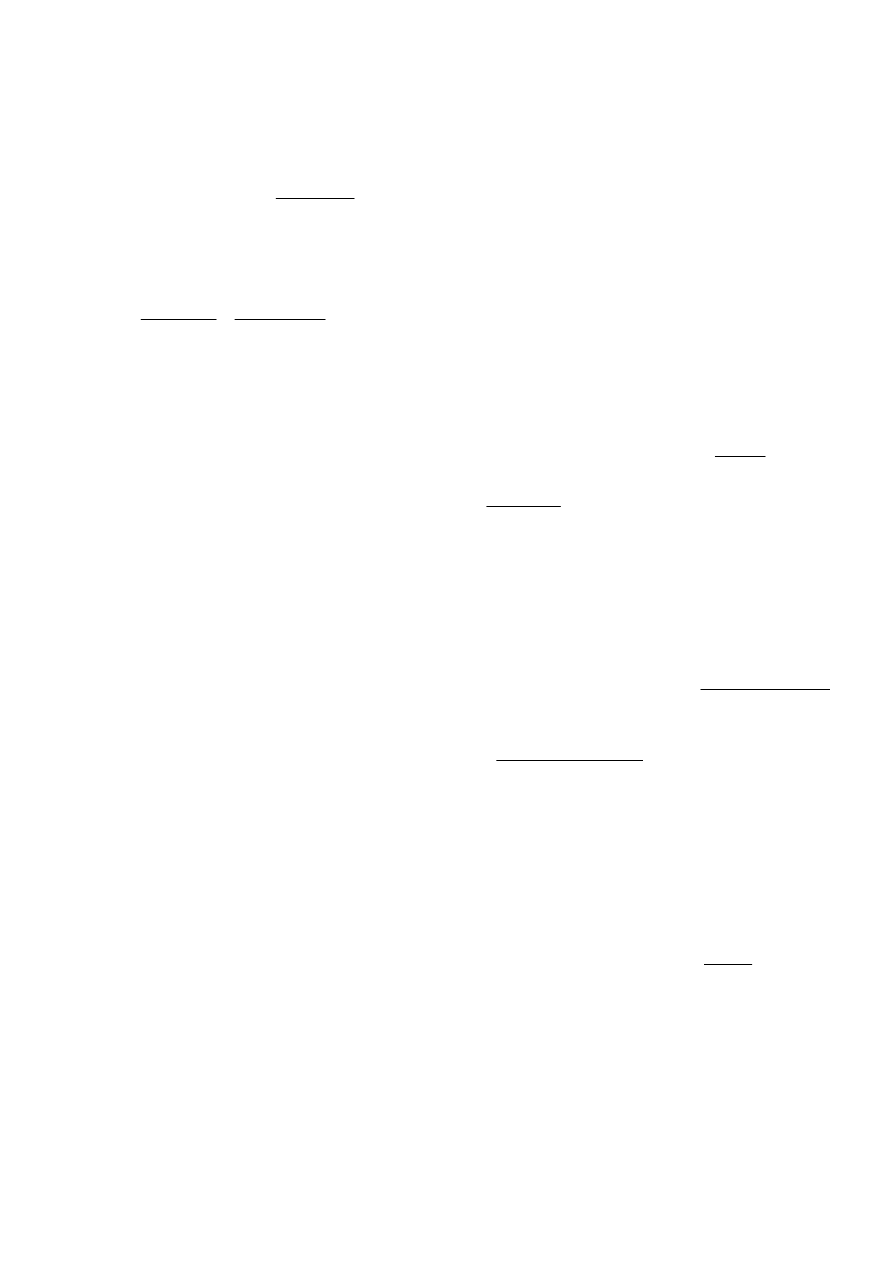
Równania różnicowe dla węzłów siatki dyskretyzacyjnej
Sztywność płyty :
(
)
2
3
1
12
ν
−
⋅
=
Eh
D
Przyjęto:
GPa
E
30
=
(B25),
2
,
0
=
ν
,
m
a
h
5
,
0
1
,
0
=
=
(
)
(
)
kNm
Eh
D
5
2
3
6
2
3
10
2552
,
3
2
,
0
1
12
5
,
0
10
30
1
12
⋅
=
−
⋅
⋅
⋅
=
−
⋅
=
ν
o
Węzeł 22
(
) (
)
D
x
q
w
w
w
w
w
w
w
w
w
w
w
w
w
⋅
∆
⋅
=
+
+
+
+
+
+
+
+
+
+
+
−
4
2
8
20
4
42
24
'
21
2
'
1
33
31
13
11
32
23
21
12
22
(
)
325520
4
25
,
1
2
2
8
20
4
42
24
22
22
33
32
23
22
⋅
⋅
=
+
+
−
−
+
+
−
w
w
w
w
w
w
w
w
m
w
w
w
w
w
w
5
42
24
33
32
23
22
10
375
,
0
2
8
8
18
−
⋅
=
+
+
+
−
−
o
Węzeł 23
(
) (
)
(
)
D
x
q
q
w
w
w
w
w
w
w
w
w
w
w
w
w
4
43
25
21
3
'
1
34
32
14
12
33
24
22
13
23
~
25
,
0
2
8
20
∆
⋅
+
+
=
+
+
+
+
+
+
+
+
+
+
+
−
(
) (
)
(
)
325520
25
,
1
6
,
9
2
25
,
0
2
8
20
4
43
23
34
32
33
24
22
23
⋅
+
⋅
=
+
−
+
+
+
+
−
w
w
w
w
w
w
w
w
m
w
w
w
w
w
w
w
5
43
34
32
33
24
22
23
10
575
,
7
2
2
8
8
8
19
−
⋅
=
+
+
+
−
−
−
o
Węzeł 24
(
) (
)
D
x
w
w
w
w
w
w
w
w
w
w
w
w
w
4
44
'
25
22
4
'
1
35
33
15
13
34
25
23
14
24
0
2
8
20
∆
⋅
=
+
+
+
+
+
+
+
+
+
+
+
−
(
)
0
2
8
20
44
24
22
24
33
34
23
24
=
+
−
+
−
+
+
−
w
w
w
w
w
w
w
w
0
2
8
8
18
44
22
33
34
23
24
=
+
+
+
−
−
w
w
w
w
w
w
o
Węzeł 32
(
) (
)
(
)
D
x
q
q
w
w
w
w
w
w
w
w
w
w
w
w
w
4
52
34
'
31
12
43
41
23
21
42
33
31
22
32
~
5
,
0
2
8
20
∆
⋅
+
=
+
+
+
+
+
+
+
+
+
+
+
−
(
)
325520
25
,
1
6
,
9
2
5
,
0
2
2
8
8
8
20
4
34
32
43
23
42
33
22
32
⋅
+
⋅
=
+
−
+
+
−
−
−
w
w
w
w
w
w
w
w
m
w
w
w
w
w
w
w
5
34
43
23
42
33
22
32
10
950
,
7
2
2
8
8
8
19
−
⋅
=
+
+
+
−
−
−
o
Węzeł 33
(
) (
)
D
x
q
w
w
w
w
w
w
w
w
w
w
w
w
w
4
53
35
31
13
44
42
24
22
43
34
32
23
33
5
,
0
2
8
20
∆
⋅
=
+
+
+
+
+
+
+
+
+
+
+
−
325520
25
,
1
2
5
,
0
2
2
2
2
8
8
8
8
20
4
44
42
24
22
43
34
32
23
33
⋅
⋅
=
+
+
+
+
−
−
−
−
w
w
w
w
w
w
w
w
w
m
w
w
w
w
w
w
w
w
w
5
44
42
24
22
43
34
32
23
33
10
750
,
0
2
2
2
2
8
8
8
8
20
−
⋅
=
+
+
+
+
−
−
−
−
o
Węzeł 34
(
) (
)
D
x
w
w
w
w
w
w
w
w
w
w
w
w
w
4
54
'
35
32
14
45
43
25
23
44
35
33
24
34
0
2
8
20
∆
⋅
=
+
+
+
+
+
+
+
+
+
+
+
−
(
) (
)
0
2
8
20
34
32
43
23
44
33
24
34
=
−
+
+
+
+
+
−
w
w
w
w
w
w
w
w
0
2
2
8
8
8
19
32
43
23
44
33
24
34
=
+
+
+
−
−
−
w
w
w
w
w
w
w
o
Węzeł 42
(
) (
)
D
x
q
w
w
w
w
w
w
w
w
w
w
w
w
w
4
2
'
5
44
'
41
22
53
51
33
31
52
43
41
32
42
5
,
0
2
8
20
∆
⋅
=
+
+
+
+
+
+
+
+
+
+
+
−
(
)
325520
25
,
1
2
5
,
0
2
8
20
4
42
44
42
22
33
43
32
42
⋅
⋅
=
−
+
−
+
+
+
−
w
w
w
w
w
w
w
w
m
w
w
w
w
w
w
5
44
22
33
43
32
42
10
750
,
0
2
8
8
18
−
⋅
=
+
+
+
−
−

o
Węzeł 43
(
) (
)
D
x
q
w
w
w
w
w
w
w
w
w
w
w
w
w
4
3
'
5
45
41
23
54
52
34
32
53
44
42
33
43
5
,
0
2
8
20
∆
⋅
=
+
+
+
+
+
+
+
+
+
+
+
−
(
) (
)
325520
25
,
1
2
5
,
0
2
8
20
4
43
23
34
32
44
42
33
43
⋅
⋅
=
−
+
+
+
+
+
−
w
w
w
w
w
w
w
w
m
w
w
w
w
w
w
w
5
23
34
32
44
42
33
43
10
750
,
0
2
2
8
8
8
19
−
⋅
=
+
+
+
−
−
−
o
Węzeł 44
(
) (
)
D
x
q
w
w
w
w
w
w
w
w
w
w
w
w
w
4
4
'
5
'
45
42
24
55
53
35
33
54
45
43
34
44
~
2
8
20
∆
⋅
=
+
+
+
+
+
+
+
+
+
+
+
−
(
)
325520
25
,
1
6
,
9
2
8
20
4
44
44
42
24
33
43
34
44
⋅
=
−
−
+
+
+
+
−
w
w
w
w
w
w
w
w
m
w
w
w
w
w
w
w
5
42
24
35
33
43
34
44
10
200
,
7
2
2
8
8
18
−
⋅
=
+
+
+
+
−
−
Układ równań algebraicznych
m
w
w
w
w
w
w
5
42
33
32
24
23
22
10
375
,
0
2
8
8
18
−
⋅
=
+
+
−
+
−
m
w
w
w
w
w
w
w
5
44
43
34
33
32
24
23
10
575
,
7
8
2
19
8
8
2
−
⋅
=
−
+
+
−
+
−
0
8
2
18
8
44
34
33
24
23
22
=
+
−
+
+
−
w
w
w
w
w
w
m
w
w
w
w
w
w
w
5
43
42
34
33
32
23
22
10
950
,
7
2
8
8
19
2
8
−
⋅
=
+
−
+
−
+
+
−
m
w
w
w
w
w
w
w
w
w
5
44
43
42
34
33
32
24
23
22
10
750
,
0
2
8
2
8
20
8
2
8
2
−
⋅
=
+
−
+
−
+
−
+
−
0
8
2
19
8
8
2
44
43
34
33
32
24
23
=
−
+
+
−
+
−
w
w
w
w
w
w
w
m
w
w
w
w
w
w
5
44
43
42
33
32
22
10
750
,
0
8
18
2
8
−
⋅
=
+
−
+
+
−
m
w
w
w
w
w
w
w
5
44
43
42
34
33
32
23
10
750
,
0
8
19
8
2
8
2
−
⋅
=
−
+
−
+
−
+
m
w
w
w
w
w
w
5
44
43
42
34
33
24
10
200
,
7
18
8
8
2
−
⋅
=
+
−
+
−
+
Postać macierzowa:
[ ]
m
w
w
w
w
w
w
w
w
w
,
10
200
,
7
10
750
,
0
10
750
,
0
0
10
750
,
0
10
950
,
7
0
10
575
,
7
10
375
,
0
18
8
1
8
2
0
1
0
0
8
19
8
2
8
2
0
1
0
1
8
18
0
2
8
0
0
1
8
2
0
19
8
1
8
2
0
2
8
2
8
20
8
2
8
2
0
2
8
1
8
19
0
2
8
1
0
0
8
2
0
18
8
1
0
1
0
2
8
2
8
19
8
0
0
1
0
2
8
1
8
18
5
5
5
5
5
5
5
44
43
42
34
33
32
24
23
22
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
⋅
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
Rozwiązanie układu równań (z programu lineq):
m
w
w
w
w
w
w
w
w
w
5
44
43
42
34
33
32
24
23
22
10
6496
,
1
9869
,
1
4818
,
1
8929
,
1
8488
,
2
3751
,
2
3670
,
1
3045
,
2
1,6258
−
⋅
=
Momenty zginające
Na kierunku x
( )
(
)
j
k
j
k
j
k
j
k
j
k
j
k
x
w
w
w
w
w
w
x
D
y
w
x
w
D
M
,
1
,
,
1
1
,
,
1
,
2
2
2
2
2
2
,
0
4
,
0
2
,
0
2
+
−
+
−
+
−
+
+
−
⋅
∆
−
≅
∂
∂
+
∂
∂
⋅
−
=
ν
( )
(
)
j
k
j
k
j
k
j
k
j
k
x
w
w
w
w
w
x
D
M
,
1
,
1
1
,
,
1
,
2
2
,
0
2
,
0
4
,
2
+
−
+
−
+
+
+
−
⋅
∆
−
=
( ) (
)
kNm
w
w
w
w
w
M
x
646
,
4
2
,
0
2
,
0
4
,
2
25
,
1
325520
42
22
33
32
31
2
32
=
+
+
+
−
⋅
−
=
( ) (
)
kNm
w
w
w
w
w
M
x
564
,
3
2
,
0
2
,
0
4
,
2
25
,
1
325520
43
23
34
33
32
2
33
=
+
+
+
−
⋅
−
=
( ) (
)
kNm
w
w
w
w
w
M
x
273
,
2
2
,
0
2
,
0
4
,
2
25
,
1
325520
44
24
35
34
33
2
34
=
+
+
+
−
⋅
−
=
o
Wykres momentu w przekroju X 3-3
3
3
4,646
3,564
2,273
M
x
[kNm]
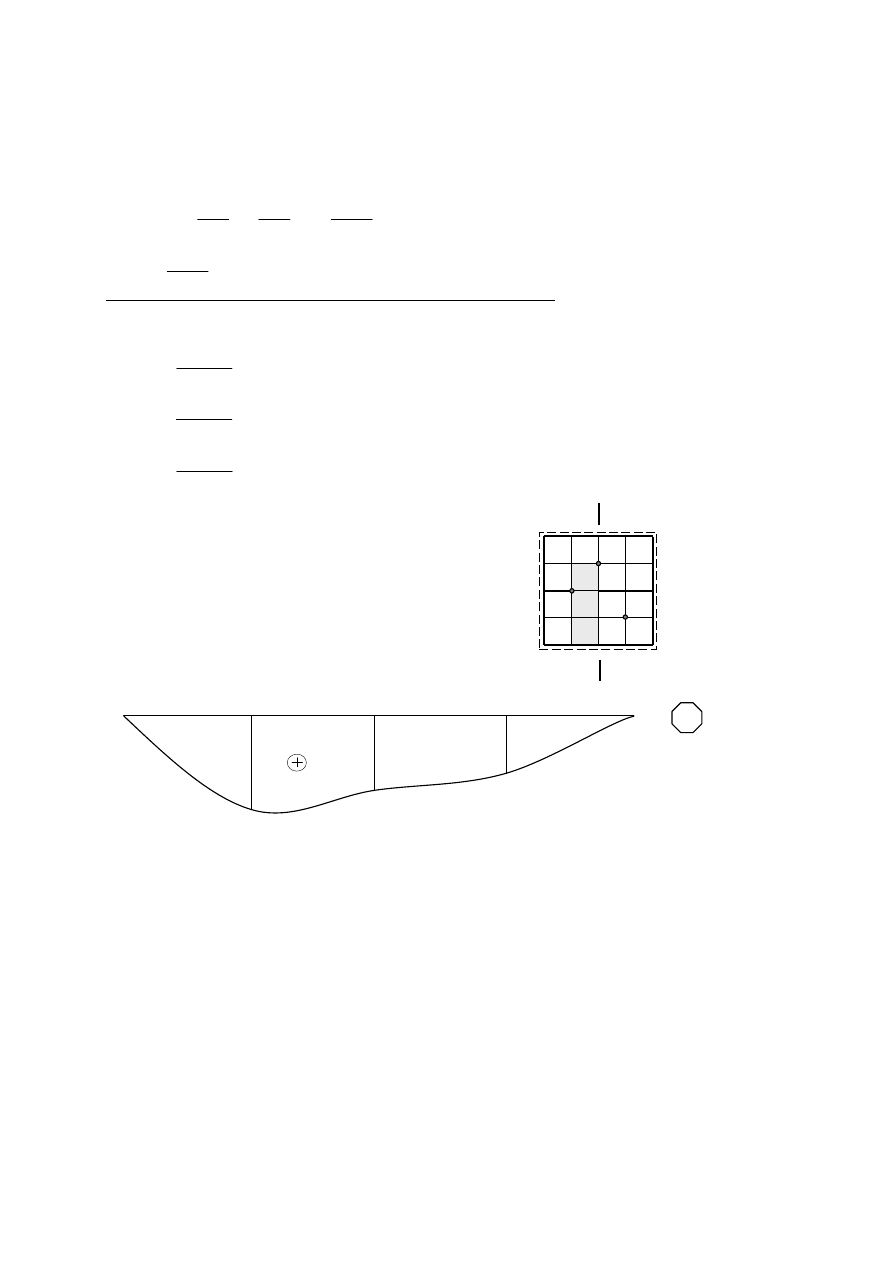
Na kierunku y
( )
(
)
1
,
,
1
,
,
1
,
,
1
2
2
2
2
2
2
,
0
4
,
0
2
,
0
2
+
−
+
−
+
−
+
+
−
⋅
∆
−
≅
∂
∂
+
∂
∂
⋅
−
=
j
k
j
k
j
k
j
k
j
k
j
k
y
w
w
w
w
w
w
x
D
x
w
y
w
D
M
ν
( )
(
)
1
,
1
,
,
1
,
,
1
2
2
,
0
2
,
0
4
,
2
+
−
+
−
+
+
+
−
⋅
∆
−
=
j
k
j
k
j
k
j
k
j
k
y
w
w
w
w
w
x
D
M
( ) (
)
kNm
w
w
w
w
w
M
y
341
,
4
2
,
0
2
,
0
4
,
2
25
,
1
325520
24
22
33
23
13
2
23
=
+
+
+
−
⋅
−
=
( ) (
)
kNm
w
w
w
w
w
M
y
525
,
3
2
,
0
2
,
0
4
,
2
25
,
1
325520
34
32
43
33
23
2
33
=
+
+
+
−
⋅
−
=
( ) (
)
kNm
w
w
w
w
w
M
y
695
,
2
2
,
0
2
,
0
4
,
2
25
,
1
325520
44
42
53
43
33
2
43
=
+
+
+
−
⋅
−
=
o
Wykres momentu w przekroju Y 3-3
2.
Wnioski.
W ćwiczeniu projektowym przedstawiono obliczenie płyty swobodnie podparta na
obwodzie. Wykresy ukazują w przybliżeniu prawidłowy przebieg momentów
zginających, jednak należy pamiętać, że metoda różnic skończonych nie oddaje
poprawnych wyników przy tak dużej dyskretyzacji. Aby uzyskać prawidłowe wartości i
dokładny przebieg wykresów sił wewnętrznych należy zagęścić siatkę dyskretyzacji.
Mimo to pozostaną błędy zaokrągleń, które przy łatwych schematach nie mają
większego wpływu na obliczone wyniki.
4,341
3,525
2,695
M
y
[kNm]
3
3
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron