Project “The development of the didactic potential of Cracow University of Technology in the range of modern
construction” is co-financed by the European Union within the confines of the European Social Fund
and realized under surveillance of Ministry of Science and Higher Education.
1
Exercise 3.
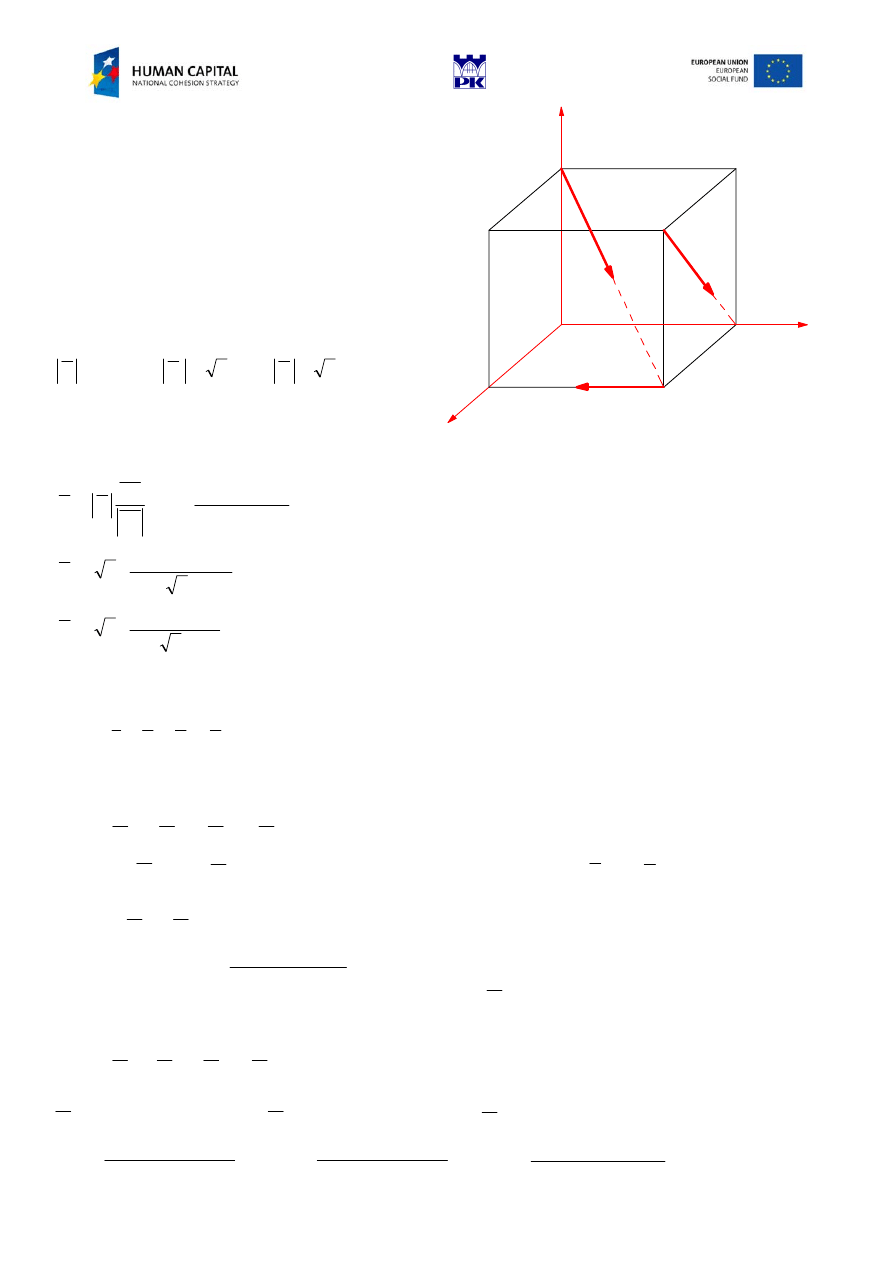
I. For a given force system find the sum vector,
the total moment about points B, O and E.
Verify the correctness of your computations.
II. Find an equivalent force couple system at point B.
III. Determine the simplest equivalent force system.
x
z
y
F
1
F
F
3
2
O
a
a
2a
A
C
E
D
B
P
F
2
1
,
P
F
2
2
,
P
F
6
3
I.
The components of the forces.
0
2
0
2
0
2
0
2
1
1
P
a
a
P
BA
BA
F
F
P
P
a
a
P
F
0
2
1
0
1
2
2
P
P
P
a
a
P
F
2
6
1
2
1
6
3
The sum vector
P
P
P
P
P
P
P
F
F
F
S
2
0
0
2
0
0
2
0
3
2
1
The total moment about point B
B
B
B
B
M
M
M
M
3
2
1
Moments
B
M
1
and
B
M
3
vanish, because the lines of actions of forces
1
F and
3
F
pass through point B.
Hence
The total moment of the force system about point B equals
0
0
Pa
M
B
.
0
0
0
0
0
2
Pa
a
P
P
M
M
B
B
The total moment about point O
O
O
O
O
M
M
M
M
3
2
1
Pa
a
a
P
M
O
2
0
0
0
2
0
2
0
1
0
2
0
0
2
3
Pa
Pa
a
P
P
P
M
O
Pa
Pa
a
a
a
P
P
M
O
2
0
2
2
0
2
Project “The development of the didactic potential of Cracow University of Technology in the range of modern
construction” is co-financed by the European Union within the confines of the European Social Fund
and realized under surveillance of Ministry of Science and Higher Education.
2
0
4
Pa
Pa
M
O
The correctness of above computations can be verified by changing the moment center.
BO
S
M
M
B
O
0
4
0
2
a
Pa
M
2
0
0
0
0
P
a
a
P
Pa
O
The total moment about point E
E
E
E
E
M
M
M
M
3
2
1
Hence
0
0
Pa
M
E
.
Verification:
BE
S
M
M
B
E
II. An equivalent force coupe system at point B
An equivalent force couple system comprises force
P
S
b
2
0
0
applied to point B, and a couple
with a moment
0
0
Pa
M
B
.
Finding a coupe of a given moment (one of infinitely many)
The couple must satisfy two conditions
1.
0
B
B
M
F
M
F
The remaining components
are arbitrary (but can’t simultaneously equal zero).
z
x
F
F ,
For example
,
, hence
P
F
x
0
z
F
0
0
P
F
i
0
0
P
F
.
2.
BG
F
M
B
)
2
(
0
2
0
0
a
y
P
Pz
z
a
y
a
x
P
BG
F
0
0
2
0
0
1
a
E
0
2
0
Pa
P
M
0
2 E
M
0
2
0
2
2
3
Pa
Pa
a
a
P
P
P
M
E
0
0
0
0
2
0
0
0
0
Pa
a
P
Pa
M
E
F
F
F
y
x
z
y
x
G
F
F
a
a
B
F
F
F
z
z
y
x
,
0
2
0
0
F
F
F
F
0
0
B
F
Pa
Pa
F
M
y
y
z
y
x
Project “The development of the didactic potential of Cracow University of Technology in the range of modern
construction” is co-financed by the European Union within the confines of the European Social Fund
and realized under surveillance of Ministry of Science and Higher Education.
3
so
2
(
0
0
0
a
y
P
Pz
Pa
)
a
z
Pa
Pz
a
y
a
y
P
2
0
)
2
(
The above set of equations defines a line. We choose one point of that line e.g.
ne of the couples resulting in a mome
II. The simplest equivalent force system.
Determining the parameter of a system
a
a
G
2
0
O
nt consists of:
0
0
Pa
M
B
a
a
G
P
F
a
a
B
P
F
2
0
0
0
,
0
2
0
0
I
0
0
0
2
0
0
Pa
P
K
Conclusion: Because
M
S
B
0
0
S
, the system of fo
reduced to a resultant force
k
rces can be
S
W
2
0
0
P applied at an unknown point
z
y
x
H
,
,
,
, about which the total moment of the force
system equals zero.
0
BH
S
M
M
B
H
0
2
2
0
0
0
0
z
a
y
a
x
P
Pa
0
0
)
(
2
)
2
(
2
Pa
a
x
P
a
y
P
2
2
0
)
(
2
0
)
2
(
2
a
x
a
y
a
x
P
a
y
P
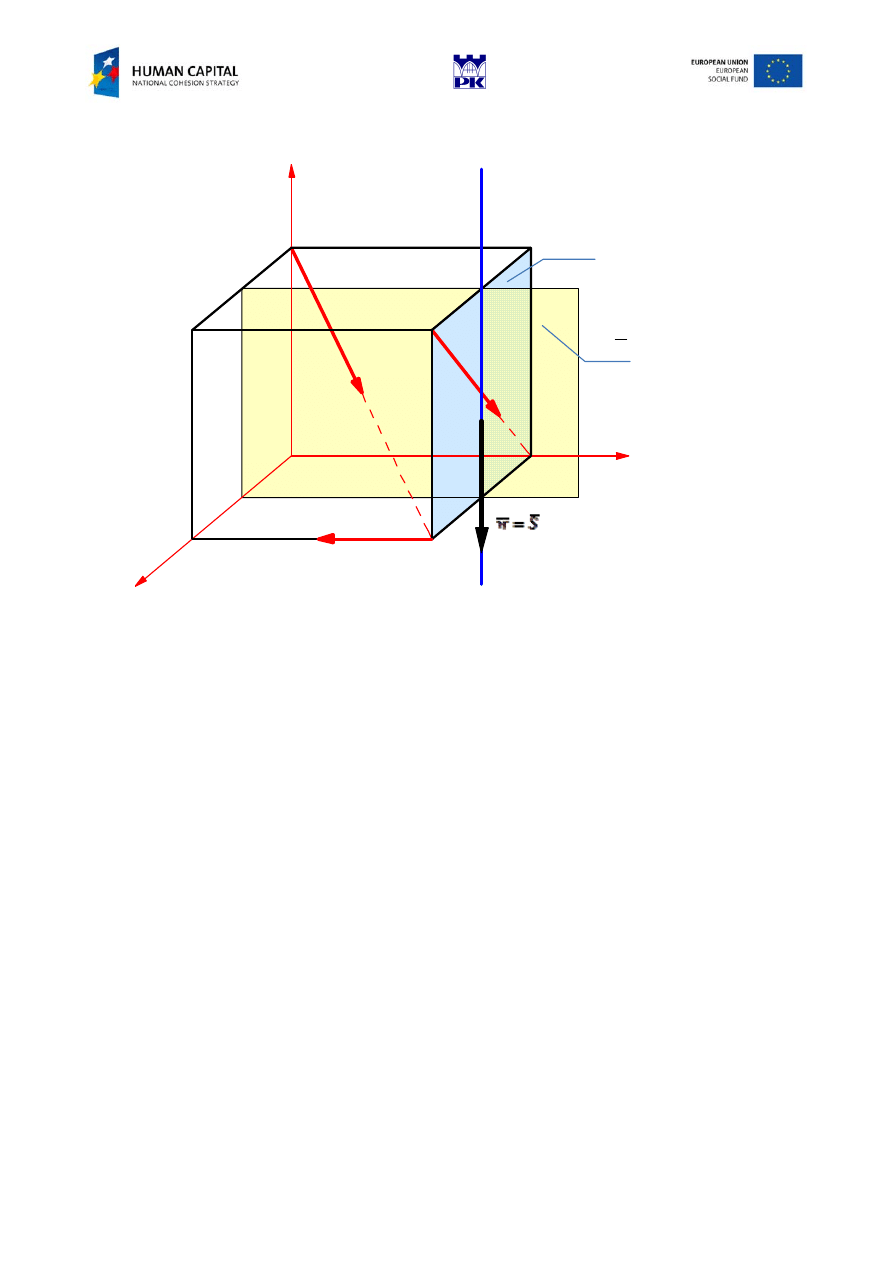
- the central axis of a system.
Setting
2
x
, we select a point on the central axis
a
a
a
H
2
2
.
The central axis contains point H an
a
d is parallel to the sum vector. Hence, the parametric equation of the
central axis takes the form:
a
z
a
y
a
x
2
2
Project “The development of the didactic potential of Cracow University of Technology in the range of modern
construction” is co-financed by the European Union within the confines of the European Social Fund
and realized under surveillance of Ministry of Science and Higher Education.
4
y
a
z
x
F
1
F
2
a
F
3
2a
A
E
B
C
D
H
O
2
a
x
a
y
2
- central axis
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron