
Treść zadań i ich rozwiązanie:
Zadanie nr 1.
Cząstki tlenku itru Y
2
O
3
o średnicy 750 Å wprowadzono do wolframu przez wewnętrzne
utlenianie. Pomiary przeprowadzone przy pomocy SEM wykazały, że na 1cm
3
przypada 5*10
14
cząstek tlenu. Oblicz pierwotną zawartość Y w % masowych w stopie W-Y. Gęstość tlenku itru
Y
2
O
3
wynosi 5,01 g/cm
3
.
Rozwiązanie:
średnica cząstek Y2O3:
d
= 750 ∗ 10 [cm]
ilość cząstek:
i = 5 ∗ 10
gęstość Y2O3:
ρ
= 5,01
g
cm
masa atomowa tlenu:
m
= 16 [u]
masa atomowa itru:
m
= 88,91 [u]
gęstość wolframu:
ρ
= 19,25
g
cm
masa atomowa jednej cząstki Y2O3
m
= m ∗ 2 + m ∗ 3 = 2 ∗ 88,91 + 3 ∗ 16 = 225,82 [u]
y =
m
∗ 2
m
∗ 100% =
2 ∗ 88,91
225,82
∗ 100% = 78,74%
objętość zajmowana przez cząstki Y2O3:
V
=
4
3
∗ π ∗
d
8
∗ i =
1
6
∗ π ∗ 750 ∗ 10
∗ 5 ∗ 10
= 0,1104 [cm ]
objętość zajmowana przez wolfram:
V = 1 − V
= 1 − 0,1104 = 0,8896 [cm ]
masa wolframu:
m
= V ∗ ρ
= 0,8896 ∗ 19,25 = 17,1248 [g]
masa Y2O3:
m
= ρ
∗ V
= 5,01 ∗ 0,1104 = 0,5531 [g]

masa itru:
m = m
∗ y = 0,55 ∗ 0,7874 = 0,4355 [g]
masa spieku przed utlenianiem:
m = m + m
= 0,4355 + 17,1248 = 17,5603 [g]
zawartość itru w spieku:
x =
m
m
∗ 100% =
0,4355
17,5603
∗ 100% = 2,48%
Zadanie nr 2.
Kompozyt w kształcie pręta o średnicy 20 mm, wykonany z żywicy epoksydowej zbrojonej
włóknami ciągłymi o udziale 40%, jest obciążany siłą 25000N. Oblicz naprężenie w każdym
włóknie.
Rozwiązanie:
d
pręta
= 20mm
udział = 40%
A
pręta
= π*d
2
pręta
/4 = 314,16mm
2
σ
c
= F/A
pręta
= 21000/314,16 = 79,58MPa
σ
w
= σ
c
*udział = 79,58*0,4 =31,83MPa
Zadanie nr 3.
Krótkie, ułożone równolegle włókna Al
2
O
3
, o średnicy 20 µm są zbrojeniem poliamidu PA6,6.
Wytrzymałość na ścinanie w strefie połączenia włókna z osnową wynosi ok. 7 MPa. Oblicz
długość krytyczną włókna i porównaj z przypadkiem, w którym zamiast włókien o średnicy 20
µm zostaną użyte whiskersy o średnicy 1 µm. Jaki jest minimalny parametr l/D w obu
przypadkach.
Rozwiązanie:
Wytrzymałość na rozciąganie włókien Al
2
O
3
R
w1
= 2100 MPa = 2,1 * 10
9
Pa
Wytrzymałość na rozciąganie whiskersów R
w2
= 21000 MPa = 2,1 * 10
10
Pa
Wytrzymałość na ścinanie w strefie połączenia włókna z osnową τ
0
= 7 MPa = 7 * 10
6
Pa
Średnica włókien Al
2
O
3
D
1
= 20 µm = 2*10
-5
m
Średnica whiskersów
D
2
= 1 µm = 1*10
-6
m

Włókna A
2
O
3
=
∗
=
2,1 ∗ 10 ∗ 2 ∗ 10
7 ∗ 10 ∗ 2
= 3
=
2 ∗
=
2,1 ∗ 10
2 ∗ 7 ∗ 10
= 150
Whiskersy
=
∗
=
2,1 ∗ 10
∗ 1 ∗ 10
7 ∗ 10 ∗ 2
= 1,5
=
2 ∗
=
2,1 ∗ 10
2 ∗ 7 ∗ 10
= 1500
Porównując otrzymane długości krytyczne widzimy że wraz ze dwudziestokrotnym zmniejszeniem
średnicy włókien otrzymujemy tylko dwukrotny spadek długości krytycznej. Wiąże się to z tym że
wraz ze spadkiem średnicy włókna, aby zachować podobną wytrzymałość kompozytu możemy
zmniejszyć długość włókien jak jest to widoczne w przypadku włókien whiskersowych. Dla włókien
whiskersowych otrzymujemy również duży stosunek l/D wynika to z tego, że dla stosunkowo małej
średnicy dostajemy dużą długość krytyczną włókien.
Zadanie nr 4.
Moduł sprężystości podłużnej (E) Mg wynosi 50 GPa, a gęstość 1,74 g/cm
3
. Znajdź udział
objętościowy włókien SiC ułożonych w jednym kierunku, który powinien być dodany do
magnezu tak, aby jego moduł właściwy wzrósł o 50%.
Rozwiązanie:
E
C
’ = 150% * E
C
= 75GPa
E
C
’ = E
Mg
*V
Mg
+ E
SiC
*V
SiC
= E
Mg
*(1- V
SiC
) + E
SiC
*V
SiC
V
SiC
=( E
C
’- E
Mg
)/(E
SiC
- E
Mg
)=(75-50)/(490-50)=0,0568=5,68%
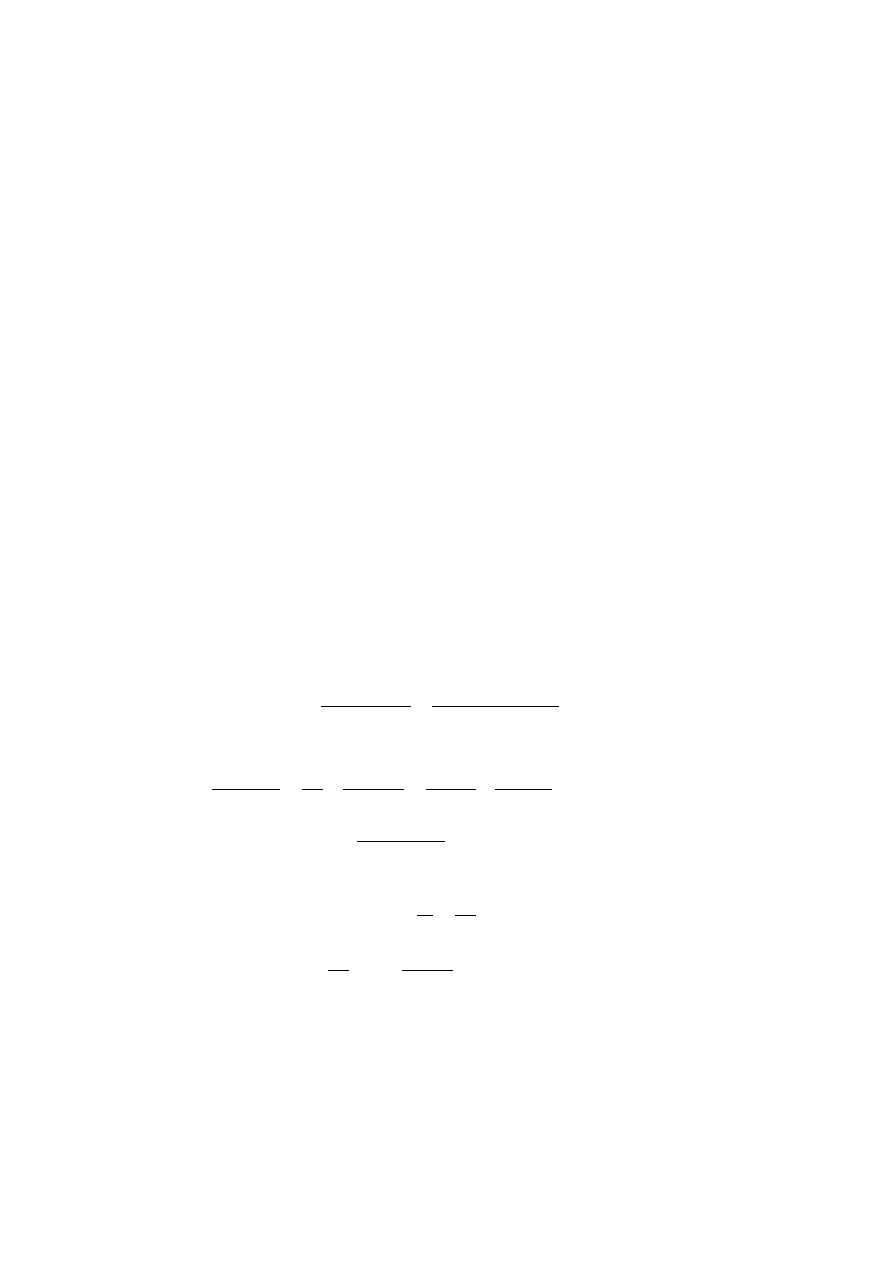
Zadanie nr 5.
Kompozyt zbrojony ciągłym włóknem posiada moduł sprężystości podłużnej E w kierunku
równoległym do kierunku ułożenia włókien równy 9 GPa przy: E
f
= 70 GPa i E
m
= 6
GPa. Oblicz moduł E w kierunku poprzecznym do kierunku ułożenia włókien tego kompozytu.
Oblicz naprężenie we włóknach przy założeniu że przyłożone obciążenie do kompozytu w
kierunku równoległym do kierunku włókien wywołuje naprężenie w osnowie równe 3 MPa.
Rozwiązanie:
Moduł sprężystości podłużnej kompozytu w kierunku równoległym E
c równ.
= 9 GPa = 9*10
9
Pa
Moduł Younga włókien E
f
= 70 GPa = 7 *10
10
Pa
Moduł Younga osnowy E
m
= 6 GPa = 6*10
9
Pa
Naprężenie w osnowie σ
m
= 3 MPa = 3*10
6
Pa
V
m
udział objętościowy osnowy
Szukane:
E
c prostop.
Moduł sprężystości podłużnej kompozytu w kierunku prostopadłym
σ
f
Naprężenie we włóknach
.
=
∗
+ (1 −
) ∗
.
=
∗
+
−
.
=
∗ (
−
) +
=
.
−
(
−
)
=
9 ∗ 10 − 7 ∗ 10
6 ∗ 10 − 7 ∗ 10
= 0,95
1
.
=
+
(1 −
)
=
0,95
6 ∗ 10
+
0,05
7 ∗ 10
= 1,59 ∗ 10
.
=
1
1,59 ∗ 10
= 6,3 ∗ 10
= 6,3
=
=
∗
=
3 ∗ 10
6 ∗ 10
∗ 7 ∗ 10
= 35

Zadanie nr 6.
Gęstość kompozytu na osnowie żywicy epoksydowej zbrojonego borowym włóknem ciągłym
wynosi 1,8 g/cm
3
. Gęstość boru wynosi 2,36 g/cm
3
, a gęstość żywicy 1,38 g/cm
3
.
Oblicz udział objętościowy włókien boru w kompozycie.
Rozwiązanie:
m
K
= m
Ż
+ m
B
ρ
K
V
K
= ρ
Ż
V
Ż
+ ρ
B
V
B
V
K
= V
Ż
+ V
B
V
K
= 1; V
Ż
= 1 - V
B
ρ
K
= ρ
Ż
(1 - V
B
) + ρ
B
V
B
=
Ż
Ż
=
,
,
,
,
= 0,429 = 42,9%
Zadanie nr 7.
Srebrowo-wolframowy kompozyt na styki elektryczne jest wykonywany technologią metalurgii
proszków w ten sposób, że najpierw jest wykonywana wypraska z czystego proszku W, która
następnie jest infiltrowana czystym srebrem. Gęstość wypraski wolframowej przed infiltracją
wynosi 13,3 g/cm
3
. Oblicz objętość porów (przed infiltracją) i końcową zawartość srebra w
kompozycie (w % masowych)
Rozwiązanie:
gęstość wolframu
= 19,25
gęstość powietrza w warunkach normalnych:
= 0,0012
gęstość wypraski
= 13,3
x= zawartość wolframu
y= zawartość porów

+
= 1 →
= 1 −
=
∗
+ (1 − ) ∗
=
− 1
−
=
13,3 − 1
19,25 − 0,0012
= 0,64
= 0,36
masa wolframu w 1 cm
3
wypraski
=
∗
= 0,64 ∗ 19,25 = 12,32 [ ]
gęstość srebra
= 10,49
masa srebra w 1 cm
3
wypraski
=
∗
= 0,36 ∗ 10,49 = 3,78 [ ]
zawartość procentowa srebra w wyprasce
=
∗ 100% =
12,32
3,78
∗ 100% = 30,68%
Zadanie nr 8.
Oblicz właściwości wytrzymałościowe : R
m
i R
c
(w obu kierunkach: prostopadłym i równoległym
do kierunku włókien) warstwy elementarnej złożonej z żywicy epoksydowej, o module E
m
= 3,1
GPa, wytrzymałości na rozciąganie i ściskanie, odpowiedni R
m
+
= 70 MPa i R
m
-
= 150 MPa
oraz włókna węglowego o module E
f
= 230 GPa i wytrzymałości na rozciąganie R
f
+
= 3430
MPa. Udział objętościowy włókien V
f
= 0,5.
Rozwiązanie:
Sprawdzenie warunku
>
∗
7 ∗ 10 > 3,43 ∗ 10 ∗
3,1 ∗ 10
2,3 ∗ 10
7 ∗ 10 > 4,62 ∗ 10
==>
ł

Kierunek równoległy
Wytrzymałość na rozciąganie R
+
c1
=
∗
+
∗ 1 −
= 3,43 ∗ 10 ∗ 0,5 +
3,1 ∗ 10
2,3 ∗ 10
∗ (1 − 0,5) = 1,74
Wytrzymałość na ściskanie R
-
c1
β = 0,7 dla włókna węglowego
=
∗
= 0,7 ∗ 1,74 = 1,218
Kierunek prostopadły
Wytrzymałość na rozciąganie R
+
c2
= 0,5 ∗
= 0,5 ∗ 7 ∗ 10 = 3,5 ∗ 10
= 35
Wytrzymałość na ściskanie R
-
c2
= 0,6 ∗
= 0,6 ∗ 1,5 ∗ 10 = 0,9 ∗ 10
= 90
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron