1
ZASADY FUNDAMENTOWANIA OBRABIAREK
Obliczanie amortyzatorów
Zastosowanie amortyzatorów w układzie obiekt izolowany - fundament - podłoże pociąga za
sobą zmianę parametrów dynamicznych tego układu w stosunku do układu nie izolowanego.
Obliczanie izolacji drganiowej polega na:
1) doborze podstawowych parametrów, określających efektywność izolacji, do których należą:
- masa względnie moment bezwładności układu drgającego,
- współczynnik sztywności amortyzatora,
- tłumienie amortyzatora;
2) określenie wymiarów i kształtu amortyzatora,
3) określeniu:
- wartości amplitud przemieszczeń drgań wymuszonych obrabiarki izolowanej oraz wartości sił
przekazywanych na podłoże w przypadku izolacji drganiowej czynnej,
- częstości skrętnych drgań własnych izolowanego obiektu, jeśli drgania te istnieją.
Uwaga: W dalszym ciągu często będzie się używać określenia częstości drgań wyrażonej nie,
jak dotychczas, w [rad/s], lecz w hercach [Hz], mianowicie częstość drgań własnych obiektu
izolowanego f
o
i częstość wymuszeń f. Związki między nimi określone są przez zależność:
π
ω
2
=
f
(4.19)
Zakładając efektywność izolacji
µ
, przy spełnieniu warunku
µ
≤
1/15 przy ξ = 0 oraz z
zależności (4.13) i (4.14) otrzymamy:
µ
µ
α
+
=
1
(4.20)
Następnie określa się wymaganą część drgań własnych obiektu izolowanego p przy zadanej
częstości wymuszeń
ω
z zależności
p
ω
α
=
:
α
ω
=
p
(4.21)
Wtedy konieczną wielkość sztywności ogólnej (zastępczej) C
z
wszystkich amortyzatorów
wyznacza się na podstawie zależności:
2
p
m
C
z
⋅
=
(4.22)
Wielkość potrzebnego współczynnika tłumienia drgań
µ
amortyzatorów można określić z
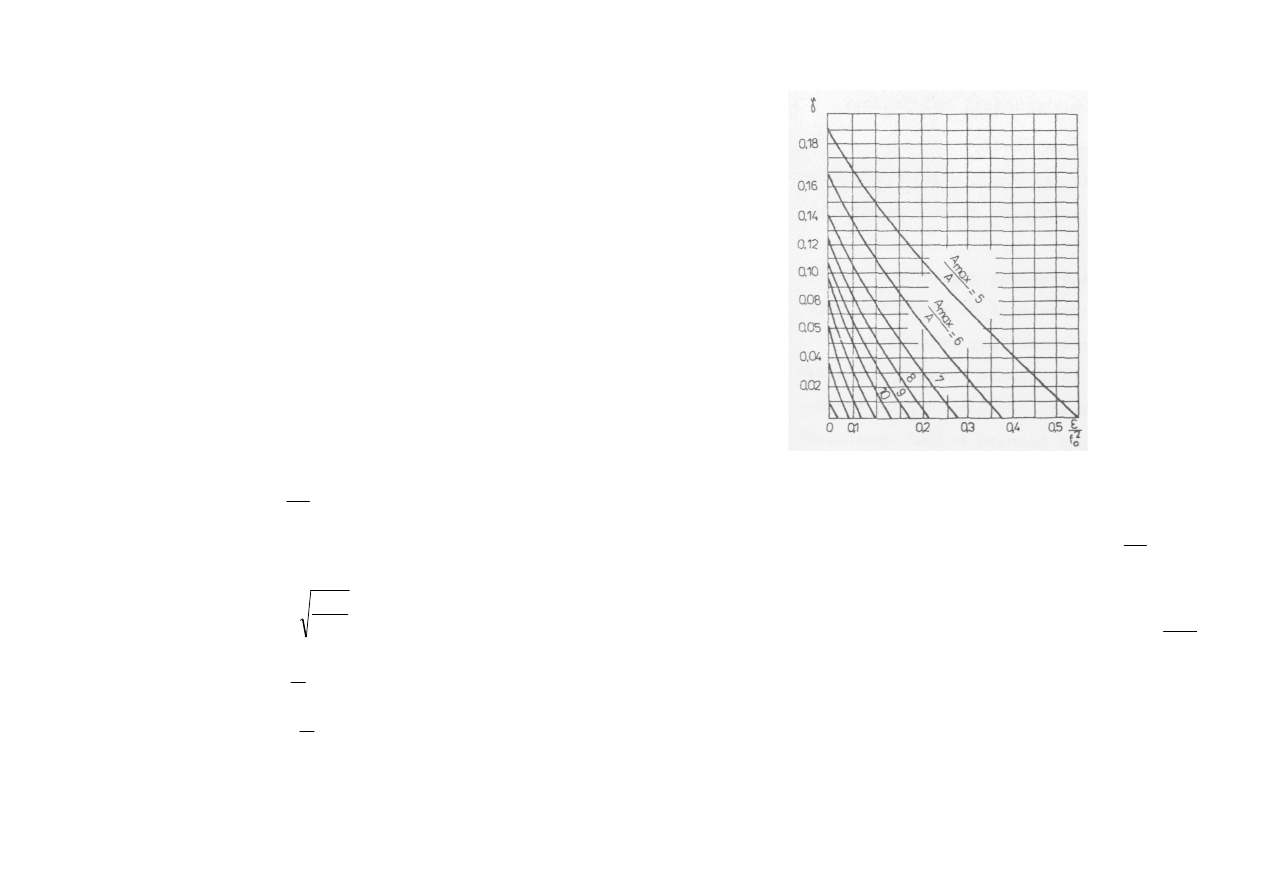
wykresu na Rys.4.5.
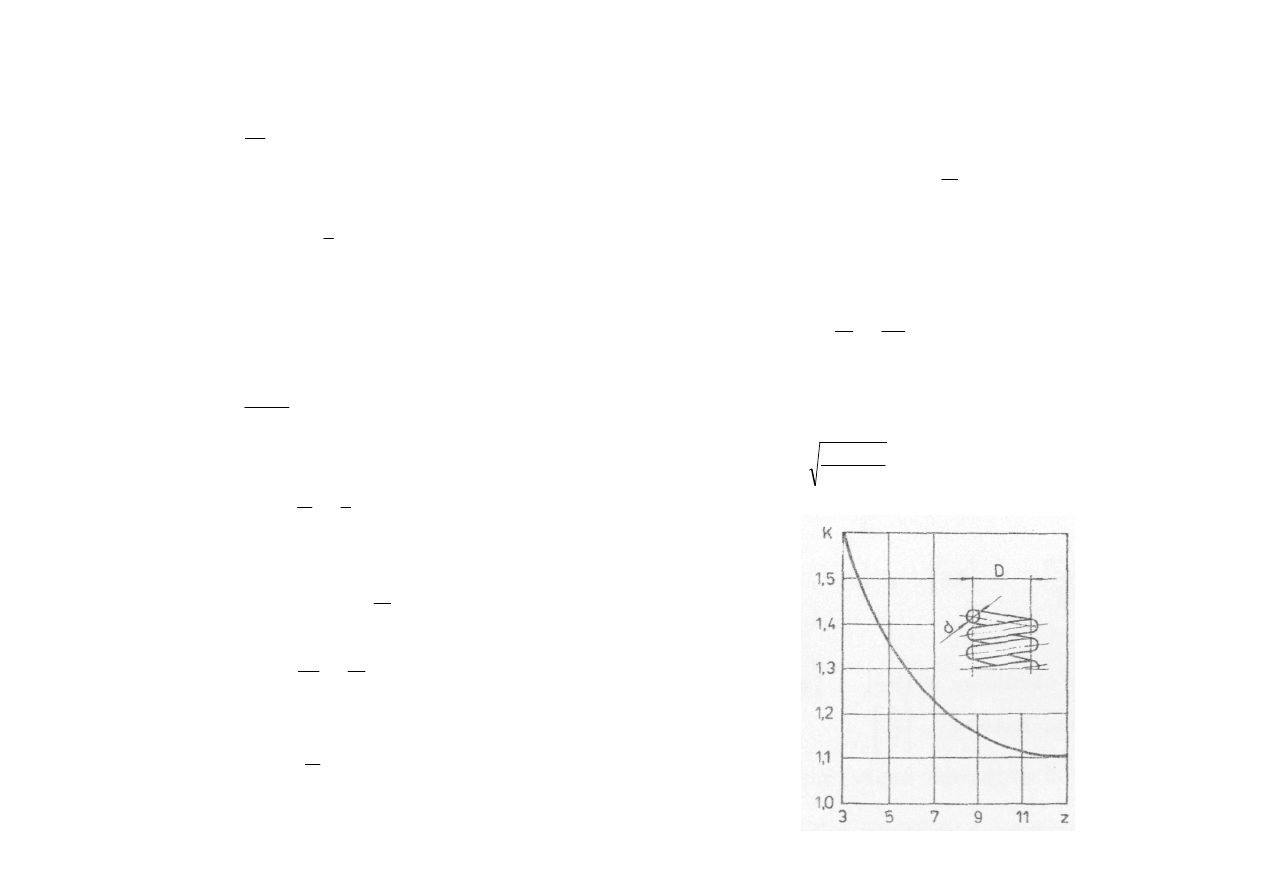
Rys.4.12. Schematy umieszczania amortyzatorów względem obrabiarki i fundamentu.
Amortyzatory sprężynowe można stosować w zależności od współczynnika oporu
niesprężystego
γ
. On z kolei zależy stosunku przyspieszenia kątowego elementów
obrotowych maszyny
ε
do kwadratu częstości jej drgań własnych f
0
(
2
0
f
ε
)
oraz w
zależności od wymaganego stosunku maksymalnej amplitudy drgań maszyny przy jej
rozruchu lub hamowaniu A
max
do amplitudy drgań maszyny w ruchu ustalonym A (
A
A
max
) -
Rys.4.12. Gdy
γ
≤
0,03
, to można stosować amortyzatory sprężynowe. Natomiast jeśli
γ
>
0,03 ,
to koniecznie należy stosować amortyzatory gumowe, względnie gumowo-
sprężynowe.
W przypadku wymuszeń bodących wynikiem ruchu nie wyważonych elementów maszyny
amplitudę siły wymuszającej obliczamy z zależności (4.8).
Obliczanie sprężyn śrubowych amortyzatorów
2
Uwaga: Poniższe obliczenia dotyczą sprężyn wykonanych z drutu o przekroju kołowrym
poddanym obciążeniu pionowemu.
1. Częstość siły wymuszającej:
[ ]
Hz
n
f
60
=
(4.23)
gdzie n - liczba obrotów (cykli) maszyny na minutę.
2. Częstość kołowa siły wymuszającej:
⋅
⋅
=
s
f
1
2
π
ω
(4.24)
3. Masa obiektu izolowanego będąca sumą mas izolowanej maszyny m
m
i
ewentualnie fundamentu m
t
:
[ ]
kg
m
m
m
t
m
+
=
(4.25)
4. Amplituda drgań pionowych obiektu izolowanego:
[ ]
m
m
F
A
2
0
ω
⋅
=
(4.26)
F
0
- amplituda siły wymuszającej [N].
5. Częstość kołowa drgań własnych obiektu izolowanego:
=
s
p
1
α
ω
(4.27)
gdzie
α
≥ 4 .
6. Sztywność zastępcza wszystkich amortyzatorów:
⋅
=
m
N
p
m
C
z
2
(4.28)
7. Sztywność jednej sprężyny:
=
m
N
w
C
C
z
,
(4.29)
w - liczba sprężyn dobrana w zależności od możliwości ich rozmieszczenia i ustawienia.
8. Obciążenie statyczne na jedną sprężynę:
[ ]
N
n
Q
F
st
=
(4.30)
9. Obciążenie dynamiczne przekazywane na jedną sprężynę w ruchu ustalonym izolowanej
maszyny:
[ ]
N
C
A
F
⋅
=
dyn
(4.31)
10. Obciążenie obliczeniowe na jedną sprężynę:
[ ]
N
F
F
F
dyn
st
obl
5
,
1
⋅
+
=
(4.32)
11. Wskaźnik sprężyny:
d
D
z
=
(4.33)
wskaźnik sprężyny przyjmuje się w granicach 4 ÷ 10.
D - średnica nawinięcia sprężyny,
d - średnica druta sprężyny.
12. Dopuszczalne naprężenie styczne materiału sprężyny:
=
2
0
m
N
k
s
τ
τ
(4.34)
τ
s
- granica plastyczności na ścinanie,
k
o
- współczynnik bezpieczeństwa, przyjmowany w granicach 1,5 ÷ 2,0 .
13. Średnica drutu sprężyny:
[ ]
m
τ
z
F
k
,
d
obl
⋅
⋅
=
6
1
(4.35)
k - współczynnik określony z wykresu na Rys.4.13.
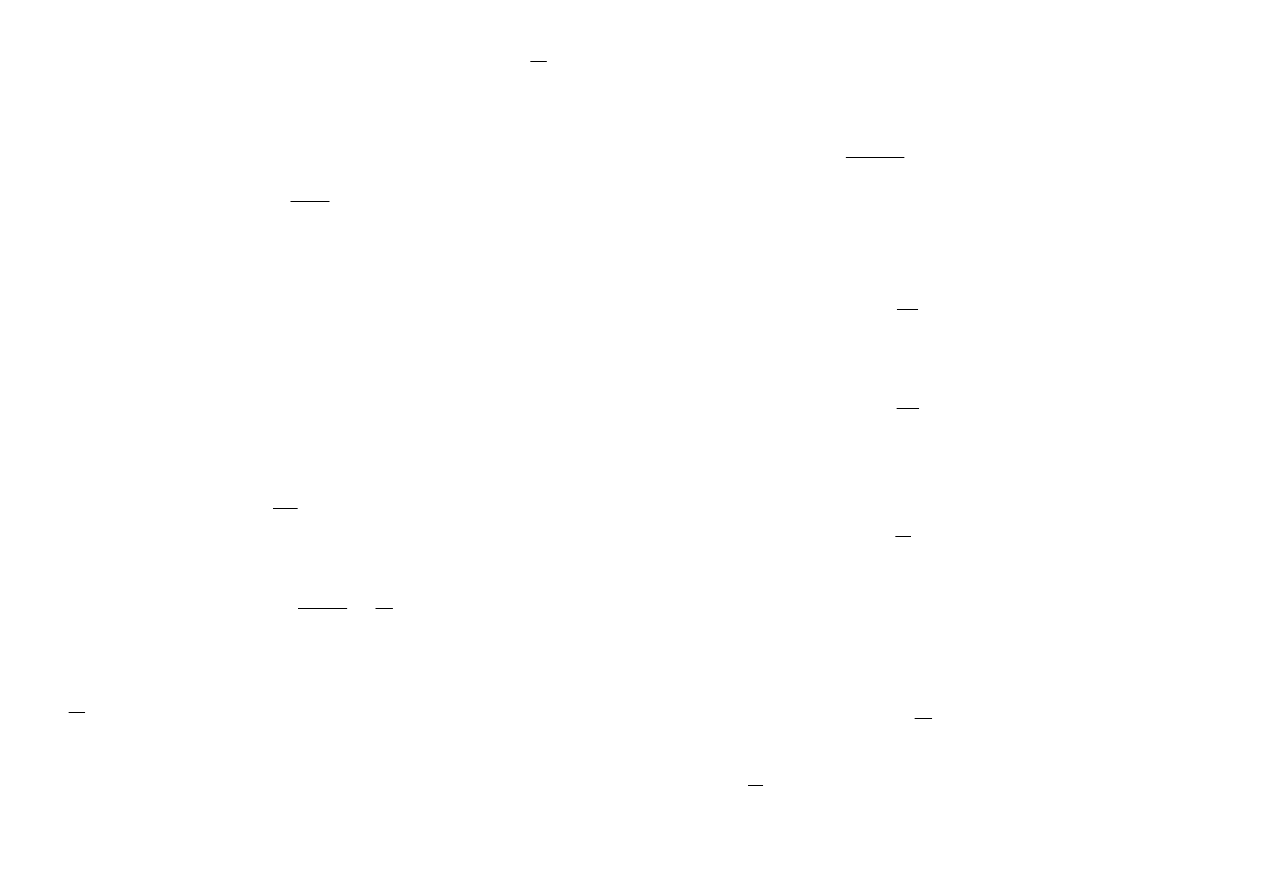
3
Rys.4.13. Przebieg wartości współczynnika k w funkcji wskaźnika sprężyny
d
D
z
=
.
14. Średnica nawinięcia sprężyny:
[ ]
m
d
z
D
⋅
=
(4.36)
15. Liczba pracujących zwojów sprężyny:
3
8
z
C
d
G
i
⋅
⋅
=
(4.37)
G - moduł sprężystości przy skręcaniu.
16. Liczba wszystkich zwojów sprężyny:
2
1
i
i
i
+
=
(4.38)
i
2
- liczba nie pracujących zwojów sprężyny: dla i < 7 i
2
= 1,5, dla i > 7 i
2
= 2,5.
17. Skok sprężyny:
(
)
[ ]
m
D
h
5
,
0
25
,
0
÷
=
(4.39)
18. Wysokość nie obciążonej sprężyny:
(
)
[ ]
m
d
i
h
i
H
5
,
0
2
0
−
+
⋅
=
(4.40)
Dla sprężyn pracujących na ściskanie musi zachodzić:
2
0
≤
D
H
(4.41)
Obliczanie amortyzatorów z jednakowymi sprężynami o zadanych wymiarach
1. Sztywność jednej sprężyny:
⋅
⋅
⋅
=
m
N
i
z
d
G
C
3
8
(4.42)
G - moduł sprężystości na skręcanie,
d - średnica drutu sprężyny,
d
D
z
=
- wskaźnik sprężyny,
i - liczba pracujących zwojów sprężyny.
2. Obciążenie dynamiczne przypadające na jedną sprężynę przy ustalonym ruchu izolowanej
maszyny:
[ ]
N
C
A
F
⋅
=
dyn
(4.43)
A - amplituda drgań izolowanej maszyny w jej ruchu ustalonym.
3. Maksymalne dopuszczalne obciążenie statyczne przypadające na jedną sprężynę:
[ ]
N
F
D
K
d
F
dyn
⋅
−
⋅
⋅
⋅
⋅
=
5
,
1
8
3
st
τ
π
(4.44)
K - współczynnik określany z wykresu na Rys.4.13,
D - średnica nawinięcia sprężyny,
τ
- dopuszczalne naprężenie na skręcanie materiału sprężyny
4. Liczba sprężyn z warunku sztywności:
C
C
w
z
≤
(4.45)
C
z
- sztywność zastępcza wszystkich sprężyn.
5. Liczba sprężyn z warunku wytrzymałości:
st
F
Q
w
≥
(4.46)
Q - ciężar izolowanego obiektu [N].
Obliczania amortyzatorów gumowych
1. Pole przekroju poprzecznego amortyzatorów gumowych:
[ ]
2
m
Q
S
σ
≥
(4.47)
Q [N] – obciążenie działające na wszystkie amortyzatory gumowe,
σ
- naprężenie statyczne w gumie,
dla gumy o twardości Shore’a < 40:
σ
= (0,1
÷ 0,3) [MPa]
dla gumy o twardości Shore’a > 40:
σ
= (0,3
÷ 0,5) [MPa]
2. Sztywność zastępcza wszystkich amortyzatorów gumowych:
⋅
=
m
N
p
m
C
z
2
(4.48)
m - masa obiektu izolowanego,
α
ω
=
p
- częstość kołowa drgań własnych obiektu izolowanego.
3. Robocza wysokość amortyzatora:
4
[ ]
m
C
S
E
H
z
d
⋅
=
1
(4.49)
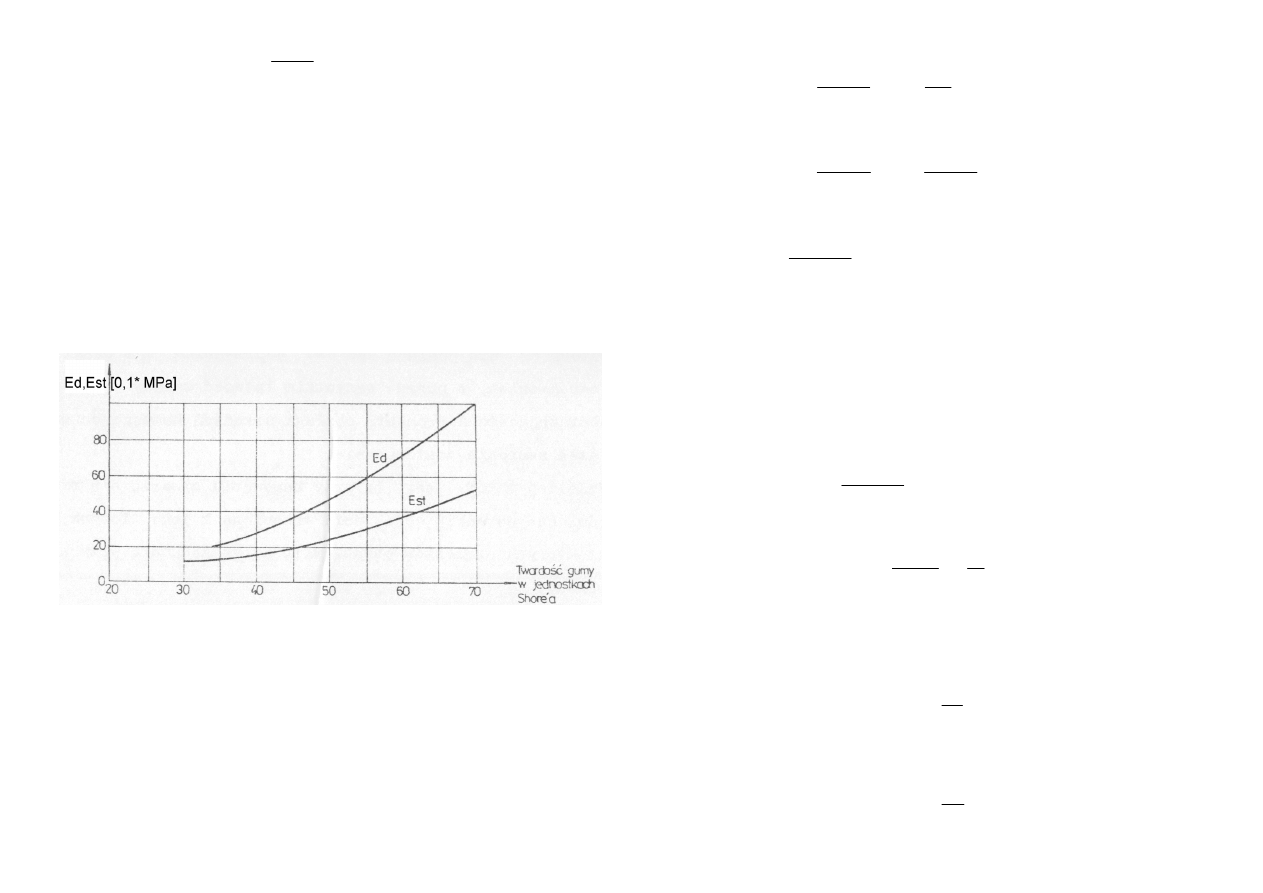
E
d
[N/m
2
] - dynamiczny moduł sprężystości gumy określany z wykresu na Rys.4.14.
4. Sumaryczny przekrój poprzeczny:
a) dla amortyzatorów o przekroju kwadratowym:
[ ]
2
2
m
b
n
S
⋅
=
(4.50)
n – liczba amortyzatorów,
b [m] – bok kwadratu amortyzatora,
b) dla amortyzatorów o przekroju kołowym:
[ ]
2
2
785
.
0
m
D
n
S
⋅
⋅
≈
(4.51)
D - średnica amortyzatora o przekroju kołowym [m],
Rys.4.14. Przebieg wartości dynamicznego i statycznego modułu sprężystości gumy w funkcji
twardości Shore’a
Uwaga: b lub D zaleca się dobierać przy warunku: H
1
≤ b (lub D) ≤ (1,5÷ 8) H
1
. Przy szerokich
amortyzatorach o małej wysokości (krępych) wysokość robocza będzie stanowiła nieznaczną
część pełnej wysokości H - dlatego amortyzator nawet z miękkiej gumy będzie bardzo sztywny.
Z tej przyczyny zaleca się stosować dla amortyzacji rowkowane lub perforowane płyty
gumowe.
5. Liczba amortyzatorów powinna się mieścić w granicach:
a) dla amortyzatorów o przekroju kwadratowym:
2
1
2
1
64
H
S
n
H
S
<
<
⋅
(4.52)
b) dla amortyzatorów o przekroju kołowym:
2
1
2
1
27
.
1
64
27
.
1
H
S
n
H
S
⋅
<
<
⋅
⋅
(4.53)
6. Pełna wysokość amortyzatora:
[ ]
m
D
b
D
b
H
H
)
(lub
)
2
.
1
125
.
0
(
8
)
(lub
1
÷
=
+
=
(4.54)
Obliczanie elementów gumowych przy zadanych ich wymiarach
1. Maksymalne obciążenie przypadające na jeden amortyzator gumowy:
[ ]
N
S
F
σ
⋅
=
1
st
(4.55)
1
S
[m
2
] - powierzchnia przekroju poprzecznego jednego amortyzatora,
σ
[N/m
2
] - obliczeniowe naprężenie statyczne w gumie,
2. Robocza wysokość amortyzatora powinna się znajdować w przedziale:
[ ]
m
D
b
D
b
H
H
)
(lub
)
2
.
1
125
.
0
(
8
)
(lub
1
÷
=
−
=
(4.56)
3. Sztywność amortyzatora:
⋅
=
m
N
H
E
S
C
d
1
1
(4.57)
E
d
[N/m
2
] - dynamiczny moduł sprężystości gumy określany z wykresu na Rys.4.14.
4. Liczba amortyzatorów:
a) z warunku sztywności:
C
C
n
z
≤
(4.58)
C
z
- sztywność zastępcza wszystkich amortyzatorów gumowych
b) z warunku wytrzymałości:
st
F
Q
n
≤
(4.59)
5
Q [N] - ciężar obiektu izolowanego.
5. Obciążenie przypadające na jeden amortyzator:
[ ]
N
n
Q
Q
1
≤
(4.60)
6. Ugięcie statyczne amortyzatora:
[ ]
m
E
S
H
Q
st
⋅
⋅
=
1
1
1
st
λ
(4.61)
E
st
[N/m
2
] - statyczny moduł sprężystości gumy określany z wykresu na Rys.4.14.
Obliczanie amortyzatorów kombinowanych gumowo - sprężynowych
1. Sztywność wszystkich amortyzatorów sprężynowych:
a)
przy równoległym połączeniu sprężyn i elementów gumowych (Rys.4.6a):
−
=
m
N
C
C
C
zg
z
zs
(4.62)
b)
przy szeregowym połączeniu sprgżyn i elementów gumowych (Rys.4.6b):
⋅
−
⋅
=
m
N
C
C
C
g
s
zg
z
zs
γ
γ
γ
(4.63)
C
z
[N/m] - sztywność zastępcza wszystkich (gumowych i sprężynowych) amortyzatorów,
γ
- współczynnik tłumienia drgań amortyzatorów kombinowanych (określa się z wykresu na
rys.4.12),
γ
s
- współczynnik tłumienia drgań sprężyny, dla sprężyn stalowych przyjmuje się:
γ
s
= 0,01,
γ
g
- współczynnik tłumienia drgań gumy, dla amortyzatorów z dużym tłumieniem przyjmuje się:
γ
g
= 0,15 ÷ 0,20 .
2. Sztywność wszystkich amortyzatorów gumowych:
a) przy równoległym połączeniu sprężyn stalowych i elementów gumowych (Rys.4.6a):
⋅
−
⋅
=
m
N
C
C
C
g
s
zs
z
zg
γ
γ
γ
(4.64)
b) przy szeregowym połączeniu sprężyn stalowych i elementów gumowych
−
⋅
=
m
N
C
C
C
C
C
z
zs
zs
z
zg
(4.65)
3. Obciążenie statyczne przenoszone przez elementy gumowe:
[ ]
N
C
A
Q
zg
g
⋅
=
max
(4.66)
A
max
[m] - amplituda drgań maszyny przy jej rozruchu lub hamowaniu.
4. Wielkość obciążenia statycznego przenoszonego przez sprężyny:
[ ]
N
Q
Q
Q
g
s
−
=
(4.67)
Q [N] - ciężar izolowanego obiektu.
5. Wymiary jak i liczbę sprężyn stalowych oraz elementów gumowych określa się wg
obliczonych wielkości C
zs
, Q
s
i C
zg
, Q
g
. W amortyzatorach kombinowanych sprężyny
powinny być obliczane wytrzymałościowo z uwzględnieniem pełnego obciążenia
przypadającego na wszystkie amortyzatory (sprężyny i elementy gumowe).
6. Wysokość elementów gumowych w amortyzatorach kombinowanych określona
obliczeniami z reguły jest mniejsza od wysokości sprężyn i dlatego w takich przypadkach
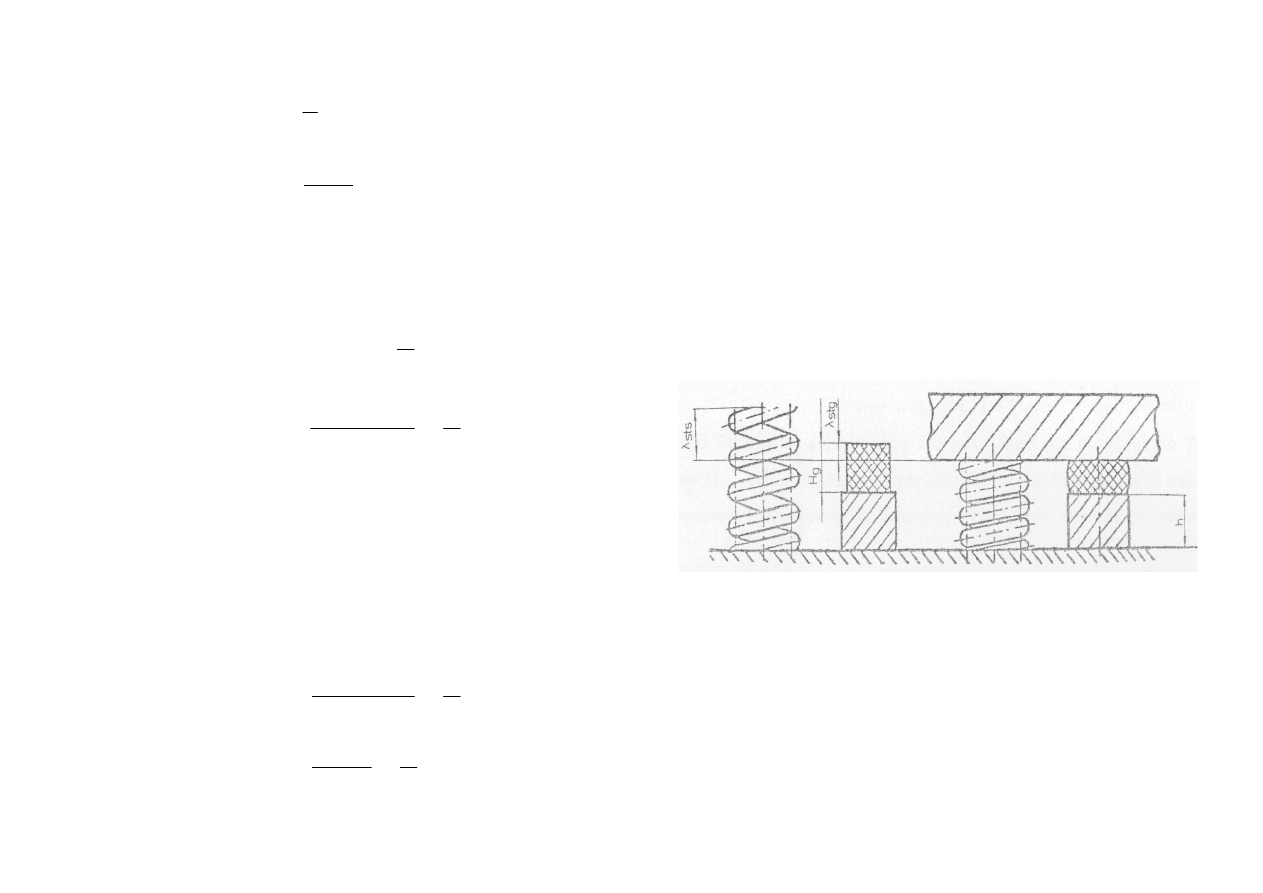
elementy gumowe należy ustawić na specjalnych podkładkach (rys.4.15).
Rys.4.15. Eliminowanie nierówności wysokości elementów gumowych i sprężyn w
amortyzatorach kombinowanych przez zastosowanie specjalnych podkładek.
[ ]
m
H
H
h
gumy
st
spr
st
g
s
_
_
λ
λ
+
−
−
=
(4.68)
H
g
- całkowita wysokość sprężymy w stanie nie obciążonym,
Hg - całkowita wysokość elementu gumowego w stanie nie obciążonym,
λ
st_spr
- statyczne ugięcie sprężyny pod obciążeniem Q
s
,
λ
st_gumy
- statyczne ugięcie gumy pod obciążeniem Q
g
.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron