Instrukcje do ćwiczeń laboratoryjnych z Drgań Mechanicznych
ĆWICZENIE NR ...
DRGANIA UKŁADÓW O CIĄGŁYM ROZKŁADZIE MASY -
DRGANIA GIĘTNE BELEK
1. Cel ćwiczenia
Celem ćwiczenia jest obserwacja drgań układów o ciągłym rozkładzie parametrów,
pomiar częstości drgań swobodnych poprzez pomiar częstości rezonansowych oraz
porównanie wyników pomiarów z wynikami obliczeń dla modeli belek.
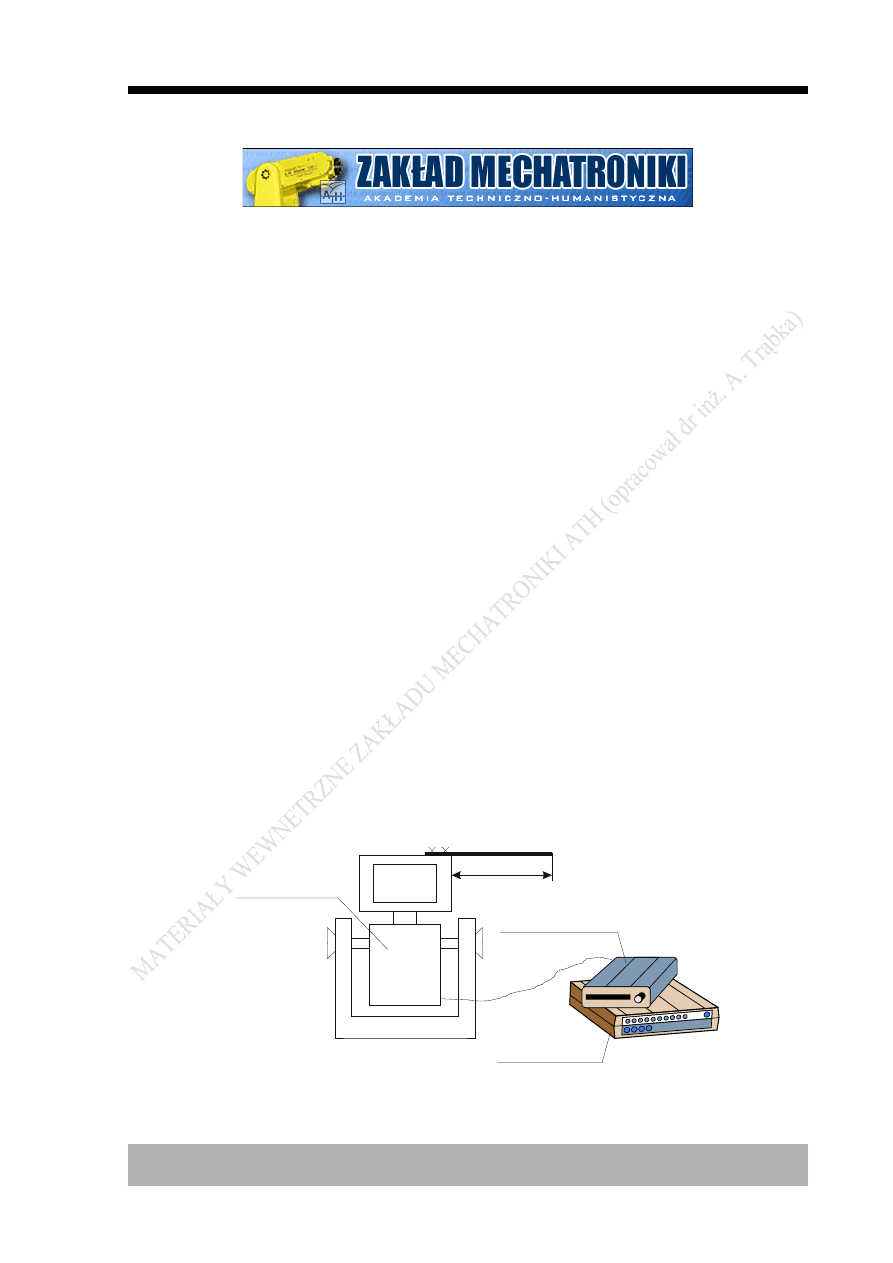
2. Opis stanowiska
Rysunek 1 przedstawia układ pomiarowy, w którym drgania są wymuszone
kinematycznie poprzez ruch podpory. Ruch wymuszający jest realizowany przez
wzbudnik drgań sterowny generatorem drgań harmonicznych.
b x h
Generator
Wzmacniacz
l
Wzbudnik
drgań
Rys. 1. Schemat układu pomiarowego do badania drgań giętnych belek
Laboratorium Drgań Mechanicznych
Bielsko-Biała 2011
opracował Arkadiusz Trąbka
opracował Arkadiusz Trąbka
2
DRGANIA UKŁADÓW O CIĄGŁYM ROZKŁADZIE MASY
Przy częstościach wymuszeń odpowiadających częstościom drgań własnych,
dominować będą odkształcenia belki odpowiadające poszczególnym postaciom
drgań. Pomiar częstotliwości rezonansowych oraz obserwacja postaci drgań pozwala
na wnioski odnośnie drgań swobodnych układu.
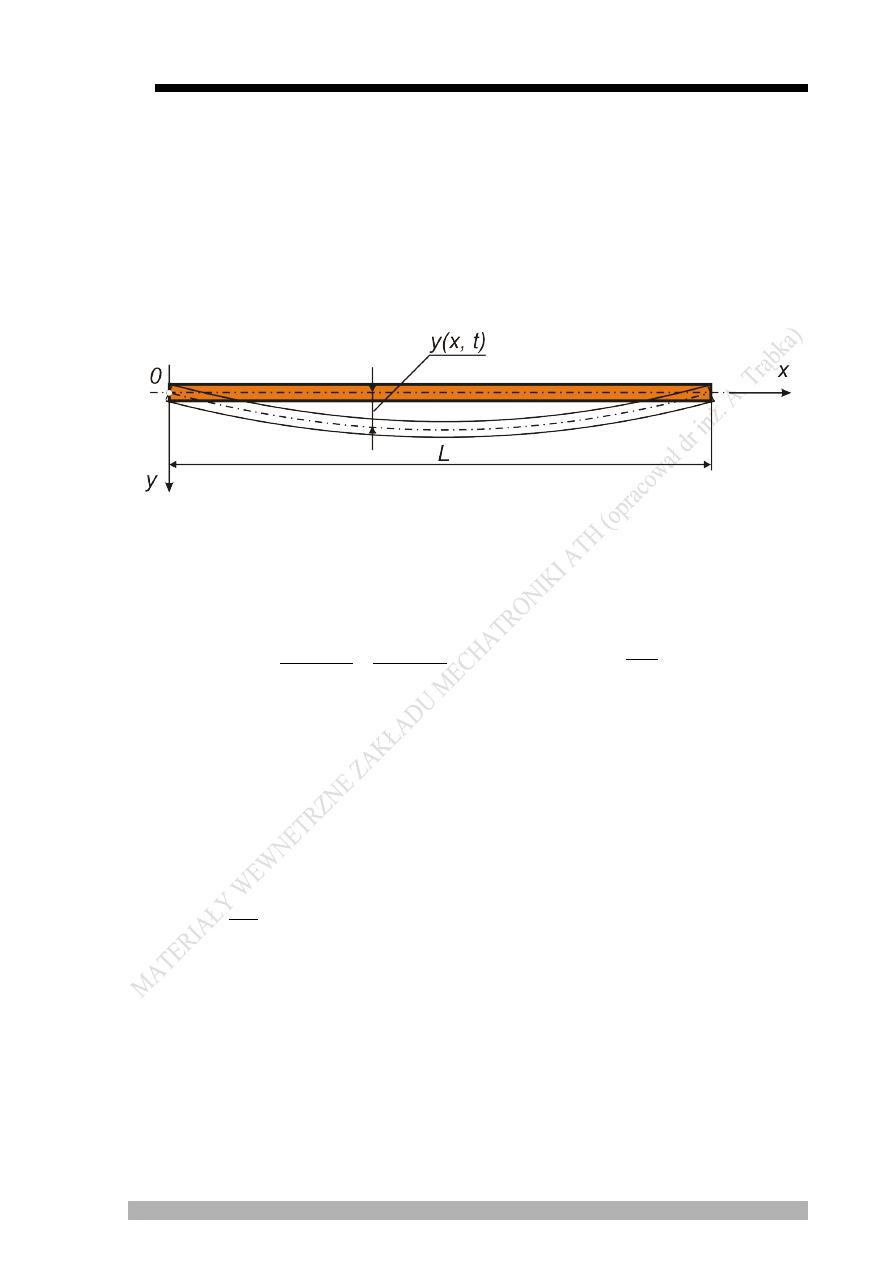
3. Zależności obliczeniowe
Rys. 2. Szkic belki wykonującej drgania giętne
Równanie drgań giętych belki o stałym przekroju (rys. 2) ma postać:
0
)
,
(
)
,
(
2
2
4
4
2
=
∂
∂
+
∂
∂
x
t
x
y
x
t
x
y
c
,
F
EI
c
ρ
=
2
(1)
Stosując metodę Fouriera zakłada się rozwiązania w postaci:
Y(x,t) = Y(x)·T(t)
(2)
Po wstawieniu (1) do (2) otrzymuje się układ równań różniczkowych zwyczajnych:
0
4
=
−
Y
y
IV
λ
0
2
=
+
T
T
ω
(3)
Gdzie:
4
2
λ
ρ
ω
F
EI
=
Rozwiązanie pierwszego z równań (3) ma postać:
Y(x) = A
1
sinλx + A
2
sinλx + A
3
sinhλx + A
4
coshλx
(4)
Uwzględniając warunki brzegowe (5) dla belki jednostronnie utwierdzonej (rys. 1):
Y(0) = 0
Y’(0) = 0
Y’’(1) = 0
Y’’’(1) = 0
(5)
Laboratorium Drgań Mechanicznych
3
Instrukcje do ćwiczeń laboratoryjnych z Drgań Mechanicznych
otrzymuje się układ równań liniowych, jednorodnych z niewiadomymi A
1
, A
2
:
(sinλl + sinhλl)A
1
+ (cosλl + coshλl)A
2
= 0
(cosλl + coshλl)A
1
+ (sinλl - sinhλl)A
2
= 0
(6)
Warunkiem istnienia niezerowych rozwiązań równań (6) jest zerowanie się
wyznacznika głównego:
(sinλl + sinhλl)
(cosλl + coshλl)
= 0
(7)
(cosλl + coshλl)
(sinλl - sinhλl)
Po rozwinięciu wyznacznika (7) otrzymuje się równanie częstości w postaci:
l
l
λ
λ
cosh
1
cos
=
(8)
którego pierwiastkami są:
l
875
,
1
1
=
λ
,
l
694
,
4
2
=
λ
,
π
λ
l
n
n
2
1
2
−
≅
dla n>2
Wartościom λ
n
odpowiadają częstości drgań swobodnych:
F
EI
n
n
ρ
λ
ω
2
=
(9)
Dla belki o przekroju prostokątnym mamy:
bh
F
=
,
12
3
bh
I
=
Stąd:
ρ
λ
ω
12
2
2
Eh
n
n
=
(10)
Każdej wartości λ
n
odpowiada postać drgań Y
n
(x):
Y
n
(x) = A[sinhλ
n
x - sinλ
n
x - a
n
(coshλ
n
x - cosλ
n
x)]
(11)
gdzie:
l
l
l
l
a
n
n
n
n
n
λ
λ
λ
λ
cos
cosh
sin
sinh
+
+
=
(12)
Laboratorium Drgań Mechanicznych
4
DRGANIA UKŁADÓW O CIĄGŁYM ROZKŁADZIE MASY
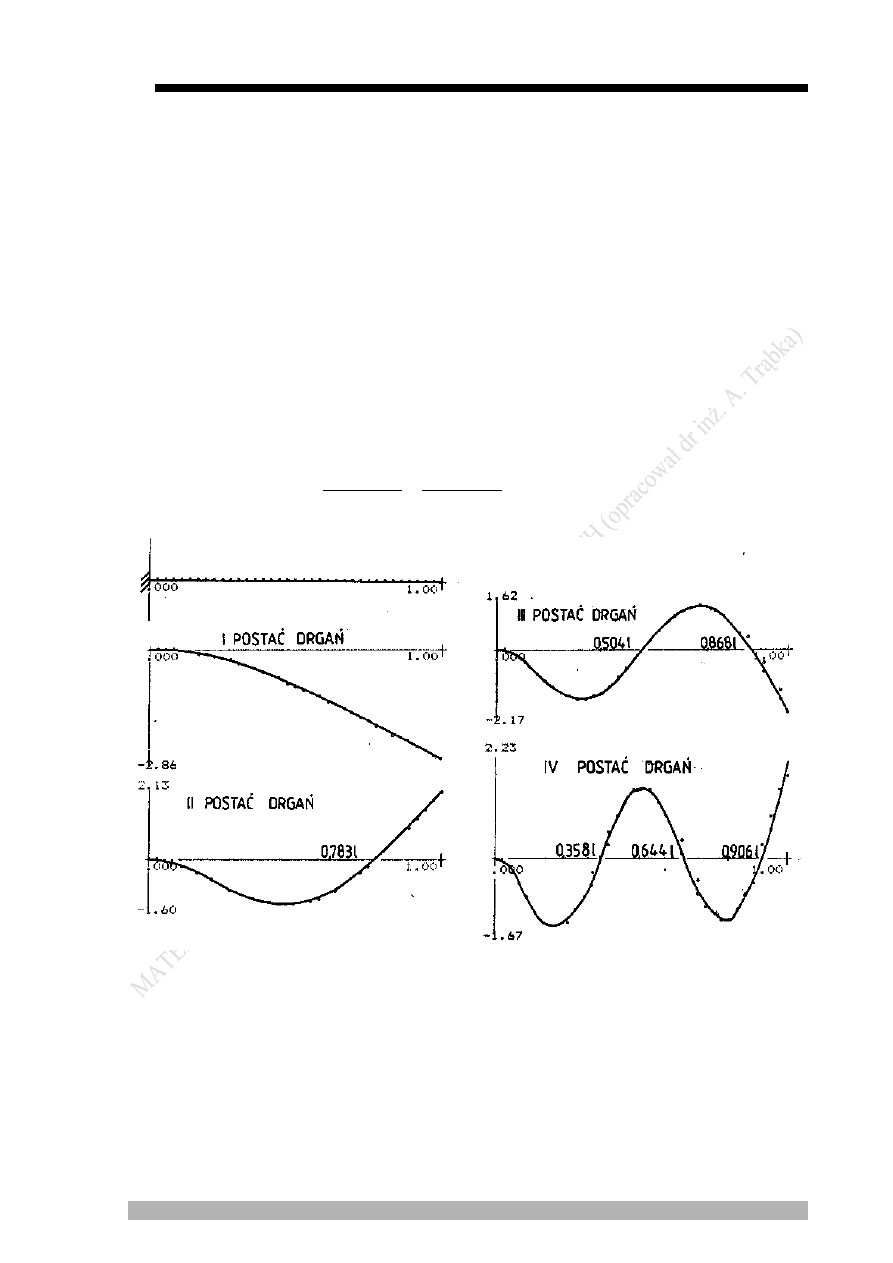
Wykresy pierwszych czterech postaci drgań przedstawiono na rys. 3 (długość l
przyjęto równą 1). Drgania wymuszone ruchami harmonicznymi podpór analizuje się
przyjmując rozwiązania równania (1) jako sumę dwóch funkcji:
y(x,t) = y
1
(x,t) + y
2
(x,t)
(13)
przy czym rozwiązanie y
2
(x,t) należy tak dobrać, aby funkcja y
1
(x,t) spełniała
jednorodne (zerowe) warunki brzegowe. W przypadku harmonicznego ruchu podpory
belki utwierdzonej, funkcję y
2
(x,t) należy przyjąć w postaci:
y
2
(x,t) = a sin ωt
(14)
Podstawiając rozwiązanie (13) do równania (1) otrzymuje się równanie opisujące
drgania wymuszone ruchem brzegu:
t
a
t
t
x
y
x
t
x
y
c
ϖ
ϖ
sin
)
,
(
)
,
(
2
2
1
2
4
1
4
2
=
∂
∂
+
∂
∂
(15)
Rys. 3. Schemat belki oraz wykresy postaci drgań
Rozwiązania y
1
(x,t) poszukujemy w postaci szeregu:
∑
∞
=
=
1
1
)
(
)
(
)
,
(
n
n
n
x
Y
t
t
x
y
ξ
(16)
Laboratorium Drgań Mechanicznych

5
Instrukcje do ćwiczeń laboratoryjnych z Drgań Mechanicznych
Prawą stronę równania (15) rozwijamy w szereg funkcji własnych:
t
a
x
Y
t
q
t
x
q
n
n
n
ϖ
ϖ
sin
)
(
)
(
)
,
(
2
1
=
=
∑
∞
=
(17)
Po pomnożeniu obu stron równania (17) przez Y
m
(x) i scałkowaniu w granicach od 0
do 1 oraz wykorzystaniu warunków ortogonalności w postaci:
m
n
dla
dx
x
Y
x
Y
m
n
≠
=
∫
0
)
(
)
(
1
0
(18)
otrzymuje się współczynniki rozwinięcia funkcji q(x,t):
[
]
∫
∫
=
1
0
2
1
0
2
)
(
)
(
sin
)
(
dx
x
Y
dx
x
Y
t
a
t
q
n
n
n
ϖ
ϖ
(19)
Podstawiając rozwiązania (16) wraz z rozwinięciem (17) do równań (15) oraz
uwzględniając powtórne warunki ortogonalizacji (18) otrzymuje się układ równań
różniczkowych pozwalający wyznaczyć funkcję ξ
n
(t).
∫ ∑
∫ ∑
∫ ∑
∞
=
∞
=
∞
=
=
+
1
0
1
1
0
1
2
1
0
1
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
n
m
n
n
n
m
n
n
n
n
m
n
n
dx
x
Y
x
Y
t
q
dx
x
Y
x
Y
t
dx
x
Y
x
Y
t
ξ
ϖ
ξ
(20)
co po uwzględnieniu (18) prowadzi do równań:
,...
2
,
1
)
(
)
(
)
(
2
=
=
+
n
t
q
t
t
n
n
n
n
ξ
ω
ξ
(21)
gdzie:
2
2
2
n
n
c
λ
ω =
Oznaczając:
∫
∫
=
1
0
2
1
0
)]
(
[
)
(
dx
x
Y
dx
x
Y
F
n
n
n
można równanie (21) zapisać w postaci:
t
a
F
t
t
n
n
n
n
ω
ω
ξ
ω
ξ
sin
)
(
)
(
2
2
=
+
(22)
Laboratorium Drgań Mechanicznych

6
DRGANIA UKŁADÓW O CIĄGŁYM ROZKŁADZIE MASY
którego rozwiązaniem są funkcje:
t
a
F
t
n
n
n
ω
ω
ω
ω
ξ
sin
)
(
2
2
2
−
=
(23)
co pozwala wyznaczyć rozwiązanie y
1
(x,t):
t
a
F
x
Y
t
x
y
n
n
n
n
ω
ω
ω
ω
sin
)
(
)
,
(
2
2
2
1
1
−
=
∑
∞
=
(24)
Pełne rozwiązanie równania (15) wynosi:
t
a
t
a
F
x
Y
t
x
y
t
x
y
t
x
y
n
n
n
n
ω
ω
ω
ω
ω
sin
sin
)
(
)
,
(
)
,
(
)
,
(
2
2
2
1
2
1
+
−
=
+
=
∑
∞
=
(25)
Z postaci rozwiązania (25) wynika, że w przypadku gdy częstość wymuszająca ω≈
ω
n
, współczynnik przy postaci Y
n
(x) osiąga wartość zmierzającą do
∞
, czyli w
rozwiązaniu będzie dominować postać drgań Y
n
(x).
Rozważany model belki nie uwzględnia tłumienia. Uwzględnienie tłumienia prowadzi
do jakościowo podobnych zależności, jednak wartości odpowiednich amplitud są
skończone.
4. Przebieg ćwiczenia
•
Trzykrotnie zmierzyć i zanotować wymiar l przedstawiony na rys. 1;
•
W trzech równomiernie od siebie oddalonych miejscach trzykrotnie zmierzyć i
zanotować wymiary b oraz h przedstawione na rys. 1;
•
Obliczyć pierwsze cztery częstości drgań własnych belki (na podstawie
zależności 9 lub 10);
•
Wyznaczyć wartości częstotliwości drgań odpowiadające obliczonym
częstościom;
•
Obliczyć współrzędne węzłów dla każdej z czterech postaci drgań belki (zgodnie
z zależnościami zamieszczonymi na rys. 3);
•
Zmieniając pokrętłem generatora częstotliwość wymuszenia harmonicznego,
odczytać wartości częstotliwości rezonansowych, przy których dominują postacie
odkształceń przedstawione na rys. 3.
UWAGA - Wartości amplitud sygnału z generatora oraz wzmocnienie
wzmacniacza dobrać tak, aby postacie drgań były dobrze widoczne, natomiast
wzbudnik drgań nie powinien być nadmiernie obciążony. Obserwacje pierwszej
postaci prowadzić przy najmniejszym wzmocnieniu i stopniowo je zwiększać przy
kolejnych postaciach drgań.
Laboratorium Drgań Mechanicznych

7
Instrukcje do ćwiczeń laboratoryjnych z Drgań Mechanicznych
•
Zanotować częstotliwości rezonansowe oraz wykreślić zaobserwowane postacie
drgań. Zmierzyć odległości punktów węzłowych.
•
Porównać otrzymane wyniki doświadczalne z wynikami teoretycznymi
(częstotliwości drgań oraz współrzędne węzłów).
5. Zawartość sprawozdania
•
Cel ćwiczenia;
•
Przebieg ćwiczenia (w punktach);
•
Schemat stanowiska laboratoryjnego (z opisem);
•
Dane wejściowe do przeprowadzanego ćwiczenia;
•
Zestawienie wyników pomiarów;
•
Przykładowe obliczenia z podaniem wzorów oraz podstawień do wzorów;
•
Zestawienie wyników obliczeń;
•
Porównanie wyników;
•
Sporządzony w trakcie ćwiczeń protokół;
•
Wnioski, spostrzeżenia i uwagi.
Laboratorium Drgań Mechanicznych
Document Outline
- Laboratorium Drgań Mechanicznych
- Laboratorium Drgań Mechanicznych
- Laboratorium Drgań Mechanicznych
- Bielsko-Biała 2011
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron