2013-03-20
1
EKONOMETRIA II
Wykład 4 Weryfikacja jednorównaniowego
liniowego modelu ekonometrycznego cd.
Dorota Perło
Wydział Ekonomii i Zarządzania, Uniwersytet w Białymstoku
2
Weryfikacja
modelu
Weryfikacja
merytoryczna
Interpretacja ocen
parametrów modelu
Sprawdzenie
sensowno
ś
ci
znaków ocen
parametrów modelu
Weryfikacja
statystyczna
Badanie stopnia
zgodno
ś
ci modelu z
danymi
empirycznymi
Badanie jako
ś
ci
ocen parametrów
strukturalnych
Badanie rozkładu
odchyle
ń
losowych
2013-03-20
2
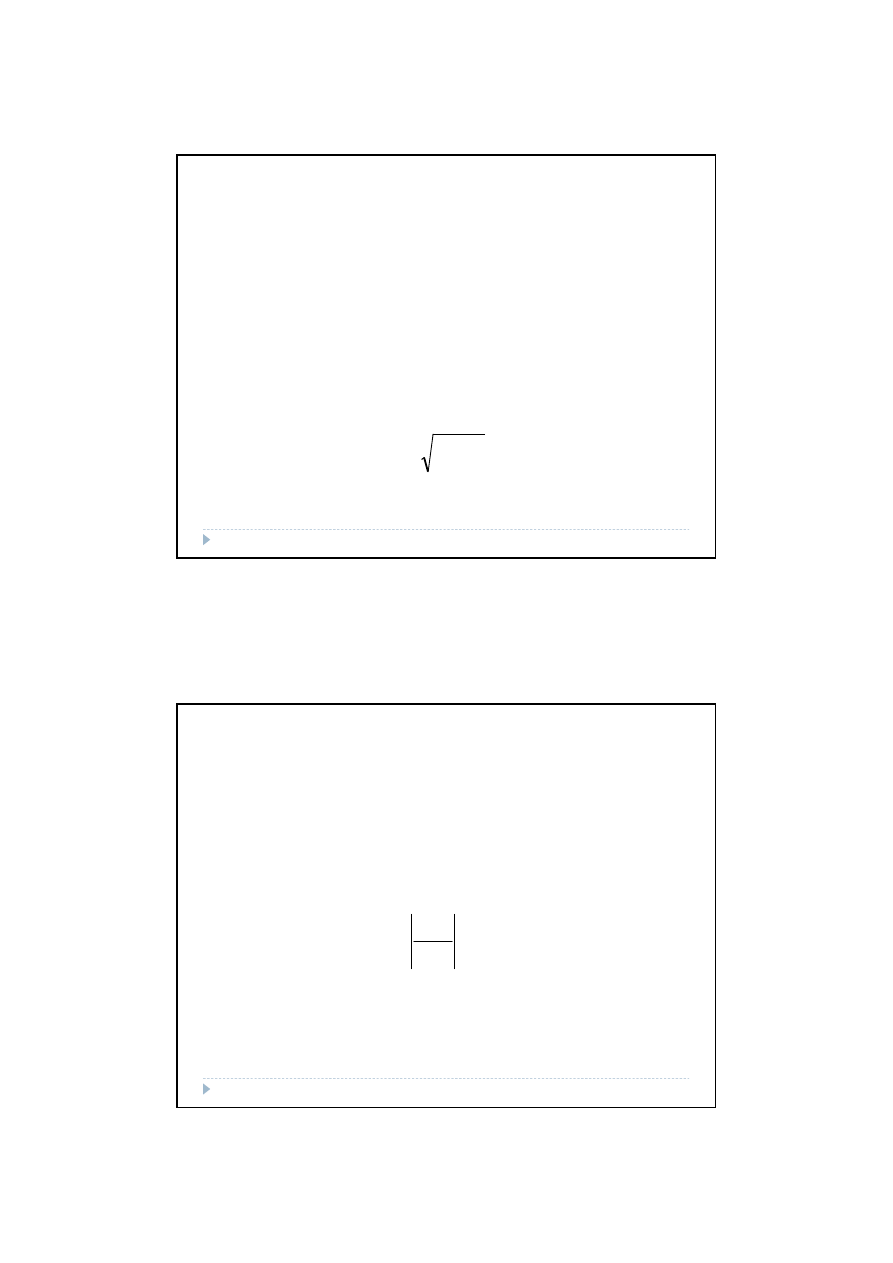
Oceny parametrów modelu są wielkościami przybliżonymi i jako
takie są obarczone błędami. Nieobciążonym i zgodnym estymatorem
macierzy kowariancji estymatora a jest macierz
Elementy diagonalne d
ij
macierzy
stanowią ocenę wariancji
estymatorów
parametrów
modelu.
O
dokładności
szacunku
parametrów
ś
wiadczy odchylenie standardowe estymatora tego
parametru
zwane średnim błędem szacunku nieznanego parametru
(j = 0, 1,…,k)
-1
T
2
2
X)
X
(
)
a
(
D
e
S
=
)
)
a
(
D
2
)
j
α
)
a
(
S
)
a
(
S
j
2
j
=
j
α
Wnioskowanie o parametrach liniowego modelu ekonometrycznego
Analiza wielkości błędów standardowych ocen parametrów
3
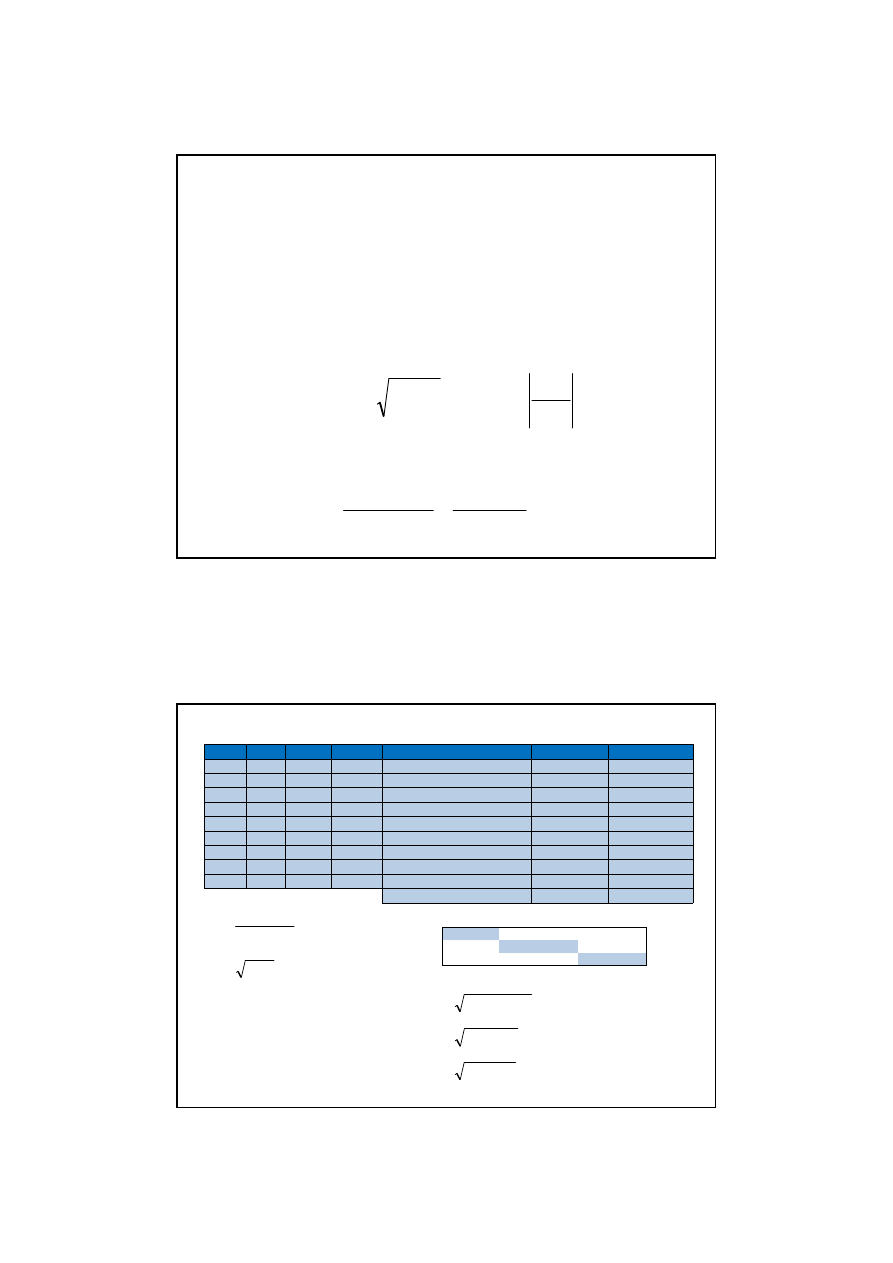
Wyznaczenie błędów szacunku parametrów S(a
j
) ma na celu
sprawdzenie,
czy
stopień
dokładności
szacunku
wszystkich
parametrów jest wystarczająco wysoki.
Do interpretacji wygodnie jest posługiwać się względnym średnim
błędem szacunku:
(j = 0, 1,…,k)
Zbyt wielki względny średni błąd szacunku (przekraczający 50%
wartości szacowanego parametru) przekreśla wartość poznawczą
liczbowej oceny parametru.
100
a
)
a
(
S
)
a
(
V
j
j
j
⋅
=
4
Wnioskowanie o parametrach liniowego modelu ekonometrycznego
Analiza wielkości błędów standardowych ocen parametrów
2013-03-20
3
Przykład 1
Na podstawie KMNK oszacowano parametry liniowego modelu
ekonometrycznego opisującego kształtowanie się stopy bezrobocia osób
w wieku 15-24 lata (Y, %) w Polsce w zależności od liczby podmiotów
gospodarczych wpisanych do rejestru REGON (X
1
, tys. jedn. gosp. ) i
ś
redniej stopy inwestycji (X
2
, %):
5
2
1
4,93X
-
0,02X
-
14
,
205
=
Y
^
Należy oszacować standardowe i względne błędy szacunku parametrów
strukturalnych.
-1
T
2
2
X)
X
(
)
a
(
D
e
S
=
)
)
1
k
(
n
e
)
1
k
(
n
)
yˆ
y
(
S
n
1
i
2
i
n
1
i
2
i
i
2
e
+
−
=
+
−
−
=
∑
∑
=
=
)
a
(
S
)
a
(
S
j
2
j
=
100
a
)
a
(
S
)
a
(
V
j
j
j
⋅
=
Przykład 1 cd.
96
,
4
=
1)
+
(2
-
9
8
,
29
=
S
2
e
23
,
2
=
96
,
4
=
S
e
D^
2
(a)=
590,25605
-0,17008
2,05448
-0,17008
0,00006
-0,00254
2,05448
-0,00254
0,36865
29519
,
24
=
25605
,
590
=
)
a
(
S
0
00771
,
0
=
00006
,
0
=
)
a
(
S
1
60717
,
0
=
36865
,
0
=
)
a
(
S
2
Rok
Y
X1
X2
Y^=205,14-0,02X
1
-4,93X
2
e
t
= y
t
-y^
t
e
t
2
= (y
t
-y^
t
)
2
2003
43
3582
18,3
39,8
3,2
10,5
2004
40,8
3577
18,1
40,9
-0,1
0,0
2005
37,8
3616
18,2
39,5
-1,7
3,0
2006
29,8
3636
19,7
31,7
-1,9
3,7
2007
21,7
3686
21,6
21,3
0,4
0,1
2008
17,3
3757
22,3
16,4
0,9
0,9
2009
20,6
3743
21,1
22,6
-2,0
3,9
2010
23,7
3910
19,9
25,0
-1,3
1,7
2011
25,8
3870
20,4
23,4
2,4
5,9
Razem:
0,0
29,8
Standardowe błędy
szacunku parametrów
strukturalnych:
2013-03-20
4
Przykład 1 cd.
%
84
,
11
=
100
•
14
,
205
29519
,
24
=
)
a
(
V
0
%
76
,
36
=
100
•
0,02
-
00771
,
0
=
)
a
(
V
1
%
32
,
12
=
100
•
4,93
-
60717
,
0
=
)
a
(
V
2
)
607
,
0
(
)
008
,
0
(
)
295
,
24
(
X
93
,
4
X
02
,
0
14
,
205
Y
ˆ
2
1
−
−
=
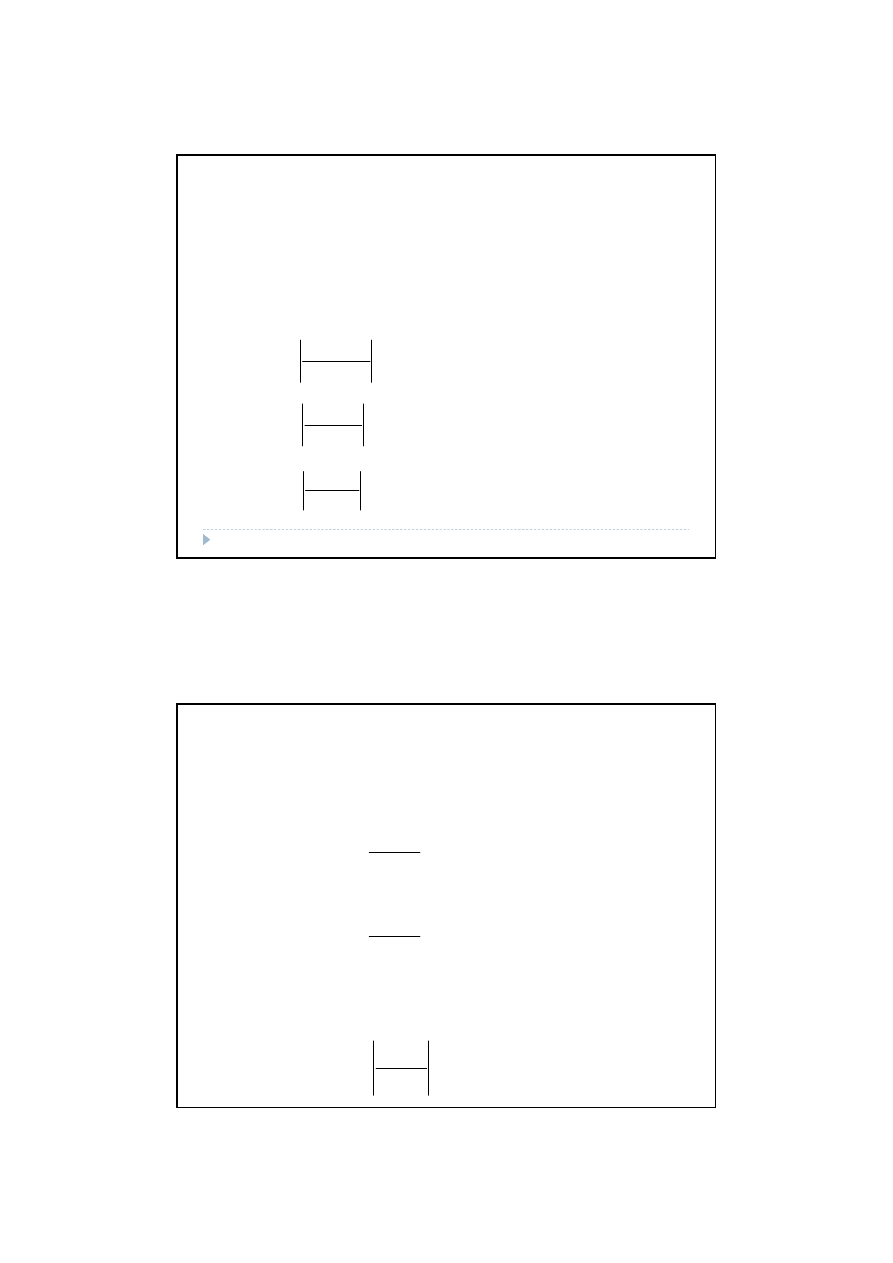
Względne błędy szacunku parametrów strukturalnych:
Oszacowany model ze standardowymi błędami szacunku parametrów
strukturalnych:
Wnioskowanie o parametrach liniowego modelu ekonometrycznego
Przedziały ufności dla parametrów strukturalnych
Estymator a
j
ma rozkład normalny o średniej
α
j
i odchyleniu
standardowym
σ
j
, co można zapisać jako a
j
: N(
α
j
,
σ
j
).
Zatem:
W praktyce zamiast nieznanego
σ
j
stosuje się S(a
j
), czyli:
Aby zbudować przedział ufności dla parametru
α
j
, j = 1, 2, …, k,
przy współczynniku ufności (1-
γ
), należy dobrać z tablic rozkładu t-
Studenta taką wartość t
γ
, n-(k+1)
, aby spełniona była relacja:
)
1
,
0
(
N
~
a
j
j
j
σ
α
−
)
1
k
(
n
j
j
j
,
t
~
)
a
(
S
a
+
−
−
γ
α
γ
α
γ
−
=
≤
−
+
−
1
)
,
t
)
a
(
S
a
(
P
)
1
k
(
n
j
j
j
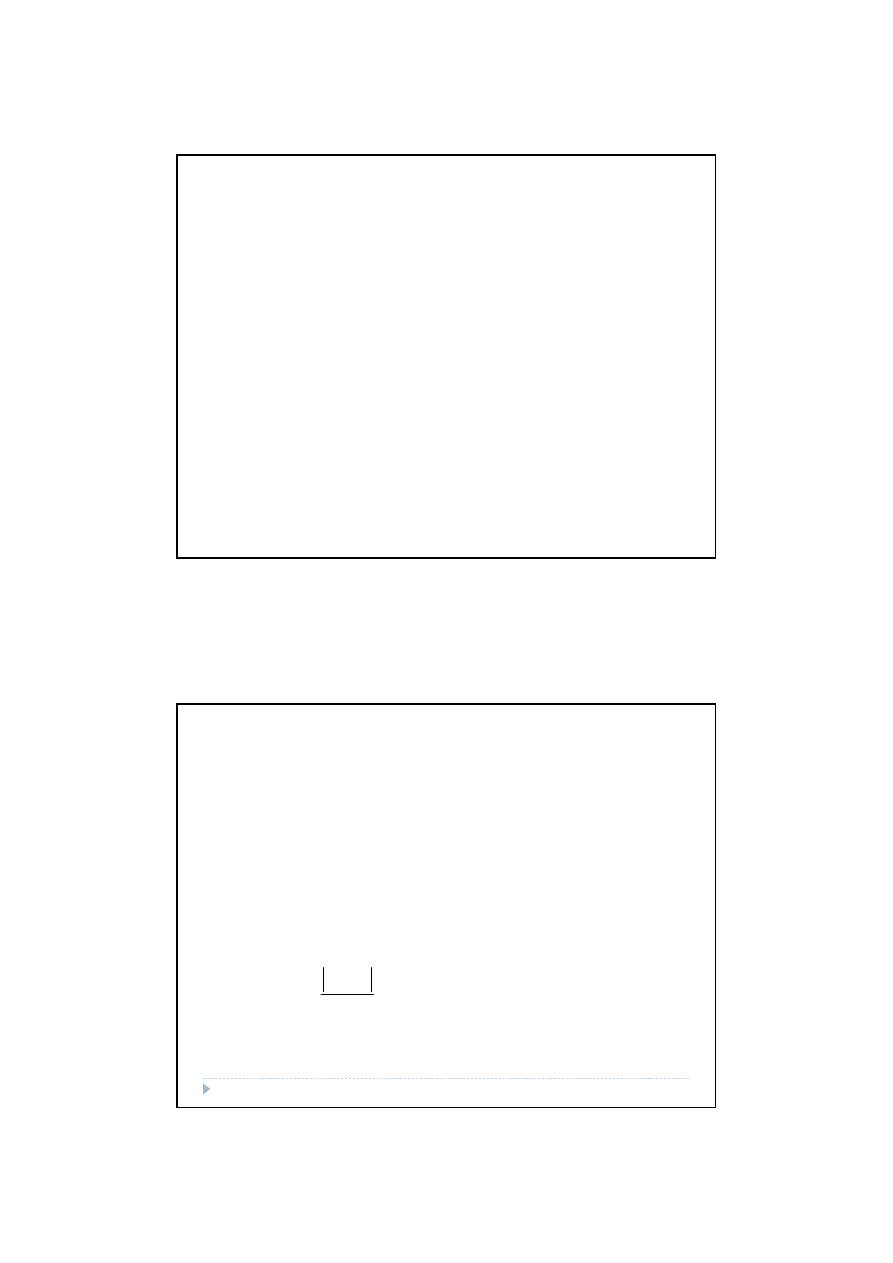
2013-03-20
5
Wnioskowanie o parametrach liniowego modelu ekonometrycznego
Przedziały ufności dla parametrów strukturalnych
Oznacza to, że:
Przedział ufności dla parametru
α
j
ma postać:
Długość przedziału ufności zależy od poziomu istotności
γ
, liczby stopni swobody
oraz wielkości standardowych błędów szacunku parametrów.
Przedział ufności jest tym węższy, im wyższa jest wartość poziomu istotności,
większa liczba stopni swobody (a więc bardziej liczna próba) oraz niższa wartość
standardowego błędu szacunku parametru.
γ
α
γ
γ
−
=
⋅
≤
−
≤
⋅
−
+
−
+
−
1
))
a
(
S
,
t
a
)
a
(
S
,
t
(
P
j
)
1
k
(
n
j
j
j
)
1
k
(
n
γ
α
γ
γ
−
=
⋅
+
−
≤
−
≤
⋅
−
−
+
−
+
−
1
))
a
(
S
,
t
a
)
a
(
S
,
t
a
(
P
j
)
1
k
(
n
j
j
j
)
1
k
(
n
j
γ
α
γ
γ
−
=
⋅
+
≤
≤
⋅
−
+
−
+
−
1
))
a
(
S
,
t
a
)
a
(
S
,
t
a
(
P
j
)
1
k
(
n
j
j
j
)
1
k
(
n
j
k
...,
,
2
,
1
j
)),
a
(
S
,
t
a
),
a
(
S
,
t
a
(
j
)
1
k
(
n
j
j
)
1
k
(
n
j
=
⋅
+
⋅
−
+
−
+
−
γ
γ
Testowanie hipotez dotyczących wartości parametrów
Testowanie hipotez dotyczących wartości parametrów
strukturalnych
strukturalnych
Badanie istotności zmiennych objaśniających
Badanie istotności zmiennych objaśniających
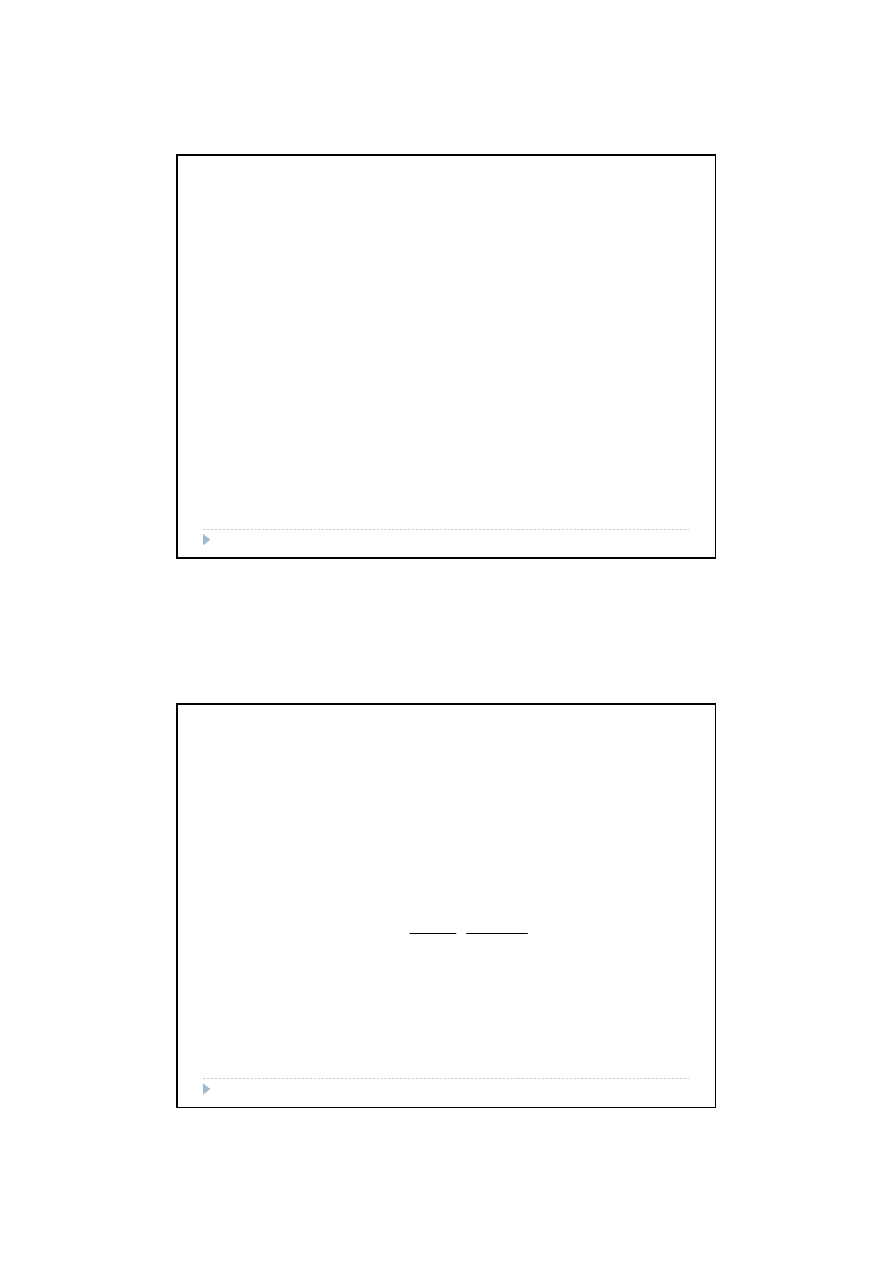
Test t-Studenta
Badając
istotność
wpływu
zmian
wartości
j-tej
zmiennej
egzogenicznej na zmiany wartości zmiennej endogenicznej można
stosować statystyczny test istotności.
Testujemy hipotezy:
H
0
:
α
j
= 0
H
A
:
α
j
0
Statystyka:
ma rozkład t-Studenta z n - (k+1) stopniami swobody.
Z tablic rozkładu t-Studenta należy odczytać wartość t* = t
γ,
n-(k+1)
.
)
a
(
S
a
t
j
j
j
α
−
=
≠
10
2013-03-20
6
Badanie istotności zmiennych objaśniających
Badanie istotności zmiennych objaśniających
Test t-Studenta
Interpretacja:
Interpretacja:
Jeżeli t>t* to hipotezę zerową odrzucamy na korzyść hipotezy
alternatywnej. Oznacza to, że zmienna X
j
ma statystycznie istotny
wpływ na zmienną objaśnianą Y. Prawdopodobieństwo popełnienia
błędu, polegającego na podjęciu błędnej decyzji weryfikacyjnej
wynosi
.
Jeżeli t<t* to nie mamy podstaw do odrzucenia hipotezy zerowej na
korzyść hipotezy alternatywnej. Oznacza to, że zmienna X
j
ma
statystycznie nieistotny wpływ na zmienną objaśnianą Y.
γ
11
Badanie istotności zmiennych objaśniających
Badanie istotności zmiennych objaśniających
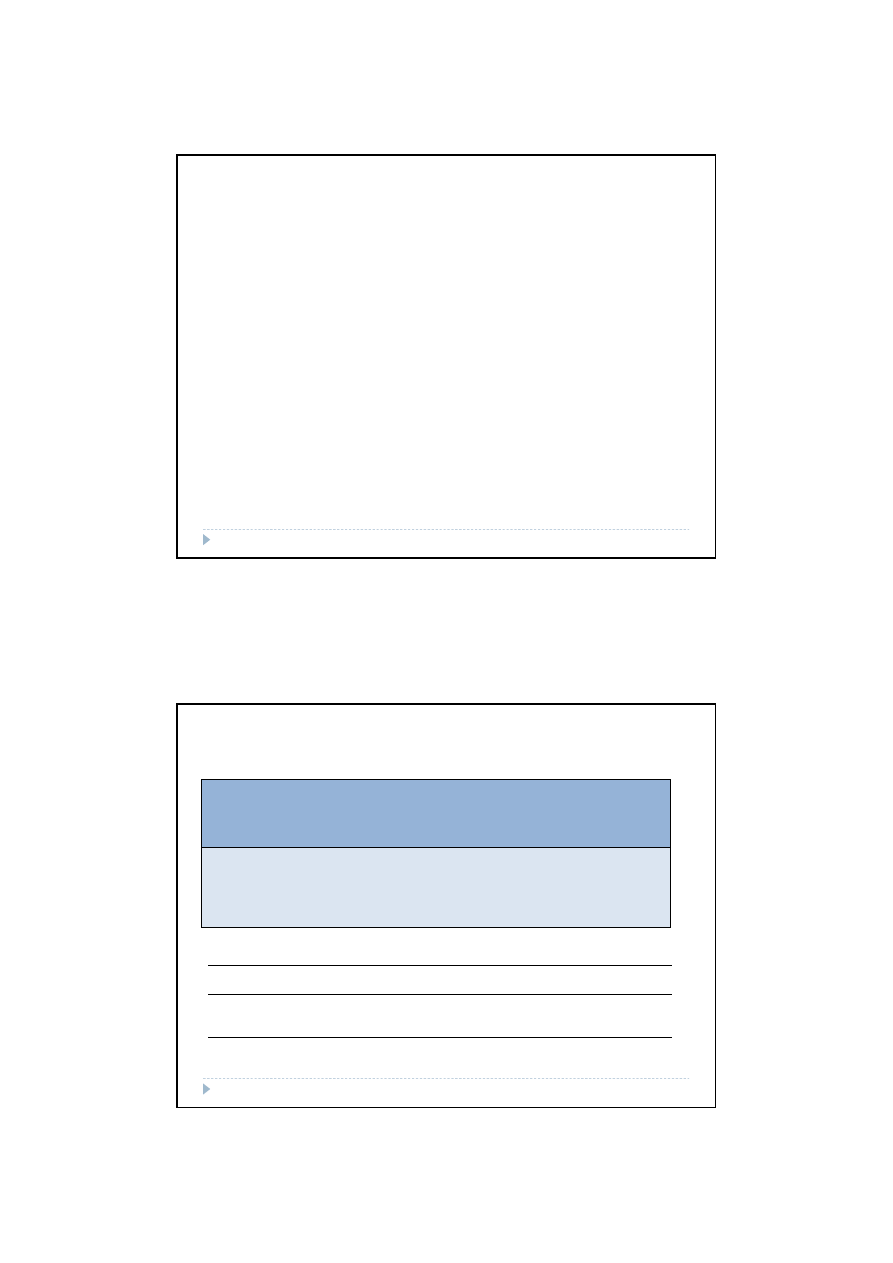
Uogólniony test
Uogólniony test Walda
Walda
Gdy istnieje potrzeba zweryfikowania hipotezy o jednoczesnej
istotności wybranego podzbioru zmiennych objaśniających można
posłużyć się hipotezami:
H
0
:
α
1
=
α
2
=…=
α
k
= 0
H
A
: co najmniej jeden z parametrów
α
j
0
Statystyka:
ma rozkład Fishera-Snedecora z r
1
= k oraz r
2
= n - (k+1) stopniami
swobody.
Z tablic rozkładu Fishera-Snedecora należy odczytać wartość F* =
F(
γ,
r
1
, r
2
).
≠
k
k
n
R
R
F
1
1
2
2
−
−
⋅
−
=
12
2013-03-20
7
Badanie istotności zmiennych objaśniających
Badanie istotności zmiennych objaśniających
Uogólniony test
Uogólniony test Walda
Walda
Interpretacja
Interpretacja
Jeżeli F>F* to hipotezę zerową odrzucamy na korzyść hipotezy
alternatywnej. Oznacza to, że istnieje taka zmienna X
j
, która ma
statystycznie
istotny
wpływ
na
zmienną
objaśnianą
Y.
Prawdopodobieństwo popełnienia błędu, polegającego na podjęciu
błędnej decyzji weryfikacyjnej wynosi
γ.
Jeżeli F<F* to nie mamy podstaw do odrzucenia hipotezy zerowej na
korzyść hipotezy alternatywnej. Oznacza to, że nie ma takiej
zmiennej X
j
, która ma statystycznie istotny wpływ na zmienną
objaśnianą Y.
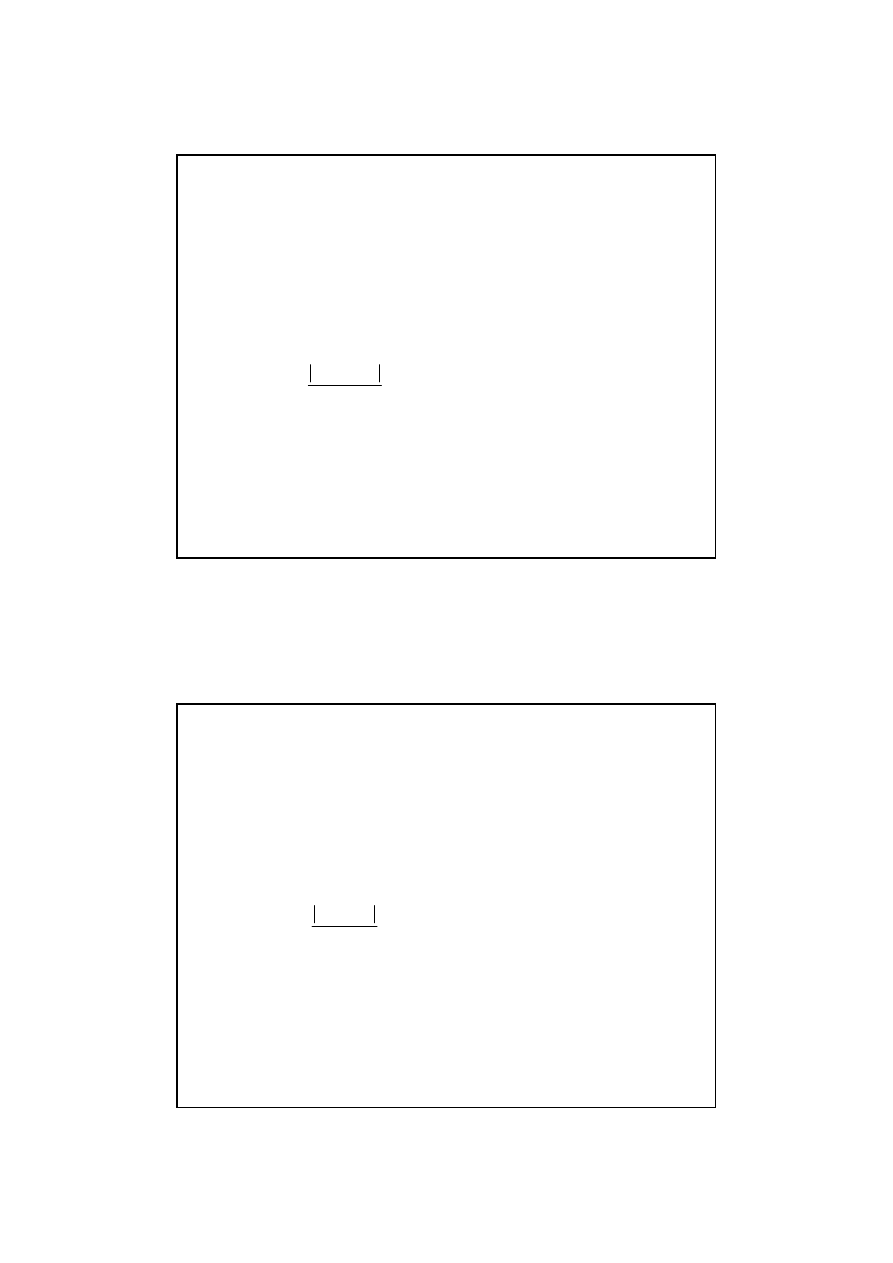
13
Zmienna
Ocena
parametru
Standardowy
bł
ą
d
szacunku
Warto
ść
statystyki
t-Studenta
Warto
ść
-p
Dolny kraniec 95%
przedziału ufno
ś
ci
Górny kraniec 95%
przedziału ufno
ś
ci
Stała
a
0
S(a
0
)
t
1
poziom
X
1
a
1
S(a
1
)
t
2
istotno
ś
ci
X
2
a
2
S(a
2
)
t
3
Precyzja oszacowań parametrów strukturalnych
modelu ekonometrycznego w programie Excel
)
a
(
S
,
t
a
1
)
1
k
(
n
1
⋅
−
+
−
γ
)
a
(
S
,
t
a
0
)
1
k
(
n
0
⋅
+
+
−
γ
)
a
(
S
,
t
a
2
)
1
k
(
n
2
⋅
−
+
−
γ
)
a
(
S
,
t
a
0
)
1
k
(
n
0
⋅
−
+
−
γ
)
a
(
S
,
t
a
1
)
1
k
(
n
1
⋅
+
+
−
γ
)
a
(
S
,
t
a
2
)
1
k
(
n
2
⋅
+
+
−
γ
Współczynniki Bł
ą
d standardowy
t Stat
Warto
ść
-p
Dolne
95%
Górne
95%
Przeci
ę
cie
205,14
24,29519
8,44
0,00015
145,69
264,59
X1
-0,02
0,00771
-2,72
0,03461
-0,04
0,00
X2
-4,93
0,60717
-8,12
0,00019
-6,41
-3,44
2013-03-20
8
Przykład 2
Należy sprawdzić, czy parametry strukturalne poniższego modelu
ekonometrycznego są istotne statystycznie?
15
Test t-Studenta
)
607
,
0
(
)
008
,
0
(
)
295
,
24
(
X
93
,
4
X
02
,
0
14
,
205
Y
ˆ
2
1
−
−
=
H
0
:
α
0
= 0
H
A
:
α
0
≠
0
44
,
8
=
295
,
24
0
-
2
=
t
05,14
Statystyka:
ma rozkład t-Studenta o parametrach
γ = 0,05
i n – (k+1) = 6 df.
Wartość krytyczna: t* = t
γ,
n-(k+1)
= t(0,05; 6) = 2,447
W związku z tym, że t>t* hipotezę zerową odrzucamy na korzyść hipotezy
alternatywnej. Oznacza to, że parametr strukturalny
α
0
jest istotny statystycznie.
Prawdopodobieństwo popełnienia błędu, polegającego na podjęciu błędnej decyzji
weryfikacyjnej wynosi 0,05.
Przykład 2 cd.
16
Test t-Studenta
)
607
,
0
(
)
008
,
0
(
)
295
,
24
(
X
93
,
4
X
02
,
0
14
,
205
Y
ˆ
2
1
−
−
=
H
0
:
α
1
= 0
H
A
:
α
1
≠
0
72
,
2
=
00771
,
0
0
-
0,02
-
=
t
Statystyka:
ma rozkład t-Studenta o parametrach
γ = 0,05
i n – (k+1) = 6 df.
Wartość krytyczna: t* = t
γ,
n-(k+1)
= t(0,05; 6) = 2,447
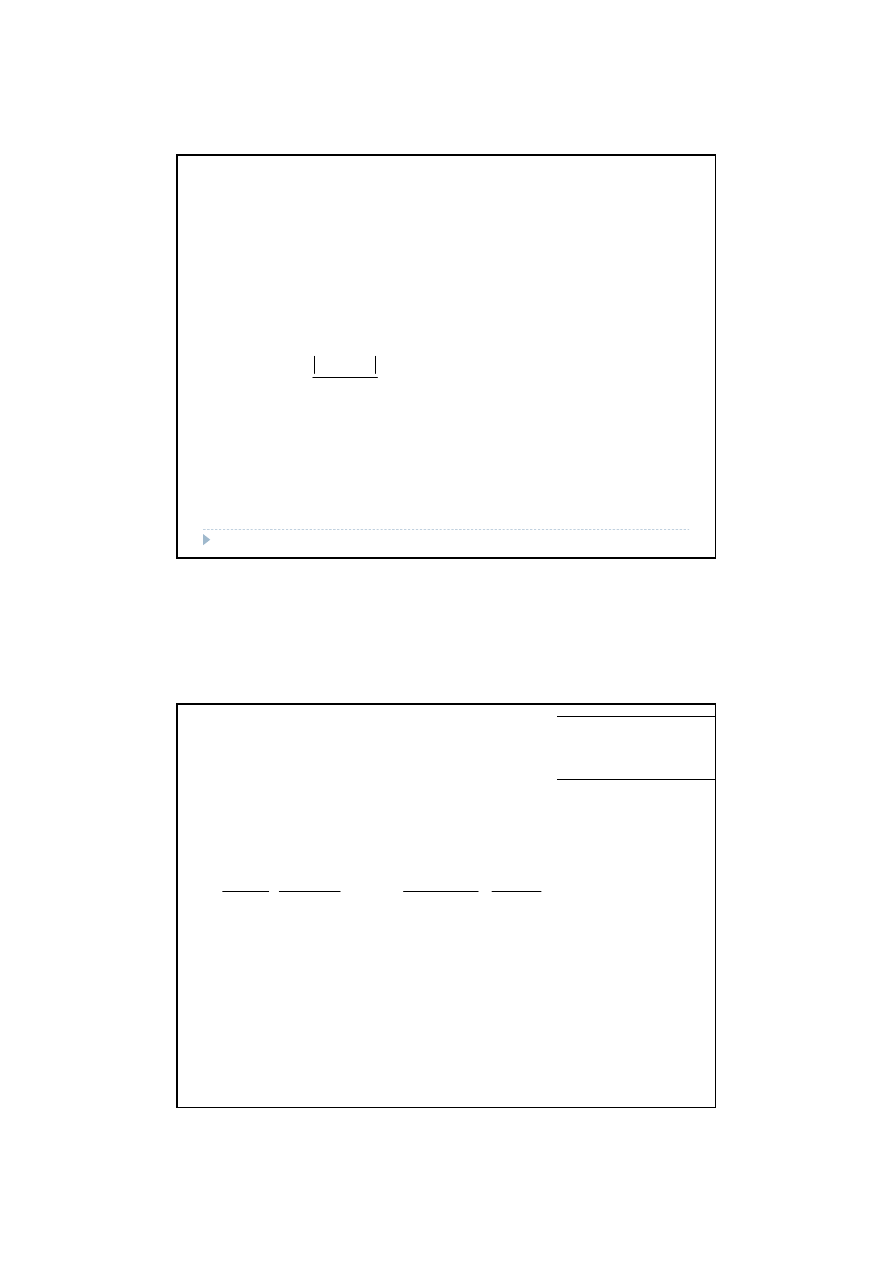
W związku z tym, że t>t* hipotezę zerową odrzucamy na korzyść hipotezy
alternatywnej. Oznacza to, że zmienna X
1
ma statystycznie istotny wpływ na
zmienną objaśnianą Y. Prawdopodobieństwo popełnienia błędu, polegającego na
podjęciu błędnej decyzji weryfikacyjnej wynosi 0,05.
2013-03-20
9
Przykład 2 cd.
17
Test t-Studenta cd.
)
607
,
0
(
)
008
,
0
(
)
295
,
24
(
X
93
,
4
X
02
,
0
14
,
205
Y
ˆ
2
1
−
−
=
H
0
:
α
2
= 0
H
A
:
α
2
≠
0
12
,
8
=
60717
,
0
0
-
4,93
-
=
t
Statystyka:
ma rozkład t-Studenta o parametrach
γ = 0,05
i n – (k+1) = 6 df.
Wartość krytyczna: t* = t
γ,
n-(k+1)
= t(0,05; 6) = 2,447
W związku z tym, że t>t* hipotezę zerową odrzucamy na korzyść hipotezy
alternatywnej. Oznacza to, że zmienna X
1
ma statystycznie istotny wpływ na
zmienną objaśnianą Y. Prawdopodobieństwo popełnienia błędu, polegającego na
podjęciu błędnej decyzji weryfikacyjnej wynosi 0,05.
Przykład 2 cd.
18
Test F-Snedecora
H
0
:
α
1
=
α
2
= 0
H
A
: co najmniej jeden z parametrów
α
j
≠
0, j = 1, 2.
Statystyka:
ma rozkład F-Snedecora o parametrach
γ = 0,05
i n – (k+1) = 6 i
k = 2 df.
Wartość krytyczna: F* =F(0,05; 6; 2) = 19,32953
W związku z tym, że F>F* hipotezę zerową odrzucamy na korzyść hipotezy
alternatywnej. Oznacza to, że istnieje taka zmienna X
j
, która ma statystycznie
istotny wpływ na zmienną objaśnianą Y. Prawdopodobieństwo popełnienia błędu,
polegającego na podjęciu błędnej decyzji weryfikacyjnej wynosi
0,05.
k
k
n
R
R
F
1
1
2
2
−
−
⋅
−
=
819
,
68
=
2
1
-
2
-
9
•
0,95823
-
1
95823
,
0
=
F
Statystyki regresji
Wielokrotno
ść
R
0,97889
R kwadrat
0,95823
Dopasowany R kwadrat
0,94430
Bł
ą
d standardowy
2,22698
Obserwacje
9

2013-03-20
10
1.
Na podstawie KMNK oszacowano parametry liniowego
modelu ekonometrycznego:
a)
model jest koincydentny,
b)
model nie jest koincydentny,
c)
weryfikacja modelu jest negatywna,
d)
ż
adne z powy
ż
szych.
2
1
X
90
,
0
X
60
,
0
78
,
0
Y
ˆ
+
+
−
=
Dane s
ą
macierze:
=
990
,
0
980
,
0
R
0
=
1
962
,
0
962
,
0
1
R
Które ze zda
ń
jest prawdziwe:
Przykładowe pytania testowe
2.
Dany jest cz
ęś
ciowy wydruk komputerowy analizy regresji
obliczonej w programie Excel:
a)
Estymator wariancji składnika losowego wynosi 0,006.
b)
Odchylenie standardowe reszt modelu jest równe 0,029.
c)
Model zbudowano na podstawie 9 obserwacji.
d)
Ż
adne z powy
ż
szych zda
ń
nie jest prawdziwe.
ANALIZA
WARIANCJI
df
SS
MS
F
Istotno
ść
F
Regresja
2
0,594
0,297
346,5
1E-07
Resztkowy
7
0,006
0,000857143
Razem
9
0,6
Przykładowe pytania testowe
2013-03-20
11
3.
Dany jest cz
ęś
ciowy wydruk komputerowy analizy regresji
obliczonej w programie Excel:
a)
Współczynnik determinacji wynosi 0,594.
b)
Współczynnik zbie
ż
no
ś
ci jest równy 0,01.
c)
Ś
rednia suma kwadratów regresji wynosi 346,5.
d)
Ż
adne z powy
ż
szych zda
ń
nie jest prawdziwe.
ANALIZA
WARIANCJI
df
SS
MS
F
Istotno
ść
F
Regresja
2
0,594
0,297
346,5
1E-07
Resztkowy
7
0,006
0,000857143
Razem
9
0,6
Przykładowe pytania testowe
4.
Oszacowano klasyczny model jednorównaniowy otrzymuj
ą
c
mi
ę
dzy innymi wektor reszt [-5;10;0;-5;0;0]. Wiadomo,
ż
e
wariancja zmiennej obja
ś
nianej wynosi 500. Wówczas R
2
jest
równy
a)
0,9480
b)
0,9500
c)
0,9750
d)
0,9800
Przykładowe pytania testowe

2013-03-20
12
5.
Oszacowano model opisuj
ą
cy kształtowanie si
ę
wielko
ś
ci
sprzeda
ż
y pewnego towaru (w kg) w zale
ż
no
ś
ci od jego ceny
(w PLN) i wydatków na promocj
ę
(w PLN) otrzymuj
ą
c poni
ż
szy
wydruk komputerowy.
współczynniki
t Stat
Wartość-p
Przecięcie
116.1568
4.7131
0.0011
Cena
-1.3079
-10.1095
0.0000
Promocja
11.2459
4.0389
0.0029
a)
Wzrost ceny o 1 PLN nie spowoduje spadku sprzeda
ż
y.
b)
Wpływ promocji nie jest istotny przy istotno
ś
ci 0.005.
c)
Przy braku promocji i cenie=2PLN, mo
ż
na si
ę
spodzie-
wa
ć
sprzeda
ż
y około mi
ę
dzy 113 a 114 PLN.
d)
Ż
adne z powy
ż
szych zda
ń
nie jest prawdziwe.
Przykładowe pytania testowe
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron