1. Cel ćwiczenia
Celem ćwiczenia było wyznaczenie reakcji strumienia cieczy na nieruchomą
przeszkodę. Do wyznaczenia wartości siły posłużymy się ramką o znanej masie i
odczytanym wychyleniem z pozycji równowagi.
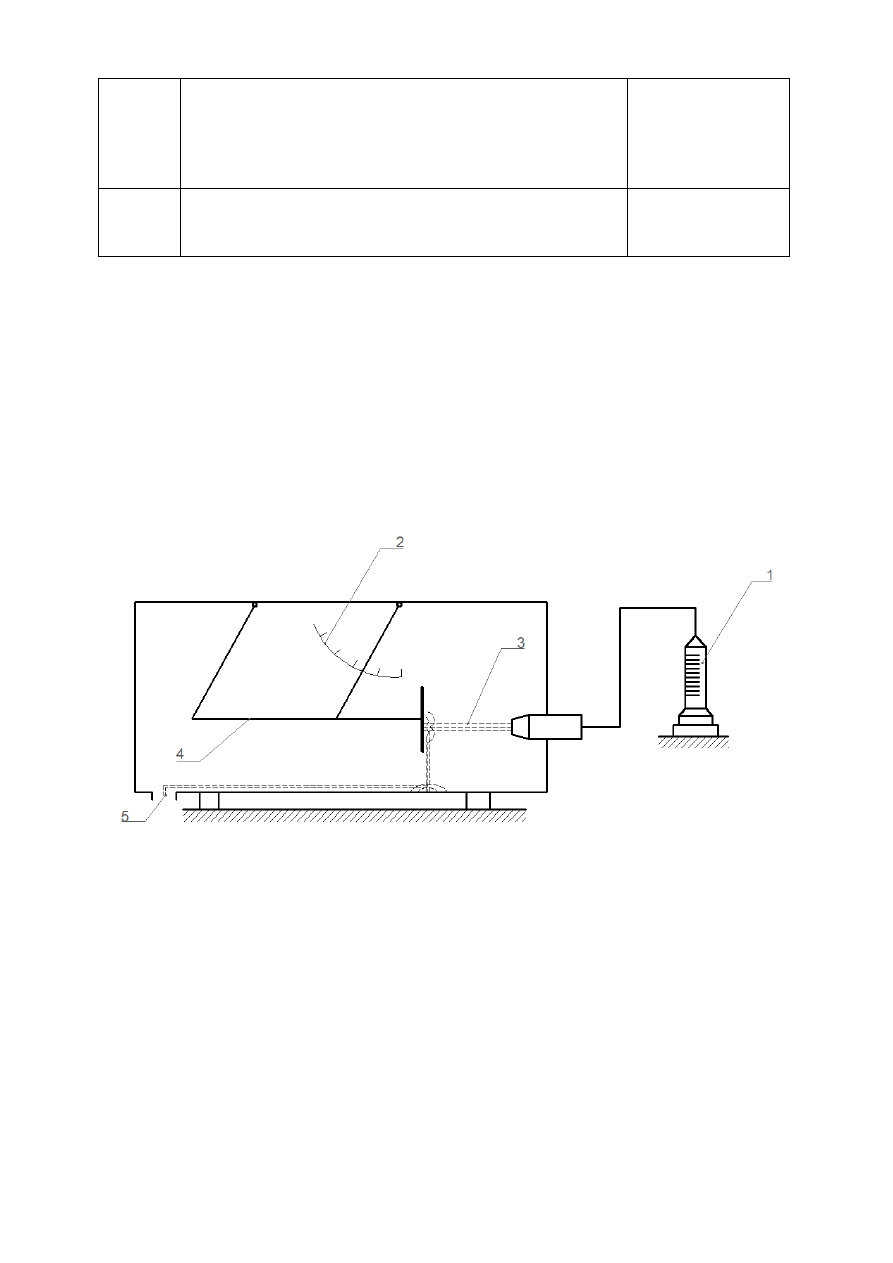
2. Schemat stanowiska
1. Rotametr
2. Podziałka kąta
3. Strumień cieczy
4. Ramka
5. Odpływ
Katedra Energetyki i Ochrony Środowiska
MECHANIKA PŁYNÓW
„Wyznaczanie reakcji hydrodynamicznej
strumienia cieczy na nieruchomą przeszkodę”
Data:
30 III 2010
Gr13A
Tomasz Olchawski
WIMIR, AiR
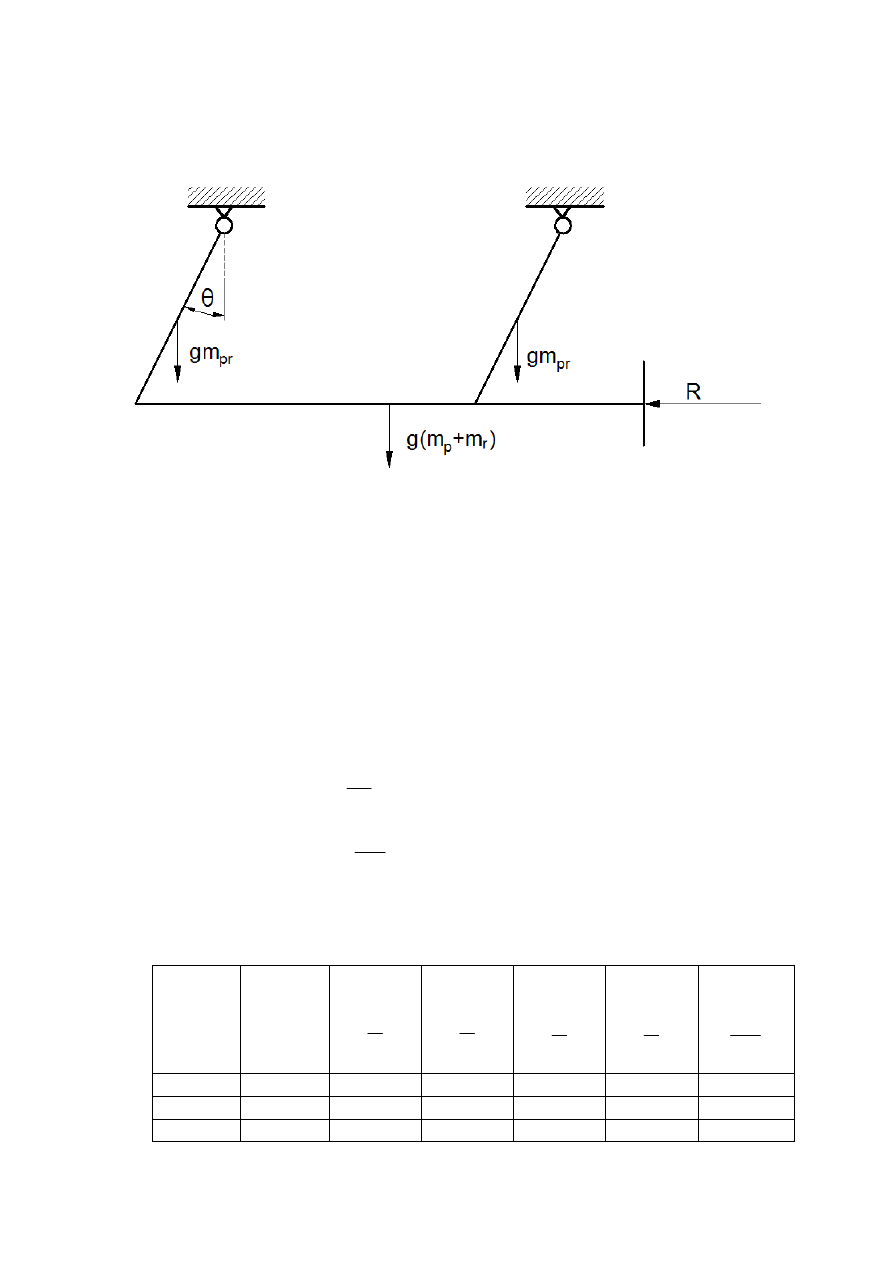
3. Wychylenie ramki
Gdzie: m
r
– masa tarczy
m
pr
- masa pręta
m
p
– masa poprzeczki
4. Dane
kg
m
pr
01705
,
0
=
kg
m
p
0669
,
0
=
kg
m
r
04525
,
0
=
m
d
004
,
0
=
2
81
,
9
s
m
g =
3
1000
m
kg
=
ρ
d – średnica strumienia cieczy,
ρ
- gęstość wody
5. Pomiary
Lp.
θ
[ ]
°
1
Q
h
l
2
Q
h
l
3
Q
h
l
sr
Q
h
l
Q
s
m
3
1
12
215
215
215
215
5,97*10
-5
2
22
290
290
290
290
8,06*10
-5
3
38
385
385
390
387
1,075*10
-4
6. Obliczenia
Wzór teoretyczny:
θ
tg
g
m
m
m
R
pr
r
p
⋅
⋅
+
+
=
)
(
[ ]
s
m
kg
=
⋅
2
]
[
2694
,
0
12
81
,
9
)
01705
,
0
04525
,
0
0669
,
0
(
1
tg
R
≈
°
⋅
⋅
+
+
=
]
[
5124
,
0
22
81
,
9
)
01705
,
0
04525
,
0
0669
,
0
(
2
tg
R
≈
°
⋅
⋅
+
+
=
]
[
9902
,
0
38
81
,
9
)
01705
,
0
04525
,
0
0669
,
0
(
3
tg
R
≈
°
⋅
⋅
+
+
=
Wzór obliczeniowy:
2
2
4
d
Q
R
obl
⋅
⋅
⋅
=
π
ρ
[ ]
s
m
kg
m
s
m
m
kg
=
⋅
=
⋅
2
2
2
3
3
(
)
]
[
2836
,
0
004
,
0
10
97
,
5
1000
4
2
2
5
1
R
obl
≈
⋅
⋅
⋅
⋅
=
−
π
(
)
]
[
5170
,
0
004
,
0
10
06
,
8
1000
4
2
2
5
2
R
obl
≈
⋅
⋅
⋅
⋅
=
−
π
(
)
]
[
9196
,
0
004
,
0
10
075
,
1
1000
4
2
2
4
3
R
obl
≈
⋅
⋅
⋅
⋅
=
−
π
Obliczenia błędów:
%
100
⋅
−
=
obl
obl
R
R
R
ε
[%]
%
=
⋅
%
5
%
100
2836
,
0
2694
,
0
2836
,
0
1
≈
⋅
−
=
ε

%
8
,
0
%
100
5170
,
0
5124
,
0
5170
,
0
2
≈
⋅
−
=
ε
%
6
,
7
%
100
9196
,
0
9902
,
0
9196
,
0
3
≈
⋅
−
=
ε
7. Wnioski
Wyłączając pomiar drugi błędy względne pomiaru i wartości teoretycznej są zbyt
duże by uznać podany wzór za przybliżający to zjawisko w stopniu wystarczającym.
Powodem tak wysokich błędów (do 7,6%) może być nieuwzględnienie
współczynników oddających rzeczywiste warunki pomiaru (jak tarcie w łożyskach) lub
niedoskonałość urządzeń pomiarowych czy dokładność odczytu.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron