1
Więźba dachowa
Zaprojektować wiązar jętkowy z drewna klasy C-30 o rozpiętości L = 10,50 m, jeżeli:
nachylenie połaci dachowych α = 41°, rozstaw krokwi a = 0,80 m, w poziomie jętek
zastosowano usztywnienie z desek w postaci skratowania (dzięki temu można zało-
żyć nieprzesuwność węzłów układu jętkowego), dach jest pokryty dachówką kar-
piówką podwójnie, wymiary budynku odpowiadają warunkom H/L <2 oraz H< 10 m,
budynek znajduje się w II strefie obciążenia śniegiem i w I strefie obciążenia wiatrem.
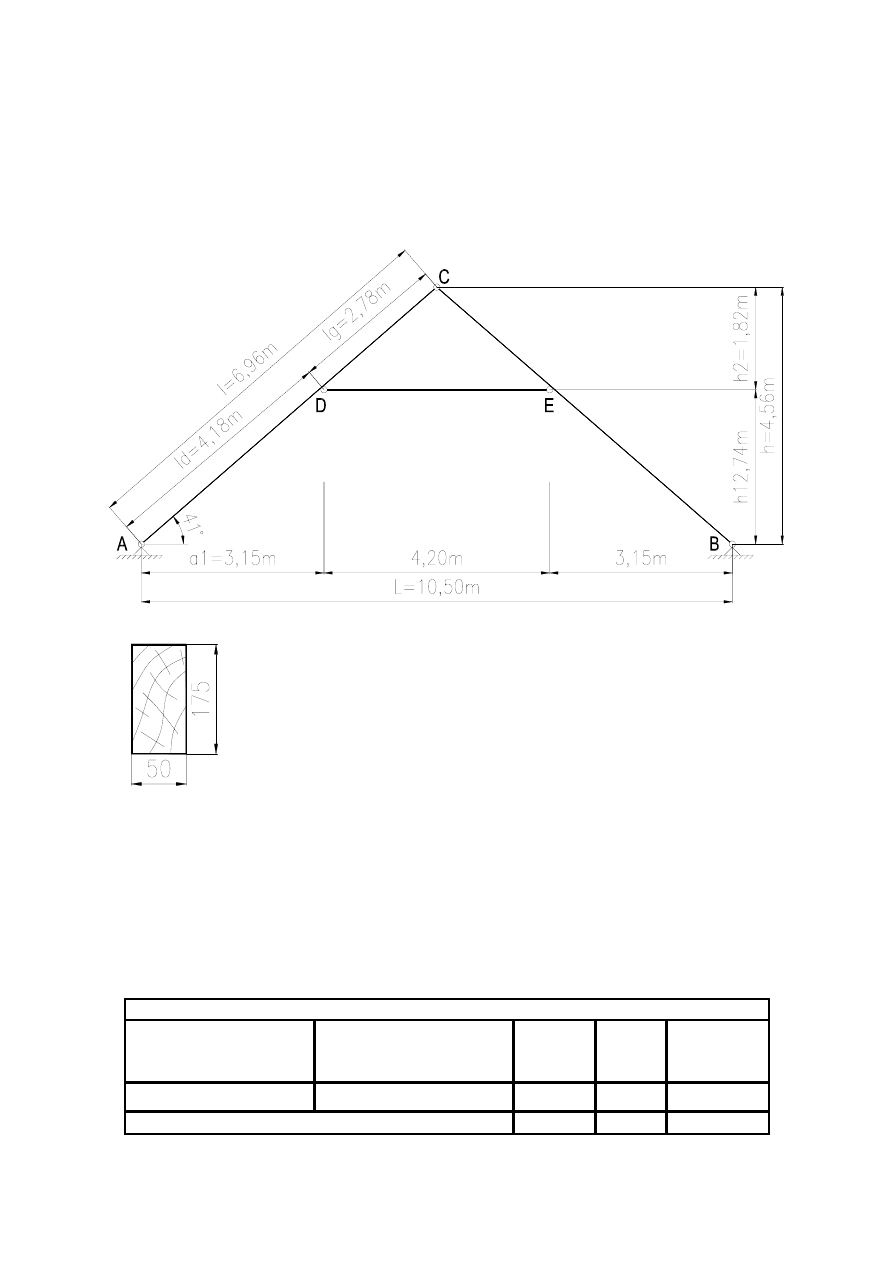
a)
b)
Wiązar jętkowy: a) schemat, b) przekrój krokwi
1. Dane geometryczne wiązara.
h = 0,5·L·tg
α = 0,5·10,50·0,8693 = 4,56 m
l = L/(2·cos
α) = 10,50/(2·0,7547) = 6,96 m
ν= l
d
/l = 0,6 (wartość przyjęta) l
d
=
ν·l⇒ 0,6·6,96 = 4,18 m
a
1
= l
d
·cos
α = 4,18·0,7547 = 3,15 m
h
1
= a
1
·tg
α = 3,15·0,8693 = 2,74 m
l
g
= l-l
d
⇒ 6,96-4,18 = 2,78 m
2. Zebranie obciążeń.
g
k
=0,9
1,2
g
d
=1,08
0,9
1,08
Nazwa obciążenia: stałe dachu
Nazwa materiału
Wyrażenie matematyczne
obc.char.
kN/m
2
wsp.obc
γ
f
obc.obl. kN/m
2
RAZEM
g=0,9
Ciężar własny pokrycia
2
S
k
=0,46
1,4
S
d
= 0,644
p
k1
=0,187
1,3
p
d1
= 0,243
p
k1
= -0,18
1,3
p
d1
= -0,234
Śnieg
Połać nawietrzna p
1
0,187
Połać nawietrzna p
2
-0,18
Nazwa obciążenia: zmienne dachu
Nazwa materiału
Wyrażenie matematyczne
obc.char.
kN/m
2
wsp.obc
γ
f
obc.obl. kN/m
2
0,46
Śnieg S=Q*C
Wiatr
Obliczenie obciążeń składowych prostopadłych do połaci dachowej od strony na-
wietrznej:
g
⊥
= a·g·cos
α = a·0,7547·g
S
⊥
= a·S·cos
2
α = a·0,7547
2
·S = 0,5696·S
g
k
⊥1
=0,8m·0,9kN/m
2
·cos41
0
⇒ 0,543 kN/m
g
d
⊥1
= 0,8m·1,08 kN/m
2
·cos41
0
⇒ 0,652 kN/m
S
k
⊥1
=0,8m·0,46 kN/m
2
·cos
2
41
0
⇒ 0,210 kN/m
S
d
⊥1
=0,8m·0,644 kN/m
2
·cos
2
41
0
⇒ 0,293 kN/m
3. Wymiarowanie krokwi.
W tym rozwiązaniu przewidziano krokwie o jednakowym przekroju na całej długości
l = 6,96 m, projektowane z jednego elementu.
3.1. Stan graniczny nośności.
Momenty zginające i siła podłużna:
E
= M
max
= -3,126 kNm
AD
= 2,507 kNm
N
B
= -7,156 kN.
Przyjęto przekrój 5,0 x 17,5 cm o polu przekroju A = 8750 mm
2
⇒0,00875m
2
, którego
W
y
= 255,21·10
3
mm
3
⇒0,00025521m
3
I
y
=22,33·10
3
mm
4
⇒0,00002233m
4
i
y
= 50,52mm
⇒0,05052m
Sprawdzenie naprężeń w przęśle AD:
l
y
= l
d
= 4,18 m
y
i
y
l
µ
y
λ
⋅
=
740
,
82
0,05052m
m
18
4,
0
,
1
y
λ
=
⋅
=
Naprężenia krytyczne przy ściskaniu:
0,05
= 8000 MPa
1
Wartość momentu w punkcie D lub E
2
Wartość momentu w przęśle A-D lub B-E
3
wg tab. Z-2.2.3-1

3
2
y
λ
0,05
E
2
π
y
crit,
c,
σ
⋅
=
11,533MPa
82,740
8000MPa
3,14
σ
2
2
y
crit,
c,
=
⋅
=
β
c
-współczynnik dotyczący prostoliniowości elementów
dla drewna litego β
c
=0,2
f
c,0,k
= 23 MPa
Smukłość sprowadzona przy ściskaniu:
1,412
11,533MPa
23MPa
y
crit,
c,
σ
c,0,k
f
y
rel,
λ
=
⇒
=
Składowa współczynnika wyboczenia:
⎥⎦
⎤
⎢⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
−
⋅
+
⋅
=
2
y
rel,
λ
0,5
y
rel,
λ
c
β
1
0,5
y
k
(
)
588
,
1
2
412
,
1
0,5
412
,
1
2
,
0
1
0,5
y
k
=
⎥⎦
⎤
⎢⎣
⎡
+
−
⋅
+
⋅
=
Współczynnik wyboczeniowy:
2
y
rel,
λ
2
y
k
y
k
1
y
c,
k
−
+
=
432
,
0
2
412
,
1
2
588
,
1
588
,
1
1
y
c,
k
=
−
+
=
Współczynnik modyfikujący parametry wytrzymałościowe z uwagi na czas trwania
obciążenia i zmiany wilgotności materiałów:
mod
=0,9 — przyjęto dla klasy trwania obciążenia = krótkotrwale (wiatr) i klasy użyt-
kowania konstrukcji = 2
Wytrzymałość obliczeniowa na ściskanie wzdłuż włókien f
c.0,k
M
γ
mod
k
c,0,k
f
d
c,0,
f
⋅
=
15,923MPa
1,3
9
,
0
23MPa
d
c,0,
f
=
⋅
=
Częściowy współczynnik bezpieczeństwa
M
=1,3
f
m,y,k
- zginanie
4
wg tab. Z-2.2.3-1
5
Przyjąć w projekcie
6
Wg tab. Z-2.2.3-1
7
Współczynnik bezp. Przyjąć w projekcie
γ
M
=1,3
8
Wg tab. Z-2.2.3-1

4
M
γ
mod
k
k
y,
m,
f
d
y,
m,
f
⋅
=
MPa
769
,
0
2
1,3
9
,
0
30MPa
d
y,
m,
f
=
⋅
=
Naprężenie obliczeniowe ściskające:
A
y
c,
k
N
d
c,0,
σ
⋅
=
MPa
893
,
1
Pa
5
,
1892975
2
8750m
00
,
0
0,432
7156N
d
c,0,
σ
⇒
=
⋅
=
Sprawdzenie naprężeń w przęśle A-D
Naprężenia od zginania:
W
AD
M
d,AD
y,
m,
σ
=
9,824MPa
Pa
7
,
823667
9
0,0002552m
2507Nm
AD
d,
y,
m,
σ
3
⇒
=
=
0
d,AD
m,z,
σ
=
Stan graniczny nośności elementów ściskanych osiowo;
1
d
m,z,
f
d
m,z,
σ
m
k
d
y,
m,
f
d
y,
m,
σ
d
c,0,
f
y
c,
k
d
c,0,
σ
≤
+
+
⋅
1
748
,
0
0
20,769MPa
9,824MPa
15,923MPa
0,432
1,893MPa
≤
=
+
+
⋅
Sprawdzenie naprężeń w punkcie E:
W
E
M
E
d,
y,
m,
σ
=
12,249MPa
Pa
3
,
12249216
0,0002552m
3126Nm
E
d,
y,
m,
σ
3
⇒
=
=
Normalna w punkcie E
N
E
= 7,011kN
A
k
N
σ
y
c,
E
d,
c,0,
⋅
=
1,855MPa
761,9Pa
1854
0,00875m
0,432
7011N
σ
2
E
d,
c,0,
⇒
=
⋅
=
5
1
d
m,z,
f
d
m,z,
σ
m
k
d
y,
m,
f
d
y,
m,
σ
2
d
c,0,
f
d,E
c,0,
σ
≤
+
+
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
1
0,597
0
20,769
12,249
2
15,923
1,855
≤
=
+
+
⎟
⎠
⎞
⎜
⎝
⎛
Naprężeń w przęśle DC nie sprawdza się.
3.2 Stan graniczny użytkowalności -sprawdzenie ugięć.
Krokiew pracuje jako belka dwuprzęsłowa o różnej długości przęseł, obciążona ob-
ciążeniem prostopadłym równomiernie rozłożonym. Jako układ statyczny do oblicze-
nia ugięć należy przyjąć belkę jednoprzęsłową obciążoną obciążeniem ciągłym q
k
,
siłą osiową ściskającą P oraz momentem odciążającym M
p
przyłożonym na podporze
środkowej. Przybliżona, ostateczna wartość ugięcia dolnej części krokwi.
ost
= u
fin
·k < u
net, fin
gdzie:
u
fin
- ugięcie finalne od obciążenia prostopadłego,
k -współczynnik wpływu siły osiowej na ugięcie krokwi.
Ponieważ w przykładzie występują różne rodzaje obciążeń i związane z nimi różne
wartości współczynnika k
def
wiec ugięcia obliczono od poszczególnych obciążeń
(wartości charakterystycznych g, S).
Normalna na podporze B
P = 7,156 kN
crit
P
P
1
1
k
−
=
2
1
2
l
I
E
π
crit
P
⋅
⋅
=
E=
mean
=12000 MPa=0,012
⋅
10
6
N/m
2
l
1
=4,180m
(
)
151,362kN
N
1
,
151362
P
4,18m
m
10
22,33
m
N
10
12000
3,14
P
crit
2
4
6
-
2
6
2
crit
⇒
=
⇒
⋅
⋅
⋅
⋅
=
1,050
k
151,12kN
7,156kN
1
1
k
=
⇒
−
=
9
Ostateczna wartość ugięcia
10
Wg tab. Z-2.2.3-1

6
(
)
def
k
1
ins
u
fin
+
⋅
=
1
/h
>20
4180/175=23,89
>20
Ponieważ l
1
/h
>20 stosujemy następujący wzór na ugięcie doraźne:
13
I
mean
E
384
4
l
q
5
M
u
ins
u
⋅
⋅
⋅
⋅
=
=
Ugięcie od obciążenia ciężarem własnym g
k
⊥1
=0,543 kN/m;
def
=0,6
(
)
8,10mm
0,0081m
ins1
u
4
m
6
-
10
22,33
2
m
N
6
10
12000
384
4
4,18m
m
N
3
10
0,543
5
ins1
u
⇒
=
⇒
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
(
)
mm
96
,
12
fin
u
0,6
1
10
,
8
fin1
u
=
⇒
+
⋅
=
Ugięcie od obciążenia śniegiem S
k
⊥1
=0,201 kN/m;
def
=0,25
(
)
mm
115
,
3
3115m
00
,
0
ins1
u
4
m
6
-
10
22,33
2
m
N
6
10
12000
384
4
4,18m
m
N
3
10
0,210
5
ins2
u
⇒
=
⇒
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
(
)
mm
89
,
3
fin
u
0,25
1
115
,
3
fin2
u
=
⇒
+
⋅
=
Ugięcie od obciążenia wiatrem pominięto (obciążenie śniegiem jest większe od ob-
ciążenia wiatrem).
Ugięcie finalne od obciążenia prostopadłego:
fin2
u
fin1
u
fin
u
+
=
16,85mm
fin
u
3,89mm
12,96mm
fin
u
=
⇒
+
=
Ostateczna wartość ugięcia dolnej części krokwi:
fin
net,
u
k
fin
u
ost
u
≤
⋅
=
9mm
6
,
17
050
,
1
16,85mm
ost
u
=
⋅
=
net, fin
= l/200 = 4180/200 = 20,9 mm> u
ost
= 17,69 mm.
11
Przemieszczenie końcowe.
12
Jeżeli warunek nie zostanie spełniony wówczas u
ins
=u
M
·[1+19,2·(h/l)
2
]
13
Przemieszczenie doraźne
14
To samo przyjąć w projekcie.
15
To samo przyjąć w projekcie.
16
Wartość graniczna ugięcia.
7
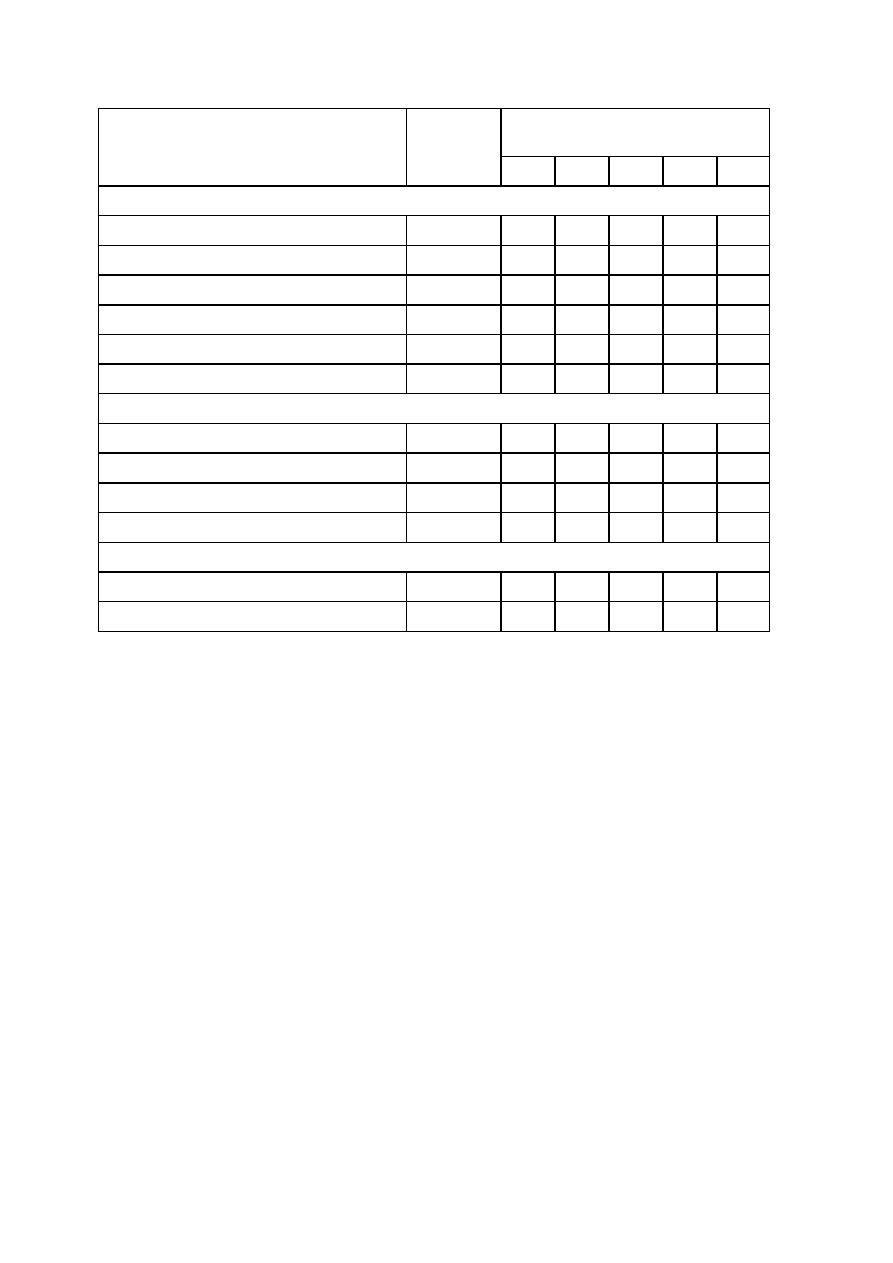
Klasy wytrzymałości – wartości charakterystyczne drewna litego
Klasy drewna konstrukcyjnego litego o
wilgotności 12 %
Rodzaje właściwości Oznaczenie
C18 C24 C30 C35 C40
Wytrzymałość, w N/mm
2
(MPa)
Zginanie
f
m,k
18 24 30 35 40
Rozciąganie wzdłuż włókien
f
t,0,k
11 14 18 21 24
Rozciąganie w poprzek włókien
f
t,90,k
0,3 0,4 0,4 0,4 0,4
Ściskanie wzdłuż włókien
f
c,0,k
18 21 23 25 26
Ściskanie w poprzek włókien
f
c,90,k
4,8 5,3 5,7 6,0 6,3
Ścinanie
f
v,k
2,0 2,5 3,0 3,4 3,8
Sprężystość, w kN/mm
2
(GPa)
Średni moduł sprężystości wzdłuż włókien
E
0,mean
9 11 12 13 14
5% kwantyl modułu sprężystości wzdłuż włókien
E
0,05
6,0 7,4 8,0 8,7 9,4
Średni moduł sprężystości w poprzek włókien
E
90,mean
0,30 0,37 0,40 0,43 0,47
Średni moduł odkształcenia postaciowego
G
mean
0,56 0,69 0,75 0,81 0,88
Gęstość, w kg/m
3
Wartość charakterystyczna
ρ
k
320 350 380 400 420
Wartość średnia
ρ
mean
380 420 460 480 500
Document Outline
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron