ILP + Równoleglosc poziomu watku

1/45

Krótka historia ILP cz.2

+ równoleglosc poziomu watku

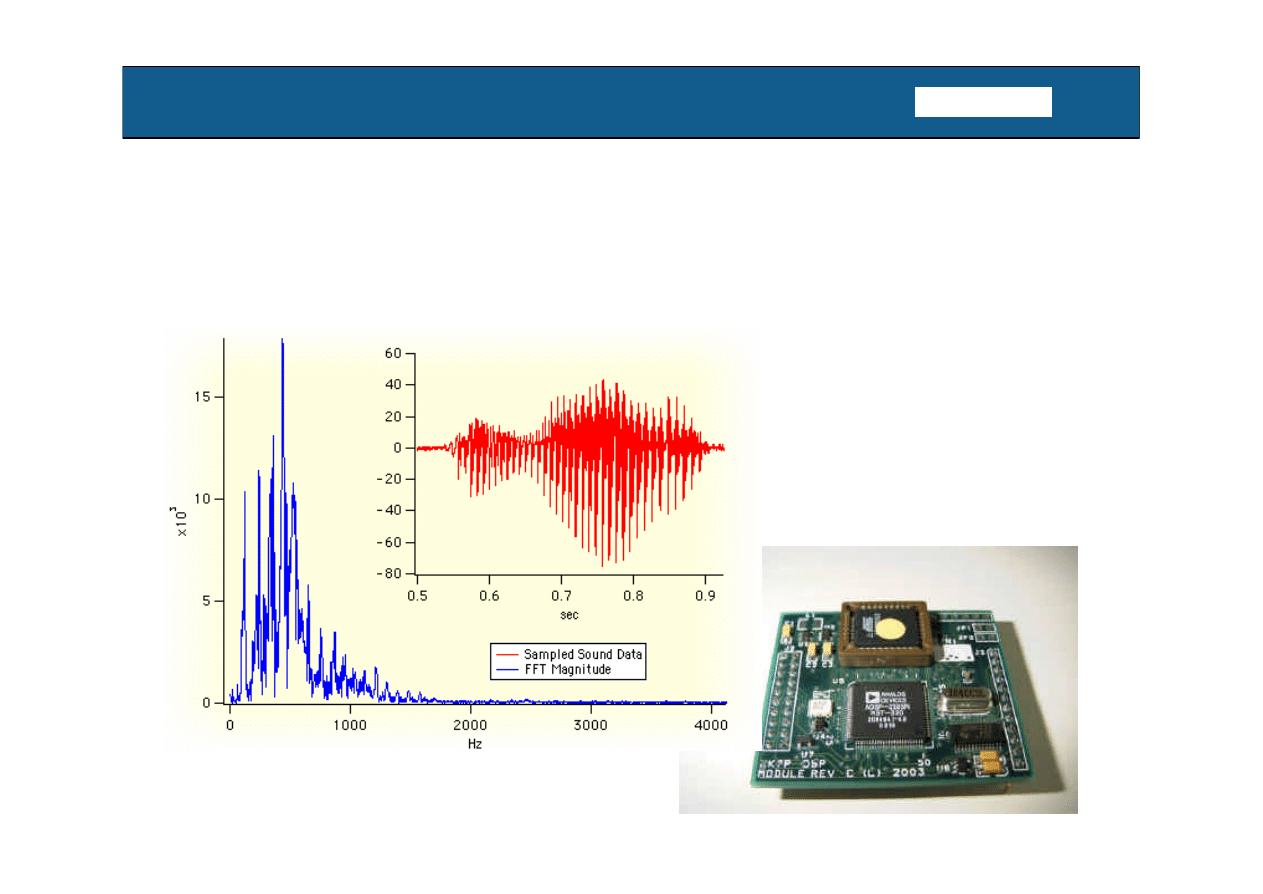
DSP – Digital Signal Processing

1. Wstep i algorytmy DSP

2/45

1

2

3

4

5

Atmel has created the first processor architected specifically for 21st century
applications. The AVR32 32-bit RISC processor core is designed to do
more processing per clock cycle so the same throughput can be ac hieved at a
lower clock frequency.

Most traditional processors were developed in the 1970's and 198 0's, before
the advent of MP3 players, digital video, GPS, voice recognition or, most
importantly, small footprint, batterypowered, hand-held products. The only
way for 20th century processors to meet 21st century performance
requirements is to turn up the clock rate. Unfortunately, turnin g up the
processor clock also increases power consumption and heat dissip ation.

Pomysl „prawie” nowy ;))

http://www.atmel.com/products/avr32/overview.asp

…

…

1. Wstep i algorytmy DSP

3/45

1

2

3

4

5

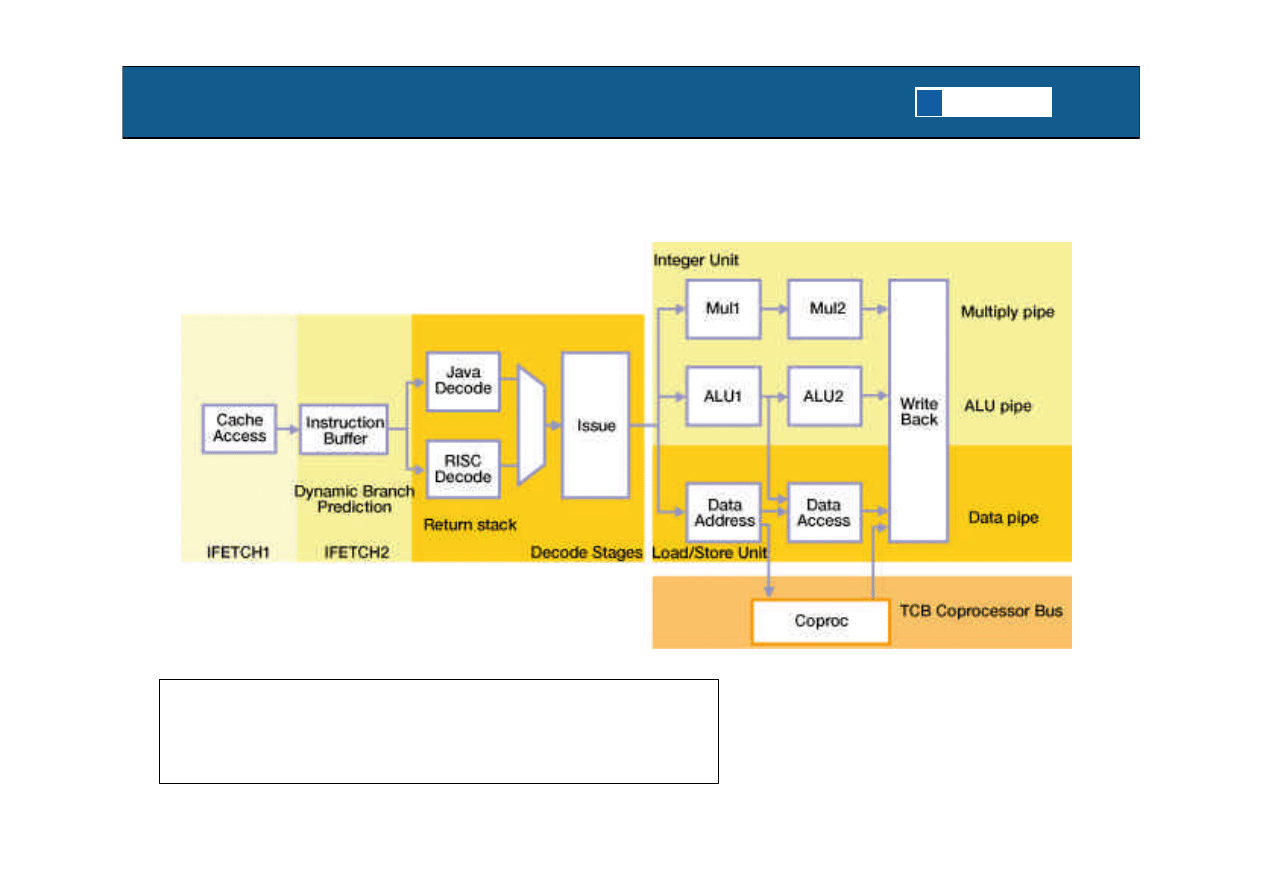
AVR32

Out of Order Execution

Single-Instruction Multiple Data (SIMD)

1. Wstep i algorytmy DSP

4/45

1

2

3

4

5

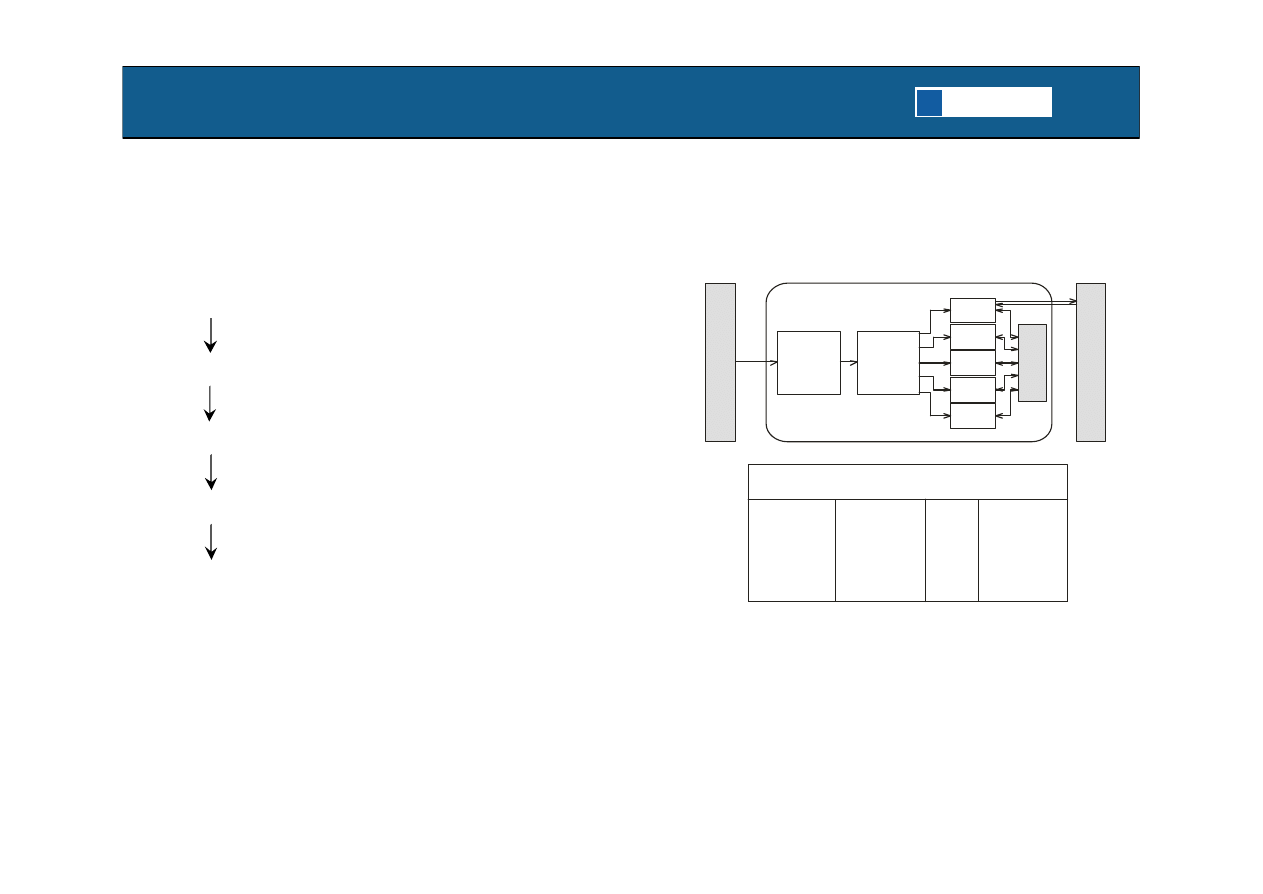
VLIW

1980 - Uniwersytet w Yale, prof. J. Fisher

MIKROKOD

Atom

Instrukcji

Operacja

dla FU-1

Atom

Instrukcji

Operacja

dla FU-2

Atom

Instrukcji

Operacja
dla FU-N

...

Molekul Instrukcji

FU-1

FU-2

FU-3

Jednostka

dekodujaca

instrukcje

Jednostka

pobierajaca

instrukcje

IDU

IFU

Pamiec programu

Pamiec danych

CPU

FU-4

FU-5

RF

blok rejestrów

1984 - Multiflow

1988 – Multiflow TRACE

1990 – UPADEK Multiflow

1. Wstep i algorytmy DSP

5/45

1

2

3

4

5

Daggerwrist

1. Wstep i algorytmy DSP

6/45

1

2

3

4

5

Digital Signal Processing

Sygnal

Przestrzenie sygnalów:

Przestrzen funkcyjna sygnalów o ograniczonej energii
Przestrzen funkcyjna sygnalów o ograniczonej mocy sr.
….

Metryczne przestrzenie sygnalów : Przestrzen Hilberta

( )

1

,

n

i i

i

x y

x y

=

=

∑

Iloczyn skalarny:

Korelacja:

Definicja 1: Dwa sygnaly x

1

i x

2

maja ten sam ksztalt, jezeli istnieja takie

liczby rzeczywiste a,b,c i d, ze dla kazdego t spelniona jest równosc:

( )

2

1

t

b

x

t

a x

d

c

−





= ⋅

+









a – skalowanie wartosci
b – przesuniecie w czasie
c – skalowanie w czasie
d – przesuniecie wartosci

1. Wstep i algorytmy DSP

7/45

1

2

3

4

5

(

)

(

) (

)

( ) ( )

1

2

12

1

2

1

2

1

1

1

,

,

,

n

i

x x

x x

x i x

i

x x

α

=

=

=

∑

:

Korelacja:

( )

2

1

t

b

x

t

a x

d

c

−





= ⋅

+









Wspólczynnik korelacyjny

Digital Signal Processing

a – skalowanie wartosci
b – przesuniecie w czasie
c – skalowanie w czasie
d – przesuniecie wartosci

( )

1

,

n

i i

i

x y

x y

=

=

∑

Uogólniona transformata Fouriera: Baza sygnalów ortogonalnych + zupelna

Funkcje harmoniczne rzeczywiste
(trygotnometryczny szereg Fouriera)

Funkcje harmoniczne zespolone
(zespolony szereg Fouriera)

Wielomiany Lagendre’a

Wielomiany Czebyszewa

Funkcje Haara + falki

Funkcje Walsha + rozpraszanie widma

1

2

2

2

2

,

cos

,

sin

,...

1,2,....

n

t

n

t

n

T

T

T

T

T

π

π

















=





























2

1

:

0, 1,....

j n

t

T

e

n

T

π

⋅









= ±













( )

2

1

2

2

2 !

1

1

1

:

1,2,....

(2 )!

n

n

n

n

n

d

t

t

n

n

dt

−









−

−

−

=













( )

2

2

1

1

1

:

1,2,....

2

2

!

n

n

n

n

n

d

t

n

n dt





+





−

=













1. Wstep i algorytmy DSP

8/45

1

2

3

4

5

( )

1

,

n

i i

i

x y

x y

=

=

∑

Digital Signal Processing

Suma wazona (iloczyn i suma wykonywane jednoczesnie)

Korelacja:

Splot:

Filtracja liniowa FIR:

Filtracja liniowa IIR:

Filtry adaptacyjne:

DCT:

( )

( ) (

)

k

y n

a k

x n

k

∞

=−∞

=

⋅

+

∑

( )

( ) (

)

k

y n

x k

h n

k

∞

=−∞

=

⋅

−

∑

( )

(

)

1

0

M

k

k

y n

b

x n

k

−

=

=

⋅

−

∑

( )

(

)

(

)

1

1

1

N

M

k

k

k

k

y n

a

y n

k

b

x n

k

−

=

=

= −

⋅

− +

⋅

−

∑

∑

( ) (

)

( ) ( )

1

h n

h n

e n U n

µ

=

− + ⋅

⋅

( ) ( )

(

) ( )

1

T

e n

d n

H

n

U n

=

−

− ⋅

( ) ( )

( )

(

)

1

0

2

1

cos

,

0,1,...,

1

2

N

k

n

k

X n

e k

x n

k

N

N

π

−

=





+

=

⋅

=

−









∑

1. Wstep i algorytmy DSP

9/45

1

2

3

4

5

Digital Signal Processing

DWT:

(

)

( )

( )

1

min

, ,

1,2,...,

j

i

ij

i

x

n

x n

a

n

i j

N





+ =

+

=





Inne operacje

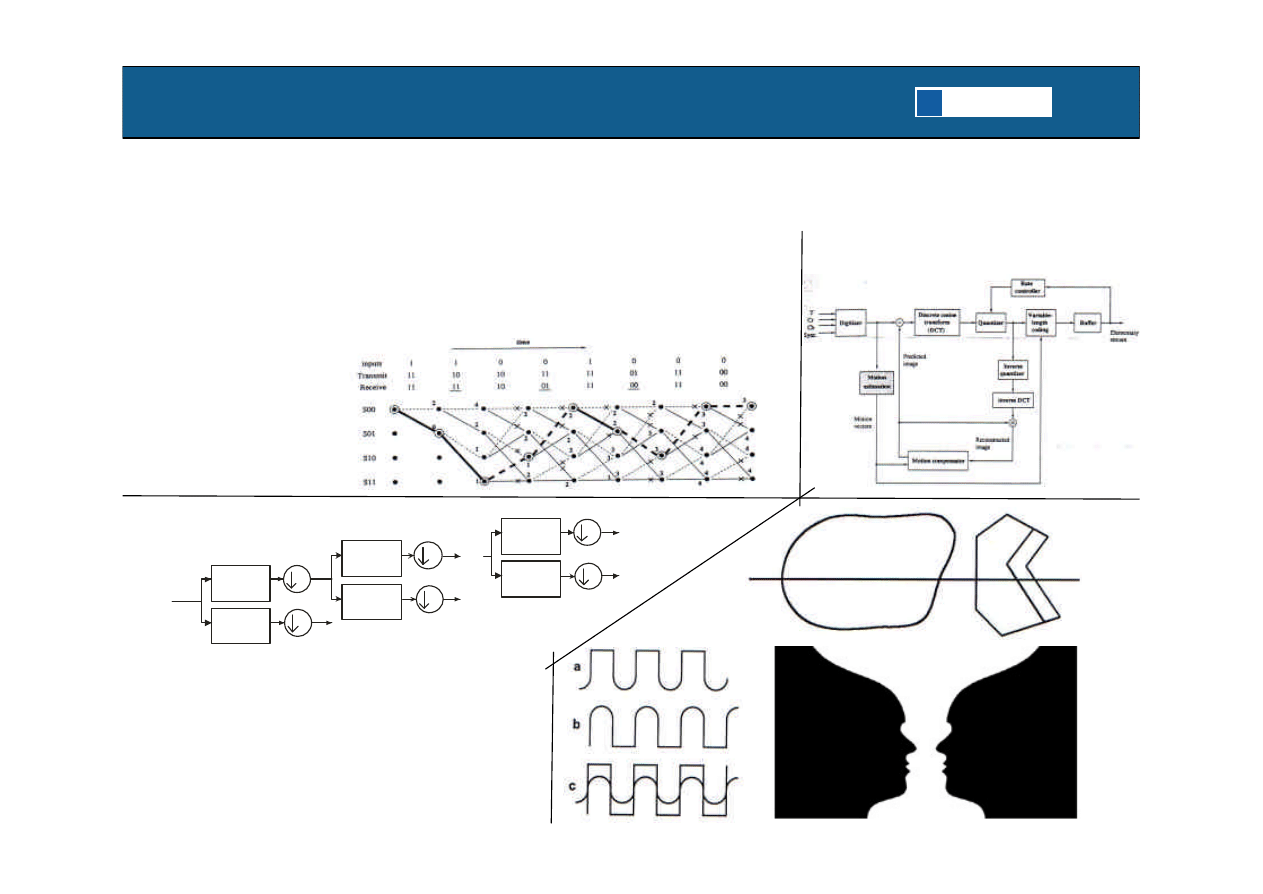
Algorytm Viterbiego :

Filtr

dolno-

przepustowy

Filtr

górno-

przepustowy

2

2

2

2

Wejscie

X

Wyjscie J

Wyjscie J-1

...

Filtr

dolno-

przepustowy

Filtr

górno-

przepustowy

2

2

Wyjscie 1

Filtr

dolno-

przepustowy

Filtr

górno-

przepustowy

Wyjscie 0

MPEG-2:

1. Wstep i algorytmy DSP

10/45

1

2

3

4

5

Digital Signal Processing

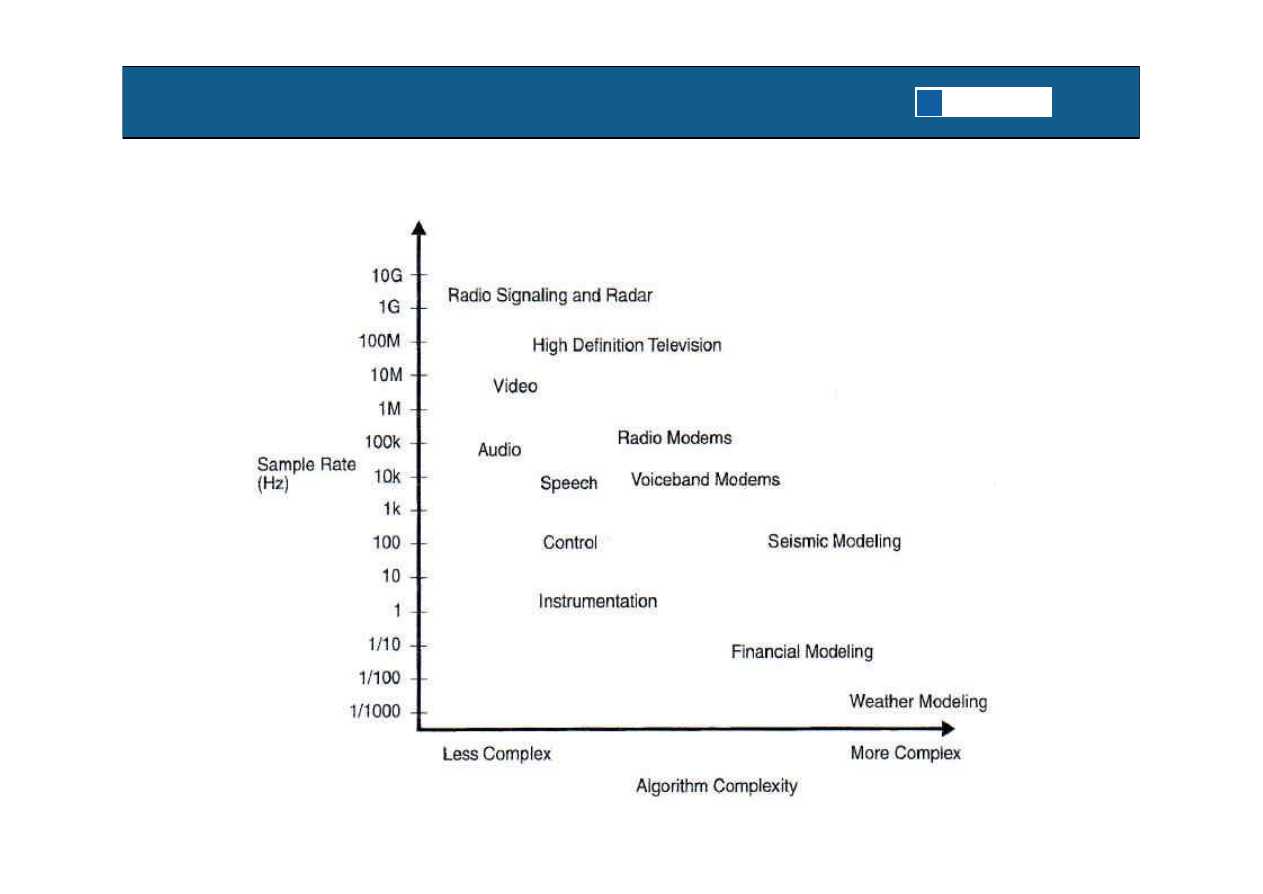
P. Lapsley, J. Bier, A. Shoham, DSP Processor Fundamentals,

Architectures and Features, IEEE Press 1997

2. Dataflow processor

11/45

1

2

3

4

5

2. Dataflow processor

12/45

1

2

3

4

5

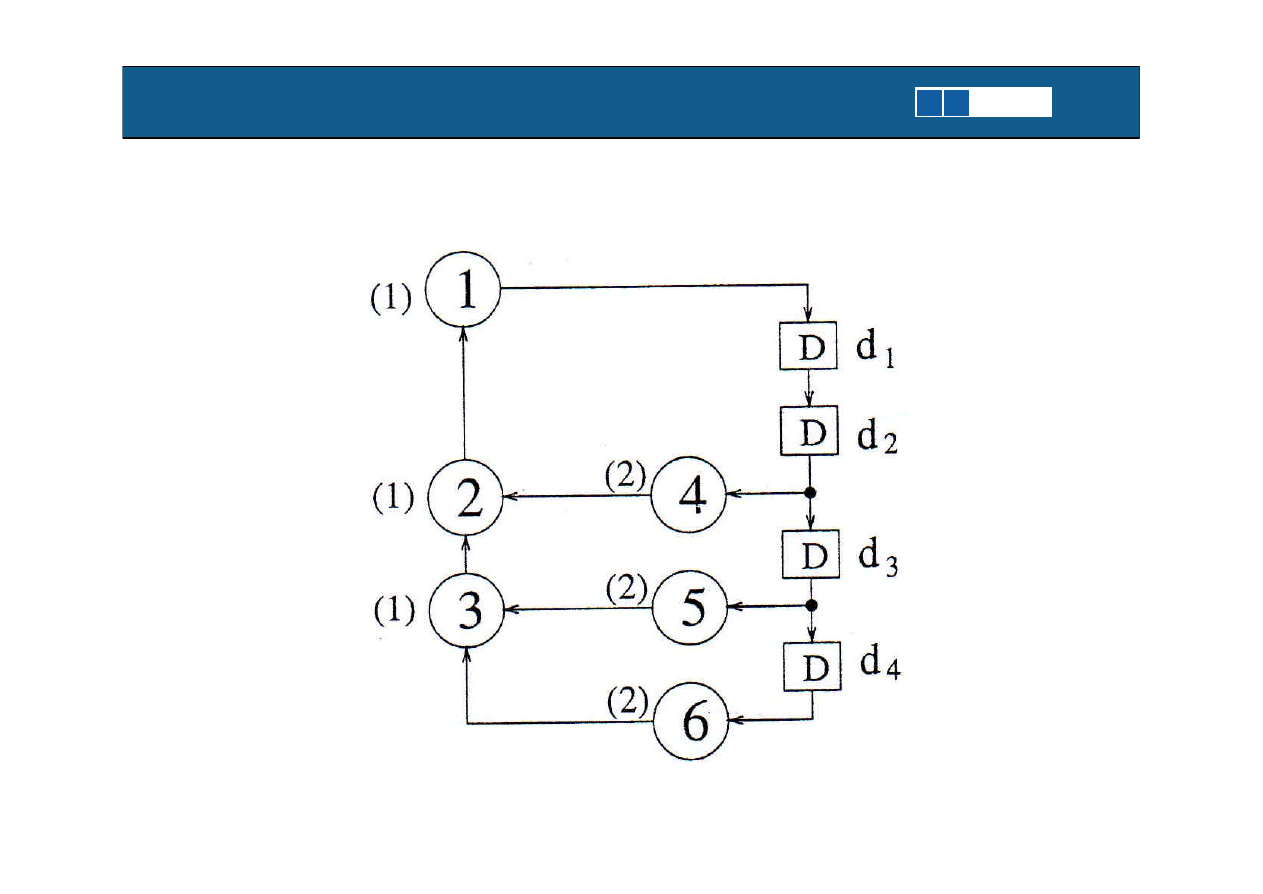
Data Flow Graph

2. Dataflow processor

13/45

1

2

3

4

5

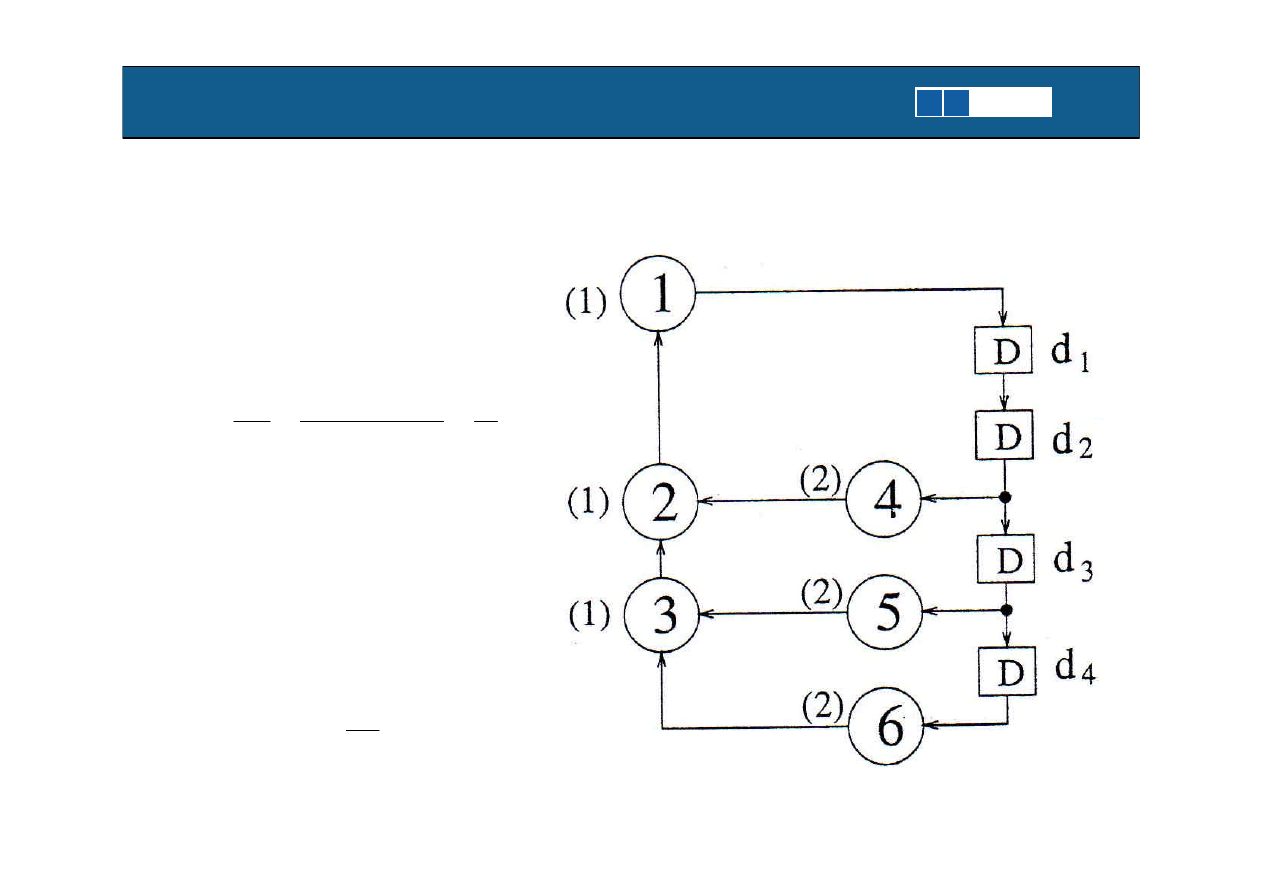
Iteration Bound – ograniczenie DSP

Prawo Amdahla:

max

l

l L

l

t

T

w

∞

∈

 

=

 

 

Iteration Bound:

Pipeline

(

)

1

1

1

T

T

T

α

α

∞

=

+ −

(

)

1

1

1

1

T

N

S

T

N

α α

∞

∞

=

=

=

+

−

2. Dataflow processor

14/45

1

2

3

4

5

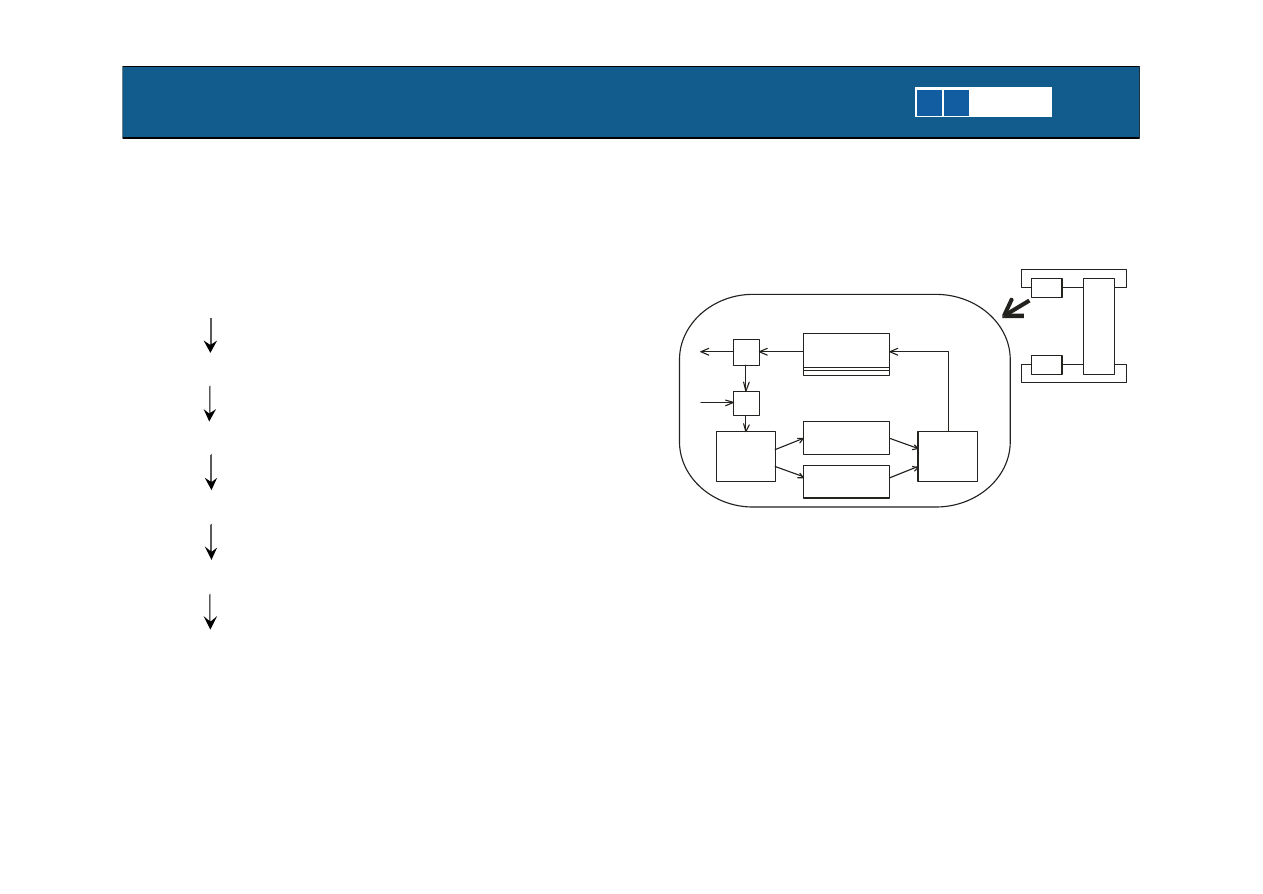
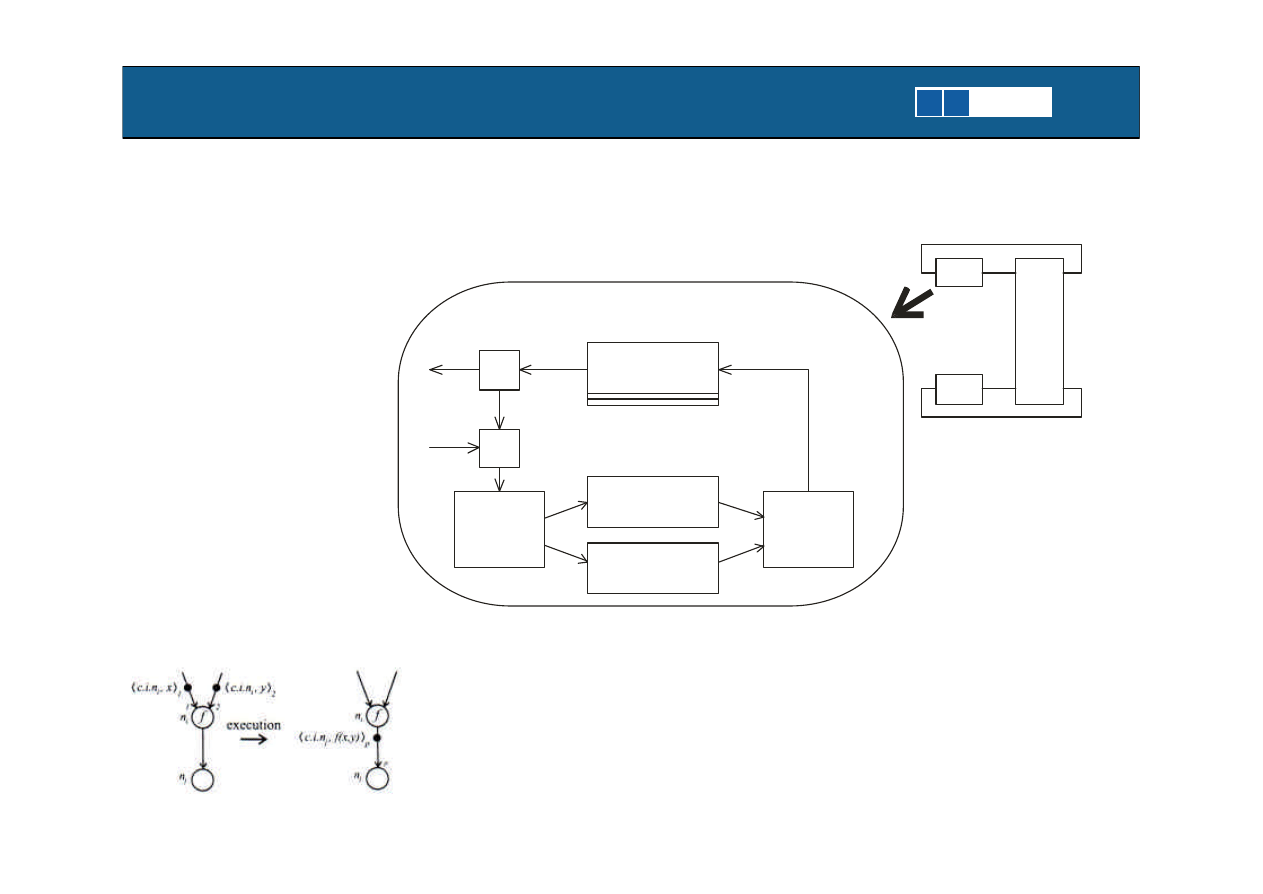
Dataflow Processor

1975 – Dennis, Dataflow Computing

DFG

1980 – MIT Static Dataflow Machine

1981 – Arvind I-structure

1981 – Manchester Dataflow Machine (MDM)

1990 – MIT Monsoon

PE

PE

CN

siec komunikacyjna

SU

RU

UU

Jednostka
uaktualniania

IQ

AS

Kolejka instrukcji

Pamiec aktywnych
operacji

IFU

Jednostka
pobierajaca
instrukcje

OUs

Jednostki
przetwarzajace

CN

do/od

lokalna
komunikacja

PE

Jednostka przetwarzajaca

...

Motto: Instrukcja jest aktywna gdy wszystkie
argumenty do jej wykonania sa dostepne

2. Dataflow processor

15/45

1

2

3

4

5

Static Dataflow Processor

PE

PE

CN

siec komunikacyjna

SU

RU

UU

Jednostka
uaktualniania

IQ

AS

Kolejka instrukcji

Pamiec aktywnych
operacji

IFU

Jednostka
pobierajaca
instrukcje

OUs

Jednostki
przetwarzajace

CN

do/od

lokalna
komunikacja

PE

Jednostka przetwarzajaca

...

Motto: Instrukcja jest aktywna gdy wszystkie
argumenty do jej wykonania sa dostepne
Cecha specyficzna: tylko jeden token na krawedzi
grafu

3. VLIW i procesory DSP

16/45

1

2

3

4

5

Planeta Darwin

Eosapien

Groveback

Daggerwrist

Butcher tree

Crawler

3. VLIW i procesory DSP

17/45

1

2

3

4

5

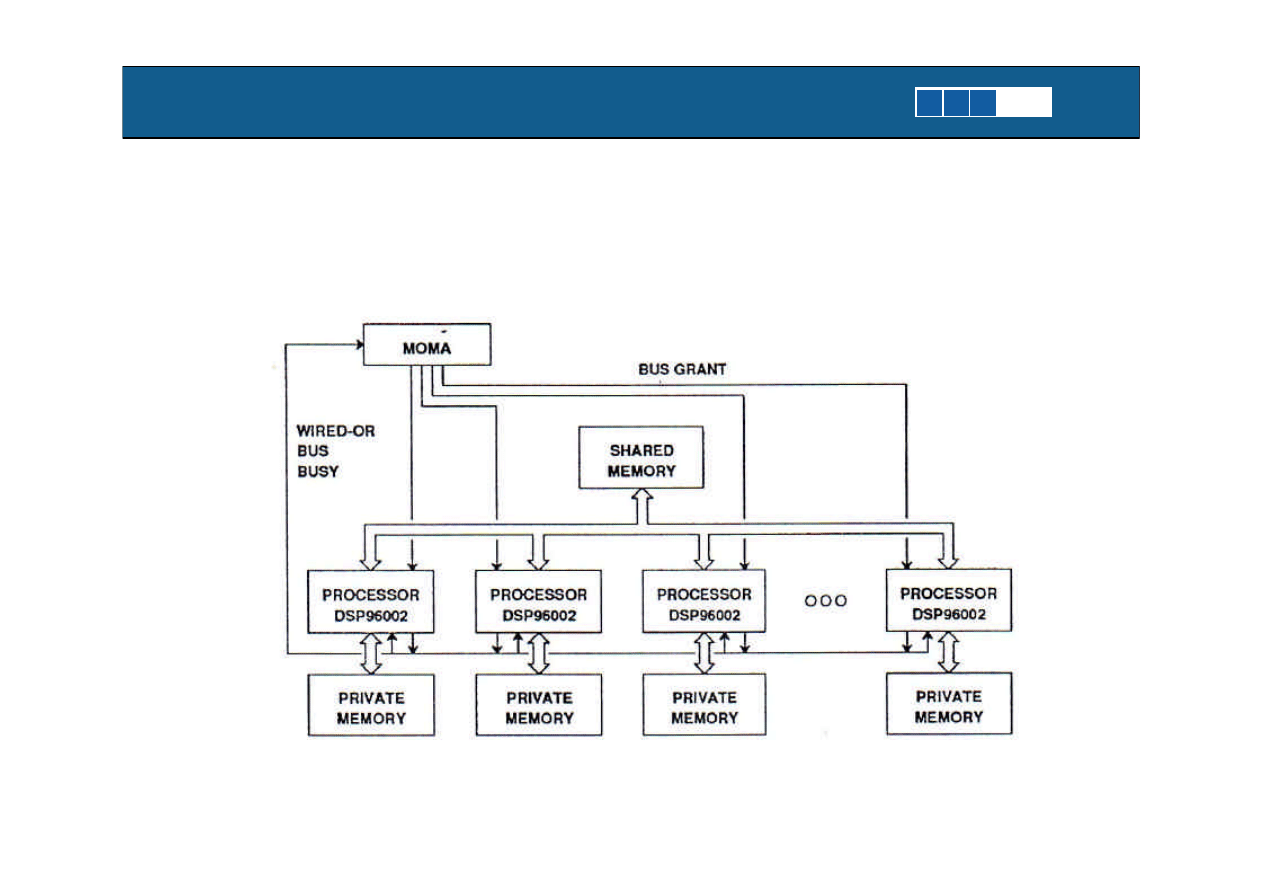
E.A. Lee, J. Bier, Architectures for

Statically Scheduled Dataflow

3. VLIW i procesory DSP

18/45

1

2

3

4

5

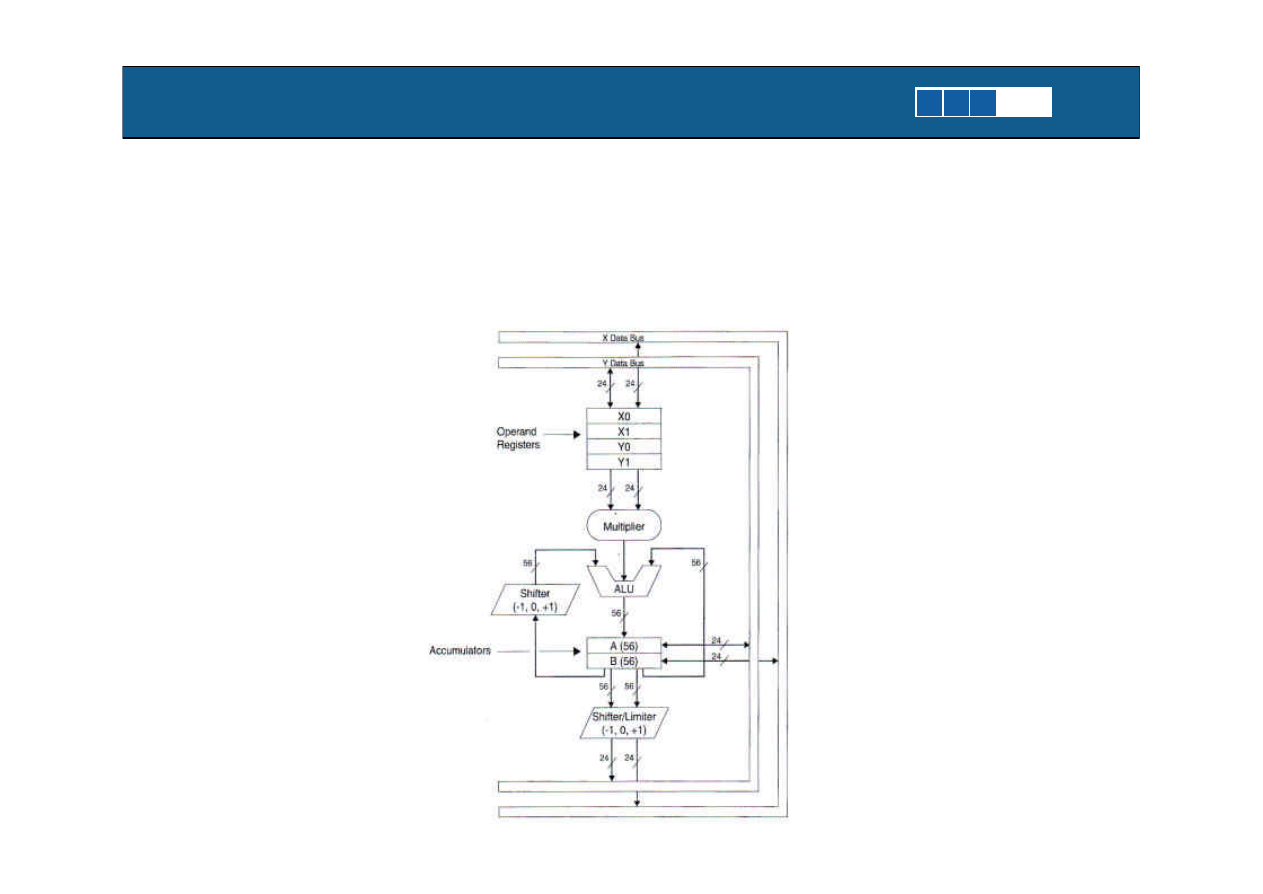
P. Lapsley, J. Bier, A. Shoham,

DSP Processor Fundamentals, Architectures

and Features, IEEE Press 1997

3. VLIW i procesory DSP

19/45

1

2

3

4

5

1) Statyczna struktura
2) Duza liczba operacji wymagajacych mnozenia i

akumulacji

3) Operacja mnozenia i akumulacji dwu-

argumentowa (potrzeba dwóch szyn danych)

4) Algorytmy najczesciej opisywane jako operacje

na wektorach lub macierzach

5) Relatywnie mala liczba skoków warunkowych

Cechy algorytmów DSP lat 90-tych

3. VLIW i procesory DSP

20/45

1

2

3

4

5

1) Instrukcja mnozenia i akumulacji w

jednym cyklu

2) Barrel-shifter
3) Dwie albo wiecej szyn danych (nie jedna)

Cechy procesorów DSP

VLIW

3. VLIW i procesory DSP

21/45

1

2

3

4

5

Przeglad procesorów DSP

Analog Devices

1) ADSP-21xx – niskomocowe procesory DSP
2) Blackfin – procesory do obróbki audio i wideo
3) SHARC – procesory zmiennopozycyjne
4) TigerSHARC – wysoka wydajnosc, wieloprocesory

3. VLIW i procesory DSP

22/45

1

2

3

4

5

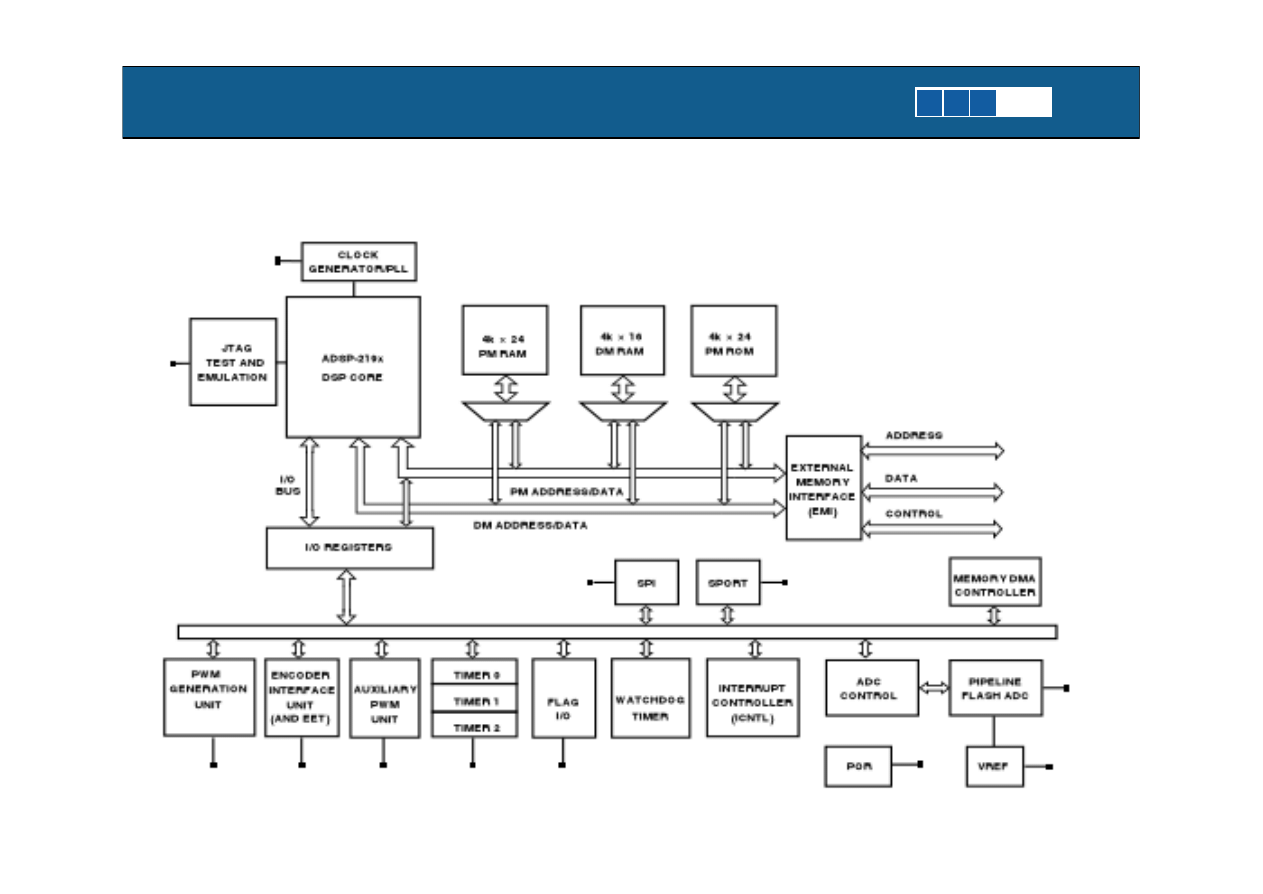
Przyklad: ADSP-21990

3. VLIW i procesory DSP

23/45

1

2

3

4

5

Staly przecinek

8 4 2 1 1/2 1/4 1/8 1/16

0 0 0 0 0 0 1 0

0,125

1,5

8 4 2 1 1/2 1/4 1/8 1/16

0 0 0 1 1 0 0 0

8,25

8 4 2 1 1/2 1/4 1/8 1/16

1 0 0 0 0 1 0 0

64 32 16 8 4 2 1 1/2

1 1 0 0 1 0 0 1

100.5

3. VLIW i procesory DSP

24/45

1

2

3

4

5

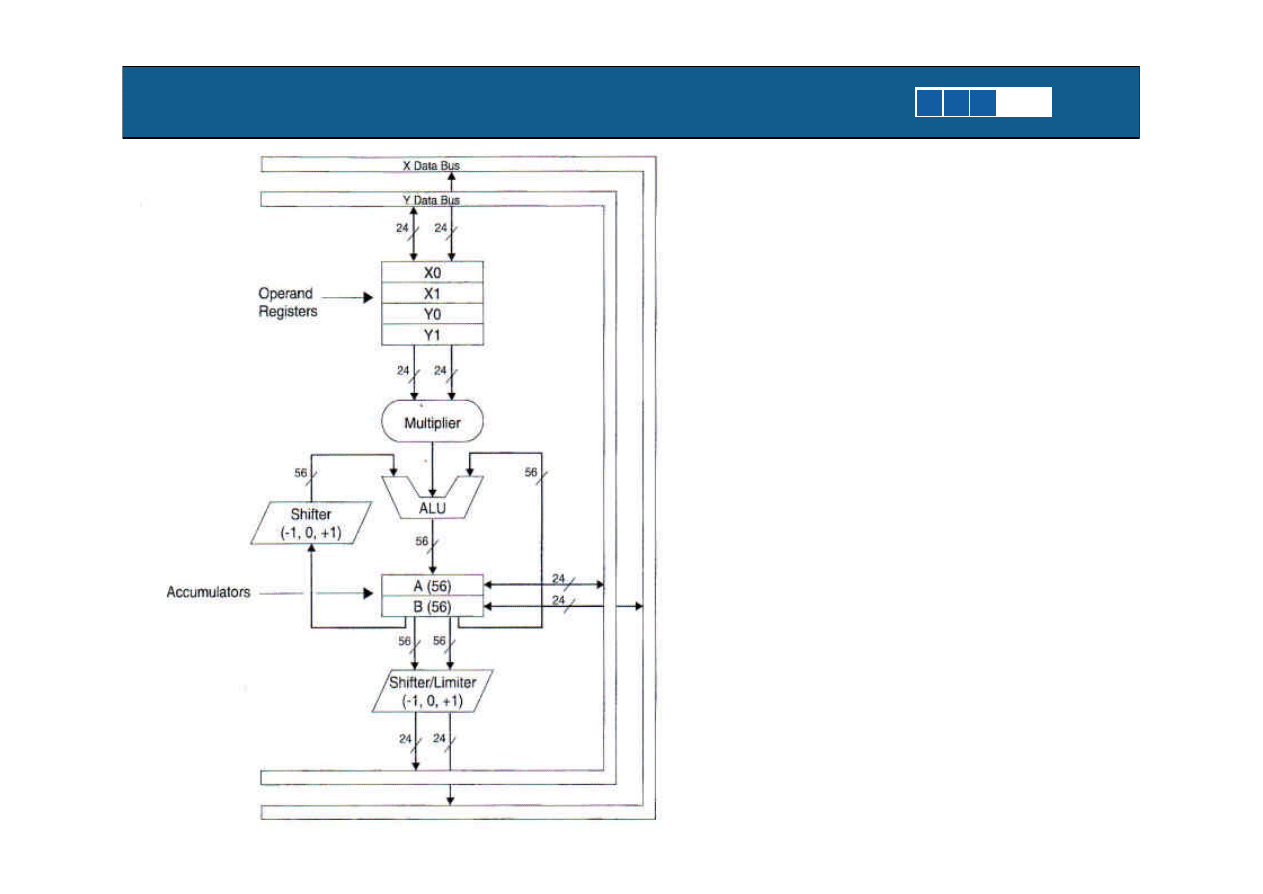
Sciezka danych dla

procesora stalo-

pozycyjnego

3. VLIW i procesory DSP

25/45

1

2

3

4

5

arrowtongue

Littoralope

3. VLIW i procesory DSP

26/45

1

2

3

4

5

Format zmiennopozycyjny - koncepcja

E

x

M B

=

⋅

M – mantysa

E – wykladnik

1 1/2 1/4 1/8

2 1

Mantysa

Wykladnik

0,125

1,5

8,25

1

0

0

0

1

1

0

0

1

1

0

0

0

0

0

1

0

0

1

0

1

0

1

0

x

3. VLIW i procesory DSP

27/45

1

2

3

4

5

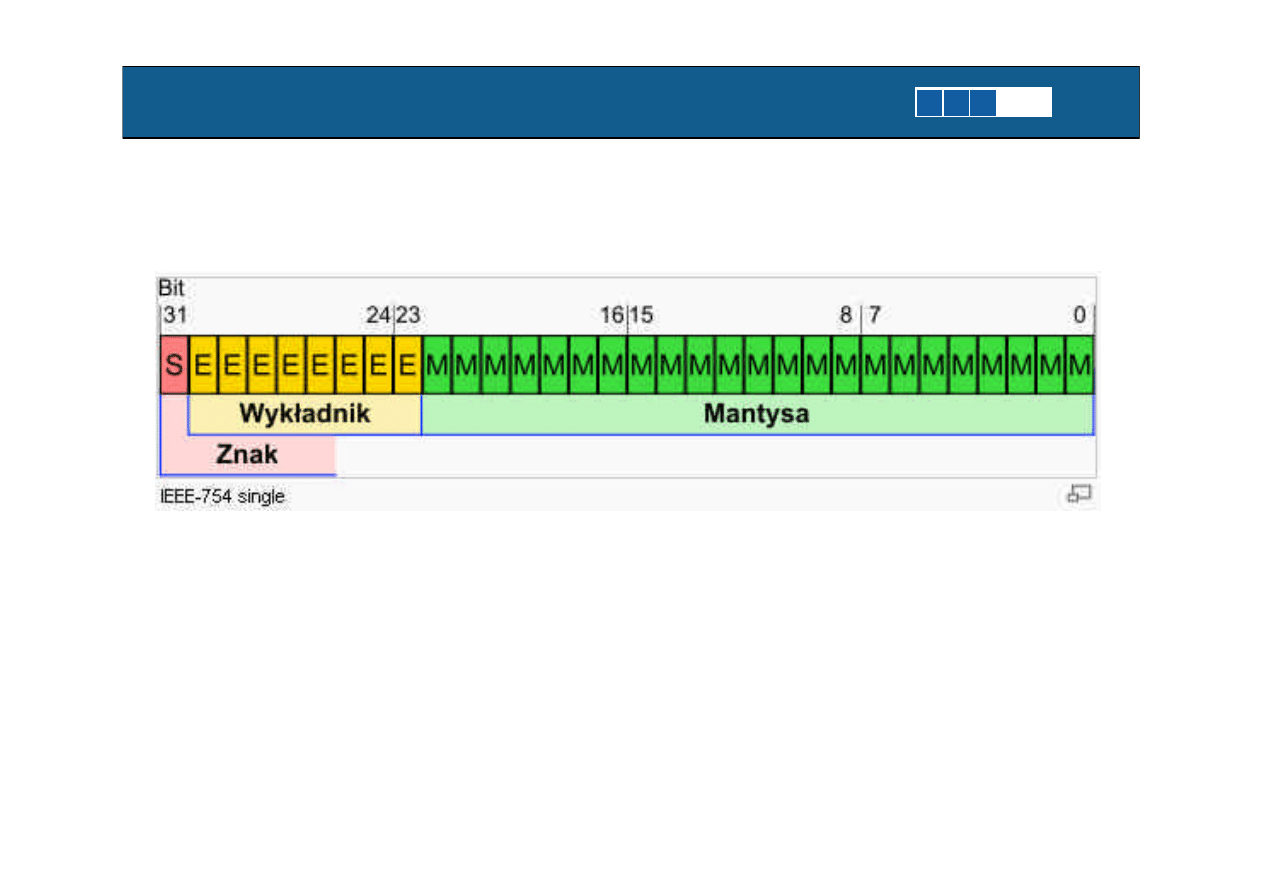
Formaty zapisu liczb zmiennopozycyjnych

( )

1

S

E

x

M B

= −

⋅ ⋅

S – znak liczby

M – mantysa

E – wykladnik

Wikipedia – liczby zmiennopozycyjne

3. VLIW i procesory DSP

28/45

1

2

3

4

5

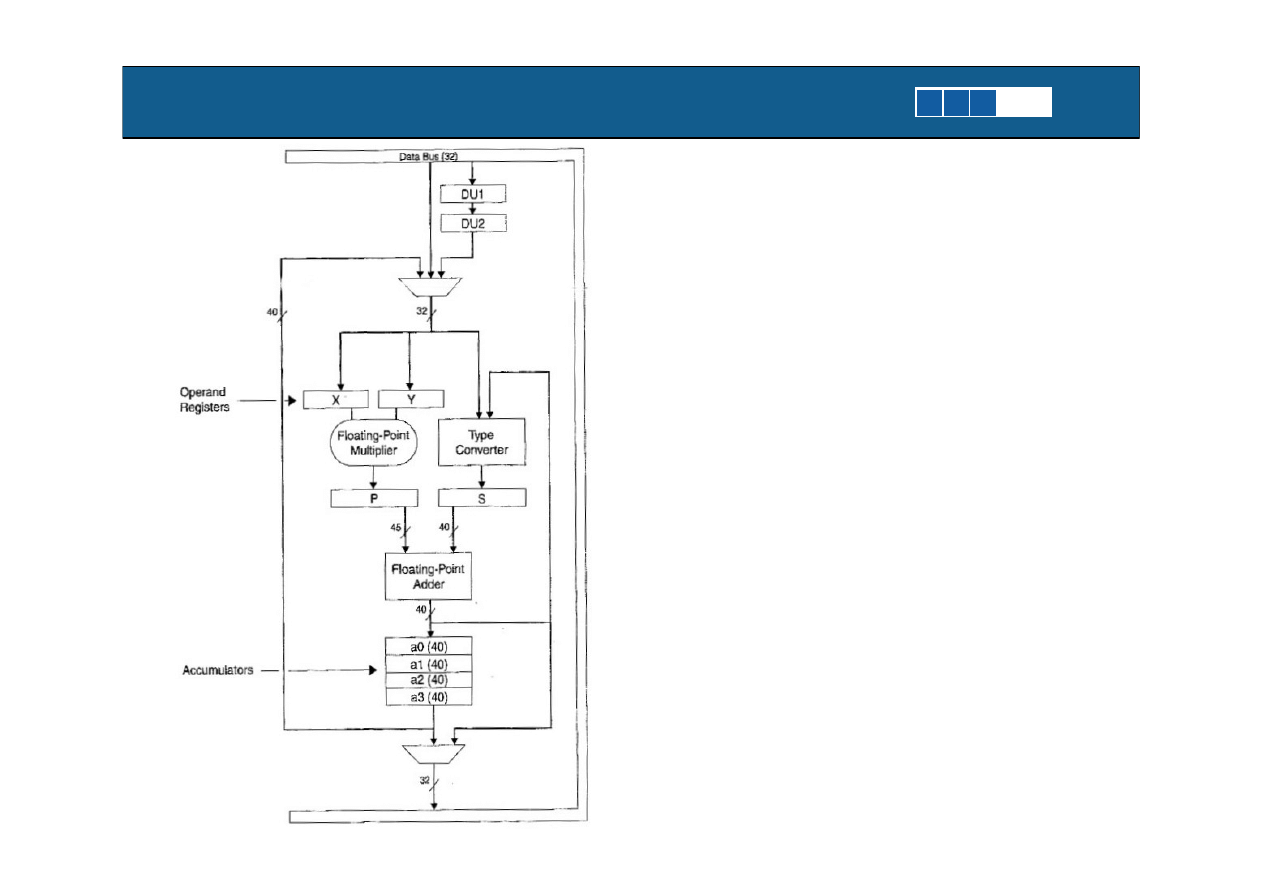
Sciezka danych dla

procesora zmienno-

pozycyjnego

3. VLIW i procesory DSP

29/45

1

2

3

4

5

Groveback

3. VLIW i procesory DSP

30/45

1

2

3

4

5

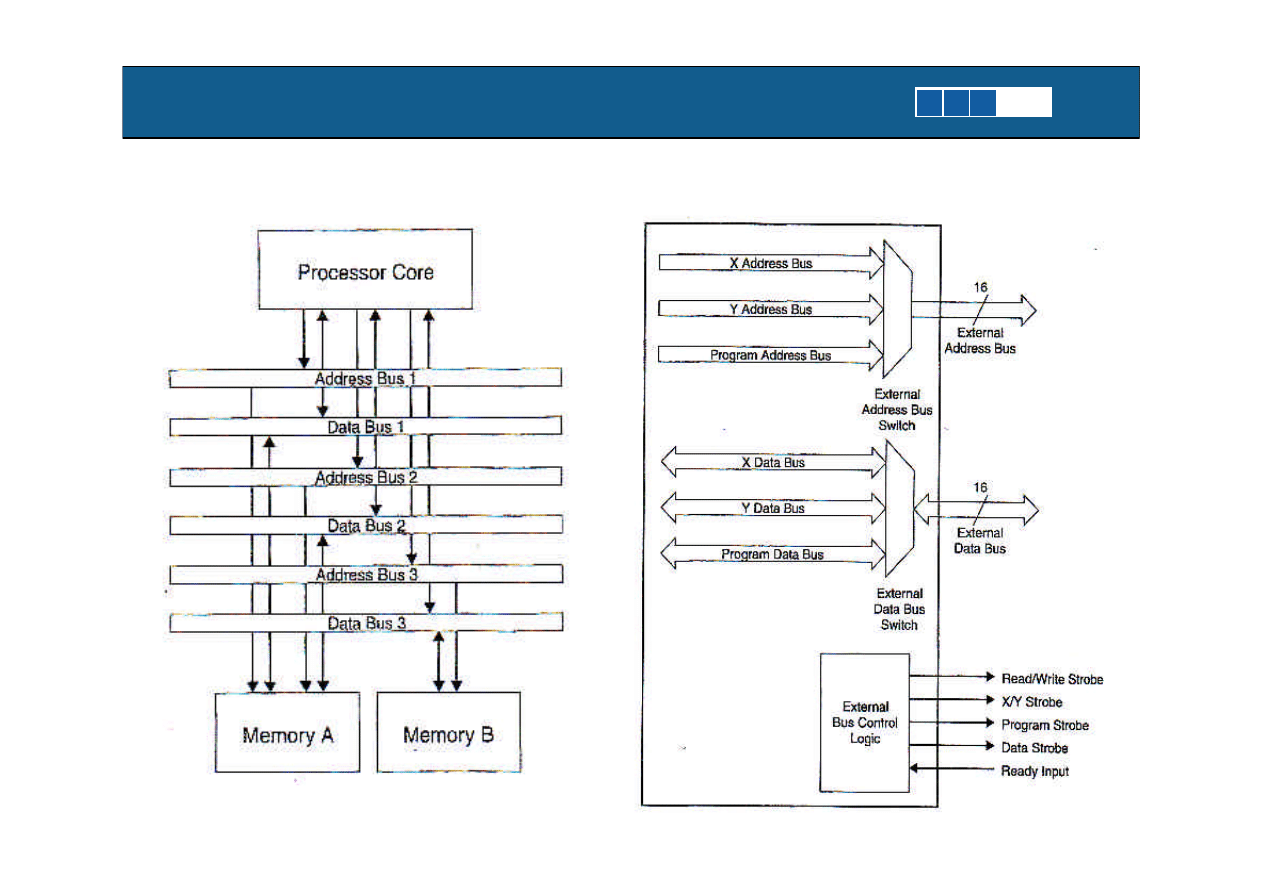
Specyficzne architektury pamieci procesorów DSP

3. VLIW i procesory DSP

31/45

1

2

3

4

5

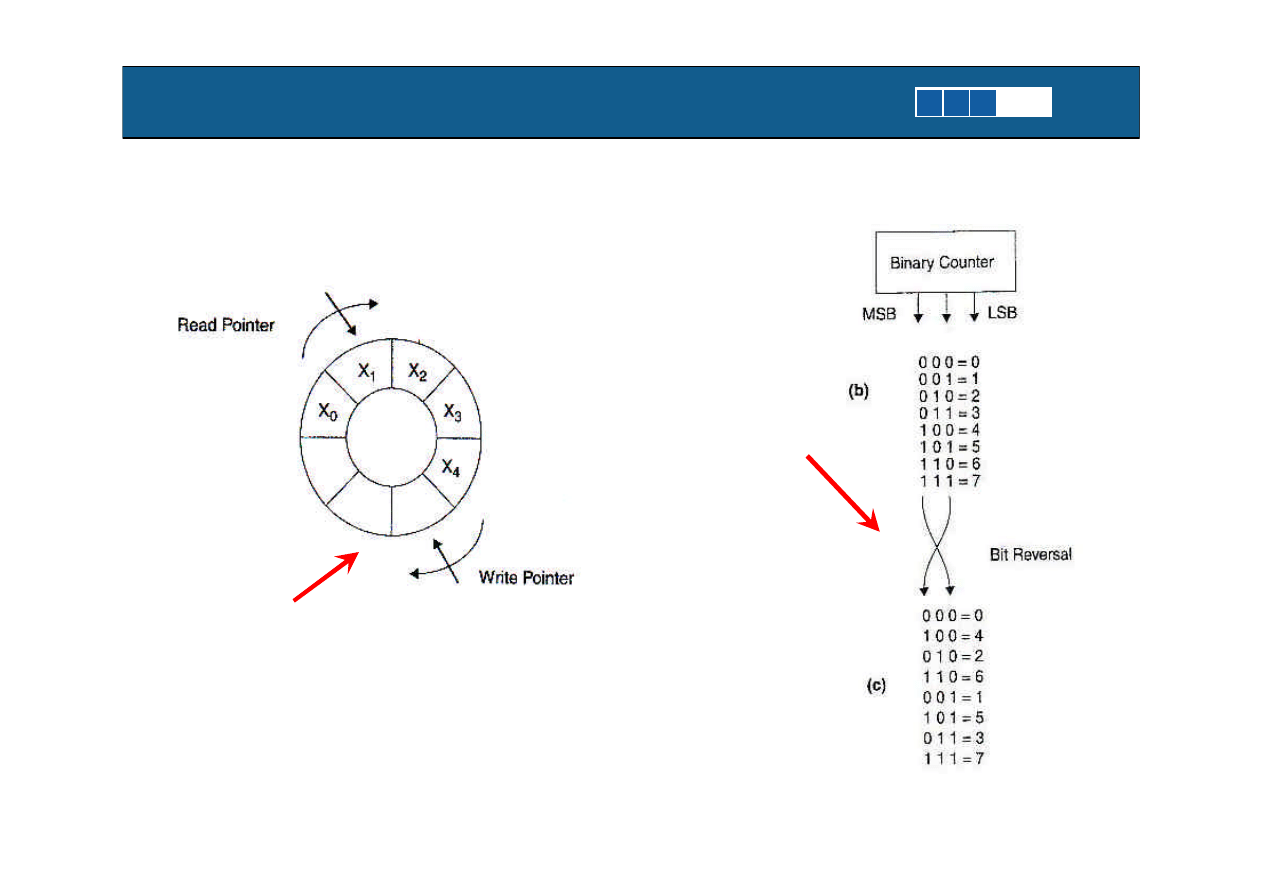
Specyficzne tryby adresowania procesorów DSP

Adresowanie Modulo

Adresowanie z

odwróceniem bitowym

(bit reversal)

32/45

1

2

3

4

5

4. VLIW i procesory DSP - przyklady

Przeglad procesorów DSP

Texas Instruments

1) C2000 – wysokowydajne 32-bitowe kontrolery
2) C5000 – energoszczedne procesory
3) C6000 – wysokowydajne procesory DSP
4) C6700 – TMS320C67xx – zmiennopozycyjne DSP
5) DaVinchi Media Processors - TMS320DM646x itp..

33/45

1

2

3

4

5

4. VLIW i procesory DSP - przyklady

Przeglad procesorów DSP

Freescale

1) DSP563XX – szeroka rodzina w oparciu o core

DSP56300

2) 56800/E – Kontrolery DSP (DSC = Digital Signal

Controller)

3) StarCore – multiprocesor – „system-on-chip” ;)

5. Równoleglosc poziomu watku

34/45

1

2

3

4

5

Eosapien

5. Równoleglosc poziomu watku

35/45

1

2

3

4

5

Wieloprogramowanie i wieloprzetwarzanie

5. Równoleglosc poziomu watku

36/45

1

2

3

4

5

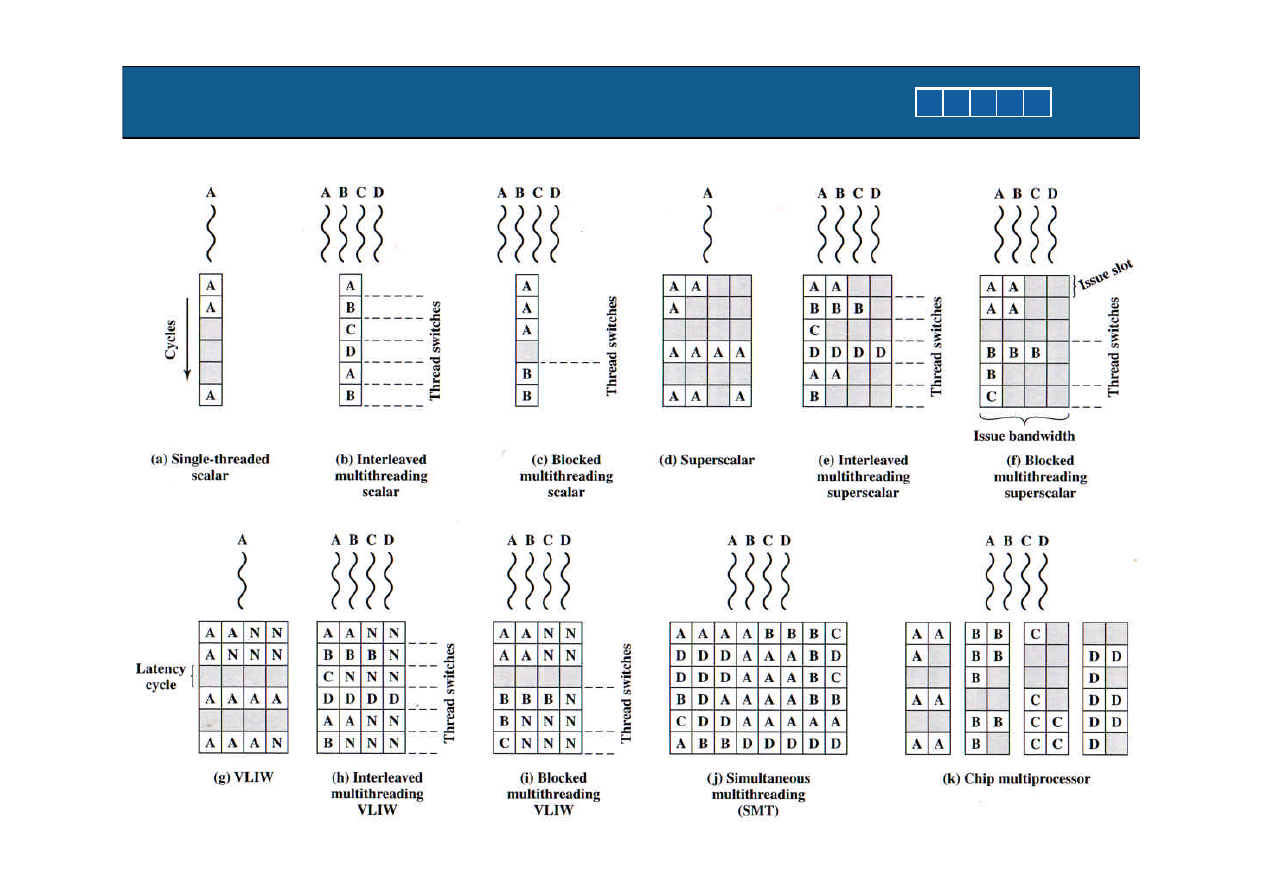
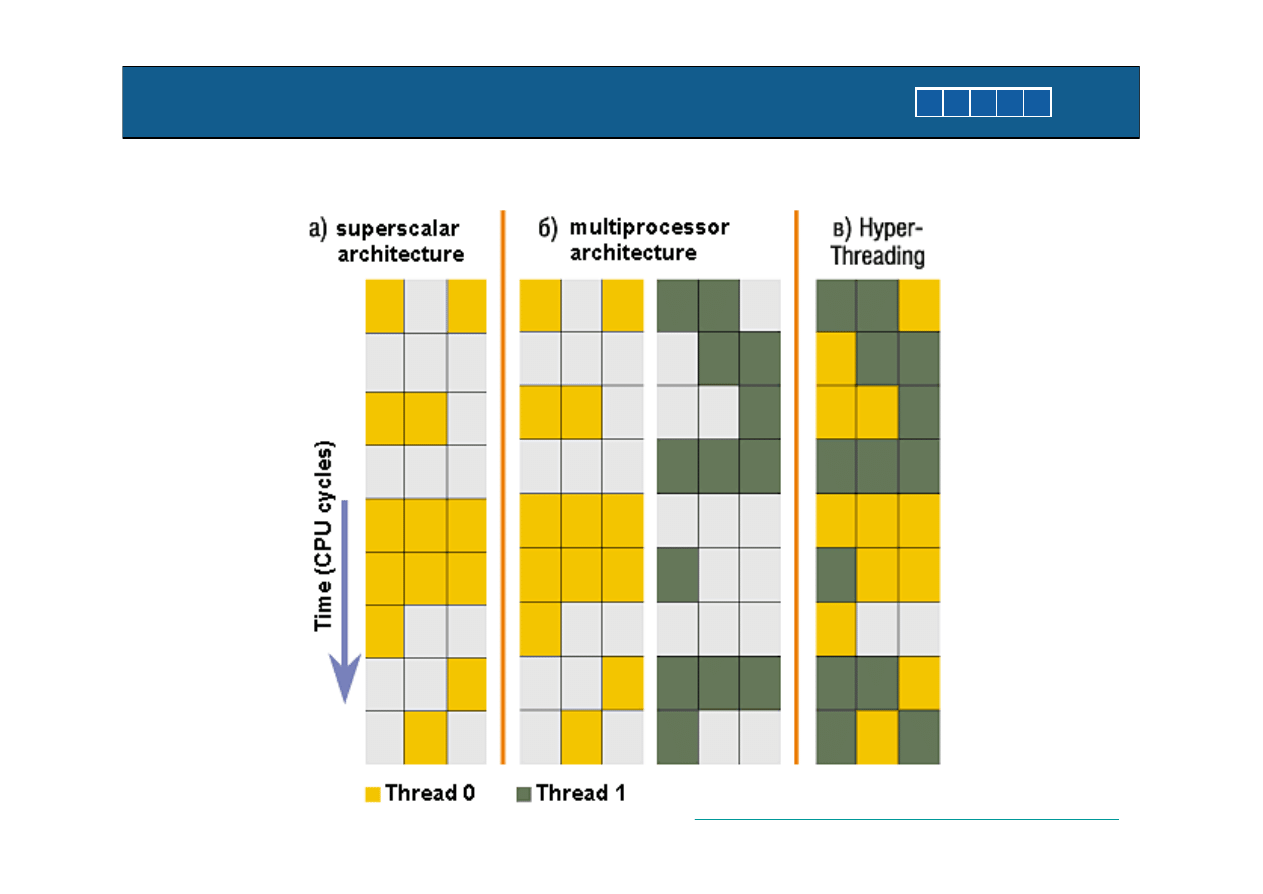
Wielowatkowosc – rodzaje i wsparcie sprzetowe

Interleaved multithreading

Blocked multithreading

Simultaneous multithreading (SMT)

Chip multiprocessing

5. Równoleglosc poziomu watku

37/45

1

2

3

4

5

Wielowatkowosc – rodzaje i wsparcie sprzetowe str.2

5. Równoleglosc poziomu watku

38/45

1

2

3

4

5

Hyperthreading

ixbtlabs.com/articles/pentium4xeonhyperthreading/

5. Równoleglosc poziomu watku

39/45

1

2

3

4

5

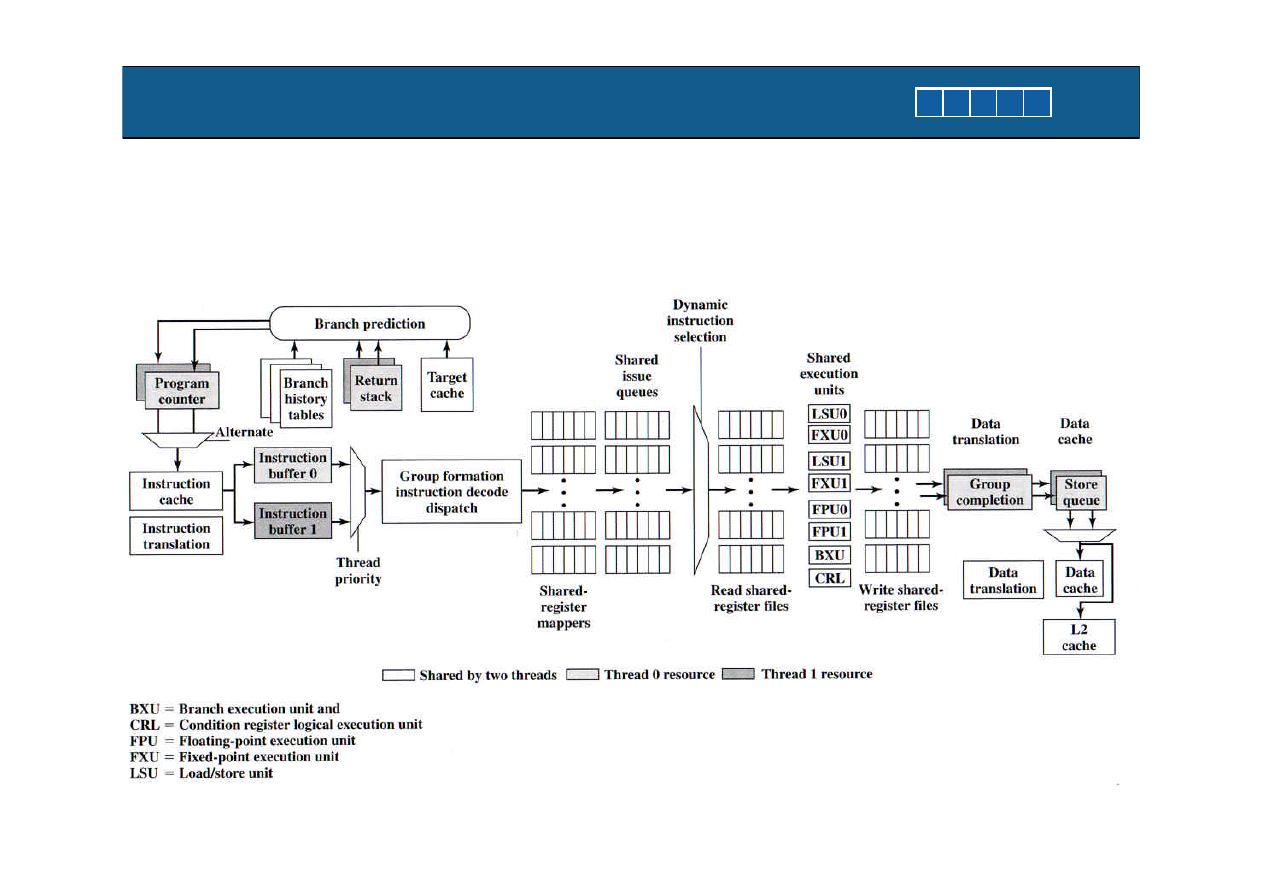
Pentium 4 hyperthreading i IBM Power5

Pentium 4 – hyperthreading = SMT z

dwoma watkami.

IBM Power5 – SMT + multiprocessing

5. Równoleglosc poziomu watku

40/45

1

2

3

4

5

Przyklad IBM Power5

5. Równoleglosc poziomu watku

41/45

1

2

3

4

5

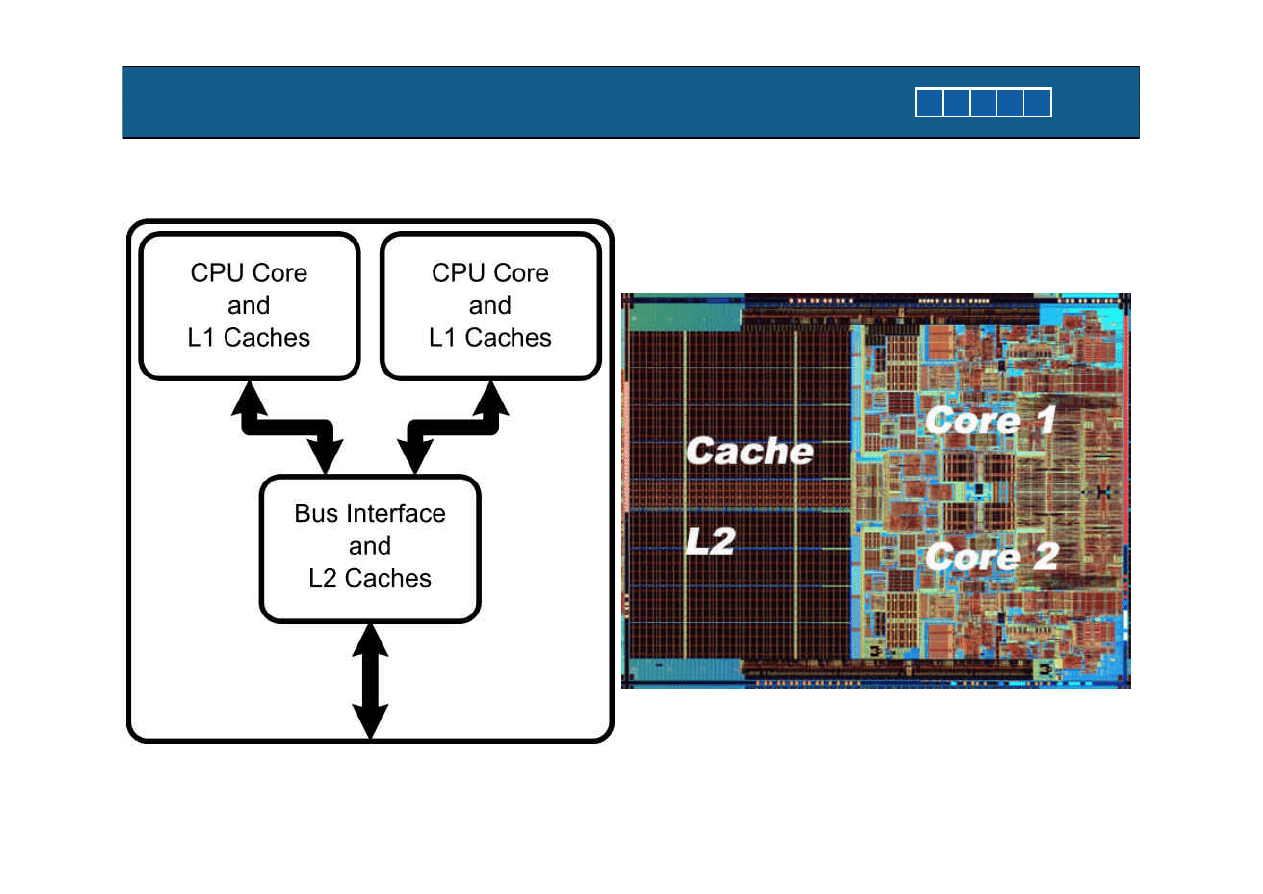
Dual - core

5. Równoleglosc poziomu watku

42/45

1

2

3

4

5

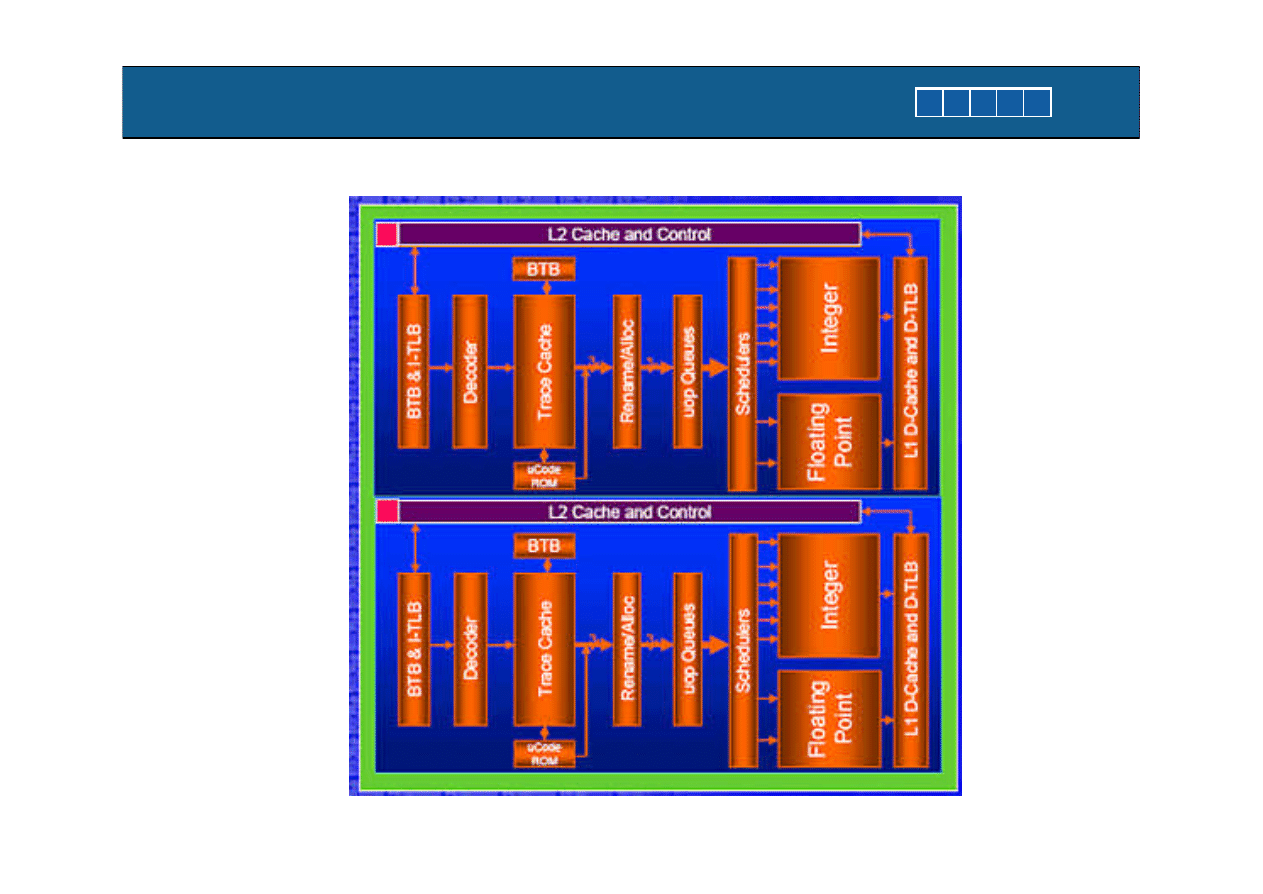
Dual - core

http://hothardware.com/Articles/Intel-Pentium-Extreme -Edition-840-Preview1/

5. Równoleglosc poziomu watku

43/45

1

2

3

4

5

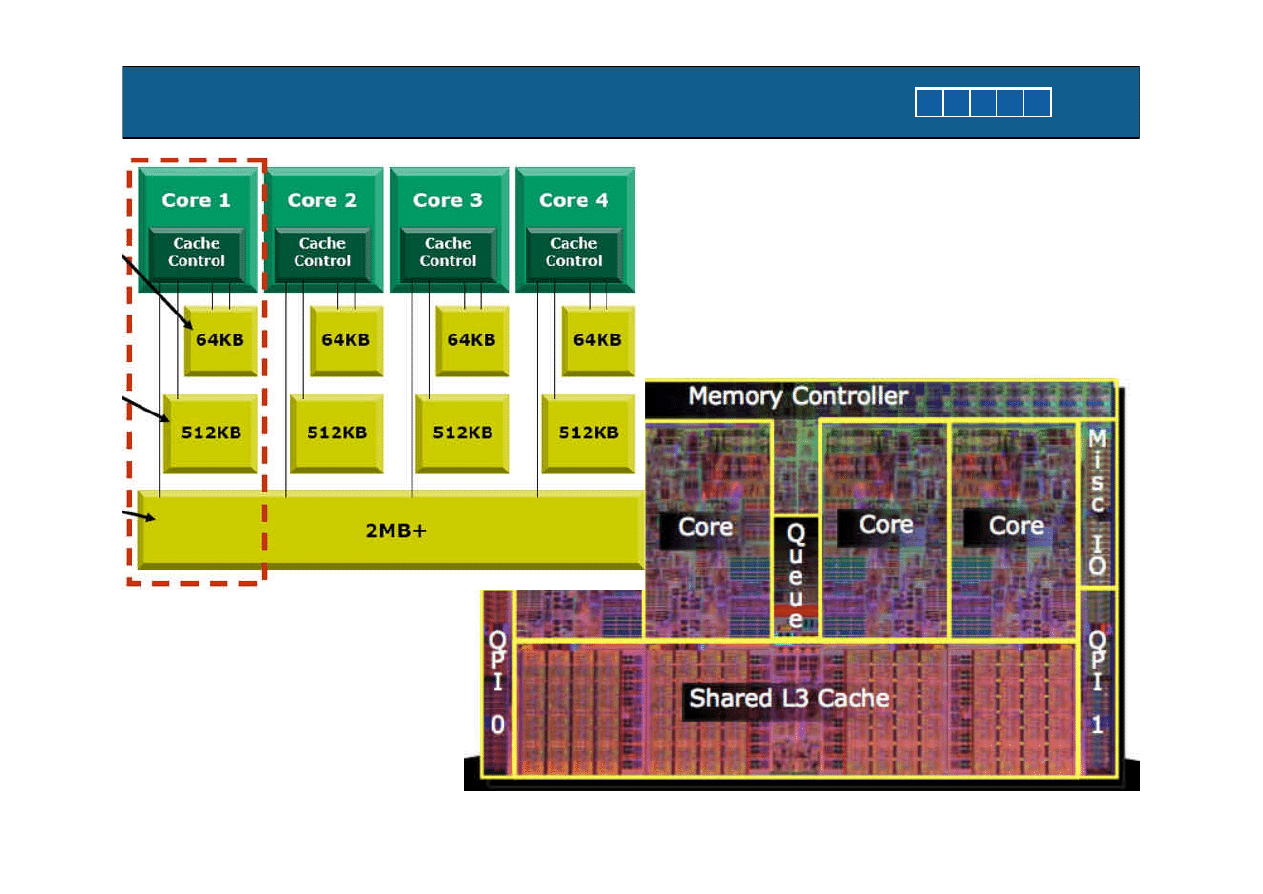
Quad - core

http://www.hwupgrade.com/articles/print/cpu/10/quad-fx-the-first-quad-core -amd-platform_index.html

ILP + Równoleglosc poziomu watku

44/45

Polecana literatura

1) P. Raghavan, A. Lad, S. Neelakandan, Embedded Linux System Design and

Development, Auerbach Publications 2006

2) D. Bovet, Understanding the Linux Kernel, O’Reilly 2005

ILP + Równoleglosc poziomu watku

45/45

KONIEC

dr inz. Mariusz Kapruziak

[e-mail]

pok. 107, tel. [phone]

http://www.allmoviephoto.com/photo /2005_alien_planet_007_big.html