
POLITECHNIKA L SKA
WYDZIAŁ IN YNIERII RODOWISKA I ENERGETYKI
INSTYTUT MASZYN I URZ DZE ENERGETYCZNYCH
LABORATORIUM ELEKTRYCZNE
Obwody sprz one magnetycznie.
(E – 5)
www.imiue.polsl.pl/~wwwzmiape
Opracował: Dr in . Włodzimierz OGULEWICZ
Sprawdził: Dr in . Włodzimierz OGULEWICZ
Zatwierdził: Dr hab. in . Janusz KOTOWICZ
1. Cel wiczenia.
Celem wiczenia jest poznanie sposobów opisu elementów sprz onych
magnetycznie (transformator powietrzny lub rdzeniowy) w układzie
elektrycznym oraz nabycie umiej tno ci do wiadczalnego wyznaczenia
indukcyjno ci własnej – L i indukcyjno ci wzajemnej – M.
2. Wprowadzenie.
2.1. Czwórniki. Okre 1enia i poj cia podstawowe.
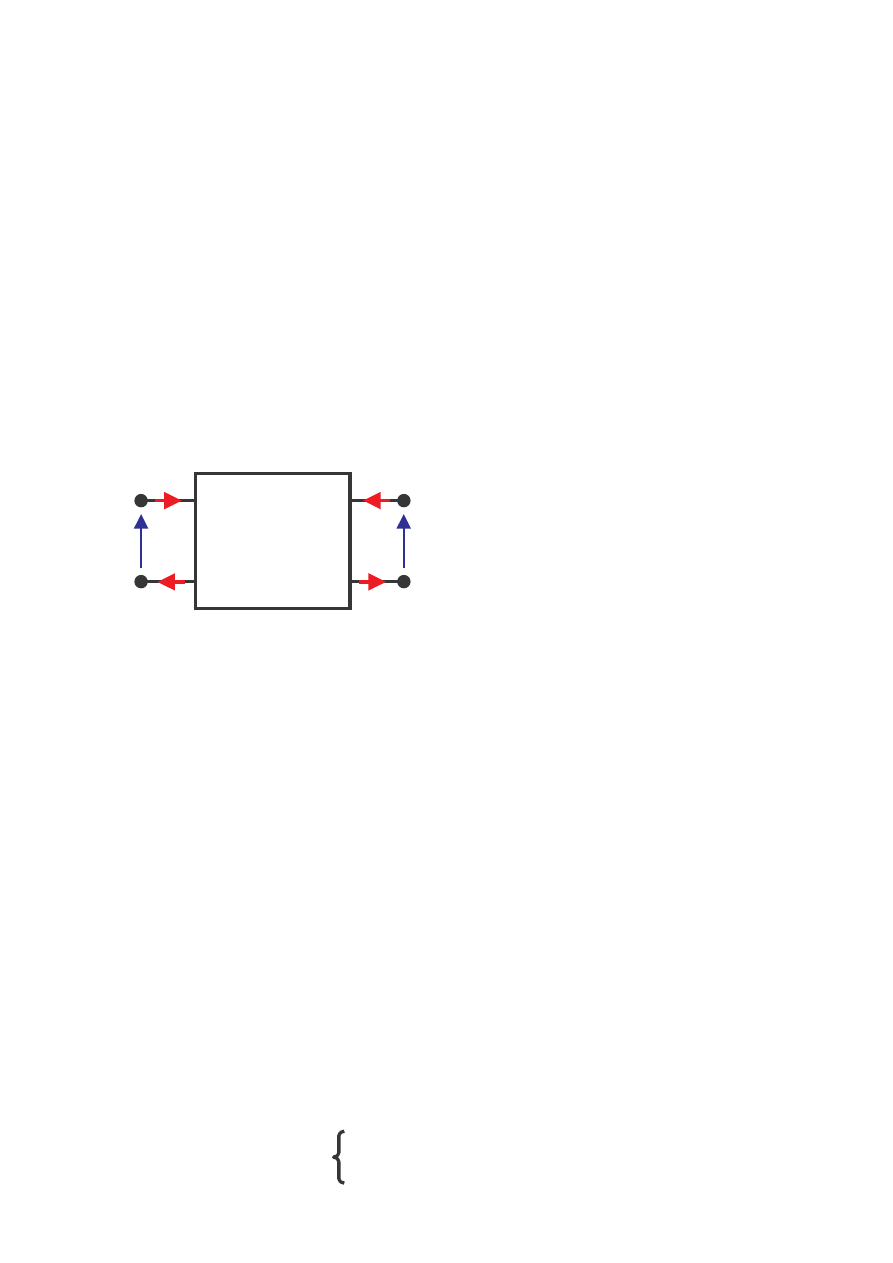
Obwód, który posiada cztery wyró nione zaciski, poprzez które mo e by
poł czony z innymi obwodami nazywa si czterobiegunnikiem, natomiast
czwórnikiem nazywa si czterobiegunnik poł czony z innymi obwodami w ten
sposób, e ka demu zaciskowi, przez który pr d wpływa do czterobiegunnika,
odpowiada zacisk, przez który taki sam pr d wypływa.
Poniewa przy ustaleniu zacisku z pr dem dopływaj cym, drugi zacisk mo e
by wybrany na trzy sposoby, z
czterobiegunnika mo na utworzy trzy
zupełnie ró ne czwórniki. Zwykle zaciski
czwórnika porz dkujemy i oznaczamy jak
na rys.1. Gdy czwórnik wł czony jest
pomi dzy
ródłem
a
odbiornikiem
rozró nia si ponadto zaciski wej ciowe (1,
1’) i wyj ciowe (2, 2’). Charakter
czwórnika
posiada
wiele
obwodów
elektrycznych takich jak filtry, linie
transmisyjne, transformatory, wzmacniacze.
Dzi ki wprowadzeniu uogólniaj cego poj cia czwórnika, do analizy ró nych
obwodów mo na u y
jednolitego aparatu matematycznego, którego zalet jest
uniezale nienie si od wewn trznej struktury i parametrów obwodu (układu). Dla
czwórnika okre la si jedynie współczynniki równa (wspólne dla wszystkich
układów), wi
ce z sob pr dy i napi cia na zaciskach układu czwórnika.
2.2. Równania czwórników.
Równania czwórnika s równaniami wi
cymi pr dy i napi cia na zaciskach
czwórnika (U
1
; I
1
; U
2
; I
2
). Dwie spo ród tych wielko ci s zmiennymi
niezale nymi, dwie pozostałe zmiennymi zale nymi. Ró ny wybór zmiennych
niezale nych prowadzi oczywi cie do ró nych postaci równa czwórnika. Sposób
wyboru jest dowolny, lecz otrzymana posta równania, zale nie od konkretnego
zagadnienia, mo e by mniej lub bardziej dogodna.
Zale nie od wyboru
zmiennych, równania te posiadaj ró ne nazwy:
1. Gdy zmiennymi niezale nymi s pr dy I
1
, I
2
równanie nazywa si
równaniem impedancyjnym
. Ma ono posta :
U
1
= Z
11
I
1
+ Z
12
I
2
(1)
U
2
= Z
21
I
1
+ Z
22
I
2
2’
1’
U
1
U
2
I
2
I
2
’
I
1
’
I
1
1
2
I
1
= I
1
’ I
2
= I
2
’
Rys.1. Czwórnik

2
.
Gdy zmiennymi niezale nymi s napi cia U
1
, U
2
równanie nazywa si
równaniem admitancyjnym
. Ma ono posta :
I
1
= Y
11
U
1
+ Y
12
U
2
(2)
I
2
= Y
21
U
1
+ Y
22
U
2
3. Gdy zmiennymi niezale nymi s wielko ci wej ciowe U
1
; I
1
lub wyj ciowe
U
2
; I
2
równanie nazywa si
równaniem ła cuchowym
:
U
1
= A U
2
+ B I
2
(3)
I
1
= C U
2
+ D I
2
4. Gdy zmiennymi niezale nymi jest pr d wej ciowy I
1
i napi cie wyj ciowe
U
2
lub wielko ci pozostałe (U
1
, I
2
) równania nazywa si
równaniem
mieszanym
lub
równaniem hybrydowym
:
U
1
= h
11
I
1
+ h
12
U
2
(4)
I
2
= h
21
I
1
+ h
22
U
2
Współczynniki poszczególnych równa , s liczbami rzeczywistymi w
przypadku obwodów pr du stałego, lub liczbami zespolonymi w obwodach z
przebiegami sinusoidalnymi o stałej cz stotliwo ci. Mog by równie funkcjami
cz stotliwo ci lub funkcjami zmiennej zespolonej.
2.3. Współczynniki równania impedancyjnego.
Współczynniki równania impedancyjnego mo na wyznaczy , gdy kolejno
zało ymy, e pr d I
2
jest równy zeru (przerwa w obwodzie odbiornika), wówczas:
Z
11
= ; Z
21
=
(5)
oraz gdy pr d I
1
jest równy zeru (czwórnik zasilany od strony zacisków 2-2’),
wówczas:
Z
22
= ; Z
12
=
(6)
Indeks ,,
0
” przy poszczególnych napi ciach i pr dach podkre la, e s one
mierzone w stanie nieobci onym czwórnika. Z tego te powodu współczynniki
Z
11
, Z
12
, Z
21
, Z
22
nazywa si parametrami rozwarciowymi czwórnika.
Współczynniki Z
11
i Z
22
s impedancjami rozwarciowymi, a Z
21
i Z
12
transmitancjami rozwarciowymi.
2.4. Cewki indukcyjne sprz one magnetycznie.
W ród cewek indukcyjnych nale y wyró ni dwa zasadnicze typy:
• Układ jednej cewki, której parametrem dominuj cym jest
indukcyjno
własna – L
.
U
10
I
20
U
20
I
20
U
10
I
10
U
20
I
10
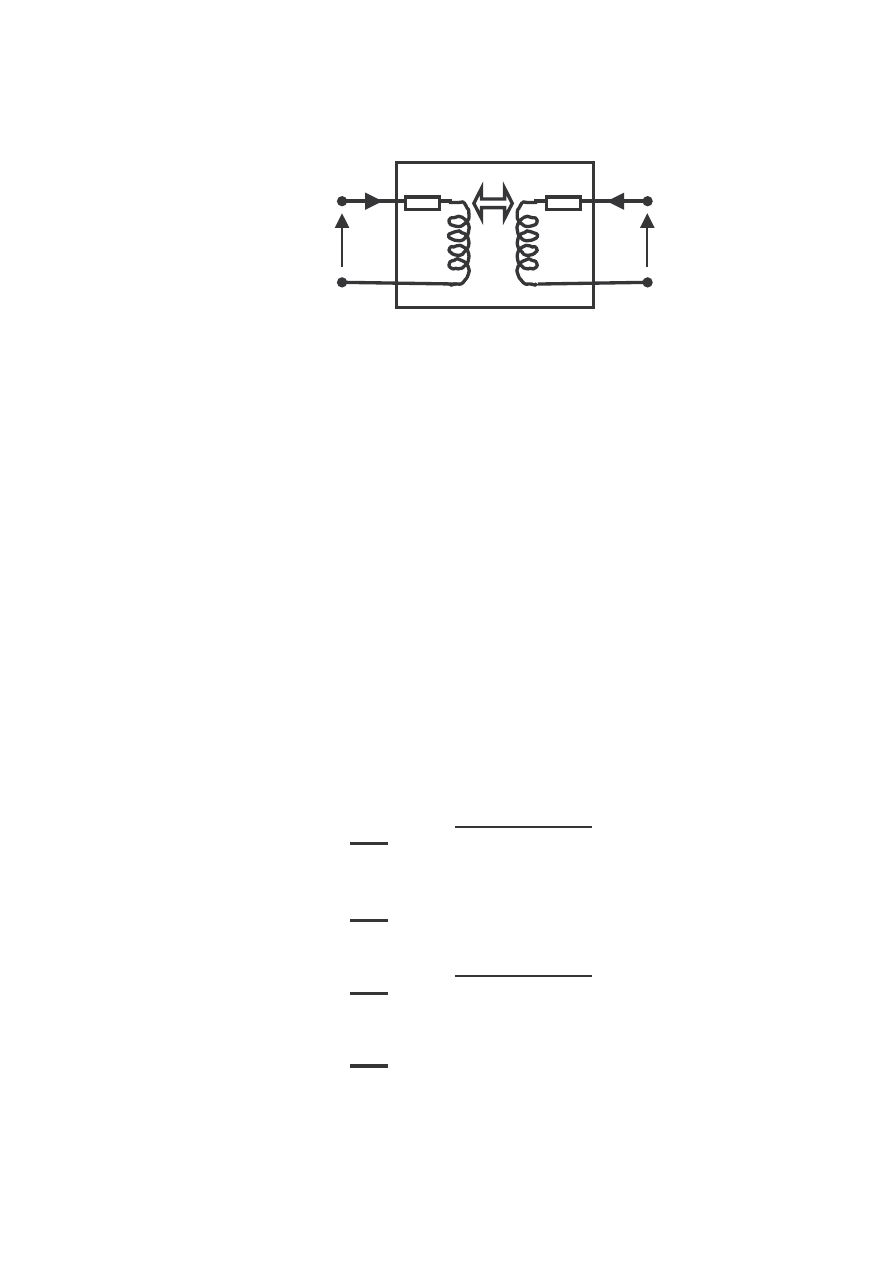
• Układ dwóch cewek sprz onych magnetycznie, których głównym
parametrem, oprócz indukcyjno ci własnych obydwu cewek (odpowiednio
L
1
i L
2
), jest
indukcyjno wzajemna – M
.
Rys.2. Układ dwóch cewek sprz onych magnetycznie.
Cewki indukcyjne mog by bezrdzeniowe (powietrzne) i wówczas obwód
magnetyczny (magnetowód) stanowi powietrze, oraz rdzeniowe (dławiki) o
magnetowodzie z materiału ferromagnetycznego (ze szczelin powietrzn lub
bez). U ycie rdzenia ferromagnetycznego powoduje zwi kszenie indukcyjno ci
własnej ( L ), a w cewkach sprz onych magnetycznie - zwi kszenie równie
indukcyjno ci wzajemnej ( M ).
W tradycyjnym wykonaniu cewki indukcyjne nawija si jednowarstwowo lub
wielowarstwowo. Mog by one wykonane jako cylindryczne (solenoidalne),
płaskie, lub toroidalne (o przekrojach kołowych lub wielobocznych).
2.5. Zwi zek parametrów równania impedancyjnego z warto ciami
indukcyjno ci własnych i wzajemnych cewek sprz onych
magnetycznie.
Traktuj c układ dwóch cewek sprz onych magnetycznie (z których ka da
charakteryzuje si indukcyjno ci własn L
1
lub L
2
oraz rezystancj odpowiednio
R
1
lub R
2
) jako czwórnik opisany układem równa impedancyjnych (4)
dochodzimy do wniosku, e:
(7)
(8)
(9)
(10)
gdzie:
= 2 f (w przypadku wiczenia f = 50 Hz)
1’
U
1
U
2
I
2
I
1
1
2’
2
R
1
R
2
L
1
L
2
M
12
=M
21
Z
11
=
Z
21
=
Z
22
=
Z
11
=
U
10
I
10
= R
1
2
+ ( L
1
)
2
U
20
I
20
= R
2
2
+ ( L
2
)
2
U
20
I
10
= M
21
U
10
I
20
= M
12
Z podanych zale no ci mo na wyznaczy parametry L
1
, L
2
, M
12
i M
21
, które przy
zało eniu R
1
= 0 oraz R
2
= 0 wynios :
(11)
(12)
(13)
(14)
2.6. Szeregowe poł czenie cewek sprz onych magnetycznie.
Warto indukcyjno ci wzajemnej – M wyznacza si jako stosunek strumienia
magnetycznego wytworzonego w jednej cewce i skojarzonego z drug cewk
(
Ψ
12
) do pr du (I
1
) cewki wywołuj cej ten strumie . Cewki magnetycznie
sprz one mog mie dwa rodzaje nawini cia:
•
zgodne
(pr dy płyn ce w cewkach wywołuj strumienie o tym samym
zwrocie),
•
przeciwne
(pr dy płyn ce w cewkach wywołuj strumienie o przeciwnym
zwrocie).
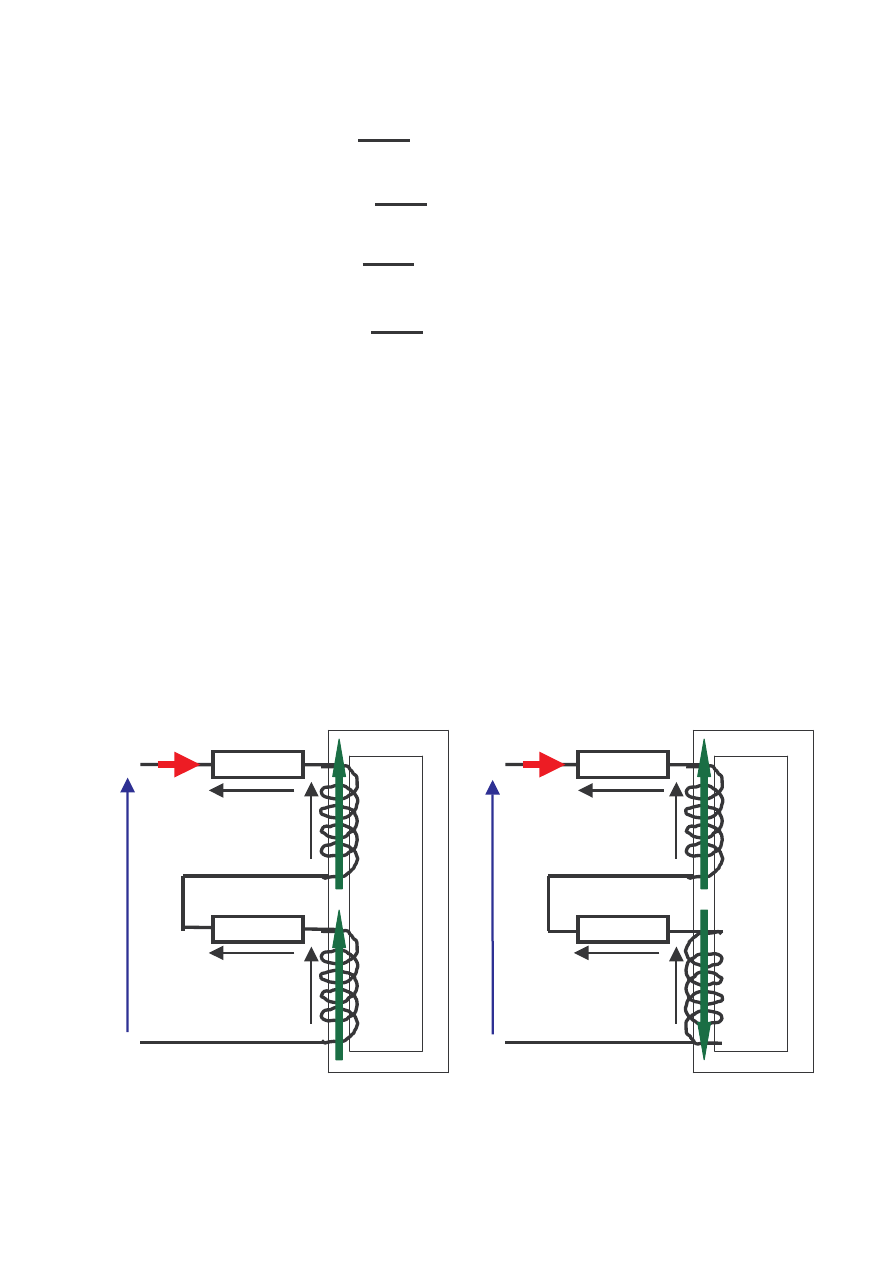
Ł cz c cewki sprz one magnetycznie szeregowo raz zgodnie i raz przeciwnie
(rys. 3.) mo na wyznaczy warto indukcyjno ci wzajemnej tych cewek.
Rys.3. Układy poł cze dwóch cewek sprz onych magnetycznie zasilanych
szeregowo.
L
1
=
M
21
=
L
2
=
M
12
=
U
1
I
1
U
2
I
2
U
20
I
1
U
10
I
2
u
R2
u
R1
φφφφ
2
L
φφφφ
1
L
R
2
u
L1
i
Z
R
1
L
1
u
L2
u
L
2
u
R2
u
R1
φφφφ
2
L
φφφφ
1
L
R
2
u
L1
i
P
R
1
L
1
u
L2
L
2
u
• dla zgodnego poł czenia cewek:
u
− R
1
i
Z
− L
1
(di
Z
/dt)
− M(di
Z
/dt)
− R
2
i
Z
− L
2
(di
Z
/dt)
− M(di
Z
/dt) = 0
u
− (R
1
+ R
2
)i
Z
− (L
1
+ L
2
+ 2M)(di
Z
/dt) = 0
w zapisie symbolicznym
U −−−− (R
1
+ R
2
)I
Z
−−−− jω
ω
ω
ω(L
1
+ L
2
+ 2M)I
Z
= 0
• dla przeciwnego poł czenia cewek:
u
− R
1
i
P
− L
1
(di
P
/dt) + M(di
P
/dt)
− R
2
i
P
− L
2
(di
P
/dt) + M(di
P
/dt) = 0
u
− (R
1
+ R
2
)i
P
− (L
1
+ L
2
− 2M)(di
P
/dt) = 0
w zapisie symbolicznym
U −−−− (R
1
+ R
2
)I
P
−−−− jω
ω
ω
ω(L
1
+ L
2
−−−− 2M)I
P
= 0
Wyznaczamy impedancj obu rodzajów poł cze oraz ich ró nic :
Z
Z
= U/I
Z
= R
1
+ R
2
+ j
ω(L
1
+ L
2
+ 2M)
Z
P
= U/I
P
= R
1
+ R
2
+ j
ω(L
1
+ L
2
− 2M)
Z
Z
− Z
P
= R
1
+ R
2
+ j
ω(L
1
+ L
2
+ 2M)
− R
1
− R
2
− jω(L
1
+ L
2
− 2M)
Z
Z
− Z
P
= j
ω2M + jω2M
j4
ωM = Z
Z
− Z
P
Warto indukcyjno ci wzajemnej – M wyniesie:
M = (Z
Z
−−−− Z
P
)/j4ω
ω
ω
ω
Je eli
R
1
≈ 0 oraz R
2
≈ 0 to Z
Z
= jX
Z
oraz Z
P
= jX
P
to
(15)
gdzie:
oraz
M =
X
Z
−−−− X
P
4ω
ω
ω
ω
X
Z
=
U
I
Z
X
P
=
U
I
P
3. Badania i pomiary.
3.1. Okre lenie wielko ci mierzonych.
Wielko ciami mierzonymi (pomiar po redni) s warto ci indukcyjno ci
własnych uzwoje transformatora bezpiecze stwa L
1
, L
2
oraz warto
indukcyjno ci wzajemnej tych uzwoje – M. Warto ci indukcyjno ci własnych i
wzajemnej wyznacza si z bezpo redniego pomiaru pr dów i napi , zgodnie z
zale no ciami (11) i (13) dla indukcyjno ci własnych oraz zgodnie z
zale no ciami (12), (14) i (15) dla indukcyjno ci wzajemnej.
3.2. Schematy układów pomiarowych.
W celu wyznaczenia warto ci indukcyjno ci własnych i wzajemnej na
podstawie parametrów równania impedancyjnego nale y zestawi układy
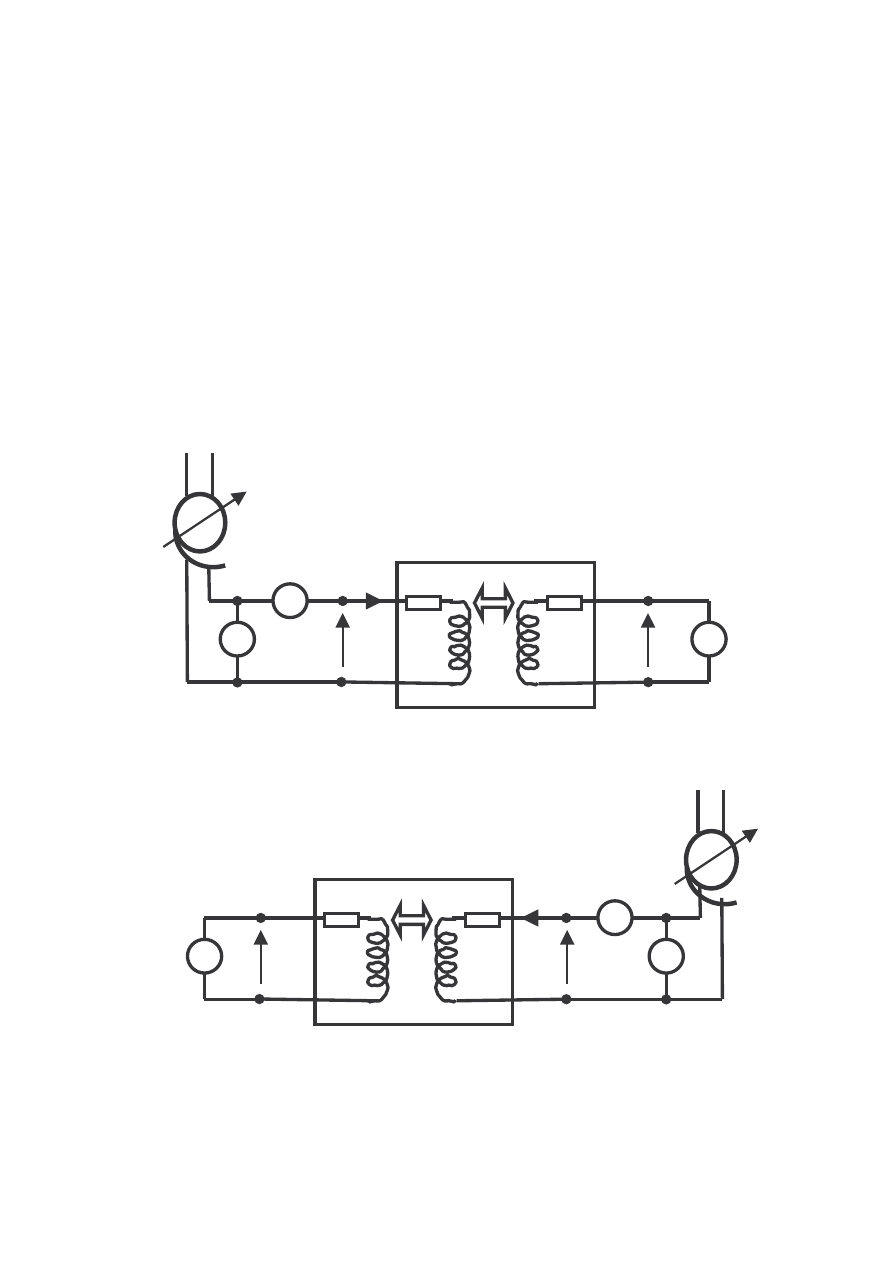
pomiarowe zgodnie ze schematami przedstawionymi na rys. 4 i 5.
Rys.4. Układ pomiarowy do wyznaczania L
1
i M
12
Rys.5. Układ pomiarowy do wyznaczania L
2
i M
21
W celu wyznaczenia warto ci indukcyjno ci wzajemnej na podstawie
pomiarów pr dów szeregowego poł czenia (zgodnego i przeciwnego) uzwoje
transformatora nale y zestawi układy pomiarowe zgodnie ze schematami
przedstawionymi na rys. 6a i 6b.
ATr
N
L
1’
U
1
U
20
I
1
1
2’
2
R
1
R
2
L
1
L
2
M
12
=M
21
V
V
A
N
L
1’
U
10
U
2
I
2
1
2’
2
R
1
R
2
L
1
L
2
M
12
=M
21
V
V
A
ATr
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron