Imię i Nazwisko
Gliwice, dnia ..10.03.2008..
...Projekt przykładowy..................
PROJEKT Z GEOTECHNIKI NR 1
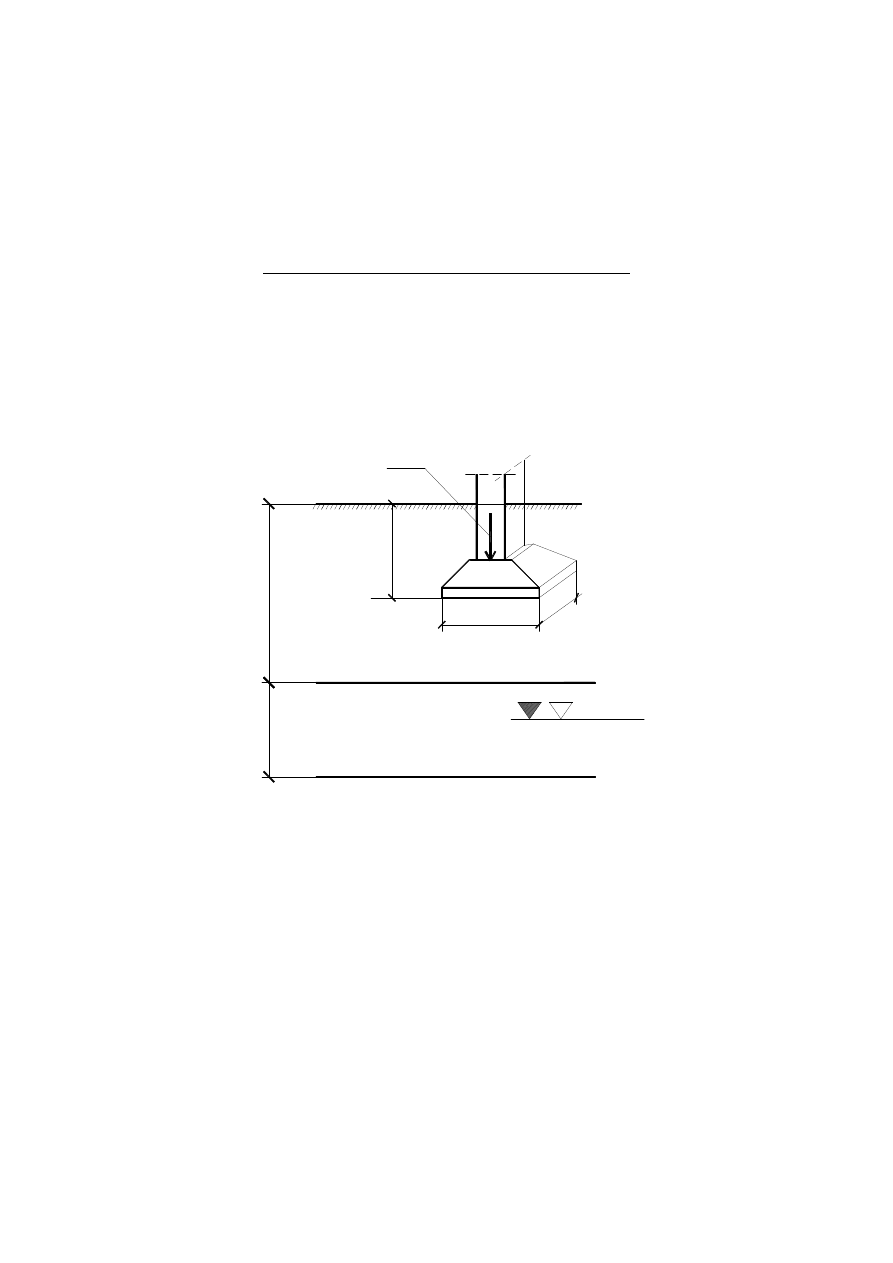
Zaprojektować fundament pod słup stropu technologicznego w hali przemysłowej dla
poniższych warunków gruntowo – wodnych:
N
B
D
r
[I = 0,39 ]
1
,8
4
,8
L
Gπ (b)
L
[I = 0,52 ]
Ps
D
2,8 m
Lokalizacja: .......Gliwice.................
Temat wydał: .........Marian Łupieżowiec..............
1.
Zestawienie obciążeń
Na podstawie projektu zintegrowanego przyjęto wartość obciążenia na stopę:
charakterystyczną:
N
k
= 435 kN,
obliczeniową: N
r
= 513 kN.
Przyjęto mimośród działania siły pionowej: e
0
= 10 mm, co daje moment obliczeniowy:
M
B
r
= 513
× 0,01 = 5,13 kNm,
M
L
r
= 513
× 0,01 = 5,13 kNm.
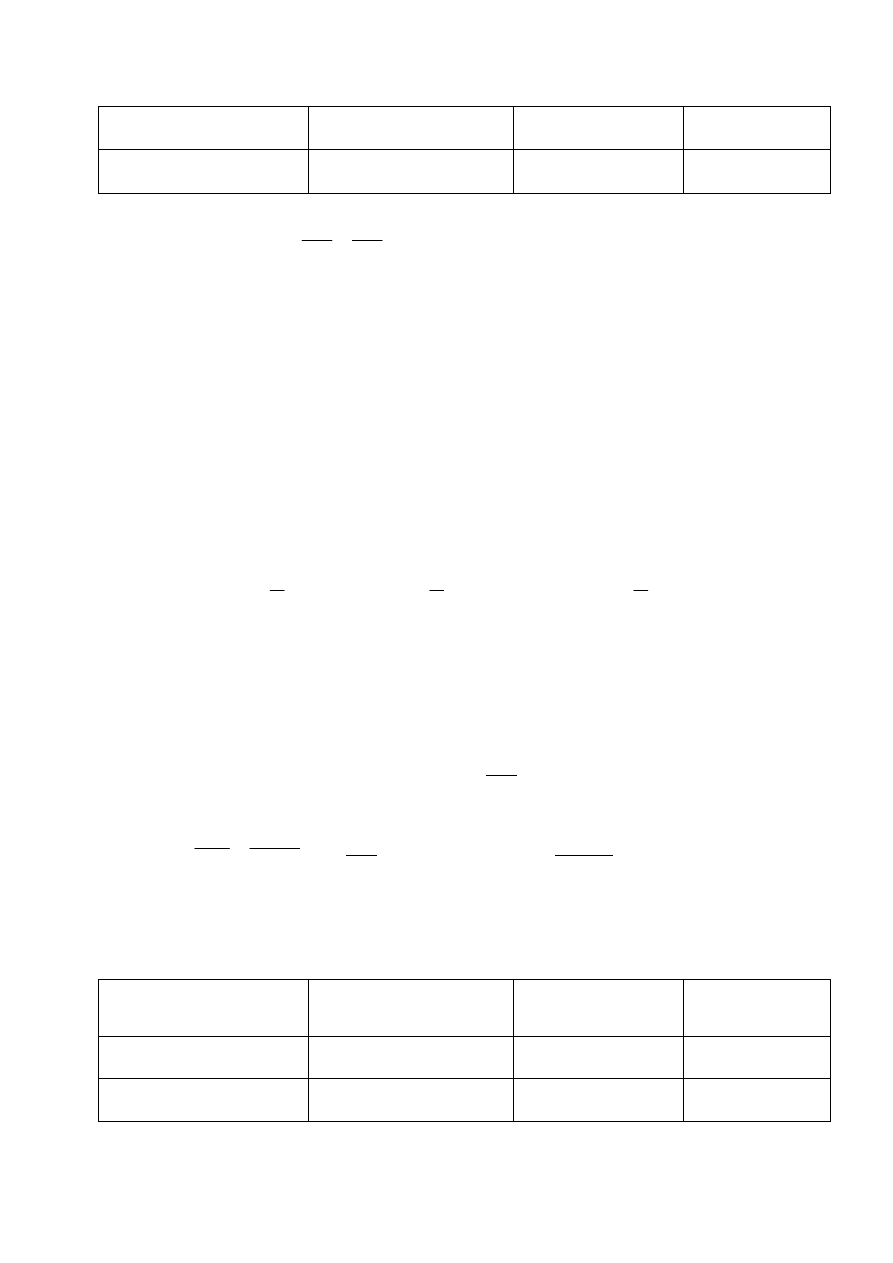
Zestawienie ciężaru własnego stopy oraz zasypki – przyjęto stopę kwadratową 2,0
× 2,0 m
o wysokości 60 cm posadowioną na głębokości 1,2 m:
Obciążenie:
charakterystyczne
[kN]
współczynnik obciążenia
γ
f
obliczeniowe
[kN]
Obciążenie z konstrukcji
435
-
513
Stopa fundamentowa
2,0
×2,0×0,6×25,0
= 60
1,1
66
Zasypanie wykopu
2,0
×2,0×0,6×20,0
= 48
1,2
58
RAZEM
543
-
637
Mimośród obciążenia:
=
=
=
637
13
,
5
r
r
N
M
e
0,008 m
2.
Podłoże gruntowe
Parametry charakterystyczne (na podst. PN-81/B-03020):
Rodzaj gruntu
stan
gruntu
I
L
/ I
D
ciężar
objętościowy
[kN/m
3
]
spójność
[kPa]
kąt tarcia
wewn.
[
°]
Moduł
ś
ciśliwości
edometrycznej
pierwotnej,
M
0
[MPa]
Moduł
ś
ciśliwości
edometrycznej
wtórnej
, M
[MPa]
Glina pylasta G
π
(nie morenowy grunt spoisty
skonsolidowany – krzywa b)
I
L
= 0,39
2,0
× 9,8
=
19,6
24
16
24
75
,
0
24
= 32
Piasek średni
Ps
I
D
= 0,52
1,85
× 9,8
=
18,1
-
33
95
9
,
0
95
= 106
Piasek średni
Ps
(pod poziomem wody)
I
D
= 0,52
2,0
× 9,8 – 10
= 9,6
-
33
95
9
,
0
95
= 106
Parametry obliczeniowe:
przyjęto:
γ
m
= 0,9
Współczynniki nośności
Rodzaj gruntu
ciężar
objętościowy
[kN/m
3
]
spójność
[kPa]
kąt tarcia
wewn.
[
°]
N
D
N
C
N
B
Glina pylasta G
π
(nie morenowy grunt spoisty
skonsolidowany – krzywa b)
19,6
× 0,9 =
17,6
24
× 0,9 =
21,6
16
× 0,9 =
14,4
3,7
10,6
0,5
Piasek średni
Ps
18,1
× 0,9
=
16,3
-
33
× 0,9 =
29,7
17,8
29,5
7,2
Piasek średni
Ps
(pod poziomem wody)
9,6
× 0,9
=
8,6
-
33
× 0,9 =
29,7
17,8
29,5
7,2
3.
Dobór rodzaju posadowienia
Ze względu na wartości sił działających na fundament oraz warunki gruntowe:
- brak gruntów organicznych
- dla piasku średniego I
D
> 0,2
- dla gliny pylastej I
L
< 0,5
- dla wszystkich gruntów edometryczne moduły ściśliwości nie mniejsze niż 1 MPa,
słup hali można posadowić bezpośrednio, jako stopę fundamentową pod słup stropu.
4.
Szacunkowe nośności warstw tworzących podłoże
Przyjmujemy:
B = L = 1,0 m,
D = 1,0 m,
obliczamy nośność podłoża wg wzoru:
r
B
B
r
D
D
r
u
c
f
B
N
L
B
D
N
L
B
c
N
L
B
q
γ
γ
⋅
⋅
⋅
⋅
−
+
⋅
⋅
⋅
⋅
+
+
⋅
⋅
⋅
+
=
25
,
0
1
5
,
1
1
3
,
0
1
,
dla gliny pylastej:
6
,
17
0
,
1
5
,
0
75
,
0
6
,
17
0
,
1
7
,
3
5
,
2
6
,
21
6
,
10
3
,
1
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
f
q
= 467 kPa,
dla piasku średniego (nad poziomem wody gruntowej):
3
,
16
0
,
1
2
,
7
75
,
0
6
,
17
0
,
1
8
,
17
5
,
2
0
⋅
⋅
⋅
+
⋅
⋅
⋅
+
=
f
q
= 871 kPa.
dla piasku średniego (pod poziomem wody gruntowej):
6
,
8
0
,
1
2
,
7
75
,
0
6
,
17
0
,
1
8
,
17
5
,
2
0
⋅
⋅
⋅
+
⋅
⋅
⋅
+
=
f
q
= 829 kPa.
Ponieważ decydujemy się na posadowienie w G
π
(nośność q
f
= 467 kPa), a poniżej
występujące warstwy mają większą nośność, więc wynika z tego, że podłoże pod
fundamentem jest jednorodne (do głębokości 2
⋅B nie występuje warstwa słabsza niż ta, na
której posadawiamy).
5.
Dobór głębokości posadowienia
Warunki ograniczające poziom posadowienia od góry:
− D
min.
= 0,5 m,
− głębokość przemarzania – dla Gliwic: h
z
= 1,0 m,
− do głębokości przemarzania występuje grunt wysadzinowy (glina pylasta) ⇒ D ≥ 1,0 m,
− występowanie słabej warstwy gruntowej blisko powierzchni terenu – brak,
− względy technologiczne i funkcjonalne – fundament powinien być w całości zasypany
gruntem,
Warunki ograniczające poziom posadowienia od dołu:
− występowanie słabej warstwy pod fundamentem – brak,
− względy technologiczne, funkcjonalne – brak,
− względy ekonomiczne – posadowić możliwie najpłycej.
Na podstawie powyższych warunków przyjęto głębokość posadowienia D = 1,0 m.
6.
Dobór wymiarów fundamentu
Korzystając z oszacowania nośności podłoża pod stopą oraz wartości obciążeń na nią
przekazywanych, przyjęto stopę kwadratową o wymiarach:
467
637
=
=
=
f
r
q
N
L
B
= 1,17 m ⇒ przyjęto: B = L = 1,2 m,
Ponieważ przyjęte wymiary stopy różnią się o ponad 10% od założonych w zestawieniu,
dlatego zachodzi konieczność korekty.
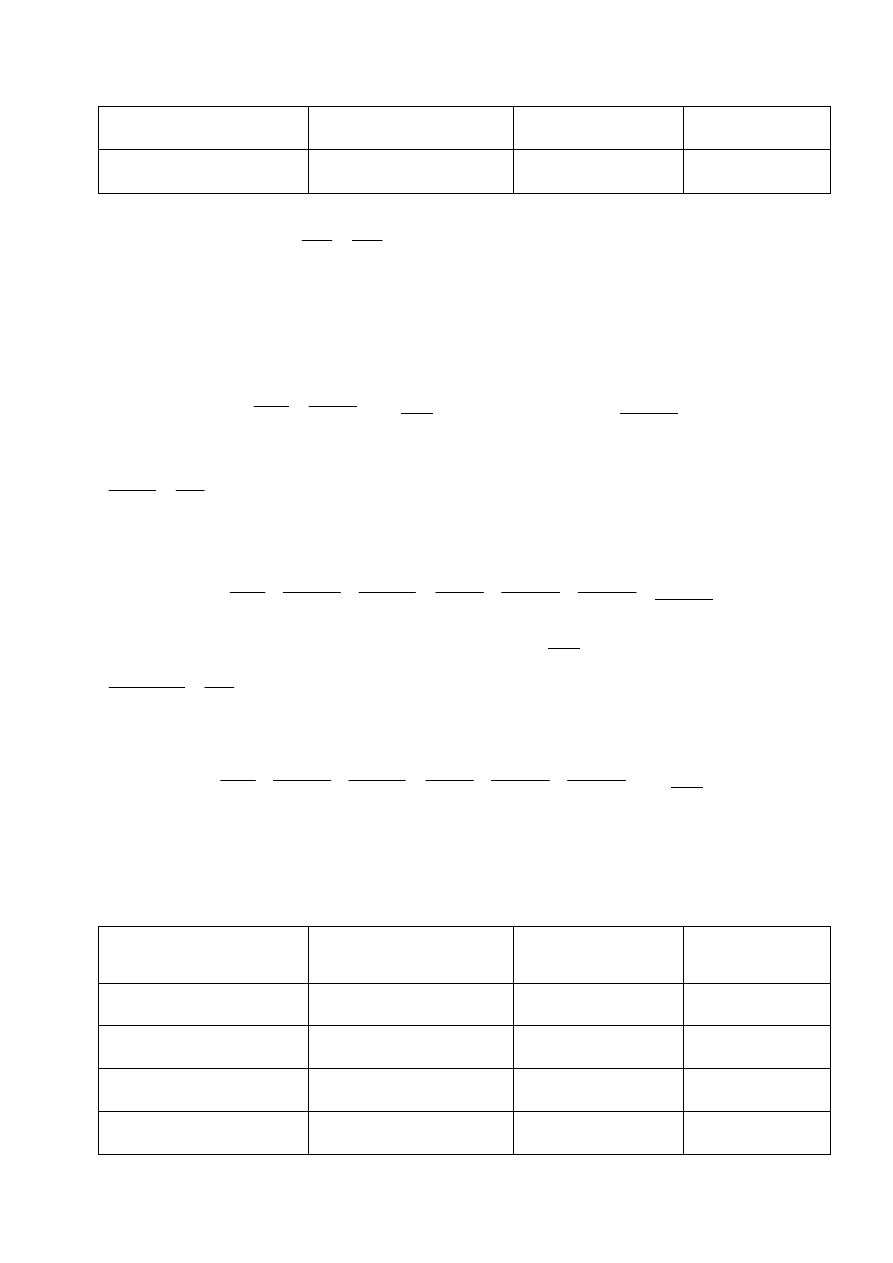
Korekta zestawienia obciążeń na stopę:
Obciążenie:
charakterystyczne
[kN]
współczynnik obciążenia
γ
f
obliczeniowe
[kN]
Obciążenie z konstrukcji
435
-
513
Stopa fundamentowa
1,2
×1,2×0,5×25,0
= 18
1,1
20
Zasypanie wykopu
1,2
×1,2×0,5×20,0
= 14
1,2
17
RAZEM
467
-
550
Mimośród obciążenia:
=
=
=
550
13
,
5
r
r
N
M
e
0,009 m.
7.
Sprawdzenie I stanu granicznego
Ponieważ w przypadku projektowania przedmiotowej stopy zachodzi:
− siła pozioma nie przekracza 10% siły pionowej,
− budowla nie jest usytuowana na zboczu lub w jego pobliżu,
− obok budowli nie przewiduje się głębokich wykopów lub dodatkowego obciążenia,
− mimośród obciążenia e = 0,008 m < 0,035⋅B = 0,042 m,
można skorzystać ze wzoru uproszczonego na sprawdzenie nośności.
Obliczenie nośności podłoża pod stopą w poziomie posadowienia:
r
B
B
r
D
D
r
u
c
f
B
N
L
B
D
N
L
B
c
N
L
B
q
γ
γ
⋅
⋅
⋅
⋅
−
+
⋅
⋅
⋅
⋅
+
+
⋅
⋅
⋅
+
=
25
,
0
1
5
,
1
1
3
,
0
1
,
6
,
17
2
,
1
5
,
0
75
,
0
6
,
17
0
,
1
7
,
3
5
,
2
6
,
21
6
,
10
3
,
1
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
f
q
= 468 kPa,
Ze względu na zastosowanie metody stanów granicznych w szacowaniu nośności fundamentu
oraz oznaczenie parametrów geotechnicznych metodą B, współczynnik korekcyjny przyjmuje
wartość:
m = 0,9
⋅ 0,9 = 0,81
Naprężenie średnie pod stopą fundamentową:
2
,
1
2
,
1
550
⋅
=
⋅
=
L
B
N
q
r
rs
= 381 kPa >
468
81
,
0
⋅
=
⋅
f
q
m
= 379 kPa ⇒
warunek
niespełniony, należy zwiększyć wymiary stopy.
Przyjmujemy wymiary stopy: B = L = 1,3 m, D = 1,0 m, wysokość stopy: H = 0,5 m.
Korekta zestawienia obciążeń na stopę:
Obciążenie:
charakterystyczne
[kN]
współczynnik obciążenia
γ
f
obliczeniowe
[kN]
Obciążenie z konstrukcji
435
-
513
Stopa fundamentowa
1,3
×1,3×0,5×25,0
= 21
1,1
23
Zasypanie wykopu
1,3
×1,3×0,5×20,0
= 17
1,2
20
RAZEM
473
-
556
Mimośród obciążenia:
=
=
=
556
13
,
5
r
r
N
M
e
0,009 m.
Nośność stopy w poziomie posadowienia:
6
,
17
3
,
1
5
,
0
75
,
0
6
,
17
0
,
1
7
,
3
5
,
2
6
,
21
6
,
10
3
,
1
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
f
q
= 469 kPa,
Naprężenie średnie pod stopą fundamentową:
3
,
1
3
,
1
556
⋅
=
⋅
=
L
B
N
q
r
rs
= 329 kPa <
469
81
,
0
⋅
=
⋅
f
q
m
= 379 kPa,
Wykorzystanie nośności podłoża:
87
,
0
379
329
=
=
⋅
f
rs
q
m
q
< 0,90
Naprężenia maksymalne:
3
,
1
3
,
1
13
,
5
6
3
,
1
3
,
1
13
,
5
6
3
,
1
3
,
1
556
6
6
2
2
2
2
max
⋅
⋅
+
⋅
⋅
+
⋅
=
⋅
⋅
+
⋅
⋅
+
⋅
=
L
B
M
L
B
M
L
B
N
q
r
L
r
B
r
r
= 357 kPa <
469
81
,
0
2
,
1
2
,
1
⋅
⋅
=
⋅
⋅
f
q
m
= 456 kPa,
78
,
0
456
357
2
,
1
max
=
=
⋅
⋅
f
r
q
m
q
< 0,90
Sprawdzenie warunku na odrywanie (naprężenia minimalne):
2
2
2
2
min
3
,
1
3
,
1
7
,
25
6
3
,
1
3
,
1
7
,
25
6
3
,
1
3
,
1
556
6
6
⋅
⋅
−
⋅
⋅
−
⋅
=
⋅
⋅
−
⋅
⋅
−
⋅
=
L
B
M
L
B
M
L
B
N
q
r
L
r
B
r
r
= 301 kPa > 0,
Z powyższego wynika, że wymiary stopy są zbyt duże (zbyt duży zapas bezpieczeństwa),
ustalamy: B = L = 1,25 m, D = 1,0 m, wysokość stopy: H = 0,5 m.
Kolejna korekta zestawienia obciążeń na stopę:
Obciążenie:
charakterystyczne
[kN]
współczynnik obciążenia
γ
f
obliczeniowe
[kN]
Obciążenie z konstrukcji
435
-
513
Stopa fundamentowa
1,25
×1,25×0,5×25,0
= 19,5
1,1
21,5
Zasypanie wykopu
1,25
×1,25×0,5×20,0
= 15,6
1,2
18,7
RAZEM
470
-
553
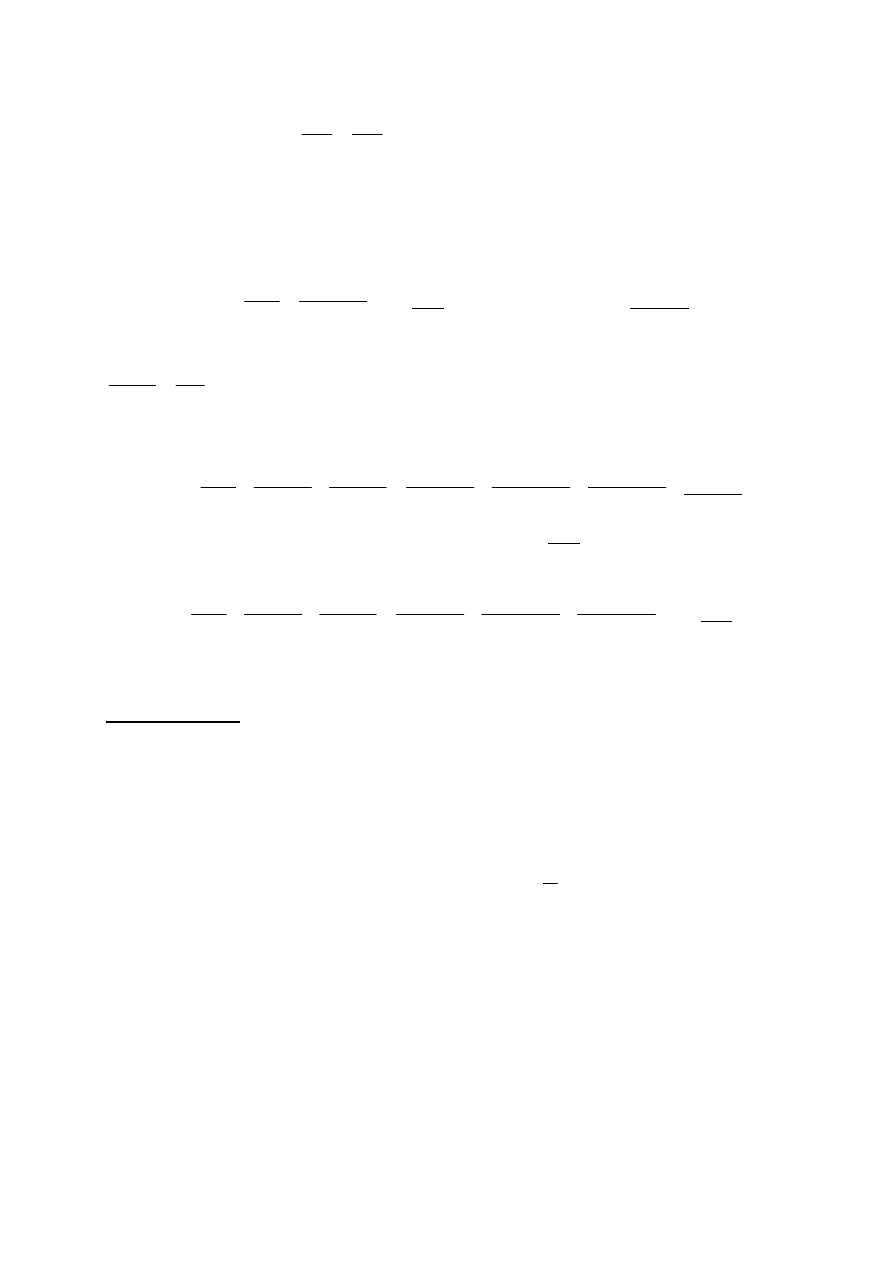
Mimośród obciążenia:
=
=
=
553
13
,
5
r
r
N
M
e
0,009 m.
Nośność stopy w poziomie posadowienia:
6
,
17
25
,
1
5
,
0
75
,
0
6
,
17
0
,
1
7
,
3
5
,
2
6
,
21
6
,
10
3
,
1
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
f
q
= 469 kPa,
Naprężenie średnie pod stopą fundamentową:
25
,
1
25
,
1
553
⋅
=
⋅
=
L
B
N
q
r
rs
= 354 kPa <
469
81
,
0
⋅
=
⋅
f
q
m
= 379 kPa,
Wykorzystanie nośności podłoża:
93
,
0
379
354
=
=
⋅
f
rs
q
m
q
> 0,90
Naprężenia maksymalne:
25
,
1
25
,
1
13
,
5
6
25
,
1
25
,
1
13
,
5
6
25
,
1
25
,
1
553
6
6
2
2
2
2
max
⋅
⋅
+
⋅
⋅
+
⋅
=
⋅
⋅
+
⋅
⋅
+
⋅
=
L
B
M
L
B
M
L
B
N
q
r
L
r
B
r
r
= 385 kPa <
469
81
,
0
2
,
1
2
,
1
⋅
⋅
=
⋅
⋅
f
q
m
= 456 kPa,
Sprawdzenie warunku na odrywanie (naprężenia minimalne):
2
2
2
2
min
25
,
1
25
,
1
7
,
25
6
25
,
1
25
,
1
7
,
25
6
25
,
1
25
,
1
556
6
6
⋅
⋅
−
⋅
⋅
−
⋅
=
⋅
⋅
−
⋅
⋅
−
⋅
=
L
B
M
L
B
M
L
B
N
q
r
L
r
B
r
r
= 323 kPa > 0,
Podsumowywując powyższe obliczenia można stwierdzić, że warunki I stanu granicznego
zostały spełnione dla: B = L = 1,25 m, D = 1,0 m, wysokość stopy: H = 0,5 m.
8.
Sprawdzenie II stanu granicznego
Wyznaczenie osiadania pod środkiem fundamentu. Obciążenie charakterystyczne działające
poprzez stopę fundamentową na podłoże: N
k
= 470 kN.
Podłoże dzielimy na warstwy o miąższości nie większej niż
m
63
,
0
2
=
B
.
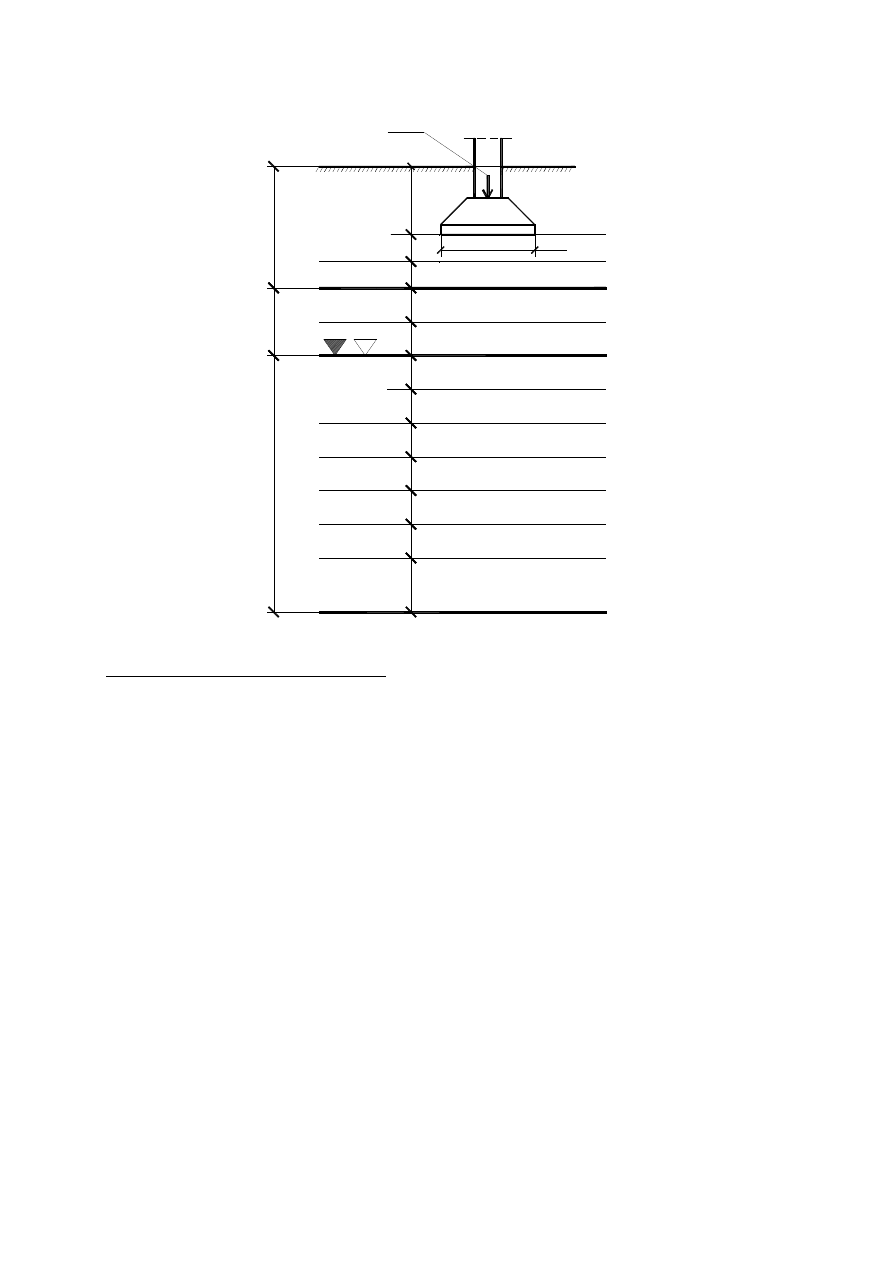
N
D
=
1
,0
k
1
,8
3
,8
Gπ
Ps
0
,4
0
.4
1
,0
0
,5
0
,5
0
,5
0
,5
0
,5
0
,5
0
,5
0
,5
0
,8
B
1
0
2
3
4
5
6
7
8
9
10
11
Wyznaczenie naprężeń początkowych:
=
terenu
poz.
,
ρ
σ
z
0,0 kPa,
D
G
z
⋅
=
π
ρ
γ
σ
0
= 19,6
⋅ 1,0 = 19,6 kPa,
1
0
0
1
−
⋅
+
=
h
G
z
z
π
ρ
ρ
γ
σ
σ
= 19,6 + 19,6
⋅ 0,4 = 27,4 kPa,
2
1
1
2
−
⋅
+
=
h
G
z
z
π
ρ
ρ
γ
σ
σ
= 27,4 + 19,6
⋅ 0,4 = 35,2 kPa,
3
2
2
3
−
⋅
+
=
h
Ps
z
z
γ
σ
σ
ρ
ρ
= 35,2 + 18,1
⋅ 0,5 = 44,3 kPa,
4
3
3
4
−
⋅
+
=
h
Ps
z
z
γ
σ
σ
ρ
ρ
= 44,3 + 18,1
⋅ 0,5 = 53,4 kPa,
5
4
4
5
'
−
⋅
+
=
h
Ps
z
z
γ
σ
σ
ρ
ρ
= 53,4 + 9,6
⋅ 0,5 = 58,2 kPa,
6
5
5
6
'
−
⋅
+
=
h
Ps
z
z
γ
σ
σ
ρ
ρ
= 58,2 + 9,6
⋅ 0,5 = 63,0 kPa,
7
6
6
7
'
−
⋅
+
=
h
Ps
z
z
γ
σ
σ
ρ
ρ
= 63,0 + 9,6
⋅ 0,5 = 67,8 kPa,
8
7
7
8
'
−
⋅
+
=
h
Ps
z
z
γ
σ
σ
ρ
ρ
= 67,8 + 9,6
⋅ 0,5 = 72,6 kPa,
9
8
8
9
'
−
⋅
+
=
h
Ps
z
z
γ
σ
σ
ρ
ρ
= 72,6 + 9,6
⋅ 0,5 = 77,4 kPa,
10
9
9
10
'
−
⋅
+
=
h
Ps
z
z
γ
σ
σ
ρ
ρ
= 77,4 + 9,6
⋅ 0,5 = 82,2 kPa,
11
10
10
11
'
−
⋅
+
=
h
Ps
z
z
γ
σ
σ
ρ
ρ
= 82,2 + 9,6
⋅ 0,8 = 89,9 kPa.
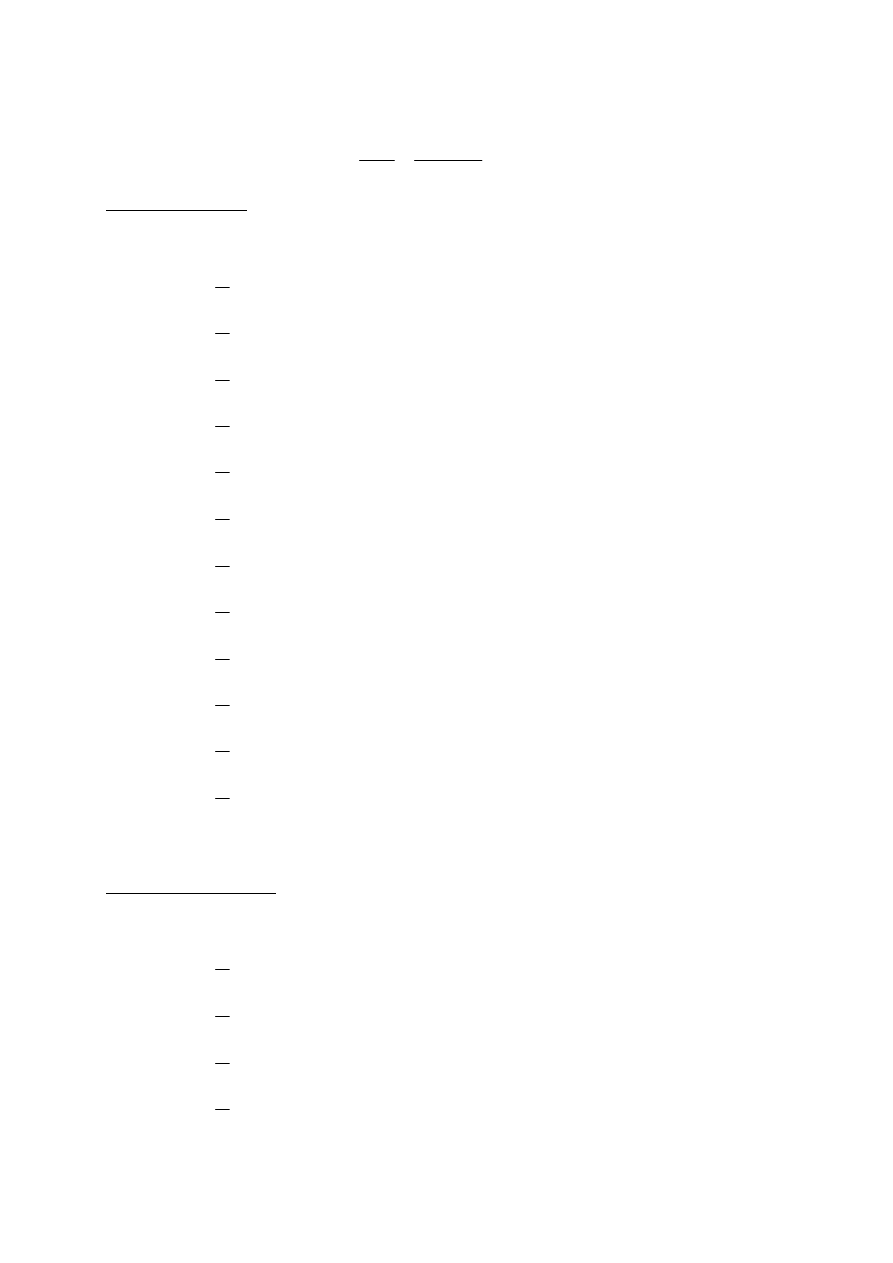
Ś
redni nacisk pod stopą fundamentową:
25
,
1
25
,
1
470
⋅
=
⋅
=
L
B
N
q
k
sr
= 300,8 kPa.
Naprężenia wtórne:
m
z
zs
η
σ
σ
ρ
⋅
=
0
,
η
m
– na podstawie nomogramu Z2-12.
z = 0,0 m,
B
z
= 0,0,
00
,
1
=
m
η
⇒
00
,
1
6
,
19
0
⋅
=
zs
σ
= 19,6 kPa,
z = 0,4 m,
B
z
= 0,286,
90
,
0
=
m
η
⇒
90
,
0
6
,
19
1
⋅
=
zs
σ
= 17,6 kPa,
z = 0,8 m,
B
z
= 0,571,
63
,
0
=
m
η
⇒
63
,
0
6
,
19
2
⋅
=
zs
σ
= 12,3 kPa,
z = 1,3 m,
B
z
= 0,929,
37
,
0
=
m
η
⇒
37
,
0
6
,
19
3
⋅
=
zs
σ
= 7,3 kPa,
z = 1,8 m,
B
z
= 1,286,
24
,
0
=
m
η
⇒
24
,
0
6
,
19
4
⋅
=
zs
σ
= 4,7 kPa,
z = 2,3 m,
B
z
= 1,643,
16
,
0
=
m
η
⇒
16
,
0
6
,
19
5
⋅
=
zs
σ
= 3,1 kPa,
z = 2,8 m,
B
z
= 2,000,
11
,
0
=
m
η
⇒
11
,
0
6
,
19
6
⋅
=
zs
σ
= 2,2 kPa,
z = 3,3 m,
B
z
= 2,357,
08
,
0
=
m
η
⇒
08
,
0
6
,
19
7
⋅
=
zs
σ
= 1,6 kPa,
z = 3,8 m,
B
z
= 2,714,
06
,
0
=
m
η
⇒
06
,
0
6
,
19
8
⋅
=
zs
σ
= 1,2 kPa,
z = 4,3 m,
B
z
= 3,071,
04
,
0
=
m
η
⇒
04
,
0
6
,
19
9
⋅
=
zs
σ
= 0,8 kPa,
z = 4,8 m,
B
z
= 3,429,
03
,
0
=
m
η
⇒
03
,
0
6
,
19
10
⋅
=
zs
σ
= 0,6 kPa,
z = 5,6 m,
B
z
= 4,000,
025
,
0
=
m
η
⇒
025
,
0
6
,
19
11
⋅
=
zs
σ
= 0,5 kPa.
Naprężenia dodatkowe:
(
)
s
z
zd
q
η
σ
σ
ρ
⋅
−
=
0
,
η
s
– na podstawie nomogramu Z2-13.
z = 0,0 m,
B
z
= 0,0,
00
,
1
=
s
η
⇒
(
)
00
,
1
6
,
19
8
,
300
0
⋅
−
=
zd
σ
= 281,2 kPa,
z = 0,4 m,
B
z
= 0,286,
68
,
0
=
s
η
⇒
68
,
0
2
,
281
1
⋅
=
zd
σ
= 191,2 kPa,
z = 0,8 m,
B
z
= 0,571,
47
,
0
=
s
η
⇒
47
,
0
2
,
281
2
⋅
=
zd
σ
= 132,2 kPa,
z = 1,3 m,
B
z
= 0,929,
30
,
0
=
s
η
⇒
30
,
0
2
,
281
3
⋅
=
zd
σ
= 84,4 kPa,

z = 1,8 m,
B
z
= 1,286,
19
,
0
=
s
η
⇒
19
,
0
2
,
281
4
⋅
=
zd
σ
= 53,4 kPa,
z = 2,3 m,
B
z
= 1,643,
13
,
0
=
s
η
⇒
13
,
0
2
,
281
5
⋅
=
zd
σ
= 36,6 kPa,
z = 2,8 m,
B
z
= 2,000,
10
,
0
=
s
η
⇒
10
,
0
2
,
281
6
⋅
=
zd
σ
= 28,1 kPa,
z = 3,3 m,
B
z
= 2,357,
07
,
0
=
s
η
⇒
07
,
0
2
,
281
7
⋅
=
zd
σ
= 19,7 kPa,
z = 3,8 m,
B
z
= 2,714,
06
,
0
=
s
η
⇒
06
,
0
2
,
281
8
⋅
=
zd
σ
= 16,9 kPa,
z = 4,3 m,
B
z
= 3,071,
05
,
0
=
s
η
⇒
05
,
0
2
,
281
9
⋅
=
zd
σ
= 14,1 kPa,
z = 4,8 m,
B
z
= 3,429,
04
,
0
=
s
η
⇒
04
,
0
2
,
281
10
⋅
=
zd
σ
= 11,2 kPa,
z = 5,6 m,
B
z
= 4,000,
03
,
0
=
s
η
⇒
03
,
0
2
,
281
11
⋅
=
zd
σ
= 8,4 kPa.
Wykresy naprężeń pierwotnych, wtórnych i dodatkowych:
Ps
G
π
3
,8
1
,0
1
,8
z [m]
σ
zd
19,6
27,4
35,2
44,3
53,4
58,2
63,0
67,8
72,6
77,4
82,2
89,9
z
ρ
σ
17,6
12,3
7,3
4,7
3,1
2,2
1,6
1,2
0,8
0,6
0,5
z max
281,2 [kPa]
191,2
132,2
84,4
53,4
36,6
28,1
19,7
16,9
14,1
11,2
8,4
Wyznaczenie głębokości aktywnej:
warunek:
ρ
σ
σ
z
zd
⋅
≤
3
,
0
jest spełniony na głębokości: z
max
= 3,3 m
kPa
3
,
20
8
,
67
3
,
0
3
,
0
kPa
7
,
19
=
⋅
=
⋅
≤
=
ρ
σ
σ
z
zd
.
Obliczenie osiadań:
Osiadanie warstwy gruntu:
(
)
(
)
0
2
1
2
1
2
2
M
h
M
h
s
zd
zd
zs
zs
⋅
⋅
+
+
⋅
⋅
+
⋅
=
σ
σ
σ
σ
λ
,
przyjmujemy:
λ = 1,0 (czas budowy ponad 1 rok).
(
)
(
)
24
2
4
,
0
2
,
191
2
,
281
32
2
4
,
0
6
,
17
4
,
19
0
,
1
1
0
⋅
⋅
+
+
⋅
⋅
+
⋅
=
−
s
= 0,2 + 3,9 = 4,1 mm,

(
)
(
)
24
2
4
,
0
2
,
132
2
,
191
32
2
4
,
0
3
,
12
6
,
17
0
,
1
2
1
⋅
⋅
+
+
⋅
⋅
+
⋅
=
−
s
= 0,2 + 2,7 = 2,9 mm,
(
)
(
)
95
2
5
,
0
4
,
84
2
,
132
106
2
5
,
0
3
,
7
3
,
12
0
,
1
3
2
⋅
⋅
+
+
⋅
⋅
+
⋅
=
−
s
= 0,0 + 0,6 = 0,6 mm,
(
)
(
)
95
2
5
,
0
4
,
53
4
,
84
106
2
5
,
0
7
,
4
3
,
7
0
,
1
4
3
⋅
⋅
+
+
⋅
⋅
+
⋅
=
−
s
= 0,0 + 0,4 = 0,4 mm,
(
)
(
)
95
2
5
,
0
6
,
36
4
,
54
106
2
5
,
0
1
,
3
7
,
4
0
,
1
5
4
⋅
⋅
+
+
⋅
⋅
+
⋅
=
−
s
= 0,0 + 0,2 = 0,2 mm,
(
)
(
)
95
2
5
,
0
1
,
28
6
,
36
106
2
5
,
0
2
,
2
1
,
3
0
,
1
6
5
⋅
⋅
+
+
⋅
⋅
+
⋅
=
−
s
= 0,0 + 0,2 = 0,2 mm,
(
)
(
)
95
2
5
,
0
7
,
19
1
,
28
106
2
5
,
0
6
,
1
2
,
2
0
,
1
7
6
⋅
⋅
+
+
⋅
⋅
+
⋅
=
−
s
= 0,0 + 0,1 = 0,1 mm.
Osiadanie całkowite:
mm
8,5
=
=
∑
i
s
s
<
s
dop
.
= 50 mm
(tab. 4 Normy – Hale przemysłowe).
Warunek II stanu granicznego został spełniony.
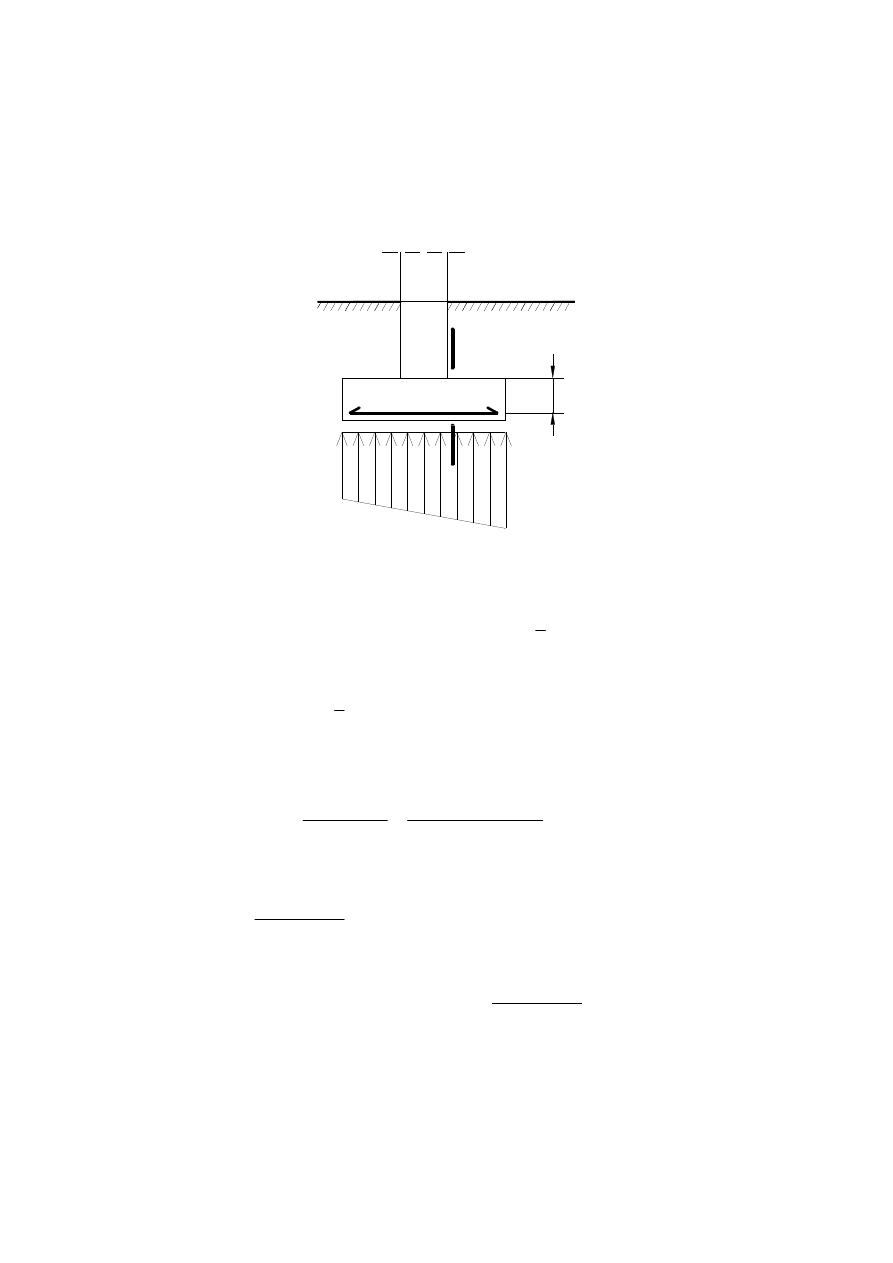
9.
Wymiarowanie zbrojenia stopy
Ostatecznie przyjmujemy stopę prostopadłościenną o wysokości H = 0,50 m. Obliczenia
przeprowadzamy metodą wydzielonych wsporników prostokątnych.
σ
max
I
I
h
0
Maksymalny odpór gruntu działający na stopę:
σ
max
= 385 kPa.
Moment siły działający na stopę w przekroju I – I:
(
)
L
b
B
M
s
I
I
⋅
−
⋅
=
−
2
max
8
1
σ
,
obliczenia przeprowadzamy dla danych: B = L = 1,25 m, b
s
= 0,40 m:
(
)
25
,
1
40
,
0
25
,
1
385
8
1
2
⋅
−
⋅
⋅
=
−I
I
M
= 43,5 kNm.
Zakładamy h
0
= 50 – 4 – 3 = 43 cm, ramię sił wewnętrznych: z = 0,9
⋅h
0
, stal zbrojeniowa
St3S-b (A-I): f
yd
= 210 MPa, obliczamy potrzebny przekrój zbrojenia:
2
3
0
cm
35
,
5
10
210
43
,
0
9
,
0
5
,
43
9
,
0
=
⋅
⋅
⋅
=
⋅
⋅
=
−
yd
I
I
s
f
h
M
A
,
przyjmujemy 5 prętów
φ 12 ⇒ A
s
rz.
= 5,65 cm
2
.
Rozstaw prętów
=
⋅
−
=
4
70
2
1250
l
278 mm
=
⋅
=
⋅
>
mm
mm
h
250
600
500
2
,
1
2
,
1
.
min
,
Ze względu na zbyt duży rozstaw prętów, przyjmujemy konstrukcyjnie:
6 prętów
φ 12 ⇒ A
s
rz.
= 6,79 cm
2
, w rozstawie:
=
⋅
−
=
5
70
2
1250
l
222 mm < 250 mm
Ponieważ stopa fundamentowa jest mała, to przyjmujemy ten sam rozstaw wkładek – bez
zagęszczania i bez skracania ich długości.
Przyjęto beton C20/25.

Ponieważ wysokość stopy: H = 500 mm > 0,3
⋅ (B – b
s
) = 0,3
⋅ (1400 – 400) = 300 mm, nie
ma potrzeby sprawdzenia przebicia stopy.
Obliczenia statyczne zakończono.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron