
Zadania z Podstaw Matematyki
dla studentów
Wy·
zszej Szko÷
y
Informatyki Stosowanej i Zarz ¾
adzania
w Warszawie.
Materia÷y uzupe÷niaj ¾
ace do wyk÷adu Micha÷a Szurka z podstaw matematyki,
do nast ¾
epuj ¾
acego programu:
Wyk÷
ad 1. Podstawowe poj ¾
ecia logiki.
Wyk÷
ad 2. Indukcja matematyczna. Rekursja.
Wyk÷
ad 3. Podstawowe operacje na zbiorach.
Wyk÷
ad 4. Zliczanie (najprostsze sytuacje kombinatoryczne).
Wyk÷
ad 5. Relacje.
Wyk÷
ad 6. Funkcje. Obraz, przeciwobraz zbioru.
Wyk÷
ad 7. Permutacje.
Wyk÷
ad 8. Zbiór pot ¾
egowy.
Wyk÷
ad 9. Iloczyn kartezja´nski i ci ¾
agi.
Wyk÷
ad 10. Relacje równowa·
zno´sci. Zasada abstrakcji.
Wyk÷
ad 11. Relacje porz ¾
adkuj ¾
ace.
Wyk÷
ad 12. Ró·
zne rodzaje relacji porz ¾
adkuj ¾
acych.
Wyk÷
ad 13. Przeliczalno´s´c i nieprzeliczalno´s´c. Moc zbioru.
Wyk÷
ad 14. Paradoksy logiczne i antynomie teorii mnogo´sci.
Wyk÷
ad 15. Jak si ¾
e uczy´c ( w szczególno´sci matematyki)?
1

Wyk÷
ad 1
. Logika
Logika – osoba podejrzana, stale prze´sladowana przez wy·zszych dygnitarzy,
pos÷ów, powa·zne instytucje i dziennikarzy. K.Bartosiewicz
Rozumujemy najcz ¾
e´sciej indukcyjnie b ¾
ad´z dedukcyjnie. Rzadziej stosu-
jemy redukcj ¾
e. Indukcja bywa okre´slana mianem rozumowania „od szczegó÷
u do
ogó÷
u”. Je·
zeli zobaczymy, ·
ze ka·
zdy napotkany Japo´nczyk ma czarne w÷
osy, do-
jdziemy do wniosku, ·
ze jest to ich cecha genetyczna: tylko wyj ¾
atkowo rodowity
Japo´nczyk mo·
ze by´c szatynem. Takie wnioskowanie to najprostsza indukcja:
przez wyliczenie. Drugi, bardziej skomplikowany typ indukcji mamy w rozu-
mowaniu takim jak:
Do tej pory jako´s zawsze tak by÷
o, ·
ze po deszczu ulice by÷
y mokre. Wi ¾
ec i
teraz te·
z tak b ¾
edzie.
Arystoteles ujmuje to tak. Pierwszym typem indukcji nazywa proste wylicze-
nie.
Je·
zeli co´s jest prawd ¾
a dla wielu indywiduów danego gatunku,
to
uz-
najemy, ·
ze jest to prawd ¾
a dla ca÷
ego gatunku
Je·
zeli co´s jest prawd ¾
a dla wielu gatunków nale·
z ¾
acych do tego samego rodzaju,
to
uznajemy, ·
ze jest prawd ¾
a dla ca÷
ego tego rodzaju.
Drugi typ indukcji, w klasy…kacji Arystotelesa, mo·
zna opisa´c jako bezpo´sred-
nie intuicyjne uj ¾
ecie zasad ogólnych na podstawie obserwacji zjawisk szczegó÷
owych.
Filozof podaje przyk÷
ad uczonego, który zauwa·
za wiele razy, ·
ze Ksi ¾
e·
zyc zwró-
cony jest jasn ¾
a stron ¾
a ku S÷
o´ncu. Uczony ten wyprowadza wniosek, ·
ze Ksi ¾
e·
zyc
´swieci odbitym ´swiat÷
em s÷
onecznym. Tak ¾
a indukcj ¾
a mo·
zna nazwa´c przenikli-
wo´sci ¾
a.
W drugim etapie badania naukowego do g÷
osu dochodzi dedukcja, tak jak
we wnioskowaniu:
Je·
zeli pada deszcz, to z nieba leci woda.
Woda moczy wszystkie przedmioty, na które spadnie.
A zatem: je·
zeli pada deszcz, to ulice b ¾
ed ¾
a mokre.
Wydaje nam si ¾
e to dzi´s proste i oczywiste. A jest to wed÷
ug Arystotelesa na-
jwa·
zniejszy typ wnioskowania, tak zwany sylogizm Barbara. Arystoteles uwa·
za÷
,
·
ze w÷
asno´sci ogólne tkwi ¾
a w sposób istotny w indywidualnych obiektach pewnej
klasy i ·
ze zdania postaci „ka·
zde S jest P” oddaj ¾
a struktur ¾
e tej relacji. Wed÷
ug
niego, zdania naukowe powinny by´c w÷
a´snie tej postaci. Dlatego po´swi ¾
eci÷wiele
wysi÷
ku analizie opisanej regu÷
y dowodzenia.
Od strony metodologicznej, wyró·
zniamy jeszcze rozumowanie redukcyjne.
W nim ze skutków wnioskujemy o przyczynach:
Ulice s ¾
a mokre. Zatem pada÷deszcz, bo co innego zmoczy÷
oby jezdni ¾
e?
2

Matematycy s ¾
a przyzwyczajeni do dowodów niewprost. S ¾
a one nietrudne,
ale dawniej uchodzi÷
y za zbyt "wyra…nowane". Oto rozumowanie Archimedesa,
prowadz ¾
ace do dowodu twierdzenia:
Ci ¾
e·
zary pozostaj ¾
ace w równowadze, po÷
o·
zone w jednakowych odleg÷
o´sciach
od punktu podparcia, s ¾
a równe.
Wychodzimy z tego, ·
ze równe ci ¾
e·
zary, po÷
o·
zone w równych odleg÷
o´sciach
od punktu podparcia, równowa·
z ¾
a si ¾
e. Chcemy, mówi ¾
ac dzisiejszym j ¾
ezykiem,
wykaza´c twierdzenie odwrotne. Przypu´s´cmy, ·
ze nie jest ono jest prawdziwe. A
zatem przyjmujemy, ·
ze prawd ¾
a jest, i·
z równowa·
z ¾
ace si ¾
e ci ¾
e·
zary s ¾
a nierównej
wielko´sci. Jeden z tych ci ¾
e·
zarów jest wobec tego wi ¾
ekszy. Zmniejszmy go tak,
by by÷równy drugiemu. Ale z obserwacji wiemy, ·
ze je·
zeli jeden z ci ¾
e·
zarów
pozostaj ¾
acych w równowadze zmniejszymy, to d´zwignia przechyli si ¾
e w stron ¾
e
ci ¾
e·
zaru niezmniejszonego. D´zwignia nie b ¾
edzie pozostawa´c w równowadze, a
jest sprzeczne z za÷
o·
zeniem.
Najwa·
zniejsze b÷¾
edy logiczne.
Dialela –b÷¾
edne ko÷
o w dowodzie.
Idem per idem: (to samo przez to samo): jak zrobi´c bieniaszki? Wzi ¾
a´c pó÷
funta ciel ¾
eciny, posoli´c, ubi´c t÷
uczkiem, pokroi´c na drobne i zrobi´c bieniaszki.
Ignotum per ignotum (nieznane przez nieznane): co to s ¾
a bieniaszki? Och,
to po prostu to samo co sepulki !
Zadanie 1.1. Które z poni·
zszych zda´n s ¾
a prawdziwe, a które fa÷
szywe:
a) 2 2 = 4 ;
b) 2 2 6= 5 ;
c) 2
100
= 1267 650 600 228 229 401 496 703 205 3767 ;
d) Nieprawda, ·
ze liczba rozwi ¾
aza´n równania x
2
4x+3 = 0 jest parzysta
;
e) Nieprawda, ·
ze liczba rozwi ¾
aza´n równania x
2
4x + 3 = 0 nie jest
nieparzysta ;
f) Je·
zeli
1
x
= 0, to x
2
x = 2008 ;
g) Je·
zeli x
2
= y
2
; to x
3
= y
3
; (x; y oznaczaj ¾
a tu liczby rzeczywiste) ;
h) Je·
zeli x
3
= y
3
; to x
2
= y
2
; (x; y oznaczaj ¾
a tu liczby rzeczywiste);
i) Je·
zeli x
2
= y
2
; to x
3
= y
3
; (x; y oznaczaj ¾
a tu liczby zespolone) ;
j) Je·
zeli x
3
= y
3
; to x
2
= y
2
; (x; y oznaczaj ¾
a tu liczby zespolone);
k) Je·
zeli A
3
= B
3
; to A
2
= B
2
; (A; B oznaczaj ¾
a tu macierze kwadra-
towe);
Przypomn ¾
e, ·
ze je·
zeli prawdziwa jest implikacja
)
, to
jest warunkiem wystarczaj ¾
acym (dostatecznym) na to, by zachodzi÷
o
;
jest warunkiem koniecznym na to, by
.
Gdy prawdziwa jest równowa·
zno´s´c
,
, to
jest warunkiem koniecznym
i dostatecznym na to, by . Mówimy te·
z, ·
ze
zachodzi wtedy i tylko wtedy, gdy
.
Okre´sle´n „warunek dostateczny”i „warunek wystarczaj ¾
acy”u·
zywamy wymi-
ennie.
Zadanie 1.2. Które z poni·
zszych zda´n jest prawdziwe:
3

a) Warunkiem koniecznym na to, by trójk ¾
at by÷równoboczny jest, by
by÷równoramienny;
b) Warunkiem dostatecznym na to, by trójk ¾
at by÷równoboczny jest, by
by÷równoramienny;
c) Warunkiem koniecznym na to, by trójk ¾
at by÷równoramienny jest, by
by÷równoboczny;
d) Warunkiem dostatecznym na to, by trójk ¾
at by÷równoramienny jest,
by by÷równoboczny;
e) Warunkiem dostatecznym na to, by liczba naturalna by÷
a podzielna
przez 2 jest, by by÷
a podzielna przez 4;
f) Warunkiem dostatecznym na to, by liczba naturalna by÷
a podzielna
przez 4 jest, by by÷
a podzielna przez 2;
g) Warunkiem koniecznym na to, by liczba naturalna by÷
a podzielna
przez 2 jest, by by÷
a podzielna przez 4;
h) Warunkiem koniecznym na to, by liczba naturalna by÷
a podzielna przez
4 jest, by by÷
a podzielna przez 2;
i) Warunkiem wystarczaj ¾
acym do prawdziwo´sci zdania 9
x
2R
x
2
a+1
jest a
0;
j) Warunkiem koniecznym prawdziwo´sci zdania 9
x
2R
x
2
a + 1 jest
a
0;
k) Warunkiem wystarczaj ¾
acym do prawdziwo´sci zdania 9
x
2R
x
2
a + 1
jest a
1;
l) Warunkiem koniecznym prawdziwo´sci zdania 9
x
2R
x
2
a + 1 jest
a
1;
m) Warunkiem koniecznym prawdziwo´sci zdania 9
x
2R
x
2
a + 1 jest
j a j
1;
n) Warunkiem wystarczaj ¾
acym do prawdziwo´sci zdania 9
x
2R
x
2
a + 1
jest j a j
1;
o) Warunkiem koniecznym na to, by ci ¾
ag by÷
a zbie·
zny jest, by spe÷
nia÷
warunek Cauchy’ego;
p) Warunkiem koniecznym i dostatecznym na to, by macierz kwadra-
towa mia÷
a nacierz odwrotn ¾
a jest, by jej wyznacznik by÷ró´zny od zera;
q) Warunkiem wystarczaj ¾
acym do zbie·
zno´sci szeregu liczbowego
P
a
n
jest
zbie·
zno´s´c ci ¾
agu (a
n
);
r) Warunkiem koniecznym do zbie·
zno´sci szeregu liczbowego
P
a
n
jest
zbie·
zno´s´c ci ¾
agu (a
n
);
s) Warunkiem wystarczaj ¾
acym do zbie·
zno´sci ci ¾
agu (a
n
) jest zbie·
zno´s´c
szeregu liczbowego
P
a
n
;
t) Warunkiem koniecznym do zbie·
zno´sci ci ¾
agu (a
n
) jest zbie·
zno´s´c sz-
eregu liczbowego
P
a
n
;
u) Warunkiem koniecznym do zdobycia mistrzostwa ´swiata w rzucie
dyskiem jest, by umie´c nim rzuca´c;
v) Warunkiem wystarczaj ¾
acym do zdobycia mistrzostwa ´swiata w rzucie
dyskiem jest, by umie´c nim rzuca´c;
w) Warunkiem wystarczaj ¾
acym do tego, by zosta´c Miss World jest, by
by´c kobiet ¾
a,
4

x) Warunkiem koniecznym do tego, by zosta´c Miss World jest, by by´c
kobiet ¾
a,
y) Warunkiem wystarczaj ¾
acym do tego, by umie´c rozwi ¾
aza´c wszystkie
zadania z tego skryptu jest, by umie´c czyta´c;
z) Warunkiem koniecznym i dostatecznym do tego, by zosta´c królem
Togo jest, by by´c Eskimosem.
Zadanie 1.3. Które z podanych ni·
zej zda´n s ¾
a warunkami dostatecznymi, a
które wystarczaj ¾
acymi do prawdziwo´sci zdania 9
x
2R
x
2
a + 1
a) a
0
b) a =
1
c) a < 0
d) a
1
e) j a j
1
Odpowied´z: Konieczne s ¾
a a; c; d; e
Dostateczne s ¾
a: b; d:
Jak to rozwi ¾
aza´c? Wystarczy si ¾
e zastanowi´c, co to znaczy „konieczny” i
"dostateczny" (=„wystarczaj ¾
acy”).
Je·
zeli z alf a wynika beta, to alf a jest
wystarczaj ¾
acy dla beta: Bo przecie·
z wystarczy, ·
zeby zasz÷
o alf a; ·
zeby beta te·
z
si ¾
e zdarzy÷
o. Z tego, ·
ze deszcz pada, wynika, ·
ze ulice sa mokre. A wi ¾
ec wystar-
czy, ·
zeby troch ¾
e popada÷
o i ju·
z jest mokro. Przeciwnie, beta jest konieczny dla
alf a:Na przyk÷
ad, z tego, ·
ze pada deszcz, wynika, ze ulice s ¾
a mokre. Je·
zeli
zobaczymy, such ¾
a ulic ¾
e, to znaczy, ·
ze deszcz nie pada. Ulice musz ¾
a by´c mokre
po deszczu.
Nst ¾
epnie, trzeba oswoi´c podany warunek z kwanty…katorem. Co znaczy po-
dany warunek: istnieje iks o tej w÷
asno´sci, ·
ze liczba przeciwna do jego kwadratu
spe÷
nia co´s tam? Otó·
z przecie·
z „liczb ¾
a przeciwn ¾
a do kwadratu”mo·
ze by´c ka·
zda
liczba ujemna (i zero) i odwrotnie, ka·
zda liczba ujemna (tak·
ze i zero) jest liczb ¾
a
przeciwn ¾
a do pewnego kwadratu. Na przyk÷
ad -2008 jest liczb ¾
a przeciwn ¾
a do
kwadratu liczby
p
2008: A zatem zdanie zamieszczone znaczy ni mniej ni wi ¾
ecej
tylko: a + 1 jest liczb ¾
a ujemn ¾
a (b ¾
ad´z zerem). Co wystarcza, by a + 1
0?
Oczywi´scie jest to to samo, co a
1. Zatem ten warunek jest i konieczny
i dostateczny. Warunek a) jest oczywi´scie za s÷
aby, bo
1
2
0, ale nie jest
1:Podobnie z c) . Warunek b) wystarcza, ale nie jest konieczny. Wreszcie,
je·
zeli liczba jest mniejsza od
1, to jej modu÷(warto´s´c bezwzgl ¾
edna) jest wi ¾
ek-
szy od 1, ale nie na odwrót.
Zadanie 1.4.
Sformu÷
owa´c twierdzenie odwrotne do twierdzenia Pitago-
rasa, twierdzenia Talesa i twierdzenia Bezouta. Sformu÷
owa´c twierdzenie prze-
ciwne do twierdzenia Pitagorasa, twierdzenia Talesa i twierdzenia Bezouta.
Sformu÷
owa´c twierdzenie przeciwstawne do twierdzenia Pitagorasa, twierdzenia
Talesa i twierdzenia Bezouta.
Zadanie 1.5. Na p÷
aszczy´znie zaznacz zbiór tych punktów (x; y), których
wspó÷
rz ¾
edne nie spe÷niaj ¾
a warunku x 6= 0 ) y 6= 0:
Zadanie 1.6. Jakich trójk ¾
atów dotyczy nast ¾
epuj ¾
ace twierdzenie:
Je·zeli trójk ¾
at jest prostok ¾
atny, to kwadrat przeciwprostok ¾
atnej jest równy
sumie kwadratów przyprostok ¾
atnych.
Zadanie 1.7.
Dla jakich liczb m i n jest prawd ¾
a, ·
ze nast ¾
epuj ¾
ace dwa zdania s ¾
a równowa·
zne?
5

Liczba k jest podzielna przez mn : Liczba k jest podzielna przez m i jest
podzielna przez n .
Zadanie 1.8. Uzupe÷
nij
K ¾
at wpisany w okr ¾
ag jest . . . . . , k ¾
at jest oparty na ´srednicy.
Zadanie 1.9. Uzupe÷
nij nast ¾
epuj ¾
ace twierdzenia, wstawiaj ¾
ac w miejsce kropek
s÷
owa konieczny, dostateczny, albo konieczny i dostateczny:
a)
Warunkiem ... ... na to, by trójk ¾
at by÷równoramienny, jest, aby dwa
jego k ¾
aty mia÷
y te same miary;
b)
Podzielno´s´c liczby ca÷
kowitej przez 2 i przez 3 jest warunkiem ... ...
jej podzielno´sci przez 6 ;
c)
Warunkiem ... ... na to, by trójk ¾
at by÷równoramienny, jest przys-
tawanie dwóch jego k ¾
atów.
Zadanie 1.10.
a) O co chodzi w tej wypowiedzi: Nie ma powodu, ·zebym nie ca÷kowicie si ¾
e
z tob ¾
a nie zgadza÷. Wypowiedz t ¾
e my´sl pro´sciej.
b) Czy to jest podstawa do dyskwali…kacji: Zwyci ¾
ezca Tour de France nie
zaprzeczy÷doniesieniom o niestosowaniu przez niego niedozwolonych ´srodków.
c) Czy to dobrze, czy ´zle, ·
ze w pewnej instytucji nikt nigdy niczego niepotrzeb-
nego nie robi ?
d) Przet÷umacz na strawn ¾
a polszczyzn ¾
e: Nie s ¾
adz ¾
e, abym nie mog÷
a Ci nie
powiedzie´c o tym, ·
ze nie przemy´sla÷
am decyzji o powtórnej zmianie decyzji, ·
ze
nie wyjd ¾
e za ciebie za m ¾
a·
z.
W logice klasycznej odró·
znia si ¾
e starannie terminy „znaczy” i „oznacza”.
Dwie nazwy mog ¾
a znaczy´c to samo, a oznacza´c co innego. Oznaczenie odnosi
si ¾
e do zakresu, znaczenie do tre´sci. „Stolica Wielkopolski”i „najwi ¾
eksze miasto
nad Wart ¾
a” oznaczaj ¾
a to samo, ale znacz ¾
a co innego. Tre´sci ¾
a poj ¾
ecia „stolicy”
jest to, ·
ze urz ¾
eduj ¾
a tam w÷
adze (wojewódzkie, pa´nstwowe). Gdy us÷
yszymy za´s
„najwi ¾
eksze miasto nad Wart ¾
a” , by´c mo·
ze najpierw wyobrazimy sobie du·
ze
miasto nad malownicz ¾
a rzek ¾
a, a dopiero po chwili dotrze do nas, ·
ze to Pozna´n.
Zakresem obu poj ¾
e´c jest zbiór, którego jedynym elementem jest miasto z ra-
tuszem z trykaj ¾
acym si ¾
e w po÷
udnie kozio÷
kami na Starym Rynku, nieopodal
ulicy ´Swi ¾
ety Marcin.
Zawieranie si ¾
e zakresów poj ¾
e´c (inkluzja zbiorów) nazywa÷
o si ¾
e w dawniejszej
logice stosunkiem podporz ¾
adkowania i nadrz ¾
edno´sci, na zbiory o niepustym
przeci ¾
eciu mówi „poj ¾
ecia krzy·
zuj ¾
ace si ¾
e”, poj ¾
ecia reprezentowane przez zbiory
roz÷¾
aczne nazywano „wykluczaj ¾
acymi si ¾
e”, a roz÷¾
aczne i dope÷
niaj ¾
ace do ca÷
ej
przestrzeni „przeciwnymi”(zatem ‘zielony’i ‘czerwony’to poj ¾
ecia wykluczaj ¾
ace
si ¾
e i sprzeczne, a przeciwnym do ‘zielonego’jest ‘niezielony’).
Zadanie 1.11.
Okre´sli´c, w jakim stosunku pozostaj ¾
a do siebie zakresy
nast ¾
epuj ¾
acych poj ¾
e´c: trójk ¾
at równoboczny, trójk ¾
at równok ¾
atny, papie·
z, biskup
rzymski, pierwszy cesarz Francji, zwyci ¾
ezca spod Austerlitz, sole, cia÷
a chemiczne
z÷
o·
zone, dzie÷
a S÷
owackiego, Kordian, wieloboki, utwory geometryczne p÷
askie,
…gury maj ¾
ace przek ¾
atne, ksi ¾
a·
zki naukowe, ksi ¾
a·
zki zajmuj ¾
ace, mahometanie,
6

mieszka´ncy Europy, ciecze, cia÷
a l·
zejsze od wody, niziny, miejsca bagniste, pros-
tok ¾
at, czworobok maj ¾
acy ko÷
o wpisane, prze·
zuwacz, zwierz ¾
e mi ¾
eso·
zerne, wulkan,
góra w Polsce.
Zadanie 1.12.
Poda´c poj ¾
ecia a) równowa·
zne, b) nadrz ¾
edne, c) krzy·
zuj ¾
ace
si ¾
e, d) podrz ¾
edne, e) przeciwne, f) sprzeczne wzgl ¾
edem ka·
zdego z nast ¾
epuj ¾
acych
poj ¾
e´c: woda, sze´scian, ptak, pierwszy po÷
udnik, wszystko, nic.
Zadanie 1.13. Czy prawdziwe jest zdanie:
Je´sli na ´swi ¾
etego Prota jest pogoda albo s÷
ota, na ´swi ¾
etego Hieronima jest
deszcz, albo go nie ma;
Zadanie 1.14. Wyra´z w inny sposób zaprzeczenie zda´n:
a) nieprawda, ·
ze niebo jest niebieskie,
b) nie jestem m ¾
adry,
c) 8
">0
9 j x
1
x
2
j < ) j f(x
1
)
f (x
2
) j < " = 0
d) w niedziele nikt tu nigdy niczego niepotrzebnego nie robi.
Zadanie 1.15.
Skonstruuj, wska·
z albo opisz, jak mog ¾
a wygl ¾
ada´c kontr-
przyk÷
ady do nastepuj ¾
acych fa÷
szywych stwierdze´n:
a) ka·
zda liczba podzielna przez 2 jest podzielna przez 4;
b) w ka·
zdym trójk ¾
acie ´srodek okr ¾
egu opisanego pokrywa si ¾
e ze ´srodkiem
okr ¾
egu wpisanego;
c) na ka·
zdym czworok ¾
acie da si ¾
e opisa´c okr ¾
ag;
d) W ka·
zdy czworok ¾
at mo·
zna wpisa´c ko÷
o.
e) W ·
zaden czworok ¾
at nie mo·
zna wpisa´c ko÷
a.
f) Na ka·
zdym czworok ¾
acie mo·
zna opisa´c ko÷
o.
g) Na ·
zadnym czworok ¾
acie nie mo·
zna opisa´c ko÷
a.
h) je·
zeli funkcja jest rosn ¾
aca dla x < 0 i jest rosn ¾
aca dla x > 0 , to jest
rosn ¾
aca dla wszystkich x;
i) ka·
zdy m ¾
e·
zczyzna jest wy·
zszy od ka·
zdej kobiety;
j) ·
zaden student nie umie algebry;
k) ka·
zdy student zna dobrze algebr ¾
e;
l) wszyscy studenci chodz ¾
a zawsze na zaj ¾
ecia;
m) gdy tylko wychodz ¾
e z domu, ·
zona pyta, dok ¾
ad id ¾
e;
n) Ka·
zda liczba podzielna przez 3 jest podzielna przez 7.
o) Je·
zeli dwie liczby maj ¾
a równe kwadraty, to s ¾
a równe.
p) Je·
zeli sin a = sin b , to a = b.
q) Ka·
zda liczba pierwsza jest nieparzysta.
r) Nie ma dwóch liczb pierwszych ró·
zni ¾
acych si ¾
e tylko o 3 .
s) Nie istniej ¾
a rozwi ¾
azania równania x
n
+ y
n
= z
n
w liczbach ca÷
kowitych.
t) Je·
zeli a; b; c s ¾
a d÷
ugo´sciami boków trójk ¾
ata prostok ¾
atnego, to a
2
+ b
2
= c
2
;
u) Je·
zeli wczoraj by÷dzie´n 28 lutego, to dzi´s jest 1 marca.
v) Je·
zeli wczoraj by÷dzie´n 28 lutego, to dzi´s jest 29 lutego.
x) Prezydent pa´nstwa musi by´c kobiet ¾
a.
y) Ka·
zdy Polak uwielbia chipsy czekoladowe.
z) Jak przygoda, to tylko we Lwowie.
7

Zadanie 1.16.
Skonstruuj, wska·
z albo opisz, jak mog ¾
a wygl ¾
ada´c kontr-
przyk÷
ady do nast ¾
epuj ¾
acych fa÷
szywych stwierdze´n:
a) Je´sli Barbara po lodzie, to Bo·
ze Narodzenie po wodzie.
b) Je´sli na ´swi ¾
etego Jana pada wieczór albo z rana, na ´swi ¾
etego Izydora pada
rano lub z wieczora.
c) Dzieckiem w kolebce kto ÷
eb urwa÷hydrze, ten m÷
ody zdusi centaury.
d) Pi÷
ka no·
zna jest takim sportem, gdzie dwie dru·
zyny graj ¾
a 90 minut, a
wygrywaj ¾
a Niemcy.
e) Z punktu widzenia kobiety m ¾
e·
zczyzna jest jak telefon.
Albo jej nie
odpowiada, albo jest zaj ¾
ety.
f) Ka·
zde zwierz ¾
e,co ma pierze, fruwa.
g) Matematyka? Nikt jej nie lubi i nikt jej nie umie.
Zadanie 1.17.
1. Zdanie p brzmi: Bitwa pod Grunwaldem odby÷a si ¾
e przed rokiem 1500 lub
bitwa pod Grunwaldem odby÷a si ¾
e po roku 1450.
Zdanie q brzmi: Je·zeli 1 = 2, to 2 = 10. Wtedy (wybierz prawid÷
ow ¾
a
odpowied´z):
a) obydwa zdania p i q s ¾
a prawdziwe,
b) p jest prawdziwe, q fa÷
szywe,
c) p jest fa÷
szywe, q prawdziwe,
d) obydwa zdania s ¾
a fa÷
szywe.
Zadanie 1.18.
Zdanie p ) ( p ) q) jest fa÷szywe, gdy (wybierz prawid÷ow ¾
a odpowied´z)
a) obydwa zdania p i q s ¾
a prawdziwe,
b) p jest prawdziwe, q fa÷
szywe,
c) p jest fa÷
szywe, q prawdziwe,
d) obydwa zdania s ¾
a fa÷
szywe.
Rozwi ¾
azanie. Trudno´sci ¾
a w zadaniu tym mo·
ze by´c samo zrozumienie tre´sci.
Poprawnej odpowiedzi mo·
zna najlepiej udzieli´c, podstawiaj ¾
ac za p , q warto´sci
logiczne 0, 1. W a) mamy 1 ) ( 1 ) 1) ; jest to zdanie prawdziwe. W b) mamy
1 ) ( 1 ) 0) , jest to zdanie fa÷szywe. W c) mamy 0 ) ( 0 ) 1) ; jest to
zdanie prawdziwe. W d) mamy 0 ) ( 0 ) 0) ; jest to zdanie prawdziwe.
Zadanie 1.19. Kulturalny doping. W czasie meczu pi÷
karskiego rzucono na
muraw¾
e stadionu butelk¾
e, która tra…÷
a bramkarza dru·
zyny go´sci. Oskar·
zono o
to czterech kibiców: Antoniego, Mariana, Witolda i Bogdana. Ka·
zdy da÷jedn ¾
a
odpowied´z fa÷
szyw ¾
a i dwie prawdziwe:
Antoni: To nie ja. Witold nie wie, kto rzuci÷butelk¾
e. Wie to Marian.
Bogdan: To nie ja. Pierwszy raz widz ¾
e Mariana. Butelk¾
e rzuci÷Witold.
Marian: To nie ja. To zrobi÷Antoni. Przez ca÷
y mecz pi÷
em piwo z Bog-
danem.
Witold: To nie ja. To zrobi÷Marian. Bogdan k÷
amie, ·
ze to ja.
Kto rzuci÷butelk¾
e?
8

Rozwi ¾
azanie. Butelk¾
e rzuci÷Antoni. Przypu´s´cmy bowiem, ·
ze to Bogdan.
Jego pierwsza wypowied´z jest zatem fa÷
szywa, wi ¾
ec dwie pozosta÷
e prawdziwe.
W szczególno´sci prawdziwa by÷
aby wypowied´z o winie Witolda. A zatem z
przypuszczenia, ·
ze to Bogdan, wynika, ·
ze to nie Bogdan. Regu÷
a Claviusa mówi,
·
ze to nie Bogdan. Przypu´s´cmy, ·
ze to Marian. Zatem jego pierwsza wypowied´z
o w÷
asnej niewinno´sci jest fa÷
szywa. Musi by´c zatem prawd ¾
a, ·
ze butelk¾
e rzuci÷
Antoni. Mamy t ¾
e sam ¾
a sytuacj ¾
e:
z za÷
o·
zenia, ·
ze to Marian wynika, ·
ze to nie on. A zatem (regu÷
a Claviusa) to
nie Marian. Tak samo przekonujemy si ¾
e o niewinno´sci Witolda. Zostaje Antoni.
Zadanie 1.20. Po maturze. Na spotkaniu z okazji dziesi ¾
eciolecia matury
kto´s powiedzia÷
: „Ka·
zdy absolwent naszego liceum uko´nczy÷potem studia wy·
zsze”.
Czy z tego wynika, ·
ze ci, co nie uko´nczyli studiów wy·
zszych, byli absolwentami
innych liceów? Czy te zdania s ¾
a równowa·
zne?
Odpowied´z. S ¾
a ludzie doro´sli, którzy nie sko´nczyli liceów. Ka·
zdy z nich
stanowi kontrprzyk÷
ad na stwierdzenie, ·
ze podane zdania s ¾
a równowa·
zne.
Zadanie 1.21. Student rozwi ¾
azywa÷test. Mia÷udzieli´c odpowiedzi „tak”
lub „nie”na pi ¾
e´c pyta´n. Wiedzia÷
, ·
ze w te´scie by÷
o wi ¾
ecej odpowiedzi twierdz ¾
a-
cych ni·
z przecz ¾
acych i ·
ze nie by÷
o tej samej odpowiedzi na trzy kolejne pytania.
Domy´sli÷si ¾
e, ·
ze pytanie pierwsze i ostatnie maj ¾
a przeciwne odpowiedzi. Zna÷
tylko odpowied´z na pytanie drugie i siedzia÷bezradnie, dopóki nauczyciel nie
podpowiedzia÷mu: „skoro znasz odpowied´z na drugie, to tak, jak by´s zna÷na
wszystkie”. Jakie by÷
y odpowiedzi na test?
Zadanie 1.22. Matematycy na balu. Czterej ma÷·
ze´nstwa wybra÷
y si ¾
e na
bal sylwestrowy. Z pocz ¾
atku ka·
zdy ta´nczy÷z w÷
asn ¾
a ·
zon ¾
a, ale wkrótce pary
si ¾
e przemiesza÷
y. Basia ta´nczy÷
a z Edwardem, Ola z m ¾
e·
zem Karoliny, Dorota
z m ¾
e·
zem Oli, Franciszek z ·
zon ¾
a Janka i Janek z ·
zon ¾
a Edwarda. W przerwie
Hubert opowiada÷dowcipy. Podaj imiona wspó÷
ma÷·
zonków i kto z kim ta´nczy÷
.
Rozwi ¾
azanie. Ponumerujmy informacje.
1. Basia ta´nczy÷
a z Edwardem, 2. Ola ta´nczy÷
a z m ¾
e·
zem Karoliny, 3. Dorota
ta´nczy÷
a z m ¾
e·
zem Oli, 4. Franciszek ta´nczy÷z ·
zon ¾
a Janka, 5. Janek ta´nczy÷z
·
zon ¾
a Edwarda, 6. Jeden z m ¾
e·
zów (ten dowcipny) ma na imi ¾
e Hubert.
Z przes÷
anki 1 wiemy, ·
ze Basia nie jest ·
zon ¾
a Edwarda. Jak ma na imi ¾
e
tancerz Oli? Kto jest ·
zon ¾
a Edwarda? Nie Ola, bo z m ¾
e·
zem Oli ta´nczy÷
a Dorota
(przes÷
anka nr 3), a z Edwardem Basia. Nie Karolina, bo z m ¾
e·
zem Karoliny
ta´nczy÷
a Ola (przes÷
anka nr 2), a z Edwardem Basia (przes÷
anka nr 1). Zatem
Edward i Dorota to ma÷·
ze´nstwo. Zatem Janek ta´nczy÷z Dorot ¾
a (przes÷
anka nr
5). Z przes÷
anki nr 3 wynika zatem, ·
ze Janek jest m ¾
e·
zem Oli. Przes÷
anka nr 4
powiada, ·
ze Franciszek ta´nczy÷z Ol ¾
a, a wi ¾
ec (nr 2) m ¾
a·
z Karoliny to Franciszek.
Basi przypada zatem dowcipny Hubert. A zatem:
Ta´nczyli: Basia - Edward, Dorota - Janek, Ola - Franciszek, Karolina -
Hubert.
9
Ma÷·
ze´nstwa: Dorota - Edward, Ola - Janek, Karolina - Franciszek, Basia -
Hubert.
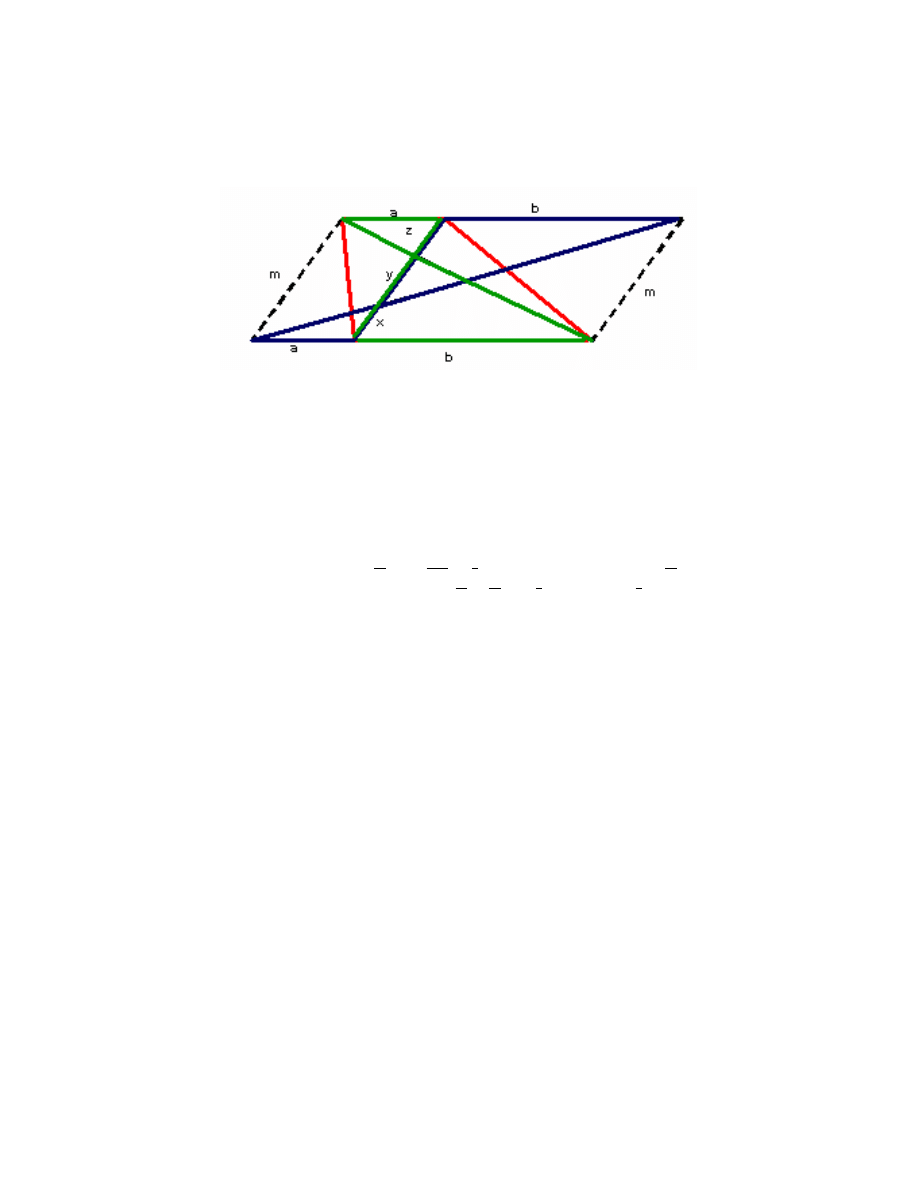
Zadanie 1.23. Trapez nie istnieje. Wyka·
zemy, ·
ze …gura zwana trapezem nie
istnieje. Przypu´s´cmy, ·
ze jest co´s takiego, jak trapez. Przed÷
u·
zmy podstawy
w sposób pokazany na rysunku tak, ·
zeby utworzy÷si ¾
e równoleg÷
obok. Jego
przek ¾
atne dziel ¾
a drug ¾
a z przek ¾
atnych trapezu na odcinki, których d÷
ugo´sci oz-
naczymy przez x; y; z, jak na rysunku. Z podobie´nstwa odpowiednich trójk ¾
atów
mamy proporcje: x + y =
bz
a
oraz
y+z
x
=
b
a
; sk ¾
ad wyznaczamy y + z =
bx
a
.
Zatem x
z = (x + y)
(y + z) =
bz
a
bx
a
=
b
a
(x
z), czyli
b
a
=
1
Ale liczby a; b to d÷
ugo´sci podstaw trapezu. Je·
zeli ich suma wynosi zero, to
one same s ¾
a zerami. To znaczy, ·
ze nie mo·
ze istnie´c …gura taka jak trapez.
Znajd´z b÷¾
ad w tym rozumowaniu.
Zadanie 1.24. (z podr ¾
ecznika Gda´nskiego Wydawnictwa O´swiatowego). Oce´n
warto´s´c logiczn ¾
a podanych zda´n. Wypowiedz je pro´sciej, w formie twierdz ¾
acej.
a) Nieprawda, ·
ze niebo czasem jest niebieskie.
b) Nieprawda, ·
ze nie ma dymu bez ognia.
c) Nie ka·
zdy Polak jest lekarzem.
d) Nieprawda, ·
ze istnieje ÷
abed´z, który nie jest bia÷
y.
Zadanie 1.25. Ucz si ¾
e logiki! S ¾
edzia na rozprawie:
–Je´sli oskar·
zony pope÷
ni÷to przest ¾
epstwo, to mia÷wspólnika.
Obro´nca:
–To nieprawda!
Dlaczego jest to najgorsza rzecz, jak ¾
a móg÷powiedzie´c? Wskazówka: przy-
pomnij sobie prawo zaprzeczenia implikacji!
Zadanie 1.26. Kto´s naby÷jaki´s artyku÷za 100 z÷
, sprzeda÷za 200 z÷
,
odkupi÷znów za 300 z÷i sprzeda÷za 400 z÷
. Ile na tym zyska÷
?
Zadanie 1.27. Kto´s poprosi÷w restauracji o piwo . Kelner przyniós÷
,
ale go´s´c w tym czasie si ¾
e rozmy´sli÷i poprosi÷o coca-col ¾
e w tej samej cenie.
Po wypiciu wsta÷i skierowa÷si ¾
e do wyj´scia. Kelner dogoni÷go przy wyj´sciu
i upomnia÷si ¾
e o zap÷
at ¾
e.
„Za co?” zdumia÷si ¾
e go´s´c?
„Jak to za co?
Za
10

lemoniad ¾
e!”. „Przecie·
z za col ¾
e da÷
em panu piwo, które pan zabra÷
!”. „W takim
razie prosz ¾
e zap÷
aci´c za piwo!”. „Zap÷
aci´c za piwo? Przecie·
z ja piwa nie pi÷
em!”.
Gdzie jest b÷¾
ad w tym rozumowaniu?
Zadanie 1.28. Dwie monety daj ¾
a ÷¾
acznie 3 z÷
ote, cho´c jedna z nich nie jest
z÷
otówk ¾
a. Jak to mo·
zliwe?
Zadanie 1.29. Pan A mia÷fa÷
szyw ¾
a stuz÷
otówk¾
e. Zap÷
aci÷ni ¾
a denty´scie
za plomb ¾
e. Dentysta wraca÷taksówk ¾
a do domu i zap÷
aci÷tym banknotem za
kurs. Taksówkarz wyda÷banknot na benzyn ¾
e. W÷
a´sciciel stacji benzynowej
podarowa÷banknot swojemu synowi, który kupi÷za niego kalkulator w sklepie
obok. Akurat zaraz potem do tego samego sklepu przyszed÷pan A. Za swój
zakup warto´sci 100 z÷
otych da÷200 z÷
otych i jako reszt ¾
e otrzyma÷ow ¾
a fa÷
szyw ¾
a
stuz÷
otówk¾
e. Kto na tych transakcjach straci÷i ile? Czy kto´s zarobi÷
?
Zadanie 1.30. Urz ¾
ad miasta chcia÷zmieni´c zasady ruchu w centrum. Pra-
cownik dosta÷zadanie zawieszenia trzech znaków drogowych na jednym s÷
upku.
Nie wzi ¾
a÷instrukcji, w jakiej kolejno´sci je umieszcza´c i nie obejrza÷tych znaków.
Na miejscu okaza÷
o si ¾
e, ·
ze s ¾
a to znaki: nakaz skr ¾
etu w prawo, zakaz skr ¾
etu w
prawo i tabliczka "nie dotyczy autobusów". Czy istnieje takie ustawienie tych
znaków, ·
zeby ta kombinacja mia÷
a sens? Czy wszystkie logiczne ustawienia b ¾
ed ¾
a
znaczy´c to samo?
Zadanie 1.31. Które z nastepuj ¾
acych zda´n s ¾
a prawdziwe dla liczb rzeczy-
wistych a; b; c:
9
a
9
b
9
c
a + b + c = 0
9
a
9
b
8
c
a + b + c = 0
9
a
8
b
8
c
a + b + c = 0
8
a
9
b
9
c
a + b + c = 0
8
a
8
b
9
c
a + b + c = 0
8
a
8
b
8
c
a + b + c = 0
Zadanie 1.32. Które z podanych ni·
zej zda´n s ¾
a warunkami dostatecznymi, a
które wystarczaj ¾
acymi do prawdziwo´sci zdania 9
x
2R
x
2
a + 1
a) a
2009
b) a =
1
c) a
1
d) a
2009
e)
j a j
1
Rozwi ¾
azanie.
Przepiszmy zdanie 9
x
2R
x
2
a + 1 tak 9
x
2R
x
2
a
1 .
A zatem kwadrat pewnej liczby rzeczywistej jest mniejszy (b ¾
ad´z równy)
a
1:
Takie stwierdzenie jest równowa·
zne z tym, ·
ze liczba
a
1 jest dodatnia b ¾
ad´z
równa zero, a
1
0, st ¾
ad a
1. Zatem warunkiem równowa·
znym (=
koniecznym i dostatecznym) stwierdzeniu, jest a
1: Warunek a
2 jest
wystarczaj ¾
acy, ale nie konieczny. Wystarczy bowiem, by liczba a by÷
a mniejsza
od 2009, by a + 1 by÷
a liczba ujemna, a wtedy znajdziemy odpowiednie x; na
przyk÷
ad ka·
zde x nie wi ¾
eksze ni·
z
p
a
1. Ale liczba a nie musi wcale by´c „a·
z
tak ma÷
a” , mo·
ze by´c np. równa 2006. Podobnie z warunkiem a =
1. Je·
zeli
a =
1, to x = 0: Ale liczba a nie musi by´c dok÷
adnie równa
1: Wystarczy ,
by nie przekracza÷
a
1:Warunek d) jest oczywi´scie konieczny. Aby liczba mog÷
a
by´c mniejsza od
1, musi „najpierw” by´c mniejsza od 2009. Warunek ten jest
zatem konieczny, ale oczywi´scie nie jest wystarczaj ¾
acy. Podobnie z warunkiem
j a j
1:
11

Zadanie 1.33. W reklamach telewizyjnych cz ¾
esto powtarza si ¾
e zwrot "aby
wygra´c samochód, wystarczy wys÷
a´c kupon". Oce´n prawdziwo´s´c tego zdania z
punktu widzenia logiki matematycznej.
Zadanie 1.34. Które z poni·
zszych zda´n s ¾
a prawdziwe:
a) warunkiem wystarczaj ¾
acym na to, by dru·
zyna polska wygra÷
a Euro
2008 jest, by wygra÷
a wszystkie mecze;
b) warunkiem koniecznym na to, by dru·
zyna polska wygra÷
a Euro 2008
jest, by wygra÷
a wszystkie mecze;
c) warunkiem koniecznym do wygrania Euro 2008 jest, by nie przegra´c
·
zadnego meczu;
d) warunkiem wystarczaj ¾
acym do wygrania Euro 2008 jest, by nie prze-
gra´c ·
zadnego meczu;
Zadanie 1.35. (Hugo Steinhaus, "100 zada´n").
Uczniów klasy A nazwiemy akami, uczniów klasy B bekami. Aki chwal ¾
a
si ¾
e, ·
ze s ¾
a wy·
zszego wzrostu ni·
z beki, a beki uchodz ¾
a za lepszych matematyków.
Gdy raz jeden z aków popattrzy÷z góry na beka, ten zapyta÷
: Co to w÷
a´sciwie
znaczy, ·
ze jeste´scie wy·
zsi od nas. Czy to znaczy, ·
ze:
1) ka·
zdy ak jest wy·
zszy od ka·
zdego beka?
2) najwi ¾
ekszy ak jest wy·
zszy od najwi ¾
ekszego beka?
3) ka·
zdy ak ma beka, od którego jest wy·
zszy?
4) ka·
zdy bek ma aka, od którego jest ni·
zszy?
5) ka·
zdy ak ma beka, i to ka·
zdy innego, od którego jest wy·
zszy?
6) ka·
zdy bek ma aka, i to ka·
zdy innego, od którego jest ni·
zszy?
7) najmniejszy bek jest ni·
zszy od najmniejszego aka?
8) suma wzrostu aków jest wi ¾
eksza od sumy wzrostu beków?
9) najmniejszy ak przewy·
zsza wi ¾
ecej beków ni·
z najwi ¾
ekszy bek aków?
10) wi ¾
ecej jest takich aków, które przewy·
zszaj ¾
a jakiego´s beka ni·
z beków,
którzy przewy·
zszaj ¾
a jakiego´s aka?
11) ´srednia arytmetyczna wzrostu aków jest wi ¾
eksza od ´sredniej arytmety-
cznej wzrostu beków?
12) wiecej jest aków wzrostu wy·
zszego od ´sredniej wzrostu beków niz beków
wy·
zszego wzrostu od ´sredniej aków?
13) mediana wzrostu aków jest wi ¾
eksza od mediany wzrostu beków?
Jak pisze Hugo Steinhaus, oblany potokiem pyta´n ak zmala÷
. A pytanie
w zadaniu jest nast ¾
epuj ¾
ace: czy i które z podanych 13 kwestii s ¾
a zale·
zne od
siebie? Inaczej mówi ¾
ac, trzeba znale´z´c takie pary pyta´n, ·
ze odpowied´z "tak" na
pierwsze zmusza do odpowiedzi "tak" na drugie. Czy sa pytania równowa·
zne,
to znaczy, czy sa pary, ·
ze odpowiedzi na obydwa pytania musza by´c jednakowe.
Czy s ¾
a pary zale·
zne, ale nierównowa·
zne.
Odpowiedzi uzasadni´c, podaj ¾
ac ewentualne kontrprzyk÷
ady.
12

Pocz ¾
atek rozwi ¾
azania. Jest zupe÷
nie jasne, ·
ze odpowied´z "tak" na pierwsze
wymusza taka odpowied´z na wszystkie inne pytania. Zagadnienie drugie jest
niezale·
zne od pozosta÷
ych. Porównanie wzrostu najwy·
zszych cz÷
onków grupy
nie mówi nic o ca÷
ej grupie. Pytanie 3 rozpatrzmy na przyk÷
adzie: wzrost w
klasie A to 160, 159, 155,154, 152, natomiast w B to 180, 179, 175, 174 i 151.
Wtedy ka·
zdy ak ma beka, od którego jest ni·
zszy, mianowicie tego ostatniego,
natomiast w ka·
zdym innym sensie aki sa ni·
zsze.
Zadanie 1.36.
Zasi ¾
eganie informacji na wycieczce.
W dolinie w górach
mieszka dwóch gospodarzy. Jeden z nich jest przyja´znie nastawiony do turystów:
zaprasza do siebie, cz ¾
estuje kaw ¾
a, a pytany o drog ¾
e, zawsze udziela poprawnej
odpowiedzi. Drugi nie lubi turystów i z÷
o´sliwie udziela fa÷
szywych informa-
cji. Obaj maj ¾
a tylko jedn ¾
a wspóln ¾
a cech ¾
e. S ¾
a mianowicie bardzo ma÷
omówni
i w szczególno´sci odpowiadaj ¾
a tylko na jedno zadane pytanie.
Jak zadaj ¾
ac
tylko jedno pytanie, dowiedzie´c si ¾
e, który ze szlaków (czerwony czy niebieski)
prowadzi na szczyt? Nie wiemy, z którym z nich rozmawiamy.
Zadanie 1.37. Jak nauczy´c si ¾
e lokalnego j ¾
ezyka? Na pewnej wyspie ·
zyj ¾
a
dwa niech ¾
etne sobie wzajemnie plemiona: Fitumitu i Bajtata. Ka·
zdy Bajtata
k÷
amie, ka·
zdy Fitumitu mówi prawd ¾
e. Rozumiej ¾
a po polsku, ale odpowiadaj ¾
a
w swoim j ¾
ezyku: huhu lub uhuhu. Nie wiemy, które z tych s÷
ów znaczy „tak”,
a które „nie”. Jak dowiedzie´c si ¾
e o to za pomoc ¾
a tylko jednego pytania?
Zadanie 1.38. Z kim mamy do czynienia? Jak, równie·
z za pomoc ¾
a
jednego pytania, dowiedzie´c si ¾
e, do którego plemienia nale·
zy tubylec, z którym
rozmawiamy? Je´sli zapytamy go, czy jest Bajtat ¾
a, ka·
zdy odpowie, ·
ze nie. Je´sli
zapytamy, czy jest Fitumitu, w odpowiedzi us÷
yszymy zawsze „tak”.
Zadanie 1.39. Stosunki rodzinne . Pewnego razu królowa ze swoj ¾
a córk ¾
a,
wygnane z domu, ucieka÷
y przez obcy las. Miejscowy król, wdowiec, i jego
syn polowali w lesie i natkn ¾
eli si ¾
e na ´slady kobiecych stóp. ´Slady te tak im si ¾
e
spodoba÷
y, ·
ze postanowili si ¾
e o·
zeni´c z tymi damami. Postanowili, ·
ze król we´zmie
za ·
zon ¾
e kobiet ¾
e o wi ¾
ekszych stopach, a syn o mniejszych. Co postanowiwszy,
pop ¾
edzili koni, a gdy ju·
z dogonili królow ¾
a i córk¾
e, uczynili, jak postanowili.
Odby÷si ¾
e skromny ´slub i huczne weselisko –jak to w bajkach bywa. Tyle ·
ze to
królewna mia÷
a wi ¾
eksz ¾
a stop ¾
e ni·
z jej matka królowa i to ona zosta÷
a ·
zon ¾
a króla.
Król po´slubi÷królewn ¾
e. Po jakim´s czasie z obu ma÷·
ze´nstw przysz÷
y na ´swiat
dzieci. Jakie jest pokrewie´nstwo mi ¾
edzy owymi dzie´cmi?
Zadanie wydaje si ¾
e ÷
atwe. Przecie stosunek pokrewie´nstwa jest ´sci´sle
zde…niowany...
Zadanie 1.40. (na 1 kwietnia, ale nie rozwi ¾
azuj eksperymentalnie!)
Jedno piwo to nie jest nic. To si ¾
e w ogóle nie liczy. To po prostu mniej
ni·
z zero. Dopiero dwa piwa to jest tak, jak zero. Dwa razy po dwa piwa jedno
po drugim to ju·
z co´s pozytywnego, wi ¾
ekszego od zera. Gdy to powtórzymy,
to b ¾
edzie ju·
z w porz ¾
adku, o.k.! To dopiero jest ma÷
e piwo. Dwa ma÷
e piwa to
podwójne ma÷
e. Du·
ze piwo to nie to samo co podwójne ma÷
e. Dopiero cztery
ma÷
e piwa (czyli dwa podwójne) to jest tak, jak jedno du·
ze. Dwa du·
ze piwa to
13

zwyk÷
e piwo. Je´sli chc ¾
e si ¾
e porz ¾
adnie napi´c piwa, to bior ¾
e cztery zwyk÷
e. Ile
piwa wypi÷
em, je·
zeli pewnego wieczoru najpierw napi÷
em si ¾
e porz ¾
adnie w domu,
a potem jeszcze porz ¾
adnie z kolegami z klubu?
14

Wyk÷
ad 2. Indukcja i rekursja.
Zasada indukcji matematycznej jest ciekawa cho´cby dlatego, ·
ze nie by÷
a
znana w staro·
zytno´sci i w ´sredniowieczu, a dok÷
adniej: nie by÷
a sformu÷
owana
w wyra´zny sposób. By÷
a oczywi´scie okazjonalnie stosowana: pierwszy raz ter-
minu induction u·
zy÷John Wallis w 1656 roku a Augustus de Morgan w 1838
roku nazywa÷ten proces successive induction, a jeden raz u·
zy÷zwrotu mathe-
matical induction. W swojej s÷
ynnej pracy Was sind und was sollen die Zahlen
(1887) Richard Dedekind u·
zywa÷konsekwentnie zarówno terminu indukcja zu-
pe÷
na (vollständige Induktion), jak i samej techniki dowodów indukcyjnych z
obecnymi wymogami ´scis÷
o´sci. Jednak do ko´nca XIX wieku w najpowa·
zniejszych
pracach matematycznych u·
zycie zwrotu und so weiter, e cosi via, and so on (po
polsku: i tak dalej) nie by÷
o b÷¾
edem formalnym. Uj ¾
ecie, które znamy dzisiaj,
wykrystalizowa÷
o si ¾
e na prze÷
omie wieku XIX i XX.
Pomówimy dok÷
adniej o indukcji i rekursji. Pierwszy termin pochodzi od
÷
aci´nskiego inductio (= wp÷
yw). Algorytm indukcyjny to taki, w którym robi si ¾
e
wszystko po kolei, systematycznie, w naturalnej kolejno´sci: obieramy ziemniaki,
wstawiamy je do wody, solimy, zapalamy gaz. Wymaga to posiadania od razu
planu dzia÷
ania.
W przypadku gotowania ziemniaków ten przepis jest nieskomplikowany, mogliby´smy
pomy´sle´c tak: “aha, widzia÷
em kiedy´s, jak ·
zona gotowa÷
a karto‡e, pami ¾
etam,
·
ze woda musia÷
a zawrze´c, no to nastawmy wod ¾
e. Aha, mówi÷
a, ·
zeby osoli´c,
no to wsypmy sól. No, ´swietnie, pocz ¾
atek ju·
z mamy, co teraz, aha, karto‡e,
gdzie·
z one s ¾
a, o, mam, no, to wrzucamy, stop, jako´s dziwnie wygl ¾
adaj ¾
a, ju·
z
wiem, trzeba je obra´c..., u¤, nie wiedzia÷
em, ·
ze to takie trudne, no, ale wszystko
si ¾
e uda÷
o...” . To jest w÷
a´snie rekursja: zaczynamy od czynno´sci, któr ¾
a przy
indukcji wykonujemy na ko´ncu.
Indukcyjny algorytm na zdanie egzaminu polega÷
by na uczeniu si ¾
e wszys-
tkiego po kolei, w logicznej kolejno´sci: najpierw naucz ¾
e si ¾
e A, bo to jest potrzebne
do B, a bez B nie zrozumiem C. Rekursja polega÷
aby na tym: bior ¾
e si ¾
e za C, ale
po chwili odkrywam, ·
ze musz ¾
e opanowa´c B, wi ¾
ec rozgrzebuj ¾
e zagadnienie B i na-
gle zauwa·
zam, ·
ze jeszcze nie umiem A. Ucz ¾
e si ¾
e A, na kupie papierów znajduj ¾
e
otwarte notatki do B i po opanowaniu B wracam do C. Podobnie przy remoncie
domu czy samochodu: mo·
zna robi´c systematycznie, od podstaw, lub zacz ¾
a´c od
rzeczy najbardziej widocznych, a potem „zobaczymy, co tam w ´srodku”.
Zadanie 2.1. Udowodni´c przez indukcj ¾
e nastepuj ¾
ace wzory:
1
3
+ 2
3
+ ::: + n
3
= (1 + 2 + 3 + ::: + n)
2
;
1
4
+ 2
4
+ ::: + n
4
=
n(n+1)(2n+1)(3n2+3n+1)
30
;
1
2
+ 3
2
+ 5
2
+ 7
2
+ ::: + (2n + 1)
2
=
(n+1)(2n+1)(2n+3)
3
;
1
3
+ 3
3
+ 5
3
+ 7
3
+ ::: + (2n + 1)
3
= (n + 1)
2
(2n
2
+ 4n + 1) ;
1 2 + 2 3 + 3 4 + ::: + (n
1)n =
n(n 1)(n+1)
3
;
X
n
k=1
(4k
3) = n(2n
1) ;
X
n
k=1
(4k
3)
2
=
n(16n
2
12n 1)
3
;
15

X
2n
k=1
( 1)
k+1
(2k
1) =
2n;
X
2n
k=1
( 1)
k+1
(2k
1)
2
=
8n
2
;
Zadanie 2.2. Udowodni´c indukcyjnie nierowno´sci
a) Je·
zeli n
4, to n! > 2n:
b) Je·
zeli n > 4, to 2
n
> n
2
:
Zadanie 2.3. Wykaza´c, ·
ze je·
zeli a
1
= 1 oraz a
n+1
=
a
n
+ 6n + 5, to
a
n
= 3n
2
+ 2n
4:
Zadanie 2.4.
Liczbami trójk ¾
atnymi nazywamy liczby T
n
= 1 + 2 + 3 +
::: + n =
n(n+1)
2
. Wyka·
z, ·
ze
a) T
2
n
+ T
2
n+1
= T
(n+1)
2
,
b) T
2
n
T
2
n+1
=
(n + 1)
3
.
Zadanie 2.5. Ci ¾
ag Fibonacciego okre´slamy w ten sposób. F
1
= 1; F
2
= 1,
F
n+2
= F
n
+ F
n+1
: Pocz ¾
atkowymi wyrazami tego ci ¾
agu s ¾
a zatem 1, 1, 2, 3, 5,
8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ... Wykaza´c indukcyjnie, ·
ze
a) liczby F
3n
s ¾
a parzyste;
b) liczby F
4n
s ¾
a podzielne przez 3;
c) co pi ¾
ata liczba ci ¾
agu Fibonacciego, pocz ¾
awszy od 5 , jest podzielna przez
5;
d) F
1
+ F
3
+ F
5
::: + F
2n 1
= F
2n
;
e) F
2
+ F
4
+ F
6
+ ::: + F
2n
= F
2n+1
1
f) F
p+q
= F
p 1
F
q
+ F
p
F
q+1
;
g) zachodzi ogólny wzór: F
n
=
1
p
5
h
1+
p
5
2
n
1
p
5
2
n
i
.
Komentarz. Na przyk÷
adzie ci ¾
agu Fibonacciego mo·
zna zobaczy´c olbrzymi ¾
a
ró·
znic ¾
e w informatyce mi ¾
edzy programami, w których u·
zywamy indukcji, a tymi,
w których u·
zywamy rekursji. Programy, procedury i funkcje, które wywo÷
uj ¾
a
same siebie (tylko ze zmienionymi parametrami) s ¾
a prostsze do napisania, ale
wolniej dzia÷
aj ¾
a. Na ogó÷bowiem „nie widz ¾
a”, ·
ze mog ¾
a skorzysta´c z niedawno
przeprowadzonych oblicze´n. Na przyk÷
ad, je·
zeli b ¾
ed ¾
e chcia÷obliczy´c n-ty wyraz
ci ¾
agu Fibonacciego, to najbardziej naturalny wydaje si ¾
e program wed÷
ug takiego
schematu:
Je·
zeli n = 1, to tym wyrazem jest 0. Je·
zeli n = 2, to tym wyrazem jest 1.
W przeciwnym razie do obliczenia tego wyrazu musisz obliczy´c najpierw wyraz
o numerze n
1 , potem wyraz o numerze n
2 i wyniki doda´c.
Taki program b ¾
edzie dzia÷
a÷nies÷
ychanie powoli, a procesor naszego kom-
putera b ¾
edzie pracowa÷w pocie czo÷
a. Dlaczego? Pomy´slmy.
·
Zeby obliczy´c
siódmy wyraz, program musi wyliczy´c wyraz szósty i pi ¾
aty. Program zabiera si ¾
e
do wyrazu szóstego. My´sli sobie przy tym tak (kto my´sli? No, ten program...)
–Aha, musz ¾
e w tym celu obliczy´c pi ¾
aty i czwarty. Wezm ¾
e si ¾
e za pi ¾
aty.
Jak mam obliczy´c ten wyraz? Zobaczmy, co ka·
ze programista. Tak, w porz ¾
adku:
mam obliczy´c wyraz czwarty i trzeci. Ju·
z si ¾
e robi. Ju·
z biegn ¾
e do czwartego...
16

Ju·
z czytam instrukcj ¾
e: ·
zeby obliczy´c wyraz czwarty, oblicz najpierw trzeci,
potem drugi, a wyniki dodaj. To proste. A jak si ¾
e oblicza trzeci? S÷
ucham
rozkazów: Trzeci to drugi plus pierwszy. No, wreszcie jakie´s konkrety. Drugi
wyraz to ... ojej, gdzie·
z on jest... , a tu. Równy jest 1. Pierwszy wyraz? Zero.
Mam to doda´c? No, to proste. O co tyle krzyku. Dodaj ¾
e, Wynik jest równy
jeden. Mam trzeci wyraz ci ¾
agu. Co to ja teraz mam robi´c? Aha, oblicza´c wyraz
czwarty.....
Przerwijmy mu ten monolog wewn ¾
etrzny. Za ka·
zdym razem program
powtarza wszystkie obliczenia od nowa –bo tak mu ka·
ze rekursja.
Napisz program indukcyjny na obliczanie kolejnych wyrazów ci ¾
agu Fibonac-
ciego.
Zadanie 2.6. Udowodni´c indukcyjnie, ·
ze je·
zeli po·
zyczamy z banku kapita÷K
na p procent na n lat (okresów) i chcemy sp÷
aca´c po tyle samo, to wielko´s´c sta÷
ej
raty jest równa K
r
n
(r
1)
r
n
1
, a po a po k-tym roku (okresie) zostaje kapita÷
u do
sp÷
aty Krk
Kr
n r
k
1
r
n
1
.
Zadanie 2.7. Wykaza´c, ·
ze ´srednia arytmetyczna 2
n
liczb dodatnich jest
wi ¾
eksza lub równa od ´sredniej geometrycznej tych liczb.
Zadanie 2.8. W pudle by÷
o 5 kapeluszy, dwa czarne i dwa bia÷
e. Ustaw-
iono trzech panów w rz ¾
edzie, jednego za drugim i ka·
zdemu w÷
o·
zono kapelusz
na g÷
ow¾
e. Nikt nie widzia÷ani w÷
asnego kapelusza, ani kapeluszy panów sto-
j ¾
acych za nim. Zapytano pana stoj ¾
acego z ty÷
u, czy wie, jakiego koloru jest
jego kapelusz. Odpowiedzia÷
, ·
ze nie wie. Zapytano o to samo pana stoj ¾
acego w
´srodku. Odpowiedzia÷
, ·
ze te·
z nie wie. Na to pan trzeci o´swiadczy÷
, ·
ze wobec
takich odpowiedzi poprzedników on ju·
z wie, jaki ma kapelusz.
Jaki by÷kolor kapelusza trzeciego pana?
Rozwi ¾
azanie.
Je´sli pan stoj ¾
acy z ty÷
u nie móg÷okre´sli´c koloru swojego
kapelusza, to znaczy, ·
ze nie widzia÷przed sob ¾
a dwóch bia÷
ych. Gdyby pier-
wszy z panów mia÷bia÷
y kapelusz, to ´srodkowy rozumowa÷
by tak: on ma bia÷
y,
a ja i on razem nie mamy dwóch bia÷
ych, zatem ja mam czarny. Pan stoj ¾
acy
z przodu rozumowa÷tak: skoro mój poprzednik nie móg÷zastosowa´c takiego
rozumowania, to ja mam czarny kapelusz!
Bardzo efektowne jest zastosowanie indukcji do zadania logicznego, stanow-
i ¾
acego rozszerzenie zadania o panach w kapeluszach na g÷
owie. Podajemy tre´s´c
zadania i wskazówk¾
e, jakiego twierdzenia dowodzi´c indukcyjnie. Z niego ju·
z
wyniknie od razu teza.
By÷
o n panów, n kapeluszy czarnych i n–1 bia÷
ych. Ustawiono n panów
w rz ¾
edzie, jednego za drugim i ka·
zdemu w÷
o·
zono kapelusz na g÷
ow¾
e.
Nikt
nie widzia÷ani w÷
asnego kapelusza, ani kapeluszy panów stoj ¾
acych za nim.
Zapytano pana stoj ¾
acego z ty÷
u, czy wie, jakiego koloru jest jego kapelusz.
Odpowiedzia÷
, ·
ze nie wie. Zapytano o to samo nast ¾
epnego pana. Odpowiedzia÷
,
·
ze te·
z nie wie ... i tak dalej a·
z do przedostatniego: „nie wiem”. Ostatni z
panów (ten, który nie widzia÷·
zadnego kapelusza) o´swiadczy÷
, ·
ze wobec takich
odpowiedzi poprzedników on ju·
z wie, jaki ma kapelusz.
Jaki by÷kolor kapelusza tego pana?
17

Wskazówka: Udowodni´c przez indukcj ¾
e nast ¾
epuj ¾
ace
Twierdzenie. Je·
zeli k -ty pan nie widzi przed sob ¾
a czarnych kapeluszy, a
poprzednik nie móg÷rozstrzygn ¾
a´c zagadnienia, to k -ty pan wie, ·
ze ma na g÷
owie
czarny kapelusz.
Zadanie 2.9. Komputer podpowiada ciekawe rozk÷
ady:
25 = 1 25
252525 = 91 2775
2525252525 = 9091 277775
25252525252525 = 909091 27777775
252525252525252525 = 90909091 2777777775
2525252525252525252525 = 9090909091 277777777775
...
Jaka jest regu÷
a budowy tej piramidki? Sformu÷
owa´c odpowiednie twierdze-
nie i udowodni´c je –oczywi´scie przez indukcj ¾
e.
Zadanie 2.10. Udowodnij, ·
ze je·
zeli d
n
oznacza d÷
ugo´sc boku n k ¾
ata forem-
nego, to d
2k
=
r
2
2
q
1
(d
k
)
2
4
:
Zadanie 2.11. W pewnym wierzcho÷
ku czworo´scianu siedzi paj ¾
ak, w innym
mucha. Mucha zaczyna spacerowa´c po kraw¾
edziach czworo´scianu. Przej´scie
ka·
zdej (od wierzcho÷
ka do wierzcho÷
ka) zajmuje jej minut ¾
e. W ka·
zdym naro·
zniku
(wierzcho÷
ku) czworo´scianu wybiera losowo kraw¾
ed´z do dalszej w¾
edrówki. Oczy-
wi´scie wszystko ko´nczy si ¾
e, gdy wskutek z÷
ego wyboru wpadnie na paj ¾
aka, który
ma na to oczywi´scie inny punkt widzenia: oto nadszed÷obiad!
Wykaza´c, ·
ze prawdopodobie´nstwo, ·
ze paj ¾
ak doczeka si ¾
e obiadu nie
pó´zniej ni·
z po n minutach wynosi p
n
=
2
3
n
.
Zadanie 2.12. Mucha i paj ¾
ak siedz ¾
a w przeciwleg÷
ych wierzcho÷
kach sze´s-
cianu. Mucha w¾
edruje po kraw¾
edziach sze´scianu, wybieraj ¾
ac za ka·
zdym razem
(to znaczy w ka·
zdym wierzcho÷
ku) losowo jedn ¾
a z nich. Na przej´scie ka·
zdej z
nich potrzebuje minuty. Wykaza´c, ·
ze prawdopodobie´nstwo, ·
ze paj ¾
ak doczeka
si ¾
e obiadu nie pó´zniej ni·
z po n minutach wynosi p
2k+1
= p
2k+2
=
7
9
k
.
18

Wyk÷
ad 3. Zbiory
Zadanie 3.1. Wyznacz (i naszkicuj na osi liczbowej lub w uk÷
adzie wspó÷
rz ¾
ed-
nych) zbiory A [ B, A \ B, A n B, B n A, je·
zeli zbiory A ; B s ¾
a okre´slone
nast ¾
epuj ¾
aco:
a) A = fx 2 R : x
2
> 9g, B = fx 2 R : x > 1g:
b) A = fx 2 R : x
2
> 1g, B = fx 2 R : x < 9g:
c) A = f(x; y) 2 R
2
: y
x > 0g, B = f(x; y) 2 R
2
: x + y < 3g:
d) A = f(x; y) 2 R
2
: y = j x jg, B = f(x; y) 2 R
2
: x = j y jg:
e) A = f (x; y) 2 R
2
: j x j < 1 g , B = f (x; yg 2 R
2
: x
2
+ y
2
6x g:
Zadanie 3.2 (a - e) . Opisz i naszkicuj uzupe÷
nienie zbioru C na p÷
aszczy´znie,
wiedz ¾
ac, ·
ze C jest sum ¾
a uzupe÷
nie´n zbiorów A i B z poprzedniego zadania.
Funkcja charakterystyczna zbioru.
Rozpatrujemy podzbiory ustalonego zbioru X: Niech A b ¾
edzie takim zbiorem,
tj.
A
X.
Okre´slamy funkcj ¾
e charakterystyczn ¾
a zbioru A w nast ¾
epuj ¾
acy
sposób:
ch
A
(x) =
1, je·
zeli x 2 A
0, je·
zeli x =
2 A
. Jest to funkcja, której dziedzin ¾
a jest zbiór
X, a warto´sciami - liczby 0 i 1. Je·
zeli interpretujemy te liczby jako „fa÷
sz" i
„prawd ¾
e", to funkcja ch „stwierdza jak jest" dla przynale·
zno´sci elementu do
zbioru. Zauwa·
zmy, ·
ze liczby 0 i 1 maj ¾
a wiele charakterystycznych, unikatowych
w÷
asno´sci, z których najcz ¾
e´sciej b ¾
edziemy wykorzystywa´c to, ·
ze s ¾
a one równe
swoim kwadratom. Istotnie: 0
2
= 0, 1
2
= 1: S ¾
a to jedyne liczby o tej w÷
asno´sci.
Wynika to st ¾
ad, ·
ze równanie x
2
= x ma tylko dwa pierwiastki (jako równanie
kwadratowe).
Funkcje charakterystyczne pozwalaj ¾
a na sprowadzenie niektórych dzia÷
a´n na
zbiorach do prostych rachunków algebraicznych. Pomys÷ten zrealizowa÷matem-
atyk angielski George Boole (w po÷
owie XIX wieku). Wyprowadzimy funkcje
charakterystyczne dla podstwowych dzia÷
a´n na zbiorach.
1. Funkcja charakterystyczna iloczynu (przeci ¾
ecia, cz ¾
e´sci wspólnej) zbiorów:
ch
A
\B
= ch
A
ch
B
Wzór ten nale·
zy rozumie´c nast ¾
epuj ¾
aco: je·
zeli warto´sci ¾
a funkcji ch
A
w
pewnympunkcie x jest a , a warto´sci ¾
a funkcji ch
B
w tym punkcie jest b, to
warto´sci ¾
a funkcji ch
A
\B
w tym punkcie jest iloczyn ab.
Dowód. Rozpatrzymy poszczególne przypadki i w ka·
zdym z nich porównamy
warto´sci funkcji. Je·
zeli x 2 A a tak·
ze x 2 B, to funkcja charakterystyczna
ch
A
\B
przybiera w tym punkcie warto´s´c 1, ch
A
\B
(x) = 1: Mamy tak·
ze ch
A
(x) =
1; ch
B
(x) = 1, zatem ch
A
ch
B
(x) = 1:Warto´sci obu funkcji sa równe.
Je·
zeli x 2 A ale x =
2 B, to funkcja charakterystyczna ch
A
\B
przybiera w
tym punkcie warto´s´c 0, ch
A
\B
(x) = 0: Mamy ch
A
(x) = 1; ch
B
(x) = 0, zatem
ch
A
ch
B
(x) = 0:Warto´sci obu funkcji sa równe.
19

Je·
zeli x =
2 A i x 2 B, to funkcja charakterystyczna ch
A
\B
te·
z przybiera
w tym punkcie warto´s´c 0, ch
A
\B
(x) = 0: W tym przypadku mamy ch
A
(x) =
0; ch
B
(x) = 1, zatem ch
A
ch
B
(x) = 0:Warto´sci obu funkcji sa równe.
Je·
zeli x =
2 A i x =
2 B, to funkcja charakterystyczna ch
A
\B
przybiera w
tym punkcie warto´s´c 0, ch
A
\B
(x) = 0: W tym przypadku mamy ch
A
(x) =
0; ch
B
(x) = 0, zatem ch
A
ch
B
(x) = 0:Warto´sci obu funkcji sa równe.
Rozumowanie to mo·
zna przeprowadzi´c inaczej, znacznie pro´sciej. Rozpa-
trzmy iloczyn ab: Czynniki a ; b sa równe 0 albo 1. W tym przypadku iloczyn
jest równy 1 wtedy i tylko wtedy, gdy obydwa czynniki sa równe 1. A to jest
równowa·
zne przynale·
zno´sci x do obydwu zbiorów A; B:
2. Funkcja charakterystyczna sumy zbiorów. Mamy
ch
A
[B
= ch
A
+ ch
B
ch
A
ch
B
Wzór ten nale·
zy rozumie´c nast ¾
epuj ¾
aco: je·
zeli warto´sci ¾
a funkcji ch
A
w
pewnympunkcie x jest a , a warto´sci ¾
a funkcji ch
B
w tym punkcie jest b, to
warto´s´c funkcji ch
A
[B
w tym punkcie jest równa a + b
ab.
Dowód. Rozpatrzymy poszczególne przypadki i w ka·
zdym z nich porów-
namy warto´sci funkcji. Je·
zeli punkt x nale·
zy do cho´c jednego ze zbiorów A ,
B , to funkcja charakterystyczna ch
A
[B
przybiera w tym punkcie warto´s´c 1,
ch
A
[B
(x) = 1: Przynajmniej jedna z liczb a = ch
A
(x); b = ch
B
(x) jest równa
1. Wtedy a + b
ab = 1: Warto´sci obu funkcji sa równe.
Je·
zeli x =
2 A i x =
2 B, to funkcja charakterystyczna ch
A
[B
przybiera w
tym punkcie warto´s´c 0, ch
A
[B
(x) = 0: W tym przypadku mamy ch
A
(x) =
0; ch
B
(x) = 0, zatem ch
A
+ ch
B
(x)
ch
A
ch
B
= 0:Warto´sci obu funkcji sa
równe.
3. Funkcja charakterystyczna ró·
znicy zbiorów. Mamy
ch
A
n B
= ch
A
(1 n ch
B
):
Wzór ten nale·
zy rozumie´c nast ¾
epuj ¾
aco: je·
zeli warto´sci ¾
a funkcji ch
A
w
pewnympunkcie x jest a , a warto´sci ¾
a funkcji ch
B
w tym punkcie jest b, to
warto´s´c funkcji ch
A
n B
w tym punkcie jest równa a(1
b):
Dowód. Aby iloczyn a(1
b) by÷równy 1, potrzeba i wystarcza, by obydwa
czynniki by÷
y równe 1. A to jest równowa·
zne stwierdzeniu, ·
ze x 2 A n B:
4. Funkcja charakterystyczna ró·
znicy symetrycznej zbiorów.
Mamy
ch
A B
= ch
A
+ ch
B
2 ch
A
ch
B
Wzór ten nale·
zy rozumie´c nast ¾
epuj ¾
aco: je·
zeli warto´sci ¾
a funkcji ch
A
w
pewnympunkcie x jest a , a warto´sci ¾
a funkcji ch
B
w tym punkcie jest b, to
warto´s´c funkcji ch
A B
w tym punkcie jest równa a + b
2ab.
Dowód. Warto´s´c funkcji ch
A B
(x) jest równa 1 wtedy i tylko wtedy, gdy
x nale·
zy do jednego ze zbiorów A; B , lecz nie nale·
zy do drugiego. Warto´s´c
wyra·
zenia a + b
2ab (gdzie liczby a oraz b s ¾
a zerami albo jedynkami) mo·
ze by´c
równa 1 wtedy i tylko wtedy, gdy jedna z tych liczb jest równa 0, a druga 1,
a zatem gdy jedna z warto´sci funkcji charakterystycznych ch
A
(x) , ch
B
(x) jest
20

rowna zero, a ta druga 1. To znaczy, ·
ze x nale·
zy do jednego ze zbiorów A; B ,
lecz nie nale·
zy do drugiego
Funkcje charakterystyczne iloczynu (produktu), sumy, ró·
znicy i ró·
znicy sym-
etrycznej zbiorów A; B b ¾
edziemy oznacza´c odpowiednio przez P (A; B), S(A; B); R(A; B) ;
X(A; B): Ma÷
e litery b ¾
eda oznacza´c odpowiednie funkcje liczbowe:
p(a; b) = ab ; s(a; b) = a + b
ab ; r(a; b) = a(1
b) ; x(a; b) = a + b
2ab
Zadanie 3.3. Za pomoc ¾
a funkcji charakterystycznych udowodnij nast ¾
epuj ¾
ace
wzory:
a) rozdzielno´s´c mno·
zenia zbiorów wzgl ¾
edem dodawania : A \ (B [
C) = (A \ B) [ (A \ C);
b) rozdzielno´s´c dodawania zbiorów wzgl ¾
edem mno·
zenia : A [ (B \
C) = (A [ B) \ (A [ C);
c) pierwsze prawo DeMorgana: A n (B [ C) = (A n B) \ (A n C);
d) drugie prawo DeMorgana: A n (B \ C) = (A n B) [ (A n C);
e) An(BnC) = (AnB) [ (A \ C);
f) A \ (B
C) = (A \ B)
(A \ C):
Rozwi ¾
azanie.
a) Przyjmijmy, ·
ze warto´sci ¾
a funkcji ch
A
w pewnympunkcie x jest a , warto´s-
ci ¾
a funkcji ch
B
w tym punkcie jest b; za´s warto´sci ¾
a funkcji ch
C
w tym punkcie
jest c:Wtedy funkcja charakterystyczna zbioru A \ (B [ C) przybiera w tym
punkcie warto´s´c
p(a; s(b; c)) = a s(b; c) = a (b + c
bc) = ab + ac
abc:
Przy obliczeniu warto´sci prawej strony skorzystamy z tego, ·
ze a
2
= a:Prawa
strona przybiera zatem warto´s´c
s(p(a; b); p(a; c)) = s(ab; ac) = ab + ac
abac = ab + ac
abc:
Obie strony s ¾
a zatem równe.
b) Przyjmijmy, ·
ze warto´sci ¾
a funkcji ch
A
w pewnympunkcie x jest a , warto´s-
ci ¾
a funkcji ch
B
w tym punkcie jest b; za´s warto´sci ¾
a funkcji ch
C
w tym punkcie
jest c:Wtedy funkcja charakterystyczna zbioru stoj ¾
acego po lewej stronie rowno´sci,
tj. A [ (B \ C) przybiera w tym punkcie warto´s´c
s(a; p(b; c)) = s(a; bc) = a + bc
abc:
Natomiast funkcja charakterystyczna zbioru stoj ¾
acego po prawej stronie
równo´sci, tj. zbioru (A [ B) \ (A [ C) ; ma w tym punkcie warto´s´c
p(s(a; b); s(a; c)) = p(a + b
ab ; a + c
ac) = (a + b
ab) (a + c
ac) =
= a
2
+ ac
a
2
c + ab + bc
abc
a
2
b
abc + a
2
bc = a + ac
ac + ab + bc
abc
ab
abc = a + bc
abc:
Przy obliczeniu warto´sci prawej strony skorzystali´smy z tego, ·
ze a
2
= a:
Obie strony s ¾
a zatem równe.
c) Przyjmijmy, ·
ze warto´sci ¾
a funkcji ch
A
w pewnympunkcie x jest a , warto´s-
ci ¾
a funkcji ch
B
w tym punkcie jest b; za´s warto´sci ¾
a funkcji ch
C
w tym punkcie
jest c:Warto´s´c funkcji charakterystycznej zbioru A n (B[C) jest równa r(a; s(b; c)) =
a(1
s(b; c)) = a(1
b
c + bc) ; za´s warto´s´c funkcji charakterystycznej
zbioru po prawej stronie równo´sci , to jest zbioru (A n B) \ (A n C) , wynosi
21

p(r(a; b); r(a; c)) = r(a; b) r(a; c) = a(1
b) a(1
c) = (a
ab)(a
ac) =
a
2
a
2
c
a
2
b + a
2
bc = a
ac
ab + abc
A zatem obydwie strony sa równe.
Zadanie 3.4. Zilustruj dzia÷
ania wyst ¾
epuj ¾
ace w poprzednim zadaniu na dia-
gramach Venna.
Zadanie 3.5. Wyka·
z za pomoc ¾
a funkcji charakterystycznych, ·
ze dzia÷
anie
„ró·
znica symetryczna” jest ÷¾
aczne, to znaczy, ·
ze zawsze jest A
(B
C) =
(A
B)
C:
Rozwi ¾
azanie. Przyjmijmy, ·
ze warto´sci ¾
a funkcji ch
A
w pewnympunkcie x
jest a , warto´sci ¾
a funkcji ch
B
w tym punkcie jest b; za´s warto´sci ¾
a funkcji ch
C
w
tym punkcie jest c:Funkcja charakterystyczna zbioru A
(B
C) ma w tym
punkcie warto´s´c
x(a; x(b; c)) = a + x(b; c)
2 a x(b; c) = a + b + c
2bc
2 a (b + c
2bc) =
= a + b + c
2bc
2ab
2ac + 4abc:
Dla zbioru (A
B)
C otrzymujemy
x(x(a; b); c) = x(a + b
2ab; c) = a + b
2ab + c
2(a + b
2ab)c = a +
b + c
2bc
2ab
2ac + 4abc:
Obie strony s ¾
a zatem równe.
Zadanie 3.6. Zilustruj ÷¾
aczno´s´c ró·
znicy symetrycznej na diagramie Venna.
Zadanie 3.7. Wykaza´c, ·
ze zbiór (A [ B)
(A [ C) zawsze zawiera si ¾
e w
zbiorze A
B
C:
Rozwi ¾
azanie. Wyznaczamy funkcj ¾
e charakterystyczn ¾
a zbioru (A [ B) (A [
C). Jej warto´sci ¾
a w punkcie x jest b + c
ab
2bc
ac + 2abc: W poprzednim
zadaniu wyznaczyli´smy warto´s´c funkcji charakterystycznej zbioru A
B
C.
Mamy wykaza´c, ·
ze
b + c
ab
2bc
ac + 2abc
a + b + c
2bc
2ab
2ac + 4abc:
Upraszczamy nierówno´s´c (dodajemy do obu stron ab + ac + 2bc
b
c
2abc)
0
a
ab
ac + 2abc:
0
a(1
b
c + 2bc):
Nierowno´s´c ta jest równowa·
zna z wyj´sciow ¾
a. Nietrudno zauwazy´c, ·
ze jest
spe÷
niona dla wszystkich liczb a; b; c b ¾
ed ¾
acych zerami lub jedynkami.
Mo·
zemy wyra·
zenie a(1
b
c + 2bc) przekszta÷
ci´c tak:
a(1
b
c + 2bc) = a(1
b
2
c
2
+ 2bc) = a(1
(b
c)
2
):
I to, ·
ze jest to zawsze nieujemne, jest teraz zrozumia÷
e.
Zadanie 3.8. W oznaczeniach poprzedniego zadania, znale´z´c przyk÷
ad, ·
ze
(A [ B)
(A [ C) A
B
C:
Rozwi ¾
azanie. Za pomoc ¾
a funkcji charakterystycznych mo·
zna taki przyk÷
ad
znale´z´c nast ¾
epuj ¾
aco.
Szukamy takich liczb a; b; c (równych 0 lub 1), by
b + c
ab
2bc
ac + 2abc
a + b + c
2bc
2ab
2ac + 4abc:
Widzieli´smy, ·
ze sprowadza si ¾
e to do podania takich warto´sci, by
0 < a(1
(b
c)
2
):
22
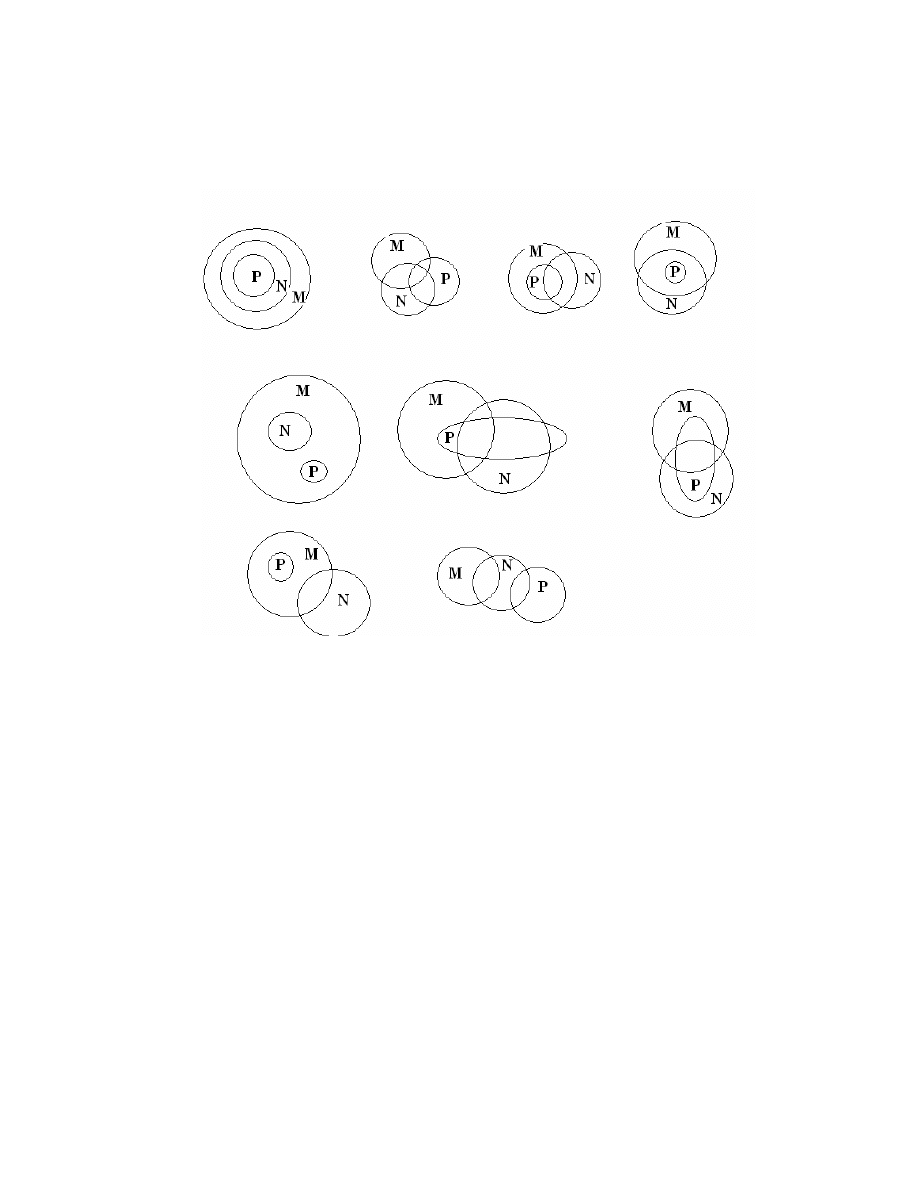
Jest to mo·
zliwe w dwóch przypadkach: a = 1; b = c = 0
oraz a = 1; b =
c = 1. W pierwszym przypadku znaczy to, ·
ze zbiory A; B; C s ¾
a takie, ·
ze istnieje
punkt x 2 A, który nie nale·
zy ani do B, ani do C: Przypadek drugi zachodzi
wtedy, gdy zbiory A; B; C maj ¾
a pewien punkt wspólny x:
Zadanie 3.9. Wyka·
z, za pomoc ¾
a funkcji charakterystycznych, ·
ze
a) (A [ B) n B = A wtedy i tylko wtedy, gdy A \ B = ?:
b) (A n B) [ B = A wtedy i tylko wtedy, gdy B
A:
Zadanie 3.10. Poni·
zej widzisz kilka mo·
zliwych po÷
o·
ze´n zbiorów. Podaj po
trzy poj ¾
ecia, których stosunek zakresów mo·
zna przedstawi´c ni·
zej podanymi
schematami,
23

Wyk÷
ad 4
. Ile tego jest?
Zadanie 4.1.
Przyjmijmy, ·
ze zbiór K ma k elementów, zbiór M ma m
elementów i ·
ze zbiór N ma n elementów. Przyjmijmy, ·
ze 0 < k
m
n.
a) Ile najmniej a ile najwi ¾
ecej elementów mog ¾
a mie´c nast ¾
epuj ¾
ace zbiory: a)
A [ B , b) A \ B , c) A [ B(\C) ; d) A \ (B [ C) , e) A n B; f) A n(B nC)
, g) (A n B) n C , h) A n (B [ C) , i) A
B; j) (A
B)
C ; k) (A
B) n C ; l) (A \ B)
C ; m) (A
B) n (A n C);
b) Zaznaczy´c zbiory wynienione powy·
zej na diagramie Venn’a,
c) wyliczy´c funkcje charakterystyczne tych zbiorów.
Zadanie 4.2. Ile elementów ma iloczyn kartezja´nski zbioru m-elementowego
i zbioru n-elementowego?
Odpowied´z. mn: W matematyce szkolnej nazywa si ¾
e to twierdzeniem o
mno·
zeniu.
Zadanie 4.3. W tylnej pia´scie roweru jest 7 trybów; w przedniej s ¾
a 3 prze÷
o·
ze-
nia. Ile jest mo·
zliwo´sci tryb-prze÷
o·
zenie?
Odp. Ustawienie przód-ty÷mo·
ze by´c interpretowane jako element iloczynu
kartezja´nskiego f1; 2; 3g
f1; 2; 3; 4; 5; 6; 7g: Jest zatem 3 7 = 21 mo·
zliwo´sci.
Zadanie 4.4.
Z Ku´znic na Hal ¾
e G ¾
asienicow ¾
a s ¾
a 2 szlaki turystyczne, z
Hali G ¾
asienicowej do doliny Pi ¾
eciu Stawów cztery, z doliny Pi ¾
eciu Stawów do
Morskiego Oka dwa. Ile jest mo·
zliwo´sci wycieczek Ku´znice-Hala G ¾
asienicowa-
Dolina Pi ¾
eciu Stawów-Morskie Oko?
Odp. 2 4 2 = 16.
Zadanie 4.5.
a) Mam do wykonania 2 czynno´sci. Ka·
zd ¾
a mog ¾
e wykona´c na 3 sposoby. Na
ile sposobów mog ¾
e wykona´c ten zestaw czynno´sci?
Odp. 3
2
= 9.
b) Mam do wykonania 3 czynno´sci. Ka·
zd ¾
a mog ¾
e wykona´c na 2 sposoby.
Na ile sposobów mog ¾
e wykona´c ten zestaw?
Odp. 2
3
= 8.
c) Mam do wykonania 2 czynno´sci. Ka·
zd ¾
a mog ¾
e wykona´c na 10 sposobów.
Na ile sposobów mog ¾
e wykona´c ten zestaw czynno´sci?
Odp. 10
2
= 100.
d) Mam do wykonania 10 czynno´sci. Ka·
zd ¾
a mog ¾
e wykona´c na 2 sposoby.
Na ile sposobów mog ¾
e wykona´c ten zestaw?
Odp. 2
10
= 1024.
Zadanie 4.6. Ile dzielników ma liczba naturalna n , której rozk÷
adem na
czynniki piewsze jest n = p
n
1
1
p
n
1
1
:::: p
n
k
k
?
Odpowied´z: (n
1
+ 1)(n
2
+ 1)::::(n
k
+ 1):Na przyk÷
ad dla liczby 24 = 2
3
3
mamy 4 2 = 8 dzielników. S ¾
a nimi 1; 2; 3; 4; 6; 8; 12; 24:
Zadanie 4.7. Ile dzielników ma liczba 360?
24

Rozwi ¾
azanie. Mamy 36 = 2
3
3
2
5
1
.
Liczba d jest dodatnim dzielnikiem
liczby 360, gdy d jest postaci 2
n
3
k
5
l
, gdzie wyk÷
adnik n jest niewi ¾
ekszy niz
3, wyk÷
adnik k jest niewi ¾
ekszy ni·
z 2, a wyk÷
adnik l jest niewi ¾
ekszy ni·
z 1. Zatem
(n; k; l) 2 f0; 1; 2; 3g
f0; 1; 2g
f0; 1g: S ¾
a zatem 4 3 2 = 24 ró·
zne dodatnie
dzielniki liczby 360. Oto one: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36,
40, 45, 60, 72, 90, 120, 180, 360.
Zadanie 4.8. Ile jest dodatnich dzielników liczby 3118500?
Odpowied´z. Poniewa·
z 3118500 = 2
2
3
4
5
3
7 11;wi ¾
ec liczba ta ma 3 5 4 2 2 =
240 czynników.
Zadanie 4.9. Ile dodatnich dzielników maj ¾
a liczby 111, 1111, 10000, 1234,
999999, 1000000 ?
Zadanie 4.10. Ile dodatnich dzielników ma liczba 2 3 5 7 11 13 17 19
23 29 31 37 = 7420 738 134 810 ?
Zadanie 4.11.
Ile dodatnich czynników ma liczba 2
64
= 18 446 744 073
709 551 616 ?
Zadanie 4.12.
Ile dodatnich czynników ma liczba 2
10
3
11
5
12
7
13
=
4290 899 381 642 207 250 000 000 000 ?
Zadanie 4.13. Numer dowodu osobistego sk÷
ada si ¾
e z trzech liter (na pocz ¾
atku)
i sze´sciu cyfr (potem). W gr ¾
e wchodzi 26 liter. Ile jest teoretycznie mo·
zliwych
róznych numerów dowodów osobistych?
Rozwi ¾
azanie. Uk÷
ad trzy litery - sze´s´c cyfr mo·
ze by´c interpretowany jako
element iloczynu kartezja´nskiego A
B
C
P
Q
R
S
T
U , gdzie
zbiory A; B; C maj ¾
a po 26 elementów, a pozosta÷
e po 10. Razem jest zatem do
dyspozycji 26
3
10
6
= 17 576 000 000 mo·
zliwych numerów; oko÷
o dwa i pó÷raza
wi ¾
ecej ni·
z wynosi liczba ludno´sci ca÷
ego ´swiata.
Zadanie 4.14. Has÷
o dost ¾
epu sk÷
ada si ¾
e z dziewi ¾
eciu symboli, w´sród których
s ¾
a trzy litery i sze´s´c cyfr. Ile jest mo·
zliwych hase÷
?
Odpowied´z.
9
3
26
3
10
6
= 1476 384 000 000.
Zadanie 4.15. Has÷
o dost ¾
epu sk÷
ada si ¾
e z dziewi ¾
eciu symboli, wybranych
spo´sród 26 liter i 10 cyfr. Ile jest mo·
zliwych hase÷
?
Odpowied´z. 36
9
= 101 559 956 668 416.
Zadanie 4.16. Ile jest podzbiorów o k elementach w zbiorze o n elementach?
Odpowied´z: Oczywi´scie zak÷
adamy, ·
ze k
n. Jest tych zbiorów
n
k
=
n(n k)!
k!
=
n(n 1)(n 1):::(n k+1)
1 2 3 ::: k
. Wspó÷
czynniki
n
k
nazywaja
si ¾
e wspó÷
czynnikami dwumianowymi albo wspó÷
czynnikami Newtona. Tworz ¾
a
one trójk ¾
at Pascala. W tym trójk ¾
acie liczbowym ka·
zdy wyraz (z wyj ¾
atkiem
skrajnych jedynek) jest sum ¾
a dwóch stoj ¾
acych bezpo´srednio nad nim.
25

1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
1
8
28
56
70
56
28
8
1
1
9
36
84
126
126
84
36
9
1
1
10
45
120
210
252
120
120
45
10
1
1
11
55
165
240
462
462
240
165
55
11
1
Mamy zatem
n
k
=
n
1
k
1
+
n
1
k
:
Zadanie 4.17. Ile jest
a) wszystkich podzbiorów danego zbioru n elementowego X ?
b) tych podzbiorów danego zbioru n elementowego X, które zawieraj ¾
a
ustalony element?
c) tych podzbiorów danego zbioru n elementowego X, które zawieraj ¾
a
dwa ustalone elementy?
Odpowied´z.
Zbiór n elementowy ma 2
n
podzbiorów.
Podamy dowód,
który da od razu algorytm ustawiania owych podzbiorów w pewnym porz ¾
adku.
Porz ¾
adek ten nazwiemy indukcyjnym. Zak÷
adamy, ·
ze X = f1; 2; :::; ng: Przyj-
muj ¾
ac tak, zak÷
adamy zatem, ·
ze elementy zbioru s ¾
a ustawione w jakim´s porz ¾
adku.
Jest to zatem zbiór uporz ¾
adkowany w sensie de…nicji podanej ni·
zej.
Zbiór jednoelementowy f1g ma dwa podzbiory: zbiór pusty ? i pe÷ny zbiór
f1g:Ustawmy je w tej w÷a´snie kolejno´sci. Poniewa·
z 2
1
= 2, zatem dla n = 1
wzór o liczbie elementów zbioru jest prawdziwy. Za÷
ó·
zmy, ·
ze jest prawdziwy
dla pewnej liczby naturalnej n
1. To znaczy, ·
ze wszystkie podzbiory zbioru
X = f1; 2; :::; ng sa ustawione w pewnym porz ¾
adku. Z ka·
zdego z tych zbiorów
tworzymy nowy zbiór przez dodanie liczby n + 1: Zatem liczba zbiorów zwi ¾
eksza
si ¾
e dwukrotnie. Poniewa·
z 2 2
n
= 2
n+1
, wi ¾
ec dowód jest zako´nczony.
Zbiór podzbiorów zbioru X
nazywamy zbiorem pot ¾
egowym i oznaczamy
jednym z symboli 2
X
lub P (X): Z przedstawionego dowodu wynika algorytm
ustawiania zbioru pot ¾
egowego w pewnej kolejno´sci. Dla kolejnych n jest to:
? , f1g ;
? , f1g , f2g , f1; 2g ;
? , f1g , f2g , f1; 2g , f3g , f1; 3g , f2; 3g , f1; 2; 3g ;
? , f1g , f2g , f1; 2g , f3g , f1; 3g , f2; 3g , f1; 2; 3g , f4g , f1; 4g , f2; 4g ,
f1; 2; 4g , f3; 4g , f1; 3; 4g , f2; 3; 4g , f1; 2; 3; 4g ;
? , f1g , f2g , f1; 2g , f3g , f1; 3g , f2; 3g , f1; 2; 3g , f4g , f1; 4g , f2; 4g ,
f1; 2; 4g , f3; 4g , f1; 3; 4g , f2; 3; 4g , f1; 2; 3; 4g; f5g , f1; 5g , f2; 5g , f1; 2; 5g ,
26

f3; 5g , f1; 3; 5g , f2; 3; 5g , f1; 2; 3; 5g , f4; 5g , f1; 4; 5g , f2; 4; 5g , f1; 2; 4; 5g ,
f3; 4; 5g , f1; 3; 4; 5g , f2; 3; 4; 5g , f1; 2; 3; 4; 5g .
b) podzbiorów danego zbioru n elementowego X, które zawieraj ¾
a ustalony
element, a, jest 2
n 1
: Mo·
zemy bowiem te zbiory utworzy´c tak: rozww ¾
azmy
zbiór X z usuni ¾
etym elementem a, czyli X nfag: Ma on 2
n 1
podzbiorów.
Do ka·
zdego z nich do÷¾
aczamy element a: W ten sposób otrzymamy wszystkie
podzbiory zbioru X , które zawieraj ¾
a ustalony element.
c) dla n
2 liczba podzbiorów danego zbioru n elementowego X, które
zawieraj ¾
a dwa ustalone elementy, jest równa 2
n 2
.
Zadanie 4.18. Dany jest zbiór X o m elementach i jego podzbiór Y
o n
elementach. Ile jest podzbiorów, które s ¾
a
a) roz÷¾
aczne z Y ,
b) maj ¾
a niepuste przeci ¾
ecie ze zbiorem Y ,
c) maj ¾
a k elementów i zawieraj ¾
a jeden element ze zbioru Y;
d) maj ¾
a k elementów i niepuste przeci ¾
ecie ze zbiorem Y:
Rozwi ¾
azanie. a) Jest m
n elementów, które nale·
z ¾
a do X, ale nie nale·
z ¾
a do
Y: Zatem jest 2
m n
takich zbiorów.
b) do ka·
zdego niepustego podzbioru zbioru Y mo·
zna do÷¾
aczy´c dowolny zestaw
m
n elementów nie nale·
z ¾
acych do Y: ×¾
acznie jest zatem (2
n
1) 2
m n
=
2
m
2
m n
takich zbiorów. Na przyk÷
ad gdy X = f1; 2; 3; 4; 5g, Y = f1; 2; 3g;
otrzymujemy nast ¾
epuj ¾
ace zbiory (jest ich cztery razy siedem):
f1g; f2g; f3g; f1; 2g; f1; 3g; f2; 3g; f1; 2; 3g;
f1; 4g; f2; 4g; f3; 4g; f1; 2; 4g; f1; 3; 4g; f2; 3; 4g; f1; 2; 3; 4g;
f1; 5g; f2; 5g; f3; 5g; f1; 2; 5g; f1; 3; 5g; f2; 3; 5g; f1; 2; 3; 5g;
f1; 4; 5g; f2; 4; 5g; f3; 4; 5g; f1; 2; 4; 5g; f1; 3; 4; 5g; f2; 3; 4; 5g; f1; 2; 3; 4; 5g:
Zgadza si ¾
e ze wzorem, który daje 2
5
2
5 3
= 28 zbiorów.
c) (wskazówka) nale·
zy oczywi´scie przyj ¾
a´c za÷
o·
zenie, ·
ze n
k
m. Do
ka·
zdego elementu zbioru Y mo·
zna dobra´c n
k elementów spoza Y:
Zadanie 4.19. Dany jest zbiór m elementach i jego dwa roz÷¾
aczne podzbiory:
jeden o k elementach, drugi o n elementach.
a) ile jest podzbiorów zbioru X, które maj ¾
a z ka·
zdym z tych zbiorów po
jednym wspólnym elemencie?
b) ile jest podzbiorów zbioru X, które maj ¾
a niepust ¾
a cz ¾
e´s´c wspóln ¾
a z ka·
zdym
z tych zbiorów?
Rozwi ¾
azanie, (a). Oznaczmy "du·
zy" zbiór m-elementowy przez X ; ten zbiór
k-elementowy przez A, a zbiór n-elementowy przez B:Oczywi´scie musi by´c k +
n
m: Wybieramy wszystkie pary elementów: pierwszy ze zbioru A, drugi ze
zbioru B:Tych par jest k n. Zbiór X n (A [ B) ma m
(k + n) elementów.
Mo·
zeny z nich utworzy´c 2
m (k+n)
podzbiorów, a do ka·
zdego z nich do÷¾
aczy´c
27
ka·
zd ¾
a z wybranych par. ×¾
acznie otrzymujemy k n 2
m (k+n)
podzbiorów. Na
przyk÷
ad, gdy m = 7; k = 2; n = 3; wzór podaje liczb ¾
e 2 3 2
7 (2+3)
= 24:
Istotnie, dla X = f1; 2; 3; 4; 5; 6; 7g ; A = f1; 2g ; B = f3; 4; 5g otrzymujemy
takie podzbiory:
f1; 3g;
f1; 4g;
f1; 5g;
f2; 3g;
f2; 4g;
f2; 5g;
f1; 3; 6g;
f1; 4; 6g;
f1; 5; 6g;
f2; 3; 6g;
f2; 4; 6g;
f2; 5; 6g;
f1; 3; 7g;
f1; 4; 7g;
f1; 5; 7g;
f2; 3; 7g;
f2; 4; 7g;
f2; 5; 7g;
f1; 3; 6; 7g; f1; 4; 6; 7g; f1; 5; 6; 7g; f2; 3; 6; 7g; f2; 4; 6; 7g; f2; 5; 6; 7g:
Zadanie 4.20. Danych jest n roz÷¾
acznych podzbiorów A
1
; A
2
; A
3
; ::: ; A
k
zbioru m-elementowego X: Kolejne te podzbiory maj ¾
a 1; 2; 3; :::; k elementów.
Ile jest
a) podzbiorów n elementowych zbioru X, które maj ¾
a z ka·
zdym zbiorem A
j
po jednym wspólnym elemencie?,
b) wszystkich podzbiorów zbioru X, które maj ¾
a z ka·
zdym zbiorem A
j
po
jednym wspólnym elemencie ?
c) wszystkich podzbiorów n elementowych zbioru X, które maj ¾
a niepuste
przeci ¾
ecie z ka·
zdym zbiorem A
j
?
d) wszystkich podzbiorów zbioru X, które maj ¾
a niepuste przeci ¾
ecie z ka·
zdym
zbiorem A
j
?
Rozwi ¾
azanie (punkt a). Najpierw przeprowadzimy krótk ¾
a dyskusj ¾
e warunków
zadania. Oczywi´scie musi by´c 1 + 2 + 3 + ::: + k
=
k(k+1)
2
m oraz
k
n
m. Spe÷
niaj ¾
a to na przyk÷
ad liczby k = 3 , m = 10 ; n = 5:
Oznaczmy liczb ¾
e m
k(k+1)
2
przez K :Wybierzmy z ka·
zdego ze zbiorów
A
1
; A
2
; A
3
; ::: ; A
k
po jednym elemencie. Mo·
zemy to zrobi´c na 1 2 3
:::
k = k! sposobów. Do ka·
zdego z tych zbiorów k-elementowych dobieramy
po n
k elementów. Mo·
zemy to zrobi´c na
m
K
n
k
sposobów. Otrzymujemy
k!
m
K
n
k
zbiorów.
Gdy k = 3 , m = 10 ; n = 5, przyjmijmy A
1
= f1g; A
2
= f2; 3g ; A
2
=
f4; 5; 6g . Naszym zadaniem jest wybra´c zbiory o 5 elementach spo´sród liczb
f1; 2; 3; 4; 5; 6; 7; 8; 9; 10g maj ¾
acych po jednym elemencie z f1g; f2; 3g ; f4; 5; 6g: Wybieramy
najpierw po jednym elemencie z tych zbiorów, ortrzymuj ¾
ac sze´s´c zbiorów:
f1; 2; 4g; f1; 2; 5g ; f1; 2; 6g , f1; 3; 4g; f1; 3; 5g ; f1; 3; 6g .
Do ka·
zdego z tych zbiorów mo·
zemy doda´c dowolnie dwie liczby spo´sród
7; 8; 9; 10:Takich par jest sze´s´c. Zatem szukanych zbiorów jest 36. Zgadza si ¾
e to
ze wzorem, bo 3!
10
6
5
3
= 36:
28

Rozwi ¾
azanie (punkt b). Pocz ¾
atek rozumowania jest tak
R
sam, jak w a).
Wybieramy z ka·
zdego ze zbiorów A
1
; A
2
; A
3
; ::: ; A
k
po jednym elemencie.
Mo·
zemy to zrobi´c na 1 2 3 :::
k = k ! sposobów. Zostaje m
K =
m
k(k+1)
2
elementów. Mo·
zemy z nich utworzy´c 2
m K
podzbiorów. ×¾
aczymy
je z wybranymi wcze´sniej k! zbiorami. Otrzymujemy razem k! 2
m K
. Gdy
k = 3 , m = 10 ; n = 5, otrzymamy 3! 2
10 6
= 96 zbiorów.
Zadanie 4.21. Ile jest permutacji zbioru o n elementach?
Odpowied´z (szkic dowodu). Permutacji zbioru n-elementowego jest n!. Po-
damy dowód, z którego wynika te·
z algorytm ustawiaj ¾
acy te permutacje w ci ¾
ag.
Dla n = 1 jest tylko jedna permutacja. Za÷
o·
zymy, ·
ze wszystkie permutacje
zbioru o n s ¾
a ustawione w ci ¾
ag o n! elementach:Do ka·
zdej permutacji dostaw-
iamy liczb ¾
e n + 1 na ka·
zdym mo·
zliwym miejscu. Tych miejsc jest n + 1: Zatem
przy przej´sciu od liczby n do n + 1 liczba permutacji zwi ¾
eksza si ¾
e n + 1 razy.
To ko´nczy dowód.
Oto ustawienie wszystkich permutacji liczb 1; 2; 3 oraz permutacji liczb
1; 2; 3; 4 w ci ¾
ag:
123; 132; 312; 213 ; 231 ; 321
oraz
1234; 1243 ; 1423; 4123 ;
1324 ; 1342 ; 1432 ; 1432 ;
3124; 3142; 3412; 4312;
2134 ; 2143 ; 2413 ; 4213 ;
2314 ; 2341 ; 2431 ; 4231 ;
3214 ; 3241 ; 3421 ; 4321
Zadanie 4.22. Ile jest permutacji zbioru f1; 2; 3; :::; ng , które zachowuj ¾
a
liczby 1; 2; 3; :::; k w ich naturalnym porz ¾
adku? Zak÷
adamy, ·
ze k
n:
Zadanie 4.23. Poda´c interpretacj ¾
e geometryczn ¾
a wszystkich 6 permutacji
zbioru o 3 elementach (jako izometrii trójk ¾
ata równobocznego).
Zadanie 4.24. Poda´c interpretacj ¾
e geometryczn ¾
a wszystkich 24 permutacji
zbioru o 4 elementach (jako izometrii czworo´scianu foremnego).
Zadanie 4.25.
Ile jest permutacji n elementów, które nie maj ¾
a punktu
sta÷
ego?
29

Wyk÷
ad 5
. Relacje
Ogólnie o relacjach. W j ¾
ezyku potocznym s÷
owo relacja znaczy mniej wi ¾
ecej
tyle co „zwi ¾
azek, powi ¾
azanie, wspó÷
zale·
zno´s´c”. Mamy relacje pokrewie´nstwa,
zale·
zno´sci s÷
u·
zbowej i znajomo´sci. W matematyce szkolnej mówimy o relacji
podzielno´sci. Relacj ¾
a jest ka·
zda zale·
zno´s´c funkcyjna. Precyzyjna matematyczna
de…nicja relacji jest do´s´c skomplikowana.
De…nicja. Niech A i B b ¾
ed ¾
a dwoma dowolnymi zbiorami. Relacj ¾
a mi ¾
edzy
elementami zbioru A i elementami zbioru B nazywamy dowolny podzbiór R
iloczynu kartezja´nskiego A
B . Mówimy, ·
ze elementy a 2 A i b 2 B s ¾
a ze sob ¾
a
w relacji R , gdy (a; b) 2 R .
Jest to cz ¾
esto spotykane w matematyce zjawisko: chc ¾
ac co´s wyrazi´c pre-
cyzyjnie, musimy uciec si ¾
e do skomplikowanych sformu÷
owa´n. Tak ¾
a cen ¾
e p÷
acimy
za precyzj ¾
e. Poni·
zej wyja´sniamy, jak t ¾
e de…nicj ¾
e prze÷
o·
zy´c na codzienn ¾
a prak-
tyk¾
e matematyczn ¾
a.
Wykresy relacji.
Przyk÷
ad 5.1. Przyjrzyjmy si ¾
e najpierw relacji podzielno´sci dla liczb ca÷
kow-
itych:
m jest dzielnikiem przez n .
Wypiszmy wszystkie pary liczb nie wi ¾
ekszych ni·
z 15, dla których ta relacja
zachodzi.
S ¾
a to: wszystkie pary (1; n) oraz pary (2; k), gdzie k jest liczb ¾
a
parzyst ¾
a,
nast ¾
epnie pary (3,3), (3,6), (3,9), (3,12) i (3,15) , potem (4,4), (4,8), (4,12),
(5,5), (5,10), (5,15), (6,6), (6,12), (7,7), (7,14), (8,8), (9,9), (10,10), (11,11),
(12,12) (13,13) (14,14) i (15,15).
Zaznaczaj ¾
ac je na p÷
aszczy´znie, otrzymamy wykres relacji.
Na oznaczenie ogólnej relacji u·
zywamy cz ¾
esto litery R albo stosownego sym-
bolu. Tu zrobimy wyj ¾
atek i oznaczymy relacj ¾
e przez P, bo litera P jest bardziej
naturalna (od s÷
owa podzielno´s´c). Piszemy:
mP n , m jest dzielnikiem n
Przyk÷
ad 5.2. Post ¾
apmy podobnie (to jest narysujmy wykres) dla relacji R
okre´slonej wzorem
x R y , y = x + 1 .
Tu sprawa jest prosta: punkty (x,y) spe÷
niaj ¾
ace te relacj ¾
e to punkty na
wykresie funkcji y = x + 1 :
Post ¾
apmy teraz przeciwnie.
Zaznaczmy na p÷
aszczy´znie jaki´s zbiór R i
postarajmy si ¾
e odczyta´c, jak ¾
a relacj ¾
e on opisuje. Je´sli zbiorem R b ¾
edzie ko÷
o o
´srodku w (0,0) i promieniu 1, to relacj ¾
a b ¾
edzie oczywi´scie
xR y , x
2
+ y
2
= 1 .
Niech teraz zbiorem R b ¾
edzie obszar, po÷
o·
zony na p÷
aszczy´znie „pod”prost ¾
a
x = y. Obszar ten sk÷
ada si ¾
e z punktów (x; y), dla których x > y . Mamy zatem
w tym przyk÷
adzie:
x R y , x > y .
Relacj ¾
e mo·
zemy uto·
zsami´c z jej wykresem !
30

Ka·
zdy zbiór na p÷
aszczy´znie (ogólniej: w iloczynie kartezja´nskim) wyznacza
pewien zwi ¾
azek mi ¾
edzy x i y, a wi ¾
ec pewn ¾
a relacj ¾
e.
Ka·
zda funkcja F: X ! Y
jest rodzajem relacji. Nie ka·
zda relacja jest funkcj ¾
a.
Widzimy zatem, ·
ze podanie zbioru punktów, których wspó÷
rz ¾
edne spe÷
niaj ¾
a
dany zwi ¾
azek wystarcza do pe÷
nego opisania tego zwi ¾
azku, tej zale·
zno´sci.
´Cwiczenie 5.1. Narysowa´c wykres relacji równo´sci (liczb).
´Cwiczenie 5.2. Narysowa´c wykres relacji mniejszo´sci: x < y gdzie x, y 2 R.
´Cwiczenie 5.3. Narysowa´c wykres relacji wi¾ekszo´sci: xRy wtedy i tylko
wtedy, gdy x > y .
´Cwiczenie 5.4. Przedstawi´c gra…cznie relacj¾e zachodz ¾
ac ¾
a mi ¾
edzy liczbami
rzeczywistymi:
x R y , x
y
2
> 2 .
´Cwiczenie 5.5. Poniewa·
z relacje s ¾
a podzbiorami iloczynu kartezja´nskiego,
mo·
zna mówi´c o ich sumach, iloczynach itp. Rozpatrzmy dwie relacje zachodz ¾
ace
mi ¾
edzy liczbami naturalnymi. S ¾
a one wi ¾
ec podzbiorami iloczynu kartezja´nskiego
N
N :
a)
relacja przystawania dwóch liczb modulo 2,
b)
relacja przystawania liczb modulo 3.
Jak ¾
a relacj ¾
a jest ich cz ¾
e´s´c wspólna ?
´Cwiczenie 5.6. Jak ¾
a relacj ¾
e opisuje pusty podzbiór iloczynu kartezja´nskiego?
Opisa´c j ¾
a wzorem lub s÷
ownie.
´Cwiczenie 5.7. Jak ¾
a relacj ¾
e mi ¾
edzy liczbami opisuje pe÷
ny podzbiór iloczynu
kartezja´nskiego X
X, to znaczy ca÷
y zbiór X
X ? Opisa´c j ¾
a wzorem lub
s÷
ownie.
´Cwiczenie 5.8. Jak ¾
a relacj ¾
e mi ¾
edzy liczbami opisuje jednopunktowy podzbiór
iloczynu kartezja´nskiego R
R, na przyk÷ad A = f(1; 2)g? Opisa´c t ¾
e relacj ¾
e
wzorem lub s÷
ownie.
´Cwiczenie 5.9. Jaki podzbiór p÷aszczyzny odpowiada relacji okre´slonej jak
nast ¾
epuje:
x R y wtedy i tylko wtedy, gdy x i y maj ¾
a t ¾
a sam ¾
a cz ¾
e´s´c ca÷
kowit ¾
a ?
´Cwiczenie 5.10. Jaki podzbiór p÷aszczyzny odpowiada relacji okre´slonej jak
nast ¾
epuje:
x R y wtedy i tylko wtedy, gdy x i y maj ¾
a tak ¾
a sam ¾
a cz ¾
e´s´c u÷
amkow ¾
a?
31

Wyk÷
ad 6. Funkcje.
Zadanie 6.1. Niech f (x) = x
2
5 j x j + 6. Wyznaczy´c obrazy przedzia÷ów
[0; 1]; [2; 3]; [ 1; 6]. Wyznaczy´c przeciwobrazy zbiorów [0; 2], [
1
4
; 0]:
Zadanie 6.2. Niech f (x) = x
2
2 j x j +1. Wyznaczy´c obrazy przedzia÷ów
[ 1; 1]; [ 2; 2]; [ 1; 0]. Wyznaczy´c przeciwobraz zbiorów [0; 1]:
Zadanie 6.3. Dla podanej funkcji f
: R ! R
i podanego przedzia÷
u I
wyznaczy´c jego obraz f (I):
a) f (x) = x
2
5x + 6 , I = [0; 4] ,
b) f (x) = x
2
5x + 6 , I = [2; 3] ,
c) f (x) = j x j, I = [ 1; 1) ,
d) f (x) = sin x , I = [0; 2 ] ,
e) f (x) = x
2
+ x + 1 , I = [ 1; 10] .
Zadanie 6.4. Dla podanej funkcji f : R ! R
i podanego przedzia÷
u J
wyznaczy´c jego przeciwobraz f
1
(J ):
a) f (x) = x
2
5x + 6 , J = [0;
1
4
] ,
b) f (x) = x
2
5x + 6 , J = [0; 6] ,
c) f (x) = j x j, J = [1; 1) ,
d) f (x) = sin x , J = [0; 1] ,
e) f (x) = x
2
+ x + 1 , J = [111; 133].
Zadanie 6.5. Niech m; n b ¾
ed ¾
a dwiema liczbami ca÷
kowitymi dodatnimi i niech
f
: R ! R b ¾
edzie funkcj ¾
a okre´slon ¾
a tak: f (x) =
x
m
dla
x
0
x
n
dla
x
0
:Dla
jakich par m; n
a) funkcja ta jest róznowarto´sciowa,
b) funkcja ta jest surjekcj ¾
a,
c) obrazem przedzia÷
u [-1,1] jest ten sam przedzia÷
,
d) obrazem przedzia÷
u [-1;1] jest przedzia÷[0; 1] ?
Zadanie 6.6. Niech f
b ¾
edzie funkcj ¾
a przyporz ¾
adkowuj ¾
ac ¾
a ka·
zdemu nie-
pustemu zbiorowi z÷
o·
zonemu z liczb naturalnych, najmniejsz ¾
a liczb ¾
e tego zbioru.
Czy ta funkcja jest róznowarto´sciowa? Okre´sli´c jej dziedzin ¾
e i wyznaczy´c jej
obraz. Opisa´c przeciwobraz liczby 2008.
Zadanie 6.7. Niech f b ¾
edzie funkcj ¾
a przyporz ¾
adkowuj ¾
ac ¾
a ka·
zdemu sko´nc-
zonemu i niepustemu zbiorowi z÷
o·
zonemu z liczb naturalnych, najwi ¾
eksz ¾
a liczb ¾
e
tego zbioru. Czy ta funkcja jest róznowarto´sciowa? Okre´sli´c jej dziedzin ¾
e i
wyznaczy´c jej obraz. Opisa´c przeciwobraz liczby 2008.
Zadanie 6.8. Poda´c wzór funkcji wzajemnie jednoznacznej, przeprowadza-
j ¾
acej
a) przedzia÷domkni ¾
ety [0;1] na przedzia÷domkni ¾
ety [0;2] ,
b) przedzia÷domkni ¾
ety [0;1] na przedzia÷domkni ¾
ety [-3;2] ,
c) przedzia÷domkni ¾
ety [2008;2009] na przedzia÷domkni ¾
ety [-100;100],
32
d) przedzia÷domkni ¾
ety [3;6] na przedzia÷domkni ¾
ety [4;8] tak, by obrazem
punktu 4 by÷punkt 6;
e) przedzia÷domkni ¾
ety [-3,3] na przedzia÷domkni ¾
ety [-3,3] tak, by obrazem
punktu -2 by÷punkt -1, obrazem -1 by÷
o 0, obrazem 0 by÷punkt 1, a obrazem
1 punkt 2.
Zadanie 6.9. Zrobi´c wykresy funkcji z zadania 6.8.
Zadanie 6.10. Funkcja f : R ! R jest dana wzorem f(x) =
8
<
:
1
dla x < 3
1
x
2
gdy -3
x < 3
3
dla x
3
:
a) Wyznaczy´c obraz przedzia÷
u otwartego (1; 6). Odpowied´z: (-8;0) [ f3g
;
b) wyznaczy´c przeciwobraz przedzia÷
u domkni ¾
etego [ 3; 2] . Odp. ( 1; 3)[
[ 2; 2] ;
c) wyznaczy´c zbiór warto´sci funkcji f :
Odpowied´z: [ 8; 1]
[ f3g:
-5
-4
-3
-2
-1
1
2
3
4
5
-8
-6
-4
-2
2
x
y
Zadanie 6.11. Niech A = f x 2 R : x
2
> 9 ^ x < 4 g. Niech f; g
b ¾
ed ¾
a funkcjami R ! R okre´slonymi jak ni·
zej: g(x) = 2x + 1 , za´s f (x) =
x
2
+ 1 dla x =
2 A
1 dla x 2 A
: Zaznaczy´c zbiór A na osi. Wyznaczy´c obraz przedzia÷
u
domkni ¾
etego [ 5; 5] przy funkcji f . Wyznaczy´c przeciwobraz zbioru A przy
funkcji g. Obliczy´c f (g(1)). Obliczy´c g(f (4)):
Odpowied´z. Funkcj ¾
e f warto przedstawi´c nieco innym wzorem. Okre´slona
jest ona tak:
33
f (x) =
8
>
>
<
>
>
:
1 dla x <
3
1
x
2
dla
3 < x < 3
1 dla 3 < x < 4
1
x
2
dla x > 4
-5
-4
-3
-2
-1
1
2
3
4
5
-20
-15
-10
-5
Po naszkicowaniu wykresu funkcji f widzimy, ·
ze obrazem przedzia÷
u [ 5; 5]
jest suma przedzia÷
ów, których ko´ncami s ¾
a
24 i
15 oraz
8 i 1. Do pe÷
nego
rozwi ¾
azania zadania nale·
zy rozstrzygn ¾
a´c, czy s ¾
a to przedzia÷
y domkni ¾
ete, czy
otwarte, czy domkni ¾
ete.
Poniewa·
z g(1) = 3; a liczba 3 nale·
zy do zbioru A, wi ¾
ec f (g (1)) = f (2 1+1) =
1. Poniewa·
z liczba 4 nie nale·
zy do zbioru A, wi ¾
ec f (4) =
4
2
+ 1 =
15, zatem
g(f (4)) = g(15) =
29:
Wyznaczamy przeciwobraz zbioru A przy funkcji g: Jest to suma przeciwo-
brazu przedzia÷
u ( 1;
3) i przeciwobrazu przedzia÷
u [3; 4): Jest to zatem
suma ( 1;
2) [ [1;
3
2
):
Zadanie 6.12. Funkcja g : R ! R jest dana wzorem g(x) =
8
<
:
1
dla x 2 ( 1; 3]
1
x
2
dla x 2 ( 3; 3]
3
dla x 2 (3; +1)
:
a) Wyznaczy´c obraz przedzia÷
u otwartego ( 3; 5).
b) wyznaczy´c przeciwobraz przedzia÷
u domkni ¾
etego [1; 6] .
c) poda´c argument, uzasadniaj ¾
acy, ·
ze h nie jest funkcj ¾
a ró·
znowarto´sciow ¾
a :
Zadanie 6.13. Funkcja h : R ! R jest dana wzorem h(x) =
8
<
:
2
dla x 2 ( 1; 2)
x
2
+ 2 dla x 2 [ 2; 2)
2 dla x 2 [2; +1)
:
a) Wyznaczy´c obraz przedzia÷
u otwartego ( 1; 3). Odpowied´z: ( 7; 2]
34

b) wyznaczy´c przeciwobraz przedzia÷
u domkni ¾
etego [ 2; 0] . Odp.( 1;
p
2)[
(
p
2; 1)
c) wyznaczy´c zbiór warto´sci funkcji h :
Odpowied´z: [ 2; 2]
Zadanie 6.14. Wyznaczy´c funkcje odwrotne do funkcji:
a) f (x) =
1
x
; b) f (x) =
x+1
x+2
; c) f (x) =
2x 1
x 2
; d) f (x) =
7 6x
7x 8
;
Zadanie 6.15. Wyznaczy´c wspó÷
czynniki a; b; c; d tak, by funkcj ¾
a odwrotn ¾
a
do f (x) =
ax+b
cx+d
by÷
a ta sama funkcja.
35

Wyk÷
ad 7
. Permutacje
Zadanie 7.1. Permutacja
1
2
3
4
5
6
2
3
4
5
6
1
, czyli cykl (123456):
1 ! 2 ! 3 ! 4 ! 5 ! 6 ! 1 . Jest to permutacja nieparzysta, ma pi ¾
e´c
inwersji: pary (2,1), (3,1), (4,1), (5,1) i (6,1). Permutacja do niej odwrotna
to
1
2
3
4
5
6
6
1
2
3
4
5
: Ma te·
z 5 inwersji. Rysunek permutacji odwrotnej
powstaje z rysunku danej przez odwrócenie strza÷
ek. Narysowa´c (przedstawi´c
gra…cznie) tak ¾
a permutacj ¾
e.
Odpowied´z: To cykl
1 ! 6 ! 5 ! 4 ! 3 ! 2 ! 1:
Zadanie 7.2. Permutacja
1
2
3
4
5
6
2
6
5
1
4
3
: Jest to cykl (126354).
Inwersje tworz ¾
a pary (6,3), (6,5), (6,4), (5,4), (5,3), (5,1), (4,3). Jest to zatem
permutacja nieparzysta.
Ile inwersji ma permutacja odwrotna? Zapisa´c j ¾
a w postaci
1
2
3
4
5
6
:
Zadanie 7.3. Permutacja
=
1
2
3
4
5
6
4
2
3
6
5
1
: Jest ona iloczynem
cykli (164)(2)(3)(5); cykle jednoelementowe (czyli punkty sta÷
e) mo·
zemy op-
u´sci´c. Zatem
= (164): Ile inwersji ma ta permutacja? Napisa´c permutacj ¾
e
odwrotn ¾
a.
Zadanie 7.4. Dane s ¾
a permutacje s = (145)(23) oraz t =
1
2
3
4
5
5
4
3
2
1
. Obliczy´c liczb ¾
e inwersji w tych permutacjach. Obliczy´c ts
3
oraz t
3
: Wyniki
przedstawi´c w postaci funkcji oraz w postaci roz÷¾
acznych cykli.
Rozwi ¾
azanie. Zapis s = (145)(23) oznacza, ·
ze jest to permutacja, w której
1 ! 4 ; 4 ! 5 ; 5 ! 1 ;
oraz 2 ! 3, 3 ! 2: Mo·
zna to zapisa´c s =
1
2
3
4
5
4
3
2
5
1
: Nast ¾
epuj ¾
ace pary tworz ¾
a inwersje: (4,3), (4,2), (4,1),
(3,2), (3,1), (2,1), (5,1). Jest zatem 7 inwersji. Permutacja jest nieparzysta.
Permutacja t odwraca naturalny porz ¾
adek liczb. Ka·
zda para tworzy inwersj ¾
e.
Jest zatem 10 inwersji.
Obliczymy teraz s
3
: Po trzykrotnym z÷
o·
zeniu tej permutacji otrzymamy s
3
=
1
2
3
4
5
1
3
2
4
5
.
Z÷
o·
zenie ts
3
oznacza, ·
ze wykonujemy najpierw s
3
, potem t: A zatem ts
3
=
1
2
3
4
5
5
3
4
2
1
:Rozk÷
adem na cykle tej permutacji jest (1; 5)(2; 3; 4). Aby
obliczy´c t
3
, przypomnijmy sobie, ·
ze permutacja t odwraca naturalny porz ¾
adek
liczb. Zatem t
1
= t, a st ¾
ad wynika, ·
ze t
1
= t
3
= t: Rozk÷
adem na cykle
permutacji t jest (1; 5)(2; 4) = (1; 5)(2; 4)(3).
Zadanie 7.5. Dane s ¾
a permutacje g =
1
2
3
4
5
6
7
8
9
3
5
1
6
2
4
9
8
7
,
36

h =
1
2
3
4
5
6
7
8
9
2
4
5
3
6
9
1
7
8
:
a) Obliczy´c g
1
:
Rozwi ¾
azanie. Obliczaj ¾
ac permutacj ¾
e odwrotn ¾
a, zamieniamy wiersze i porz ¾
ad-
kujemy wzgl ¾
edem górnego (po zamianie) : g
1
=
1
2
3
4
5
6
7
8
9
3
5
1
6
2
4
9
8
7
b) przedstawi´c h jako z÷
o·
zenie roz÷¾
acznych cykli. Odpowied´z: h jest cyklem
(124356987):
c) obliczy´c g
h
2
:
Rozwi ¾
azanie: h
2
to cykl (145972368);czyli permu-
tacja h
2
=
1
2
3
4
5
6
7
8
9
4
3
6
5
9
8
2
1
7
:Odwrotna do niej to
h
2
=
1
2
3
4
5
6
7
8
9
8
7
2
1
4
3
9
6
5
; z÷
o·
zenie g h
2
=
1
2
3
4
5
6
7
8
9
8
9
5
3
6
1
7
4
2
d) okre´sli´c znak permutacji h:
Ma ona 8 inwersji; tworz ¾
a je pary: (2,1),
(4.3), (4,1), (5,3), (5,1), (6,1), (9,7), (9,8). Jest to permutacja parzysta.
Zadanie 7.6. Napisa´c wszystkie permutacje liczb 1,2,3 w porz ¾
adku induk-
cyjnym. Narysowa´c wszystkie te permutacje w tym porz ¾
adku. Jakim izometriom
trójkata równobocznego odpowiadaj ¾
a kolejno te permutacje?
Odpowied´z. W skróconym zapisie: [1,2,3], [1,3,2], [3,1,2], [2,1,3], [2,3,1],
[3,1,2], czyli
1
2
3
1
2
3
;
1
2
3
1
3
2
;
1
2
3
3
1
2
;
1
2
3
2
1
3
;
1
2
3
2
3
1
;
1
2
3
3
1
2
:
Permutacje te odpowiadaj ¾
a kolejno nastepuj ¾
acym izometriom trójk ¾
ata równobocznego:
identyczno´s´c, symetria osiowa wzgl ¾
edem wysoko´sci wyprowadzonej z wierzcho÷
ka
1 prostopadle do boku 12, obrót o 120 stopni, symetria wzgl ¾
edem wysoko´sci
wyprowadzonej z wierzcho÷
ka 3 prostopadle do boku 12, obrót o 240 stopni,
symetria wzgl ¾
edem wysoko´sci wyprowadzonej z wierzcho÷
ka 2 prostopadle do
boku 13.
Zadanie 7.7. Wypisa´c wszystkie permutacje liczb 1,2,3 w porz ¾
adku leksyko-
gra…cznym. Zilustrowa´c rysunkiem.
Odpowied´z.
1
2
3
1
2
3
;
1
2
3
1
3
2
;
1
2
3
2
1
3
;
1
2
3
2
3
1
;
1
2
3
3
1
2
;
1
2
3
3
2
1
:
Zadanie 7.8. Zmiana porz ¾
adku permutacji zbioru o trzech elementach z
porz ¾
adku indukcyjnego na porz ¾
adek leksykogra…czny generuje pewna permu-
tacj ¾
e zbioru sze´scioelementowego. Wyznaczy´c t ¾
e permutacj ¾
e.
Rozwi ¾
azanie. Z zada´n 1 i 2 wynika, ·
ze jest to permutacja
1
2
3
4
5
6
1
2
5
3
4
6
,
czyli cykl (354).
37

Zadanie 7.9. Napisa´c wszystkie permutacje zbioru (1,2,3,4} w porz ¾
adku
indukcyjnym. Pierwszych 5 z nich zilustrowa´c rysunkiem.
Zadanie 7.10. Napisa´c wszystkie permutacje zbioru (1,2,3,4} w porz ¾
adku
indukcyjnym. Pierwszych 5 z nich zilustrowa´c rysunkiem.
Zadanie 7.11. Wyja´sni´c, jakim izometriom czworo´scianu foremnego odpowiadaj ¾
a
poszczególne permutacje zbioru {1,2,3,4}.
Szkic odpowiedzi.
Obrót czworo´scianu foremnego o 180 stopni wokó÷osi przechodz ¾
acej przez
´srodki przeciwleg÷
ych boków. Jest to permutacja parzysta
a
b
c
d
c
d
a
b
;
jest iloczynem transpozycji (ac)(bd), na liczbach (13)(24) =
1
2
3
4
3
4
1
3
.
Czworo´scian ma trzy pary przeciwleg÷
ych kraw¾
edzi, zatem sa trzy takie obroty.
Dwa pozosta÷
e to (14)(23) =
1
2
3
4
4
3
2
1
i (12)(34) =
1
2
3
4
2
1
4
3
:
Zadanie 7.12. Jaka permutacja znajduje si ¾
e na miejscu 37 w grupie per-
mutacji 5 elementów w porz ¾
adku leksykogra…cznym, w porz ¾
adku indukcyjnym?
Odp. W porz ¾
adku leksykogra…cznym
1 2 3 4 5
2 4 1 3 5
:
Dla porz ¾
adku indukcyjnego mamy tak. Wypiszmy najpierw porz ¾
adek induk-
cyjny permutacji dwóch elementów: to [1,2], potem [2,1]. Porz ¾
adek indukcyjny
dla trzech to [1,2,3], [1,3,2], [3,1,2], [2,1,3], [2,3,1], [3,1,2]. Dla czterech otrzy-
mujemy:
[1,2,3,4], [1,2,4,3], [1,4,2,3], [4,1,2,3],
[1,3,2,4], [1,3,4,2], [1,4,3,2], [4,1,3,2],
.... potem cztery permutacje powstaj ¾
ace z [3,1,2] przez dopisywanie czwórki,
..... potem [2,1,3,4], [2,1,4,3], [2,4,1,3] i [4,2,1,3]. Permutacja [2,4,1,3] czyli
1 2 3 4
2 4 1 3
znajduje si ¾
e na 15 miejscu w S
4
. Z ka·
zdej poprzedzaj ¾
acej j ¾
a pow-
staje 5 nowych permutacji liczb 1,2,3,4,5. Permutacja, o któr ¾
a chodzi, jest na
miejscu 71.
Zadanie 7.13. Na którym miejscu w ka·
zdym z tych porz ¾
adków znajduje si ¾
e
permutacja
1 2 3 4 5
5 2 1 3 4
?
Rozwi ¾
azanie. W porz ¾
adku leksykogra…cznym grupy S
5
pierwszych 24 per-
mutacji to te, które s ¾
a postaci
1 2 3 4 5
1
; nast ¾
epnych 24 to
1 2 3 4 5
2
,
potem id ¾
a
1 2 3 4 5
3
;
1 2 3 4 5
4
:×¾
acznie 96 permutacji. Nast ¾
epuje teraz 6
permutacji postaci
1 2 3 4 5
5 1
;razem 102. Potem dopiero
1 2 3 4 5
5 2 1 3 4
. Znaj-
duje si ¾
e zatem ona na 103 miejscu.
Zadanie 7.14. Wyznaczy´c setn ¾
a od ko´nca permutacj ¾
e w porz ¾
adku leksyko-
gra…cznym w S
9
:
38

Odp.
1 2 3 4 5 6 7 8 9
9 8 7 6 1 5 3 2 4
.
Zadanie 7.15. Wyznaczy´c permutacj ¾
e, która jest na miejscu 2007 w S
9
.
Odp.
1 2 3 4 5 6 7 8 9
1 2 5 8 7 6 4 3 9
:
Wyk÷
ad 8
. Zbiór pot ¾
egowy.
Rodzin ¾
e podzbiorów zbioru {1,2,3,...,n} mo·
zna na przyk÷
ad uporz ¾
adkowa´c
leksykogra…cznie: najpierw zbiór pusty ?, potem zbiory zawieraj ¾
ace 1 , potem
zbiory, których najmniejszym elementem jest 2 itd. Dla n = 3 daje to porz ¾
adek
?, {1}, {1,2}, {1,2,3}, {1,3}, {2}, {2,3}, {3}.
Porz ¾
adek leksykogra…czny z gradacj ¾
a polega na ustawieniu najpierw zbiorów
jednoelementowych, potem dwuelementowych itd. Z tym, ·
ze na pocz ¾
atku staw-
iamy zbiór pusty. Dla n = 3 jest to porz ¾
adek
?; f1g; f2g; f3g; f1; 2g; f1; 3g; f2; 3g; f1; 2; 3g
Ale porz ¾
adek indukcyjny daje lepszy algorytm. Zaczynamy od zbioru pustego.
Zak÷
adaj ¾
ac, ·
ze podzbiory o n elementach ju·
z s ¾
a ustawione, dopisujemy nowoprzy-
by÷
y element do ka·
zdego kolejnego wyrazu ci ¾
agu. Daje to nastepuj ¾
acy porz ¾
adek
(gdy n = 3):
?; f1g; f2g; f1; 2g; f3g; f1; 3g; f2; 3g; f1; 2; 3g:
Twierdzenie. W porz ¾
adku indukcyjnym zbioru pot ¾
egowego 2
f1;2;3;:::;ng
, to
jest w rodzinie podzbiorów zbioru (1,2,3,...,n}, zbiór z÷
o·
zony z liczb fa
1
; a
2
; :::; a
k
g
, gdzie a
1
< a
2
< ::: a
k
, znajduje si ¾
e na miejscu o numerze 1+2
a
1
1
+ 2
a
2
1
+ ::: +
2
a
k
1
:
Przyk÷
ad-sprawdzenie. W zbiorze podzbiorów {1,2,3} mamy:
dla zbioru {1} miejsce 1 + 2
0
= 2;
dla zbioru {2} miejsce 1 + 2
1
= 3;
dla zbioru {1,2} miejsce 1 + 2
0
+ 2
1
= 4;
dla zbioru {3} miejsce 1 + 2
2
= 5;
dla zbioru {1,3} miejsce 1 + 2
0
+ 2
2
= 6;
dla zbioru {2,3} miejsce 1 + 2
1
+ 2
2
= 7;
dla zbioru {1,2,3} miejsce 1 + 2
0
+ 2
1
+ 2
2
= 8:
Przyk÷
ad. W rodzinie podzbiorów liczb ca÷
kowitych dodatnich niewi ¾
ekszych
ni·
z 10 zbiór z÷
o·
zony ze wszystkich liczb nieparzystych znajduje si ¾
e na miejscu
1 + 2
0
+ 2
2
+ 2
4
+ 2
6
+ 2
8
=
342 .
Dowód twierdzenia. Zastosujemy indukcj ¾
e wzgl ¾
edem n: Twierdzenie jest
prawdziwe dla n = 2. Powy·
zej zosta÷
o te·
z sprawdzone dla n = 3. Za÷
ó·
zmy,
·
ze jest ono prawdziwe dla pewnej liczby naturalnej n i rozpatrzmy rodzin ¾
e
podzbiorów zbioru f1; 2; 3; :::; n + 1g. Widzieli´smy, ·
ze przy porz ¾
adku induk-
cyjnym pierwszych 2
n
wyrazów to podzbiory, w których nie ma n + 1: Je´sli
zatem a
1
< a
2
< ::: < a
k
s ¾
a ró·
znymi liczbami mniejszymi od n, to zbiór
z÷
o·
zony z tych liczb jest na miejscu 1 + 2
a
1
1
+ 2
a
2
1
+ ::: + 2
a
k
1
:Ze
sposobu ustawiania zbiorów w ci ¾
ag wynika, ·
ze A = f a
1
; a
2
; :::; a
k
; n + 1g
39

znajduje si ¾
e 2
n
miejsc za f a
1
; a
2
; :::; a
k
g: Jest to zatem miejsce o numerze
1 + 2
a
1
1
+ 2
a
2
1
+ ::: + 2
a
k
1
+ 2
n
. To jest zgodne z wyprowadzanym
wzorem. Na mocy zasady indukcji twierdzenie jest udowodnione.
Z twierdzenia tego wynika te·
z algorytm ustalenia, który zbiór jest na danym
miejscu m w porz ¾
adku indukcyjnym. Przedstawiamy liczb ¾
e m
1 w uk÷
adzie
dwójkowym:
m
1 = 2
a
k
+ 2
a
k
1
+ ::: + 2
a
1
. Na danym miejscu znajduje si ¾
e zbiór
fa
1
+ 1; a
2
+ 1; :::; a
k
+ 1g
Przyk÷
ad-sprawdzenie. Jaki zbiór znajduje si ¾
e na miejscu 342 w rodzinie
podzbiorów zbioru liczb naturalnych nie wi ¾
ekszych ni·
z 10?
Przedstawiamy liczb ¾
e 341 w uk÷
adzie dwójkowym:
341 = 2
8
+ 2
6
+ 2
4
+ 2
2
+ 2
0
: Widzimy, ·
ze na miejscu 342 znajduje si ¾
e zbiór
{1,3,5,7,9}.
Zadanie 8.1. Wypisa´c wszystkie 32 podzbiory zbioru pot ¾
egowego 2
f1;2;3;4;5g
w porz ¾
adku leksykogra…cznym.
Odp.
{?}, {1}, {1, 2}, {1, 2, 3}, {1, 2, 3, 4}, {1, 2, 3, 4, 5}, {1, 2, 3, 5}, {1, 2, 4},
{ 1, 2, 4, 5}, {1, 2, 5}, {1, 3}, {1, 3, 4}, {1, 3, 4, 5}, {1, 3, 5}, {1, 4}, {1, 4,
5}, {1, 5}, {2}, {2, 3}, {2, 3, 4},
{2, 3, 4, 5}, { 2, 3, 5}, {2, 4}, {2, 4, 5}, {2, 5}, {3}, {3, 4}, {3, 4, 5}, {3, 5},
{4}, {4, 5}, {5}
Zadanie 8.2. Wypisa´c wszystkie 32 podzbiory zbioru pot ¾
egowego 2
f1;2;3;4;5g
w porz ¾
adku leksykogra…cznym z gradacj ¾
a.
Odp. {?}, {1}, {2}, {3}, {4}, {5}, {1, 2}, {1, 3}, {1, 4}, {1, 5}, {2, 3}, {2,
4}, {2, 5}, {3, 4}, {3, 5}, {4, 5}, {1, 2, 3},
{1, 2, 4}, {1, 2, 5}, {1, 3, 4}, {1, 3, 5}, {1, 4, 5}, {2, 3, 4}, { 2, 3, 5}, {2, 4,
5}, {3, 4, 5}, {1, 2, 3, 4},
{1, 2, 3, 5}, {1, 2, 4, 5}, {1, 3, 4, 5}, {2, 3, 4, 5}, {1, 2, 3, 4, 5}
Zadanie 8.3. Wypisa´c wszystkie 32 podzbiory zbioru pot ¾
egowego 2
f1;2;3;4;5g
w porz ¾
adku indukcyjnym.
Odp. {?}, {1}, {2}, {1, 2}, {3}, {1, 3}, {2, 3}, {1, 2, 3}, {4}, {1, 4}, {2,
4}, {1, 2, 4}, {3, 4},
{1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}, {5}, {1, 5}, {2, 5}, {1, 2, 5}, {3, 5}, {1, 3,
5}, {2, 3, 5}, {1, 2, 3, 5},
{4, 5}, {1, 4, 5}, {2, 4, 5}, {1, 2, 4, 5}, {3, 4, 5}, {1, 3, 4, 5}, {2, 3, 4, 5},
{1, 2, 3, 4, 5} .
Zadanie 8.4. Który zbiór jest na miejscu 2007 w rodzinie podzbiorów X =
f1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11g w ka·
zdym z tych trzech porz ¾
adków?
Odp. Poniewa·
z 2006 = 2
10
+ 2
9
+ 2
8
+ 2
7
+ 2
6
+ 2
4
+ 2
2
+ 2
1
;wi ¾
ec w porz ¾
adku
indukcyjnym jest to {2,3,5,7,8,9,10,11}.
W porz ¾
adku leksykogra…cznym jest to {6,8,9,10,11}.
40

W porz ¾
adku leksykogra…cznym z gradacj ¾
a jest tak.
Najpierw stoi zbiór
pusty, potem 11 zbiorów jednoelementowych, potem
11
2
= 55
zbiorów
dwuelementowych, potem kolejno
11
3
= 165 trójelementowych,
11
4
=
330 czteroelementowych,
11
5
= 462 pi ¾
ecioelementowych,
11
6
= 462
sze´scioelementowych,
11
7
= 330 siedmioelementowych i
11
8
= 165 o´smioelementowych:
Poniewa·
z 1 + 11 + 55 + 165 + 330 + 462 + 462 + 330 + 165 = 1981; za´s 1981 +
11
9
= 2036 > 2007, wi ¾
ec interesuj ¾
acy nas zbiór ma 9 elementów i znajduje
si ¾
e na miejscu 2007
1981 = 26 w´sród dziewi ¾
ecioelementowych. Pierwszych
7
5
= 21 z nich to f1; 2; 3; 4; x; y; z; t; ug - ostatnim jest f1; 2; 3; 4; 8; 9; 10; 11g.
Po nim nast ¾
epuj ¾
a te, których najmniejsze liczby to 1; 2; 3; 5:S ¾
a to po kolei
f1; 2; 3; 5; 6; 7; 8; 9; 10g; f1; 2; 3; 5; 6; 7; 8; 9; 11g; f1; 2; 3; 5; 6; 7; 8; 10; 11g; :f1; 2; 3; 5; 6; 7; 9; 10; 11g.
Bezpo´srednio za tym zbiorem znajduje si ¾
e {1,2,3,5,6,8,9,10,11}.
Zadanie 8.5.
Znale´z´c miejsce zbioru {3,6,7} w rodzinie 2
X
, gdy X =
f1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11g:
Odp. W porz ¾
adku indukcyjnym to miejsce nr 101, w porz ¾
adku leksyko-
gra…cznym to 1732. W porz ¾
adku leksykogra…cznym z gradacj ¾
a to 162.
Zadanie 8.6. Napisa´c trzy zbiory poprzedzaj ¾
ace {3,6,7} i trzy zbiory nastepu-
j ¾
ace po {3,6,7} w ka·
zdym z tych trzech porz ¾
adków.
Zadanie 8.7. Ile jest zbiorów mi ¾
edzy {3,6,7} a {4,5,6} w ka·
zdym z tych
porz ¾
adków?
Zadanie 8.8. Wyznaczy´c pi ¾
e´c ko´ncowych zbiorów w rodzinie podzbiorów
zbioru stuelementowego w porzadku leksykogra…cznym, leksykogra…cznym z
gradacj ¾
a i indukcyjnym.
Zadanie 8.9. Zbiór P (f1; :::101g); czyli rodzin ¾
e wszystkich podzbiorów zbioru
liczb naturalnych 1, 2, 3, ..., 99,100,101 porz ¾
adkujemy indukcyjnie.
a) poda´c najbli·
zszy zbiór dwuelementowy, który wyst ¾
epuje po {1,8,13}.
b) ile podzbiorów o trzech elementach znajduje si ¾
e przed {1,3,12,14}?
Rozwi ¾
azanie. Porz ¾
adek indukcyjny zaczyna si ¾
e od ? ; f1g; f2g; f1; 2g, potem
dostawiamy liczb ¾
e 3, otrzymuj ¾
ac dalszy ci ¾
ag: {3}, {1,3}, {2,3}, {1,2,3}. W
rozpatrywanym przyk÷
adzie przed {1,8,13} znajduj ¾
a si ¾
e wszystkie zbiory za-
wieraj ¾
ace liczby od 1 do 12. Ostatni z nich, maj ¾
acy numer 2
12
= 4096 to
{1,2,3,4,5,6,7,8,9,10,11,12}. Najwcze´sniejszy jednoelementowy to, jak widzieli´smy,
zbiór f1g:Najpó´zniejszy to {12}. Dostawiamy teraz do ka·
zdego z nich 13. {12,
13} jest zbiorem o dwóch elementach najbli·
zszym {1,8,13}.
Wszystkie z÷
o·
zone z trójek (a; b; c), gdzie a; b; c s ¾
a liczbami
14: Jest to
równe
14
3
=
14 13 12
1 2 3
= 14 13 2 = 14 26 = 364:
Pierwszych osiem zbiorów to ? ; f1g; f2g; f1; 2g; f3g; f1; 3g; f2; 3g; f1; 2; 3g:
Zadanie 8.10.
Zbiór P (f1; :::100g); czyli rodzin ¾
e wszystkich podzbiorów
zbioru liczb naturalnych 1, 2, 3, ..., 99,100 porz ¾
adkujemy indukcyjnie.
41

a) poda´c najbli·
zszy zbiór dwuelementowy, który wyst ¾
epuje po {1,12,13}.
b) ile podzbiorów o trzech elementach znajduje si ¾
e przed {1,5,18,12}?
Zadanie 8.11. W zbiorze P (f1; :::10g); czyli w rodzinie wszystkich podzbiorów
zbioru liczb naturalnych 1, 2, 3, ..., 10 rozpatrujemy porz ¾
adek nast ¾
epuj ¾
acy:
A poprzedza B , je·
zeli ma mniej elementów, a je·
zeli obydwa zbiory maj ¾
a tyle
samo elementów, to wcze´sniejszy jest ten, który jest wcze´sniejszy w porz ¾
adku
leksykogra…cznym.
a) Wyznaczy´c zbiór, znajduj ¾
acy si ¾
e na miejscu 99.
b) wyznaczy´c numer miejsca, na którym znajduje si ¾
e zbiór {3,9,10}.
Zadanie 8.12. W zbiorze P (f1; :::11g); czyli w rodzinie wszystkich podzbiorów
zbioru liczb naturalnych 1, 2, 3, ..., 11 rozpatrujemy porz ¾
adek nast ¾
epuj ¾
acy:
A poprzedza B , je·
zeli ma mniej elementów, a je·
zeli obydwa zbiory maj ¾
a tyle
samo elementów, to wcze´sniejszy jest ten, który jest wcze´sniejszy w porz ¾
adku
leksykogra…cznym.
a) Wyznaczy´c zbiór, znajduj ¾
acy si ¾
e na miejscu 66.
Rozwi ¾
azanie. Jest to zbiór {9,11}. Mo·
zna to obliczy´c ,licz ¾
ac "od ko´nca".
W tym porz ¾
adku na pierwzym miejscu stoi zbiór pusty, potem 11 zbiorów jed-
noelementowych i
11
2
= 55 zbiorów o dwóch elementach. Daje to 1+11+55
= 67 zbiorów. Ostatni z nich to {10,11} a przedostatni to {9,11}.
b) wyznaczy´c numer miejsca, na którym znajduje si ¾
e zbiór {4,7,10}.
Rozwi ¾
azanie. Jest to zbiór o trzech elementach, zatem przed nim stoi zbiór
pusty, 11 zbiorów jednoelementowych i
11
2
= 55 zbiorów o dwóch elemen-
tach. Przed nim znajduj ¾
a si ¾
e te·
z zbiory f1; ; g; f2; ; g ; f3; ; g
jest ich
odpowiednio
10
2
= 45 ;
9
2
= 36 ;
8
2
= 28: Mamy 1 + 11 + 55 + 45 +
36 + 28 = 176: Przed zbiorem {4,7,10} znajduje si ¾
e jeszcze 6 zbiorów f4; 5; g , 5
zbiorów f4; 6; g oraz 2 zbiory {4,7,8}, {4,7,9}. To daje ÷¾
acznie 176 + 6 + 5 + 2 =
189:Zbiór {4,7,10} jest na 190 miejscu.
Wyk÷
ad 9. Ci ¾
agi. Iloczyn kartezja´
nski
f1; 2; 3; :::; mg
f1; 2; 3; :::ng
lub
fa; b; c; :::; mg
fa; b; c; :::ng
Zadanie 9.1. Wypisa´c wszystkie elementy zbioru f1; 2; 3g f1; 2; 3g w porz ¾
adku
leksykogra…cznym, antyleksykogra…cznym, odwrotnym leksykogra…cznym, odwrot-
nym antyleksykogra…cznym i leksykogra…cznym z gradacj ¾
a (=przek ¾
atniowym).
Odp.: W porz ¾
adku leksykogra…cznym: (1,1), (1,2), (1,3), (2,1), (2,2), (2,3),
(3,1), (3,2), (3,3).
Porz ¾
adek odwrotny do danego to wypisanie elementów
od ko´nca, zatem: (3,3), (3,2), (3,1), (2,3), (2,2), (2,1), (1,3), (1,2), (1,1).
Porz ¾
adek antyleksykogra…czny to taki, w którym najpierw patrzymy na drug ¾
a
wspó÷
rz ¾
edn ¾
a, a potem na pierwsz ¾
a: zatem (1,1), (2,1), (3,1), (1,2), (2,2), (3,2),
(1,3), (2,3), (3,3). Odwrotny antyleksykogra…czny to napisanie powy·
zszego ci ¾
agu
od ko´nca. Leksykogra…czny z gradacj ¾
a to (1,1), (1,2), (2,1), (1,3), (2,2), (3,1),
(2,3), (3,2), (3,3).
42

Zadanie 9.2. Niech A b ¾
edzie zbiorem liczb naturalnych od 1 do 17, za´s B
zbiorem liczb naturalnych od 1 do 37. Na którym miejscu w ka·
zdym z tych
porz ¾
adków znajduje si ¾
e (10,20)? Który element znajduje si ¾
e na miejscu 100?
Rozwi ¾
azanie. Ten iloczyn kartezja´nski mo·
zemy wyobrazi´c sobie jako pros-
tok ¾
atn ¾
a tablic ¾
e o podstawie 17 kropek, wysoko´sci 37.
Musimy sprawnie je
policzy´c. W porz ¾
adku leksykogra…cznym liczymy w kolumnach z do÷
u do góry a
kolumny z lewa na prawo. Para (10, 20) jest w dziesi ¾
atej kolumnie na 20 miejscu;
jest to zatem miejsce numer 9 37 + 20 = 353. ·
Zeby wyznaczy´c, który element
jest na miejscu setnym, obliczamy: w pierwszych dwóch kolumnach jest 2 37 =
74 miejsc, zatem szukana para jest w trzeciej kolumnie na miejscu 100
74 = 26.
Jest to wi ¾
ec para (3,26). Z tego przyk÷
adu wida´c, ·
ze aby wyznaczy´c, jaka para
jest na miejscu s w iloczynie kartezja´nskim f1; 2; :::mg f1; 2; :::ng (w porz ¾
adku
leksykogra…cznym) nale·
zy podzieli´c s przez m tak, by reszta by÷
a niewi ¾
eksza ni·
z
n:
W porz ¾
adku odwrotnym leksykogra…cznym para (10,20) jest na 353 miejscu
"od ko´nca", to jest na miejscu 17 37
353 = 276. W porz ¾
adku antyleksyko-
gra…cznym liczymy w warstwach poziomych z lewa na prawo a warstwy z do÷
u
do góry. Element (10, 20) jest w dwudziestej warstwie (wierszu) na dziesi ¾
atym
miejscu. Ogó÷
em jest to zatem miejsce numer 19 17 + 10 = 333: W porz ¾
adku
odwrotnym antyleksykogra…cznym jest to 333 od ko´nca, czyli 17 37
333 =
296:Przyjrzyjmy si ¾
e porz ¾
adkowi z gradacj ¾
a. W nim najpierw "id ¾
a" rz ¾
edy uko´sne
z÷
o·
zone z 1, 2, 3, ..., 16 elementów (÷¾
acznie
16 17
2
= 136 = elementów). Nast ¾
epuje
21 rz ¾
edów po 17 elementów, a potem znowu 16 rz ¾
edów, w których jest kolejno
16, 15, 13, ...,3, 2, 1 elementów. Para (10,20) znajduje si ¾
e w uko´snym rz ¾
edzie
numer 29, jest zatem na miejscu 1 + 2 + ::: + 16 + 12 17 + 10 = 350.
Zadanie 9.3. W danych z poprzedniego zadania wyznacz poprzednik i nast ¾
ep-
nik pary (10, 20) wzgl ¾
edem ka·
zdego z porz ¾
adków wspomnianych na wst ¾
epie.
W porz ¾
adku leksykogra…cznym mamy: (10; 19)
(10; 20)
(10; 21): W
odwrotnym leksykogra…cznym na odwrót. W antyleksykogra…cznym: (9; 20)
(10:20)
(11; 20).
Zadanie 9.4. W danych z zadania 2 wyznacz element setny od ko´nca (w
ka·
zdym z porz ¾
adków).
Zadanie 9.5. W danych z zadania 2 wyznacz par ¾
e, która stoi 17 miejsc za
(7,7).
Zadanie 9.6. Je·
zeli m i n s ¾
a liczbami naturalnymi, to w iloczynie f1; 2; :::2m+
1g f1; 2; :::2n+1g jest nieparzysta liczba elementów. W ka·
zdym z tych porz ¾
ad-
ków, podanych wy·
zej, wyznaczy´c element ´srodkowy.
Rowi ¾
azanie. Element ´srodkowy zajmie miejsce
(2m+1)(2n+1)+1
2
= m + n +
2mn+1: W porz ¾
adku leksykogra…cznym, odwrotnym leksykogra…cznym, antyleksyko-
gra…cznym i odwrotnym antylekykogra…cznym jest to zawsze element (m+1; n+
1).
Zadanie 9.7. Przez N oznaczamy zbiór liczb ca÷kowitych dodatnich. Zbiór
N N porz ¾
adkujemy wed÷
ug porz ¾
adku leksykogra…cznego z gradacj ¾
a. Wyznaczy´c
element na miejscu 2007.
43

Rozwi ¾
azanie. Porz ¾
adek leksykogra…czny z gradacj ¾
a polega na tym, ·
ze na-
jpierw wypisujemy pary o sumie wspó÷
rz ¾
ednych 2, potem 3, potem 4 itd. A
zatem w kolejnych pi ¾
etrach gradacji mamy 1,2,3,4,..., n elementów. Korzys-
tamy ze wzoru 1 + 2 + 3 + ::: + n =
n(n+1)
2
:Szukamy najwi ¾
ekszego n takiego,
·
ze
n(n+1)
2
jest mniejsze od 2007. Rozwi ¾
azujemy nierówno´s´c n
2
+ n
4014 < 0 .
Mamy
= 1 + 4 4014 = 16 057 , zatem dodatnim pierwiastkiem rzeczywistym
równania n
2
+ n
4014 = 0 jest
1+
p
16057
2
= 62: 858: Poszukiwane n jest zatem
równe 62. Istotnie 1+ 2+ ...+62 =
62 63
2
= 1953: Element stoj ¾
acy na miejscu
2007 ma sum ¾
e wspó÷
rz ¾
ednych 64 i stoi na 2007
1953 = 54 miejscu w rz ¾
edzie
uko´snym. Jest to zatem (54,10).
Zadanie 9.8. Jaki element jest na miejscu 145? Odp.: (9,9).
Zadanie 9.9. Na którym miejscu znajduje si ¾
e (7,13) ? Odpowied´z: na 178.
Zadanie 9.10.
Na którym miejscu w tym samym porz ¾
adku znajduje si ¾
e
(11,111)?
Rozwi ¾
azanie. Suma wspó÷
rz ¾
ednych wynosi 122. Element ten znajduje si ¾
e
zatem na 11 miejscu w uko´snym rz ¾
edzie, w którym suma wspó÷
rz ¾
ednych jest
122. Przed nim stoi:
jeden element o sumie wspó÷
rz ¾
ednych 2 , to jest (1,1),
dwa elementy o sumie wspó÷
rz ¾
ednych 3, to jest (1,2) i (2,1),
.....,
wreszcie 110 elementów o sumie wspó÷
rz ¾
ednych 111. Razem
110 111
2
= 6105
elementów. Nasza para (11,111) znajduje si ¾
e 11 miejsc dalej, zatem na miejscu
6116.
Zadanie 9.11. Niech A = f1; 2; 3; 4; 5; 6g: W iloczynie kartezja´nskim A
A
wprowadzamy relacj ¾
e R wzorem (a; b) R (c; d)
, max fa; bg = maxfc; dg.
a) Wyznaczy´c klas ¾
e abstrakcji (=klas ¾
e równowa·
zno´sci) pary (3,4).
b) Ile elementów ma zbiór ilorazowy A
A /R ?
c) Ile elementów ma najliczniejsza klasa równowa·
zno´sci?
Rozwi ¾
azanie. Jak mo·
zna opisa´c t ¾
e relacj ¾
e, przyswoi´c j ¾
a sobie? Dwie pary uz-
najemy za równowa·
zne, je·
zeli wi ¾
eksze elementy tych par s ¾
a takie same. Przyjmi-
jmy, ·
ze liczby to numery butów m ¾
e·
za i ·
zony - no, numeracja damska jest inna,
wi ¾
ec mo·
ze si ¾
e zdarzy´c, ·
ze m ¾
a·
z ma jedynk¾
e a ·
zona szóstk¾
e, a w ogóle to prze-
cie·
z tylko dla wyobra·
zenia sobie. Jest zatem sze´s´c klas równowa·
zno´sci , zbiór
ilorazowy ma siedem elementów - odpowiadaj ¾
acych numerom butów.
Jakie ma÷·
ze´nstwa s ¾
a równowa·
zne Kowalskim, gdzie ·
zona ma trójk¾
e, a m ¾
a·
z
czwórk¾
e? S ¾
a to: Jankowscy (·
zona jedynk¾
e, m ¾
a·
z czwórk¾
e), Nowakowie (·
zona 2,
m ¾
a·
z 4), Stefa´nscy (·
z 3, m 4), Wi´sniewscy (4,4), Zieli´nscy (·
zona czwórk¾
e, m ¾
a·
z
trójk¾
e), Pietrzakowie (4,2) i Z ¾
abkowscy (·
zona czwórk¾
e, m ¾
a·
z jedyneczk¾
e). A wi ¾
ec
w klasie równowa·
zno´sci (3,4) jest ÷¾
acznie 7 par: (1,4), (2,4), (3,4), (4,4), (4,3),
(4,2), (4,1). Najliczniejsza klasa to oczywi´scie (1,6), (2,6), (3,6), (4,6), (5,6),
(6,6), (6,5), (6,4), (6,3), (6,2), (6,1).
44

Wyk÷
ad 10
. Relacje równowa·
zno´sci
Najwa·
zniejsze relacje to relacje równowa·
zno´sci i wszelkiego typu relacje
porz ¾
adkuj ¾
ace.
De…nicja.
Mówimy, ·
ze pewna relacja (któr ¾
a oznaczymy symbolem t )
okre´slona w pewnym niepustym zbiorze X
jest relacj ¾
a równowa·
zno´sci, gdy
jest
a) zwrotna: 8
x
2X
x t x ,
b) symetryczna: x t y ) y t x ,
c) przechodnia: x t y ^ y t z ) x t z.
Podstawow ¾
a w÷
asno´s´c relacji równowa·
zno´sci ujmuje
Twierdzenie o podziale (=zasada abstrakcji). Ka·
zda relacja rownowa´zno´sci,
okre´slona w niepustym zbiorze X wyznacza podzia÷tego zbioru na roz÷¾
aczne
podzbiory, zwane klasami równowa·
zno´sci (albo: klasami abstrakcji) w ten sposób,
·
ze do jednej klasy zaliczamy wszystkie te elementy, które s ¾
a wzajemnie ze sob ¾
a
w relacji. Odwrotnie, podzia÷zbioru na roz÷¾
aczne podzbiory wyznacza pewn ¾
a
relacj ¾
e równowa·
zno´sci.
Przyk÷
ad. Ustalmy liczb ¾
e ca÷
kowit ¾
a p: Relacja zachodz ¾
aca mi ¾
edzy liczbami
ca÷
kowitymi, okre´slona wzorem
m t n wtedy, gdy m
n jest liczb ¾
a podzieln ¾
a przez p
jest relacj ¾
a równowa·
zno´sci. Klasy równowa·
zno´sci to zbiory
fk pg; fk p + 1g; fk p + 2g; :::; fk p + p
1g, ,gdzie k 2 Z.
Innymi s÷
owy, s ¾
a to zbiory z÷
o·
zone z liczb, które z dzielenia przez p daj ¾
a
reszty 0, 1,...,p-1.
Zadanie 10.1. Niech R b ¾
edzie tak ¾
a relacj ¾
a w zbiorze P (N) = 2
N
wszyst-
kich podzbiorów zbioru liczb ca÷
kowitych N , ·
ze dla
A ; B
N jest A R
B
() A = B lub 5 =
2 A [ B . Opisa´c klasy równowa·
zno´sci: zbioru pustego,
zbioru {1,2,3} , zbioru {1,2,3,4,5} , zbioru, którego jedynym elementem jest
liczba 5 oraz zbioru 2N z÷o·
zonego ze wszystkich liczb parzystych.
Rozwi ¾
azanie. Przypomn ¾
e, ·
ze P (N) = 2
N
to rodzina podzbiorów zbioru liczb
naturalnych. Oznaczenie P (X) = 2
X
dla okre´slenia rodziny podzbiorów danego
zbioru pochodzi st ¾
ad, ·
ze gdy X jest zbiorem sko´nczonym o n elementach, to ma
on 2
n
elementów. Przypominam te·
z, ·
ze klasa równowa·
zno´sci danego elementu
to zbiór wszystkich elementów z nim równowa·
znych (tak, jak w.powy·
zszym
przyk÷
adzie).
W zadaniu tym klasa równowa·
zno´sci zbioru pustego ? sk÷ada si ¾
e tych zbiorów
B; dla których 5 =
2 ? [ B. Ale ? [ B = B. Zatem klas ¾
a równowa·
zno´sci zbioru
pustego jest rodzina tych zbiorów, które nie zawieraj ¾
a liczby 5. W szczegól-
no´sci {1,2,3} oraz zbiór z÷
o·
zony z liczb parzystych nale·
z ¾
a do tej rodziny. Zbiór
{1,2,3,4,5} jest w relacji tylko sam ze sob ¾
a, gdy·
z suma f1; 2; 3; 4; 5g [B zawsze
zawiera liczb ¾
e 5. Podobnie jest dla zbioru jednoelementowego {5}. Reasumuj ¾
ac,
mo·
zna powiedzie´c, ·
ze rodzina tych podzbiorow rozpada si ¾
e na klasy jednoele-
mentowe (to s ¾
a wszystkie zbiory zawieraj ¾
ace 5) oraz jedn ¾
a "du·
z ¾
a" klas ¾
e do
45

której nale·
z ¾
a wszystkie zbiory nie zawieraj ¾
ace 5. Obrazowo, mo·
zna powiedzie´c,
·
ze interesuje nas tylko to, czy zbiór zawiera 5, czy nie.
Zadanie 10.2. Niech R b ¾
edzie tak ¾
a relacj ¾
a w zbiorze P (N) = 2
N
wszystkich
podzbiorów zbioru liczb ca÷
kowitych nieujemnych N , ·
ze dla
A ; B
N
jest A R B
() A = B lub A [ B nie zawiera ·
zadnej liczby pierwszej.
Opisa´c klasy równowa·
zno´sci: zbioru pustego, zbioru {1,2,3} , zbioru {1,2,3,4,5}
, zbioru, którego jedynym elementem jest liczba 5 oraz zbioru 2N z÷o·
zonego ze
wszystkich liczb parzystych.
Rozwi ¾
azanie jest analogiczne do 10.1. Odpowied´z: Klasa zbioru pustego to
wszystkie zbiory nie zawieraj ¾
ace ·
zadnej liczby pierwszej. Poniewa·
z pozosta÷
e
podane zbiory zawieraj ¾
a liczb ¾
e pierwsz ¾
a, klasy równowa·
zno´sci tych zbiorów
sk÷
adaj ¾
a si ¾
e z nich samych.
Zadanie 10.3. W zbiorze kó÷na p÷
aszczy´znie okre´slamy relacj ¾
e
w , przyj-
muj ¾
ac, ·
ze K
1
w K
2
wtedy i tylko wtedy, gdy K
1
i
K
2
maj ¾
a ten sam
´srodek. Sprawdzi´c, ·
ze jest to relacja równowa·
zno´sci. Wykaza´c, ·
ze zbiór klas
równowa·
zno´sci mo·
ze by´c uto·
zsamiony z p÷
aszczyzn ¾
a.
Rozwi ¾
azanie. Ka·
zde ko÷
o ma ten sam ´srodek, co ono samo. Je·
zeli jedno ko÷
o
ma ten sam ´srodek, co drugie, to drugie ma ten sam ´srodek, co pierwsze. Je·
zeli
jedno ko÷
o ma ten sam ´srodek, co drugie, a drugie ten sam ´srodek, co trzecie, to
pierwsze ma ten sam ´srodek, co trzecie. Jest to zatem relacja równowa·
zno´sci.
Klasa równowa·
zno´sci (klasa abstrakcji) sk÷
ada si ¾
e z kó÷o wspólnym ´srodku.
Ka·
zdej takiej klasie mo·
zna wi ¾
ec przypisa´c punkt na p÷
aszczy´znie - wspólny
´srodek kó÷z tej klasy. Daje to wzajemnie jednoznaczn ¾
a odpowiednio´s´c mi ¾
edzy
zbiorem punktów p÷
aszczyzny a klasami równowa·
zno´sci podanej relacji.
Zadanie 10.4. W zbiorze kó÷na p÷
aszczy´znie okre´slamy relacj ¾
e
, przyj-
muj ¾
ac, ·
ze K
1
K
2
wtedy i tylko wtedy, gdy K
1
i
K
2
maj ¾
a ten sam
promie´n. Wykaza´c, ·
ze jest to relacja równowa·
zno´sci. Wykaza´c, ·
ze zbiór klas
równowa·
zno´sci mo·
ze by´c uto·
zsamiony ze zbiorem liczb rzeczywistych dodatnich.
Rozwi ¾
azanie. Wystarczy w rozwi ¾
azaniu zadania 2 zamieni´c s÷
owo "´srodek"
na "promie´n". A zatem: ka·
zde ko÷
o ma ten sam promie´n, co ono samo. Je·
zeli
jedno ko÷
o ma ten sam promie´n, co drugie, to drugie ma ten sam promie´n, co
pierwsze. Je·
zeli jedno ko÷
o ma ten sam promie´n, co drugie, a drugie ten sam
promie´n, co trzecie, to pierwsze ma ten sam promie´n, co trzecie. Jest to zatem
relacja równowa·
zno´sci. Klasa równowa·
zno´sci (klasa abstrakcji) sk÷
ada si ¾
e z kó÷
o takim samym promieniu. Promie´n jest liczb ¾
a dodatni ¾
a. Ka·
zdej takiej klasie
mo·
zna wi ¾
ec przypisa´c liczb ¾
e dodatni ¾
a: wspólny promie´n kó÷z tej klasy. Daje to
wzajemnie jednoznaczn ¾
a odpowiednio´s´c mi ¾
edzy liczbami dodatnimi a klasami
równowa·
zno´sci podanej relacji.
Zadanie 10.5 . W zbiorze wszystkich kwadratów po÷
o·
zonych na p÷
aszczy´znie
wprowadzamy relacj ¾
e
l w ten sposób, ·ze K
1
l K
2
wtedy i tylko wtedy, gdy
kwadraty te maj ¾
a równe ´srodki i równe pola.
Rozwi ¾
azanie. Sprawdzenie, ·
ze podana relacja jest zwrotna, symetryczna i
przechodnia, wykonujemy podobnie jak w zadaniach 10.3 i 10.4.
46

Zadanie 10.10. W zbiorze liczb rzeczywistych R okre´slamy relacj ¾
e
wzorem
a
b () 9 m 2 Z : m
a < m + 1 ; m
b < m + 1 .
Wykaza´c, ·
ze jest to relacja równowa·
zno´sci. Wykaza´c, ·
ze zbior ilorazowy
R=
mo·
ze by´c uto·
zsamiony ze zbiorem liczb rzeczywistych R . Opisa´c klas ¾
e
równowa·
zno´sci liczby
:
Rozwi ¾
azanie. Aby przekona´c sie, ·
ze jest to relacja równowa·
zno´sci, mo·
zna
zauwa·
zy´c, ·
ze podan ¾
a zale·
zno´s´c mo·
zna opisa´c tak: dwie liczby s ¾
a w relacji, je·
zeli
nale·
z ¾
a do tego samego przedzia÷
u [m; m + 1) gdzie m jest liczba ca÷
kowit ¾
a. Z
tej samej uwagi wynika równie·
z, ·
ze klas ¾
a równowa·
zno´sci liczby
jest przedzia÷
[3; 4).
Zadanie 10.7. Rozpatrujemy relacje o polu Z. Które z poni·
zszych relacji s ¾
a
relacjami równowa·
zno´sci? Opisa´c klasy równowa·
zno´sci tych relacji.
a) m R n
() 7 j m
n ,
b) m S n
() m = n lub 7 j m + n ,
c) m T n
() m = n lub m
2
+ n
2
= 1 ,
d) m U n
() (m
n)
2
= 1 ,
e) m V n
() (m
n)
2
< 1 ,
f) m W n , gdy albo obie liczby m; n s ¾
a równe zero, albo m n > 0 ,
g) m X n
() 2
mn
> 1 (w tym przyk÷
adzie polem relacji jest zbiór
ca÷
kowitych ró·
znych od zera.)
g) m Y n
() m = n lub (m
2008 i n
2008),
h) m Z n ()
m
2
+ n > 0.
Rozwi ¾
azania, uwagi.
R
jest relacj ¾
a równowa·
zno´sci, poniewa·
z jest zwrotna ( bo 0 jest podzielne
przez 7), symetryczna (liczba jest podzielna przez 7 wtedy i tylko wtedy, gdy
liczba do niej przeciwna jest podzielna przez 7) i przechodnia (bo je·
zeli m
n
dzieli si ¾
e przez 7 oraz n k dzieli sie przez 7, to m k = (m n)+(n k) dzieli si ¾
e
przez 7). Klasy równowa·
zno´sci tej relacji to zbiory liczb daj ¾
ace z dzielenia przez
7 t ¾
e sam ¾
a reszt ¾
e. Jest zatem siedem klas równowa·
zno´sci, ka·
zda reprezentowana
przez pewn ¾
a liczb ¾
e 0, 1, 2, 3, 4, 5, 6 i ka·
zda zawiera niesko´nczenie wiele liczb.
Mo·
zna to uj ¾
a´c inaczej: Relacja R zachodzi mi ¾
edzy dwiema liczbami wtedy
i tylko wtedy, gdy daj ¾
a one z dzielenia przez 7 t ¾
e sam ¾
a reszt ¾
e. Z tego natych-
miast wynika, ·
ze jest to relacja równowa·
zno´sci, a zbiór liczb ca÷
kowitych jest
podzielony na klasy równowa·
zno´sci [0], [1], [2], [3], [4], [5], [6].
S
nie jest to relacj ¾
a równowa·
zno´sci. Jest wprawdzie zwrotna i symetryczna,
ale nie jest przechodnia, bo na przyk÷
ad 1 S 6 oraz 6 S 15 , ale nieprawda, ·
ze
1 S 15 .Do klasy [j] zaliczamy te liczby, które z dzielenia przez 7 daj ¾
a reszt ¾
e j
. . Relacja T nie jest zwrotna ani przechodnia, na przyk÷
ad 0 T 1 oraz 1 T 0 ,
ale nieprawda, ·
ze 0 T 0. Relacja U nie jest zwrotna, relacja V nie jest prze-
chodnia. Relacj ¾
e W mo·
zna opisa´c tak: zachodzi ona mi ¾
edzy dwiema liczbami
wtedy i tylko wtedy, gdy maj ¾
a one ten sam znak , przy czym rozumiemy, ·
ze
znakiem liczby dodatniej jest plus, ujemnej minus, a znakiem liczby zero jest
zero. Jest to wi ¾
ec relacja równowa·
zno´sci i dzieli zbiór wszystkich liczb na trzy
klasy: liczby ujemne, liczba zero i liczby dodatnie. Warunek w de…nicji relacji X
47

jest równowa·
zny temu, by mn > 0. A zatem relacj ¾
e t ¾
e mo·
zna opisa´c podobnie,
jak relacj ¾
e W: zachodzi ona mi ¾
edzy dwiema liczbami ró·
znymi od zera wtedy
i tylko wtedy, gdy maj ¾
a one ten sam znak. W tym przypadku s ¾
a zatem tylko
dwie klasy równowa·
zno´sci: zbiór liczb ujemnych oraz zbiór liczb dodatnich.
Aby przekona´c si ¾
e, ·
ze Y jest relacj ¾
a równowa·
zno´sci, opiszmy j ¾
a nieco inaczej:
ró·
zne liczby s ¾
a w relacji Y , gdy obydwie s ¾
a wi ¾
eksze lub równe 2008. Klasami
równowa·
zno´sci s ¾
a tu: zbiory jednoelementowe z÷
o·
zone z liczb mniejszych od
2008, oraz "du·
zy" zbiór z÷
o·
zony ze wszystkich liczb
2008: Relacja Z nie jest
oczywi´scie symetryczna.
Zadanie 10.8. W zbiorze wielomianów drugiego stopnia postaci x
2
+ px + q
, spe÷
niaj ¾
acych warunek p
2
4q > 0 okre´slamy relacj ¾
e, uznaj ¾
ac za równowa·
zne te
wielomiany, które maj ¾
a t ¾
e sam ¾
a sum ¾
e pierwiastków. Opisa´c klas ¾
e równowa·
zno´sci
wielomianów x
2
1 , x
2
5x + 6. Wykaza´c, ·
ze zbiór klas równowa·
zno´sci mo·
zna
uto·
zsami´c ze zbiorem wszystkich liczb rzeczywistych R.
Szkic rozwi ¾
azania. Ze wzorów Viete’a wynika, ·
ze wielomiany równowa·
zne
wzgl ¾
edem tej relacji maj ¾
a ten sam wspó÷
czynnik p przy x:Przyporz ¾
adkowanie
wielomianowi tego wspó÷
czynnika wyznacza uto·
zsamienie zbioru wielomianów z
e zbiorem wszystkich liczb rzeczywistych R :
Zadanie 10.9. Wykaza´c, ·
ze klasy równowa·
zno´sci relacji okre´slonej dla liczb
ca÷
kowitych ró·
znych od zera wzorem
m
n () m n > 0 i m
2
= n
2
s ¾
a jednoelementowe.
Zadanie 10.10. Opisa´c klasy równowa·
zno´sci relacji okre´slonej dla liczb ze-
spolonych wzorem
z
1
z
2
() z
2
1
= z
2
2
:
Zadanie 10.11. Dana jest liczba naturalna n > 1:Opisa´c klasy równowa·
zno´sci
relacji okre´slonej dla liczb zespolonych wzorem
z
1
z
2
() z
n
1
= z
n
2
:
Zadanie 10.12. Opisa´c klasy równowa·
zno´sci relacji
` okre´slonej dla liczb
rzeczywistych przez
x
` y () sin x = sin y i cos x = cos y:
Zadanie 10.13. Niech f : X ! N b ¾
edzie funkcj ¾
a przekszta÷
caj ¾
ac ¾
a zbiór
X w zbiór liczb naturalnych N . Okre´slamy relacj ¾
e w zbiorze X wzorem
x
1
+ x
2
wtedy i tylko wtedy, gdy f (x
1
) = f (x
2
). Wykaza´c, ·
ze jest to relacja
równowa·
zno´sci.
a) Opisa´c klasy równowa·
zno´sci relacji okre´slonej tak dla liczb rzeczywistych
za pomoc ¾
a funkcji f (x) = x
2
+ x :
b) Opisa´c klasy równowa·
zno´sci relacji okre´slonej tak dla liczb rzeczywistych
za pomoc ¾
a funkcji f (x) = x
2
3x:
c) Opisa´c klasy równowa·
zno´sci relacji okre´slonej tak dla liczb ca÷
kowitych za
pomoc ¾
a funkcji f (m) = m + j m j :
d) Opisa´c klasy równowa·
zno´sci relacji okre´slonej tak dla liczb ca÷
kowitych
za pomoc ¾
a funkcji f (n) = n
2
( 1)
n
:
Rozwi ¾
azanie.
Jest do´s´c oczywiste, ·
ze z podanych warunków wynika, ·
ze
relacja jest zwrotna, symetryczna i przechodnia. Istotnie, f (a) = f (a), a to
48

znaczy, ·
ze relacja jest zwrotna. Podobnie: je·
zeli f (a) = f (b) , to bez w ¾
atpi-
enia f (b) = f (a); relacja jest wi ¾
ec symetryczna. Wreszcie, je·
zeli f (a) = f (b) i
f (b) = f (c), to oczywi´scie f (a) = f (c).
a) W tym przyk÷
adzie klasa równowa·
zno´sci danej liczby rzeczywistej y zaw-
iera te liczby x , dla których x
2
+x
(y
2
+y) = 0:Rozwa·
zamy to jako równanie ze
wzgl ¾
edu na x . Wyró·
znikiem tego równania jest
= 1 + 4(y
2
+ y) = (2y + 1)
2
;
zatem pierwiastkami s ¾
a
x
1
=
1 (2y+1)
2
= 1
y ; x
2
=
1+(2y+1)
2
= y: S ¾
a to liczby symetrycznie
po÷
o·
zone wzgl ¾
edem
1
2
:
c) Zauwa·
zmy, ·
ze dla liczb nieujemnych x mamy x + j x j = 2x. Dla liczb
ujemnych mamy x + j x j = x
x = 0 = 0 + j 0 j . Oczywi´scie z tego, ·
ze
2m = 2n wynika, ·
ze m = n: Zatem dla liczb dodatnich relacja jest to·
zsamo´sci ¾
a
a poza tym jest jedna "du·
za" klasa równowa·
zno´sci, z÷
o·
zona z liczb ujemnych i
zera.
d) Rozwa·
zmy liczb ¾
e ca÷
kowit ¾
a n. Zauwa·
zmy, ·
ze f (n) = f ( n) . Zatem
klasa równowazno´sci ka·
zdej liczby zawiera liczb ¾
e do niej przeciwn ¾
a. Wystarczy
zatem ograniczy´c si ¾
e do liczb nieujemnych. Mamy f (0) = 0
2
( 1)
0
=
1 oraz
f (1) = 1
2
( 1)
1
= 2 ; f (2) = 2
2
( 1)
2
= 3 ; f (4) = 4
2
( 1)
2
= 15.
Dla dodatnich warto´sci argumentu funkcja ta jest funkcj ¾
a rosn ¾
ac ¾
a. Zatem klasy
równowa·
zno´sci s ¾
a dwuelementowe (liczba i liczba do niej przeciwna) z jednym
wyj ¾
atkiem: klasa liczby 0.
Zadanie 10.14. Wykaza´c, ·
ze relacja s , okre´slona dla macierzy kwadratowych
nieosobliwych ustalonego rozmiaru wzorem
M s N , istnieje taka macierz nieosobliwa A, ·
ze M = A
1
N A;
jest relacj ¾
a równowa·
zno´sci. Wyznaczy´c macierz, której klasa równowa·
zno´sci
jest jednoelementowa.
Rozstrzygn ¾
a´c, czy macierze
1
0
0
2
i
1
0
0
3
s ¾
a równowa·
zne. Rozstrzygn ¾
a´c,
czy macierze
1
2
3
4
i
4
2
3
1
s ¾
a równowa·
zne.
Rozwi ¾
azanie. Je·
zeli pami ¾
etamy, ·
ze relacja ta zachodzi mi ¾
edzy macierzami
wtedy i tylko wtedy, gdy s ¾
a one macierzami tego samego przekszta÷
cenia lin-
iowego, tylko byc mo·
ze w ró·
znych bazach, to zadanie jest oczywiste. Macierze
1
0
0
2
i
1
0
0
3
nie s ¾
a równowa·
zne, na przyk ¾
a÷
d dlatego, ·
ze maj ¾
a ró·
zne
warto´sci w÷
asne. Mo·
zemy rozwi ¾
aza´c zadanie inaczej, bez odwo÷
ywania si ¾
e do
znajomo´sci algebry liniowej. Relacja s jest oczywi´scie zwrotna (wystarczy wzi ¾
a´c
za A macierz jednostkow ¾
a). Dalej, je·
zeli M = A
1
N A , to N = AM A
1
:Relacja
jest wi ¾
ec symetryczna. Wreszcie, je·
zeli M = A
1
N A oraz N = B
1
KB, to
M = A
1
B
1
KBA = (BA)
1
K
(BA):
Relacja jest wi ¾
ec przechodnia:
Aby przekona´c si ¾
e, ·
ze macierze
1
0
0
2
i
1
0
0
3
nie s ¾
a równowa·
zne,
mo·
zemy zauwa·
zy´c, ·
ze maj ¾
a ró·
zne wyznaczniki, albo obliczy´c to wprost. Niech
A =
a
b
c
d
. Wtedy
a
b
c
d
1
0
0
2
=
a
2b
c
2d
oraz
1
0
0
3
49

a
b
c
d
=
a
b
3c
3d
. Z równo´sci macierzy wynika, ·
ze b = c = d = 0. Taka
macierz A jest osobliwa.
Aby rozstrzygn ¾
a´c, czy macierze
1
2
3
4
i
4
2
3
1
s ¾
a równowa·
zne, mo·
zemy
poszuka´c, jak wy·
zej, macierzy A =
a
b
c
d
: Mamy wtedy
a
b
c
d
1
2
3
4
=
a + 3b
2a + 4b
c + 3d
2c + 4d
oraz
1
3
2
4
a
b
c
d
=
a + 3c
b + 3d
2a + 4c
2b + 4d
.
Z uk÷
adu równa´n
a + 3b = a + 3c ;
2a + 4b
=
b + 3d ; c + 3d =
2a+4c ; 2c+4d = 2b+4d wyznaczamy wiele mo·
zliwo´sci otrzymania nieosobliwej
macierzy A: Na przyk÷
ad mo·
zna wzi ¾
a´c A =
3
1
1
1
:
3
1
1
1
1
2
3
4
=
0
2
2
2
1
3
2
4
3
1
1
1
=
0
2
2
2
Macierze
1
2
3
4
i
4
2
3
1
s ¾
a zatem równowa·
zne.
Zadanie 10.15. Wykaza´c, ·
ze relacja, zachodz ¾
aca mi ¾
edzy macierzami kwadra-
towymi nieosobliwymi, gdy istnieje taka macierz nieosobliwa A, ·
ze M = A
T
N A;
jest relacj ¾
a równowa·
zno´sci. Rozstrzygn ¾
a´c, czy macierze
1
0
0
1
i
1
0
0
1
s ¾
a równowa·
zne.
Szkic rozwi ¾
azania. Je·
zeli wiemy, ·
ze relacja podana opisuje macierze, które sa
macierzami formy kwadratowej w róznych bazach, to zadanie jest banalne. Je·
zeli
tego wiemy, mo·
zemy ÷
atwo rozwi ¾
aza´c zadanie, na´sladuj ¾
ac rozwi ¾
azanie zadania
poprzedniego. Relacja jest oczywi´scie zwrotna (wystarczy wzi ¾
a´c za A macierz
jednostkow ¾
a). Dalej, je·
zeli M = A
T
N A , to N = AM A
T
:Relacja jest wi ¾
ec sym-
etryczna. Wreszcie, je·
zeli M = A
T
N A oraz N = B
T
KB, to M = A
T
B
T
KBA
= (BA)
T
K
(BA):
Relacja jest wi ¾
ec przechodnia: Aby przekona´c si ¾
e, ·
ze
macierze
1
0
0
1
i
1
0
0
1
nie s ¾
a równowa·
zne, poszukajmy macierzy A:
Niech b ¾
edzie ona równa A =
a
b
c
d
.
Wtedy
a
b
c
d
1
0
0
1
a
c
b
d
=
a
2
+ b
2
ac + bd
ac + bd
c
2
+ d
2
.
To nie
mo·
ze by´c równe
1
0
0
1
, bo w prawym dolnym naro·
zniku s ¾
a liczby róznych
znaków.
Zadanie 10.16. Dana jest macierz A =
1
1
0
0
. W zbiorze macierzy
kwadratowych 2 2 rozpatrujemy relacj ¾
e: M
N , AM = AN: Rozstrzygn ¾
a´c,
50

czy jest to relacja równowa·
zno´sci. Opisa´c klas ¾
e równowa·
zno´sci macierzy
1
2
2
1
:Czy
wszystkie klasy równowa·
zno´sci sa równoliczne?
Zadanie 10.17.
W zbiorze macierzy kwadratowych n
n wprowadzamy
relacj ¾
e
v okre´slon ¾
a wzorem
A
v B wtedy i tylko wtedy, gdy AB = BA: Rozstrzygn ¾
a´c, czy jest to relacja
zwrotna, symetryczna i czy jest przechodnia.
Rozwi ¾
azanie. Jest to relacja zwrotna, bo A A = A A. Jest symetryczna, bo
je·
zeli AB = BA, to BA = AB. Nie jest to relacja przechodnia. Ka·
zda macierz
kwadratowa jest bowiem przemienna z nacierz ¾
a jednostkow ¾
a, A:I = I:A. A za-
tem gdyby okre´slona tu relacja by÷
a przechodnia, to ka·
zde dwie macierze by÷
yby
przemienne, to znaczy dla ka·
zdych dwóch macierzy ich iloczyn nie zale·
za÷
by od
kolejno´sci. Wiemy jednak, ·
ze tak nie jest.
Zadanie 10.18. Poda´c przyk÷
ad zbioru niesko´nczonego X i takiej relacji
równowa·
zno´sci o polu X , która ma dok÷
adnie 2008 klas równowa·
zno´sci.
Szkic rozwi ¾
azania. Wystarczy poda´c rozbicie zbioru X na 2008 roz÷¾
acznych
podzbiorów.
Zadanie 10.19. Sprawdzi´c, czy relacja R zachodz ¾
aca mi ¾
edzy liczbami ze-
spolonymi, a okre´slona wzorem:
z
1
R
z
2
wtedy i tylko wtedy, gdy j z
1
j + j z
2
j
3
jest zwrotna, czy jest symetryczna i czy jest przechodnia.
Odpowied´z: Nie jest zwrotna, jest symetryczna, nie jest przechodnia.
Zadanie 10.20. Sprawdzi´c, czy relacja T zachodz ¾
aca mi ¾
edzy liczbami ze-
spolonymi, a okre´slona wzorem:
z
1
T
z
2
wtedy i tylko wtedy, gdy z
1
z
2
2 R
jest zwrotna, czy jest symetryczna i czy jest przechodnia.
Rozwi ¾
azanie. Relacja jest zwrotna, bo zawsze gdy od pewnej liczby ode-
jmiemy liczb ¾
e równ ¾
a, to otrzymamy zero. Relacja jest symetryczna, bo je·
zeli
z
1
z
2
jest liczb ¾
a rzeczywist ¾
a, to z
2
z
1
te·
z. Jest to te·
z relacja przechodnia. Is-
totnie, je·
zeli z
1
z
2
2 R oraz z
2
z
3
2 R, to z
1
z
3
= (z
1
z
2
)+(z
2
z
3
) 2 R:
Klasy równowa·
zno´sci [z]
s ¾
a jednoelementowe, gdy z 2 R i dwuelementowe
(z÷
o·
zone z danej liczby i liczby do niej sprz ¾
e·
zonej), gdy z =
2 R.
Zadanie 10.21. Sprawdzi´c, czy relacja U zachodz ¾
aca mi ¾
edzy liczbami ze-
spolonymi, a okre´slona wzorem:
z
1
U
z
2
wtedy i tylko wtedy, gdy z
1
z
2
2 R
jest zwrotna, czy jest symetryczna i czy jest przechodnia.
Rozwi ¾
azanie. Relacja nie jest zwrotna, bo kwadrat liczby zespolonej nie musi
by´c liczb ¾
a rzeczywist ¾
a. Jest oczywi´scie symetryczna. Nie jest relacj ¾
a przechod-
ni ¾
a. Na przyk÷
ad (1 + i) (1 + i)
3
=
4 jest liczb ¾
a rzeczywist ¾
a, podobnie jak
(1 + i)
3
(1 + i). Natomiast (1 + i) (1 + i) = 2i =
2 R.
Zadanie 10.22. Okre´sli´c pole relacji tak, ·
zeby mia÷
a ona sens i rozstrzygn ¾
a´c,
czy jest ona relacj ¾
a równowa·
zno´sci: prostopad÷
o´s´c, równoleg÷
o´s´c, równoliczno´s´c,
podobie´nstwo, przystawanie, posiadanie wspólnego czynnika > 1.
Zadanie 10.23. W zbiorze ci ¾
agów spe÷
niaj ¾
acych warunek Cauchy’ego wprowadzamy
relacj ¾
e wzorem:
51

ci ¾
ag (a
n
) jest w relacji z ci ¾
agiem (b
n
), je·
zeli ci ¾
ag a
1
; b
1
; a
2
; b
2
; a
3
; b
3
; :::
te·
z
jest ci ¾
agiem Cauchy’ego. Wykaza´c, ·
ze jest to relacja równowa·
zno´sci i ·
ze zbiór
ilorazowy mo·
zna uto·
zsami´c ze zbiorem liczb rzeczywistych R .
Zadanie 10.24. W zbiorze ci ¾
agów o wyrazach rzeczywistych wprowadzamy
relacj ¾
e wzorem:
ci ¾
ag (a
n
) jest w relacji z ci ¾
agiem (b
n
), je·
zeli ci ¾
agi te ro·
zni ¾
a si ¾
e na conajwy·
zej
sko´nczonej liczbie miejsc. Wykaza´c, ·
ze jest to relacja równowa·
zno´sci.
Zadanie 10.25. W zbiorze funkcji ci ¾
ag÷
ych na odcinku [0; 1] wprowadzamy
relacj ¾
e uznaj ¾
ac za równowa·
zne te funkcje, których warto´sci w punkcie x =
1
2
s ¾
a
równe. Wykaza´c, ·
ze jest to istotnie relacja równowa·
zno´sci i ·
ze zbiór ilorazowy
mo·
zna uto·
zsami´c ze zbiorem liczb rzeczywistych R .
Zadanie 10.26.
Poda´c przyk÷
ad takiej relacji równowa·
zno´sci, nieb ¾
ed ¾
acej
relacj ¾
a przystawania modulo 2, która rozbija zbiór liczb ca÷
kowitych na klasy
dwuelementowe.Opisa´c t ¾
e relacj ¾
e s÷
ownie i wzorem.
Zadanie 10.27. Niech A = f1; 2; 3; 4; 5; 7g: W iloczynie kartezja´nskim A
A
wprowadzamy relacj ¾
e R wzorem (a; b) R (c; d)
, min fa; bg = minfc; dg.
a) Wyznaczy´c klas ¾
e abstrakcji (=klas ¾
e równowa·
zno´sci) pary (4,6).
b) Ile elementów ma zbiór ilorazowy A
A /R ?
c) Ile elementów ma najliczniejsza klasa równowa·
zno´sci?
Rozwi ¾
azanie.
Co znaczy okre´slona tu relacja? Jak mo·
zna j ¾
a opisa´c bez
wzoru? Bardzo prosto. W ka·
zdej parze liczbowej zwracamy uwag ¾
e tylko na
mniejsz ¾
a. A zatem pary równowa·
zne z (4,6) to wszystkie te, w których mniejsza
z liczb jest równa 4: (4,4), (4,5), (4,6), (4,7), (5,4), (6,4), (7,4).
Zbiór ilorazowy to zbiór wszystkich klas równowa·
zno´sci. Jest zatem siedem
klas: Najliczniejsza z nich to ta, gdzie mniejsza z liczb jest 1: (1,1), (1,2), (1,3),
(1,4), (1,5), (1,6), (1,7), (7,1), (6,1), ..., (2,1).
Maj ¾
a one kolejno 13, 11, 9, 7, 5, 3, 1 elementów. Najmniejsza jest klasa
jednoelementowa, z÷
ozona z pary (7,7). Sprawdzamy: 13+11+9+7+5+3+1 =
49 = 7
2
:
Zadanie 10.28. Niech A = f 4; 3; 2; 1; 0; 1; 2; 3; 4g: W iloczynie kartez-
ja´nskim A A wprowadzamy relacj ¾
e
wzorem (a; b)
(c; d) , j max fa; bg j =
j maxfc; dg j.
a) Wyznaczy´c klas ¾
e abstrakcji (=klas ¾
e równowa·
zno´sci) pary (3,4).
b) Ile elementów ma zbiór ilorazowy A
A /
?
c) Wskaza´c najmniej liczn ¾
a klas ¾
e równowa·
zno´sci.
Rozwi ¾
azanie.
Klasa równowa·
zno´sci pary (3,4) sk÷
ada si ¾
e z tych par, gdzie
najwiekszym elementem jest 4 albo -4, a zatem z nast ¾
epuj ¾
acych par: (-4,-4),
(*,4) oraz (4,*), gdzie * oznacza kolejne liczby -4, ..., 4. Zbiór ilorazowy ma
5 elementów, bo tylko 0, 1,2,3,4 mog ¾
a by´c najwi ¾
ekszymi warto´sciami funkcji
"modu÷maksimum". Jest jedna jednoelementowa klasa: z÷
o·
zona z pary (0,0).
52

Wyk÷
ad 11. Relacje porz ¾
adkujace
.
Trzecim najwa·
zniejszym typem relacji –po relacjach równowa·
zno´sci i funkc-
jach –
s ¾
a rozmaite relacje porz ¾
adkuj ¾
ace. Ogólnie rzecz bior ¾
ac, w relacji porz ¾
adku-
j ¾
acej musimy umie´c
elementy porównywa´c: który jest mniejszy (wcze´sniejszy), a który wi ¾
ekszy
(pó´zniejszy). Ale nawet ta prosta relacja
ma inne w÷
asno´sci, gdy rozpatry-
wana jest na zbiorze liczb naturalnych, liczb ca÷
kowitych lub liczb rzeczywistych.
Na przyk÷
ad w zbiorze liczb naturalnych ka·
zdy niepusty podzbiór ma element
najmniejszy, co nie jest prawd ¾
a dla relacji mniejszo´sci w zbiorze Z liczb ca÷kow-
itych, ani w zbiorze R wszystkich liczb rzeczywistych. Z kolei liczby rzeczywiste
uporz ¾
adkowane s ¾
a w sposób g ¾
esty: mi ¾
edzy dwie liczby rzeczywiste zawsze mo·
zna
wstawi´c trzeci ¾
a. Przyk÷
ady te pokazuj ¾
a, ·
ze relacja porz ¾
adkuj ¾
aca mo·
ze by´c "lep-
sza" lub "gorsza", a w ka·
zdym razie mie´c wiele specy…cznych w÷
asno´sci.
Dla informatyka relacje porz ¾
adkuj ¾
ace maj ¾
a z oczywistych wzgl ¾
edów du·
ze
znaczenie. Na przyk÷
ad, dobre uporz ¾
adkowanie zbioru (w sensie de…nicji po-
danej ni·
zej) umo·
zliwia konstruowanie programów rekurencyjnych i indukcyjnych.
Przypominam, ·
ze relacja w zbiorze X to pewien podzbiór R iloczynu kartez-
ja´nskiego X
X i ·
ze zamiast pisa´c (x; y) 2 R, piszemy xRy i mówimy, ·
ze
x jest w relacji z elementem y. Zbiór X
nazywamy polem relacji. Omówimy systematycznie ró·
zne typy relacji porz ¾
ad-
kuj ¾
acych. Poniewa·
z porz ¾
adek przypomina nierówno´s´c, b ¾
edziemy u·
zywa´c sym-
bolu a
b na zaznaczenie, ·
ze elementy a oraz b s ¾
a zwi ¾
azane ogóln ¾
a relacj ¾
a
porz ¾
adkuj ¾
ac ¾
a. Jest to zapis bardziej przejrzysty ni·
z aRb:
Pierwszym warunkiem, który nak÷
adamy na relacje porz ¾
adkuj ¾
ace, jest zwrot-
no´s´c: ka·
zdy element jest sam ze sob ¾
a w relacji:
8 a 2 X zachodzi a
a:
Na przyk÷
ad relacja
spe÷
nia ten warunek w ka·
zdym zbiorze liczbowym.
Drugim wspólnym warunkiem dla wszystkich relacji porz ¾
adkuj ¾
acych jest jej
przechodnio´s´c. Znaczy to, ·
ze dla wszystkich a; b; c nale·
z ¾
acych do pola tej relacji
ma by´c spe÷
niony warunek:
je·
zeli a
b i tak·
ze b
c, to a
c
Ten warunek jest równie·
z spe÷
niony przez zwyk÷¾
a relacj ¾
e
w ka·
zdym zbiorze
liczbowym.
De…nicja
. Mówimy, ·
ze pewna relacja
polu X jest w tym zbiorze X relacj ¾
a
cz ¾
e´sciowego porz ¾
adku wtedy i tylko wtedy, gdy jest zwrotna, przechodnia oraz
dla ka·
zdych a2 X, b2 X jest prawd ¾
a, ·
ze
a
b oraz b
a , to a = b
to znaczy, ·
ze je·
zeli z ka·
zdych dwóch elementów pierwszy jest mniejszy (wcze´sniejszy)
od drugiego, a drugi mniejszy (wcze´sniejszy) od pierwszego (w sensie rozpatry-
wanej relacji) , to jest to mo·
zliwe tylko wtedy, gdy elementy te s ¾
a identyczne.
Je·
zeli relacja spe÷
nia powy·
zszy trzeci warunek, to mówimy, ·
ze jest
na wpó÷przeciwsymetryczna. Nie jest to specjalnie szcz ¾
e´sliwy termin, ale
utar÷si ¾
e i jest u·
zywany. Oznacz ¾
e go skrótem NWP. Nazywa si ¾
e go te·
z s÷
ab ¾
a
antysymetri ¾
a.
53

Spójrzmy na relacje z przyk÷
adu 10.6 (poni·
zej). Widzimy, ·
ze liczby wi ¾
eksze
od 2 s ¾
a w tej relacji uporz ¾
adkowane "normalnie", wed÷
ug "starsze´nstwa". Zero
jest mniejsze ni·
z dwa,
liczba 1 te·
z jest mniejsza ni·
z dwa, ale 0 i 1 s ¾
a nieporównywalne:
nie jest prawd ¾
a, ·
ze 0
1, ale te·
z nie jest prawd ¾
a, ·
ze 1
0.
Mimo to warunek NWP jest spe÷
niony.
Cwiczenie. Chcemy okre´sli´c w zbiorze wszystkich liczb ca÷
kowitych relacj ¾
e
porz ¾
adkuj ¾
ac ¾
a tak, by otrzyma´c porz ¾
adek cz ¾
e´sciowy i by
liczba 0 by÷
a mniejsza od wszystkich innych (poprzedza÷
a wszystkie inne),
a poza tym porz ¾
adek by÷
by "normalny" : dla liczb ró·
znych od zera m
n
gdy m
n:
Teori ¾
e b ¾
edziemy ilustrowa´c na kilku przyk÷
adach, do których b ¾
edziemy si ¾
e
najcz ¾
esciej odwo÷
ywa´c.
Przyk÷
ad 10.1 . Relacja mniejszo´sci
w zbiorze liczb naturalnych; na t ¾
e
relacj ¾
e mówimy zwyczajowo relacja mniejszo´sci, ale powinno si ¾
e nazywa´c si ¾
e j ¾
a
relacja niewi ¾
ekszo´sci, bo nierówno´s´c jest nieostra.
Przyk÷
ad 11.2. Relacja mniejszo´sci
w zbiorze liczb ca÷
kowitych.
Przyk÷
ad 11.3. Relacja mniejszo´sci
w zbiorze liczb wymiernych.
Przyk÷
ad 11.4. Relacja zawierania (inkluzji) zbiorów: A
B, b ¾
ed ¾
acych
podzbiorami pewnego ustalonego zbioru X. Polem tej relacji jest zbiór pot ¾
egowy
2
X
= P (X)
–zbiór wszystkich podzbiorów zbioru X.
Przyk÷
ad 11.5. Relacja
zachodz ¾
aca mi ¾
edzy wielomianami zmiennej x o
wspó÷
czynnikach rzeczywistych:
je·
zeli stopie´n f jest mniejszy ni·
z stopie´n g, to f
g;
–je·
zeli stopnie f i g s ¾
a ró·
zne, to f
g gdy st f < st g ,
- je·
zeli stopnie f i g s ¾
a ró·
zne i równe n, to f
g , gdy wspó÷
czynnik
przy x
n
w wielomianie f jest mniejszy od wspó÷
czynnika przy x
n
w
wielomianie g
–je·
zeli stopnie s ¾
a równe i równe s ¾
a wspó÷
czynniki przy
najwy·
zszej pot ¾
edze x, to porównujemy wspó÷
czynniki przy kolejnej
pot ¾
edze x
n 1
je´sli i te s ¾
a równe, to patrzymy na wspó÷
czynnik
przy x
n 2
i tak dalej.
Przyk÷
ad 11.6. W zbiorze liczb naturalnych z zerem w÷¾
acznie N= { 0; 1; 2; 3; 4; 5,
....}
rozpatrujemy relacj ¾
e okre´slon ¾
a wzorem x
y gdy x < y + 2 .
Przyk÷
ad 11.7. Uk÷
ad katalogów na twardym dysku komputera wyznacza
pewien porz ¾
adek. Nie ma w nim cykli. Zbiór uporz ¾
adkowany o tych w÷
asno´sci-
ach (tzn. niemaj ¾
acy cykli) nazywamy drzewem.
Przyk÷
ad 11.8. Inna relacj ¾
a porzadkuj ¾
ac ¾
a liczb naturalnych mo·
ze by´c
m
n wtedy i tylko wtedy, gdy m
2 lub m
n:
Przyk÷
ad 11. 9. W zbiorze liczb ca÷
kowitych okre´slamy relacj ¾
e
m
n wtedy i tylko wtedy, gdy m
n i jednocze´snie mn > 0
Przyk÷
ad 11.10. W zbiorze liczb ca÷
kowitych dodatnich rozpatrujemy
relacj ¾
e podzielno´sci:
m
n wtedy i tylko wtedy, gdy mjn (to znaczy, gdy m jest dzielnikiem n):
54
Zadanie 11.1. W przyk÷
adach 11.1 - 11.10 wyznaczy´c elementy minimalne i
maksymalne, najmniejsze i najwi ¾
eksze.
Zadanie 11.2. W przyk÷
adzie 11.5 uporz ¾
adkowa´c w kolejno´sci (od najm-
niejszego
do najwi ¾
ekszego) wielomiany x; 2x
2
+5x+6; 2x
2
+x+7; 2x
2
+5x+6; x
3
+1
Zadanie 11.3 W których z przyk÷
adów 11.1-11.10 mo·
ze si ¾
e zdarzy´c, ·
ze
dla pewnych elementów a; b nie zachodzi ani a
b;ani b
a ?
Porz ¾
adek leksykogra…czny w iloczynie kartezja´
nskim zbiorów
uporz ¾
adkowanych
Wszyscy znamy zasad ¾
e wed÷
ug której tworzone s ¾
a wszelkiego rodzaju listy
alfabetyczne. W szkole podstawowej poznajemy uporz ¾
adkowanie liter alfabetu.
Obecnie jest ono takie:
A ¾
ABC´CDE ¾
EFGHIJKL×MN´
NOÓPQRS´STUVWXYZ´Z ·
Z
ale za czasów szkolnych autora tego skryptu kolejno´s´c ·
Z i ´Z by÷
a przestaw-
iona i nie mówi÷
o si ¾
e o Q, V ani X. Tak czy owak, je´sli ustalimy kolejno´s´c liter
alfabetu, to nazwy porzadkujemy wed÷
ug oczywistej zasady: decyduje pierwsza
litera, potem druga, trzecia i tak dalej. Zauwa·
zmy, ·
ze z dwóch nazwisk ta-
kich Kot i Kota´nski postawimy to pierwsze wcze´sniej, tak jakby na ko´ncu sta÷
o
niesko´nczenie wiele liter wcze´sniejszych ni·
z a. Te zasady porz ¾
adkowania s ¾
a nam
dobrze znane. Matematycy nazywaj ¾
a to porz ¾
adkiem leksykogra…cznym.
De…nicja
. Niech b ¾
ed ¾
a dane dwa zbiory: zbiór X z relacj ¾
a porz ¾
adkuj ¾
ac ¾
a,
któr ¾
a oznaczymy symbolem
J i zbiór Y z relacj ¾
a porz ¾
adkuj ¾
ac ¾
a, któr ¾
a oz-
naczymy
symbolem v. Porz ¾
adkiem leksykogra…cznym w iloczynie kartezja´nskim X
Y nazywamy relacj ¾
e
okre´slon ¾
a tak
(x
1
; y
1
)
(x
2
; y
2
) gdy albo x
1
J x
2
oraz x
1
6= x
2
;albo x
1
= x
2
oraz y
1
v y
2
:
Zadanie 11.4. Przekona´c si ¾
e, ·
ze powy·
zsza de…nicja oddaje intuicj ¾
e
poj ¾
ecia porz ¾
adku leksykogra…cznego (s÷
ownikowego): decyduje porz ¾
adek na
pierwszej wspó÷
rz ¾
ednej, a w nast ¾
epnej kolejno´sci na drugiej wspó÷
rz ¾
ednej.
Zadanie 11.5. Napisa´c elementy iloczynu kartezja´nskiego
{ 1,2,3,4,5}
{ 1,2,3 } w porz ¾
adku leksykogra…cznym.
Zadanie 11.6. W zbiorze jednomianów x
m
y
n
dwóch zmiennych x i y
wprowadzamy porz ¾
adek leksykogra…czny. Opisa´c go dok÷
adniej.
Wypisa´c kilkana´scie pocz ¾
atkowych elementów ci ¾
agu
tych jednomianów uporz ¾
adkowanego leksykogra…cznie.
Zadanie 11.7. W zbiorze liczb zespolonych wprowadzamy porz ¾
adek uznaj ¾
ac
z
1
z
2
, gdy zarówno modu÷z
1
, jak i argument (g÷
ówny) z
1
jest niewi ¾
ekszy
ni·
z modu÷i argument z
2
: Naszkicowa´c diagram Hassego dla tego porz ¾
adku w
zbiorze zespolonych ca÷
kowitych, to jest postaci m + ni, gdzie m; n sa liczbami
ca÷
kowitymi.
Szkic rozwi ¾
azania. Podane okre´slenie nie wyja´snia, czy 0 jest mniejsza od
innych liczb. Liczba 0 nie ma bowiem argumentu. Przyjmijmy, ·
ze jest ona
mniejsza od wszystkich innych. Nast ¾
epuj ¾
a cztery liczby o module 1, w kolejno´sci
1, i;
i;
1: Nast ¾
epne s ¾
a liczby module
p
2; s ¾
a to 1 + i;
1 + i;
1
i; 1
i
55

. Mamy
:::
2i
"
1 + i
i
1 + i
.
"
-
"
::: !
2
!
1
0
!
1
! 2
! :::
#
&
#
#
1
i
i
! 1
i
#
2i
:::
Zadanie 11.8. W zbiorze macierzy 2 na 2 o wyrazach b ¾
ed ¾
acych liczbami
ca÷
kowitymi 0 i 1 wprowadzamy porz ¾
adek nast ¾
epuj ¾
acy: M
N , gdy det
M
det N:Gdy za´s wyznaczniki sa równe, macierz M uznajemy za mniejsz ¾
a
(wcze´sniejsz ¾
a) ni·
z N , gdy jest od niej wcze´sniejsza w porz ¾
adku leksykogra…cznym.
Wypisa´c wszystkie te macierze w porz ¾
adku tak okre´slonym.
Rozwi ¾
azanie. Jest 2
4
= 16 takich macierzy. Z liczb 0, 1 ustawionych w
macierz kwadratow ¾
a 2 na 2 mo·
zna uzyska´c tylko wyznaczniki -1, 0 +1. Zatem
najpierw wypiszemy macierze o wyznaczniku -1.
0
1
1
0
,
0
1
1
1
;
1
1
1
0
, potem te o wyznaczniku 0 :
0
0
0
0
,
0
0
0
1
;
0
0
1
0
,
0
0
1
1
;
0
1
0
0
,
0
1
0
1
;
1
0
0
0
,
1
0
1
0
;
1
1
0
0
;
1
1
1
1
, wreszcie o wyznaczniku 1
1
0
0
1
;
1
0
1
1
,
1
1
0
1
:
Zadanie 11.9. W zbiorze macierzy 3 na 3 o wyrazach b ¾
ed ¾
acych liczbami
ca÷
kowitymi 0 i 1 wprowadzamy porz ¾
adek nast ¾
epuj ¾
acy: M
N , gdy det
M
det N:Gdy za´s wyznaczniki s ¾
a równe, macierz M uznajemy za mniejsz ¾
a
(wcze´sniejsz ¾
a) ni·
z N , gdy jest od niej wcze´sniejsza w porz ¾
adku leksykogra…cznym.
Napisa´c trzy pierwsze i trzy ostatnie macierze. Na którym miejscu jest macierz
jednostkowa?
Zadanie 11.10. W zbiorze macierzy 3 na 3 o wyrazach b ¾
ed ¾
acych liczbami
ca÷
kowitymi 0 i 1 wprowadzamy porz ¾
adek nast ¾
epuj ¾
acy: M
N , gdy jdet
M j
j det Nj:Gdy za´s wyznaczniki s ¾
a równe, to macierz M uznajemy za
mniejsz ¾
a (wcze´sniejsz ¾
a) ni·
z N , gdy jest od niej wcze´sniejsza w porz ¾
adku leksyko-
gra…cznym. Napisa´c pierwszych sto macierzy wzgl ¾
edem tego porz ¾
adku.
Zadanie 11.11. W zbiorze macierzy 2 na 2 o wyrazach b ¾
ed ¾
acych liczbami
ca÷
kowitymi 0 i 1 wprowadzamy porz ¾
adek nast ¾
epuj ¾
acy: M
N , gdy jdet
56

M j
j det Nj:Gdy za´s modu÷y wyznaczników s ¾
a równe, to macierz M uzna-
jemy za mniejsz ¾
a (wcze´sniejsz ¾
a) ni·
z N , gdy jest od niej wcze´sniejsza w porz ¾
adku
leksykogra…cznym z gradacj ¾
a na ci ¾
agach czteroelementowych. Napisa´c wszys-
tkie te macierze w opisanym porz ¾
adku.
Zadanie 11.12. W zbiorze macierzy 2 na 2 o wyrazach b ¾
ed ¾
acych liczbami
ca÷
kowitymi 0 i 1 wprowadzamy porz ¾
adek nast ¾
epuj ¾
acy: M
N , gdy albo
macierze s ¾
a równe, albo det M < det N:Opisa´c ten porz ¾
adek.
Zadanie 11.13. W zbiorze macierzy 2 na 2 o wyrazach b ¾
ed ¾
acych liczbami
ca÷
kowitymi 0 i 1 wprowadzamy porz ¾
adek nast ¾
epuj ¾
acy: M
N , gdy
je·
zeli wyznacznik macierzy M jest równy zero, a wyznacznik macierzy N
nie, to M
N ,
je·
zeli wyznaczniki macierzy M i N s ¾
a równe i niezerowe, to M
N ,
gdy M jest wcze´sniejsza w porz ¾
adku leksykogra…cznym z gradacj ¾
a na ciagach
czteroelementowych,
je·
zeli wyznaczniki macierzy M i N s ¾
a ró·
zne i niezerowe, to M
N gdy
wyznacznik M jest wi ¾
ekszy ni·
z wyznacznik N:
Zadanie 11.14. W zbiorze iloczynie kartezja´nskim (1; 2; 3; 4; 5; ::mg (1; 2; 3; ::::; ng
wprowadzamy porz ¾
adek
C wzorem (a; b) C (c; d) gdy a c i b
_
d:Wyznaczy´c
elementy minimalne i maksymalne. Poda´c przyk÷
ady ÷
a´ncuchów. Niech teraz
m = n = 5. Wyznaczyc kresy, je·
zeli istniej ¾
a, par (1; 2) i (2; 1) oraz (2,3) i
(4,2).
Rozwi ¾
azanie wynika z nast ¾
epuj ¾
acej interpretacji tego porz ¾
adku: para (a; b) poprzedza (c; d);
je·
zeli na obu wspó÷
rz ¾
ednych jest spe÷
niona zwyk÷
a nierówno´s´c
.
A za-
tem (1; 2)
C (2; 3) C (2; 4) C (5; 5):Ale pary (1; 2) i (2; 1) s ¾
a nieporówny-
walne. Geometrycznie, punkt A poprzedza B, je·
zeli le·
zy od niego "ni·
zej lub
nie wy·
zej" i "na lewo lub chocia·
z nie na prawo". Na diagramie poni·
zej mamy
A
C B ; A C D ; B C C ; C C D, ale mi¾edzy punktami B; D nie jest prawd ¾
a,
·
ze B
C D, ani D C B:
Zadanie 11.15. W zbiorze macierzy 2 na 2 o wyrazach b ¾
ed ¾
acych 0 lub 1
wprowadzamy porz ¾
adek w nast ¾
epuj ¾
acy sposób. Ka·
zdej macierzy przyporz ¾
ad-
kujemy dwie liczby: jej wyznacznik W (M ) i jej ´slad S(M ). ´Sladem macierzy
nazywamy sum ¾
e elementów na przek ¾
atnej. Porz ¾
adek okre´slamy tak:
M
N gdy albo M = N albo para (W (M ); S(M )) poprzedza (W (N ); S(N ))
w porz ¾
adku leksykogra…cznym. Narysowa´c diagram Hassego tego porz ¾
adku.
Wskaza´c elementy minimalne i maksymalne, najwi ¾
ekszy i najmniejszy (je´sli
s ¾
a). Czy istnieje kres górny zbioru z÷
o·
zonego z macierzy zerowej i macierzy
jednostkowej?
Rozwi ¾
azanie. Wypiszmy wszystkie macierze 2 na 2 o wyrazach 0,1 wraz z
ich wyznacznikami i ´sladami (´slad oznaczamy przez tr, od angielskiego trace ):
A =
0
0
0
0
, det A = 0, tr A = 0;
B =
1
0
0
0
, det B = 0, tr
B = 1;
57

C =
0
1
0
0
, det C = 0, tr C = 0;
D =
0
0
1
0
, det D = 0, tr
D = 0;
E =
0
0
0
1
, det E = 0, tr E = 1;
F =
1
1
0
0
, det F = 0, tr
F = 1;
G =
1
0
1
0
, det G = 0, tr G = 1;
I =
1
0
0
1
, det I = 1, tr I = 2;
J =
0
1
1
0
, det J =
1, tr J = 0;
K =
0
1
0
1
, det K = 0, tr
K = 1;
L =
0
0
1
1
, det L = 0, tr L = 1;
M =
1
1
1
0
, det M =
1, tr
M = 1;
N =
1
1
0
1
, det N = 1, tr N = 2;
P =
1
0
1
1
, det P = 1, tr
P = 2;
R =
0
1
1
1
, det R =
1, tr R = 1;
S =
1
1
1
1
, det S = 0, tr
S = 2:
Inaczej mówi ¾
ac, poszczególne macierze odpowiadaj ¾
a nast ¾
epuj ¾
acym parom
(det; tr) :
( 1; 0) ! J ; (0; 0) ! A; C ; D ; ( 1; 1) ! M; R ; (0; 1) ! B; E; F; G; K ; L; ;
(0; 2) ! S ;
(1; 2) ! I; N; P ;
W porz ¾
adku leksykogra…cznym s ¾
a one uporz ¾
adkowane liniowo w ten sposób:
J; (M; R); (A; C; D); (B; E; F; G; K ; L) ; S; (I; N; P ). Mi ¾
edzy macierzami
z tej samej grupy (wzi ¾
etej w nawias) nie zachodzi relacja. Zatem elementem
minimalnym jest J i jest to te·
z element najmniejszy. Elementami maksymal-
nymi s ¾
a I; N; P . Poniewa·
z zarówno macierz zerowa A , jak i macierze C; D s ¾
a
macierzami mniejszymi od macierzy jednostkowej I, zatem inf (A; I) nie istnieje.
Podobnie nie istnieje sup (A; I):
Zadanie 11.16. Przy oznaczeniach z poprzedniego zadania wprowadzamy
ma macierzach porz ¾
adek nast ¾
epujacy M
N , gdy para (det M ; trM ) jest
mniejsza od (det M; tr N ) w sensie porz ¾
adku opisanego w zadaniu 11.14.
Narysowa´c diagram Hassego tego porz ¾
adku. Wskaza´c elementy minimalne i
maksymalne, najwi ¾
ekszy i najmniejszy (je´sli s ¾
a). Czy istnieje kres górny zbioru
z÷
o·
zonego z macierzy zerowej i macierzy jednostkowej?
Rozwi ¾
azanie. Wszystko ÷
atwo wynika z diagramu Hassego:
Zadanie 11.17. Niech dla macierzy M symbol k(M ) oznacza sum ¾
e elemen-
tów pierwszej kolumny macierzy. W oznaczeniach zadania 11.15 wprowadzamy
porz ¾
adek
n, uznaj ¾
ac, ·
ze M
n N gdy albo M = N albo (det M; k(M))
58

poprzedza (det M; k(M )) w porz ¾
adku opisanym w zadaniu 11.14. Powtórzy´c
zadanie 11.15 dla tego porz ¾
adku
n.
Rozwi ¾
azanie. W oznaczeniach z rozwi ¾
azania zadania 11.15 mamy
A =
0
0
0
0
, det A = 0, k (A) = 0;
B =
1
0
0
0
, det B = 0,
k (B) = 1;
C =
0
1
0
0
, det C = 0,
k(C) = 0;
D =
0
0
1
0
, det D = 0,
k(D) = 1;
E =
0
0
0
1
, det E = 0, k(E) = 0;
F =
1
1
0
0
, det F = 0,
k(F ) = 1;
G =
1
0
1
0
, det G = 0, k(G) = 2;
I =
1
0
0
1
, det I = 1, k(I) = 1;
J =
0
1
1
0
, det J =
1, k(J ) = 1;
K =
0
1
0
1
, det K = 0,
k(K) = 0;
L =
0
0
1
1
, det L = 0, k(L) = 1;
M =
1
1
1
0
, det M =
1,
k(M ) = 2;
N =
1
1
0
1
, det N = 1, k(N ) = 1;
P =
1
0
1
1
, det P = 1,
k(P ) = 2;
R =
0
1
1
1
, det R =
1, k(R) = 1;
S =
1
1
1
1
, det S = 0,
k(S) = 2:
St ¾
ad otrzymujemy diagram Hassego:
Zadanie 11.18. W zbiorze liczb naturalnych {1,2,3,.....1024} wprowadzamy
porz ¾
adek w nast ¾
epuj ¾
acy sposób. Przedstawiamy liczb ¾
e n w postaci n = 2
k
+ l,
gdzie l < 2
k
. Liczb ¾
e m uznajemy za wcze´sniejsz ¾
a ni·
z n; gdy m = 2
p
+ q, q < 2
p
i para (k; l) jest wcze´sniejsza od (p; q) w porz ¾
adku opisanym w zadaniu 11.14,
to znaczy, gdy k
p i l
q. Wyznaczy´c elementy minimalne i maksymalne, na-
jwi ¾
ekszy i najmniejszy (je·
zeli istniej ¾
a). Poda´c przyk÷
ad najd÷
u·
zszego ÷
a´ncucha.
Wyznaczy´c (je·
zeli istniej ¾
a) kresy par (1,2), (10,13), (100, 128), (256,512).
Rozwi ¾
azanie. Wynika z diagramu Hassego tego porz ¾
adku. Porz ¾
adku tego
59

u·
zywamy przy dowodzie
"
128
! 129
! 130
! 131
! 132
! 133
! 134
! 135
! 136
! ::: 257
"
64
!
65
!
66
!
67
!
68
!
69
!
70
!
71
!
72
! ::: 127
"
32
!
33
!
34
!
35
!
36
!
37
!
38
!
39
!
40
! :::
63
"
16
!
17
!
18
!
19
!
20
!
21
!
22
!
23
!
24
! :::
31
"
8
!
9
!
10
!
11
!
12
!
13
!
14
!
15
"
4
!
5
!
6
!
7
"
2
!
3
"
1
nierówno´sci mi ¾
edzy ´sredni ¾
a arytmetyczn ¾
a a ´sredni ¾
a geometryczn ¾
a.
Zadanie 11.19. W zbiorze liczb naturalnych {1,2,3,.....120} wprowadzamy
porz ¾
adek w nast ¾
epuj ¾
acy sposób. Przedstawiamy liczb ¾
e n w postaci n = k! + l,
gdzie k!
n < (k + 1)!. Liczb ¾
e m uznajemy za wcze´sniejsz ¾
a ni·
z n; gdy m =
p! + q; gdzie p!
m < (p + 1)!
i para (k; l) jest wcze´sniejsza od (p; q) w
porz ¾
adku opisanym w zadaniu 11.14, to znaczy, gdy k
p i l
q. Wyznaczy´c
elementy minimalne i maksymalne, najwi ¾
ekszy i najmniejszy (je·
zeli istniej ¾
a).
Poda´c przyk÷
ad najd÷
u·
zszego ÷
a´ncucha. Wyznaczy´c (je·
zeli istniej ¾
a) kresy par
(1,2), (5, 7),(10,13) (100, 120).
Rozwi ¾
azanie (szkic). Mamy kolejno 1 = 1! + 0; 2 = 2! + 0, 3 = 2! + 1; 4 =
2! + 2; 5 = 2! + 3; 6 = 3! + 0 ;
7 = 3! + 1; 8 = 3! + 2, 9 = 3! + 3; ::::Porz ¾
adek wygl ¾
ada tak, jak w diagramie
poni·
zej. Liczba 120 nie jest najwi ¾
eksza, bo np. nie zachodzi ani 119
120 ,
ani 120
119. Jest elementem maksymalnym.Inne elementy maksymalne to
5, 23 i 119. Liczba 1 jest najmniejsza. Najd÷
u·
zszy ÷
a´ncuch to 1 ! 2 ! 6 ! 24
! 25 ! 26 ! ::: ! 119: Mamy : inff1; 2g = 1; supf1; 2g = 2; inff5; 7g =
2; supf5; 7g nie istnieje ; inff10; 13g = 10; supf10; 13g = 13; ,
inff100; 120g = 24; supf100; 120g nie istnieje.
60

120
"
24
! 25 ! 26 ! 27 ! 28 ! 29 ! 30 ! 31 ! 32 ! ::: ! 119
"
6
!
7
!
8
!
9
! 10 ! 11 ! 12 ! 13 ! 14 ! ::: !
23
"
2
!
3
!
4
!
5
"
1
61

Wyk÷
ad 12. Elementy maksymalne i minimalne. Kresy. Porz ¾
adek
liniowy, porz ¾
adek dobry.
Okre´slenie porz ¾
adku liniowego jest bardzo proste. Zbiór X cz ¾
e´sciowo uporz ¾
ad-
kowany przez relacj ¾
e
nazywamy liniowo uporz ¾
adkowanym, je·
zeli dla ka·
zdych
dwóch elementów a 2 X, b 2 X, jest spe÷niony jeden z dwóch warunków:
a
b ; b
a: Innymi s÷
owy: ka·
zde dwa elementy tego zbioru dadz ¾
a si ¾
e porów-
na´c.
Zadanie 12.1. Które ze zbiorów z przyk÷
adu 11.1-11.12 s ¾
a liniowo uporz ¾
ad-
kowane
przez opisane tam relacje?
Zadanie 12.2. Czy pewien zbiór podzbiorów ustalonego zbioru mo·
ze by´c
liniowo uporz ¾
adkowany przez relacj ¾
e inkluzji?
Zadanie 12.4. Poda´c sposób liniowego uporz ¾
adkowania zbioru wszystkich
punktów kratowych p÷
aszczyzny, to jest punktów postaci (m; n), gdzie n oraz
m s ¾
a liczbami ca÷
kowitymi.
W zbiorze liczb naturalnych {1,2,3,4, 6,7....29,35} , z÷
o·
zonym z liczb niepodziel-
nych przez 5 i mniejszych od 30 oraz dodatkowo z liczby 35 okre´slamy relacj ¾
e
C wzorem x C y , x = y _ x + 3 y:
a) Wyznaczy´c elementy minimalne.
b) Wyznaczy´c elementy maksymalne.
c) Wyznaczy´c element najwi ¾
ekszy.
d) Wyznaczy´c element najmniejszy.
e) Wyznaczy´c kresy zbioru {4,6,7},
f) Poda´c przyk÷
ad najd÷
u·
zszego ci ¾
agu x
1
C x
2
C ::: C x
n
;w którym wszys-
tkie liczby sa ró·
zne.
Odpowied´z. Elementy minimalne to 1,2,3. Najmniejszych nie ma. Liczba
35 jest najwi ¾
eksza, zatem i maksymalna. Innych maksymalnych nie ma. Kre-
sem dolnym podanego zbioru jest 1. Kresu górnego nie ma. S ¾
a dwa ci ¾
agi
o w÷
asno´sci podanej w zadaniu: 1
C 4 C 7 C 10 C :::: C 28 C 35 oraz 2
C 5 C 8 C 11 C :::: C 29 C 35: Obydwa maj ¾
a po 11 liczb.
Zadanie 12.5. W zbiorze liczb naturalnych {1,2,3,4,5,6,8, ....27,33} , z÷
o·
zonym
z liczb niepodzielnych przez 7 i mniejszych od 28 oraz dodatkowo z liczby 33
okre´slamy relacj ¾
e R wzorem x R y , x = y _ x
y
5:
a) Wyznaczy´c elementy minimalne.
b) Wyznaczy´c elementy maksymalne.
c) Poda´c argument, rozstrzygaj ¾
acy, ·
ze porz ¾
adek nie jest liniowy.
d) Wskaza´c najd÷
u·
zszy ci ¾
ag rosn ¾
acy (wzgl ¾
edem tego porz ¾
adku).
e) Wyznaczy´c kresy zbioru {6,16,26}.
Porz ¾
adek g ¾
esty
Intuicja odpowiada nam, ·
ze liczby ca÷
kowite le·
z ¾
a rzadko na linii prostej (osi
liczbowej), a wymierne i rzeczywiste g ¾
esto. Ujmuje to nast ¾
epuj ¾
ace okre´slenie.
Porz ¾
adek nazywamy g ¾
estym, je·
zeli mi ¾
edzy dwa dowolne elementy zbioru
mo·
zemy stawi´c trzeci. Formalny zapis tego warunku wygl ¾
ada tak:
8a 2 X 8b 2 X , a 6= b 9 c 2 X; c 6= a, c 6= b ; a
c
b
A wi ¾
ec istotnie, w sposób g ¾
esty uporz ¾
adkowane s ¾
a liczby wymierne, a
tak·
ze liczby liczby rzeczywiste na prostej. Nieoczekiwanie okazuje si ¾
e, ·
ze
62

zbiór liczb naturalnych te·
z da si ¾
e uporz ¾
adkowa´c w sposób g ¾
esty.
Przyk÷
ad. Niech f : N ! Q b ¾
edzie funkcj ¾
a ustalaj ¾
ac ¾
a równoliczno´s´c
zbioru liczb naturalnych i zbioru liczb wymiernych. A zatem f jest funkcj ¾
a
wzajemnie jednoznaczn ¾
a. Okre´slmy porz ¾
adek w zbiorze N tak:
m
n je·
zeli dla odpowiadaj ¾
acych im liczb wymiernych mamy f (m) < f (n)
w zbiorze Q.
Jest to porz ¾
adek g ¾
esty, bowiem je·
zeli m; n s ¾
a dwiema ró·
znymi liczbami natu-
ralnymi, to mo·
zemy wskaza´c liczb ¾
e le·
z ¾
ac ¾
a mi ¾
edzy nimi (w sensie wprowadzonego
porz ¾
adku), na przyk÷
ad f
1
f (m)+f (n)
2
.
Porz ¾
adek dobry.
Mo·
zliwo´s´c dobrego uporz ¾
adkowania zbioru jest bardzo wa·
zna dla zastosowa´n.
Mówimy, ·
ze relacja
porz ¾
adkuje zbiór X w sposób dobry, je·
zeli w ka·
zdym nie-
pustym podzbiorze Y
X istnieje element najmniejszy. Najprostszym przyk÷
a-
dem zbioru dobrze uporz ¾
adkowanego jest zbiór liczb wszystkich liczb natural-
nych N:
12.10. Które z poni·
zszych relacji s ¾
a relacjami cz ¾
e´sciowego porz ¾
adku, do-
brego porz ¾
adku, porz ¾
adku liniowego? Które opisuj ¾
a porz ¾
adek g ¾
esty? Opisa´c el-
ementy maksymalne, minimalne, majwi ¾
eksze, najmniejsze. Wskaza´c przyk÷
ady
÷
a´ncuchów i drzew.
a) relacja
w zbiorze pot ¾
egowym 2
X
;
b) relacja
w zbiorze liczb naturalnych;
c) relacja
w zbiorze liczb rzeczywistych;
d) relacja okre´slona dla liczb zespolonych wzorem z
1
z
2
gdy j z
1
j
j z
2
j
,
e) relacja okre´slona dla macierzy wzorem M
1
M
2
, gdy det M
1
det M
2
,
f) relacja okre´slona dla macierzy o wyrazach ca÷
kowitych dodatnich, o dwóch
wierszach i dwóch kolumnach tak: A
B , gdy a
11
b
11
,
g) relacja okre´slona dla macierzy o wyrazach ca÷
kowitych dodatnich, o dwóch
wierszach i dwóch kolumnach tak: A
B , gdy a
12
b
12
; a
21
b
21
; a
22
b
22
:
h) prostopad÷
o´s´c prostych na p÷
aszczy´znie,
i) równoleg÷
o´s´c prostych na p÷
aszczy´znie,
j) relacja podzielno´sci w´sród liczb ca÷
kowitych dodatnich: m
n gdy m j n
,
k) relacja równoliczno´sci zbiorów,
l) relacja zachodz ¾
aca mi ¾
edzy liczbami ca÷
kowitymi ró·
znymi od zera, a okre´slona
tak: m
n gdy
m j n oraz m
n;
m) relacja mi ¾
edzy liczbami naturalnymi (z zerem w÷¾
acznie) okre´slona wzorem:
m
n gdy m + 10 < n;
n) relacja zachodz ¾
aca mi ¾
edzy liczbami rzeczywistymi a okre´slona tak: a
b
gdy a = 0 lub a = b,
o) relacja zachodz ¾
aca mi ¾
edzy liczbami rzeczywistymi a okre´slona tak: a
b
gdy a = 0 lub a
b.
63

Zadanie 12.11. W zbiorze Z wszystkich liczb calkowitych okre´slamy relacj ¾
e w
nastepuj ¾
acy sposób: k
l wtedy i tylko wtedy, gdy [(k l < 0 ^ k > l) _ (k l
0 ^ j k j > j l j]
. Wyka·
z, ·
zest to dobry porz ¾
adek z zbiorze Z.
64

Wyk÷
ad 13.
Przeliczalno´s´c i równoliczno´s´c
Zadanie 13.1. Które z podanych zbiorów s ¾
a przeliczalne? Uzasadni´c odpowied´z:
a) zbiór ujemnych liczb ca÷
kowitych;
b) zbiór wszystkich liczb postaci m+n
p
2, gdzie m; n s ¾
a liczbami ca÷
kow-
itymi;
c) zbiór wszystkich liczb niewymiernych;
d) zbior wszystkich liczb postaci
m+n
m
2
+n
2
+1
; gdzie m; n s ¾
a liczbami ca÷
kow-
itymi;
e) zbiór Q wszystkich liczb wymiernych;
f) zbiór Q
N ;
g) zbiór R
N ;
h) zbiór wszystkich podzbiorów zbioru N;
i) zbiór wszystkich sko´nczonych podzbiorów zbioru N;
j) zbiór wszystkich kul w przestrzeni, których promienie sa liczbami
wymiernymi, a ´srodki sa punktami o wszystkich wspó÷
rz ¾
ednych wymiernych.
Zadanie 13.2. Które z podanych zbiorów s ¾
a równoliczne?
a) zbiór wszystkich liczb rzeczywistych i zbiór wszystkich liczb rzeczy-
wistych dodatnich;
b) zbiór wszystkich liczb wymiernych i zbiór wszystkich liczb rniewymiernych;
c) zbiór liczb pierwszych i zbiór liczb podzielnych przez 2008.
Zadanie 13.3. Symbol
w oznacza równoliczno´s´c. O zbiorach A; B; C; D
zak÷
adamy, ·
ze s ¾
a niesko´nczone. Czy jest prawd ¾
a, ·
ze je·
zeli A
w B oraz C w D,
to
a) A [ C w B [ D ;
b) A \ C w B \ D ;
c) A
C
w B D ;
d) A n B w B n A ;
e) A
C
w B D ;
f) A
A
w B:
Zadanie 13.4. Uzasadni´c, ·
ze zbior liczb algebraicznych jest przeliczalny.
Wyk÷
ad 14. Paradoksy i ciekawostki logiczne; antynomie.
Omówimy tylko najbardziej charakterystyczne zagadnienia . Niektóre
zadania wygl ¾
adaj ¾
a na arytmetyczne, ale nale·
z ¾
a raczej do logiki.
1. Paradoks k÷
amcy. Znany by÷ju·
z staro·
zytnym …lozofom (wspomina
o nim ju·
z Eubulides w IV wieku p.n.e.). Za÷
ó·
zmy, ·
ze wiemy o kim´s, ·
ze jest
notorycznym k÷
amc ¾
a i zawsze mówi nieprawd ¾
e. Wyobra´zmy sobie dalej, ·
ze ten
kto´s mówi o sobie „K÷
ami ¾
e” . Poniewa·
z zawsze mówi nieprawd ¾
e, to czyni to
równie·
z i w tej chwili. Jego wypowied´z „k÷
ami ¾
e” nie jest prawdziwa. A zatem
mówi prawd ¾
e!
65

2. Krokodyl, problem Protagorasa i w¾
edrowiec u Cervantesa. Bardzo
stary jest paradoks, który w staro·
zytno´sci opisywany by÷jako paradoks z krokodylem.
Pewnemu ojcu krokodyl porwa÷syna. Na pro´sby ojca odrzek÷
, ·
ze pu´sci dziecko,
je·
zeli ojciec zgadnie prawid÷
owo, co on (krokodyl) ma zamiar zrobi´c z ch÷
opcem.
Ojciec powiedzia÷„nie pu´scisz ch÷
opca”. Rozumowa÷bowiem tak: je·
zeli krokodyl
mia÷zamiar go po·
zre´c, to odgad÷
em prawid÷
owo, a wi ¾
ec musi pu´sci´c ch÷
opca.
Je´sli za´s nie zgad÷
em, to krokodyl zwróci mi syna, bo –jak sam przyzna÷–nie ma
zamiaru go po·
zre´c. Krokodyl jednak odrzek÷
: „przeciwnie, w ka·
zdym wypadku
ch÷
opiec jest mój, bo je´sli nie mia÷
em zamiaru go po·
zre´c, to nie odgad÷
e´s moich
zamiarów, a wi ¾
ec zgodnie z nasz ¾
a umow ¾
a po·
zr ¾
e go. Je·
zeli za´s zgad÷
e´s, co b ¾
edzie,
to po·
zr ¾
e ch÷
opca –no, bo tak ma by´c.”
Wielki so…sta Protagoras (·
zy÷w latach ok. 485 – 410 p.n.e.) umówi÷
si ¾
e z jednym ze swoich uczniów, ·
ze ten zap÷
aci mu za nauk¾
e retoryki dopiero
wtedy, gdy wygra swój pierwszy proces s ¾
adowy. M÷
odzieniec zako´nczy÷nauk¾
e,
ale nie kwapi÷si ¾
e z rozpocz ¾
eciem kariery prawniczej. Po kilku latach nauczyciel
pozwa÷go do s ¾
adu o zwrot pieni ¾
edzy. Rozumowa÷tak: je´sli ucze´n wygra proces,
to zgodnie z umow ¾
a b ¾
edzie musia÷zap÷
aci´c. Je´sli przegra, to b ¾
edzie musia÷
zap÷
aci´c zgodnie z wyrokiem s ¾
adu. Tak czy owak, dostan ¾
e swoje pieni ¾
adze.
Ale ucze´n odrzek÷
: Je´sli proces wygram, to w my´sl orzeczenia s ¾
adu nie b ¾
ed ¾
e ci
musia÷nic zap÷
aci´c. A je·
zeli przegram, to nie b ¾
ed ¾
e musia÷p÷
aci´c na mocy naszej
umowy. Tak czy owak nie dostaniesz ode mnie ani obola.
Miguel Cervantes w swojej s÷
ynnej powie´sci „Don Kichot”opisuje pewn ¾
a
maj ¾
etno´s´c, przedzielon ¾
a na dwie cz ¾
e´sci wielk ¾
a rzek ¾
a.
Na rzece znajduje si ¾
e
most, a u jego wylotu dom czterech s ¾
edziów i szubienica. S ¾
edziowie maj ¾
a pil-
nowa´c prawa, ustanowionego przez w÷
a´sciciela: Kto przechodzi przez most od
brzegu do brzegu, winien pierwej zezna´c pod przysi ¾
eg ¾
a, sk ¾
ad, dok ¾
ad i po co idzie.
Je´sli powie prawd ¾
e, niechaj go puszcz ¾
a wolno, ale je´sli sk÷
amie, niechaj b ¾
edzie
powieszony na tej szubienicy bez odpuszczenia winy. Pewien w¾
edrowiec odrzek÷
,
·
ze szed÷tylko po to, by zosta´c powieszonym na tej szubienicy. Co mieli zrobi´c
s ¾
edziowie? Je´sli pu´sci go si ¾
e wolno, to znaczy ·
ze sk÷
ama÷
, a wi ¾
ec powinien zosta´c
powieszony. Je´sli powiesi si ¾
e go, to znaczy, ·
ze poda÷prawdziwy cel przybycia,
ale wtedy winien by´c puszczony wolno.
Taka sprzeczno´s´c mo·
ze si ¾
e pojawi´c wsz ¾
edzie tam, gdzie w jakiej´s wypowiedzi
mówimy co´s o niej samej. Jest to podobne do bardzo wspó÷
czesnego b÷¾
edu przy
pisaniu programów komputerowych: niesko´nczonej rekursji.
I wreszcie przytoczmy ... dowód istnienia Boga (Jean Buridan , XIV
wiek). Rozpatrzmy tak ¾
a par ¾
e zda´n:
1. Bóg istnieje.
2. Ka·
zde zdanie w tej parze jest fa÷
szywe.
Przypu´s´cmy najpierw, ·
ze zdanie 2 mówi prawd ¾
e, a wi ¾
ec, ·
ze stwierdza, jak
jest. A wi ¾
ec nie tylko zdanie pierwsze, ale i ono samo jest fa÷
szywe. Mamy
zatem sprzeczno´s´c: je·
zeli jest prawdziwe, to jest fa÷
szywe. A zatem nie mo·
ze
by´c prawdziwe. To znaczy, ·
ze jest nieprawdziwe. Nie ka·
zde zdanie w tej parze
jest fa÷
szywe. Ale przyj ¾
eli´smy, ·
ze zdanie drugie jest fa÷
szywe, zatem pierwsze
jest prawdziwe!!!
3. Pytania, na które nie mo·
zna odpowiedzie´c „tak”lub „nie”. W wielu
66

testach nale·
zy na pytania odpowiada´c „tak” lub „nie”. Jak ma odpowiedzie´c
minister na pytanie „Czy przesta÷Pan ju·
z bra´c ÷
apówki?”. Odpowied´z „nie”
znaczy, ·
ze jeszcze bierze. Odpowied´z „tak” znaczy, ·
ze bra÷
.
Po prostu: je·
zeli w pytaniu zawarta jest sugestia, nie ma na nie dobrej
odpowiedzi.
4. Ksi ¾
e·
zna i matematyka. Dowody niekonstruktywne. Anegdot ¾
e t ¾
e
przytacza Szczepan Jele´nski w Lilavati. Znany …lozof francuski Auguste Comte
próbowa÷przekona´c pewn ¾
a ksi ¾
e·
zn ¾
a, ·
ze w Pary·
zu s ¾
a dwie osoby o tej samej liczbie
w÷
osów na g÷
owie. „Przypu´s´cmy” rozpocz ¾
a÷
, „·
ze ka·
zdy z mieszka´nców stolicy
ma inna liczb ¾
e w÷
osów na g÷
owie”. Nikt nie ma wi ¾
ecej ni·
z sto tysi ¾
ecy w÷
osów,
a w Pary·
zu mieszka przecie·
z ponad sto tysi ¾
ecy ludzi. A zatem, konkludowa÷
jakie´s dwie osoby musz ¾
a mie´c po tyle samo w÷
osów.
Ksi ¾
e·
zna uzna÷
a podobno argumenty …lozofa za nieprzekonywuj ¾
ace. Rozu-
mowanie Comte’a to klasyczny przyk÷
ad dowodu niekonstruktywnego. Dowodz-
imy istnienia pewnego obiektu, nie podaj ¾
ac najmniejszej wskazówki, jak go
znale´z´c. Przypomnijmy poruszany ju·
z w tej ksi ¾
a·
zce ÷
adny przyk÷
ad matem-
atyczny na ten temat:
Istnieje liczba niewymierna, która podniesiona do pot ¾
egi niewymiernej jest
wymierna.
Samo zadanie jest mniej ciekawe ni·
z jego rozwi ¾
azanie. Rozpatrzmy liczb ¾
e
a =
p
2
p
2
. Jest ona albo wymierna, albo niewymierna. Je·
zeli jest wymierna, to
zadanie rozwi ¾
azane. Je·
zeli jest niewymierna, to obliczmy a
p
2
. Mamy a
p
2
p
2
=
p
2
2
= 2, a zatem niewymierna liczba a podniesiona do niewymiernej pot ¾
egi daje
liczb ¾
e wymiern ¾
a. Zadanie rozwi ¾
azane ... tylko wci ¾
a·
z nie znamy przyk÷
adu liczby
niewymiernej, która podniesiona do pot ¾
egi niewymiernej jest liczb ¾
a niewymiern ¾
a.
Przed podobnym dylematem stan ¾
a÷kiedy´s s ¾
ad w jednym z dawnych miast
wojewódzkich. Samochodem jecha÷
o m÷
ode ma÷·
ze´nstwo. Zmieniali si ¾
e co pewien
czas przy kierownicy. Po wielu godzinach jazdy osoba, która w÷
a´snie prowadzi÷
a
samochód, nie dostrzeg÷
a znaku „stop”. Nast ¾
api÷powa·
zny wypadek.
- Które z pa´nstwa prowadzi÷
o wtedy samochód? , zapyta÷s ¾
edzia na rozprawie.
- ·
Zona , odpowiedzia÷m ¾
a·
z. Równocze´snie ·
zona powiedzia÷
a:
- M ¾
a·
z.
-Ale·
z kochanie, przecie·
z to by÷
a´s Ty.
- Co Ty opowiadasz, to by÷
e´s Ty.
- Nie, Ty.
- Nie, Ty.
Wizja lokalna (np. analiza ustawienia fotela) nic nie da÷
a. Skazuj ¾
ac którekol-
wiek z ma÷·
zonków, s ¾
edzia móg÷skaza´c niewinnego cz÷
owieka. Zatem jednak,
mimo ·
ze sprawca wypadku stan ¾
a÷przed s ¾
adem, nie mo·
zna go by÷
o skaza´c. In-
aczej ni·
z w matematyce, dowody na sali s ¾
adowej musz ¾
a by´c konstruktywne.
Przynajmniej tak jest w prawie rzymskim.
5. Fikcja. W matematyce obiekty nieistniej ¾
ace nie maj ¾
a nazwy. Ale
w innych naukach maj ¾
a, nawet w astronomii: Wulkan to hipotetyczna planeta,
istniej ¾
aca by´c mo·
ze mi ¾
edzy S÷
o´ncem i Merkurym. O jej istnieniu mog ¾
a ´swiad-
67

czy´c niewyt÷
umaczalne zaburzenia w ruchu Merkurego. Faeton to domniemana
planeta, po której rozerwaniu, wskutek dzia÷
ania si÷przyp÷
ywowych, powsta÷
y
planetoidy.
Protagoras, autor znanego powiedzenia Anthropos metron panton, („cz÷
owiek
jest miar ¾
a wszechrzeczy”) uwa·
za÷
, ·
ze geometria nie jest nauk ¾
a, bo mówi o
rzeczach nie istniej ¾
acych: punkty, linie, bry÷
y. Takich rzeczy nie ma. To prawda,
ale jako´s nikt si ¾
e tym nie przejmuje i dzi´s ka·
zdy zaliczy geometri ¾
e do nauki. W
siedemnastym za´s wieku wielki …lozof angielski, biskup Ko´scio÷
a anglika´nskiego
George Berkeley (1685-1753), przedstawiciel kierunku …lozo…cznego zwanego
idealizmem, uwa·
za÷
, ·
ze rachunek ró·
zniczkowy Newtona nie ma sensu, bo dzieli
si ¾
e w nim zero przez zero. Berkeley pisa÷
: „Czy·
z matematycy, którzy s ¾
a tak sub-
telni w kwestiach religijnych, s ¾
a tak samo skrupulatni w swej w÷
asnej dziedzinie?
Czy nie ulegaj ¾
a autorytetowi, nie bior ¾
a rzeczy na wiar ¾
e, nie s ¾
a przekonani, ·
ze
punkty s ¾
a niewymierne? Czy·
z nie maj ¾
a swych w÷
asnych tajemnic, a co wi ¾
ecej
–swych w÷
asnych niezgodno´sci i sprzeczno´sci?”
A jak z astronomi ¾
a? W XVII wieku niektórzy uczeni s ¾
adzili, ·
ze plamy na
S÷
o´ncu to efekt powstaj ¾
acy przez przechodzenie przed S÷
o´ncem ma÷
ych planet.
Planety te mia÷
y nawet swoje nazwy: Sidera Bourbonica albo Sidera Austriaca.
6. Z fa÷
szu wynika wszystko. Ucz ¾
ac zasady logicznej, ·
ze implikacja
o fa÷
szywym poprzedniku jest prawdziwa, mo·
zemy przeprowadzi´c kilka takich
rozumowa´n. Za÷
ó·
zmy, ·
ze 5 dzielone przez dwa równa si ¾
e 3. Udowodni ¾
e, ·
ze wtedy
7 = 102. Od obu stron równo´sci 5/2 = 3 odejmuj ¾
e 5/2, otrzyman ¾
a równo´s´c
mno·
z ¾
e przez 190 i dodaj ¾
e 7 do obu stron. Mo·
zna tak wykaza´c ka·
zd ¾
a równo´s´c
liczbow ¾
a. Mog ¾
e te·
z wykaza´c, ·
ze jestem królow ¾
a angielsk ¾
a. Je·
zeli bowiem 5/2 =
3, to mno·
z ¾
ac przez dwa mam 5 = 6 , odejmuj ¾
ac od obu stron 4,otrzymuj ¾
e 1 =
2. A zatem dwie ró·
zne osoby (ja i królowa) s ¾
a naprawd ¾
e jedn ¾
a osob ¾
a.
A tak na marginesie, czy pi ¾
e´c dzielone przez dwa mo·
ze si ¾
e równa´c trzy?
Mo·
ze ... je·
zeli u·
zyjemy zbyt m ¾
adrego kalkulatora. W niektórych takich kalku-
latorach mo·
zna ustawi´c ·
z ¾
adan ¾
a dok÷
adno´s´c oblicze´n. Je´sli za·
zyczymy sobie zero
cyfr po przecinku, to mo·
zemy jako odpowied´z otrzyma´c 2 albo 3, zale·
znie od
typu kalkulatora. Kalkulator Texas Instruments TI 83 podaje 3.
68

Wyk÷
ad 15. Jak si ¾
e uczy´c (w szczególno´sci matematyki)?
Z tre´sci tego wyk÷
adu nie b ¾
edziesz egzaminowany na egzaminie z podstaw
matematyki, a ... codziennie w trakcie Twoich studiów i by´c mo·
ze pracy za-
wodowej.
Oto stara maksyma ÷
aci´nska:
Quinque sacre claves dicuntur stare sophie;
Prima frequens studium, …nem nescitque legendi.
Altera: que relegis memori commitere menti.
Tertia: que nescis percrebra rogatio rerum.
Quarta est verus honor sincero corde magistri.
Quinta iubet vanas mundi contemprere gazas.
Mówi ¾
a o istnieniu pi ¾
eciu rzeczy do ´swi ¾
etej m ¾
adro´sci;
Pierwsza to cz ¾
esta nauka nie znaj ¾
aca ko´nca czytania.
Druga: to, co powtórnie przeczytane, powierzaj rozumowi obdarzonemu
pami ¾
eci ¾
a.
Trzecia: bardzo cz ¾
esto pytaj o rzeczy, których nie wiesz.
Czwarta to prawdziwy i szczery szacunek dla mistrza.
Pi ¾
ata zaleca, by mie´c w pogardzie pró·
zne skarby ´swiata.
(Mateusz z Vendôme; t÷
um. Andrzej Borowski)
Dawno ju·
z odesz÷
y do lamusa historii teorie, w których przez prac ¾
e okre´sla÷
o
si ¾
e przede wszystkim, je´sli nie wy÷¾
acznie, robot ¾
e …zyczn ¾
a (Ojciec chleb czarny
wykuwa m÷
otem, przy igle matka blada...). Dzi´s wiemy, ·
ze uczenie si ¾
e jest te·
z
form ¾
a pracy. Bior ¾
a w niej udzia÷czynniki umys÷
owe i …zyczne, a ogólne prawa
rz ¾
adz ¾
ace prac ¾
a maj ¾
a zastosowanie i do wysi÷
ku umys÷
owego.
Ju·
z staro·
zytni zastanawiali si ¾
e nad tym, jakiego rodzaju czynno´sci ¾
a jest
my´slenie. Gdyby Platon pisa÷teraz swoje dialogi, mo·
ze pos÷
u·
zy÷
by si ¾
e metafor ¾
a
z fotogra…ki, ·
ze my´slenie to co´s jak wywo÷
ywanie.
Ka·
zdy, kto wywo÷
ywa÷
samodzielnie zdj ¾
ecie w ciemni, musia÷zachwyci´c si ¾
e, ·
ze na bia÷
ym papierze na-
gle zaczynaj ¾
a si ¾
e pojawia´c zarysy twarzy, domy, krajobraz. Tak i z nami: w
ciemno´sciach naszego umys÷
u, mo·
ze w pod´swiadomo´sci, co´s si ¾
e dzieje. My´slenie
wydobywa owo co´s z g÷¾
ebi i nagle oczami duszy, dostrzegamy owo co´s, widz-
imy jasno i klarownie: ju·
z wiemy ile pozornie traci na ci ¾
e·
zarze cia÷
o zanurzone
w wodzie, co wyjdzie, gdy do dodamy kwadraty d÷
ugo´sci przyprostok ¾
atnych, i
czemu równa si ¾
e mc
2
. Rzeczywisto´s´c (w du·
zym uproszczeniu) dociera do nas
w postaci bod´zców odbieranych przez nasze zmys÷
y. Powstaje w ten sposób
nasz w÷
asny, prywatny ´swiat. To my´sl porz ¾
adkuje ten ´swiat, który sam w sobie
uporz ¾
adkowany nie jest. Nie ma w nim góry i do÷
u, lewej ani prawej strony,
niebo nie jest niebieskie, gwiazdy nie s ¾
a du·
ze i ma÷
e, kamie´n nie jest twardy a
woda p÷
ynna. Pies nie szczeka ani kot nie miauczy. To my tworzymy poj ¾
ecia,
abstrakcyjne budowle, dzi ¾
eki którym ob÷
oki s ¾
a w górze a ziemia w dole, serce
okazuje si ¾
e by´c po lewej stronie, S÷
o´nce wi ¾
eksze od Ziemi, ska÷
a twarda a po-
duszka mi ¾
ekka. Abstrakcja to kategoria umys÷
u, dzi ¾
eki której cz÷
owiek wmawia
69

sobie, ·
ze rozumie ´swiat. Nie znam autora tego celnego powiedzenia. Ale my´sle-
nie odbywa si ¾
e jeszcze wewn ¾
atrz naszego prywatnego ´swiata. Natomiast, gdy
mówi ¾
e, to przekazuj ¾
e osobie s÷
uchaj ¾
acej informacje o tym swoim ´swiecie: w
umy´sle kogo´s, kto mnie s÷
ucha, zaczynaj ¾
a si ¾
e pojawia´c obrazy z mojego ´swiata.
Nie mo·
zemy wyrazi´c bezpo´srednio zmys÷
owego doznania (na przyk÷
ad przyjem-
no´sci), mo·
zemy jednak o nim opowiedzie´c
podzieli´c si ¾
e nim, kiedy je prze-
my´slimy (zre‡ektujemy), nadaj ¾
ac mu posta´c czego´s, co mo·
ze sta´c si ¾
e publiczne.
Nie jest to jednak jeszcze wszystko, co o my´sleniu trzeba tu powiedzie´c
(no w÷
a´snie, a mia÷
o by´c o mówieniu). Jest pewien wa·
zny element, w którym
gra s÷
ów zwi ¾
azana z wyobra·
zaniem sobie my´slenia jako wywo÷
ywania, zawodzi.
Kiedy na papierze fotogra…cznym pojawia si ¾
e obraz, jest on tylko wydobywany
przez procesy chemiczne. On tam ju·
z by÷
, tylko trzeba by÷
o wykona´c pewn ¾
a
czynno´s´c, ·
zeby go zobaczy´c. To znana z …lozo…i zasada deja vu, ju·
z to gdzie´s
widzieli´smy. Z my´sleniem jest inaczej. Cz ¾
e´s´c jego niezwyk÷
o´sci zasadza si ¾
e z
pewno´sci ¾
a na tym, ·
ze nie poprzedza go nic, co w jakikolwiek sposób mog÷
oby
stanowi´c jego wzór. S÷
owem: zanim pomy´slimy, nie wiemy jeszcze, jak to b ¾
edzie
„wygl ¾
ada÷
o”.
Psychologowie podchodz ¾
a do problemu pracy umys÷
owej bardzo rozmaicie.
Wybitny ameryka´nski psycholog Joy P.A. Guilford (1897 – 1988), znany sze-
roko ze swych bada´n nad inteligencj ¾
a, wyodr ¾
ebni÷dwa g÷
ówne typy czynników
intelektualnych: czynnik my´slowy i czynnik pami ¾
eciowy.
Czynniki my´slowe
mo·
zna sklasy…kowa´c nast ¾
epuj ¾
aco:
1. Czynniki poznawcze, a wi ¾
ec u´swiadamianie sobie tre´sci i odkrywanie
jej znaczenia. Mamy tu takie zjawiska jak rozumienie poszczególnych s÷
ów,
wi ¾
azanie ich w ci ¾
agi zale·
zno´sci, a tak·
ze orientacja przestrzenna, wykrywanie
zwi ¾
azków mi ¾
edzy poj ¾
eciami i dostrzeganie problemów. Wiemy, ·
ze znaczna cz ¾
e´s´c
doros÷
ych ma k÷
opoty ze zrozumieniem prostych tekstów. Nie chodzi tu tylko
o zadania matematyczne „z tekstem”, takie jak autentyczne zadanie z pewnego
podr ¾
ecznika z 1922 roku. Gdy dobrze zrozumiemy jego tre´s´c, rozwi ¾
azanie nie
b ¾
edzie trudne.
Wychod´zca polski, powracaj ¾
acy z Ameryki, pragn ¾
a÷przywie´z´c z sob ¾
a 4
samochody i 10 maszyn do pisania. Gdyby naby÷4 samochody i 10 maszyn,
to wyda÷
by wszystkie posiadane na ten cel pieni ¾
adze i nie wystarczy÷
oby mu
na przewóz nabytych towarów. Wobec tego wychod´zca naby÷4 samochody i
tylko 5 maszyn do pisania; po op÷
aceniu towaru i jego przewozu przeci ¾
etnie po
5 dolarów od sztuki, wychod´zcy pozosta÷
o 55 dolarów. Koszt przewozu samo-
chodu kosztowa÷tyle centów, ile zap÷
acono dolarów za wszystkie 4 samochody,
koszt przewozu ka·
zdej maszyny do pisania wynosi÷tyle centów, ile zap÷
acono
dolarów za wszystkie 5 maszyn. Ile pieni ¾
edzy mia÷wychod´zca przed kupnem i
ile kosztowa÷ka·
zdy samochód i ka·
zda maszyna do pisania?
2. W´sród czynników my´slowych mam i te, które nazywaj ¾
a si ¾
e wytwór-
czymi. Po zrozumieniu czego´s mo·
ze si ¾
e w naszym umy´sle zrodzi´c pewien pro-
dukt my´slowy –podobnie jak po g÷¾
ebokim zrozumieniu i przemy´sleniu dzia÷
ania
pewnego urz ¾
adzenia in·
zynier potra… zaprojektowa´c nowe, lepsze. W matem-
atyce czynnikami wytwórczymi s ¾
a na przyk÷
ad: nadawanie nazw tworom ab-
strakcyjnym, wyobra´znia „matematyczna” (na przyk÷
ad: jak sobie wyobrazi´c
70

kul ¾
e w przestrzeni wymiaru 4, ale tak·
ze wyobrazi´c sobie co mo·
zna, a czego
nie mo·
zna otrzyma´c w wyniku ci ¾
agu przekszta÷
ce´n algebraicznych), p÷
ynno´s´c
wys÷
awiania si ¾
e, przekszta÷
canie znacze´n (na przyk÷
ad uogólnianie), a tak·
ze ory-
ginalno´s´c.
3. Za najbardziej zaawansowane czynniki my´slowe uznajemy czynniki
oceny: ocenianie spostrze·
zeniowe, logiczne, do´swiadczalne itp. Nie chodzi tu
tylko o umiej ¾
etno´s´c stawiania stopni, a o porz ¾
adkowanie ´swiata w naszym
umy´sle. Umiej ¾
etno´s´c oceny spostrze·
zeniowej maj ¾
a i zwierz ¾
eta. W÷
a´sciwa ocena
stopnia zagro·
zenia jest cz ¾
esto warunkiem prze·
zycia. Warto´sciowanie oparte na
logicznej analizie i eksperymentach jest cech ¾
a ludzk ¾
a. Czynimy to na co dzie´n,
niekiedy nie zdaj ¾
ac sobie z tego sprawy wyra´znie. Gdy wypowiadamy kate-
goryczne s ¾
ady na temat tego, co jest pi ¾
ekne, cz ¾
esto staramy si ¾
e znale´z´c jakie´s
racjonalne uzasadnienie w÷
asnej, subiektywnej oceny. By´c mo·
ze mniej wysi÷
ku
intelektualnego w÷
o·
zymy w uzasadnienie pi ¾
ekna teorii
matematycznej. Je·
zeli nale·
zymy do grona osób podejmuj ¾
acych decyzje o
znaczeniu spo÷
ecznym, nasze warto´sciowanie wp÷
ywa na wybór strategii gospo-
darczej, kierunki rozwoju bada´n naukowych itd. Inteligencja polega w du·
zej
mierze na podejmowaniu decyzji na podstawie niepe÷
nych danych. Je·
zeli mamy
bowiem kompletny przegl ¾
ad sytuacji, to decyzj ¾
e mo·
ze podj ¾
a´c za nas ... byle
komputer. Inteligencja jest cz ¾
esto nies÷
usznie postrzegana jako wiedza plus szy-
bko´s´c kojarzenia.
´
Cwiczenie 15.1
. Czy zgadzasz si ¾
e, ·
ze my´slenie jest pewnego rodzaju czyn-
no´sci ¾
a? Na pewno! Zastanów si ¾
e wobec tego, czy bardziej przypomina ono
czynno´s´c tak ¾
a, jak malowanie obrazu, czy tak ¾
a jak jazda na rowerze? Czy w
wyniku my´slenia co´s powstaje (tak, jak obraz spod p ¾
edzla malarza), czy jest to
tylko czynno´s´c pomocnicza, czy wykonywana dla niej samej (jak jazda na row-
erze)? Jak rozumiesz nast ¾
epuj ¾
ace opinie wybitnego …lozofa, egzystencjalisty,
Martina Heideggera:
My´slenie nie daje poznania, jak czyni ¾
a to nauki. My´slenie nie jest ´zród÷em
praktycznych umiej ¾
etno´sci. My´slenie nie rozwi ¾
azuje zagadek ´swiata. My´slenie
nie wyposa·za nas bezpo´srednio w zdolno´s´c dzia÷ania.
Jak rozumiesz nast ¾
epuj ¾
ace s÷
owa ?
Aktywno´s´c my´slowa – któr ¾
a Platon nazwa÷wewn ¾
etrznym dialogiem, jaki
ka·zdy prowadzi z samym sob ¾
a – s÷u·zy jedynie otwarciu oczu i umys÷u. Innymi
s÷owy, my´slenie (u Platona, przyp. M. Sz.) ma na celu kontemplacj ¾
e i na niej
si ¾
e ko´nczy, a kontemplacja nie jest aktywno´sci ¾
a, lecz pasywno´sci ¾
a.
Tyle o czynnikach my´slowych.
Oczywiste jest, ·
ze ka·
zda praca wymaga pewnej energii, która podczas pracy
si ¾
e wyczerpuje. Po fazie wysi÷
ku musi przyj´s´c okres wypoczynku. Ka·
zdy cz÷
owiek
jest inny; ka·
zdy ma inny rytm pracy. Rytm ten zale·
zy mi ¾
edzy innymi od rodzaju
wysi÷
ku umys÷
owego, jaki wykonujemy. W pocz ¾
atkowej fazie pracy krzy·
zuj ¾
a si ¾
e
dwa czynniki: zaciekawienie (podniecenie startu) i trudno´sci z „rozp ¾
edzeniem
si ¾
e”. W szczególno´sci w prac ¾
e, któr ¾
a wykonujemy po raz pierwszy, trzeba si ¾
e
dopiero powoli wdro·
zy´c. Prze÷
amujemy tu swoj ¾
a bezw÷
adno´s´c, opór. W dalszym
ci ¾
agu pracy zwi ¾
eksza si ¾
e wprawa, a zaciekawienie tylko nieznacznie maleje. W
ko´ncu jednak wzmaga si ¾
e zm ¾
eczenie, ciekawo´s´c opada i krzywa efektywno´sci
71

„ma ujemn ¾
a pochodn ¾
a”. Mo·
ze jednak si ¾
e zdarzy´c, ·
ze gdy wiemy z góry, kiedy
nast ¾
api koniec pracy, w ostatniej chwili dostajemy nowej werwy, odzyskujemy
energi ¾
e i …niszujemy jak sportowiec na ostatniej prostej.
Gdy po pewnym okresie pracy umys÷
owej odpoczniemy, to znu·
zenie ust ¾
api,
a efekt pracy, w postaci chwilowej wprawy, utrzyma si ¾
e i po podj ¾
eciu pracy
wydajno´s´c b ¾
edzie ros÷
a szybciej ni·
z na pocz ¾
atku i stan ten utrzyma si ¾
e przez
d÷
u·
zszy czas. Na ko´ncowy wynik sk÷
ada si ¾
e tak wiele czynników, ·
ze nie mo·
zna
poda´c ogólnej recepty powodzenia w pracy umys÷
owej. Prawo uczenia si ¾
e sfor-
mu÷
owane przez Foucaulta przypomina zupe÷
nie prawa przyrody. Brzmi ono
nast ¾
epuj ¾
aco: czas potrzebny do nauczenia si ¾
e pewnego szeregu elementów jest
proporcjonalny do kwadratu d÷
ugo´sci szeregu i liniowo proporcjonalny do czasu
potrzebnego do nauczenia si ¾
e jednego cz÷
onu.
Ka·
zdy charakter pracy umys÷
owej rz ¾
adzi si ¾
e innymi prawami. J ¾
ezyków na-
jlepiej uczy´c si ¾
e wed÷
ug zasady „krótko i cz ¾
esto”. Matematyka znajduje si ¾
e na
przeciwnym biegunie: na ogó÷musimy si ¾
e najpierw skoncentrowa´c, otworzy´c na
nowe tre´sci, by potem przez stosunkowo d÷
ugi czas by´c zdolnym do skupienia
si ¾
e na de…nicjach, poj ¾
eciach, twierdzeniach i nawet rachunkach. Po zako´nczeniu
nauki matematyki ten stan „wzbudzenia” opada powoli. Dlatego nie rezygnu-
j ¾
ac z systematycznej nauki, nale·
zy na nauk¾
e matematyki przeznacza´c d÷
u·
zsze
odcinki czasu.
Pami ¾
e´c i zapami ¾
etywanie
Nie ma w tych wyk÷
adach miejsca na dok÷
adne przedstawienie ró·
znych teorii
uczenia si ¾
e.
Wspomn ¾
e tylko o najstarszej, plato´nskiej.
W dialogu Teajtet
Platon przedstawia swoj ¾
a koncepcj ¾
e odtwarzania w pami ¾
eci zdobytej wiedzy.
Zgodnie t ¾
a koncepcj ¾
a, wszyscy posiadamy w duszy jakby woskowe tabliczki o
osobniczo zró·
znicowanej jako´sci, na których odciskaj ¾
a si ¾
e spostrze·
zenia i my´sli.
W dzieci´nstwie wosk jest prawie p÷
ynny – zapominamy szybko, nowe wra·
zenia
wymazuj ¾
a stare. W wieku m÷
odzie´nczym wosk jest w najlepszym stanie: idee
odciskaj ¾
a si ¾
e szybko i na trwale. Z biegiem lat wosk krzepnie – coraz trud-
niej uczymy si ¾
e nowych rzeczy. Poznanie polega na dopasowaniu doci´sni ¾
e´c do
wzorców „wy·
zszej jako´sci” Dusza ma predyspozycje do odzyskiwania wiedzy z
jak ¾
a mia÷
a obcowa´c w poprzednich bytowaniach. Mistrz –…lozof potra… za po-
moc ¾
a odpowiednich pyta´n wydoby´c t ¾
e wiedz ¾
e z zakamarków duszy. W dialogu
Menon ta metoda zostaje zaprezentowana na m÷
odym ch÷
opcu, nie uczonym, ale
rozgarni ¾
etym umys÷
owo. Przeprowadzona próba wypada pomy´slnie i Sokrates
stwierdza: nieprawda·
z, chocia·
z go nikt nie uczy÷
, tylko mu pytania zadawa÷
, on
zacznie wiedzie´c, sam ¾
a wiedz ¾
e z g÷¾
ebi podejmuj ¾
ac.
Zwró´cmy uwag ¾
e na wiele znacze´n s÷
owa „zapami ¾
eta´c”. W zale·
zno´sci od
kontekstu „zapami ¾
eta´c tekst” znaczy:
- umie´c dos÷
ownie go powtórzy´c,
- umie´c go stre´sci´c,
- umie´c wydoby´c z niego najbardziej istotne tre´sci;
- rozpozna´c go jako ju·
z widziany przy powtórnym ogl ¾
adaniu.
Co najbardziej tra…a do nas? Obraz, d´zwi ¾
ek, czy mo·
ze zapach? W epoce
telewizyjnej panuje teoria, ·
ze obraz. Z kolei pami ¾
e´c „zapachowa” jest bardzo
72

trwa÷
a: mo·
zemy przypomnie´c sobie obraz z dzieci´nstwa, gdy nagle „co´s” za-
pachnie tak samo.
Pocz ¾
atkowo przez termin pami ¾
e´c (gr. mnéme, ÷
ac. memoria) rozumiano
uczenie si ¾
e tekstu tak, by mo·
zna go by÷
o dos÷
ownie odtworzy´c (czyli w÷
a´snie
„na pami ¾
e´c”). Wspó÷
czesne znaczenie s÷
owa pami ¾
e´c jest oczywi´scie nieco inne.
Psychologowie wyró·
zniaj ¾
a trzy zasadnicze typy pami ¾
eci: wzrokowa, s÷
uchowa
i ruchowa.
Pierwsze dwie nie wymagaj ¾
a obja´snienia, trzeci ¾
a by´c mo·
ze ma
dziecko, które „musi” si ¾
e wierci´c w klasie podczas lekcji. Oczywi´scie nie ma
cz÷
owieka, który by÷
by w stu procentach wzrokowcem, s÷
uchowcem czy ruchow-
cem. Rozpoznanie typu swojej pami ¾
eci to po÷
owa sukcesu przy zapami ¾
etywaniu.
Nauczyciel powinien oczywi´scie orientowa´c si ¾
e, jaki typ pami ¾
eci ma dany ucze´n;
jest to rzecz jasna ma÷
o realne przy kilkudziesi ¾
ecioosobowych klasach.
Formy, jakie mo·
ze przybiera´c aktywno´s´c cz÷
owieka, usi÷
uj ¾
acego przyswoi´c
sobie tre´s´c czytanego tekstu s ¾
a bardzo ró·
zne. Mo·
ze to by´c:
1.
Dok÷
adne, bardziej jasne i szczegó÷
owe ni·
z zwykle spostrzeganie (od-
czytywanie) tekstu.
2.
Wykonywanie ruchów artykulacyjnych (odczytywanie na g÷
os lub szeptem).
3.
Wykonywanie rytmicznych ruchów g÷
owy, tu÷
owia lub ko´nczyn.
4.
Ponowne odczytywanie ca÷
o´sci materia÷
u lub trudniejszych jego cz ¾
e´sci.
5.
Odtwarzanie, powtarzanie w my´sli trudniejszych fragmentów.
6.
Dzielenie tekstu na cz ¾
e´sci, stanowi ¾
ace pewne jednostki tre´sciowe.
7.
Wyodr ¾
ebnianie sensownych punktów oparcia w postaci zda´n lub poje-
dynczych s÷
ów, obrazów, które reprezentuj ¾
a tre´s´c. Najbardziej rozwini ¾
et ¾
a forma
tej czynno´sci jest uk÷
adanie planu tre´sci.
8.
Streszczanie fragmentów tekstu w÷
asnymi s÷
owami.
9.
Kojarzenie (wi ¾
azanie) fragmentów odczytywanej tre´sci pomi ¾
edzy sob ¾
a
lub z poprzednio opanowan ¾
a wiedz ¾
a.
´
Cwiczenie 15.2
. Zastanów si ¾
e, które z tych czynno´sci s ¾
a polecane dla
wzrokowca, s÷
uchowca, ruchowca. Które Ty stosujesz? Które s ¾
a najbardziej
istotne przy uczeniu si ¾
e matematyki?
Pami ¾
e´c s÷
uchowa, a w ka·
zdym razie s÷
uchowy kana÷przetwarzania informa-
cji okazuje si ¾
e wa·
zniejszy, ni·
z si ¾
e wydaje. Zwróci÷na to uwag ¾
e angielski psy-
cholog Alan Baddeley w latach osiemdziesi ¾
atych XX wieku. Pami ¾
e´c krótkotr-
wa÷
a (STM, od angielskiego short time memory) dzieli si ¾
e na trzy sektory. Do
jednego z nich (zwanego p ¾
etl ¾
a fonologiczn ¾
a) tra…aj ¾
a na kilka a najdalej na kilka-
na´scie sekund informacje s÷
owne, do drugiego obrazy (na kilkadziesi ¾
at sekund)
a centralny o´srodek wykonawczy decyduje, co zrobi´c z informacjami przeby-
waj ¾
acymi przez ten krótki czas w pami ¾
eci zmys÷
owej. Jest ona albo usuwana
(„zdeletowana!”) , albo przesy÷
ana dalej, w g÷¾
ab pami ¾
eci, do kolejnych obszarów
pami ¾
eci d÷
ugotrwa÷
ej („na twardy dysk”). Wed÷
ug wielu psychologów, w÷
a´snie
te sekundy decyduj ¾
a o ca÷
ej ludzkiej kulturze, kszta÷
tuje nasz ¾
a osobowo´s´c. Je´sli
p ¾
etla fonologiczna nie dzia÷
a prawid÷
owo, to nie jeste´smy w stanie utrzyma´c w
pami ¾
eci naszych spostrze·
ze´n na tyle d÷
ugo, by przekszta÷
ci´c je w trwa÷
y ´slad w
pami ¾
eci d÷
ugotrwa÷
ej. Szczególnie dotyczy to informacji d´zwi ¾
ekowej, a wi ¾
ec na
przyk÷
ad uczenia si ¾
e j ¾
ezyków obcych.
73

Ka·
zdy nauczyciel wie, ·
ze bardzo cz ¾
esto uczniowie czytaj ¾
a tekst zadania
nieuwa·
znie i nie próbuj ¾
a przeczyta´c powtórnie, nawet gdy nie rozumiej ¾
a przy
pierwszym czytaniu. Nie wnikaj ¾
ac w tre´s´c, dokonuj ¾
a zupe÷
nie przypadkowych
oblicze´n i gdy nie potra… ¾
a ju·
z dalej, to w÷
a´snie stadium uwa·
zaj ¾
a za ko´ncowy
wynik. Nie troszcz ¾
a si ¾
e o sprawdzenie, które bardzo cz ¾
esto jest mo·
zliwe innym
sposobem.
Do rozumienia czytanego tekstu niezb ¾
edne jest pami ¾
etanie kilku poprzed-
nich s÷
ów czy zda´n. Musz ¾
a by´c one –albo ich skróty –uwi ¾
ezione w naszej p ¾
etli
fonologicznej. Dlatego w÷
a´snie d÷
ugie instrukcje s ¾
a nieczytelne a d÷
ugie zada-
nia trudne. Przeprowadzi÷
em kiedy´s eksperyment w. W jednej z dwóch grup
studenckich w Wy·
zszej Szkole Informatyki Stosowanej i Zarz ¾
adzania da÷
em na
kolokwium to samo zadanie, co w drugiej, ale inaczej sformu÷
owane.
Zadanie 1a. Wyznaczy´c liczby zespolone, równe odwrotno´sci kwadratu swo-
jego sprz ¾
e·
zenia.
Zadanie 1b. Rozwi ¾
aza´c równanie z
=
1
z
2
.
W grupie b) wi ¾
ekszo´s´c studentów rozwi ¾
aza÷
a zadanie, w grupie a) nikt. W
niewytrenowanych umys÷
ach studentów p ¾
etla fonologiczna by÷
a za krótka na
pomieszczenie ca÷
ej frazy „odwrotno´s´c kwadratu sprz ¾
e·
zenia”. Dlatego zadania
z tekstem wymagaj ¾
a wi ¾
ekszego skupienia i kilkakrotnego czytania. Po prze÷
o·
ze-
niu tre´sci zadania mo·
zemy zachowa´c si ¾
e tak, jak mawia÷pewien m÷
ody asystent
na Politechnice Warszawskiej: „Uwaga, studenci! Wy÷¾
aczy´c my´slenie, w÷¾
aczy´c
ró·
zniczkowanie!”.
Asystent ten nie dodawa÷jednak, ·
ze po zró·
zniczkowaniu
(ogólniej: po dokonaniu rachunków) trzeba znowu w÷¾
aczy´c my´slenie.
Wyró·
zniamy trzy poziomy rozumienia tekstu matematycznego :
1)
rozumienie formalne,
2)
rozumienie operatywne,
3)
rozumienie strukturalne.
Na pierwszym poziomie rozumienia wystarczy dos÷
ownie odczyta´c tekst i
upewni´c si ¾
e, ·
ze zdajemy sobie spraw¾
e ze znaczenia wszystkich s÷
ów tam wys-
t ¾
epuj ¾
acych. Gdy ucze´n po raz pierwszy dowiaduje si ¾
e, co to jest podobie´nstwo:
Podobie´nstwo o dodatniej skali k jest przekszta÷
ceniem, w którym odleg÷
o´s´c
obrazów dwóch punktów jest k razy wi ¾
eksza od odleg÷
o´sci tych punktów,
to mo·
ze nie poj ¾
a´c, o co chodzi, nawet je´sli rozumie ka·
zde s÷
owo. Rozumienie
operatywne mo·
zna okre´sli´c jako umiej ¾
etno´s´c pos÷
ugiwania si ¾
e danym poj ¾
eciem:
umiem stwierdzi´c, ·
ze jakie´s …gury s ¾
a podobne, umiem narysowa´c obraz …gury
przy podobie´nstwie, umiem zastosowa´c podobie´nstwo, je·
zeli zajdzie potrzeba.
Wreszcie o rozumieniu strukturalnym mówimy, gdy rozumiemy miejsce danego
poj ¾
ecia matematycznego w wi ¾
ekszej teorii, gdy wiemy, dlaczego pos÷
ugujemy
si ¾
e nim ... i gdy umiemy pogl ¾
adowo odpowiedzie´c na pytanie „co to naprawd ¾
e
znaczy”. Tak, dowodem na to, ·
ze rozumiemy co´s „strukturalnie” jest umiej ¾
et-
no´s´c wyt÷
umaczenia tego laikowi.
´
Cwiczenie 15.3
. Rozumienie tekstu matematycznego ma trzy poziomy:
rozumienie formalne, strukturalne i operatywne. Prze´sled´z to na przyk÷
adzie
ci ¾
agu zda´n.
74

1.
Ci ¾
ag a
n
zbli·
za si ¾
e nieograniczenie do liczby
g
.
2.
Dla du·
zych n wyraz a
n
ró·
zni si ¾
e ma÷
o od g.
3.
Dla dostatecznie du·
zych n wyraz a
n
ró·
zni si ¾
e dowolnie ma÷
o od g .
4.
Mo·
zna dobra´c taki wska´znik, aby wyrazy ci ¾
agu a
n
o wska´znikach wi ¾
ek-
szych od tego wska´znika ró·
zni÷
y si ¾
e od liczby g tak ma÷
o, jak tylko zechcemy.
5.
Dla dowolnej dodatniej liczby mo·
zna dobra´c taki wska´znik, aby ka·
zdy
wyraz ci ¾
agu o wska´zniku wi ¾
ekszym od tego wska´znika ró·
zni÷si ¾
e od liczby g o
mniej ni·
z .
6.
8
>0
9
N
8
n>N
j a
n
g j <
7.
Je·
zeli
jest dowoln ¾
a liczb ¾
a dodatni ¾
a, to wyrazów ci ¾
agu niespe÷
niaj ¾
a-
cych warunku j a
n
g j < mo·
ze by´c tylko sko´nczenie wiele.
8.
Je·
zeli
jest dowoln ¾
a liczb ¾
a dodatni ¾
a, to do zbioru R n (g
;
g +
) mo·
ze nale·
ze´c tylko sko´nczenie wiele wyrazów ci ¾
agu a
n
.
9.
Do ka·
zdego otoczenia liczby g nale·
z ¾
a prawie wszystkie wyrazy ci ¾
agu
a
n
.
Od mglistego zdania 1 przechodzimy stopniowo do zdania 6, wyra·
zaj ¾
acego
poj ¾
ecie granicy zupe÷
nie formalnie. Te kolejne transformacje polegaj ¾
a na coraz
wyra´zniejszym ukazywaniu si ¾
e kwanty…katorów. Mo·
zna powiedzie´c, ·
ze w÷
a´snie
w ten sposób u´sci´slano poj ¾
ecie granicy od czasów Newtona.
Ale zdanie takie jak 6 oczywi´scie nie wystarcza. Zdania wcze´sniejsze s ¾
a te·
z
potrzebne, bo daj ¾
a nam niezb ¾
edn ¾
a intuicj ¾
e. Umo·
zliwiaj ¾
a przej´scie od rozu-
mienia formalnego do rozumienia operatywnego. Zdania 7, 8, 9 pomagaj ¾
a ju·
z
w rozumieniu strukturalnym tekstu.
´
Cwiczenie 15.4
; ostatnie. Zaprojektuj tak swoj ¾
a nauk¾
e, ·
zeby cel, jaki masz
- a jest nim osi ¾
agni ¾
ecie operatywnej znajomo´sci przerabianego materia÷
u - da÷
si ¾
e osi ¾
agn ¾
a´c przy maksimum twojego zadowolenia.
75
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron