AGH

Akademia Górniczo-Hutnicza

W Krakowie

Zespół nr 2

Sebastian Więcek

Grzegorz Figura

Adrian Ryczek

Tomasz Zakrzewski

LABORATORIUM ELEKRTOTECHNIKI

Wydział:

WIMiR

Rok akademicki:
2011/2012

Rok studiów:

I

Kierunek:

AiR

Grupa:

2

Temat ćwiczenia:

Badanie i pomiary układów trójfazowych
połączonych w gwiazdę i w trójkąt.

Data wykonania:

25.03.2012 12:00

Data oddania spr.:

01.06.2012

Data zaliczenia:

Ocena:

1. Cel ćwiczenia:

 Zapoznanie się ze specyfikacja przebiegów sinusoidalne zmiennych w układach trójfazowych

skojarzony w gwiazdę i trójkąt,

 Utrwalenie wiadomości o podstawowych relacjach między napięciami oraz prądami fazowymi i

przewodami,

 Pomiary mocy różnorodnie łącznych odbiorników trójfazowych z zastosowaniem rożnych układów

połączeń watomierzy.

2. Przebieg ćwiczenia:

I) Badany układ (rys.1) jest zasilany z sieci trójfazowej symetrycznej (dostępne są zaciski).
Układ dwóch watomierzy, czyli tzw. układ Arona mierzy całkowita moc czynna odbiornika
(P=P1+P2). Pozostałe trzy watomierze mierzą moce pobierane przez poszczególne
fazy odbiornika. Amperomierze A

R

, A

S

, A

T

mierzą prądy przewodowe. Voltomierze V

R

, V

S

,

V

T

mierzą napięcia fazowe na odbiorniku. Układ obciążony odbiornikami Z

R

, Z

S

, Z

T

.

Pomiary wykonać dla różnych wartości obciążenia.

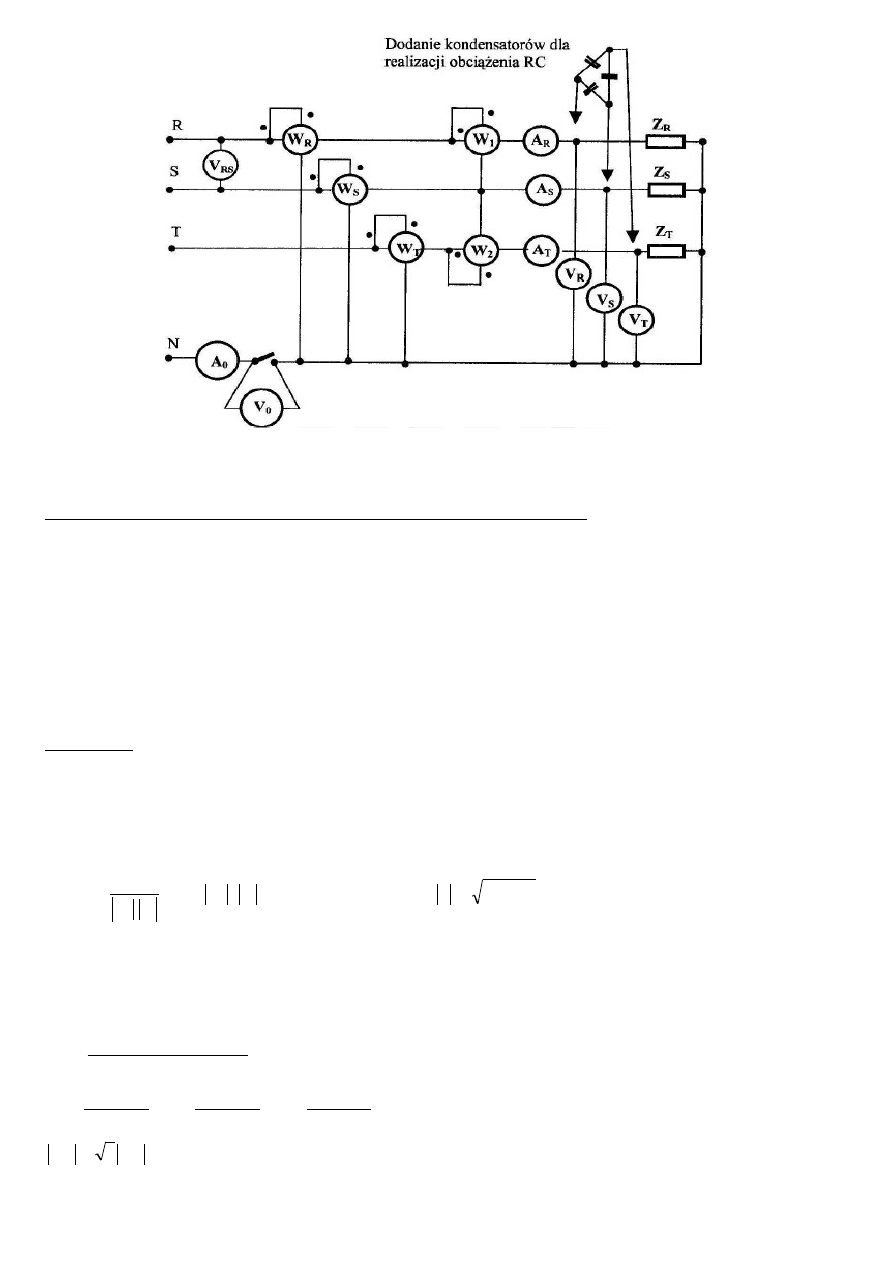
Rys.1 Układ pomiarowy.

3. Wykaz przyrządów potrzebnych do wykonania ćwiczenia:

 Tablica pomiarowa zawierająca: układ 3 watomierzy oraz amperomierze i voltomierze

wg powyższego schematu (rys.1),



Dwa watomierze analogowe (W

1

, W

2

),



Układ grzałek (Z

R

, Z

S

, Z

T

).

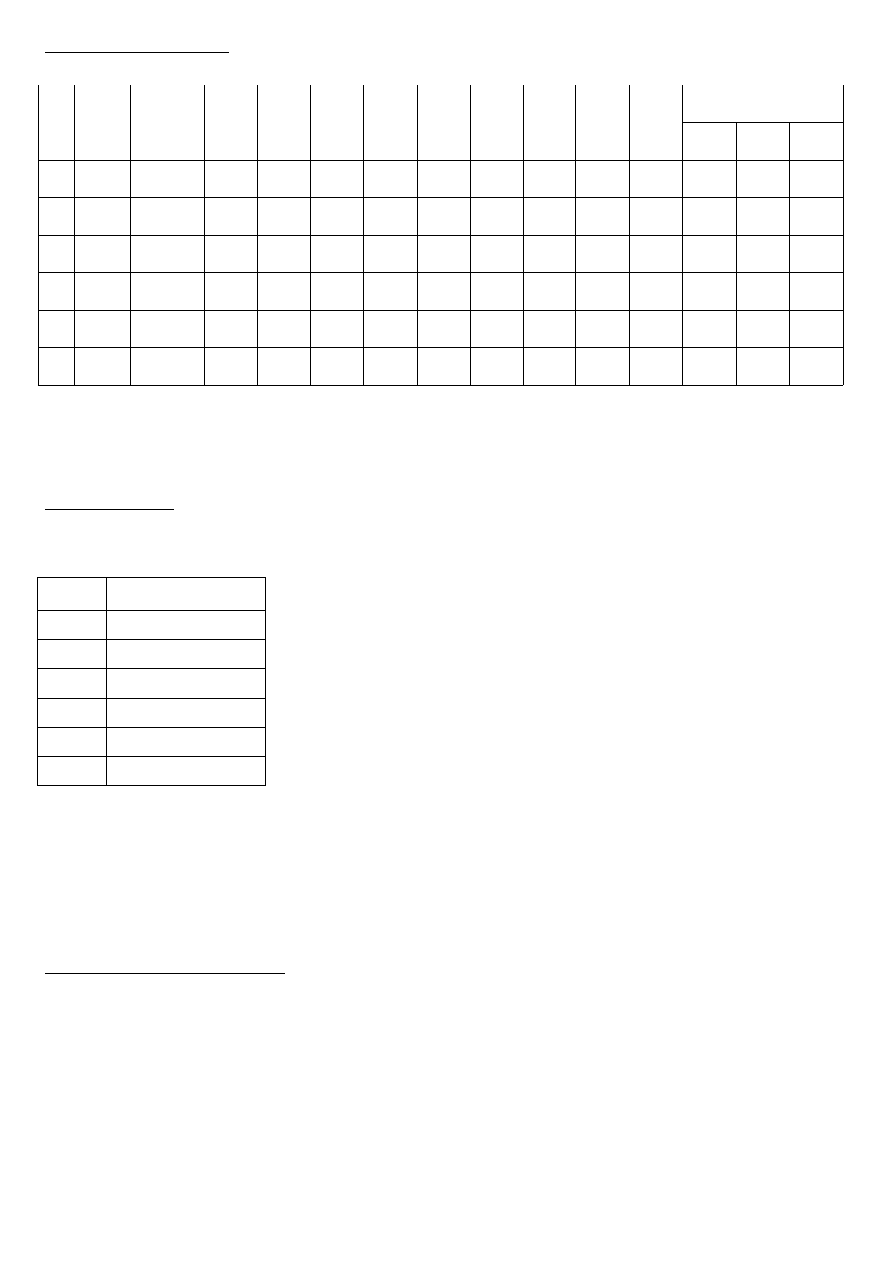
4. Wzory:

Dla odbiorników RL lub RC dla każdej fazy obliczamy:

Wzory z teorii dla połączenia w gwiazdę :

F

P

F

P

C

C

C

B

B

B

A

A

A

C

B

A

C

C

B

B

A

A

I

I

U

U

Z

U

E

I

Z

U

E

I

Z

U

E

I

Y

Y

Y

Y

E

Y

E

Y

E

U

=

=

−

=

−

=

−

=

+

+

+

+

=

3

,

,

0

0

0

0

2

,

3

,

,

sin

,

cos

Q

P

S

Q

Q

Q

Q

I

U

Q

I

U

P

i

i

i

i

i

i

i

i

+

=

+

+

=

⋅

⋅

=

⋅

=

ϕ

ϕ

5. Tabela pomiarów:

Lp. U

RS

[V]

I

R

[A]

I

S

[A]

I

T

[A]

I

0

[A]

U

R

[V]

U

S

[V]

U

T

[V]

U

0

[V]

P

1

[W]

P

2

[W]

Stany:

Z

R

Z

S

Z

T

1.

220

0

0

2.65 MAX 127

127

127

0

0

515

0

0

1

2.

220

0

2,75

2.6

MAX 127

127

127

0

0

510

0

1

1

3.

220

1

0

2.7

2.25

127

127

127

0

290

515

1

0

1

4.

220

1.1

2,7

2.65

1.20

127

127

127

0

290

515

1

1

1

5.

220

2.8

0

2.7

MAX 127

127

127

0

550

520

2

0

1

6.

220

2.8

2,7

2.65

0.2

127

127

127

0

550

520

2

1

1

5. Obliczenia :

Lp.

P= P

1

+P

2

1.

515

2.

510

3.

805

4.

805

5.

1070

6.

1070

6. Wykresy wektorowe:

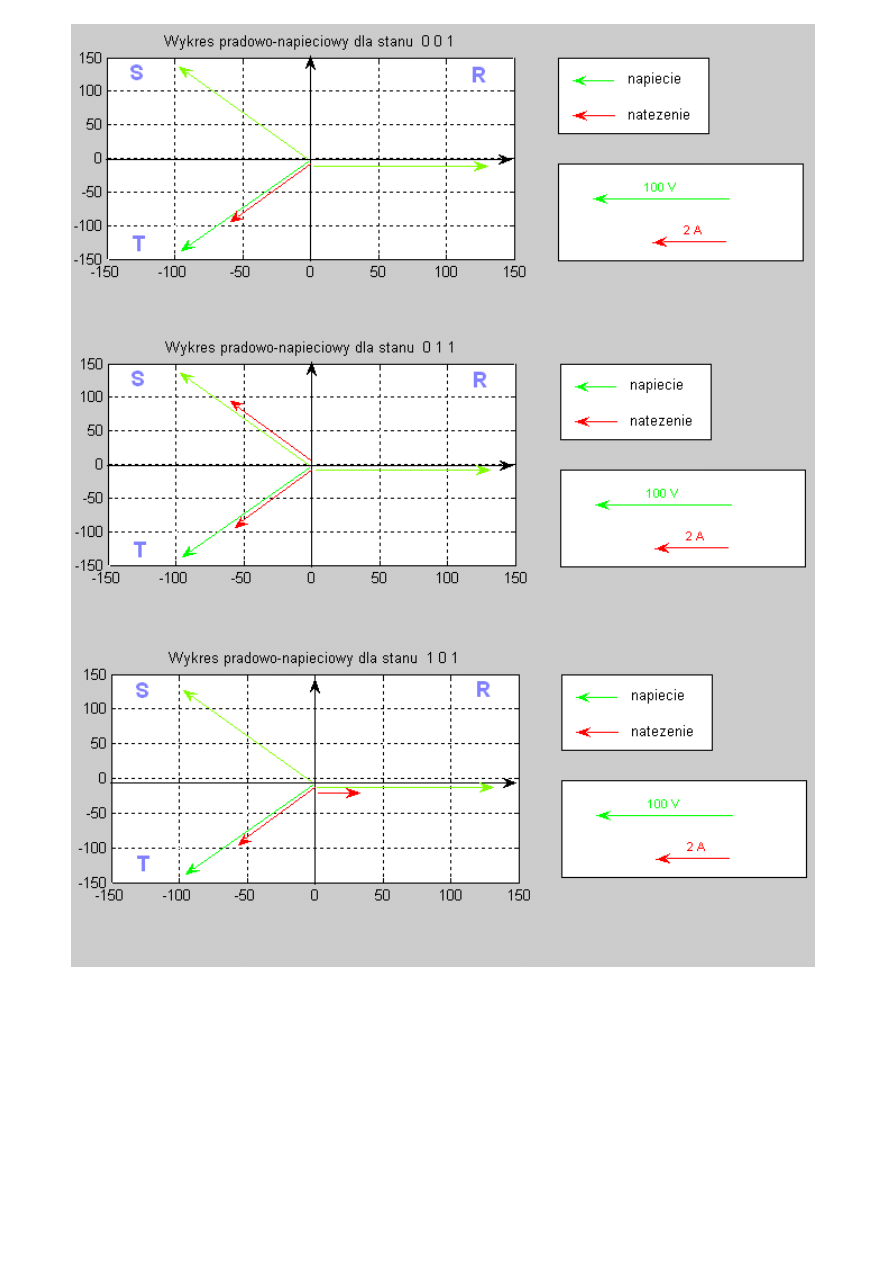
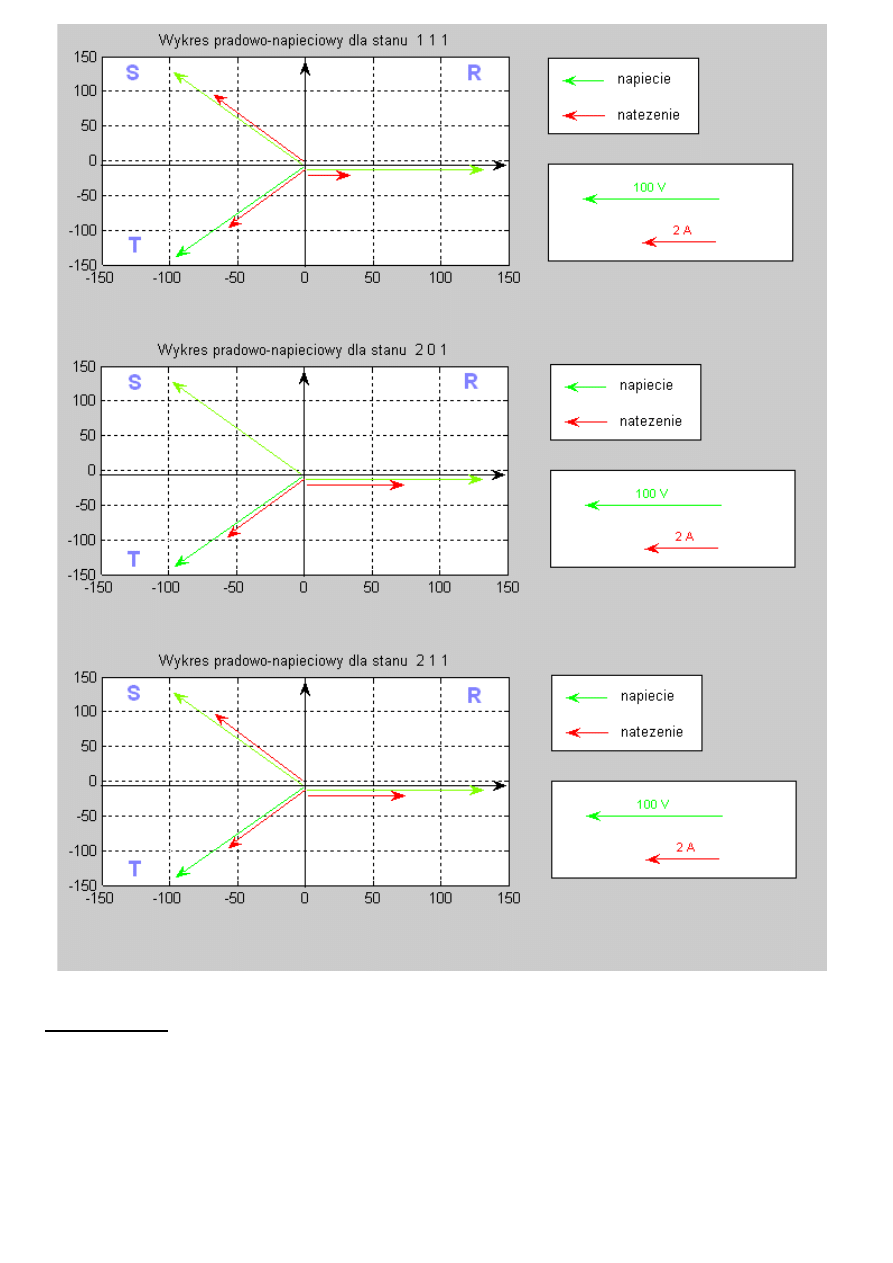
7. Wnioski :

W układach symetrycznych prądy w przewodach mają tą samą wartość dla wszystkich faz. W

przewodzie zerowym ( neutralnym ) prąd nie płynie, obecność tego przewodu nie ma wpływu na pracę układu
symetrycznego. W układach niesymetrycznych prądy w przewodach mają różną wartość dla wszystkich faz, w
przewodzie zerowym płynie prąd. W naszym przypadku prądy w poszczególnych fazach miały rożne wartości
prócz dla stanu 2 1 1, gdzie można zauważyć „prawie” symetryczny układ (I

R

=I

S

=I

T

, I

0

~0A).

Watomierze W

1

,W

2

pokazują różne wartości mocy, suma ich wskazań jest mocą czynną odbiorników jest to

tzw. układ Arona. Watomierze W

R

, W

S

, W

T

, były zamontowane na tablicy pomiarowej lecz nie widzieliśmy

ich wyników. Wyniki z watomierzy W

R

, W

S

, W

T

pozwoliłyby wyliczyć moc bierną i pozorną, a przede

wszystkim kąt przesunięcia φ. Wykonane wykresy są więc tylko czysto teoretyczne. Na rysunku nr 1
zastosowano „pare” kondensatorów, które pełnią rolę kompensatorów mocy. Dąży się w takim układzie, aby
kąt, a dokładnie sinφ był równy 1, co za tym idzie moc bierna będzie równa mocy czynnej
(U*I*sinφ = Q = P = U*I*cosφ).