Podstawy statystyki, ekonomiki i organizacji 

 
 
 
 
 
 
 
 
 
 
 
 
 

Graficzna prezentacja  

danych statystycznych 

 

 

 

 

 

 

 

 

 

 

2 

W  czasie  opracowywania  materiał  statystyczny  zostaje  uporządkowany  i 

pogrupowany. Rezultatem opracowania materiału jest przedstawienie w odpowiedniej formie 

wyników badania statystycznego, czyli prezentacja danych statystycznych. 

Istnieją trzy podstawowe metody prezentacji danych statystycznych: 

  przedstawienie w układzie tabelarycznym, czyli w tablicach statystycznych; 

  przedstawienie graficzne, czyli w formie wykresów statystycznych; 

  włączenie do tekstu opisowego. 

W  praktyce  są  stosowane  także  różne  mieszane  metody  prezentacji  danych 

statystycznych,  będące  kombinacją  wymienionych  metod  podstawowych.  Wybór  metody 

prezentacji  danych  statystycznych  powinien  zależeć  w  każdym  wypadku  od  rodzaju  danych 

wynikowych, które mają być przedstawione, oraz od celu, któremu służy prezentacja danych. 

Graficzna  prezentacja  danych  statystycznych  oznacza  obrazowanie  ich  za  pomocą 

wykresów.  Wykres  jest  wtórnym  przedstawieniem  danych  liczbowych  zawartych  w  tablicy 

statystycznej.  

Wykresy  zyskały  szerokie  zastosowania,  zarówno  przy  prezentacji  surowego,  jak  i 

opracowanego materiału statystycznego, przede wszystkim dzięki temu, że: 

 

prezentują badane zjawisko bardziej bezpośrednio, przejrzyście i obrazowo niż liczby, 

 

szybciej  przemawiają  do  wyobraźni  odbiorcy  i  pozwalają  zorientować  się  w  całości 

rozpatrywanych zagadnień; 

 

są doskonałym narzędziem popularyzowania i propagowania treści w nich zawartych. 

Warunkiem odegrania przez wykresy pozytywnej roli w prezentacji wyników badania 

statystycznego  jest bardzo staranne wykonanie graficzne, dokładne odmierzenie odcinków  i 

figur. Podobnie jak tablica, wykres składa się z kilku części. Najważniejsze z nich to: tytuł, 

pole  wykresu  i  legenda,  w  której  podaje  się  wyjaśnienia  dotyczące  skali,  stosowanych 

symboli, znaków i barw oraz informacje o źródłach danych. 

W  badaniach  statystycznych  najczęściej  stosowanymi  metodami  graficznymi  są: 

metoda liniowa, powierzchniowa, obrazkowa, ilościowa i ilościowo-symbolowa, kartogramy 

oraz wykresy w układzie współrzędnych. 

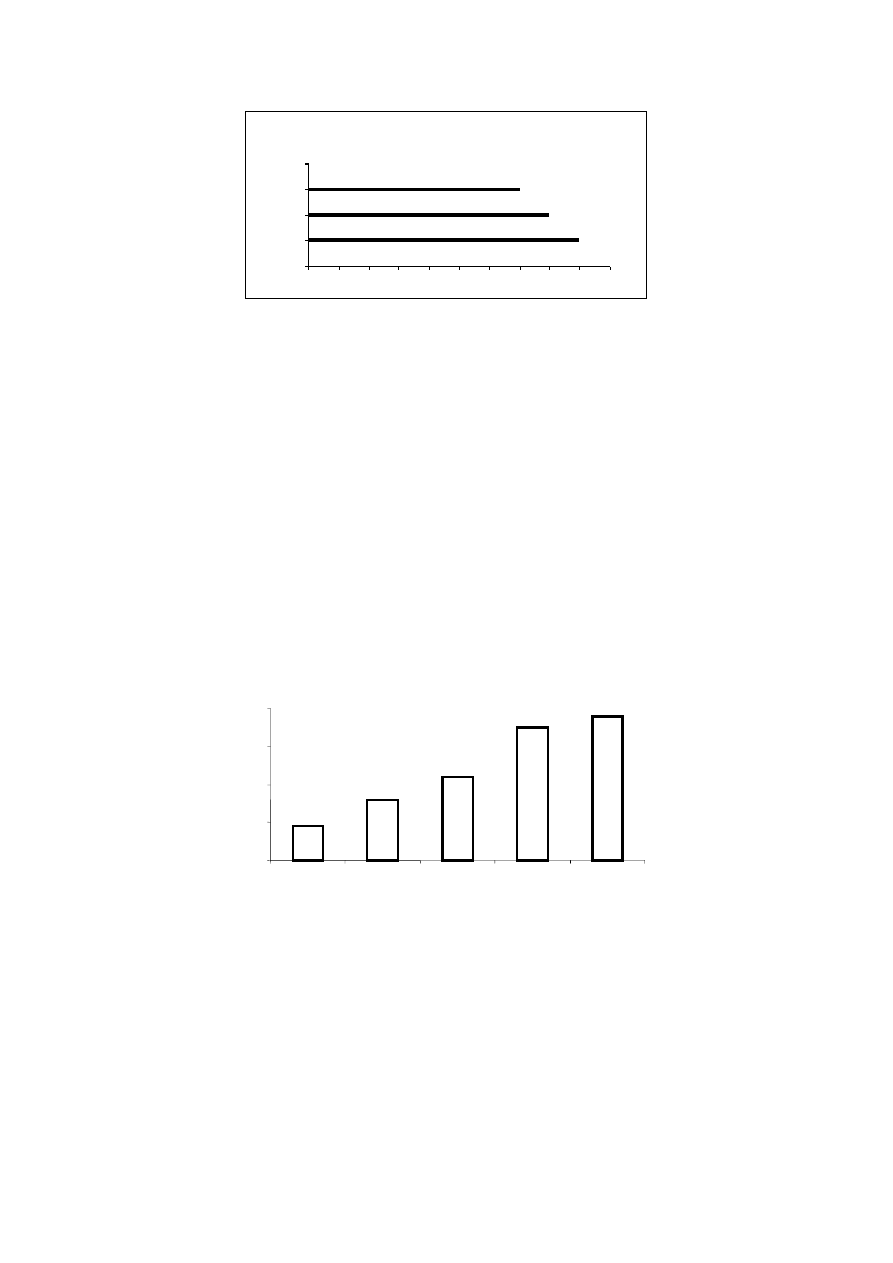
Najprostszym  sposobem  graficznego  przedstawienia  wielkości  statystycznej  jest 

metoda  liniowa,  polegająca  na  narysowaniu  odcinków  linii  prostych,  których  długość 

odpowiada  (w  odpowiedniej  skali)  liczebności  porównywanych  zbiorowości.  Linie  te  mogą 

być narysowane w płaszczyźnie rysunku poziomo (rys. 1) lub pionowo. 

 

3 

Relacja przeciętnych miesięcznych wynagrodzeń 

netto w sferze budżetowej do wynagrodzeń w sektorze 

przedsiębiorstw

1989

1992

1995

1998

2001

0

10

20

30

40

50

60

70

80

90

100

 

Rys. 1 Wykres liniowy 

 

Metoda  powierzchniowa  polega  na  stosowaniu  wykresów  powierzchniowych, 

charakteryzujących zbiorowość lub zjawiska za pomocą powierzchni figur płaskich. Metoda 

ta stosowana jest w prezentacji struktury zbiorowości lub zjawiska, do obrazowania szeregów 

rozdzielczych  oraz  prezentacji  wielkości  (liczebności)  niektórych  zjawisk.  Generalnie 

obowiązującą  zasadą  w  stosowaniu  wykresów  powierzchniowych  jest  zachowanie 

proporcjonalności powierzchni figur do prezentowanych wielkości. 

Szczególnie powszechnie stosowane są wykresy oparte na wydłużonych prostokątach, 

zwane wykresami słupkowymi. Wykonywane one są w ten sposób, że rysuje się równoległe 

do  siebie  prostokąty  luźno  stojące  (rys.  2)  lub  przylegające  do  siebie.  Prostokąty  te  mają 

jednakową szerokość, a wysokości proporcjonalne do liczebności, które ilustrują.  

Rys. 2 Wykres słupkowy 

 

Innym  rodzajem  wykresu  słupkowego  jest  wykres,  w  którym  zamieszczamy 

prostokąty  jednakowej  wysokości.  Szerokości  podstaw  tych  prostokątów  są  różne, 

proporcjonalne do ilustrowanych liczebności.  

Inną  postacią  wykresów  powierzchniowych  są  wykresy  kołowe,  a  także  (stosowane 

bardzo rzadko) kwadratowe i trójkątne. 

Powierzchnia  kołowa  jest  odpowiednikiem  ilustrowanej  przez  nie  wielkości  danej 

zbiorowości  prezentowanej  na  wykresie.  Istota  sporządzenia  wykresu  kołowego  polega  na 

Ilość książeczek oszczędnościowych PKO w tys.  

w latach 1960 – 1980 

0

 

10000

 

20000

 

30000

 

40000

 

1960

 

1965

 

1970

 

1975

 

1980

 

 

4 

ustaleniu  długości  promienia  dla  każdego  koła,  od  którego,  zgodnie  ze  wzorem  πr

2

,  zależy 

jego powierzchnia obrazująca określoną wielkość. Punktem wyjścia  jest określenie długości 

promienia dla koła najmniejszego.  

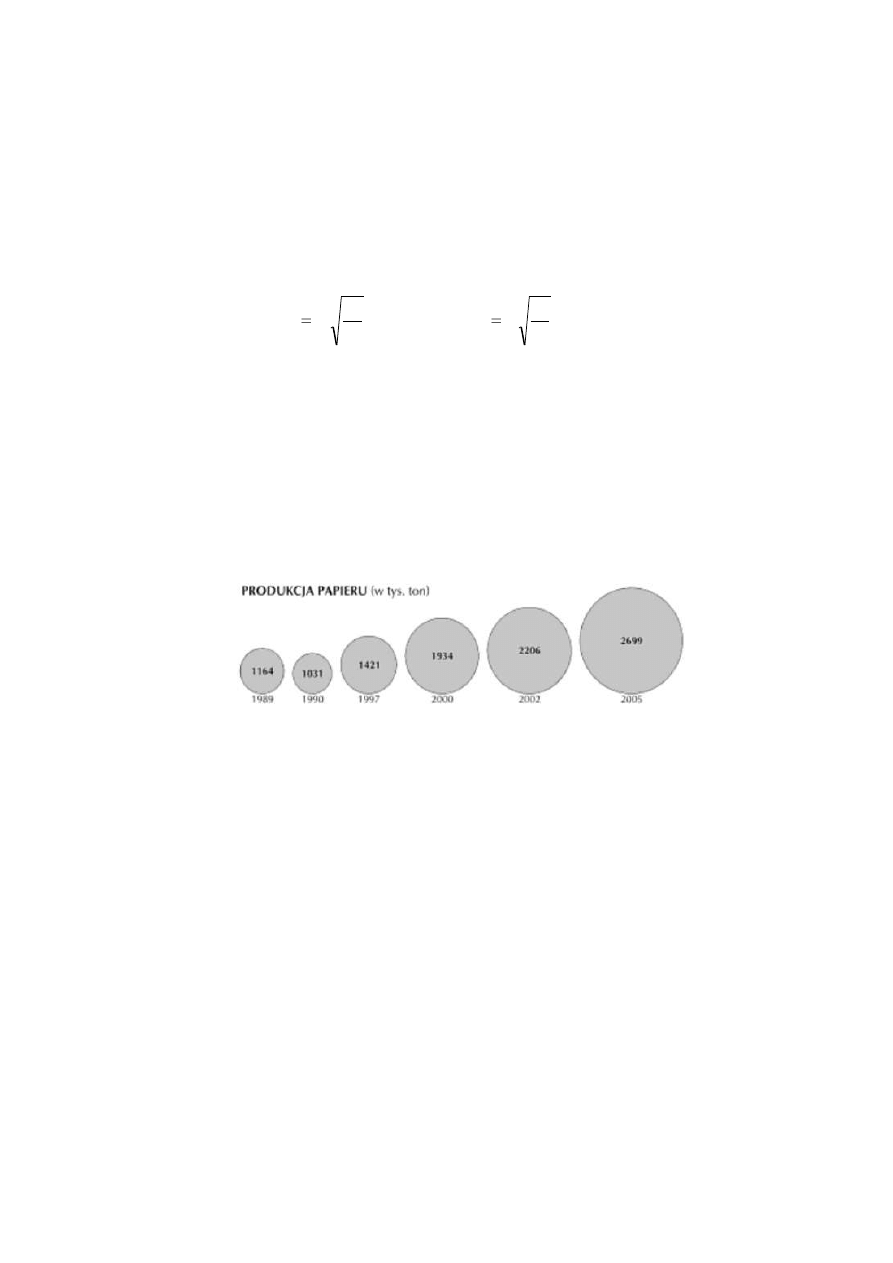
Długość  promienia  poszczególnych  kół  obliczamy  z  pierwiastka  kwadratowego 

kolejnej  liczebności  do  liczebności  najmniejszej,  dla  której  przyjęta  została  najmniejsza 

długość promienia według wzoru: 

                                       

1

2

2

1

n

n

r

r

                       

1

3

1

3

n

n

r

r

 

gdzie: 

r

1 

– promień najmniejszego koła; 

r

2

, r

3

, itd. – promienie kolejnych kół; 

n

1

 – liczebność najmniejszego koła; 

n

2

, n

3

, itd. – liczebność kolejnych kół; 

 

Wykresy  kołowe,  ilustrujące  dane  o  wielkości  produkcji  papieru  w  Polsce  w  latach 

1989, 1992, 1997, 2000, 2005 przedstawiono na rysunku 3.  

 

Rys. 3 Wykresy kołowe 

 
 

Wykresy  słupkowe  i  kołowe  są  również  przydatne  do  graficznej  ilustracji  struktury 

zbiorowości,  czyli  do  ilustrowania  podziału  tej  zbiorowości  na  części  proporcjonalne  do 

wyróżnionych podzbiorowości składowych zbiorowości głównej (przedstawionego zjawiska). 

W  metodach,  w  których  zdecydowano  się  zilustrować oprócz  struktury  również  liczebność, 

rysuje  się  słupki,  rzadziej  koła,  proporcjonalne  do  liczebności,  a  następnie  dzieli  się  je  na 

części  proporcjonalne  do  liczebności  wyróżnionych  podzbiorowości  prezentowanej 

zbiorowości głównej. 

 

Ilustracją  wielkości  i  struktury  obrotu  Obligacji  Skarbu  Państwa  o  oprocentowaniu 

stałym w latach 2002 i 2005 jest rysunek 4. 

 

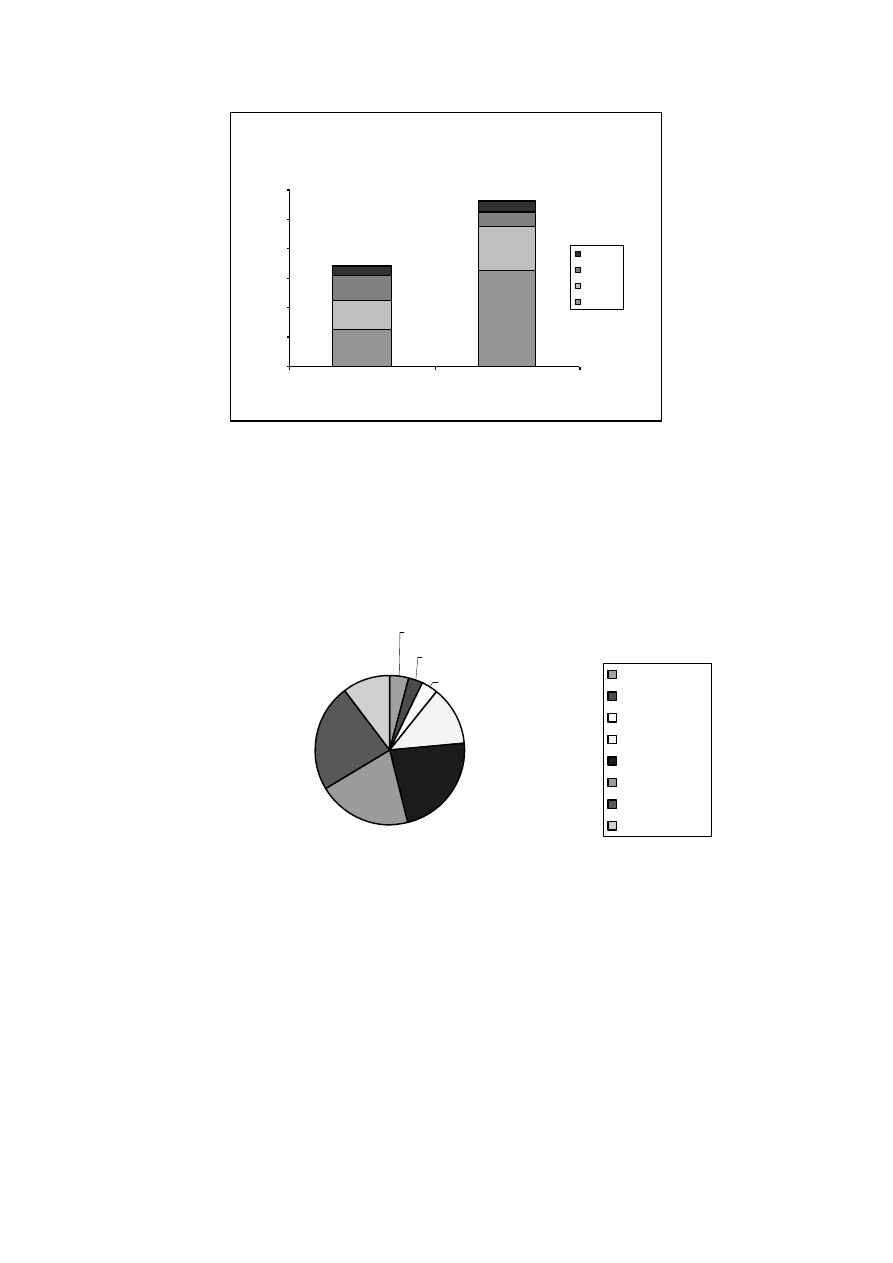
5 

Wielkość i struktura obrotów  na giełdow ym rynku 

obligacji w  latach 2002 i 2005

250

646

200

303

163

102

67

73

0

200

400

600

800

1000

1200

2002 r.

2005 r.

Lata

W

ie

lk

o

ś

ć

 o

b

ro

tu

 w

 m

ld

 z

ł

20-letnie

10-letnie

5-letnie

2-letnie

 

Rys. 4 Wykres słupkowy ilustrujący strukturę zbiorowości 

 
 

W  metodach,  w  których  ilustruje  się  tylko  strukturę,  rysujemy  prostokąt  lub  koło,  a 

następnie  dzielimy  je  proporcjonalnie  do  wyróżnionych  podzbiorowości  (części) 

przedstawionej zbiorowości głównej (rys. 5). 

Struktura niepełnosprawnych kobiet w 2002 r.

4,20%

2,90%

3,70%

12,70%

22,70%

20,30%

23,10%

10,40%

0-19 lat
20-29
30-39
40-49
50-59
60-69
70-79
80 lat i więcej

 

Rys. 5 Wykres kołowy obrazujący strukturę badanego zjawiska 

 
 

Jednym  z  bardziej  efektownych,  lecz  niezbyt  dokładnych,  sposobów  prezentacji 

danych  statystycznych  jest  metoda  obrazkowa.  W  metodzie  tej  przedstawia  się  wielkość 

zjawiska za pomocą odpowiedniej wielkości obrazka ilustrującego to zjawisko. Na przykład 

liczbę  odbiorników  telewizyjnych  w  kilku  krajach  prezentujemy  przez  narysowanie  dla 

każdego kraju telewizora odpowiedniej wielkości. 

 

Metoda  ilościowa  polega  na  tym,  że  wielkość  zjawiska  jest  prezentowana  przez 

powtarzanie  dowolnego  znaku,  który  wyraża  określoną  liczbę  jednostek.  Jeśli  np.  jeden 

 

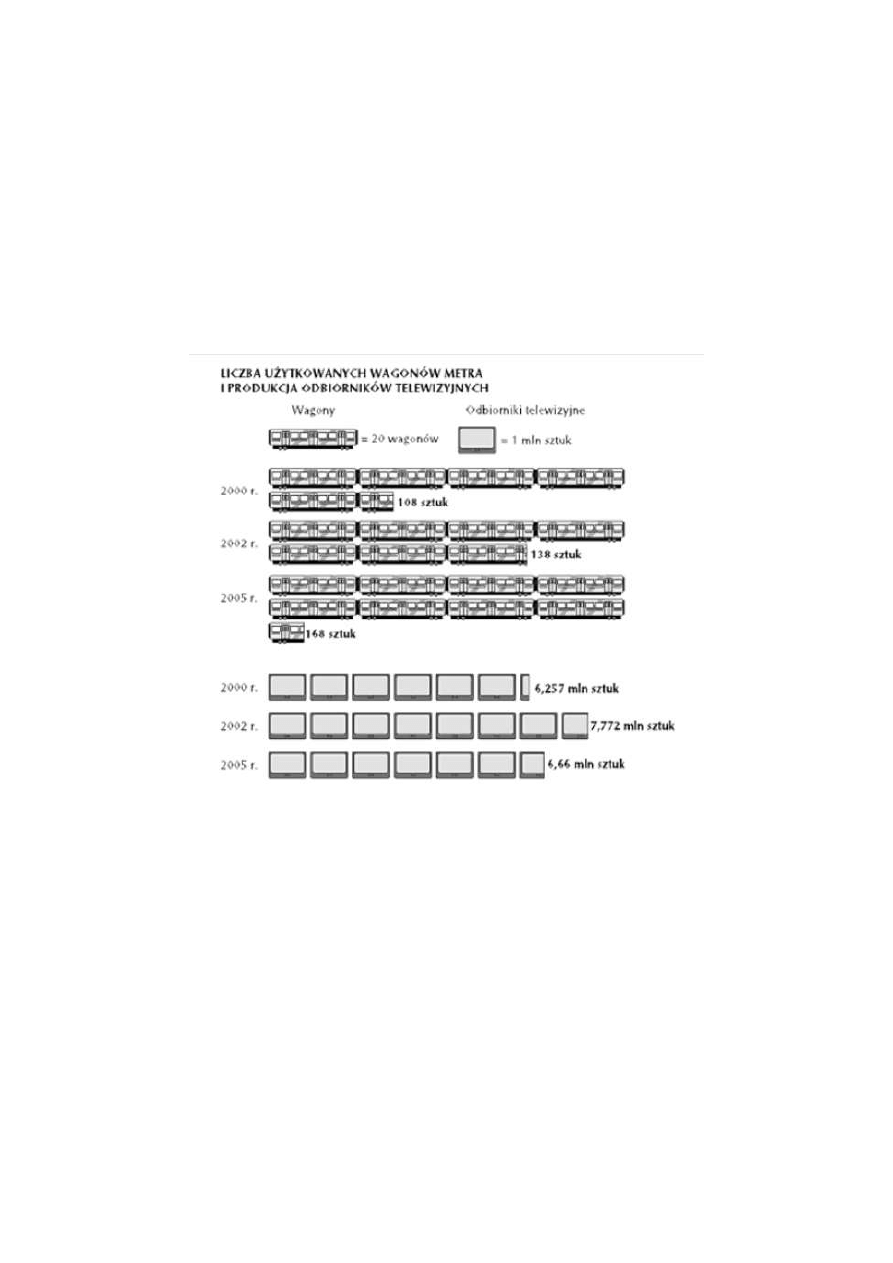
6 

przyjęty znak oznacza 1000 robotników, to w celu przedstawienia 10 000 robotników trzeba 

taki znak powtórzyć 10 razy. Metoda ta jest wyrazista i poprawna, niestety nie jest to metoda 

całkowicie dokładna. 

 

Metoda  ilościowo-symbolowa  (zwana  również  metodą  wiedeńską)  jest  odmianą 

metody  ilościowej.  Zamiast  znaków  stosuje  się  małe  rysunki-symbole,  które  przedstawiają 

prezentowane  zjawisko.  Warunkiem  stosowania  tej  metody  jest  staranny  dobór  rysunków-

symboli  oraz  staranne  wykonanie  graficzne.  Przykładem  wykresu  wykonanego  metodą 

ilościowo-symbolową jest rysunek 6. 

 

Rys. 6 Metoda ilościowo-symbolowa prezentacji danych statystycznych 

 

Często w celach popularyzatstorskich, mając na uwadze ułatwienie odbioru (przyjazny 

charakter prezentacji materiału statystycznego), stosowane są wykresy obrazujące poziom lub 

natężenie zjawiska na tle mapy obszaru, którego dane zjawisko dotyczy. Są to tzw. wykresy 

mapowe – kartogramy (rys. 7), które przedstawiają terytorialne rozmieszczenie zbiorowości 

lub  zjawiska.  Są  one  budowane  w  oparciu  o  mapę  i  zwykle  łączą  w  sobie  równocześnie 

elementy wykresów liniowych, powierzchniowych, punktowych lub obrazkowych. 

Wykresy  mapowe  wykorzystywane  są  do  prezentacji  wielkości  oraz  natężenia  (na 

jednostkę  powierzchni  lub  też  na  1000  ludności)  danego  zjawiska  w  wyodrębnionych 

jednostkach  terytorialnych.  Jest  to  znana  i  powszechnie  stosowana  forma  graficznej 

prezentacji zbiorowości lub zjawisk.  

 

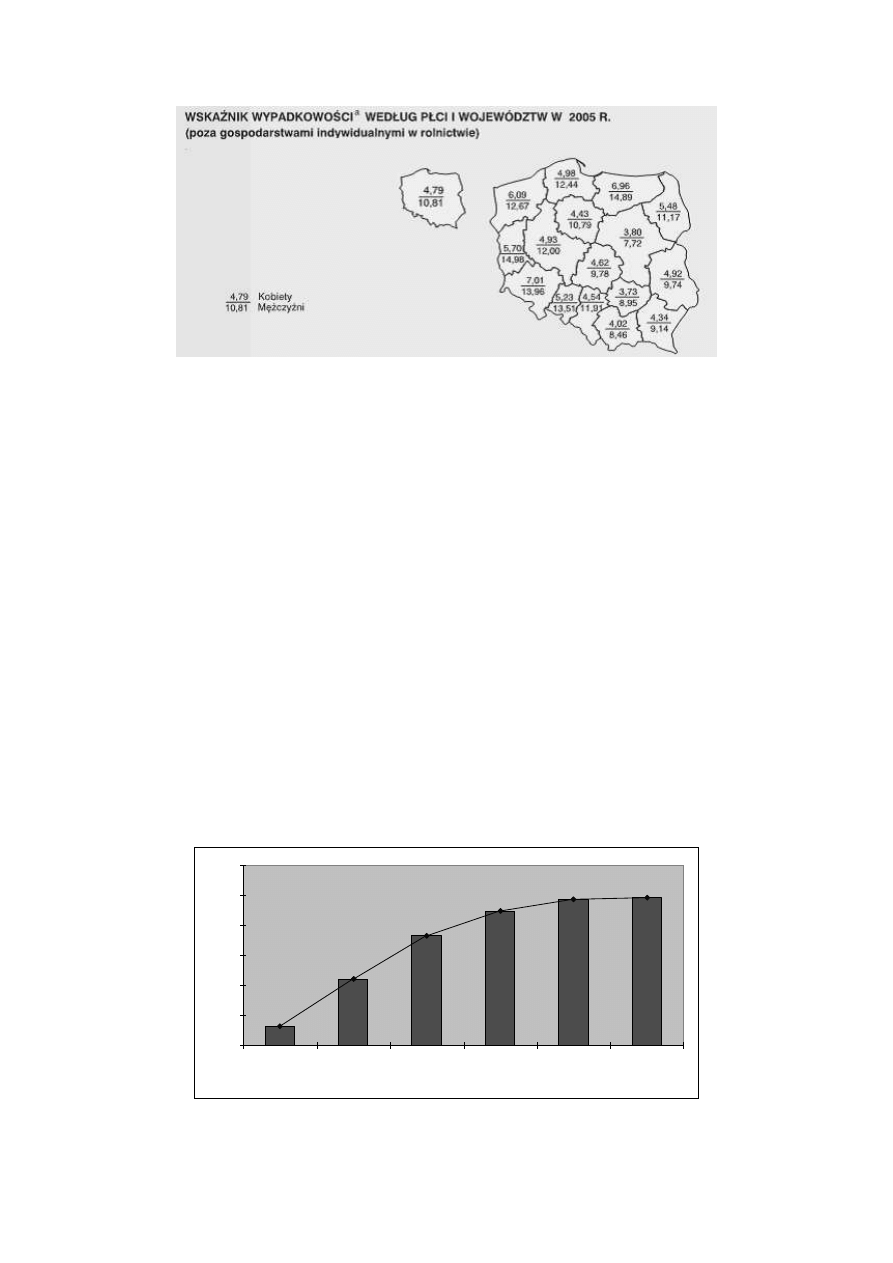
7 

 

Rys. 7 Kartogram 

 
 

Do graficznego przedstawiania liczbowych danych w statystyce są również stosowane 

wykresy w układzie współrzędnych – histogramy i diagramy.  

Diagram  jest  łamaną powstałą przez połączenie punktów, których współrzędnymi są 

środki przedziałów klasowych i odpowiadające im liczebności (częstości lub gęstości).  

Histogram  to  wykres,  w  którym  prostokąty  przylegają  do  siebie,  ich  podstawy  są 

określone  rozpiętością  przedziałów,  a  wysokości  –  liczebnością  przedziałów.  Tak  więc 

powierzchnia  poszczególnych  prostokątów  pozostaje  w  tym  samym  stosunku  do  ogólnej 

powierzchni  histogramu,  co  liczebności  poszczególnych  przedziałów  klasowych  do  ogólnej 

liczebności szeregu rozdzielczego. Budując histogram na podstawie szeregu rozdzielczego o 

nierównych przedziałach klasowych należy najpierw sprowadzić liczebności przedziałów do 

porównywalności,  tzn.  obliczyć  liczebności  przypadające  w  danym  przedziale  na  jednostkę 

jego rozpiętości.  

Na każdym histogramie może być opisany diagram. Możemy go skonstruować łącząc 

linią ciągłą środki górnych boków prostokątów w histogramach struktury i dynamiki (rys.8). 

0

10

20

30

40

50

60

1980

1985

1990

1995

2000

2005

Lata

m

ln 

os

ób

 

Rys. 8 Wykres w układzie współrzędnych 

 

 

8 

Literatura: 

 

1.  R. Seidel, Statystyka, Podręcznik z ćwiczeniami, Wydawnictwo eMPi

2

, Poznań, 2000. 

2.  Z. Peuker, Statystyka, Podręcznik dla liceum ekonomicznego, Wydawnictwo Szkolne 

i Pedagogiczne, Warszawa, 1987. 

3.  T. Michalski, Statystyka, Wydawnictwo Szkolne i Pedagogiczne, Warszawa, 2008.