K
INEMATYKA RUCHU POSTĘPOWEGO
1. PRĘDKOŚĆ STAŁA – jest to stosunek drogi do czasu jej przebycia. Ciało poruszające
się z taką prędkością przebywa w każdej jednostce czasu taką samą drogę.
[ ] [
]
2. PRĘDKOŚĆ ŚREDNIA - prędkość średnią
definiujemy jako stosunek całkowitej
przebytej drogi
do całkowitego czasu
,od początku do końca ruchu.
[
] [
]
– odległość przebyta w czasie .
3. PRĘDKOŚĆ CHWILOWA – stosunek drogi do czasu jej pokonania. Prędkość chwilowa
jest to jakby prawie prędkość średnia, ale wyznaczana w ciągu bardzo krótkiego
przedziału czasu (ściśle rzecz ujmując, powinniśmy wziąć przedział czasu
nieskończenie bliski zera). Można ją liczyć na dwa sposoby:
POSTAĆ RÓŻNICZKOWA
POSTAĆ Z GRANICĄ
POSTAĆ SKALARNA
[ ] [
]
[ ] [
]
POSTAĆ WEKTOROWA
⃗
⃗
[ ] [
]
⃗
⃗
[ ] [
]
4. PRZYSPIESZENIE JEDNOSTAJNE – występuje w ruchu jednostajnie przyspieszonym
prostoliniowym. W przyspieszeniu jednostajnym wartość, kierunek i zwrot wektora
przyspieszenia są stałe.
Stała wartość przyspieszenia oznacza, że w ciągu każdej sekundy szybkość (wartość
prędkości) wzrasta o tyle samo:
⃗⃗⃗
⃗⃗⃗
[ ] [
]
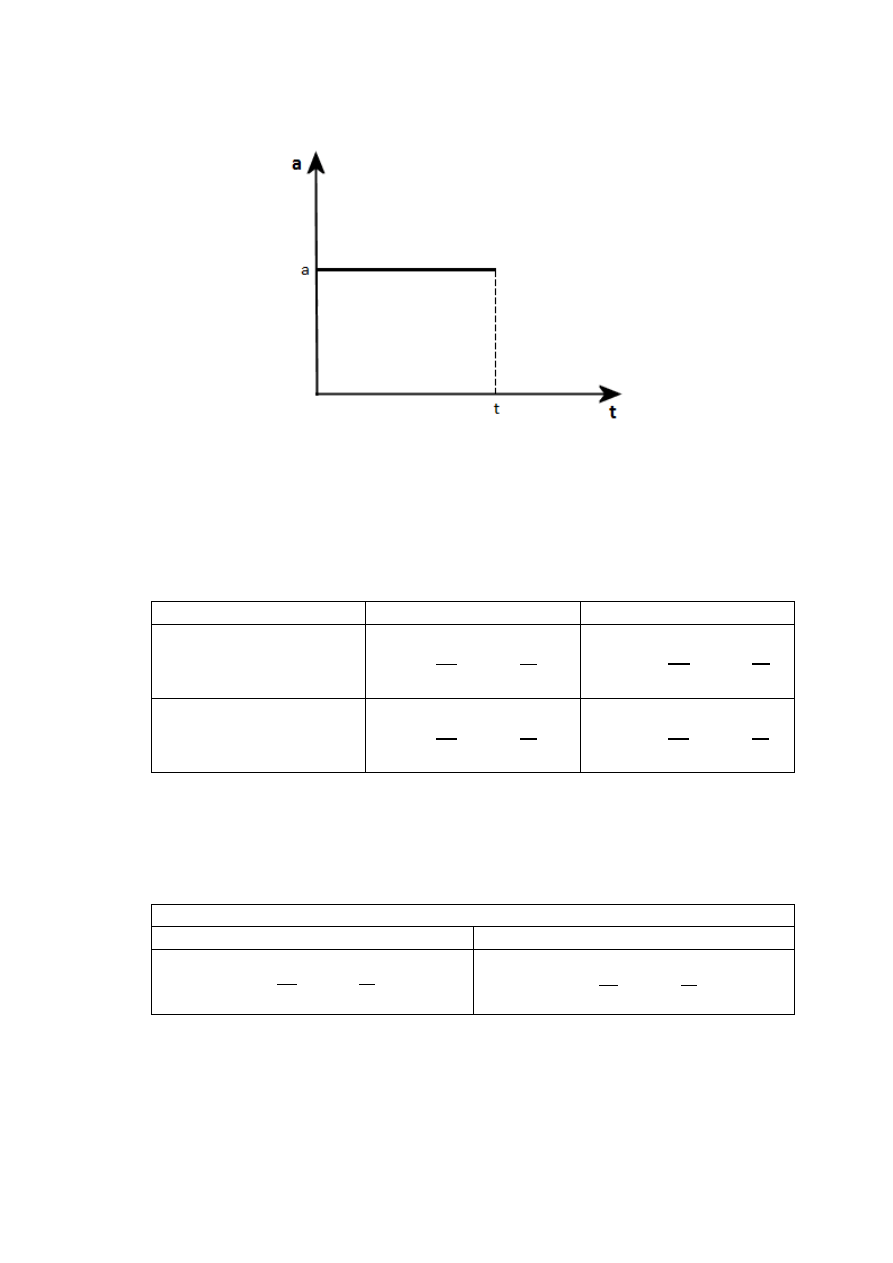
Wartość przyspieszenia nie zmienia się, co obrazuje wykres:
5. PRZYSPIESZENIE CHWILOWE – występuje w ruchu jednostajnie przyspieszonym
zmiennym. Przyspieszenie chwilowe liczone dla bardzo małych (właściwie
nieskończenie małych) odcinków drogi (lub nieskończenie małych przedziałów czasu).
Matematycznie zapisuje się to albo z użyciem pojęcia granicy, albo za pomocą notacji
różniczkowej.
POSTAĆ RÓŻNICZKOWA
POSTAĆ GRANICY
POSTAĆ SKALARNA
[ ] [
]
[ ] [
]
POSTAĆ WEKTOROWA
⃗
⃗
[ ] [
]
⃗
⃗
[ ] [
]
6. RUCH JEDNOSTAJNY, PROSTOLINIOWY – ruch ze stałą (co do wartości i kierunku)
prędkością. Torem ruchu jest linia prosta. W ruchu jednostajnym prędkość nie
zmienia się w czasie.
WZÓR NA PRĘDKOŚĆ
POSTAĆ SKALARNA
POSTAĆ WEKTOROWA
[ ] [
]
⃗
⃗
[ ] [
]
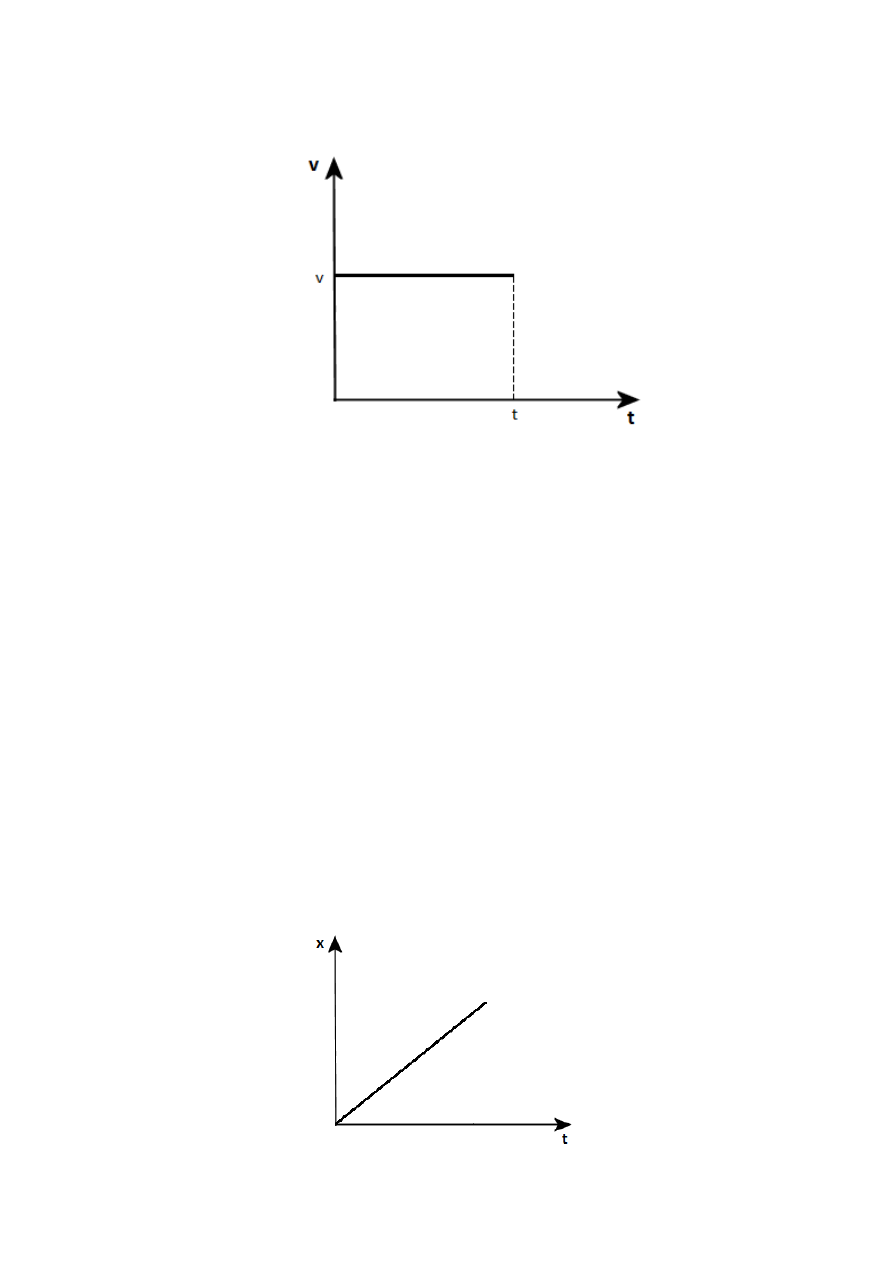
Wykres zależności prędkości od czasu:
W ruchu jednostajnym droga w każdej sekundzie przyrasta o tę samą ilość metrów.
[ ] [ ]
W niektórych przypadkach mówimy o położeniu ciała zamiast o drodze.
Ciało znajdowało się początkowo w punkcie
po czym przemieszczało się z
prędkością przez czas . Znając te wielkości, możemy podać, w jakiej odległości (od
jakiegoś miejsca) ciało znajduje się po wykonaniu ruchu - obliczamy, jaką drogę
pokonało oraz dodamy początkową odległość.
[ ] [ ]
Drogę i położenie możemy używać zamiennie - dają nam przecież tę samą informację,
tzn. o jaką odległość przemieściło się ciało.
Wykres zależności drogi od czasu:
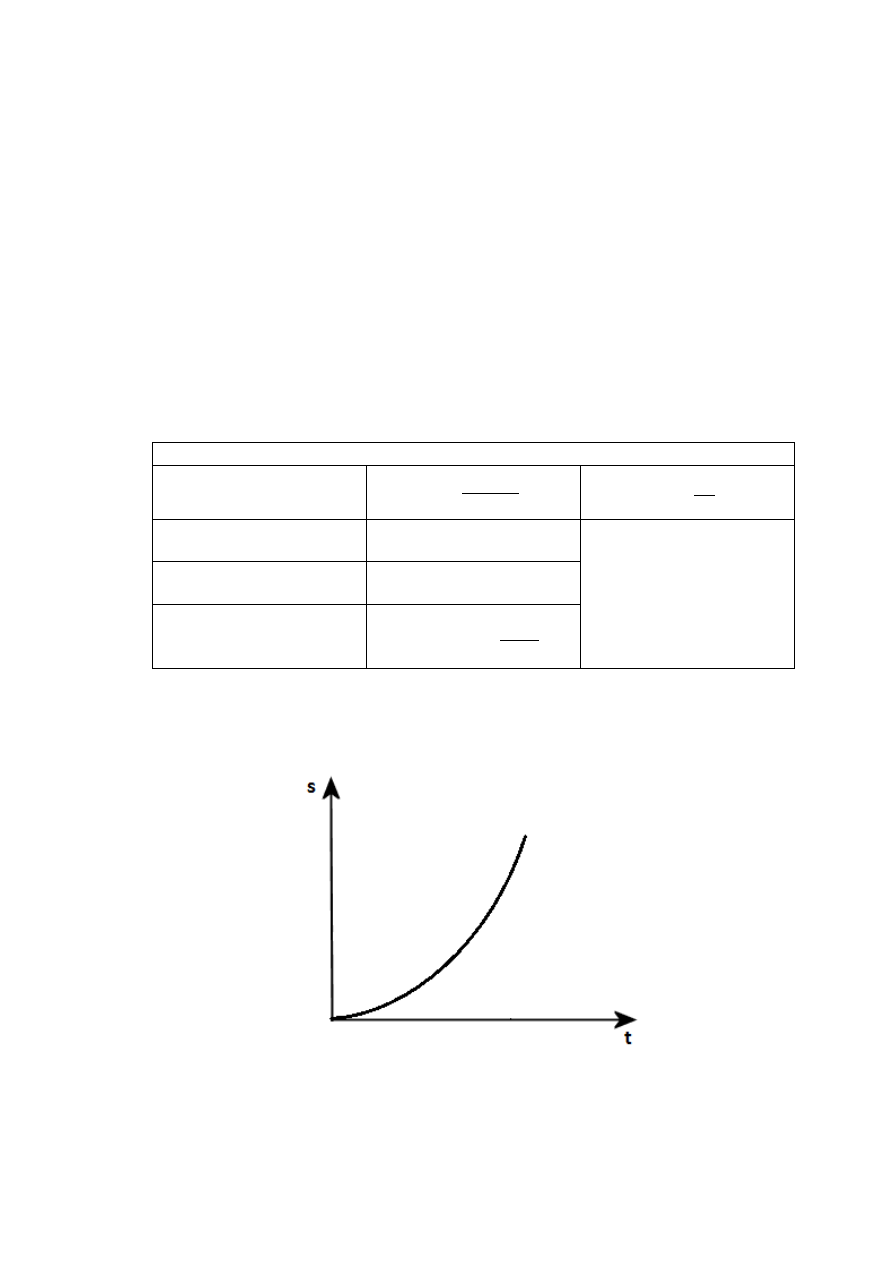
7. RUCH JEDNOSTAJNIE ZMIENNY – ruch prostoliniowy, w którym wartość
przyspieszenia jest stała.
Dzielimy go na RUCH JEDNOSTAJNIE PRZYSPIESZONY i RUCH JEDNOSTAJNIE
OPÓŹNIONY.
RUCH JEDNOSTAJNIE PRZYSPIESZONY – ruch, w którym prędkość ciała zwiększa się
o jednakową wartość w jednakowych odstępach czasu. Ciało takie ma przyspieszenie
o stałej wartości, a jego kierunek i zwrot są równe kierunkowi i zwrotowi prędkości
tego ciała.
WZORY
PRZYSPIESZENIE
PRĘDKOŚĆ KOŃCOWA
PRZYROST PRĘDKOŚCI
DROGA
Wykres zależności drogi od czasu:
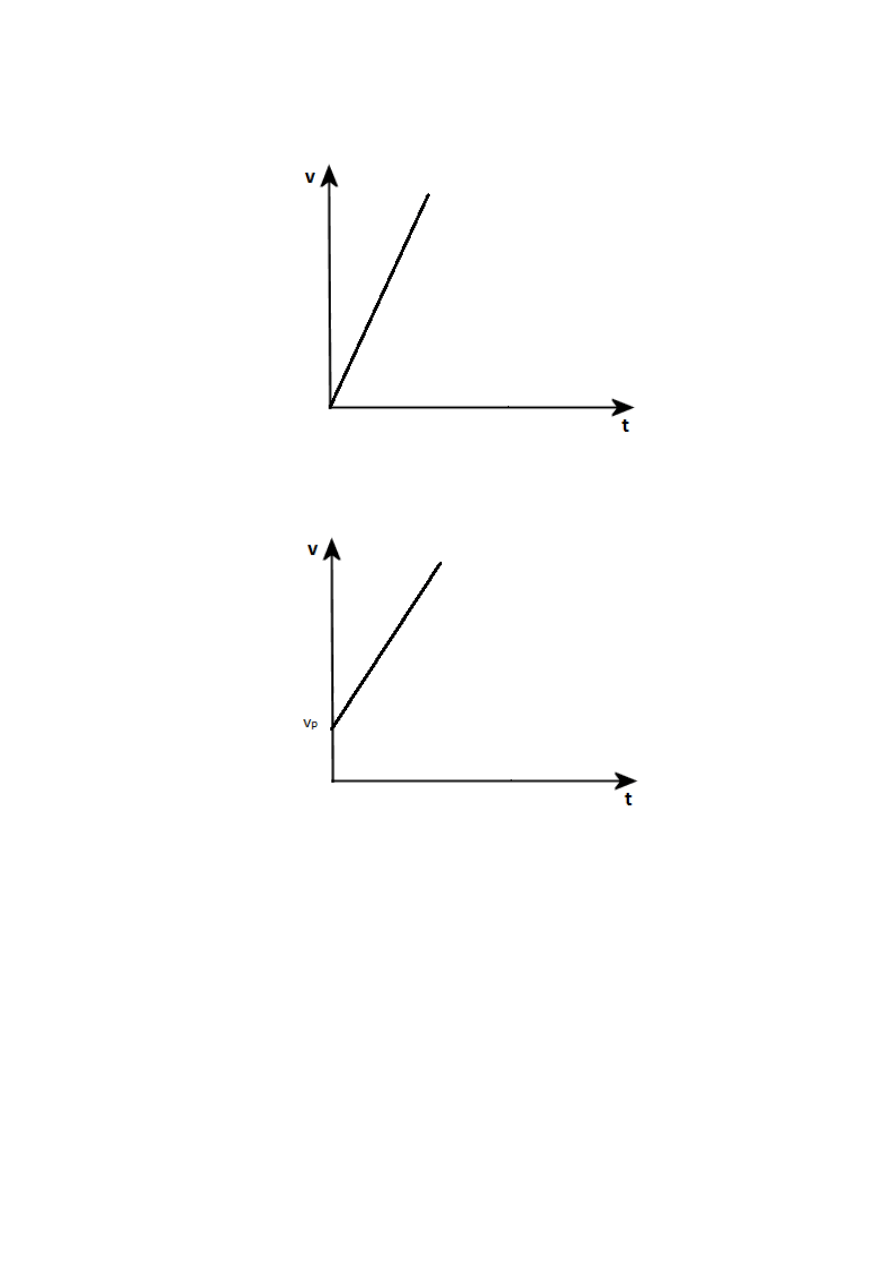
Wykres zależności prędkości od czasu dla
:
Wykres zależności prędkości od czasu dla
:
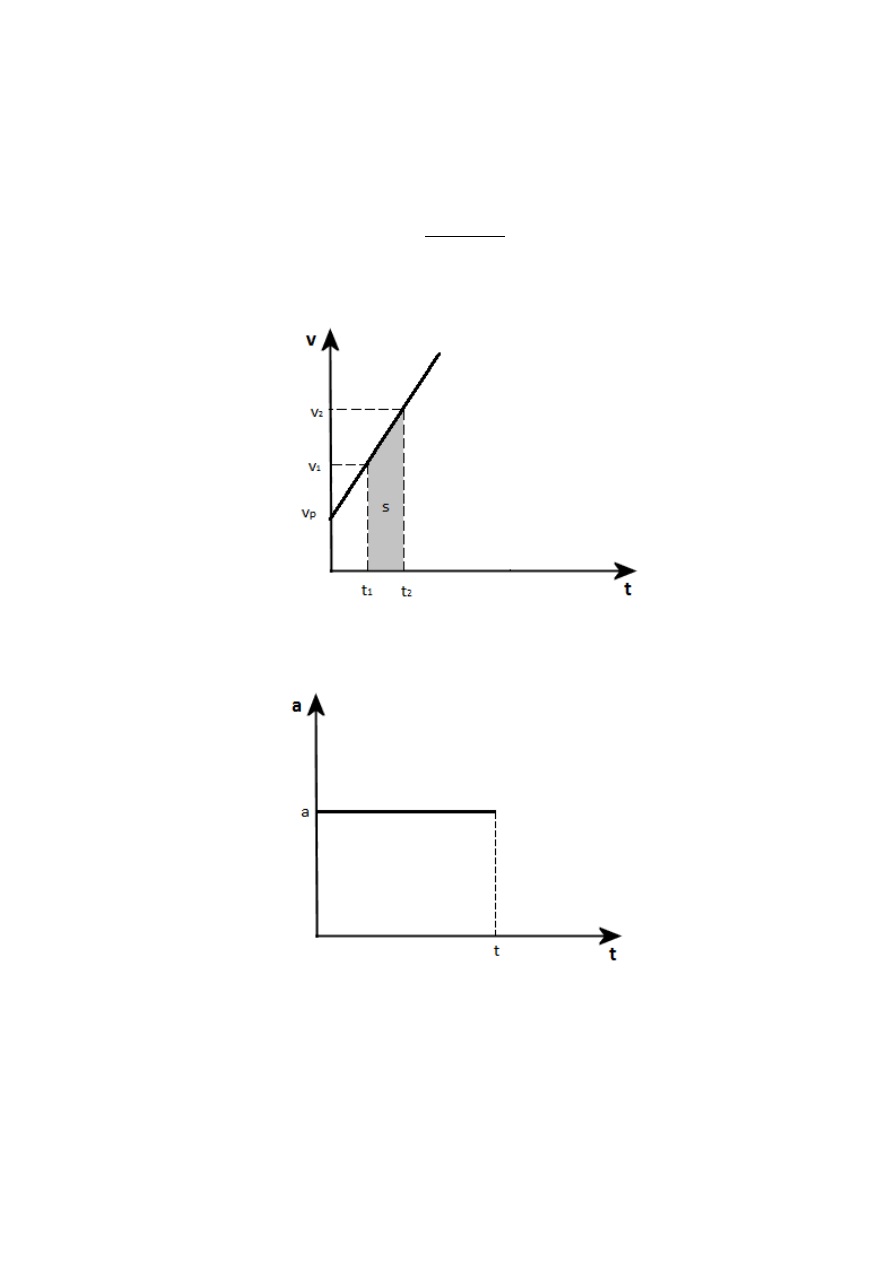
Mając wykres prędkości od czasu, można policzyć drogę przebytą przez ciało. Droga
przebyta przez ciało w przedziale czasu od
do
jest równa polu odwróconego
trapezu prostokątnego.
(
)
Wykres zależności przyspieszenia od czasu:
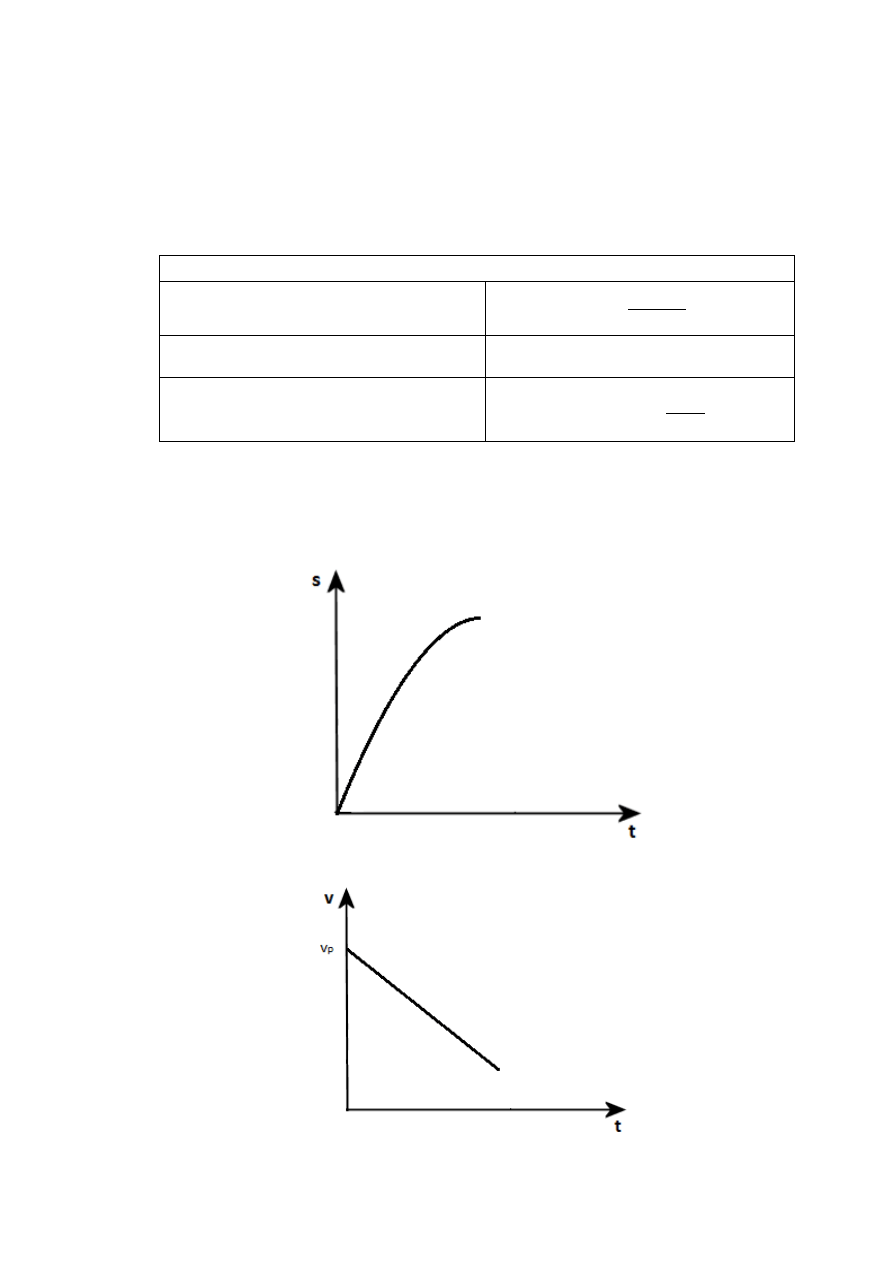
RUCH JEDNOSTAJNIE OPÓŹNIONY – ruch, w którym prędkość maleje jednostajnie, a
opóźnienie jest stałe.
WZORY
OPÓŹNIENIE
PRĘDKOŚĆ KOŃCOWA
DROGA
Wykres zależności drogi od czasu:
Wykres zależności prędkości od czasu dla
:
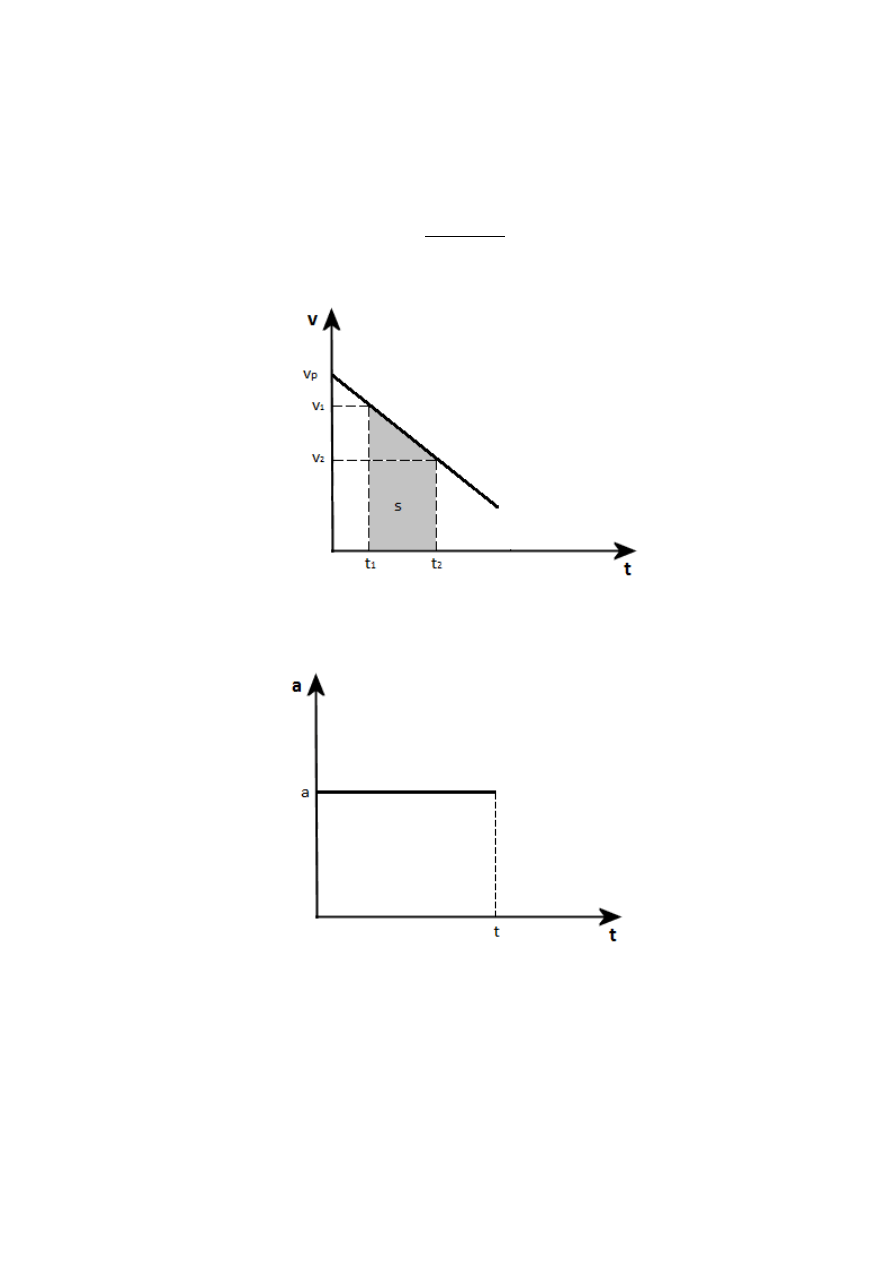
Mając wykres prędkości od czasu, można policzyć drogę przebytą przez ciało. Droga
przebyta przez ciało w przedziale czasu od
do
jest równa polu odwróconego
trapezu prostokątnego.
(
)
Wykres zależności opóźnienia od czasu:

D
YNAMIKA PUNKTU MATERIALNEGO
I zasada dynamiki Newtona(zasada bezwładności): W inercjalnym układzie
odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to
ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
II zasada: Jeśli siły działające na ciało nie równoważą się (czyli wypadkowa sił jest
różna od zera), to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły
wypadkowej, a odwrotnie proporcjonalnym do masy ciała.
III zasada(zasada akcji i reakcji): Jeżeli ciało A oddziałuje na ciało B z siłą F
BA
to ciało B
oddziałuje na ciało A z siła F
AB
o takiej samej wartości, kierunku, ale przeciwnym
zwrocie.
Siła bezwładności–siła pojawiająca się w nieinercjalnym układzie odniesienia, będąca
wynikiem przyspieszenia tego układu. Siła bezwładności nie jest oddziaływaniem z
innymi ciałami, jak to ma miejsce przykładowo w sile klasycznie rozumianej
grawitacji. Jeżeli zjawisko, w którym pojawiła się siła bezwładności, opisywane jest w
inercjalnym układzie odniesienia, wówczas siła bezwładności nie występuje,
zachowanie się ciał w takim układzie można wyjaśnić działaniem innych sił. Siła
bezwładności działająca na ciało o masie m znajdujące się w nieinercjalnym układzie
poruszającym się z przyspieszeniem a wyrażona jest wzorem:
.
Rodzaje siły bezwładności:
Efekt Coriolisa – efekt występujący w obracających się układach odniesienia. Dla
obserwatora pozostającego w takim układzie objawia się zakrzywieniem toru ciał
poruszających się wewnątrz niego. Zakrzywienie to zdaje się być wywołane jakąś siłą,
tak zwaną siłą Coriolisa. Siła Coriolisa jest pozorna, występującą jedynie w
obracających się układach nieinercjalnych. Dla zewnętrznego obserwatora siła ta nie
istnieje. Dla niego to układ zmienia położenie, a poruszające się ciało zachowuje swój
stan ruchu zgodnie z I zasadą dynamiki.
.
Siła odśrodkowa– jedna z sił bezwładności występująca w obracających się układach
odniesienia. Układy takie zalicza się do układów nieinercjalnych.
.
Transwersalna siła bezwładności– jedna z sił bezwładności występująca w
nieinercjalnym układzie odniesienia obracającym się ze zmienną prędkością. Podczas
takiego obrotu wartość przyspieszenia kątowego układu jest różna od zera.
Występowaniu tej siły towarzyszy siła odśrodkowa, a gdy ciało się porusza w
obracającym się układzie odniesienia, również siła Coriolisa. Siła ta działa zarówno na
ciała poruszające się w obracającym się układzie odniesienia, jak i nieruchome
względem niego.
.
Ruch po okręgu-prędkość jest stała, a torem jest okrąg (np. krzesełko karuzeli,
wskazówka zegara). Wektor prędkości jest styczny do okręgu w każdym punkcie tego

okręgu. Siła dośrodkowa utrzymuje ciało w stałej odległości od środka okręgu.
Kierunek wektora siły dośrodkowej jest zgodny z kierunkiem promienia okręgu, a
zwrot skierowany jest do środka okręgu. Wartość siły grawitacji działającej między
dwoma ciałami jest wprost proporcjonalna do iloczynu ich mas i odwrotnie
proporcjonalna do kwadratu odległości między tymi ciałami.
C
IĄŻENIE POWSZECHNE
–
G
RAWITACJA
1. PRACA W POLU GRAWITACYJNYM.
Jak wyraża się praca w polu grawitacyjnym?
Praca w polu grawitacyjnym jednorodnym - jednorodnym polem grawitacyjnym
nazywamy pole, ktorego w wszystkich punktach natężenie pola jest takie samo( te
same
wartości,
kierunki, zwroty), linie sił są równoległe i równo odległe. Praca w jednorodnym polu
grawitacyjnym można policzyć ze wzoru z definicji:
F - stała siła, Δr - przesunięcie, α - kąt między wektorem siły i przesunięcia.
Praca w polu grawitacyjnym centralnym - centralnym polem grawitacji jest pole,
którego linie zaczynają się w nieskończoności i kończą się na danej masie
wytwarzającej
pole.
Do policzenia pracy wykonywanej w tym polu nie można wykorzystać definicji pracy,
ponieważ wartość działającej siły nie jest stała( zależy od odległości i źródła):
(
)
Od czego zależy praca w polu grawitacyjnym?
Praca wykonywana przy przyrównaniu ciał zależy jedynie od początkowego
końcowego położenia punktu, nie zależy natomiast od kształtu toru.
2. PRAWO POWSZECHNEGO CIĄŻENIA.
Każde 2 ciała przyciągają się z siłą grawitacji F, ktorej wartość jest wprost
proporcjonalna do iloczynu mas tych ciał m
1
i m
2
, a odwrotnie proporcjonalna do
kwadratu odległości miedzy nimi

3. CIĘŻAR.
Co to jest ciężar ciała i od czego zależy?
Zależy od: źródła pola grawitacyjnego, odległości od źródła, od tego jak daleko jest
mierzony od źródła.
Ciężar ciała Q jest w przybliżeniu równy sile grawitacji F
g
wynikającej z oddziaływania
danego ciała z Ziemią. Siła ta ma postać
m - masa ciała, M
z
- masa ziemi, R
z
– promień Ziemi.
Ciężar ciała Q jest wypadkową kilku sił- głownie siły przyciągania
ziemskiego oraz siły odśrodkowej wywołanej obrotem Ziemi. Ciężar ciała jest to siła,
która nadaje ciału przyspieszenie ziemskie i wobec tego jest związany z masa ciała
wzorem:
m - masa ciała, g - przyspieszenie ziemskie w danym miejscu.
Ciężar ciała, a wiec też wartość g zależy od położenia geograficznego i od wysokości,
ponieważ:
- w skutek spłaszczenia Ziemi na biegunach, siła przyciągania jest tam większa niż na
równiku
- siła przysiadania rośnie ze wzrostem odległości od środka Ziemi, czyli ze wzrostem
wysokości
- siła odśrodkowa zależy od odległości obrotu, a wiec od prędkości geograficznej
i wysokością nad powierzchnią Ziemi
4. POTENCJAŁ POLA GRAWITACYJNEGO.
Potencjał V pola grawitacyjnego danym punkcie nazywamy stosunek energii
potencjalnej, jaka na umieszczone w tym punkcie ciało, do miary tego ciała

Jednostka potencjału pola grawitacyjnego jest [
] [
]
Potencjał pola grawitacyjnego nazywamy stosunek potencjalnej punktowego ciała
naelektryzowanego ładunkiem q do wartości tego ładunku. V=
.
Jednostką potencjału jest 1 wolt [1V].
5. WPŁYW RUCHU OBROTOWEGO ZIEMI NA WARTOŚĆ PRZYSPIESZENIA ZIEMSKIEGO.
Największa wartość przyspieszenia ziemskiego jest na biegunie 90˚.Najniższa na
równiku , wynika to z ruchu obrotowego ziemi.
6. POLE GRAWITACYJNE - pole wytwarzane przez obiekty posiadające masę. Określa
wielkość i kierunek siły grawitacyjnej działającej na znajdujące się w nim inne obiekty
posiadające masę. Pole opisuje się poprzez podanie natężenia pola grawitacyjnego γ,
czyli siły F działającej na masę jednostkową m, lub potencjału grawitacyjnego.
P
RACA I ENERGIA
1. PRACA - pracą stałej siły F nazywamy iloczyn skalarny tej siły i wektora
przemieszczenia (oraz kąta zawartego między wektorami siły i przemieszczenia).
[ ] [ ] [
]
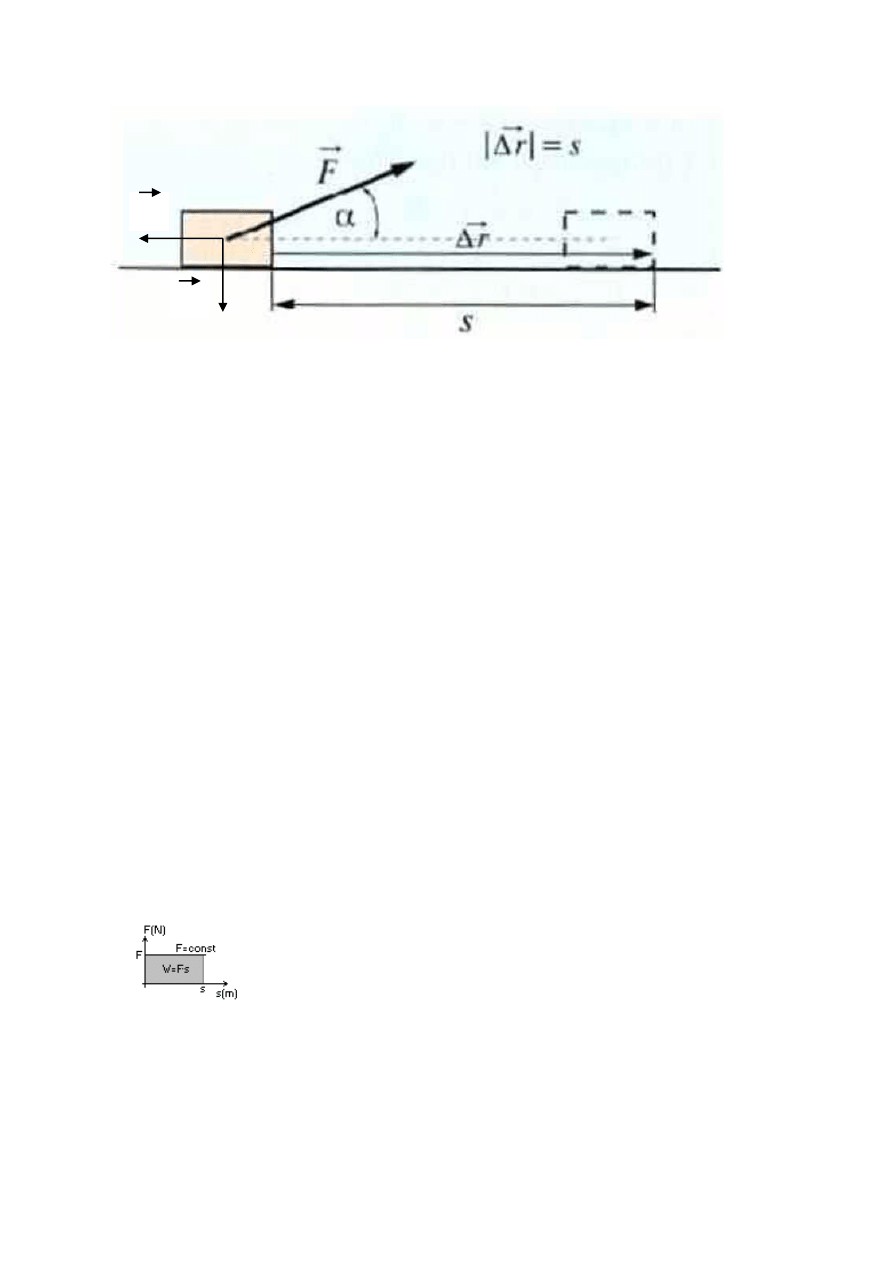
(Nad wszystkimi symbolami poza α strzałka, w sensie zapis wektorowy)
F - wartość stałej siły, której pracę obliczamy
Dr - wartość przemieszczenia
α - kąt, który tworzą wektory siły F i przemieszczenia Dr
T - siła tarcia
Fc - siła ciążenia (F
c
=Q=mg)
Dla powyższego przykładu (rysunek) PRACĘ poszczególnych sił liczymy następująco:
Wielkość pola pod wykresem działającej na ciało siły F podczas przemieszczenia s jest
wartością wykonanej pracy
a) gdy siła jest stała
b) gdy wartość siły wzrasta proporcjonalnie do przesunięcia
T
Fc
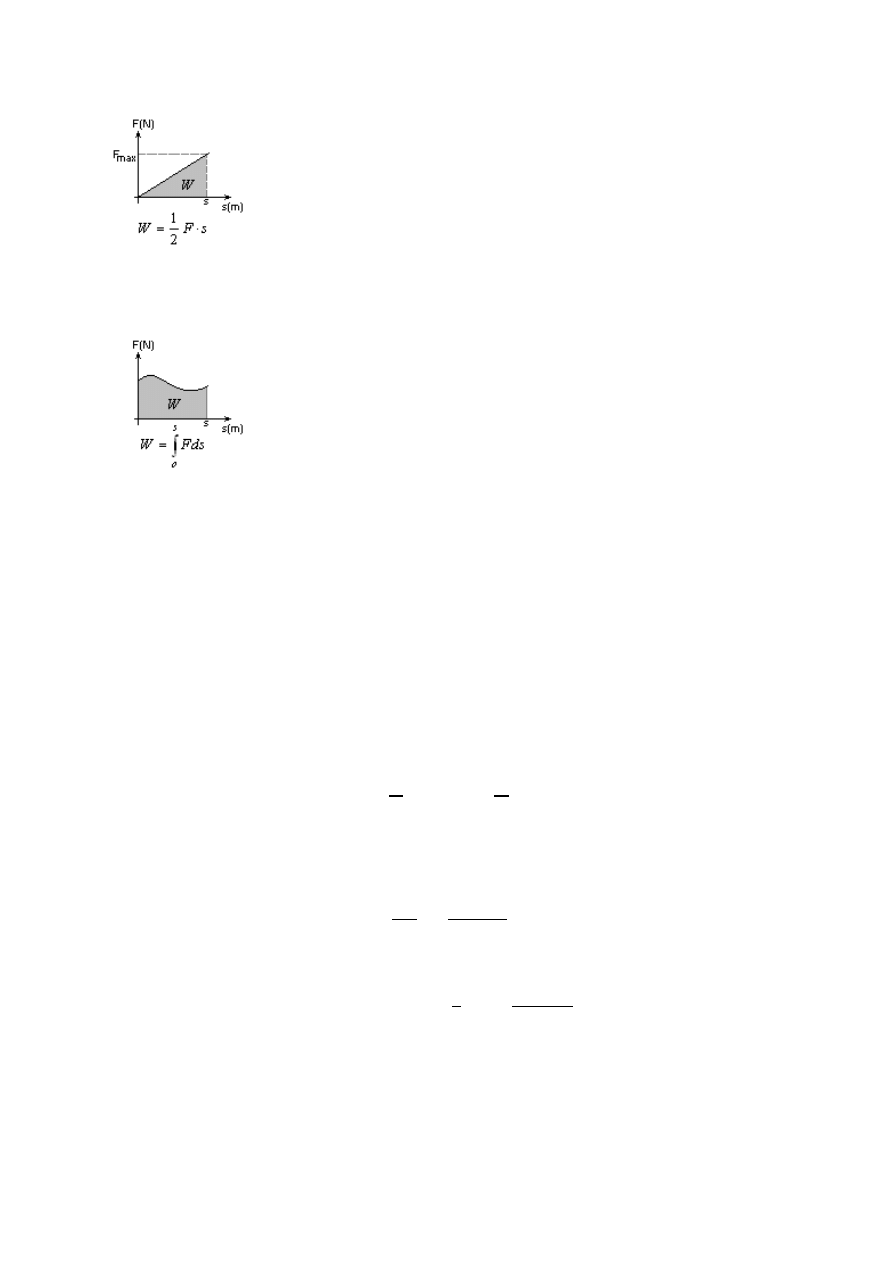
c) gdy wartość siły jest zmienna podczas przesunięcia (praca siły zmiennej)
Przykładem takiej siły (c) jest siła sprężystości sprężyny. Jeżeli rozciągamy sprężynę działając
na nią siłą F
z
i przesuwając jej koniec ruchem jednostajnym, to siła sprężystości F równoważy
w każdym punkcie siłę F
z
, czyli F
z
= - F
- wzór na siłę sprężystości sprężyny
Obliczenie pracy wykonanej przez siłę Fz podczas rozciągania sprężyny sprowadza się do
obliczenia pola powierzchni zawartej między wykresem F(x) a osią x, czyli:
2. MOC - stosunek pracy W do czasu t, w którym ta praca została wykonana, nazywamy
średnią mocą P.
[ ] [
] [
]
MOC CHWILOWA:

lub pochodna pracy w czasie
3. ENERGIA MECHANICZNA
Mówimy, że układ posiada ENERGIĘ MECHANICZNĄ, jeśli jest zdolny do wykonywania
pracy
a) Energia potencjalna ciężkości ciała o masie m znajdującego się na wysokości h nad
poziomem „zerowym” (Ep w tym punkcie równa jest 0) wyraża się wzorem:
b) Energia potencjalna sprężystości sprężyny wydłużonej o x wyraża się wzorem:
k - współczynnik sprężystości materiału, z którego wykonano sprężynę
c) Energia kinetyczna ciała o masie m poruszającego się w danym układzie odniesienia z
szybkością v wyraża się wzorem:
Zmiana energii mechanicznej wykonanej nad układem równa jest pracy siły
zewnętrznej wykonanej nad układem:
Zmiana energii potencjalnej układu ciał równa jest pracy siły zewnętrznej wziętej ze
znakiem minus:
Zmiana energii kinetycznej ciała równa jest pracy siły wypadkowej działającej na to
ciało:

4. ZASADA ZACHOWANIA ENERGII MECHANICZNEJ
Jeśli na układ ciał oddziałujących wzajemnie siłami zachowawczymi (grawitacji i
sprężystości) nie działają siły zewnętrzne lub działają, ale nie wykonują pracy, to energia
mechaniczna układu jest zachowana
Innymi słowy:
Jeżeli siły zewnętrzne nie wykonują pracy nad układem ciał, to energia mechaniczna tego
układu nie zmienia się. Zakładamy przy tym, że ciała układu oddziałują z sobą tylko siłami
zależnymi od położenia.
ZASADA
ZACHOWANIA
PĘDU
Środek masy- punkt określony przez rozkład mas w danym ciele lub układzie ciał.
Położenie środka masy wyraża się wzorem:
∑
∑
gdzie m
k
i r
k
- odpowiednio masy i promienie wodzące poszczególnych punktowych ciał
składających się na dany obiekt.
Ruch środka masy- środek masy może być w spoczynku lub poruszać się podczas ruchu
poszczególnych ciał układu.
Prędkośc środka masy obliczamy ze wzoru:
∑
∑
Pęd układu punktów materialnych-
jest równy sumie wektorowej pędów, wszystkich
punktów układu. Pęd układu punktów zmienia się tylko wtedy, gdy działa na nie siła
zewnętrzna. Zmiana pędu układu punktów materialnych jest równa popędowi sumy sił
zewnętrznych
.
Zasada zachowania pędu
Jeżeli na jakiś układ ciał nie działają siły (oddziaływania) zewnętrze to wtedy układ ten ma
stały pęd.
Za pomocą wzoru można zapisać:
Jeżeli , to .
Zderzenia sprężyste (elastyczne)- takie zderzenie dwóch ciał w którym suma energii
zderzających się ciał przed zderzeniem i po zderzeniu jest taka sama i suma pędów przed
zderzeniem i po zderzeniu jest taka sama.
Zderzenia niesprężyste- takie zderzenie dwóch ciał w którym suma energii kinetycznych
po zderzeniu jest mniejsza niż przed zderzeniem a suma pędów po zderzeniu i przed
zderzeniem jest jednakowa.
R
UCH OBROTOWY
Bryła sztywna (ciało sztywne) jest to ciało, którego cząstki składowe zachowują względem
siebie stałe odległości. W pojęciu tym zaniedbujemy ruch drgający atomów oraz cząstek
względem siebie.
Moment pędu bryły
Moment pędu bryły obracającej się wokół jednej ze swoich osi symetrii dany jest wzorem
L=Iw
gdzie:
I – moment bezwładności bryły
w – prędkość kątowa bryły
Moment pędu L(→wektor) jest wektorem. W przypadku bryły poruszającej się wokół jednej
ze swoich osi symetrii, zwrot i kierunek momentu pędu jest taki sam jak wektora prędkości
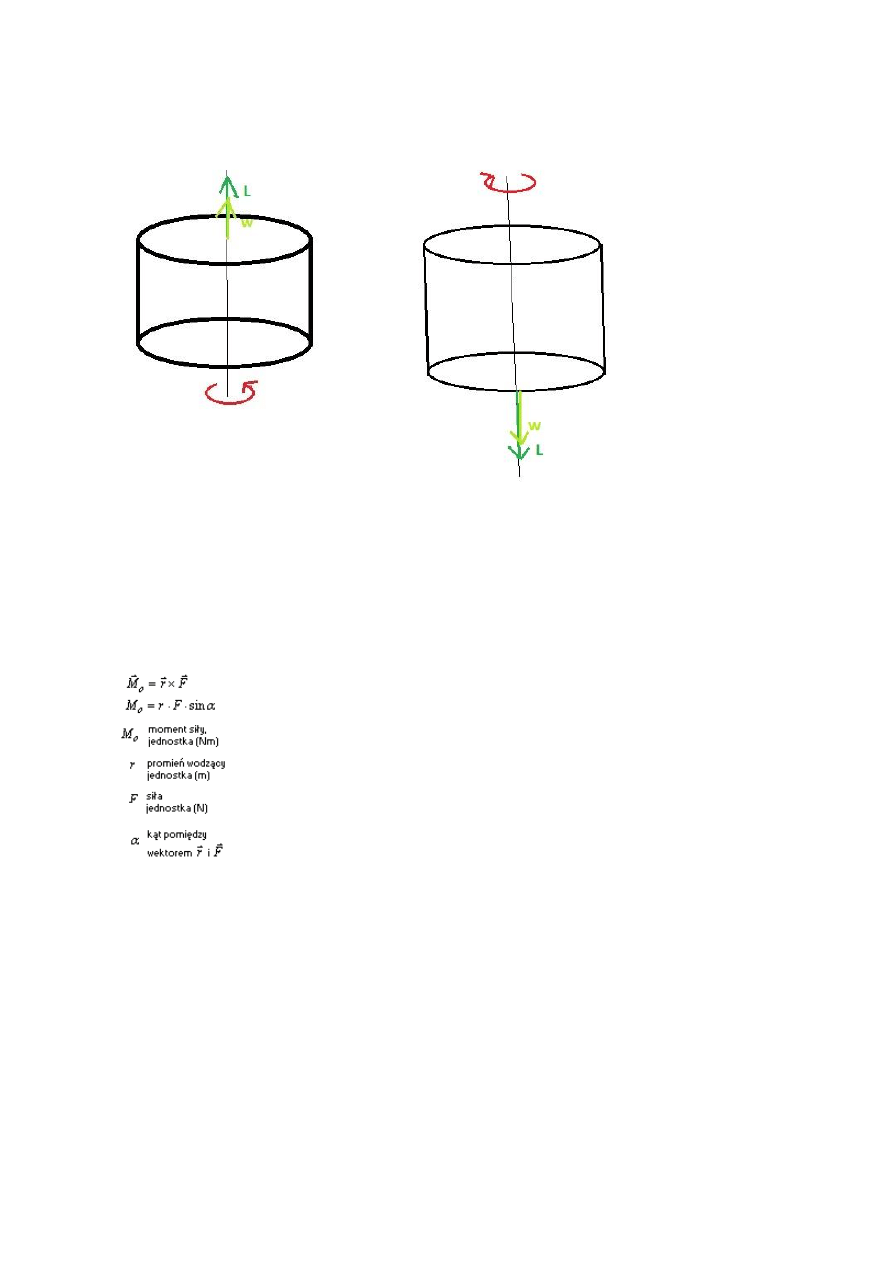
kątowej w(→wektor).
Moment siły (moment obrotowy) to iloczyn wektorowy promienia wodzącego r (o początku
w punkcie O i końcu w punkcie przyłożenia siły) oraz siły F
Jest to wielkość wektorowa. Zaczepiona jest w punkcie O (początku promienia wodzącego), a
jego jej kierunek jest prostopadły do kierunku płaszczyzny wyznaczonej przez wektor (F) i
promień wodzący (r). Zwrot wektora momentu siły określa się zgodnie z reguła śruby
prawoskrętnej.

Jednostką momentu siły jest Nm (niutonometr). Jednostka ta jest zdefiniowana analogicznie
jak dżul (jednostka energii). Uwaga: są to dwie różne jednostki!
Moment bezwładności jest to wielkość skalarna określająca bezwładność ciała w ruchu
obrotowym względem określonej osi obrotu. Im większy moment bezwładności, tym trudniej
jest zmienić ruch obrotowy ciała (zwiększyć lub zmniejszyć prędkość kątową ciała)
Moment bezwładności układu dwóch punktów materialnych jest sumą momentów
bezwładności każdego z tych punktów

Moment bezwładności dla całej bryły składającej się z dowolnej liczby elementów
Twierdzenie Steinera omawia, w jaki sposób znaleźć moment bezwładności bryły względem
dowolnej osi, jeżeli znany jest moment bezwładności względem osi równoległej i
przechodzącej przez środek tej bryły
Zasada zachowania momentu pędu
Jeśli wypadkowy moment sił zewnętrznych działających na ciało jest równy zeru wówczas
moment pędu ma wartość stałą
I
w
= const
Ruch postępowy i obrotowy
Ruch postępowy bryły sztywnej
– jest to taki ruch, w którym ustawienie bryły w przestrzeni
nie ulega zmianie.
Ruch obrotowy bryły sztywnej
- jest to taki ruch, w którym punkty materialne tworzące tę
bryłę poruszają się po okręgach o środkach leżących na jednej prostej i zwanej osią obrotu.
R
UCH DRGAJĄCY
Cechy ruchu drgającego:
ν - liczba pełnych drgań (cykli) wykonywanych w ciągu sekundy
T - okres ruchu – czas w jakim wykonane jest jedno pełne drganie
1 herc = 1Hz = jedno pełne drganie na sekundę = 1 s
-1
T= 1/ ν
1. Siła harmoniczna
W ruchu harmonicznym siła jest wprost proporcjonalna i przeciwnie skierowana do
przemieszczenia.
F= -kx
k= mω
2
k- współczynnik proporcjonalności
x- przesunięcie od położenia równowagi
2. Wahadło matematyczne
F
g
= mgsinƟ
Jeżeli kąt Ɵ jest mały( mniejszy niż 10
o
) to sin Ɵ jest bardzo bliski Ɵ
F= -mgƟ= -mg
= -
x
F= -kx
F= -mω
2
x
T= 2
√
*Wahadło to pkt materialny zawieszony na nierozciągliwej, nieważkiej nici.
3. Wahadło fizyczne
siła ciężkości działa na środek ciężkości w punkcie C, środek ciężkości znajduje się w
odległości h od punktu zawieszenia O, moment siły związany ze składową Fg ma
ramie o długości h.
M= -hF
g
sinƟ
I
ɛ
= -hF
g
sinƟ
ɛ
= -

T= 2
√
4. Rezonans
Jest to proces przekazywania jednemu ciału przez drugie o okresie równym okresowi
drgań własnych. Wyróżniamy rezonans mechaniczny, akustyczny,
elektromagnetyczny. Zjawisko rezonansu występuje w drganiach wymuszonych.
5. Logarytmiczny dekrement tłumienia
Wielkość fizyczna charakteryzująca szybkość zanikania drgań, gdy są one tłumione.
Mówi nam jak maleje amplituda.
( to logarytm naturalny dekrementu tłumienia)
β-współczynnik tłumienia drgań
T- okres drgań tłumionych
6. Jeżeli ruch oscylatora słabnie na skutek działania sił zewnętrznych, to taki oscylator
nazywamy oscylatorem tłumionym, a jego drgania nazywamy tłumionymi.
7. Oscylator harmoniczny prosty- wyidealizowany układ fizyczny - punkt materialny o
masie m, na który działa siła proporcjonalna do chwilowego wychylenia x od
pewnego położenia równowagi
8. Straty mocy
jest to zjawisko fizyczne polegające na traceniu części energii przetwarzanej
przez dany układ.
Straty mocy (a więc i energii) wywoływane są przez szereg
czynników, np: tarcie mechaniczne, promieniowanie(cieplne, elektromagnetyczne).
9. Drgania wymuszone oscylatora harmonicznego
Siła wymuszająca:
Równanie ruchu:

10. Moc absorbowana
Moc absorbowana jest największa, gdy w stanie ustalonym (drgania o stałej
amplitudzie) moc absorbowana = mocy traconej na pracę przeciw sile tłumiącej
F
ALE W OŚRODKACH SPRĘŻYSTYCH
Fale mechaniczne – fale na wodzie, dźwiękowe, sejsmiczne ; podlegają zasadom dynamiki
Newtona ; mogą istnieć wyłącznie w jakimś ośrodku materialnym.
Fale elektromagnetyczne – występują w szerokim zakresie długości fal, nie potrzebują
żadnego ośrodka materialnego do rozprzestrzeniania się. Wszystkie fale elektromagnetyczne
poruszają się w próżni z tą samą prędkością c = 299792458 m/s
Fale materii – fale związane z elektronami, protonami, cząstkami elementarnymi.
Fale mechaniczne :
a) fale poprzeczne – ruchy cząstek materii przenoszącej falę są prostopadłe do kierunku
propagacji fal
b) fale podłużne – ruchy cząstek materii przenoszącej falę są równoległe do kierunku
propagacji fali
Równanie fali : y(x,t)=x
m
sin(kx-ωt)
y – przemieszczenie ; x
m
– amplituda ; k – liczba falowa ; x – położenie ; ω – częstość kłowa ; t
– czas
Przemieszczenie y elementu znajdującego się w chwili t w położeniu x
Prędkość fali. Fala w ciągu jednego okresu drgań przebywa odległość równą jednej długości
fali :
Interferencja fal – gdy 2 fale sinusoidalne o takich samych amplitudach i długościach fali
biegną w tym samym kierunku wzdłuż naprężonej liny, interferują ze sobą, dając wypadową
falę sinusoidalną biegnącą w tym samym kierunku.

y
1
(x,t)=y
m
sin(kx - ωt)
y
2
(x,t)=y
m
sin(kx - ωt + ø)
y’(x,t)= y
1
(x,t)+ y
2
(x,t) = y
m
sin(kx - ωt) + y
m
sin(kx - ωt + ø)
y’(x,t)=[2y
m
cos ½ ø] sin (kx - ωt +½ ø)
y’ – przemieszczenie ; cos – amplituda ; sin – czynnik oscylacyjny
gdy : ø = 0 to y’(x,t)=2y
m
sin(kx - ωt)
gdy : ø = π to y’(x,t)=0
Fala stojąca - gdy 2 fale sinusoidalne o takich samych amplitudach i długościach fali biegną
w przeciwnych kierunkach wzdłuż napiętej liny, w wyniku ich interferencji powstaje fala
stojąca.
y
1
(x,t)=y
m
sin(kx - ωt)
y
2
(x,t)=y
m
sin(kx + ωt)
y’(x,t)= y
1
(x,t)+ y
2
(x,t) = y
m
sin(kx - ωt) + y
m
sin(kx + ωt)
y’(x,t)=[2y
m
sinkx]cosωt
y’ – przemieszczenie ; y
m
– amplituda drgań ; cos – czynnik oscylacyjny
amplituda fali stojącej osiąga maksimum : |sin kx| = 1
amplituda fali stojącej osiąga minimum : sin kx = 0 ; kx = nπ
Fale dźwiękowe
Fale dźwiękowe w zakresie słyszalnym – powstają w wyniku drgań (strun, słupów powietrza,
płyt, membran) powodujących zagęszczenia oraz rozrzedzenia otaczającego ośrodka;
ośrodek przenosi to zaburzenie na duże odległości od źródła w postaci fali. Fale te po
dotarciu do ucha wywołują wrażenie dźwięku.
Prędkość dźwięku- impuls zagęszczenia wysłany wzdłuż długiej rury wypełnionej
powietrzem. Obliczamy ze wzoru:
√
Gdzie:
B- moduł sciśliwości
ρ- gęstośc ośrodka
Natężenie dźwięku- miara energii fali dźwiękowej. Obliczamy ze wzoru:

Gdzie:
P
źr
- moc źródła
r
2
- promień sfery
Głośność dźwięku-
wrażenie słuchowe, spowodowane falą akustyczną rozchodzącą się
w ośrodku sprężystym. Obliczamy ze wzoru:
( )
Gdzie:
I
0
= 10
-
12
- natężenie odniesiania bliskie dolnej granicy słyszalności ucha ludzkiego
I- natężenie dźwięku
decybel- (=0.1 bela)- jednostka głośnosci
R
ÓWNANIA
M
AXWELLA
Prawo indukcji elektromagnetycznej Faradaya
Całka po dowolnej krzywej zamkniętej z natężenia pola elektrycznego jest równa minus
pochodnej po czasie (szybkości zmian) strumienia pola magnetycznego przez dowolną
powierzchnię rozpiętą na tej krzywej.
Prawo to wiąże zmienne pole magnetyczne z indukowanym przez nie polem elektrycznym:
Strumień indukcji pola elektrycznego
Uogólnione prawo Ampere'a
wiąże indukcję pola magnetycznego z wywołującymi je prądem elektrycznym oraz zmiennym
polem elektrycznym:
Całka po dowolnej krzywej zamkniętej z indukcji pola magnetycznego jest równa sumie
Przenikalnośc magnatyczna ośrodka razy całkowite natężenie prądu elektrycznego
przepływającego przez dowolną powierzchnię rozpiętą na tej krzywej,

Przenikalność magnetyczna ośrodka razy przenikalność elektryczna ośrodka razy
pochodnej po czasie (prędkości zmian) strumienia natężenia pole elektrycznego przez
tą powierzchnię
Natężenie prądu elektrycznego
|
strumień pola elektrycznego
,
|
Przenikalność magnetyczna ośrodka
Prawo Gaussa dla elektryczności
wiąże strumień pola elektrycznego z ładunkiem wytwarzającym to pole
Strumień pola elektrycznego przez dowolną powierzchnię zamkniętą przemnożony przez
przenikalność elektryczną ośrodka jest równy całkowitemu ładunkowi zawartemu wewnątrz
tej powierzchni
strumień pola elektrycznego
,
Całkowity ładunek zawarty wewnątrz powierzchni
,
Prawo Gaussa dla magnetyzmu
pole magnetyczne jest bezźródłowe – nie istnieją ładunki magnetyczne
Całkowity strumień indukcji magnetycznej przechodzący przez dowolną powierzchnię zamkniętą
równa się zeru
Indukcja magnetyczna
FALE ELEKTROMAGNETYCZNE
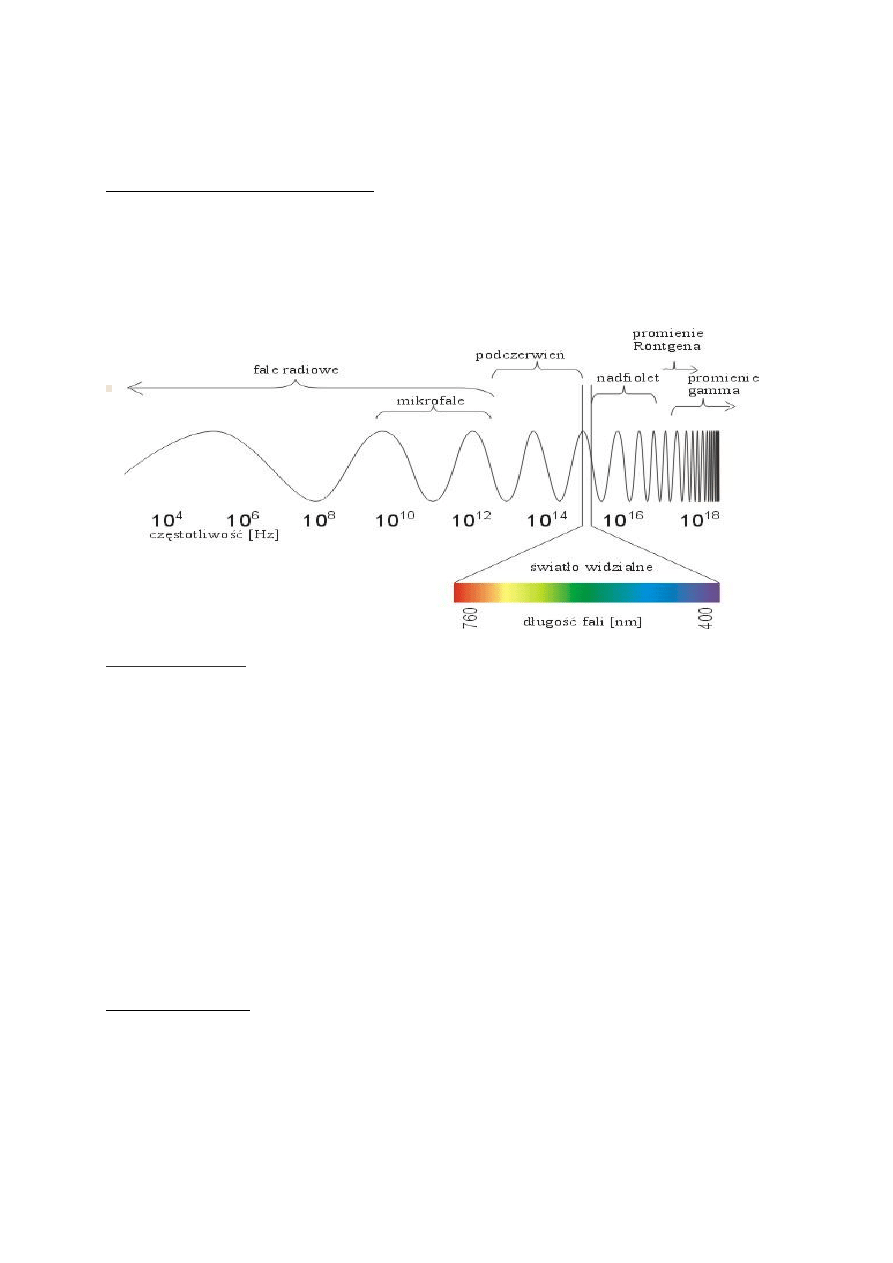
Widmo fal elektromagnetycznych- podział fal elektromagnetycznych za względu na
częstotliwośc lub długość. Obejmuje ono fale radiowe, mikrofale, promieniowanie
podczerwone, światło widzialne, promieniowanie nadfioletowe, promieniowanie
rentgenowskie, promieniowanie gamma.
Wektor Poyntinga-
wektor określający gęstość strumienia energii przenoszonej przez pole
elektromagnetyczne.
Wektor
jest
określony
jako iloczyn
wektorowy wektorów natężeń
pola
elektrycznego i magnetycznego:
⃗ ⃗⃗ ⃗⃗⃗
Gdzie:
⃗-
rzeczywisty wektor Poyntinga
⃗⃗- natężenie pola elektrycznego
⃗⃗⃗- natężenie pola magnetcznego
Polaryzacja światła- jest zjawiskiem, w którym światło ujawnia swoje właściwości jako fala
poprzeczna. Światło jest falą elektromagnetyczną polegającą na rozchodzeniu sie na
przemian zmiennych pól elektrycznych i magnetycznych, których linie są do siebie wzajemnie
prostopadłe. Gdy wektor natężenia pola elektrycznego i wektor indukcji magnetycznej mają
tylko jeden wyróżniony kierunek, to światło jest spolaryzowane liniowo. Do polaryzacji
światła służą polaryzatory, czyli substancje o takich właściwościach, że światło po przejściu
przez nie ma jeden wyróżniony kierunek, w którym drga wektor natężenia pola
elektrycznego i prostopadle do niego drga wektor indukcji magnetycznej.
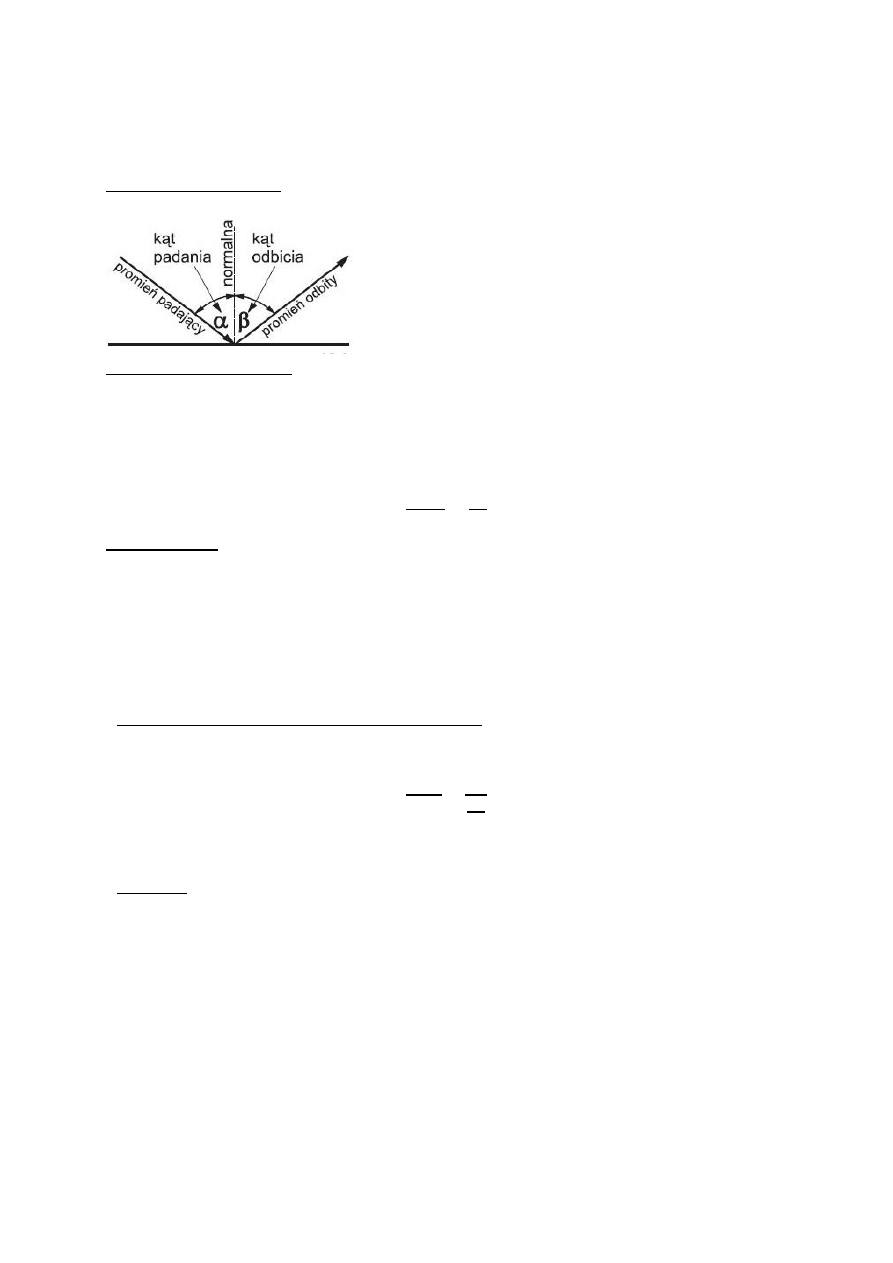
Prawo odbicia światła- mówi o tym, że jesli kąt padania i kąt odbicia leżą w jednej
płaszczyźnie, to kąt padania jest równy kątowi odbicia.
α=β
Prawo załamania światła
Gdy światło przechodzi z ośrodka o bezwzględnym współczynniku załamania n
1
do ośrodka o
bezwzględnym współczynniku załamania n
2
, to stosunek sinusa kąta padania do sinusa kąta
załamania jest równy stosunkowi bezwzględnych współczynników załamania światła w obu
ośrodkach zgodnie z wzorem:
Kąt Brewstera-
kąt padania światła na powierzchnię dielektryka, przy którym promień
odbity jest całkowicie spolaryzowany liniowo, czyli α+β=90
ο
Z definicji kąta powstał waunek Brewstera:
Gdy na granicę ośrodków przezroczystych pada światło niespolaryzowane pod takim
kątem, że promień odbity i załamany tworzą kąt prosty, to światło odbite jest całkowicie
spolaryzowane.
Zjawisko całkowitego wewnętrznego odbicia- zachodzi tylko wtedy, gdy światło
przechodzi z ośrodka gęstszego do rzadszego (załamuje sie od normalnej- rys.wyżej). W
takim przypadku role kąta padania i kąta załamania odwracają się i dlatego:
n
1,2
-
bezwzględne współczynniki załamania ośrodków
Dyfrakcja
Dyfrakcja- zjawisko polegające na zaburzeniu prostoliniowego rozchodzenia się promieni
świetlnych.
Dyfrakcji ulega światło tylko na takich przeszkodach (szczelinach), których rozmiary są
porównywalne
z
długością
fali
świetlnej.
d >> λ –
dyfrakcja
nie
występuje,
d ≈ λ – dyfrakcja zachodzi.
Dyfrakcja na pojedynczej szczelinie
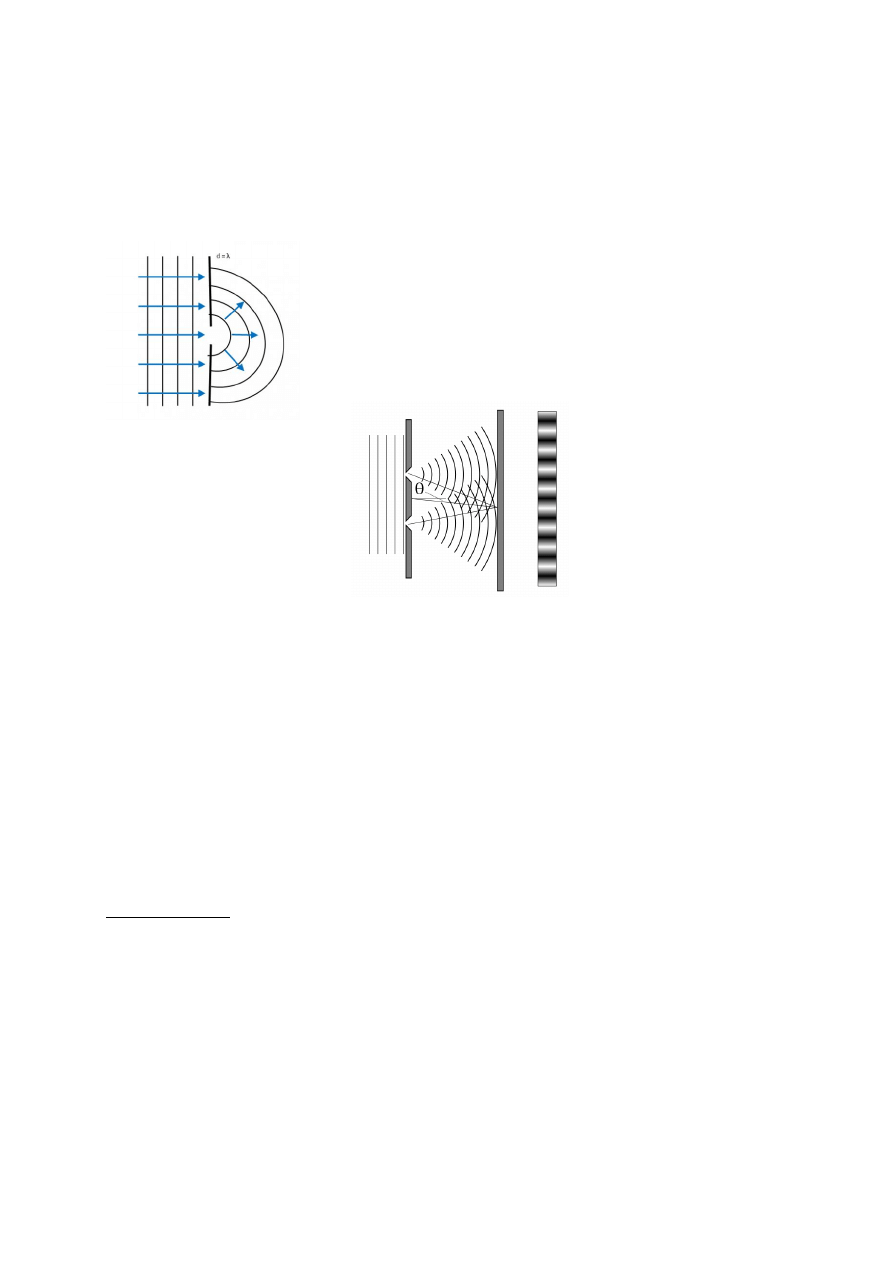
Fala świetlna padając na przeszkodę w postaci wąskiej szczeliny ulega zjawisku dyfrakcji, w
wyniku czego na ekranie pojawia się charakterystyczny obraz dyfrakcyjny, składający się z
centralnego prążka oraz mniej intensywnych, ułożonych na przemian jasnych i ciemnych
prążków pobocznych. Położenie centralnego prążka określa się wzorem:
d×sinα=λ
Interpretacja
światła
dla
dwóch szczelin
Jeżeli na układ dwóch szczelin
pada równoległa wiązka
światła, to na szczelinach
występuje dyfrakcja, co
prowadzi do nakładania się
wiązek (interferencji) i w
konsekwencji
na
ekranie
obserwuje
się
układ
ciemnych i jasnych prążków,
czyli minimów i maksimów
interferencyjnych
.
Siatka dyfrakcyjna
Układ równoległych i równo oddalonych od siebie szczelin, przepuszczających światło. Jeżeli
na siatkę pada monochromatyczna fala świetlna, to na ekranie, po drugiej stronie siatki,
otrzymujemy obraz dyfrakcyjny w postaci jasnych i ciemnych prążków.
Warunek Bragga
Warunek
opisujący
kierunek
położenia
maksimów
interferencyjnych
promieni
rentgenowskich (interferencja fal) ugiętych (dyfrakcja fal) na sieci krystalicznej kryształu:
Gdzie:
n- rząd odbicia
λ- długość fali promieniowania rentgenowskiego

d-odległość między płaszczyznami sieci krystalicznej
θ- kąt pomiędzy powierzchnią kryształu a kierunkiem padania promieni rentgenowskich
Wykorzystywany jest w badaniach struktury kryształów.
ELEMENTY FIZYKI WSPÓŁCZESNEJ
ZJAWISKO FOTOELEKTRYCZNE
Zjawisko fotoelektryczne- Zjawisko uwalniania przez światło elektronów z powierzchni
rozmaitych substancji nazwane jest zjawiskiem fotoelektrycznym. Rozróżnia się
fotoelektryczne zjawisko zewnętrzne i wewnętrzne. Zgodnie z zaproponowanym wtedy
modelem energia padającego kwantu gamma (równa hν, gdzie h - stała Plancka, ν -
częstotliwość fali świetlnej) jest przekazywana elektronowi zgodnie z równaniem hν = E+W,
gdzie E - energia kinetyczna elektronu, W - tzw. praca wyjścia (energia potrzebna do
wydostania się elektronu z substancji).
ZJAWISKO CAMPTONA
Comptona
efekt
(zjawisko), rozpraszanie
wysokoenergetycznego
promieniowania
elektromagnetycznego (gamma lub rentgenowskiego) na słabo związanych elektronach.
W
wyniku
rozpraszania elektron otrzymuje
część pędu i energii
padającego kwantu
promieniowania, przez co rozproszony kwant promieniowania ma mniejszą energię (większą
długość fali). Zjawiska tego nie można wyjaśnić na gruncie klasycznej fizyki. Z analizy procesu
zderzenia kwantu promieniowania z elektronem, gdy oba obiekty traktowane są jako
sprężyste kulki, można otrzymać wzór na wzrost długości fali promieniowania:
Δλ = 2πλ
o
(1-cosθ),
gdzie λ
o
tzw. comptonowska długość fali, θ - kąt rozproszenia.
MODEL ATOMU WODORU
Model atomu Bohra; planetarny model budowy atomu wodoru przedstawiony w 1913 roku
przez fizyka duńskiego N.H.D.Bohra. Model atomu Bohra stanowi rozwinięcie modelu atomu
Rutherforda przy założeniu, że zarówno ruch elektronu w atomie, jak i emisja
promieniowania podlegają pewnym ograniczeniom, nie mającym żadnego uzasadnienia w
fizyce klasycznej, a wręcz z nią sprzecznym. Ograniczenia te Bohr przedstawił w postaci
czterech postulatów :

1)w atomie wodoru elektron porusza się wokół jądra po orbicie kołowej w wyniku
działania siły kulombowskiej i zgodnie z zasadami mechaniki kwantowej;
2)elektron może krążyć tylko po wyróżnionych (dozwolonych) orbitach, tj. takich, dla
których moment pędu elektronu jest całkowitą wielokrotnością stałej Plancka h podzielonej
przez 2π oznaczonej przez ђ: m
e
v
n
r
n
= n ђ , gdzie: n=1,2,3…, m
e
- masa elektronu, v
n
-
prędkość elektronu na n-tej orbicie o promieniu r
n
;
3)Elektron krążący po dozwolonej orbicie nie promieniuje energii (wbrew prawom
elektrodynamiki klasycznej). Orbitę taką nazywa się orbitą stacjonarną, a odpowiedni stan
atomu- stanem stacjonarnym;
4)Przejście atomu ze stanu stacjonarnego o energii En do innego stanu stacjonarnego
energii Em jest związane z emisją lub absorbcją fotonu o energii równej różnicy energii w
stanach początkowym i końcowym: hv= En- Em ; gdzie v-częstotliwość promieniowania.
Zgodnie z drugim postulatem Bohra moment pędu elektronu jest skwantowany,
kwantowany jego dozwolonymi wartościami są: 1,ђ2ђ,3ђ…, przy czym ђ należy traktować
jako naturalną jednostkę momentu pędu. Konsekwencją kwantowania momentu pędu
elektronu w atomie jest kwantowanie promieni dozwolonych orbit oraz kwantowanie energii
atomu;
Całkowita energia atomu ma wartość ujemną (elektronowi swobodnemu umownie
przypisuje się energię potencjalną równa zero), wyznaczoną przez wartość liczby n nazywaną
główną liczbę kwantową. Stan podstawowy odpowiada n=1 i jego energia jest równa E
1
= -R
= 2,18 * 10
-18
J , odpowiada mu orbita położona najbliżej jądra ,o promieniu r
1
= 5,3*10
-11
m
nazywany promieniem Bohra oznaczanym przez a
0
. Model atomu Bohra ma znaczenie
wyłącznie historyczne.
KWANTOWA NATURA ŚWIATŁA
, zgodnie z którą
. Uważa się dziś, że zjawiska charakterystyczne dla fal, jak na
światła można wyjaśnić tylko za jej pomocą. Jednakże w
przeciwieństwie do opozycyjnej
teoria falowa nie jest w stanie wyjaśnić
innych zjawisk, jak na przykład
. Przyjmuje się więc, iż światło ma
Fale materii de Broglie'a
Fale de Broglie, fale materii, jeden z aspektów istnienia materii. Cząstki elementarne i inne
obiekty mikroświata w pewnych warunkach wykazują właściwości typowe dla fal (np. ulegają
zjawisku dyfrakcji). Każdej cząstce swobodnej o pędzie p można przypisać długość fali:
λ = h/p,
gdzie h - stała Plancka.
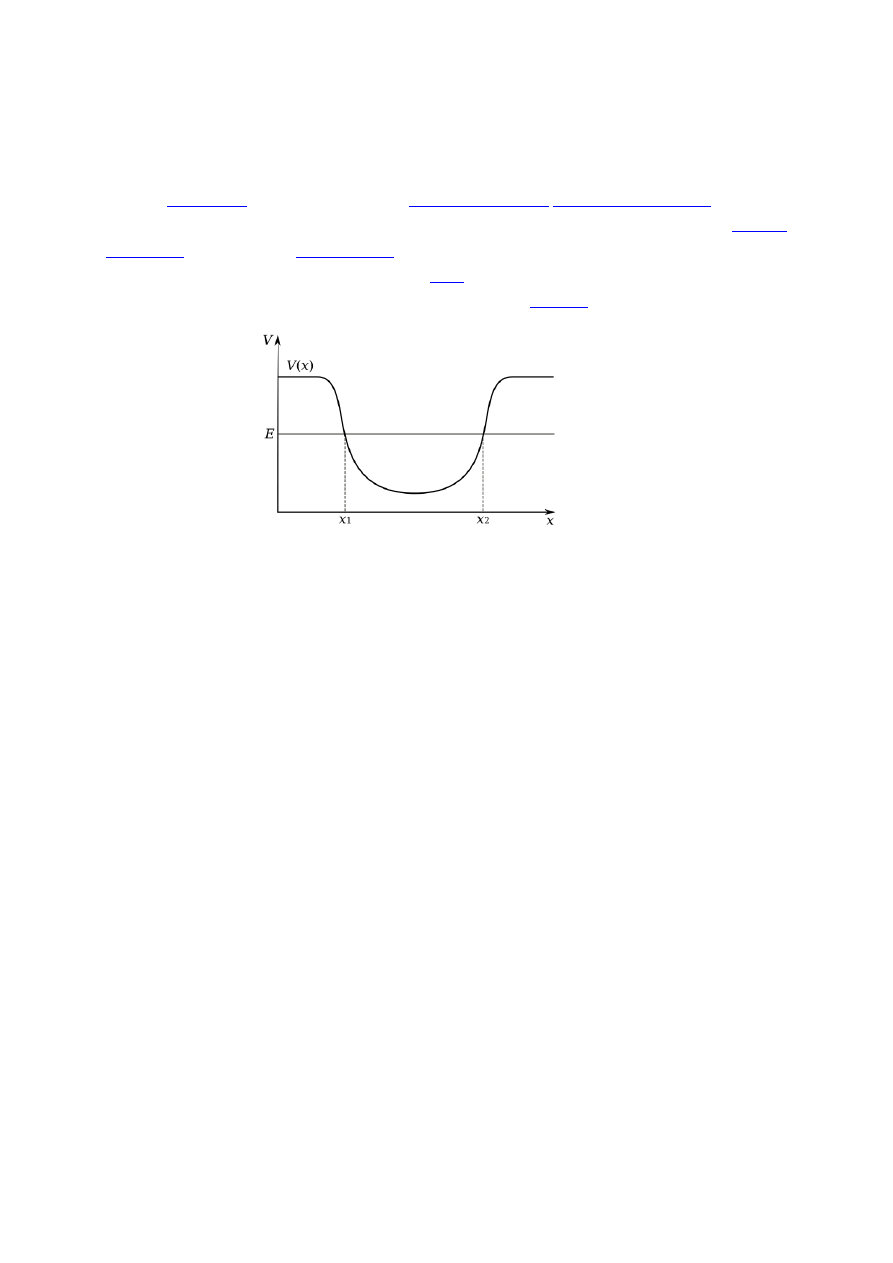
STUDNIA POTENCJAŁU
. Energia
uwięziona w studni potencjału nie może przekształcić się w inną postać energii (
studni potencjału), ponieważ jest uwięziona w
lokalnym minimum studni. Z tego względu,
nie może podążyć do globalnego minimum
energii potencjalnej tak, jak miałoby to miejsce z powodu

RÓWNANIE SCHRÖDINGERA
Schrödingera równanie, podstawowe równanie mechaniki kwantowej sformułowane w
1926 przez
(zgodne z tzw. obrazem Schrödingera ). Ogólnie Schrödingera
równanie ma postać:
gdzie: i - jednostka urojona, h = h/2π (h - stała Plancka), t - czas, H -hamiltonian układu, ψ -
funkcja falowa opisująca ten układ.
Równanie Schrödingera dla atomu wodoru ma postać:
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron