Wykład 11 

dr inż. Anna Borowska-Centkowska 

centkowska@if.pw.edu.pl

 

Gmach Mechatroniki, pok. 333, tel. 22 234 8405 

 
 

 



Teoria względności, szczególna teoria 

względności, postulaty 



Transformacja Galileusza 



Transformacja Lorentza 



Wnioski wynikające z transformacji Lorentza: 

dylatacja czasu, kontrakcja długości, 

względność jednoczesności 



Dynamika relatywistyczna: pojęcie masy, 

pędu i energii 

Teoria Względności 

• Pomiary  –  co,  gdzie,  kiedy  oraz  w  jakiej 

odległości w czasie i przestrzeni. 

• Transformowanie 

(przekształcanie) 

wyników  pomiarów  między  poruszającymi 
się układami. 

• Teoria  względności  –  dotyczy  układów, 

które mogą przyspieszać. 

• Szczególna 

teoria 

względności 

– 

dotyczy  inercjalnych 

układów  odniesienia, 

czyli  takich  w 

których  obowiązują  zasady 

dynamiki  Newtona 

(układy  poruszają  się 

względem siebie ze stałymi prędkościami). 

• Czas 

i 

przestrzeń 

są 

wzajemnie 

powiązane. 

• Czas nie płynie ze stałą szybkością. 

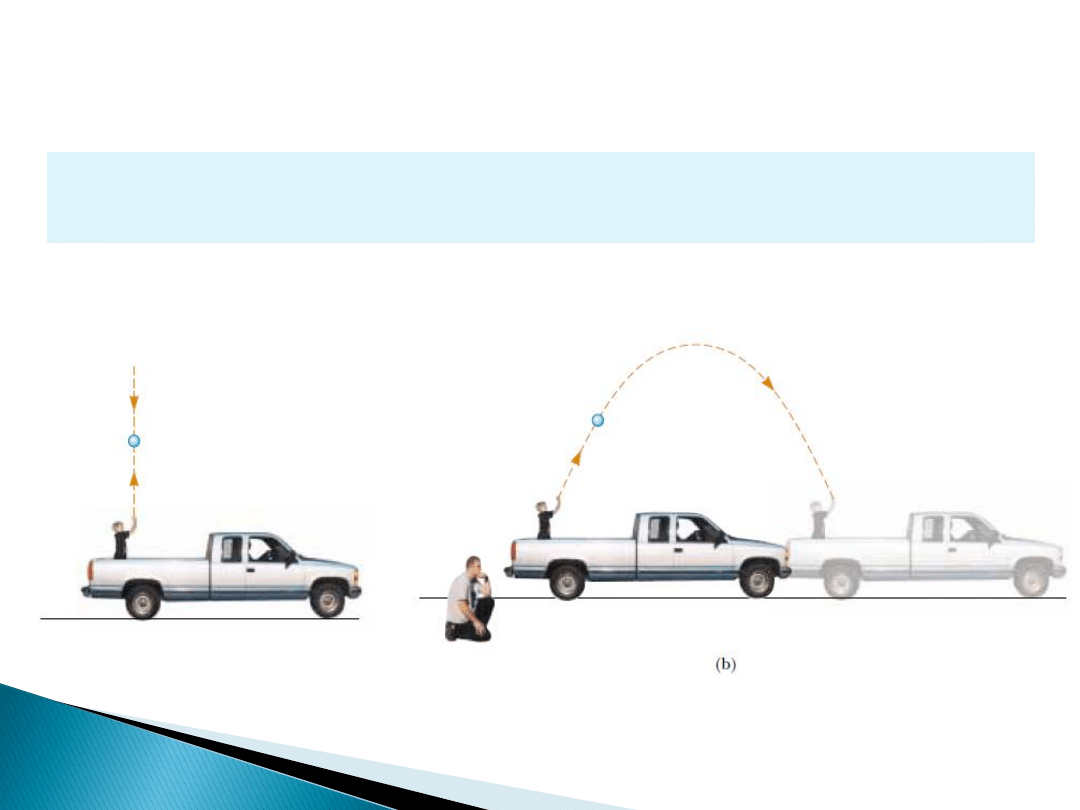
Postulaty szczególnej teorii względności 

Dla wszystkich 

obserwatorów w inercjalnych układach odniesienia 

prawa fizyki 

są takie same – żaden z układów nie jest wyróżniony. 

I postulat 

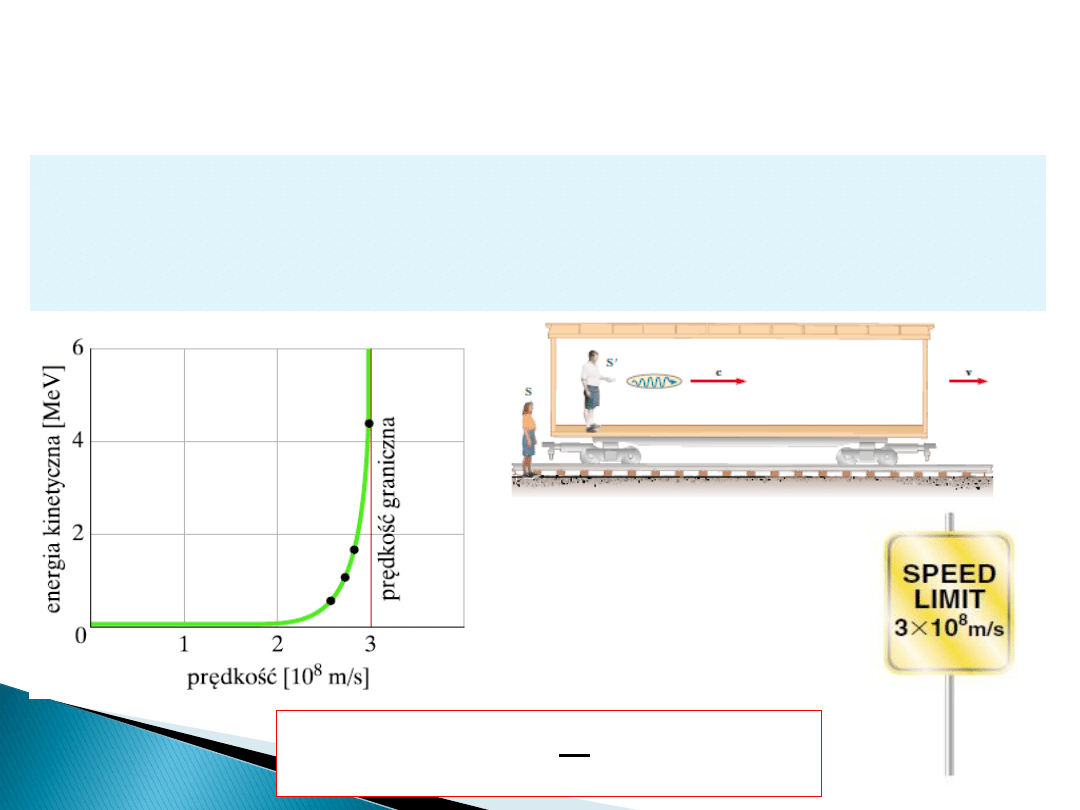
Postulaty szczególnej teorii względności 

We  wszystkich  inercjalnych 

układach  odniesienia  i  we  wszystkich 

kierunkach 

światło rozchodzi się w próżni z taką samą prędkością c. 

Prędkość  żadnego  ciała  przenoszącego  energię  lub  informacje  nie  może 
przekroczyć prędkości granicznej. 

II postulat 

𝑐 = 299 792 458

𝑚

𝑠

≈ 3 ∙ 10

8

𝑚/𝑠 

Postulaty szczególnej teorii względności 

Potwierdzenie 

doświadczalne 

(CERN, 

1964):  
- mimo 

zwiększania  energii  kinetycznej 

elektronów,  ich  prędkość  nie  przekracza 
prędkości światła 
- 

prędkość  światła  wyemitowanego  przez 

źródło poruszające się z prędkością bliską c 
wynosi zawsze c 

– tyle samo, co dla źródła 

w spoczynku. 

𝜋

0

→ 𝛾 + 𝛾

 

𝑣 = 0.999 75𝑐

 

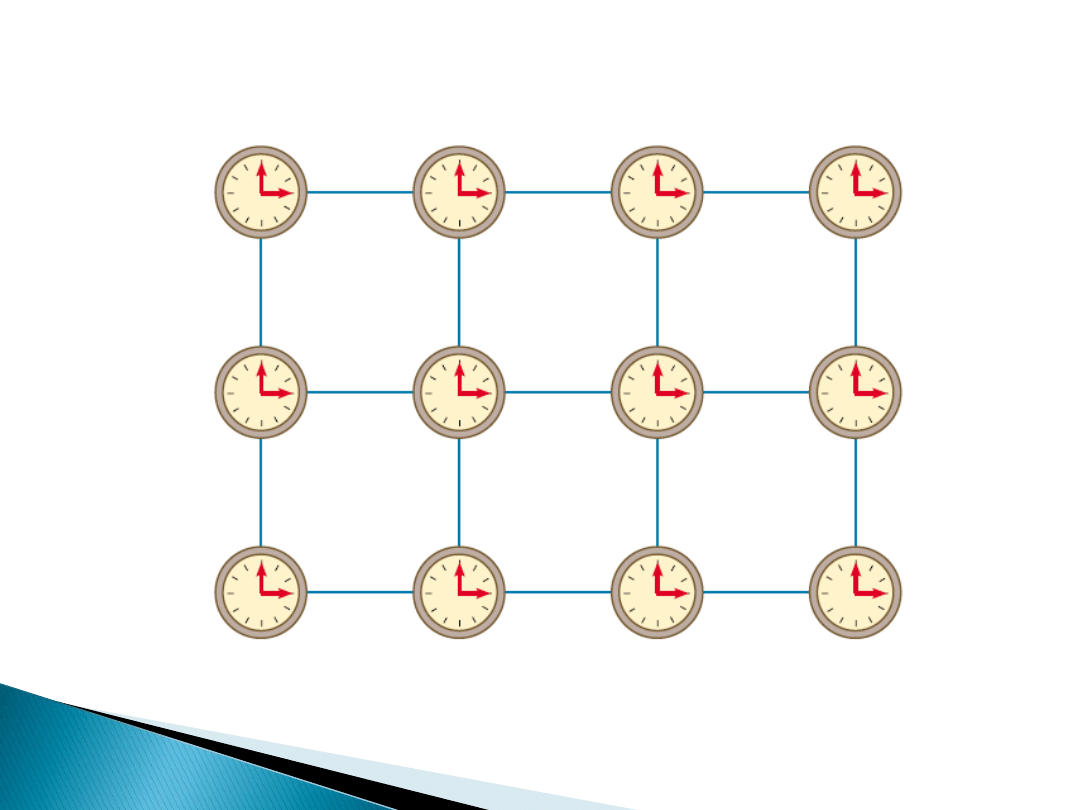
Jak „mierzyć” zdarzenie? 

1.

Współrzędne przestrzenne 

2.

Współrzędna czasowa 

3.

Współrzędne czasoprzestrzenne 

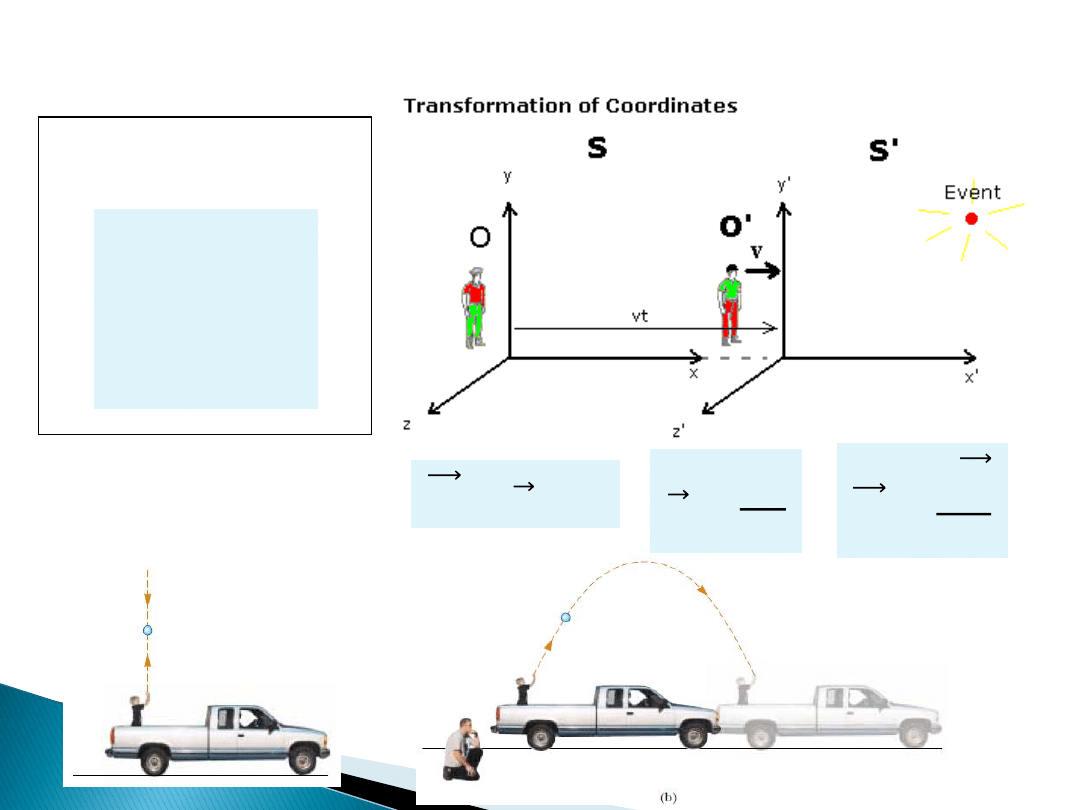
Transformacja Galileusza i Lorentza 

Galileusza (u << c) 

𝑡

′

= 𝑡

 

𝑥

′

= 𝑥 − 𝑣𝑡

 

𝑦

′

= 𝑦

 

𝑧

′

= 𝑧 

𝑢′ = 𝑢 − 𝑣  

𝑢 =

𝑑𝑥 

𝑑𝑡

 

𝑢′ =

𝑑𝑥′

𝑑𝑡

 

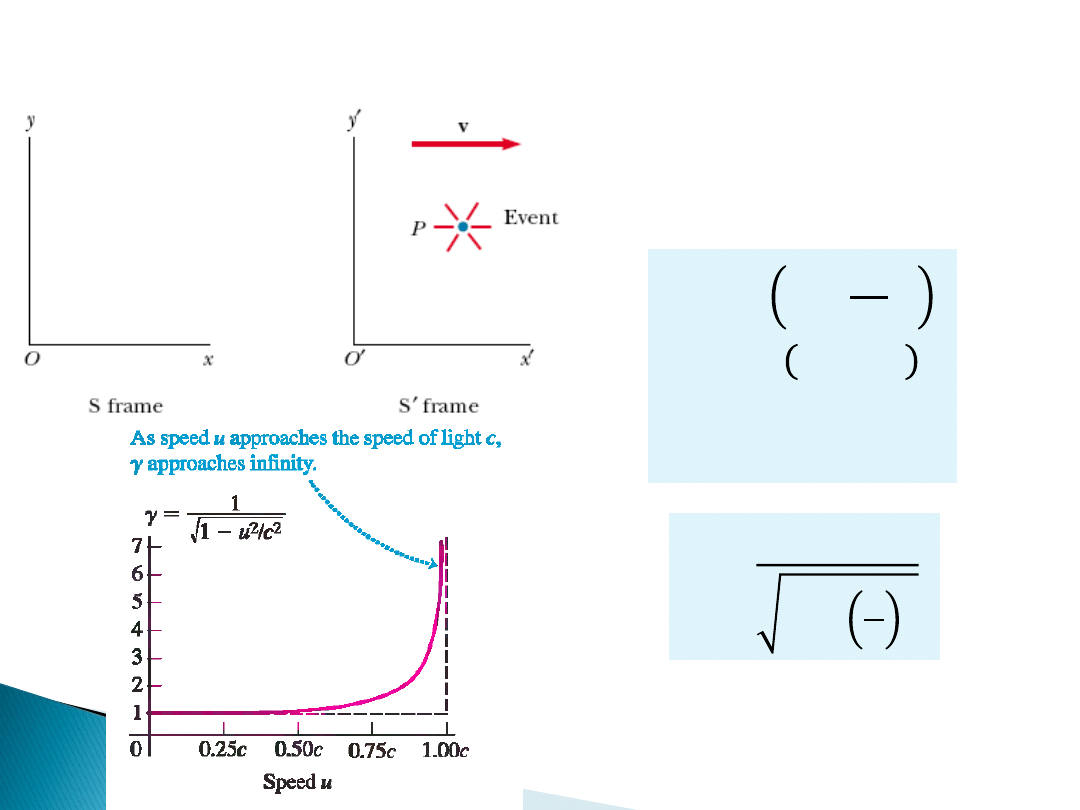
Transformacja Galileusza i Lorentza 

Transformacja Lorentza (v



c) 

𝑡

′

= 𝛾 𝑡 −

𝑣

𝑐

2

𝑥

 

𝑥

′

= 𝛾 𝑥 − 𝑣𝑡

 

𝑦

′

= 𝑦

 

𝑧

′

= 𝑧 

𝛾 =

1

1 − 𝑣𝑐

2

 

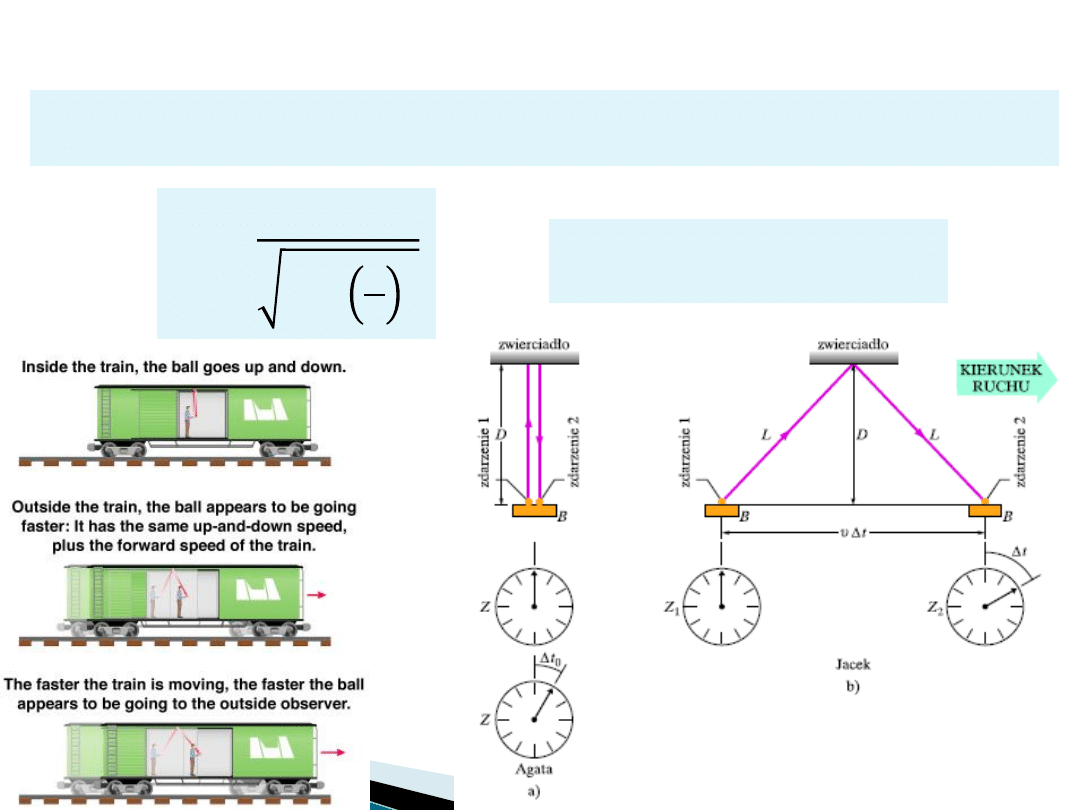
Względność czasu i dylatacja czasu 



t 

– obserwator stacjonarny 



t

0

 

– obserwator w ruchu 

Odstęp między zdarzeniami zależy od tego, w jakiej odległości od siebie 
one nastąpiły, zarówno w przestrzeni jak i w czasie.   

∆𝑡 =

∆𝑡

0

1 − 𝑣𝑐

2

 

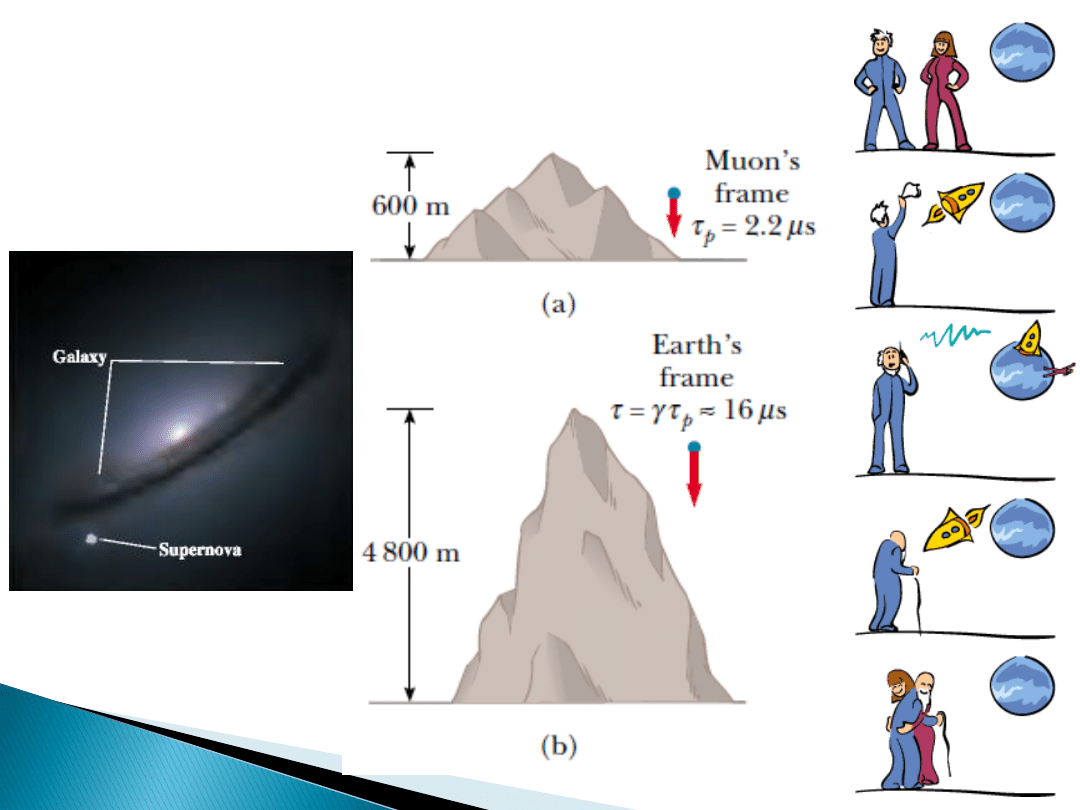
Paradoks bliźniąt 

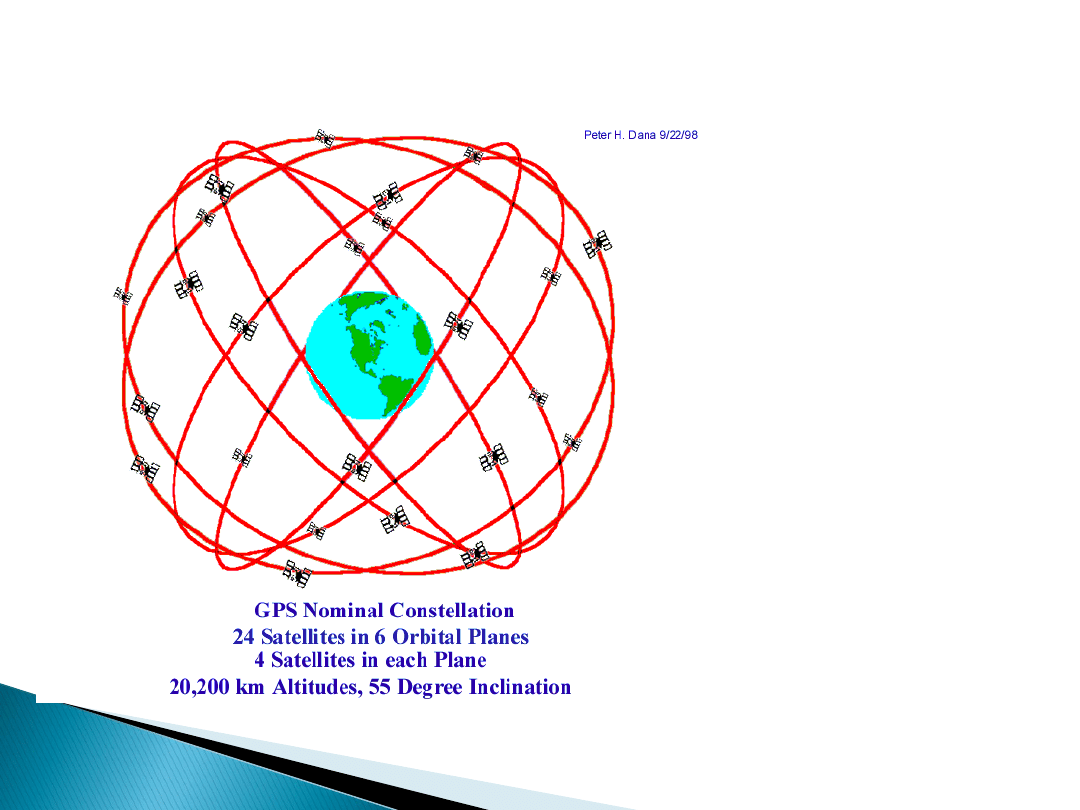
System GPS 

Wymagana 
dokładność zegara: 
20 ns/dzień 
 
Efekt 
„relatywistyczny”: 
38,600 ns/dzień