2011-01-18

1

EKONOMETRIA 1

wykład 12

dr Beata Madras-Kobus

Prognozowanie

na podstawie

modelu

ekonometrycznego

PROGNOZOWANIE

Przewidywanie przyszłości w sposób

racjonalny

z

wykorzystaniem

metod

naukowych.

PROGNOZA

Konkretny

wynik

wnioskowania

w

przyszłość

na

podstawie

znajomości

modelu

ekonometrycznego

opisującego

pewien

wycinek

sfer

zjawisk

ekonomicznych

Funkcje prognozy

z

Preparacyjna (działanie
przygotowujące inne działania)

z

Aktywizująca (pobudzanie do
podejmowania działań)

z

Informacyjną (oswajanie z
nadchodzącymi zmianami)

Klasyfikacja prognoz

Ze względu na sposób wyrażania stanu zmiennej

z

Ilościowa

-punktowa
-przedziałowa

z

Jakościowa

Ze względu na kryterium czasu

z

Krótkookresowa

z

Średniookresowa

z

Długookresowa

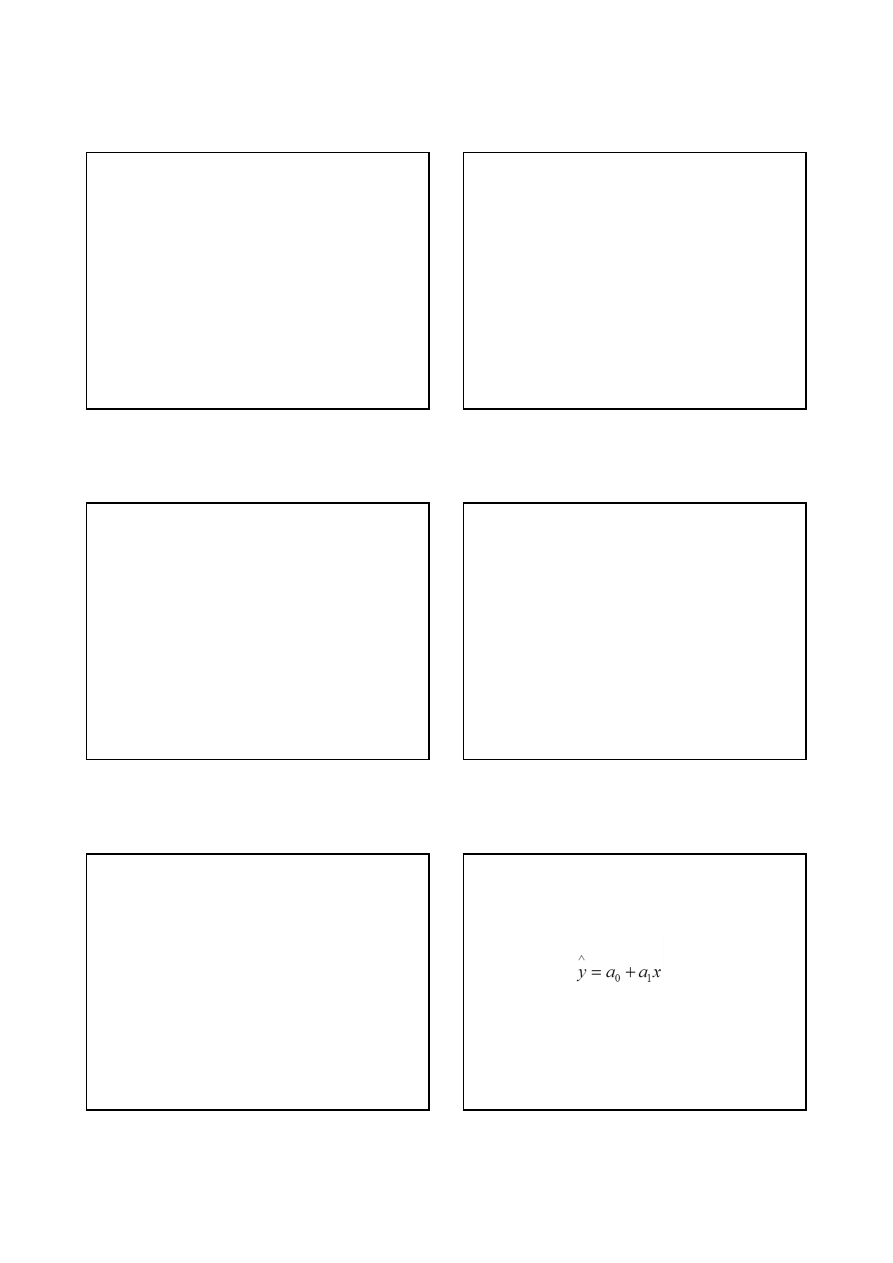
Mamy dany oszacowany model

ekonometryczny postaci:

Predykcją ekonometryczną nazywa się
proces wnioskowania w przyszłość na
podstawie modelu ekonometrycznego

2011-01-18

2

Aby można było wnioskować na podstawie
modelu ekonometrycznego, muszą być spełnione
następujące założenia:

1. znajomość modelu zmiennej prognozowanej,
2. stabilność parametrów i postaci analitycznej

modelu,

3. stabilność rozkładu odchyleń losowych

modelu,

4. znajomość wartości zmiennej objaśniającej w

okresie prognozowania,

5. dopuszczalność ekstrapolacji modelu poza

próbę statystyczną

Źródłem wartości zmiennych objaśniających w
okresie prognozowania mogą być:

1. trendy zmiennej objaśniającej,
2. modele opisowe zmiennej objaśniającej,
3. plany społeczno – gospodarcze,
4. inne studia prognostyczne

1. prognozy punktowe
2. prognozy przedziałowe

Wyróżniamy dwa rodzaje prognoz ekonometrycznych:

Etapy prognozowania ekonometrycznego

1. Sformułowanie zadania prognostycznego.
Określamy obiekt, zjawisko bądź proces będący
przedmiotem

prognozy,

czyli

zmienną

endogeniczną. Ustalamy cel wykonania prognozy,
jej pożądany horyzont i wymagalną dokładność.

2. Sformułowanie przesłanek prognozy.
Definiujemy model ekonometryczny opisujący
wybraną zmienną endogeniczną. Stosownie do tego
wyboru gromadzimy dane statystyczne, szacujemy
parametry modelu, poddajemy go weryfikacji oraz
badaniu stabilności. Ustalamy wartości zmiennej
egzogenicznej w okresie prognozy.

3. Wyznaczenie prognozy i jej interpretacja.
Obliczamy wartość zmiennej endogenicznej w
okresie prognozy oraz interpretujemy otrzymane
wyniki.

4. Ocena dokładności predykcji.
Ostatni etap

stanowi realizację jednego z

postulatów predykcji ekonometrycznej, który głosi,
żeby dla każdej prognozy obliczyć i ocenić wartość
mierników określających stopień dokładności
predykcji.

Stabilność postaci analitycznej modelu

– test Ramseya

Za pomocą testu Ramseya weryfikujemy
hipotezę o stabilności postaci analitycznej
modelu. Przeprowadzenie tego testu upewnia
nas, że wybrana – liniowa – postać analityczna
modelu

jest

dobrze

dobrana

do

opisu

zmienności

danej

zmiennej

objaśnianej

w

zależności

od

wartości

zmiennych

objaśniających.

2011-01-18

3

Krok 1: Szacujemy parametry modelu ekonometrycznego

Krok 2: Po oszacowaniu modelu obliczamy wartości
teoretyczne

zmiennej objaśnianej oraz współczynnik

determinacji. Oznaczamy go R

I

2

.

Krok 3: Szacujemy parametry modelu ekonometrycznego

Krok

4:

Po

oszacowaniu

modelu

wyznaczamy

współczynnik determinacji. Oznaczamy go R

II

2

.

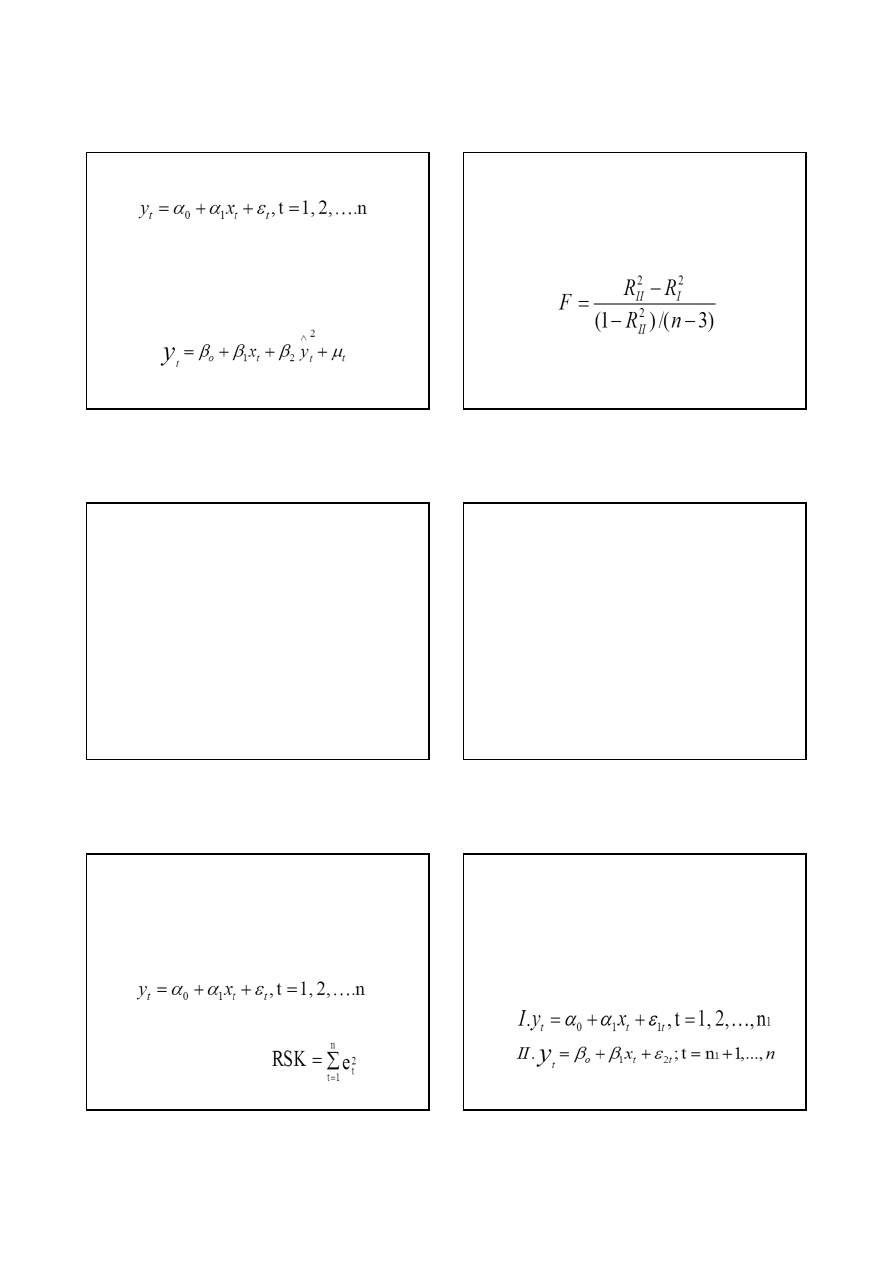
Krok 5: Badamy, czy przyrost wartości współczynnika
determinacji w modelu drugim w porównaniu z modelem
pierwszym jest statystycznie istotny. Obliczamy wartość
statystyki:

gdzie:
n - liczba obserwacji

Krok 6: Przy danym poziomie istotności weryfikujemy
hipotezy
H

0

: wybór postaci analitycznej modelu ekonometrycznego

jest prawidłowy;
H

1

: wybór postaci analitycznej modelu nie jest

prawidłowy.

Jeśli prawdziwa jest hipoteza zerowa, to statystyka F ma
rozkład F-Snedecora o r

1

= 1, r

2

= n– 3 stopniach swobody

Wartość krytyczną testu dla określonej liczby
stopni swobody oraz przy danym poziomie
istotności oznaczamy F*.

Jeśli F > F*, to hipotezę zerową odrzucamy.
W przeciwnym przypadku nie ma podstaw do
odrzucenia hipotezy

zerowej. Wnioskujemy

wtedy, że wybrana przez nas postać analityczna
modelu jest dobrze dobrana do opisu zmienności
danej zmiennej objaśnianej w zależności od
wartości zmiennych objaśniających.

Stabilność parametrów modelu – test Chowa

Test Chowa jest najczęściej używanym testem do
weryfikowania

hipotezy o stabilności parametrów

modelu ekonometrycznego.
Krok 1: Szacujemy składowe wektora parametrów
modelu ekonometrycznego:

a następnie obliczamy sumę kwadratów reszt dla tego
modelu. Przyjmujemy oznaczenie :

Krok 2: Dzielimy okres obserwacji t = 1, 2, ……, n na
dwa podokresy t = 1, 2, …, n

1

oraz t = n

1

+1, n

1

+2, …., n.

Podział ten może być podziałem subiektywnym albo
wynikającym

z

analizy

zjawiska

bądź

procesu

opisywanego przez model.
Krok 3: Szacujemy składowe wektorów parametrów
modeli ekonometrycznych I oraz II odpowiednio:

Zakładamy, że składniki losowe obu modeli spełniają
założenia KMNK.

2011-01-18

4

Krok 4: Obliczamy sumy kwadratów reszt modeli I oraz
II, czyli RSK

I

i RSK

II

.

Krok 5: Dodatkowo obliczamy: RSK

III

= RSK

I

+ RSK

II

oraz RSK

IV

= RSK – RSK

III

.

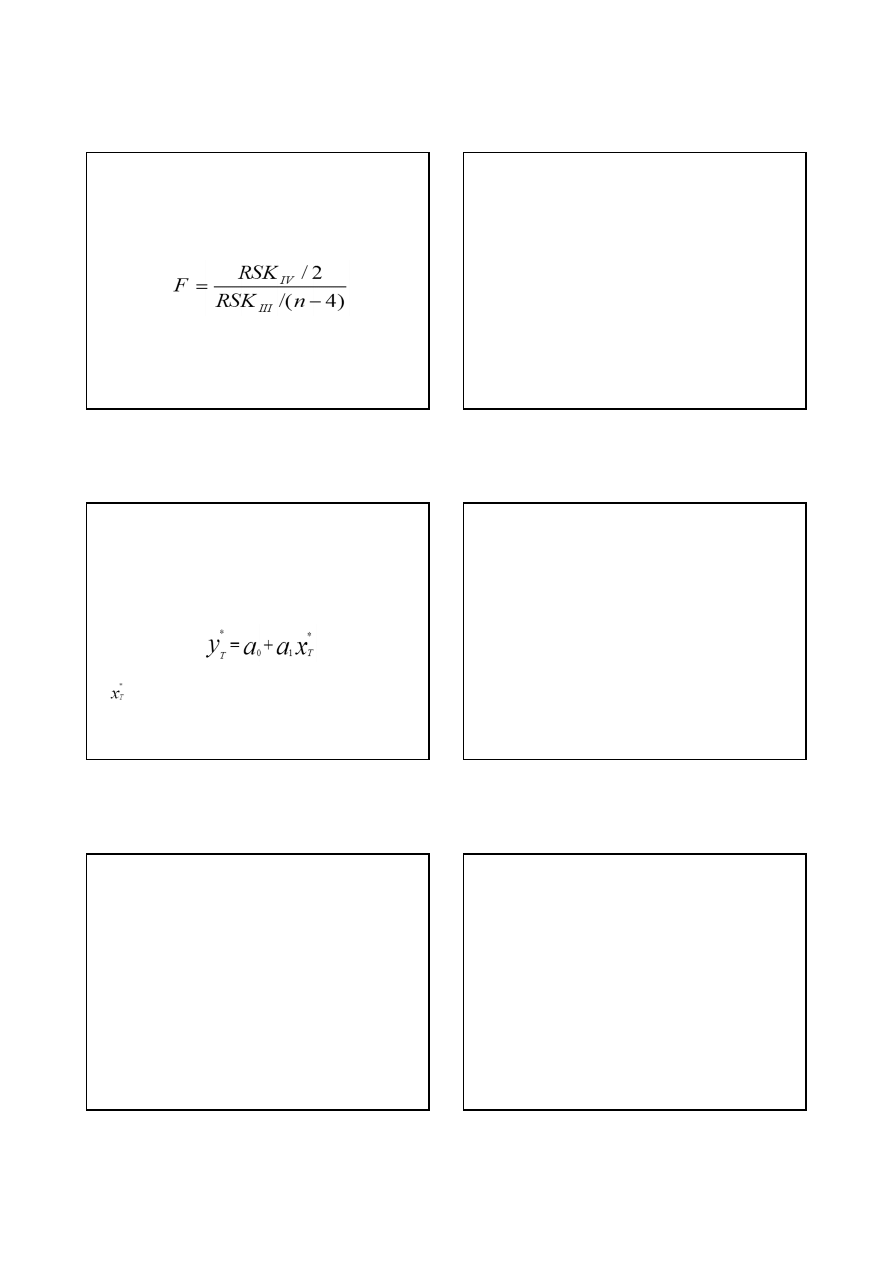
Krok 6: Wyznaczamy wartość statystyki F

Krok 7: Przy danym poziomie istotności weryfikujemy
hipotezę zerową
H

0

: α=α

I

=α

II

, czyli hipotezę o stabilności parametrów

wobec hipotezy alternatywnej
H

1

: parametry modelu nie są stabilne

Jeśli prawdziwa jest hipoteza zerowa, to statystyka F ma
rozkład F – Snedecora z r

1

=2 oraz r

2

= n-4 stopniami

swobody.
Wartość krytyczną testu dla określonej liczby stopni
swobody oraz przy danym poziomie istotności oznaczamy
F*.
Jeśli F > F*, to hipotezę zerową odrzucamy. W
przeciwnym wypadku nie ma podstaw do odrzucenia
hipotezy zerowej. Wnioskujemy wtedy, że parametry
liniowego modelu ekonometrycznego są stabilne. To
oznacza, że oceny parametrów stojących przy tych
samych zmiennych objaśniających, zyskane na podstawie
obserwacji statystycznej z różnych okresów, nie różnią się
istotnie.

Prognoza punktowa

Prognoza punktowa jest liczbą uznaną za najlepszą
ocenę wartości zmiennej prognozowanej w okresie
prognozowania.
Prognozę punktową zmiennej Y wyznacza się jako:

gdzie:

- wartość zmiennej objaśniającej w okresie
prognozowania .

Ocena prognozy

Wśród powodów dokonywania nietrafnych prognoz
ekonometrycznych najczęściej wymienia się następujące:
Błąd estymacji modelu – oszacowania parametrów różnią
się od prawdziwych nieznanych wartości tych parametrów;
Błąd struktury stochastycznej modelu

- założenia

KMNK, chociaż pozytywnie zweryfikowane, jednak nie są
spełnione;
Błąd losowy – wartość składnika losowego jest różna od
zera w okresie prognozy;
Błąd specyfikacji – pominięcie w zestawie zmiennych
egzogenicznych, zmiennych mających istotny wpływ na
wartości zmiennej endogenicznej lub wybór niewłaściwej
postaci analitycznej modelu;

Błąd warunków endogenicznych – nagła zmiana
warunków procesu kształtowania się wartości
zmiennej objaśnianej;
Błąd warunków egzogenicznych – przyjęcie
niewłaściwych wartości zmiennych objaśniających
w okresie prognozy;
Błąd pomiaru – podana do wiadomości po
oszacowaniu modelu korekta danych statystycznych.

Ocena ex ante stopnia dokładności predykcji
uwzględnia tylko pierwszą i drugą z wymienionych
przyczyn

powstawania

błędów

prognozy

ekonometrycznej.

Błąd prognozy określa się jako różnicę
między

rzeczywistą

wartością

(y

τ

),

a

wartością prognozowaną (y

τ

*

) analizowanej

zmiennej Y, wyznaczoną na moment lub
okres

τ. Błąd ten można szacować na

podstawie prognoz wygasłych (szacowanie
błędu ex post) lub stochastycznie szacować
na podstawie informacji ex ante.

2011-01-18

5

Błędy ex ante podają spodziewaną
wartość odchyleń rzeczywistych wartości
zmiennej prognozowanej od prognoz.

Błąd ex post można liczyć na jeden
moment lub okres albo, w przypadku
budowy prognoz na kilka kolejnych m
okresów: [n+1, n+2, …, T], dla każdego
momentu

lub

okresu

z

przedziału

empirycznej weryfikacji prognoz.

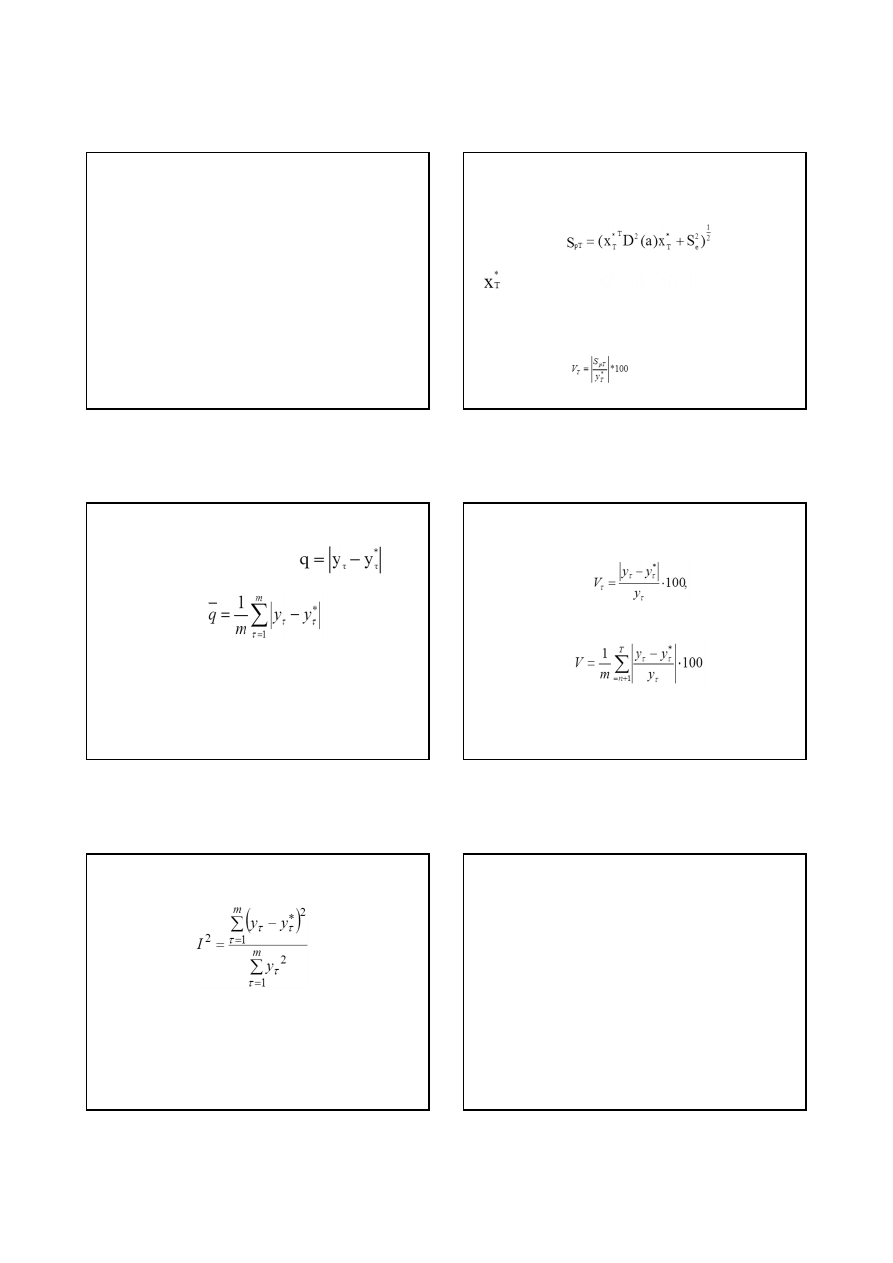
Ocena ex ante prognozy punktowej

Dla prognozy punktowej szacujemy tzw. średni błąd predykcji
ex ante:

gdzie:

- jest wektorem

Błąd ten informuje, o ile przeciętnie prognozy będą się różnić od
rzeczywistych wartości zmiennej prognozowanej w okresie
prognozowania

Wartość wyrażenia

nazywamy względnym średnim

błędem predykcji ex ante

Dla pojedynczej jednostki

τ > n licząc bezwzględny błąd

prognozy ex post stosuje się wzór:

a w przypadku przedziału średni błąd prognozy ex post:

gdzie
y

τ

* - prognoza zmiennej Y wyznaczona na moment lub okres

τ > n,

y

τ

– rzeczywista wartość zmiennej prognozowanej w momencie lub

okresie

τ > n,

n – liczba wyrazów szeregu czasowego zmiennej prognozowanej.

Wyraża on odchylenie (średnie odchylenie) prognoz
wygasłych

od

wartości

rzeczywistych

zmiennej

prognozowanej.

Miary dokładności prognozy ex post

Można

liczyć

też

względny

błąd

prognozy ex post w czasie t:

Lub średni względny błąd prognozy ex
post:

Względne błędy informują, jaki procent
rzeczywistej

wartości

stanowi

błąd

prognozy (średni błąd prognozy).

Dla przedziału weryfikacji prognoz można też liczyć
współczynnik Theila:

I informuje, jaki był przeciętny względny błąd
prognozy dla rozpatrywanych okresów.
Dla prognoz idealnych miernik ten przyjmuje
wartość 0. Im większe są różnice między
wartościami rzeczywistymi a prognozowanymi, tym
większa wartość współczynnika.

Można

przyjąć

następujące

kryteria

dopuszczalności prognoz:

V < 3% - prognozy bardzo dobre,
3%< V < 5% - prognozy dobre,
5% < V < 10% - prognozy dopuszczalne,
V > 10% - prognozy niedopuszczalne.

2011-01-18

6

Prognoza przedziałowa jest przedziałem
ufności,

który

ze

z

góry

zadanym

prawdopodobieństwem,

nazywanym

wiarygodnością prognozy, zawiera nieznaną
wartość zmiennej prognozowanej w okresie
prognozowania

Przedział

ufności ma postać:

gdzie:
1 –

α

– przyjęty poziom ufności

t

α

n-(k+1)

– wartość z rozkładu t-Studenta dla zadanego

poziomu istotności

α i n – (k+1) stopniach swobody