Oficyna Edukacyjna * Krzysztof Pazdro

PRÓBNY

EGZAMIN MATURALNY

Z MATEMATYKI

POZIOM PODSTAWOWY

1. Sprawdź, czy arkusz egzaminacyjny zawiera 16 stron

(zadania 1–34). Ewentualny brak zgłoś przewodniczącemu

zespołu nadzorującego egzamin.

2. Rozwiązania zadań i odpowiedzi wpisuj w miejscu na to

przeznaczonym.

3. Odpowiedzi do zadań zamkniętych (1–25) przenieś na kartę

odpowiedzi, zaznaczając je w części karty przeznaczonej

dla zdającego. Zamaluj pola do tego przeznaczone.

Błędne zaznaczenie otocz kółkiem i zaznacz właściwe.

4. Pamiętaj, że pominięcie argumentacji lub istotnych

obliczeń w rozwiązaniu zadania otwartego (26–34) może

spowodować, że za to rozwiązanie nie będziesz mógł dostać

pełnej liczby punktów.

5. Pisz czytelnie i używaj tylko długopisu lub pióra z czarnym

tuszem lub atramentem.

6. Nie używaj korektora, a błędne zapisy wyraźnie przekreśl.

7. Pamiętaj, że zapisy w brudnopisie nie będą oceniane.

8. Możesz korzystać z zestawu wzorów matematycznych,

cyrkla i linijki oraz kalkulatora.

9. Na karcie odpowiedzi wpisz swój numer PESEL i przyklej

naklejkę z kodem.

10. Nie wpisuj żadnych znaków w części przeznaczonej dla

egzaminatora.

PRZED MATURĄ

MAJ 2015

Czas pracy:

170 minut

Liczba punktów

do uzyskania: 50

WPISUJE ZDAJĄCY

KOD

PESEL

Próbny egzamin maturalny z matematyki. Poziom podstawowy

2

Oficyna Edukacyjna * Krzysztof Pazdro

ZADANIA ZAMKNIĘTE

W zadaniach od 1. do 25. wybierz i zaznacz na karcie odpowiedzi poprawną odpowiedź.

Zadanie 1. (1 pkt)

Liczba log

sin

cos

3 3

30

30

°

°

+ log

3 3

60

tg ° jest równa:

A. 1

B. 0

C. 3

D. 3 3 .

Zadanie 2. (1 pkt)

Liczba

6

3

2

2

−

(

)

jest równa:

A. 12 – 5 6 B.

6 C.

2

1

2

2

−

(

)

D.

6 3

2

2

+

(

)

.

Zadanie 3. (1 pkt)

Liczba o 25% mniejsza od różnicy kwadratu podwojonej liczby a i potrojonego kwadratu licz-

by b to:

A. 0,75(2a

2

– 3b

2

)

B. 0,25[(2a)

2

– (3b)

2

] C. 0,75(2a – 3b)

2

D. 0,75[(2a)

2

– 3b

2

].

Zadanie 4. (1 pkt)

Liczba y jest mniejsza niż 120% liczby x. Wynika stąd, że:

A. x = 120%y B.

x = 831

3

%y C.

x > 831

3

%y D.

x < 831

3

%y.

Zadanie 5. (1 pkt)

Funkcja f(x) = (m

2

+ 2m + 1)x + 2m jest rosnąca dla:

A. dowolnego m rzeczywistego

B. m różnego od –1

C. m różnego od 1

D. m większego od 2.

Zadanie 6. (1 pkt)

Funkcja kwadratowa y = f(x) ma dwa miejsca zerowe: –2 i 4. Równanie prostej mającej 1 punkt

wspólny z wykresem funkcji f może wyrażać się wzorem:

A. y = f(1)

B. y = f(–2)

C. y = f(4)

D. y = f(2).

Próbny egzamin maturalny z matematyki. Poziom podstawowy

3

Oficyna Edukacyjna * Krzysztof Pazdro

BRUDNOPIS (nie podlega ocenie)

Próbny egzamin maturalny z matematyki. Poziom podstawowy

4

Oficyna Edukacyjna * Krzysztof Pazdro

Zadanie 7. (1 pkt)

Dziedzinę funkcji f(x) = log 2

1

2

+ −

−

x x

x

określają nierówności:

A. –1 < x < 1 lub 1 < x < 2 B. –1 ≤ x < 1 lub 1 < x ≤ 2 C. –1 < x < 2 D. –1 ≤ x ≤ 2.

Zadanie 8. (1 pkt)

Jeden z pierwiastków równania ax

2

+ bx + c = 0 jest równy − b

a

. Wówczas c jest równe:

A. –b

B. –a

C. 0

D. 1.

Zadanie 9. (1 pkt)

Do zbioru rozwiązań nierówności x

2

> 7 nie należy liczba:

A. 3

B. –4

C. 1

D. 5.

Zadanie 10. (1 pkt)

Okrąg wpisano w romb o przekątnych mających długość 2 i 2 3. Promień tego okręgu jest

równy:

A. 3

B. 1

C. 3

2

D. 2.

Zadanie 11. (1 pkt)

Suma kątów wewnętrznych wielokąta wypukłego jest równa 720°. Wielokąt ten ma

A. 9

B. 6

C. 12

D. 15

przekątnych.

Zadanie 12. (1 pkt)

W trójkącie równobocznym o boku 9 obcięto naroża (3 trójkąty równoboczne) i otrzymano

sześciokąt foremny. Pole tego sześciokąta jest równe:

A. 27 3

4

B. 9 7

4

C. 81 3

4

D. 27 3

2

.

Zadanie 13. (1 pkt)

Równanie prostej równoległej do prostej 2x + 3y – 5 = 0 i przechodzącej przez punkt (1, –3)

ma postać:
A. 2x + 3y + 7 = 0

B. y = −

+

2
3

5
3

x

C. 2x + 3y = 5

D. 2x + 3y = 7.

Próbny egzamin maturalny z matematyki. Poziom podstawowy

5

Oficyna Edukacyjna * Krzysztof Pazdro

BRUDNOPIS (nie podlega ocenie)

Próbny egzamin maturalny z matematyki. Poziom podstawowy

6

Oficyna Edukacyjna * Krzysztof Pazdro

Zadanie 14. (1 pkt)

Współrzędne przeciwległych wierzchołków kwadratu są równe A(1, 2) i C(7, –6). Pole kwa-

dratu jest równe:

A. 80

B. 64

C. 50

D. 100.

Zadanie 15. (1 pkt)

Zapas żywności, jaki ma 12 wędrowców na pustyni, starczy im na dwa tygodnie. O ilu mniej

musiałoby być podróżników, aby jedzenia starczyło im na trzy tygodnie, przy założeniu, że

wszystkie porcje są takie same?

A. o 4

B. o 8

C. o 2

D. o 3.

Zadanie 16. (1 pkt)

W ciągu geometrycznym a

1

· a

2

= 1 i a

3

· a

4

= 16. Zatem q jest równe:

A. 2

B. 2 lub –2

C. 1

2

D. –2.

Zadanie 17. (1 pkt)

Ze zbioru liczb naturalnych od 1 do 30 losujemy jedną liczbę. Prawdopodobieństwo, że wylo-

sowana liczba jest parzysta lub podzielna przez 5, jest równe:
A. 7

15

B. 1

2

C. 3

5

D. 7

10

.

Zadanie 18. (1 pkt)

Funkcja kwadratowa o miejscach zerowych (–2) i 5, której wykres przechodzi przez punkt

A(3, 0), ma wzór:

A. y = 3(x – 2)(x + 5)

B. y = 3(x + 2)(x – 5)

C. y = (x – 2)(x + 5)

D. nie ma takiej funkcji.

Zadanie 19. (1 pkt)

Dany jest ciąg a

n

= n

n

+

−

5

3

2

. Wyrazy ciągu, które są mniejsze od 1

2

, mają numery:

A. większe od 12

B. mniejsze od 12

C. mniejsze od 5

D. większe od 5.

Zadanie 20. (1 pkt)

Przekrój osiowy walca jest prostokątem o bokach, których długości pozostają w stosunku 1 : 2

(wysokość jest 2 razy dłuższa od średnicy) i jego pole powierzchni bocznej jest równe 72π.

Objętość walca jest równa:
A. 108π

B. 54 2 π

C. 81π

D. 90π.

Próbny egzamin maturalny z matematyki. Poziom podstawowy

7

Oficyna Edukacyjna * Krzysztof Pazdro

BRUDNOPIS (nie podlega ocenie)

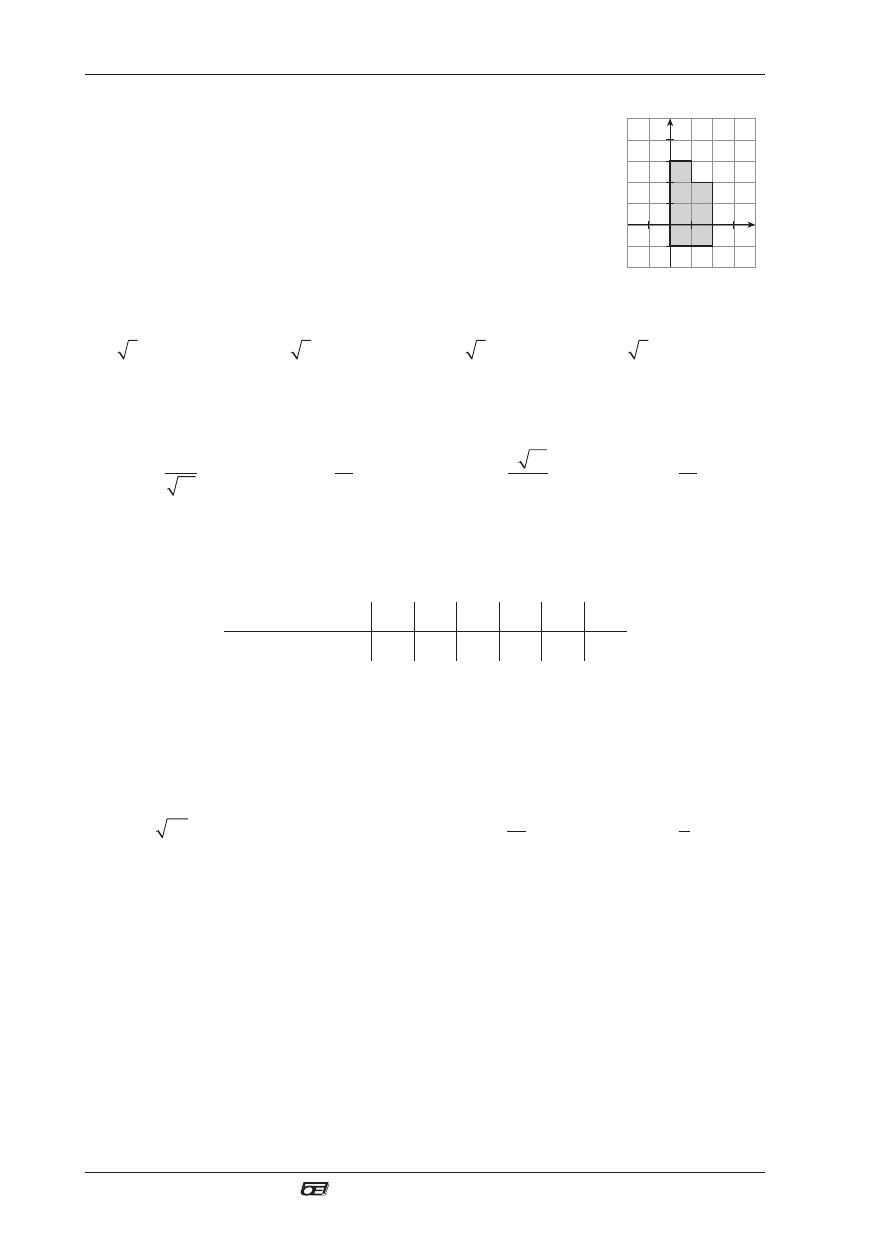
Próbny egzamin maturalny z matematyki. Poziom podstawowy

8

Oficyna Edukacyjna * Krzysztof Pazdro

Zadanie 21. (1 pkt)

Figura pokazana na rysunku obraca się wokół osi OY. Pole powierzchni

powstałej bryły jest równe:

A. 18π B. 20π C. 22π D. 19π.

Zadanie 22. (1 pkt)

Przekątna sześcianu jest o 2 cm dłuższa od jego krawędzi. Objętość sześcianu jest równa:
A. 8 3

B. 6 3 + 10

C. 16 3

D. 8 3 + 8.

Zadanie 23. (1 pkt)

Jeżeli a jest kątem ostrym i tg a = 4, to

A. sin a = 4

17

B. sin a = 4

17

C. cos a = 4 17

17

D. cos a = 4

17

.

Zadanie 24. (1 pkt)

Wyniki testu semestralnego z matematyki, którego średnia była równa 3,8, przedstawiono w ta-

beli:

Oceny

1

2

3

4

5

6

Liczba ocen

2

2

8

9

x

3

Mediana ocen jest równa:

A. 4

B. 3,5

C. 5

D. 4,5.

Zadanie 25. (1 pkt)

Która z funkcji przyjmuje wyłącznie wartości ujemne?
A. f(x) = −

x

B. f(x) = –x

2

C. f(x) = − 1

2

x

D. f(x) = − 1

x

.

0

1

2

–1

3

4

1

2 3

–1

X

Y

Próbny egzamin maturalny z matematyki. Poziom podstawowy

9

Oficyna Edukacyjna * Krzysztof Pazdro

BRUDNOPIS (nie podlega ocenie)

Próbny egzamin maturalny z matematyki. Poziom podstawowy

10

Oficyna Edukacyjna * Krzysztof Pazdro

ZADANIA OTWARTE

Rozwiązania zadań o numerach od 26. do 34. należy zapisać w wyznaczonych miejscach

pod treścią zadania.

Zadanie 26. (2 pkt)

Znajdź wartość największą funkcji f(x):

f x

x

x

( ) =

−

+

2

2

4

3

2

.

Zadanie 27. (2 pkt)

Powierzchnia boczna stożka po rozwinięciu na płaszczyźnie stanowi 1

3

koła. Oblicz kąt roz-

warcia stożka.

Próbny egzamin maturalny z matematyki. Poziom podstawowy

11

Oficyna Edukacyjna * Krzysztof Pazdro

Zadanie 28. (2 pkt)

Rozwiąż równanie:

1
2

1

16

12 21

2

8

2

4

2

0

2

log

( , )









 ⋅ +

=

(

)

⋅

x NWD

x

x

x

.

Zadanie 29. (2 pkt)

W trójkącie prostokątnym o kącie ostrym a

sinα

α

tg

= 3

2

. Wyznacz kąty ostre tego trójkąta.

Próbny egzamin maturalny z matematyki. Poziom podstawowy

12

Oficyna Edukacyjna * Krzysztof Pazdro

Zadanie 30. (2 pkt)

Pole równoległoboku jest równe 24, a jego środek symetrii jest oddalony od dwóch nierówno-

ległych boków odpowiednio o 2 i o 3. Oblicz obwód równoległoboku.

Zadanie 31. (2 pkt)

W pudełku jest 6 kul białych i 4 czarne. Losujemy 3 kule. Oblicz prawdopodobieństwo, że

wśród nich jest co najmniej jedna kula czarna.

Próbny egzamin maturalny z matematyki. Poziom podstawowy

13

Oficyna Edukacyjna * Krzysztof Pazdro

Zadanie 32. (3 pkt)

Znajdź wzór ogólny ciągu (a

n

), wiedząc, że a

1

= 3, a

2

= 5, a

3

= 10 i różnice między sąsiednimi

wyrazami ciągu (a

n

) tworzą ciąg arytmetyczny.

Próbny egzamin maturalny z matematyki. Poziom podstawowy

14

Oficyna Edukacyjna * Krzysztof Pazdro

Zadanie 33. (5 pkt)

Środek okręgu wpisanego w trapez prostokątny znajduje się w odległości 2 cm i 4 cm od koń-

ców dłuższego ramienia. Znajdź pole trapezu.

Próbny egzamin maturalny z matematyki. Poziom podstawowy

15

Oficyna Edukacyjna * Krzysztof Pazdro

Zadanie 34. (5 pkt)

W graniastosłupie prawidłowym trójkątnym przekątna ściany bocznej o długości 10 jest nachy-

lona do sąsiedniej ściany pod kątem 30°. Oblicz objętość tego graniastosłupa.

Próbny egzamin maturalny z matematyki. Poziom podstawowy

16

Oficyna Edukacyjna * Krzysztof Pazdro

PESEL

WYPEŁNIA ZDAJĄCY

WYPEŁNIA EGZAMINATOR

Nr

zad.

Punkty

0

1

2

3

4

5

26
27
28
29
30
31
32
33
34

Nr

zad.

Odpowiedzi

1

A

B

C

D

2

A

B

C

D

3

A

B

C

D

4

A

B

C

D

5

A

B

C

D

6

A

B

C

D

7

A

B

C

D

8

A

B

C

D

9

A

B

C

D

10

A

B

C

D

11

A

B

C

D

12

A

B

C

D

13

A

B

C

D

14

A

B

C

D

15

A

B

C

D

16

A

B

C

D

17

A

B

C

D

18

A

B

C

D

19

A

B

C

D

20

A

B

C

D

21

A

B

C

D

22

A

B

C

D

23

A

B

C

D

24

A

B

C

D

25

A

B

C

D

SUMA

PUNKTÓW

D

0 1 2 3 4 5 6 7 8 9

J

0 1 2 3 4 5 6 7 8 9