Autor: dr inż. Piotr Wyciślok

Strona 1 / 3

INSTRUKCJA

LABORATORIUM METOD

POLOWYCH.

TWORZENIE MODELU W

METODZIE ELEMENTÓW

SKOŃCZONYCH

MP/004

Autor: dr inż. Piotr Wyciślok

Strona 2 / 3

CEL
Celem ćwiczenia jest praktyczne zapoznanie się z budową modeli geometrii z
wykorzystaniem programu FEMAP.

WSTĘP TEORETYCZNY:
Przystępując do modelowania dowolnego problemu za pomocą metody elementów
skończonych należy pamiętać, że nasz model obejmuje pewną przestrzeń, którą
nazywamy modelem geometrycznym. Model ten b

udujemy za pomocą punktów

(point), krzywych(curve), powierzchni (surface i Boundary region)

i brył (solid). Przy

czym zawsze występuja w modelu wszystkie te elementy tzn. w oparciu o punkty
budujemy krzywe, które stanowią podstawę do opisu powierzchni. Te ostatnie zaś
słłużą do definiowania brył. Uzyskany model przestrzeni poddajemy dyskretyzacji
zgodnej ze fizykalnym modelem zjawisk zachodzących w przestrzeni modelu, np. w
przypadku analizy ugięcia belki , naszą przestrzenią modelu będzie (z zastrze-
żeniem, że rozpatrujemy belkę jako ustrój trójwymiarowy) sama belka, tj. przestrzeń
przez tę belkę zajmowana. Zaś dyskretyzacja powinna odbyć się za pomocą
elementów skończonych, które opisują zachowanie fizykalne w naszym modelu. Dla
naszego przykładu winny być to elementy bryłowe opisane równaniami znanymi z
wytrzymałości materiałów. Proces dyskretyzacji jest we współczesnych systemach
MES w dalekim stopniu zautomatyzowany. Jednakże czekają w tym procesie
również pułapki, powodujące, że niezbędny jest nad procesem podziału nadzór, jak
również dbałość o podanie właściwych parametrów generacji siatek elementów
(mesh). Te ostatnie zależą od wybranych typów elementu jak i naszych arbitralnych
decyzji (np. co do wielkości elementu). Ten ostatni może być również podany na
wiele sposobów, np. poprzez określenie gęstości węzłów na krawędziach modelu lub
zdefiniowanie średniej wielkości elementu. Zdyskretyzowany model powinien również
zawierać dyskretyzowane wartości stałych (wynikających z zastosowanej teorii),
które przypiszemy do konkretnego elementu. W naszym przykładzie będą to np.
dane materiału belki jak moduł Younga czy liczba Poissona. Kolejną czynnością jest
zdyskretyzowanie ustalonych warunków brzegowych i obciążeń modelu. Określenie
warunków brzegowych w naszym przykładzie to zdefiniowanie węzłów w których
znane są wartości przemieszczeń uogólnionych (translacji i rotacji) oraz określenie
węzłów z zadanymi obciążeniami. Co do zasady zarówno warunki brzegowe jak i
obciążenia zadawane są w węzłach, jednakże oprogramowanie preprocesora
(programu ułatwiającego przygotowanie danych) pozwala na przykładanie obciążeń i
warunków brzegowych zarówno do elementów jak i elementów geometrii (punktów,
krzywych, powierzchni). Należy jednak pamiętać, że skutkuje to w ostatecznym
rozrachunku przyłożeniem obciążenia do węzłów modelu.

WYKAZ NIEZBĘDNYCH PROGRAMÓW:

FEMAP.

MATERIAŁY DYDAKTYCZNE:

1.

Wykład.

Autor: dr inż. Piotr Wyciślok

Strona 3 / 3

2.

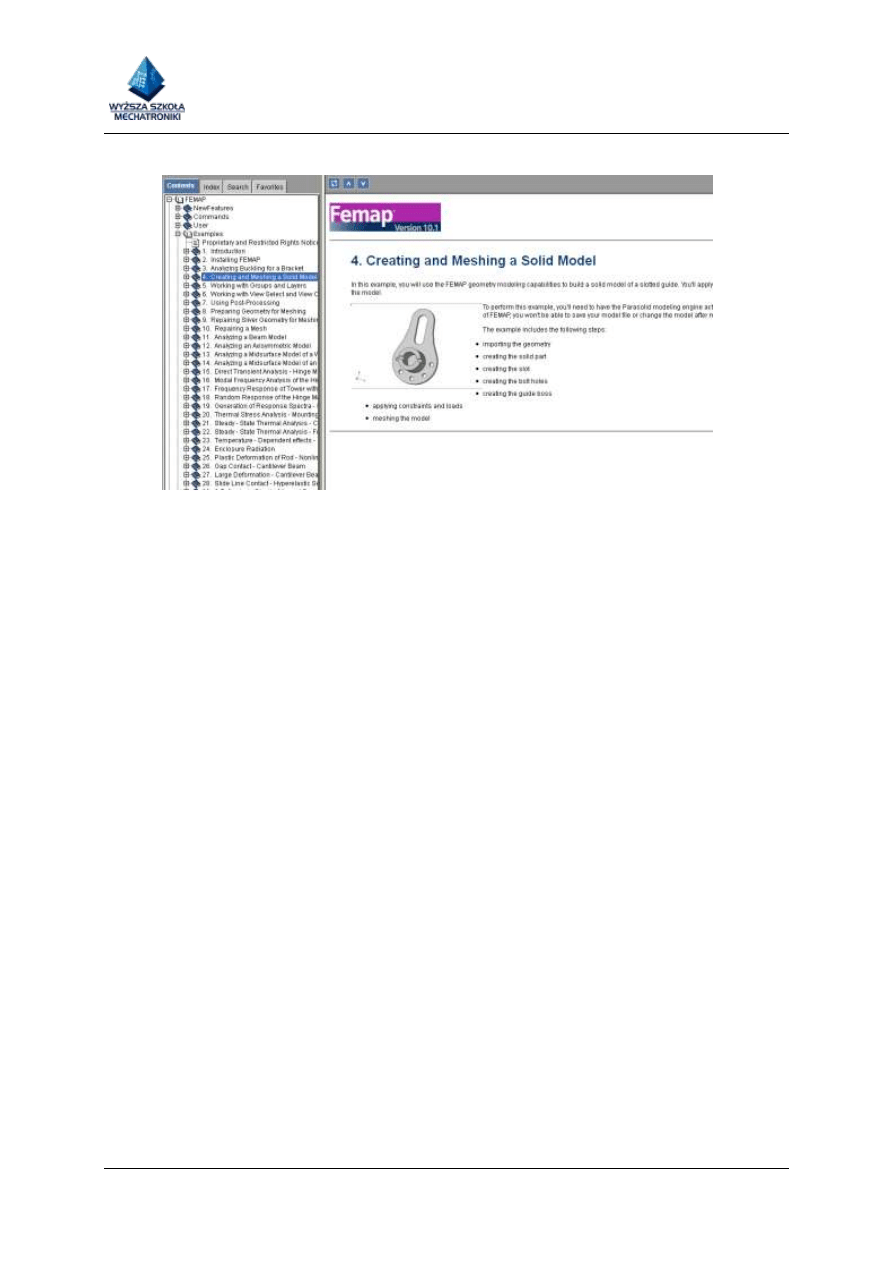
Przykład z pomocy programu FEMAP :

Rysunek 1 Przykład do realizacji w pomocy programu FEMAP

ZADANIE DO REALIZACJI:
Budowa modelu bryły , jego dyskretyzacja zgodnie z tokiem podanym w przykładzie
nr 4 pliku pomocy programu FEMAP

PRZEBIEG ĆWICZENIA

1.

Podział na grupy.

2.

Test wiadomości.

3. Wykonanie modelu

zgodnego z treścią zadania:

a. Importowanie zarysu modelu z formatu neutralnego.
b. Budowa modelu geometrii.

i.

Wyciąganie bryły

ii.

Wykonywanie otworów i wycięć

iii. Wykonywanie prowadnika

iv.

Wykonywanie nacięcia w prowadniku

4. Dyskretyzacja modelu-

podział na elementy skończone

5.

Zadanie warunków brzegowych i obciążeń.

6. Uruchamianie modelu
7.

Wykonanie obliczeń.