2.2.

Funkcja ciągła w zbiorze – ujęcie poglądowe

Otoczeniem liczby (punktu) x o promieniu r ( r > 0) nazywamy przedział (x – r, x + r).

Piszemy U(x, r). Mówimy również, że liczby tego otoczenia są bliskie x z dokładnością do r.

Przykłady

a)

)

1

;

3

(

−

U

= (

−

4,

−

2) ; b)

)

01

,

0

;

4

,

3

(

U

= (3,39 ; 3,41), (zob. rys.);

Rozważmy funkcję liczbową f o dziedzinie D

f

i wartościach w zbiorze Z, czyli

f: D

f

→

Z; niech otoczenie argumentu (punktu) a zawiera się w jej dziedzinie.

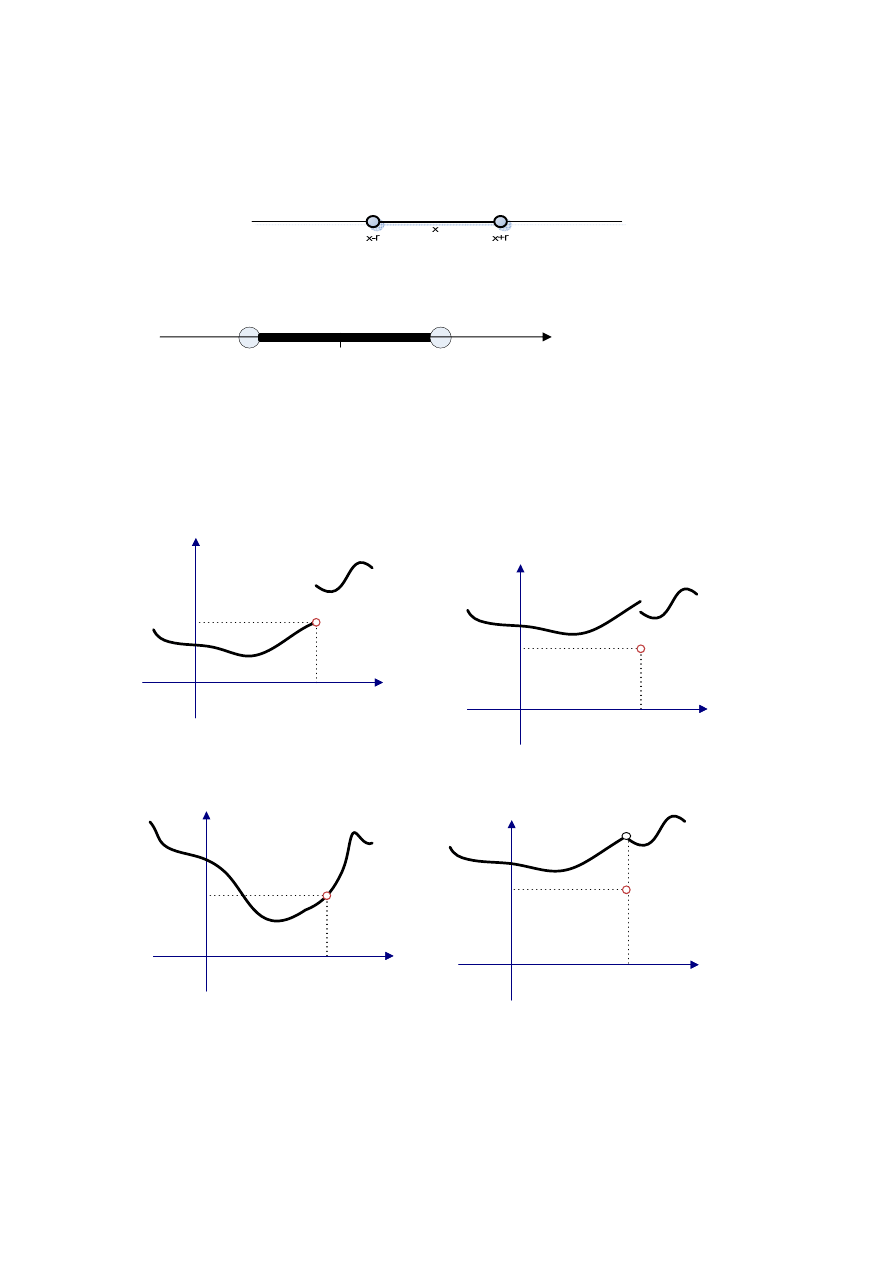
Wykresy tego rodzaju funkcji przedstawiają rysunki; punkt o współrzędnych (a, f(a) )

zaznaczony na czerwono zaliczamy również do wykresu tej funkcji.

a

f(a)

a

x

y

a

f(a)

a

x

y

a

f(a)

a

x

y

a

f(a)

x

y

Rys. a)

Rys. c)

Rys. d)

Rys. b)

Tylko funkcja f, której wykres przedstawia rysunek c) ma własność, którą można

obrazowo wyrazić następująco:

•

„mała” zmiana argumentu a niesie ze sobą „małą” zmianę wartości f(a) lub też:

•

wartości funkcji dla argumentów „bliskich” a są również „bliskie” f(a) albo też:

3,4

3,39

3,41

•

w małym otoczeniu argumentu a funkcja przybiera wartości bliskie f(a),

•

w małym otoczeniu punktu (a, f(a)) wykres tej funkcji można „narysować bez

odrywania ołówka od papieru”.

Mówimy wtedy, że funkcja liczbowa, której wykres przedstawia rys. c) jest ciągła w

punkcie a.

Inne punkty dziedziny każdej z tych funkcji różne od a również mają tę własność. Są

więc ciągłe w tych punktach.

O funkcjach, których wykresy przedstawiają rysunki a), b), d) mówimy, że nie są ciągłe

w punkcie a. Punkt a nazywamy punktem nieciągłości funkcji.

Rozważamy funkcję f, której wykres przedstawia rysunek:

Funkcja ta jest nieciągła w punkcie a. By to uzasadnić – poglądowo – rozumujemy tak:

Jakkolwiek byśmy nie wybrali liczb

bliskich argumentowi a (na rysunku

zaznaczono je kolorem niebieskim),

to ich obrazy poprzez funkcję f nie

będą liczbami bliskimi wartości f(a)

- na rysunku liczby te przedstawia

przedział zaznaczony kolorem

czerwonym.

a

f(a)

x

y

Definicja

Funkcję ciągłą w każdym punkcie podzbioru A dziedziny D

f

funkcji liczbowej f nazywamy

funkcją ciągłą w zbiorze A. W szczególnym przypadku zbiór A może być przedziałem

(otwartym, domkniętym).

Przykład

Funkcje f i g określamy następująco:

f(x) =







=

≠

+

2

3

2

1

2

x

dla

x

dla

x

, g(x) =







=

≠

−

0

0

0

1

x

dla

x

dla

x

. Dziedziną każdej z nich jest zbiór R.

Ich wykresy przedstawia rysunek.

x

y

0

2

1

3

5

y = 2x+1

Różnice między tymi funkcjami są istotne.

•

W przypadku funkcji f mamy do czynienia z tzw. nieciągłością usuwalną. Wystarczy w

tym celu zdefiniować nową funkcję f* określoną wzorem f*(x) = 2x + 1. Obie funkcje f

i f* mają równe wartości w każdym punkcie poza punktem x = 2. Przy czym funkcja f*

jest funkcją ciągłą.

•

W przypadku funkcji g mamy do czynienia z nieciągłością nieusuwalną. Nie istnieje

funkcja ciągła g*, która w każdym punkcie miałaby wartości równe wartościom funkcji

g. Mówiąc obrazowo żadne „poprawianie” w punkcie 0 nie uczyni z funkcji g funkcji

ciągłej.