Prędkośd
.
,
,
dt
dz
v
dt
dy
v
dt
dx
v
z
y
x
t
r
v
śr
dt
r
d
t
r
v
t
0
lim
jeżeli t0
W celu bardziej szczegółowego scharakteryzowania ruchu punktu materialnego
wprowadza się wielkości wektorowe –
prędkośd
i
przyśpieszenie
.
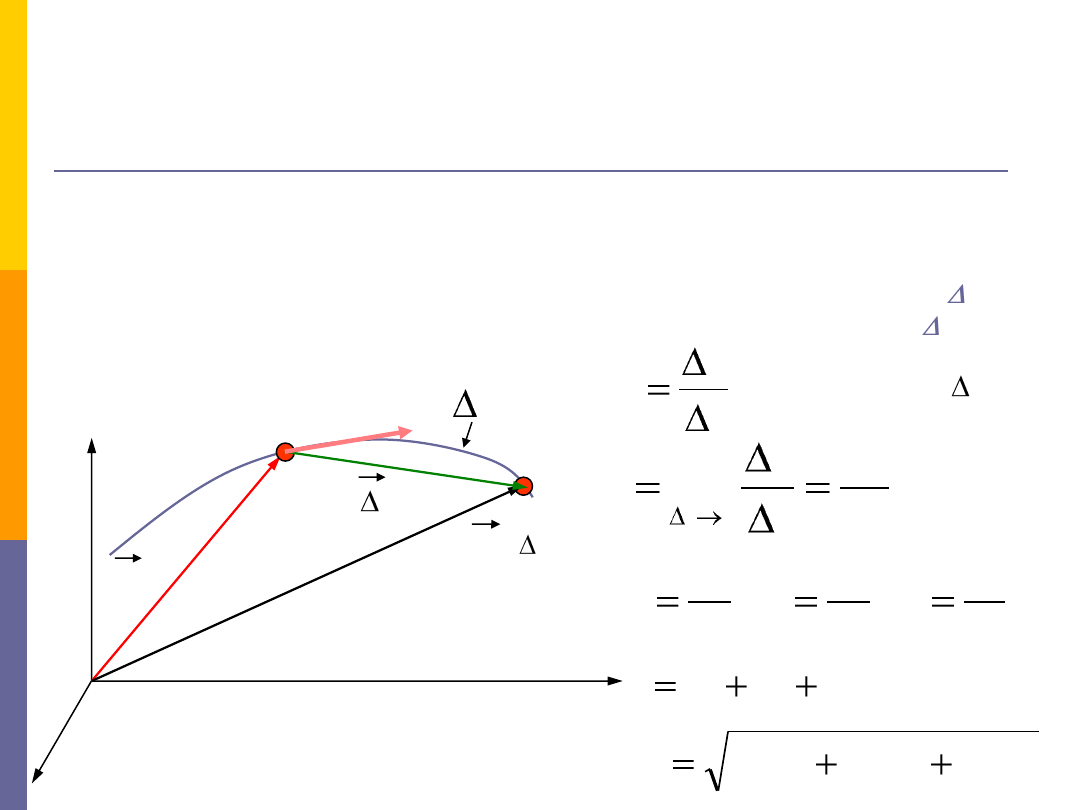
Prędkośd punktu materialnego określa zarówno szybkośd jak i kierunek ruchu
w danej chwili czasu. Wektor
średniej prędkości
v
śr
w przedziale czasu od
t
do
t+ t
określa
się jako stosunek przyrostu
r
promienia wodzącego punktu do przyrostu czasu
t.
(średnia)
v
x
y
r
r(t)
A
A’
r(t+
t
)
z
s
(chwilowa)
2
2
2
)
(
)
(
)
(
|
|
z
y
x
z
y
x
v
v
v
v
v
v
v
v
Prędkośd
dt
ds
t
s
t
v
t
0
lim
)
(
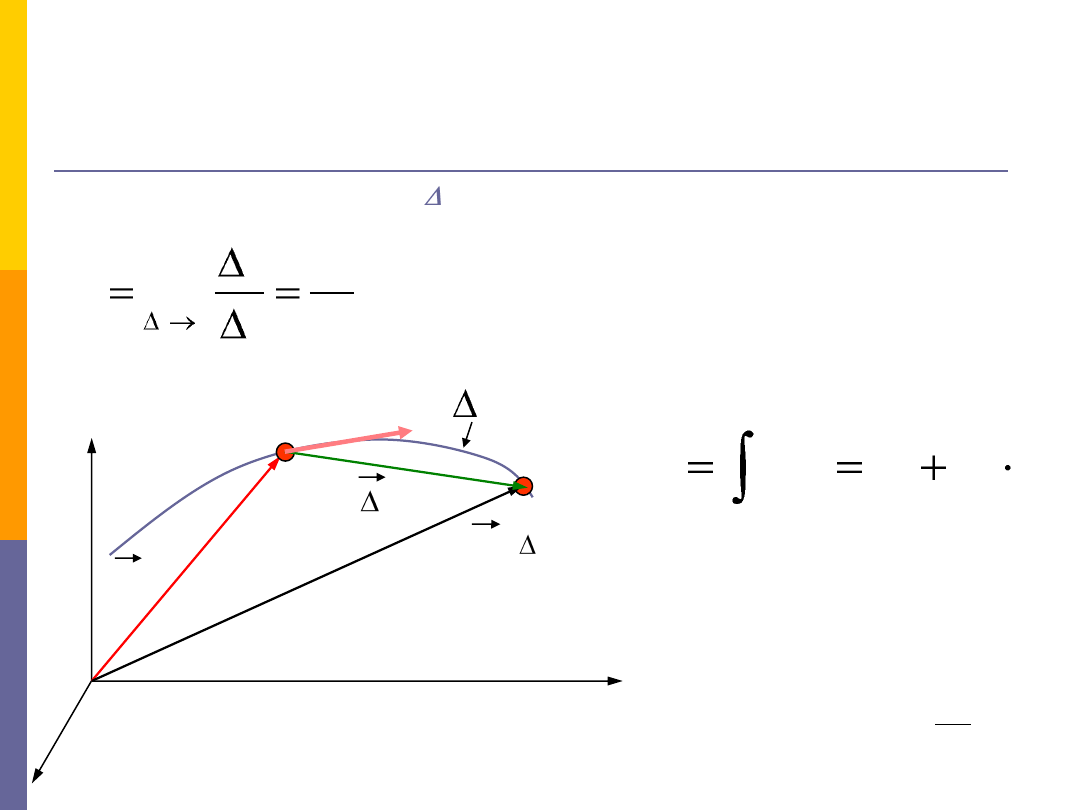
Dla małych wartości przesunięcia
r
możemy napisad:
t
v
s
dt
v
t
s
o
o
t
t
o
)
(
Zależnośd drogi od czasu
w ruchu jednostajnym!!!!!
W szczególnym przypadku, gdy nie zmienia się kierunek
I wartośd wektora prędkości, to mamy do czynienia
z ruchem jednostajnym, prostoliniowym:
v
x
y
r
r(t)
A
A’
r(t+
t
)
z
s
s
m
Jednostka:
Przyśpieszenie
s
v
v
v
t
v
a
śr
dt
v
d
t
v
a
t
0
lim
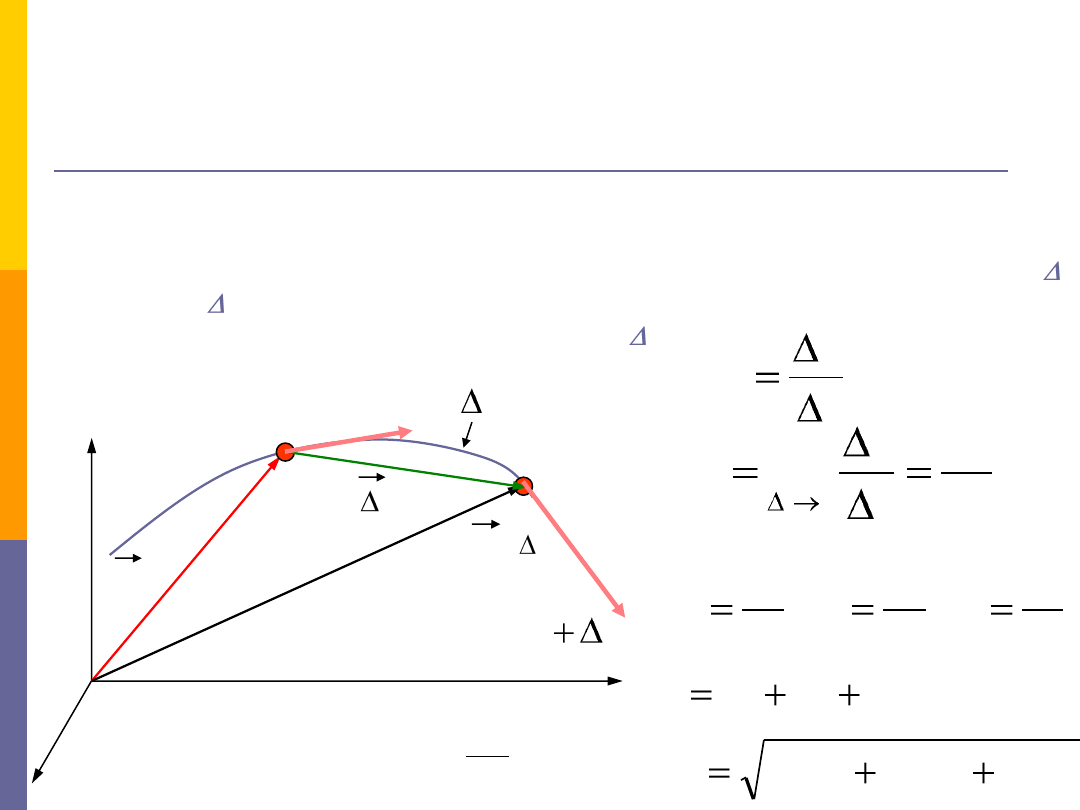
Zwykle podczas ruchu punktu materialnego jego wektor prędkości zmienia swą wartośd
i kierunek. W celu scharakteryzowania zmiany prędkości w takim ruchu wprowadza się
pojęcie
przyspieszenia
. Załóżmy, że prędkośd punktu w przedziale czasu od
t
do
t+ t
zmieniła się o
v
. Wektor
średniego przyśpieszenia
a
śr
w tym przedziale czasu określa się
jako stosunek zmiany prędkości
v
do przyrostu czasu
t
.
x
y
r
r(t)
A
A’
r(t+
t
)
z
(średnie)
(chwilowe)
.
,
,
dt
dz
a
dt
dy
a
dt
dx
a
z
y
x
2
:
s
m
Jednostka
2
2
2
)
(
)
(
)
(
|
|
z
y
x
z
y
x
a
a
a
a
a
a
a
a
Przyśpieszenie
n
s
v
v
v
n
s
a
a
a
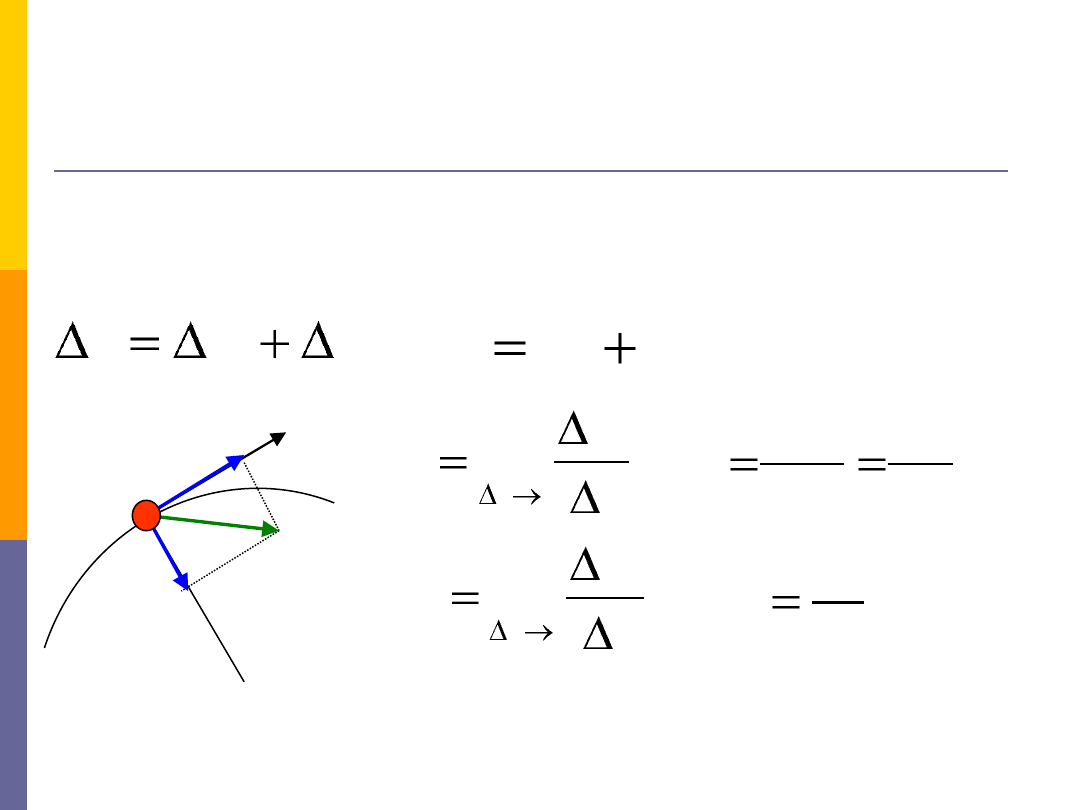
Na ogół kierunek wektora przyśpieszenia nie jest styczny do toru punktu
materialnego, w przeciwieostwie do kierunku wektora prędkości. Zmianę wektora
prędkości
v
w czasie
t
można zapisad jako:
n
a
s
a
A
a
v
t
v
a
s
t
s
0
lim
t
v
a
n
t
n
0
lim
(styczne)
(normalne)
przyśpieszenie styczne –
charakteryzuje szybkośd zmiany
bezwzględnej wartości prędkości
przyśpieszenie normalne –
charakteryzuje szybkośd zmiany
kierunku wektora prędkości
dt
v
d
dt
v
d
a
s
s
R
v
a
n
2
R
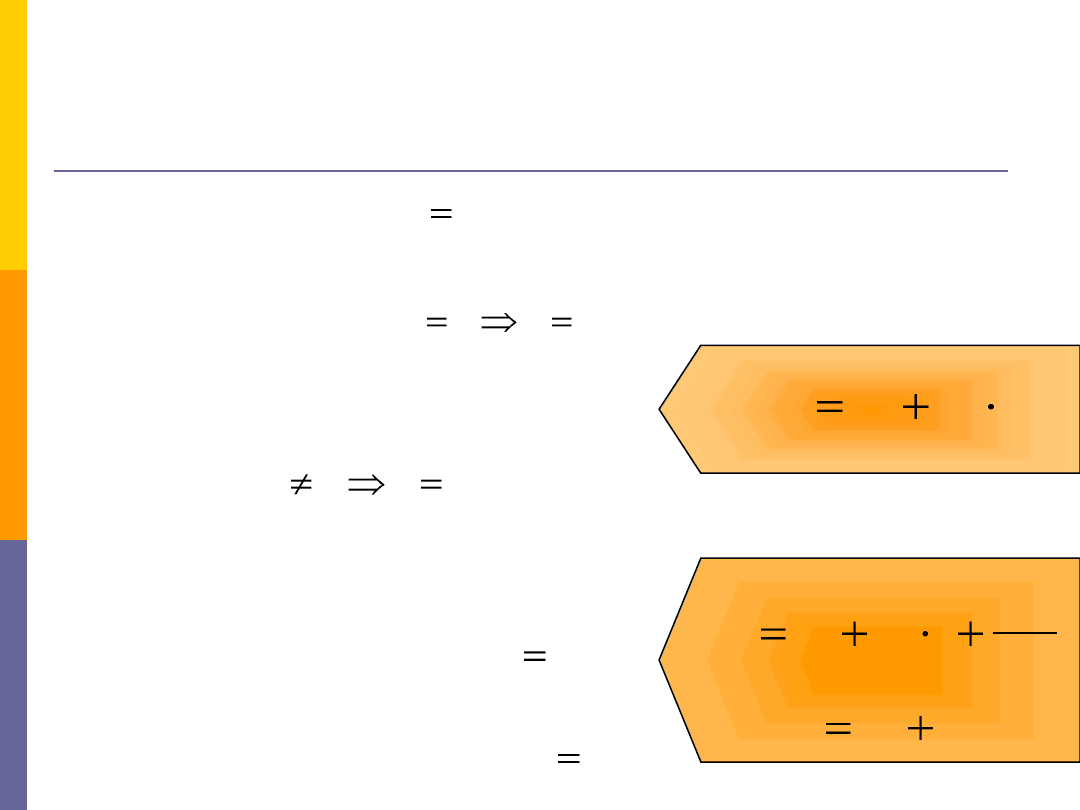
at
v
t
v
at
t
v
s
t
s
o
o
o
)
(
2
)
(
2
Szczególne przypadki ruchu
0
n
a
const
v
a
s
0
const
a
s
ruch prostoliniowy
t
v
s
t
s
o
o
)
(
)
(
0
t
f
v
a
s
)
(t
f
a
s
jeżeli
jeżeli dodatkowo
ruch prostoliniowy, jednostajny
ruch prostoliniowy, zmienny:
jednostajnie zmienny
niejednostajnie zmienny
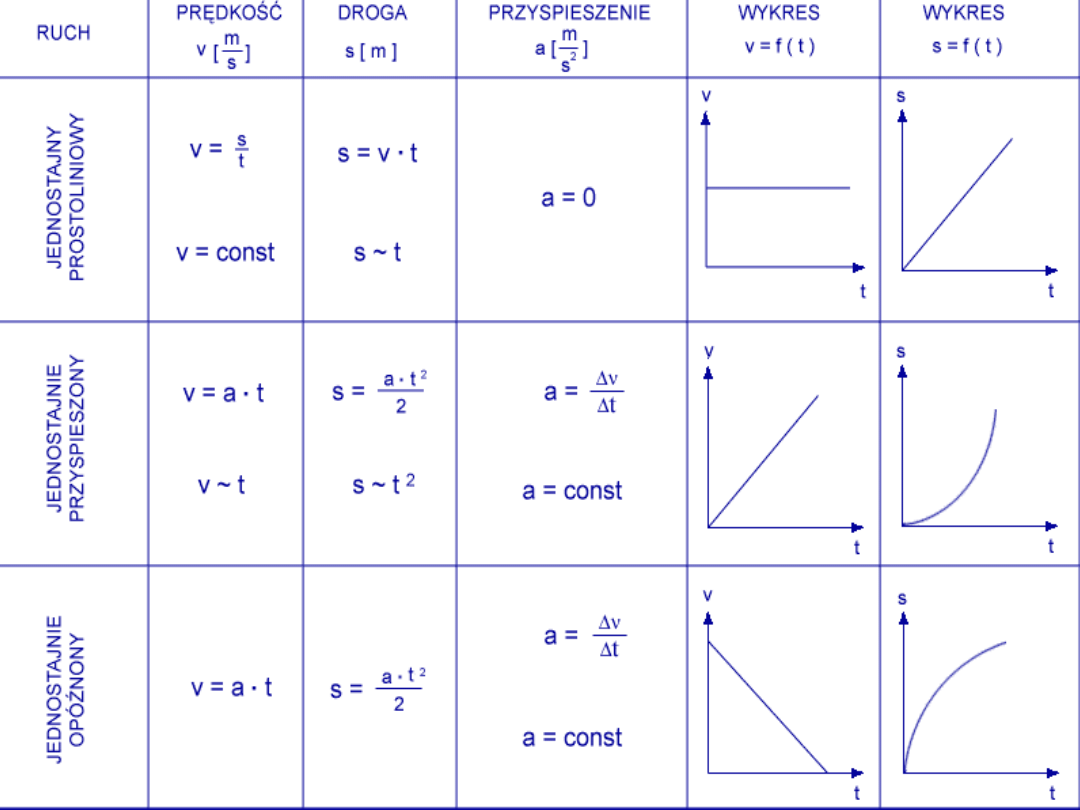
Szczególne przypadki ruchu
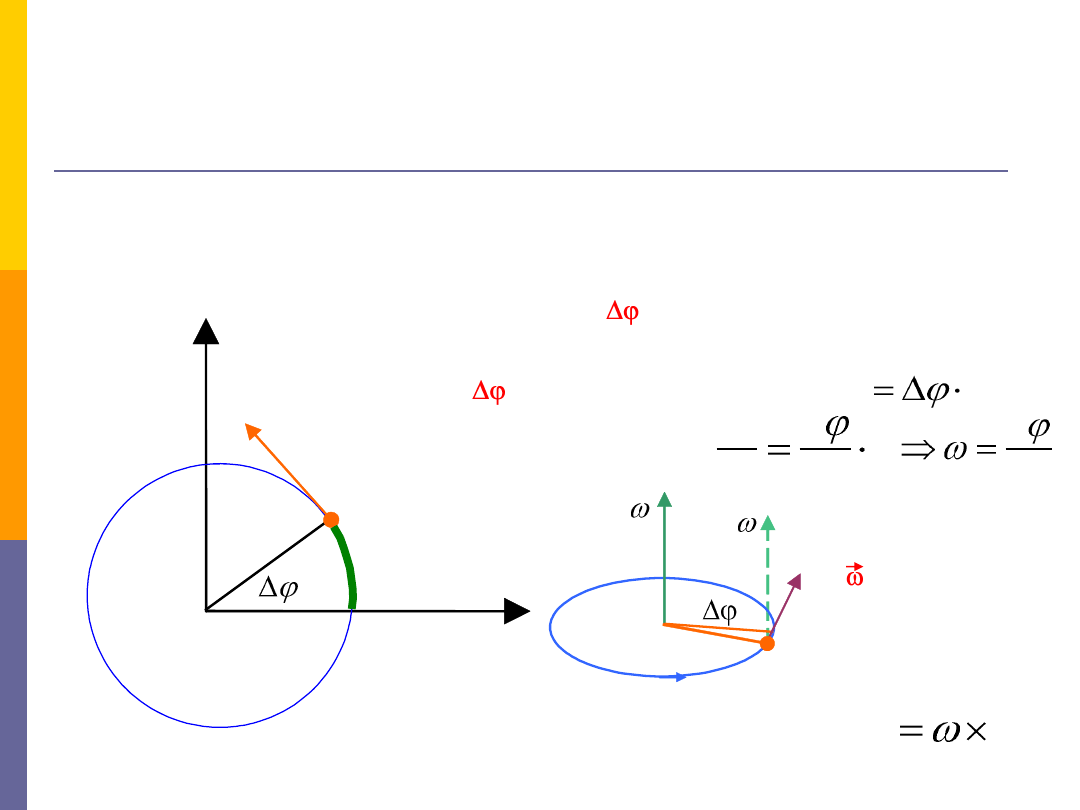
Ruch obrotowy punktu materialnego
ruch obrotowy po okręgu -
szczególny przypadek płaskiego ruchu
krzywoliniowego
r
s
x
y
v
A
droga kątowa –
położenie punktu A określamy za
pomocą kąta
r
s
droga liniowa –
wyrażamy za pomocą drogi kątowej
w sposób następujący:
prędkośd kątowa:
r
dt
d
dt
ds
dt
d
r
v
A
prędkośd liniowa punktu A:
r
v
kierunek wektora
dany jest przez
regułę śruby
prawoskrętnej
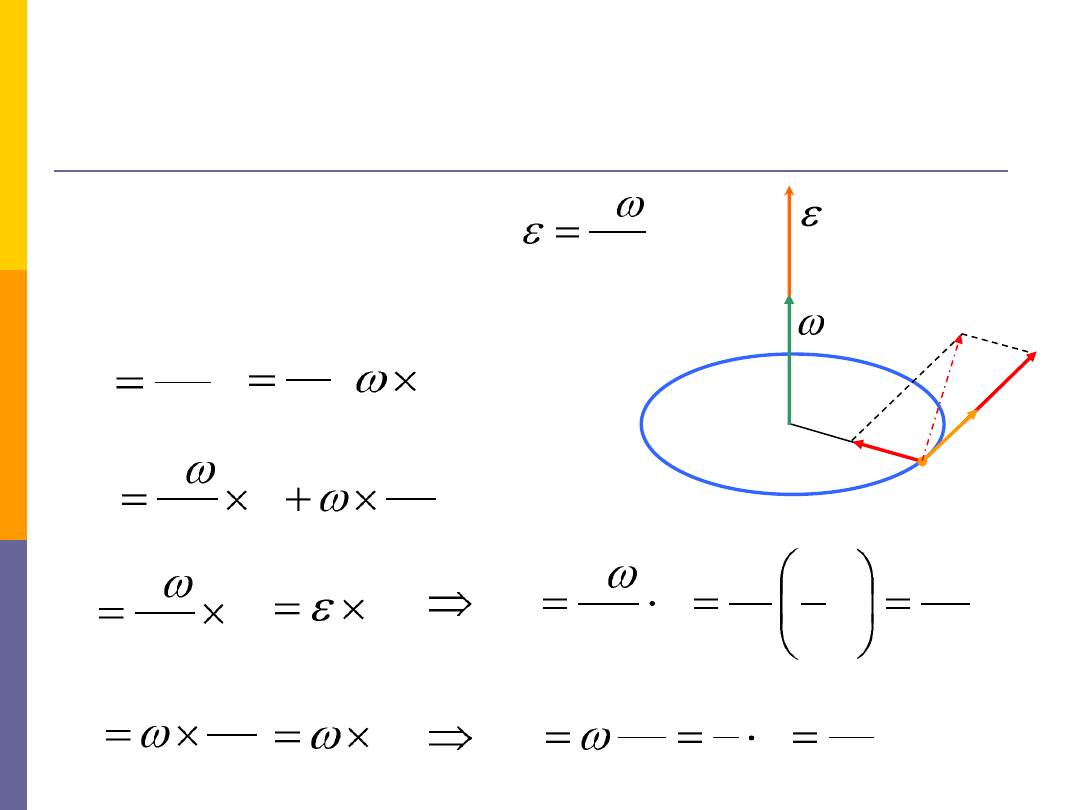
dt
d
ruch przyspieszony
ruch opóźniony
r
r
dt
v
d
a
przyspieszenie kątowe:
przyspieszenie styczne i dośrodkowe:
)
(
r
dt
d
dt
r
d
r
dt
d
r
dt
d
a
s
r
dt
r
d
a
n
v
s
a
v
n
a
a
Ruch obrotowy punktu materialnego
dt
dv
r
r
v
dt
d
r
dt
d
a
s
|
|
r
v
v
r
v
dt
dr
a
n
2
|
|
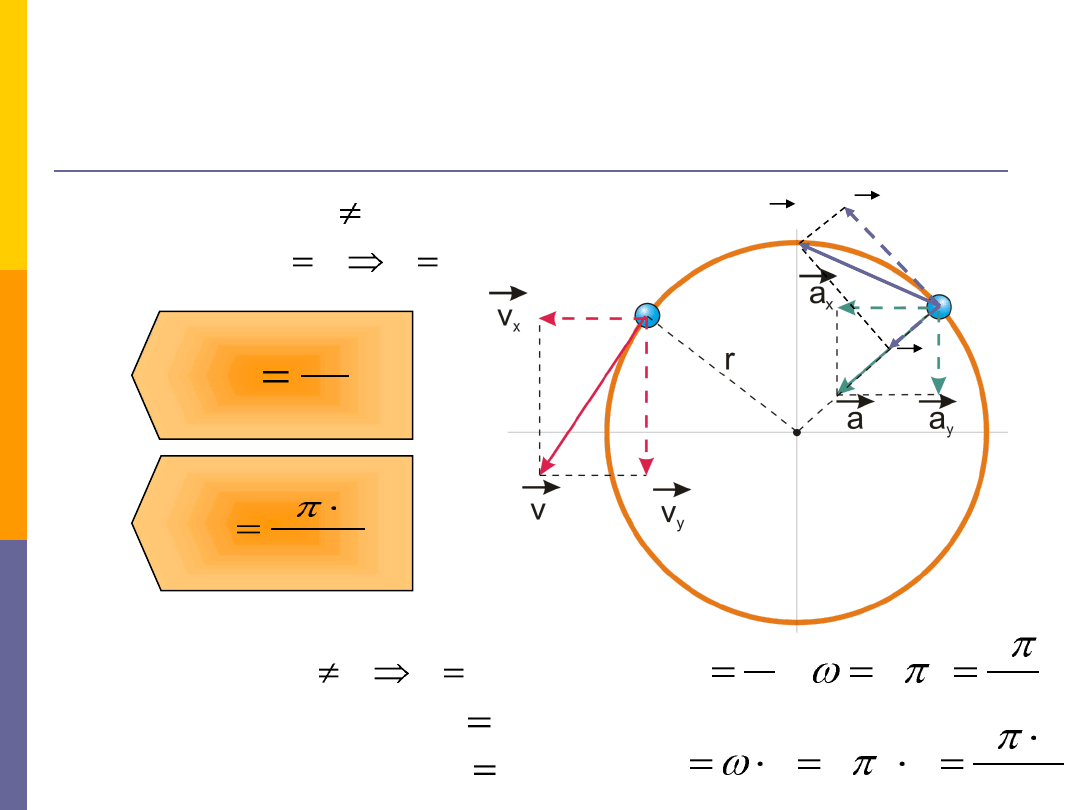
Szczególne przypadki ruchu
0
n
a
const
v
a
s
0
ruch po okręgu
const
a
s
)
(t
f
a
s
R
v
a
n
2
)
(
0
t
f
v
a
s
v
r
T
2
jednostajny
niejednostajny
jednostajnie zmienny
niejednostajnie zmienny
a
s
a
T
f
T
f
2
2
;
1
T
r
r
f
r
v
2
2
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron