Ć

wiczenie nr

3F

Badanie przepływu

pr

ą

du elektrycznego

w materiałach przewodz

ą

cych

1. Podstawy teoretyczne

1.1. Powstawanie oporu elektrycznego w metalach.

1.1.1. Podstawowe cechy modelu elektronów swobodnych.

Elektrony w metalu nie są ściśle związane z jądrem atomu – należą one do metalu jako

całości, co pozwala im na swobodne poruszanie się w jego (ograniczonej) objętości.
Ponieważ energia jonizacji wszystkich elektronów danego atomu jest zbyt wysoka, odrywane
są jedynie elektrony walencyjne z niecałkowicie obsadzonych powłok zewnętrznych.

W modelu elektronów swobodnych przyjmuje się trójwymiarową studnię potencjału

wypełnioną elektronami walencyjnymi, tworzącymi tzw. gaz Fermiego o ujemnym ładunku.
Dodatnie jony neutralizują ładunek elektronów, w wyniku czego wypadkowy ładunek metalu
jest równy zeru. Jest to równoważne założeniu, że ładunki dodatnie są rozmieszczone w
sposób ciągły w całej objętości metalu, zamiast być zlokalizowane w położeniach jonów. Jest
to przybliżenie, w rzeczywistości dodatnio naładowany jon przedstawia znaczny potencjał
przyciągający dla elektronu.

W modelu swobodnych elektronów przyjmuje się ponadto, że pole potencjału dla żadnej

z cząsteczek ładunku nie zależy od położenia pozostałych – tym samym całkowicie pomija się
oddziaływanie pomiędzy elektronami.

Gaz elektronowy (gaz Fermiego) w przestrzeni wektorowej

k

Ze względu na dużą koncentrację, gaz elektronowy w metalach podlega rozkładowi

Fermiego-Diraca. Zgodnie z tym rozkładem, dwie identyczne cząstki nie mogą zajmować
tego samego stanu energetycznego. Na podstawie równanie de Broglie’a, pęd takiej cząstki
(jeżeli opisujemy ją za pomocą funkcji falowej) wynosi:

k

p

h

=

(1)

Wektor jednostkowy k ma w przestrzeni składowe k

x

, k

y

, k

z

, natomiast skalarnie

k = 2π/λ, gdzie λ jest długością fali w kierunku jej rozchodzenia się, a ħ

= 1,0545·10

-34

Js jest

stałą Plancka.

Przestrzeń wektorowa k może być użyta do przedstawienia rozkładu energii, przy czym

skalarnie:

m

k

E

2

2

2

h

=

(2)

Tym samym, wszystkie cząsteczki mające wektory o tej samej wielkości (cząsteczki o tej

samej długości fali) mają taką samą energię (stan energetyczny). Stany te leżą na powierzchni
kuli, której promień jest równy k. Jako fermiony, elektrony podlegają zakazowi Pauliego.
Tym samym, jedynie dwa elektrony o przeciwnych spinach mogą znajdować się w tym
samym stanie energetycznym, przy czym w temperaturze zera bezwzględnego T = 0 K,
elektrony zajmują stany o najniższych energiach. Stany energetyczne zapełniane są przez
elektrony kolejno, aż do maksymalnej wartości k, odpowiadającej najwyższej energii.
Powierzchnia kuli, odpowiadająca maksymalnej energii cząsteczek w temperaturze T = 0 K
nosi nazwę powierzchni Fermiego, wektor falowy Fermiego k

F

jest jej promieniem, a energia

stanów na powierzchni Fermiego nazywana jest energią Fermiego E

F

.

Energia Fermiego dla metali ma wartość kilku, kilkunastu elektronowoltów (np. dla

miedzi E

F

= 7,07 eV, dla aluminium E

F

= 11,69 eV) i zależy od objętości atomowej Ω i

elektrowartościowości Z:

3

2

2

2

3

2













Ω

=

Z

m

E

F

π

h

(3)

Gdyby nie wpływ zakazu Pauliego dla gazu Fermiego, tzn. gdyby elektrony były

traktowane jak cząsteczki gazu klasycznego, energia taka odpowiadałaby temperaturze
(energii kinetycznej) rzędu 10

5

K.

Należy podkreślić, że powierzchnia Fermiego nie odzwierciedla żadnej rzeczywistej

powierzchni w metalach. Powierzchnia Fermiego leży w przestrzeni

k i wskazuje, że istnieje

graniczna wartość pędu elektronów w temperaturze zera bezwzględnego.

1.1.2. Przewodno

ść

elektryczna i rozpraszanie no

ś

ników ładunku.

Jeżeli zewnętrzne pole elektryczne nie występuje, dla każdego elektronu o pędzie

p = ħk

w przestrzeni

k istnieje elektron o pędzie przeciwnym p

’

= –ħ

k, co powoduje, że całkowity

pęd układu jest równy zeru.

Przyłożenie pola elektrycznego

E powoduje, że ładunki elektronów zaczynają

oddziaływać z polem z siłą

F = -eE. Siła ta dąży do przesunięcia elektronów w stronę

wyższego potencjału.

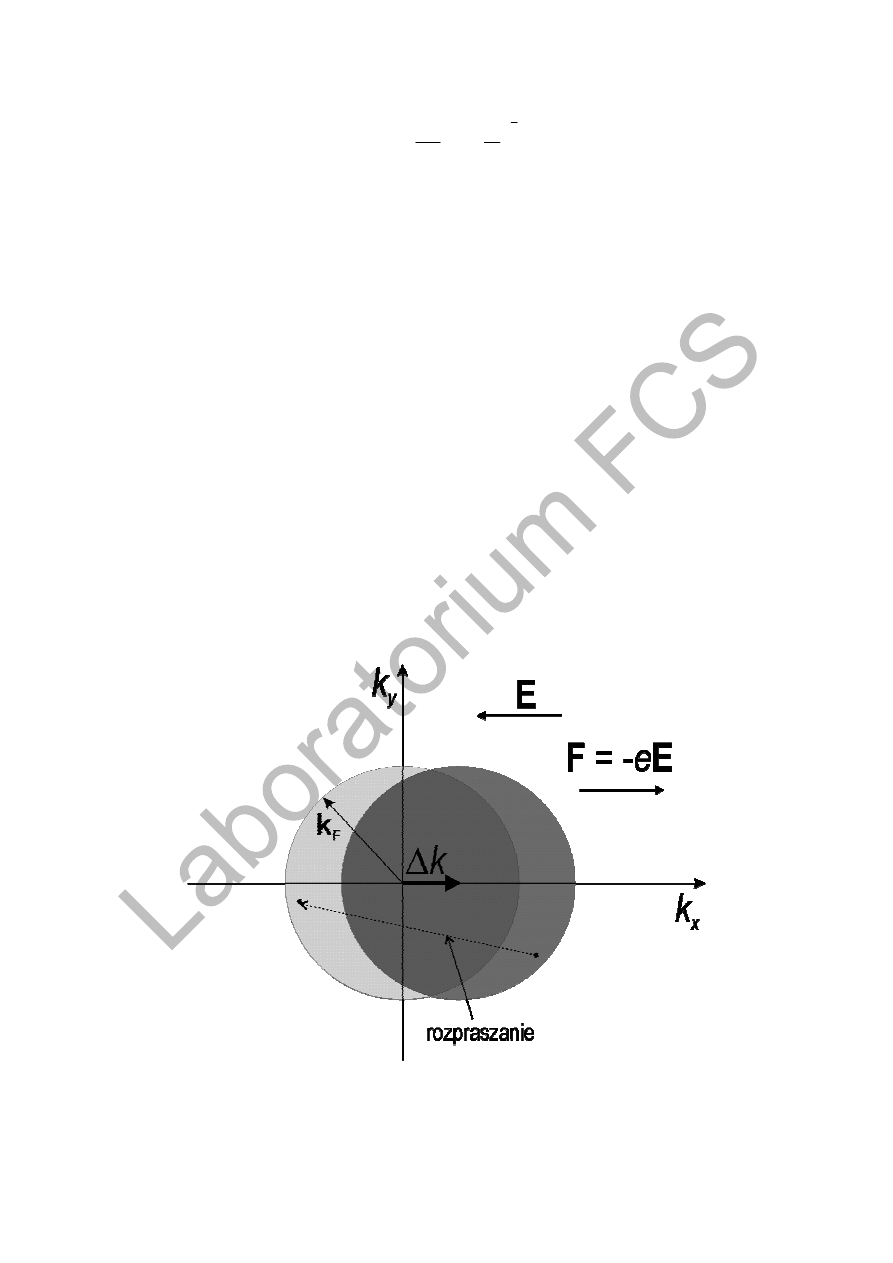
Dla przedstawienia obrazu przewodnictwa wygodnie jest posłużyć się kulą Fermiego.

Ponieważ liczby falowe są proporcjonalne do pędów (k = p/ħ), więc kulę Fermiego możemy
traktować jako rozkład pędów. Wypadkowy pęd jest wektorem łączącym początek układu
współrzędnych (pęd równy zero) ze środkiem kuli. W przypadku braku pola elektrycznego,
początek układu i środek kuli Fermiego pokrywają się ze sobą. Gdy elektrony są
przyspieszane w polu elektrycznym, wypadkowy pęd staje się różny od zera. Cała kula
Fermiego przesunięta jest wówczas z początku układu w kierunku działania siły i porusza się
w sposób ciągły w miarę upływu czasu (rys. 1).

Rys. 1. Zmiana położenia kuli Fermiego w wyniku oddziaływania pola elektrycznego E na elektrony.

Rozpraszanie powoduje powrót elektronów do nieobsadzonych stanów rozkładu pierwotnego

(dla E=0).

Gdyby na elektrony działała tylko siła związana z polem zewnętrznym

E,

otrzymalibyśmy przyspieszony ruch elektronów zgodny z gradientem potencjału. W
rzeczywistości, w stałym polu elektrycznym obserwujemy przepływ prądu stałego. Jest to
wynikiem zderzeń elektronów z fononami i domieszkami sieci krystalicznej. W wyniku tych
zderzeń powstaje pewien stan równowagi, który charakteryzuje się ustalona prędkością dryfu
v (ruch elektronów można porównać do ruchu ciała pod działaniem stałej siły w ośrodku
lepkim).

Czynnikiem ustalającym pewną prędkość dryfu

v, pomimo przyspieszającego działania

pola elektrycznego o natężeniu

E, jest wpływ jonów. Regularne ułożenie jonów w sieci

krystalicznej sprawia, że możemy przyjąć wygładzony kształt oddziaływania elektronowo-
fononowego. Jednak drgania cieplne sieci oraz występowanie różnego rodzaju defektów w
rzeczywistych metalach, powodują wiele odchyleń od doskonałej regularności sieci
krystalicznej – w kategoriach wygładzonego potencjału jest to równoznaczne ze zmianami
gęstości ładunków dodatnich.

W miarę wzrostu temperatury, wzrasta amplituda drgań cieplnych i odchylenia te stają się

coraz silniejsze. Defekty struktury krystalicznej (wakanse, dyslokacje, błędy ułożenia, granice
ziaren) także niszczą regularność sieci i powodują zmiany gęstości ładunku jonów, co z kolei
wywołuje lokalne zmiany potencjału.

Elektrony napotykając lokalne zmiany potencjału ulegają rozpraszaniu, co powoduje

zmniejszenie ich przepływu. Im większa szybkość przepływu, tym większe rozpraszanie.
Otrzymujemy równowagę pomiędzy przyspieszeniem wynikającym z istniejącego pola
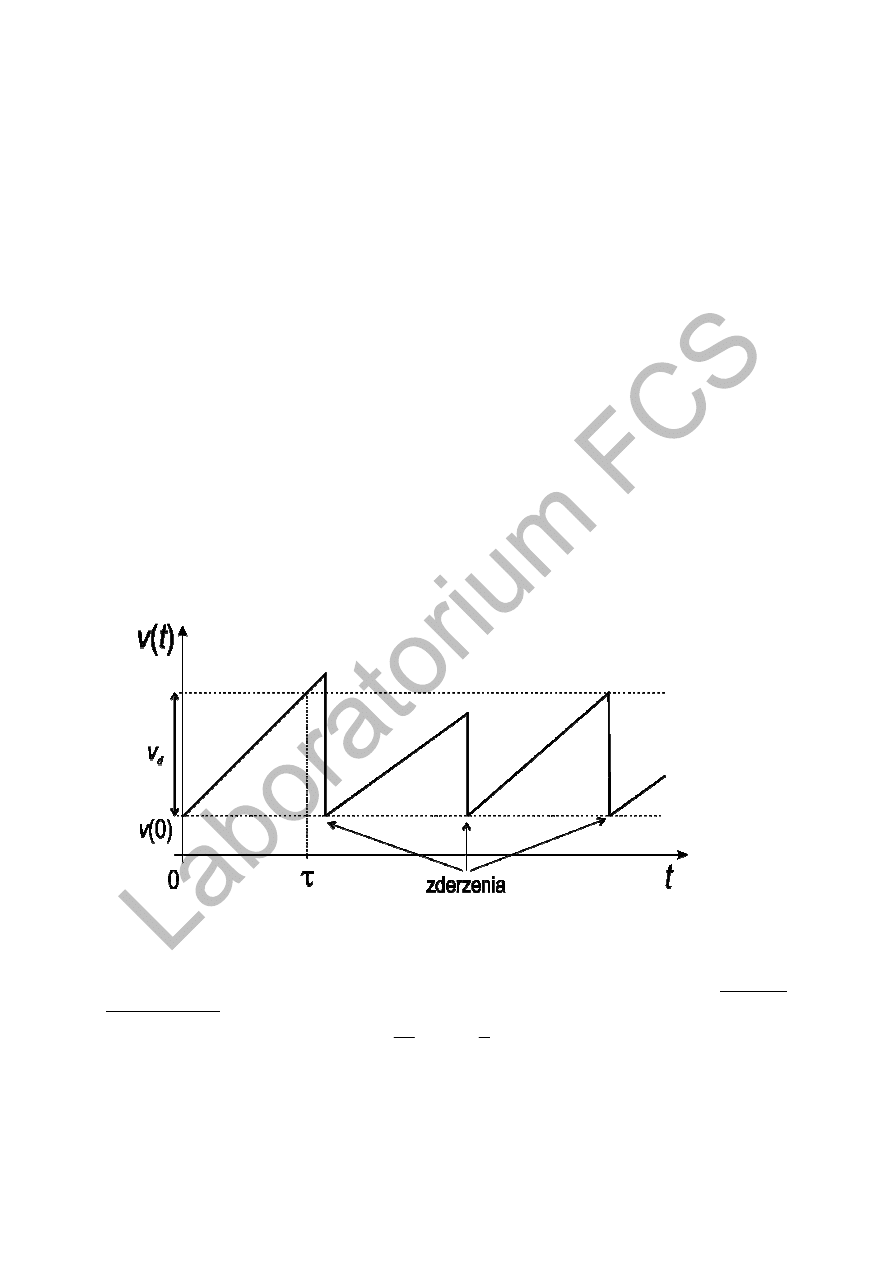
potencjału i wpływem przypadkowych zderzeń. Dla pojedynczego elektronu oznacza to, że
pomiędzy kolejnymi rozproszeniami zmniejszającymi jego prędkość, podlega on stałemu
przyspieszeniu (rys. 2).

Rys. 2. Zmiana prędkości pojedynczego elektronu jako efekt działania przyspieszającego pola

elektrycznego i procesów rozproszeniowych.

Jeżeli założyć, że siła hamująca jest proporcjonalna do prędkości dryfu, to równanie

ruchu elektronu przyjmuje postać:

v

E

v

m

e

dt

d

m

τ

1

−

−

=

(4)

gdzie τ oznacza średni czas pomiędzy zderzeniami.

Jeżeli dla czasu t=0 (moment włączenia pola elektrycznego) v=0, to rozwiązanie

równania (4) można zapisać w postaci:















−

=

−

τ

t

e

t

1

)

(

d

v

v

(5)

gdzie

τ

m

eE

v

d

−

=

- prędkość dryfu w stanie ustalonym.

Po wyłączeniu pola (E=0), równanie (4) przyjmuje postać:

τ

v

v

=

dt

d

(6)

którego rozwiązaniem jest funkcja:

τ

t

e

t

−

=

d

v

v )

(

(7)

Jak wynika z równań (5) i (7), skokowe zmiany natężenia pola elektrycznego powodują
wykładniczą zmianę prędkości elektronów w czasie.
Znając prędkość dryfu v

0

, można wyznaczyć gęstość prądu w stanie ustalonym:

τ

E

v

j

d

n

m

e

en

2

=

−

=

(8)

gdzie n – koncentracja elektronów.
Z prawa Ohma wynika, że:

E

j

γ

=

(9)

gdzie

γ

- konduktywność.

Porównując równania (8) i (9) otrzymujemy:

τ

γ

n

m

e

2

=

(10)

Stosunek prędkości dryfu w stanie ustalonym do natężenia pola elektrycznego

wywołującego uporządkowany ruch elektronów z tą prędkością, nosi nazwę ruchliwości
nośników µ:

τ

µ

m

e

=

=

E

v

d

(11)

Konduktywność metalu wyrażona za pomocą ruchliwości nośników ładunku

elektrycznego może być zapisana w postaci:

µ

γ

en

=

(12)

Ś

redni czas między zderzeniami τ dla metali o wysokiej konduktywności jest bardzo

mały. Przykładowo, dla miedzi w temperaturze 300 K wynosi on (

γ

Cu

= 6,4·10

7

S/m,

n

Cu

= 8,5·10

28

m

-3

, e = 1,6·10

-19

C, m = 9·10

-31

kg):

s

10

3

14

Cu

2

Cu

K

300

,

Cu

−

⋅

≈

=

n

e

m

γ

τ

,

(12)

a w temperaturze 4,2 K (temperatura ciekłego helu) wynosi (

γ

Cu

= 6,2·10

12

S/m):

s

10

3

9

K

2

,

4

,

Cu

−

⋅

≈

τ

(13)

Ś

redni czas pomiędzy zderzeniami τ = 10

-14

s oznacza, że w temperaturze 300 K w polu o

natężeniu 1 V/m prędkość dryfu elektronów w miedzi wynosi zaledwie:

m/s

05

,

0

≈

=

E

m

e

v

d

τ

(14)

podczas gdy w tej samej temperaturze prędkość elektronów w ruchu chaotycznym jest o 8
rzędów wielkości większa.

Przemieszczenie kuli Fermiego w miedzi w temperaturze 300 K, wywołane polem 1 V/m,

jest bardzo małe:

1

-

m

50

≈

=

∆

=

∆

τ

h

h

eE

p

k

,

(15)

podczas gdy wartość wektora falowego na poziomie Fermiego wynosi:

1

9

m

10

9

−

⋅

≈

=

=

h

h

F

mv

p

k

,

(16)

dla v

F

~ 1,5·10

6

m/s (po zamianie energii Fermiego E

F

= 7 eV na energię kinetyczną).

Niewielkie zmiany w zrównoważonym rozkładzie elektronów (∆k/k ~5·10

-9

) wskazują, że

w przewodnictwie prądu elektrycznego biorą udział tylko niewielkie ilości elektronów
znajdujących się przy powierzchni Fermiego. Elektrony znajdujące się wewnątrz kuli
Fermiego nie biorą udziału w przewodnictwie, ponieważ w ich pobliżu nie ma stanów
nieobsadzonych. Zmiana ich pędu nie jest możliwa ze względu na zakaz Pauliego.

Tym samym, prędkość elektronów rozpraszanych w wyniku zjawisk związanych z

istnieniem oporu elektrycznego (biorących udział w zderzeniach z jonami i domieszkami) jest
praktycznie równa prędkości Fermiego v

F

.

Znając czas pomiędzy zderzeniami i prędkość elektronów, można obliczyć średnią drogę

swobodną l (odległość między zderzeniami):

F

v

l

τ

=

(17)

Dla miedzi w temperaturze 300 K l

Cu

~ 4,5·10

-8

m = 4.5·10

2

Å, natomiast w temperaturze

4,2 K l

Cu

~ 4,5·10

-3

m = 4.5·10

7

Å. Wynika z tego, że średnia droga swobodna elektronów

pomiędzy zderzeniami jest około 10

2

razy większa w temperaturze 300 K, a w temperaturze

4,2 K nawet 10

7

razy większa od stałej sieci krystalicznej (odległości pomiędzy jonami).

Wynik ten wskazuje, że idealna sieć krystaliczna, w której jony są nieruchome i która nie

zawiera defektów krystalograficznych, nie może powodować powstawania oporu
elektrycznego. Spowodowane jest to falową naturą elektronu oraz faktem, że długość fali
elektronowej odpowiadającej energii Fermiego jest znacznie większa od odległości
międzyatomowych. Tym samym fala elektronowa nie oddziaływuje z nieruchomymi jonami
sieci i nie traci swojej energii.

Rozpraszanie energii elektronu w metalach następuje w wyniku dwóch zjawisk:

•

zderzenia elektron – fonon (drgania cieplne sieci);

•

zderzenia elektron – defekt sieci krystalicznej.

Opór elektryczny metali zmienia się z temperaturą, ponieważ pierwsze z tych zjawisk
(koncentracja i amplituda fononów) jest funkcją temperatury.

1.1.3. Wpływ temperatury na przewodno

ść

elektryczn

ą

metali

Ze wzorów (11) i (12), po uwzględnieniu, że τ = l/v

F

, otrzymujemy następujące wyrażenie

dla przewodności elektrycznej metali:

F

v

l

m

e

n

2

=

γ

(18)

W metalach koncentracja elektronów n, oraz prędkość Fermiego v

F

w znikomym

stopniu zależą od temperatury (ze względu na praktycznie całkowite obsadzenie stanów na
powierzchni E

F

oraz fakt, że E

F

= mv

2

/2 >> kT. Tym samym, we wzorze (18) temperatura

może wpływać na przewodność elektryczną metali jedynie poprzez zmiany średniej drogi
swobodnej elektronów l. Niezależnie od rodzaju czynnika rozpraszającego, średnia droga
swobodna jest odwrotnie proporcjonalna do koncentracji centrów rozpraszających l ~ 1/n.

Rozpraszanie elektronów na drganiach sieci krystalicznej (na fononach)

W temperaturach wysokich koncentracja fononów zmienia się liniowo w funkcji

temperatury:













Θ

=

T

n

n

A

f

2

9

(19)

gdzie n

A

jest koncentracją atomową, zaś Θ temperaturą Debye’a. Z zależności (19) wynika, że

rezystywność

ρ

= 1/

γ

~ T.

Liniowa zależność rezystywności od temperatury wynika także z faktu, że amplituda

ruchów harmonicznych jonów wokół średnich położeń w sieci jest funkcją temperatury, przy
czym średnia energia drgań na jon wynosi 3k

B

T

(3/2 k

B

T

to energia potencjalna, pozostała

część to energia kinetyczna). Prawdopodobieństwo rozpraszania jest proporcjonalne do
kwadratu średniego odchylenia, przy czym:

( )

b

T

k

x

B

2

3

2

=

(20)

gdzie b jest współczynnikiem normującym.

Ostatnie wyrażenie prowadzi bezpośrednio do liniowej zależności prawdopodobieństwa

rozpraszania w funkcji temperatury, a tym samym zależności:

T

~

ρ

(21)

W zakresie niskich temperatur, ze względu na mały pęd fononów niezbędne jest

wielokrotne zderzanie elektronu z fononami w celu jego całkowitego rozproszenia. Tym
samym, pomimo że temperaturowa zależność koncentracji fononów (wynikająca z rozkładu
Bosego-Einsteina przy małej zależności drgań jonów) jest wyrażona wzorem:

3

2

3













Θ

=

T

n

n

A

f

π

,

(22)

to eksperymentalnie obserwuje się następującą zależność rezystywności od temperatury:

5

~

1

T

γ

ρ

=

(23)

Ponieważ koncentracja fononów w niskich temperaturach jest bardzo mała, w większości

praktycznych przypadków rozpraszanie elektronów na fononach w tym zakresie temperatur
nie odgrywa większej roli.

Rozpraszanie elektronów na domieszkach

Procesy rozpraszania wywołane są nie tylko przez oddziaływanie elektronów z fononami,

ale także przez wszelkie inne zakłócenia w sieci jonów, które powodują lokalne zmiany
rozkładu ładunku struktury krystalograficznej. Takie zmiany w gęstości ładunku pochodzą z:

•

lokalnych zmian parametru sieci wywołanych atomami o różnej wielkości ( a także
wakansami oraz atomami w położeniach międzywęzłowych);

•

lokalnych różnic ładunku, wywołanych atomami o różnej wartościowości w stosunku
do wartościowości atomów osnowy (lub brakiem atomu osnowy, tzw. wakansem).

Wpływ defektów punktowych przejawia się głównie poprzez lokalne zmiany ładunku,

powodujące odchylanie torów elektronów już w dużej odległości od centrum rozpraszającego,
w wyniku działania pola kulombowskiego. Jeżeli różnica w wartościowościach atomów
wynosi ∆Z, to potencjał lokalnego ładunku w odległości r wynosi:

r

Ze

V

2

∆

=

∆

(24)

a prawdopodobieństwo rozpraszania jest proporcjonalne do kwadratu tego potencjału:

( ) ( )

2

2

~

~

1

Z

V

d

∆

∆

τ

(25)

Ponieważ wielkości po prawej stronie wzoru:

( )

2

2

2

1

~

1

1

1

Z

n

e

m

n

e

m

∆

=

=

τ

γ

ρ

(26)

nie zależą od temperatury, więc oporność elektryczna wywołana rozpraszaniem na
domieszkach także nie zależy od temperatury, a jedynie od koncentracji i ładunku domieszek.

Reguła Mathiessena

Rezystywności wynikające z niezależnych procesów rozpraszania są addytywne:

n

ρ

ρ

ρ

ρ

+

+

+

=

K

2

1

(27)

Jest to konsekwencją faktu, że jeżeli występują różne mechanizmy rozproszeń,

charakteryzujące się czasami relaksacji τ

1

, τ

2

, ... τ

n

, to równanie ruchu elektronu w polu

elektrycznym przyjmuje postać:













+

+

+

−

−

=

n

m

e

dt

d

m

τ

τ

τ

1

1

1

2

1

K

v

E

v

(28)

W tym przypadku rozpraszanie może być scharakteryzowane jednym czasem relaksacji τ,

takim że:

n

τ

τ

τ

τ

1

1

1

1

2

1

+

+

+

=

K

(29)

Wówczas:

n

l

l

l

l

1

1

1

1

2

1

+

+

+

=

K

(30)

Tak więc, na podstawie wzoru (10) można otrzymać:

n

n

n

e

m

n

e

m

ρ

ρ

ρ

τ

τ

τ

τ

ρ

+

+

+

=













+

+

+

=

=

K

K

2

1

2

1

2

2

1

1

1

1

(31)

Zgodnie z modelem elektronów swobodnych opór elektryczny metali w niskich

temperaturach (T→0) (tzw. opór resztkowy) nie zależy od temperatury, ponieważ jest
spowodowany rozproszeniami na domieszkach, a rozpraszanie na fononach nie wnosi
istotnego wkładu do oporu ze względu na bardzo małą amplitudę drgań sieci krystalicznej.
W miarę wzrostu temperatury addytywny wkład rozpraszania fononowego rośnie, powodując
wzrost rezystywności proporcjonalny początkowo do T

5

, a w wyższych temperaturach do T,

odpowiednio do zmieniającego się prawdopodobieństwa rozpraszania związanego z
kwadratem amplitudy drgań jonów.

2. Wykonanie

ć

wiczenia

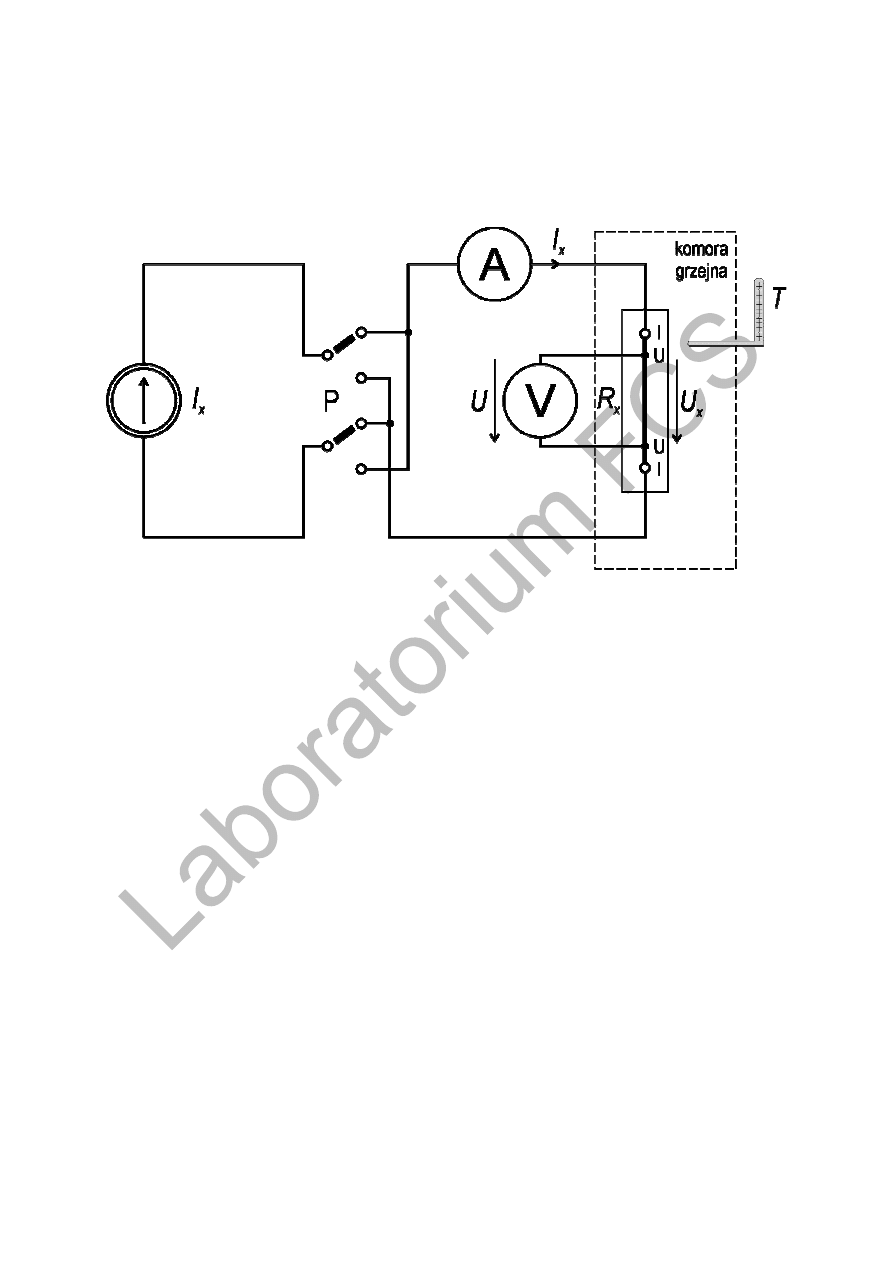
2.1. Układ pomiarowy

Oznaczenia:

I

X

– źródło prądowe (zasilacz z regulacją wartości prądu);

A – amperomierz cyfrowy;
V – woltomierz cyfrowy;
R

X

– badana próbka o średnicy d

X

oraz odległości między zaciskami l

X

;

P – przełącznik do zmiany kierunku prądu;
T – termometr.

2.2. Wyznaczanie rezystywno

ś

ci materiałów przewodowych.

2.2.1. Przebieg pomiaru.

•

Umieścić badaną próbkę w komorze grzejnej schłodzonej do temperatury otoczenia.

•

Połączyć próbkę z układem pomiarowym zgodnie ze schematem (2.1).

•

Ustawić wydajność prądową źródła prądu, odpowiednią dla każdego materiału (wg

instrukcji dodatkowej).

•

Skontrolować wartość płynącego prądu przy pomocy amperomierza A i odczytać na

woltomierzu V wartość napięcia na próbce.

•

Zmienić kierunek przepływu prądu i ponowić odczyt (wyeliminowanie wpływu

zjawisk termoelektrycznych).

•

Zanotować temperaturę otoczenia.

Wykonać pomiary dla różnych materiałów wymienionych w instrukcji dodatkowej.

2.2.2. Obliczenia

Napięcie wskazywane przez woltomierz U jest równe sumie rzeczywistego napięcia na
próbce U

X

i napięć wynikających z sił termoelektrycznych w obwodzie napięciowym E

T

.

Uwzględniając znaki mierzonego napięcia dla obu kierunków płynącego prądu (U

1

i U

2

),

rzeczywiste napięcie na próbce jest równe:

2

2

1

U

U

U

X

−

=

(32)

Jeżeli |U

X

| > |E

T

|, napięcie na próbce można wyznaczyć ze wzoru:

2

2

1

U

U

U

X

+

=

(33)

Wykorzystując wzór (32) lub (33) obliczyć rezystancję próbki R

X

:

X

X

X

I

U

R

=

(34)

Rezystywność

ρ

x

oraz konduktywność

γ

x

materiału próbki obliczyć ze wzorów:

X

X

X

X

l

S

R

=

ρ

(35)

X

X

X

X

X

S

l

R

ρ

γ

1

1

=

=

(36)

gdzie S

x

– pole powierzchni przekroju poprzecznego przewodu:

4

2

X

X

d

S

π

=

.

(37)

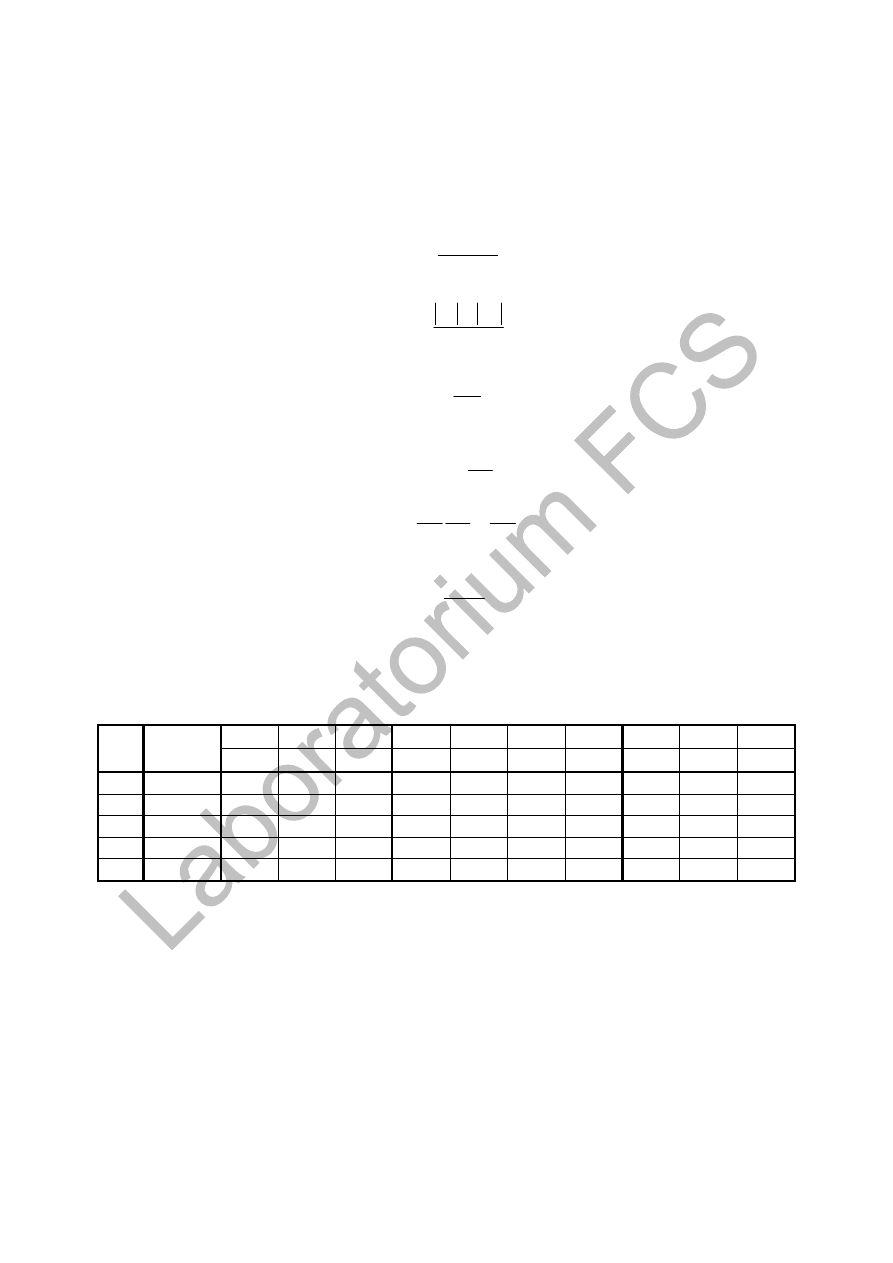
2.2.3. Wyniki.

Wyniki pomiarów i obliczeń zanotować w tabeli 1.

ρ

l

X

d

X

|I

X

|

U

1

U

2

U

X

R

X

ρ

X

γ

X

L.p. Materiał

[

Ω

m]

[m]

[m]

[mA] [mV] [mV] [mV]

[

Ω

]

[

Ω

m] [S/m]

1

2

3

4

5

2.3. Badanie wpływu temperatury na rezystywno

ść

materiałów

przewodowych

2.3.1 Przebieg pomiaru.

•

Umieścić badaną próbkę w komorze grzejnej schłodzonej do temperatury otoczenia.

•

Połączyć próbkę z układem pomiarowym zgodnie ze schematem (2.1).

•

Ustawić wydajność prądową źródła prądu, odpowiednią dla badanego materiału (wg

instrukcji dodatkowej).

•

Odczytać wskazania termometru oraz wskazania amperomierza i wskazania

woltomierza dla dwóch kierunków płynącego prądu.

•

Ustawić początkową temperaturę grzania (wg instrukcji dodatkowej), a następnie

włączyć ogrzewanie komory i po ustaleniu się temperatury odczytać wskazania
przyrządów postępując jak w poprzednim punkcie.

•

Zwiększając, kolejno co 10 ºC, temperaturę w komorze powtórzyć opisane wcześniej

czynności aż do uzyskania temperatury około 100 ºC.

•

Po zakończeniu cyklu pomiarów schłodzić wnętrze komory do temperatury otoczenia.

Wykonać pomiary dla próbki wykonanej z czystego metalu oraz próbki wykonanej ze stopu
metali.

2.3.2. Obliczenia.

Parametrem określającym reakcję rezystancji (rezystywności) materiału na zmianę

temperatury jest temperaturowy współczynnik rezystancji

α

(TWR):

dT

dR

R

O

1

=

α

(38)

W literaturze technicznej jest podawany temperaturowy współczynnik zmian rezystancji

dla temperatury odniesienia 20 ºC. Ze względu na praktycznie liniową zależność między
rezystancją i temperaturą dla większości metali (dla temperatur zbliżonych do temperatury
otoczenia), temperaturowy współczynnik rezystancji

α

20

(dla temperatury odniesienia 20 ºC)

jest wyznaczany ze wzoru:

C

R

R

R

X

X

°

−

−

=

20

1

20

20

20

ϑ

α

(39)

gdzie: R

20

– rezystancja w temperaturze 20 ºC;

R

X

– rezystancja w temperaturze

ϑ

X

.

Jeżeli temperatura odniesienia jest inna wzór (39) ulega odpowiednim zmianom.

2.3.3. Wyniki.

Wyniki pomiarów i obliczeń zanotować w tabeli 2.

ϑ

|I

X

|

U

1

U

2

U

X

R

X

α

ϑ

1

Materiał

L.p.

[ºC]

[mA]

[mV]

[mV]

[mV]

[

Ω

]

[1/K]

1

..

9

1

..

9

Współczynniki

α

ϑ

1

wyznaczyć metodą aproksymacji liniowej (prosta aproksymująca musi

przechodzić przez punkt odpowiadający temperaturze odniesienia

ϑ

1

).

Na podstawie otrzymanych wyników wyznaczyć charakterystyki temperaturowe rezystancji
badanego metalu i stopu metali R

X

= f(

ϑ

). Dodatkowo wykonać na jednym układzie

współrzędnych wykresy (R

X

/R

ϑ

1

)-1 = f(

ϑ

) dla obu próbek.