
Wykład 9
27 11 2006
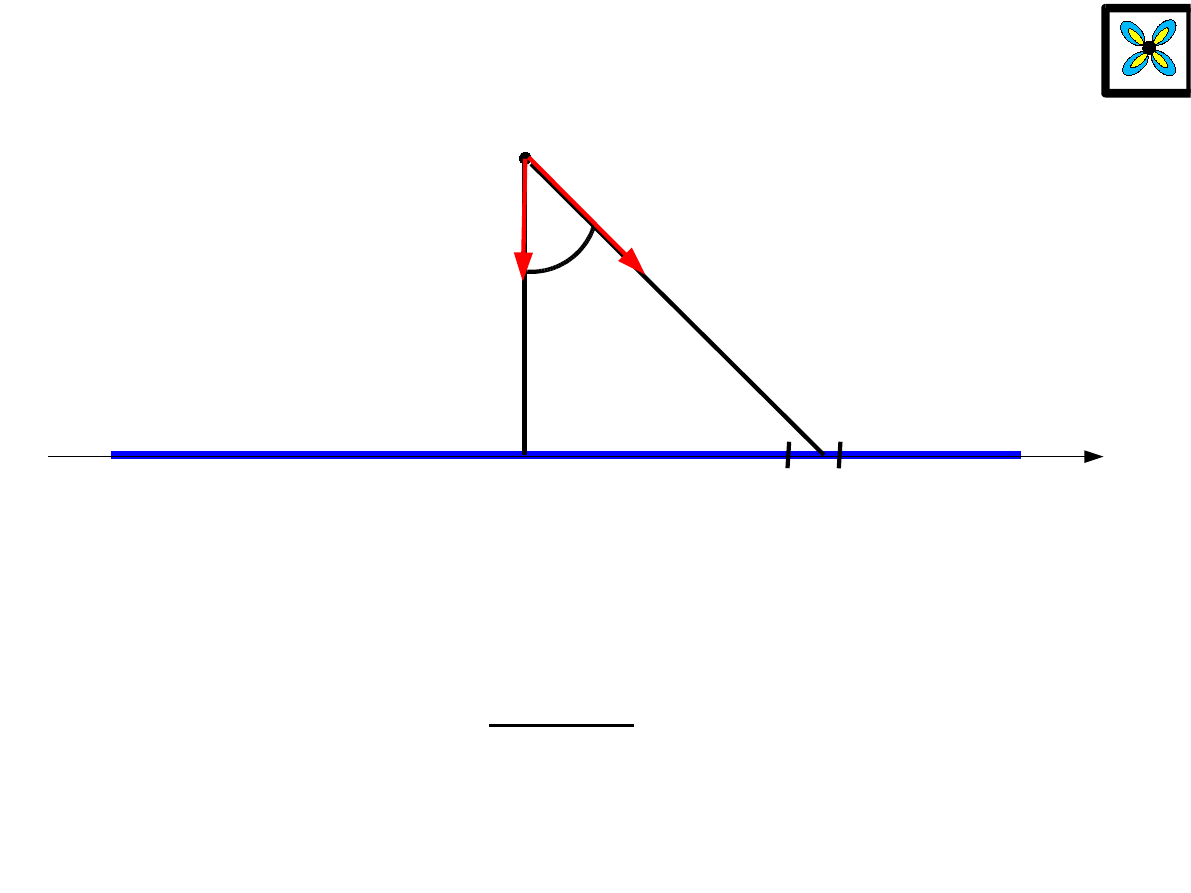
h
x
x
dx
r
=const
dE
dE
⊥
E
=
2 G
h
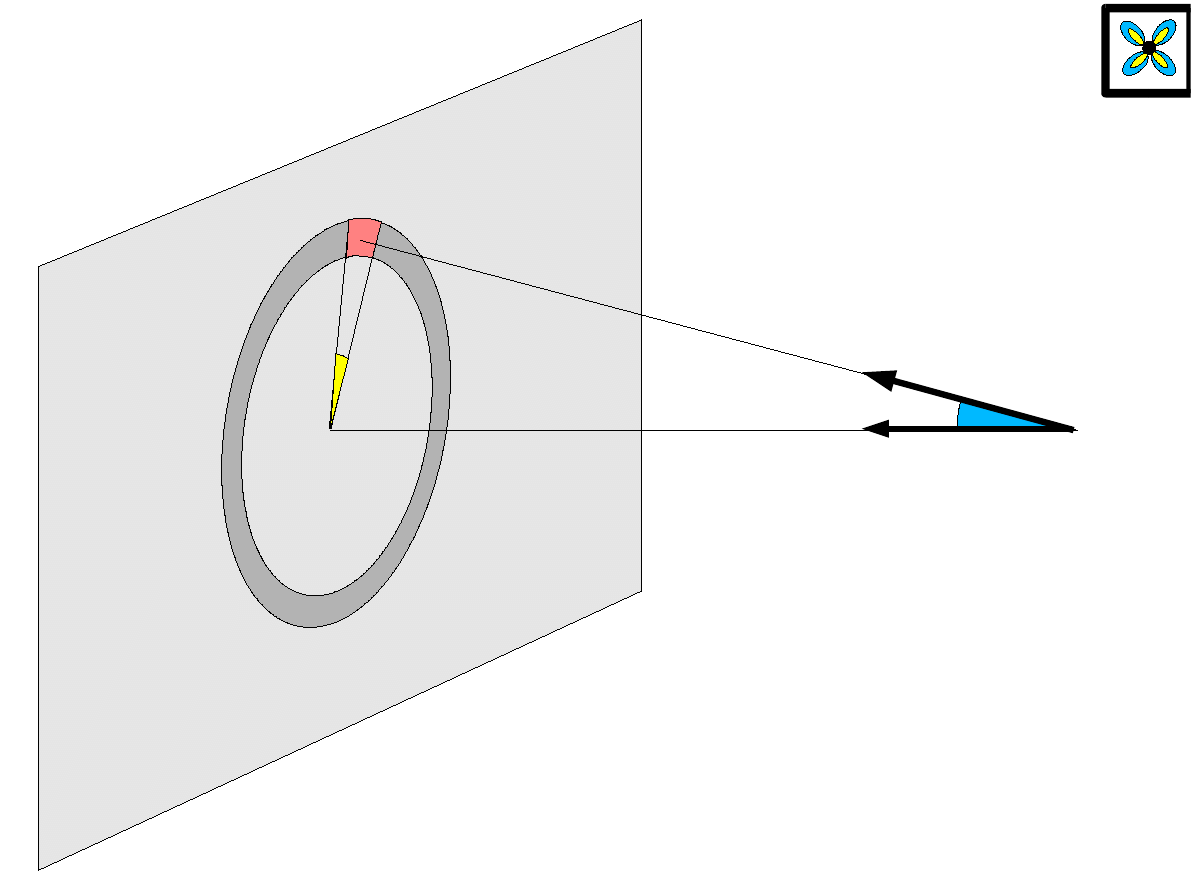
dE
dE
⊥
r
h
R
dR
d
E
= 2 G
= const
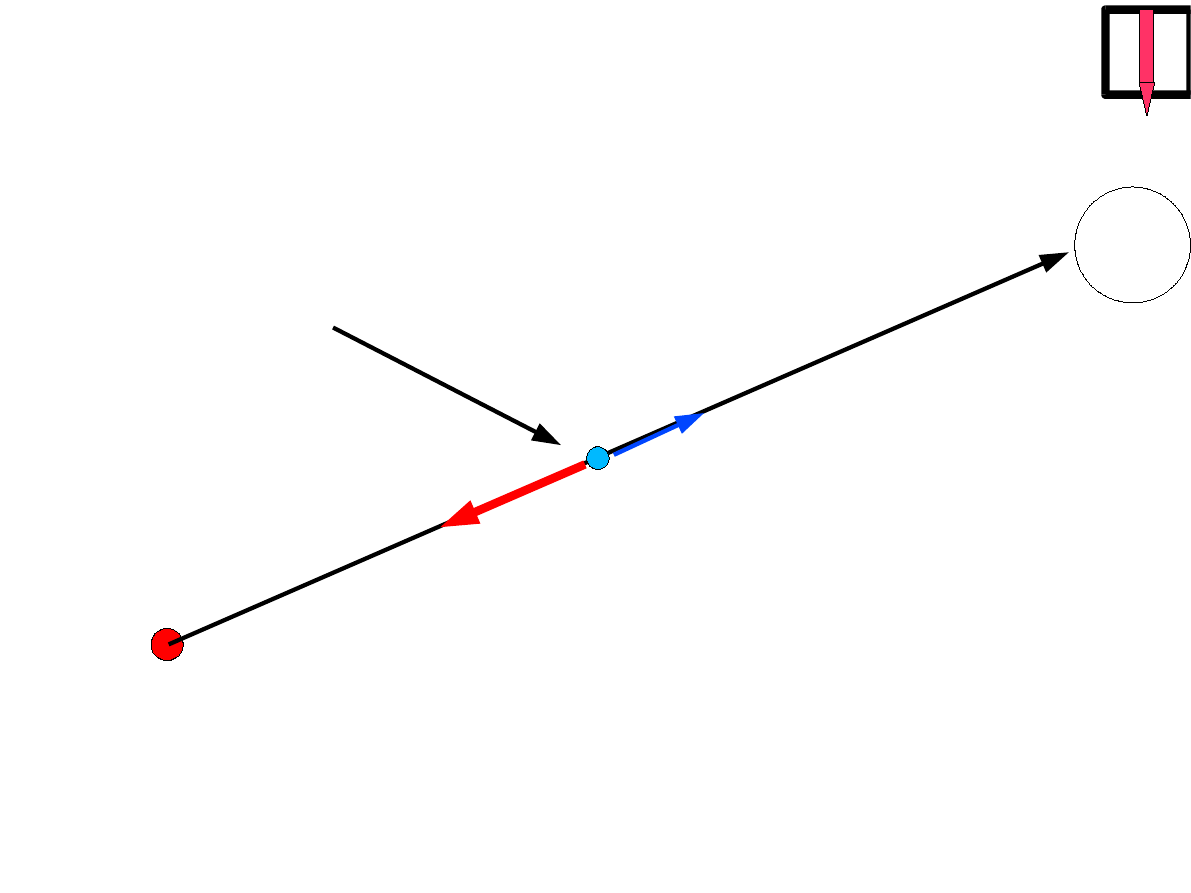
r
M
m
F
dr
∞
praca siły grawitacji
praca siły grawitacji
W
=
∫
r
∞
F⋅dr =
∫
r
∞
F dr cos
F ,
dr
= −1
∫
r
∞
G M m
r
2
dr
W
= −G M m
∫
r
∞
1
r
2
dr
= −G M m
−1
r
r
∞
W
= G M m
1
∞ −
1
r
=−
G M m
r

W
=
∫
r
∞
F⋅dr =
∫
r
∞
−dE
p
= −1E
p
∞
−E
pr
= E
pr
−E
p
∞
E
p
∞
= 0
E
pr
= E
p
r = −
G M m
r
W
= E
pr
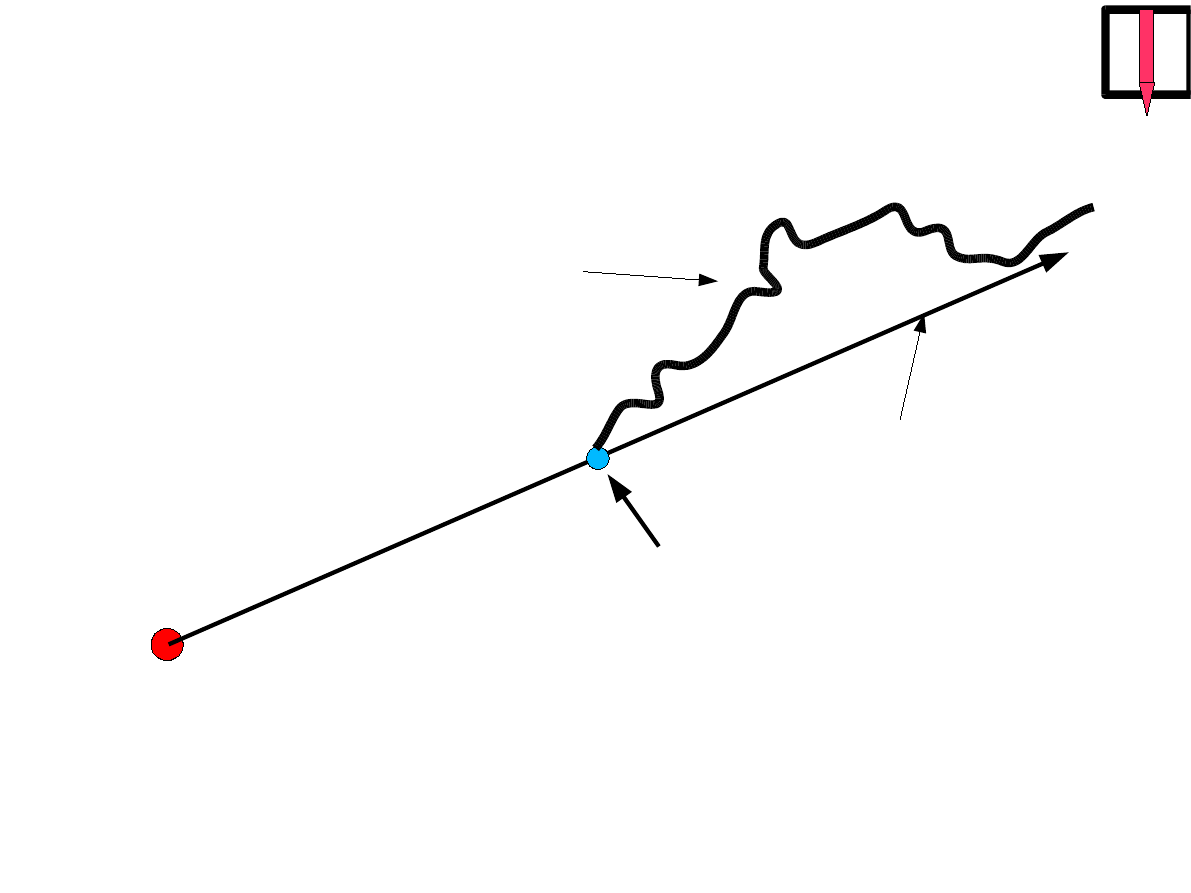
r
M
m
∞

E
pr
= E
p
r = −
G M m
r
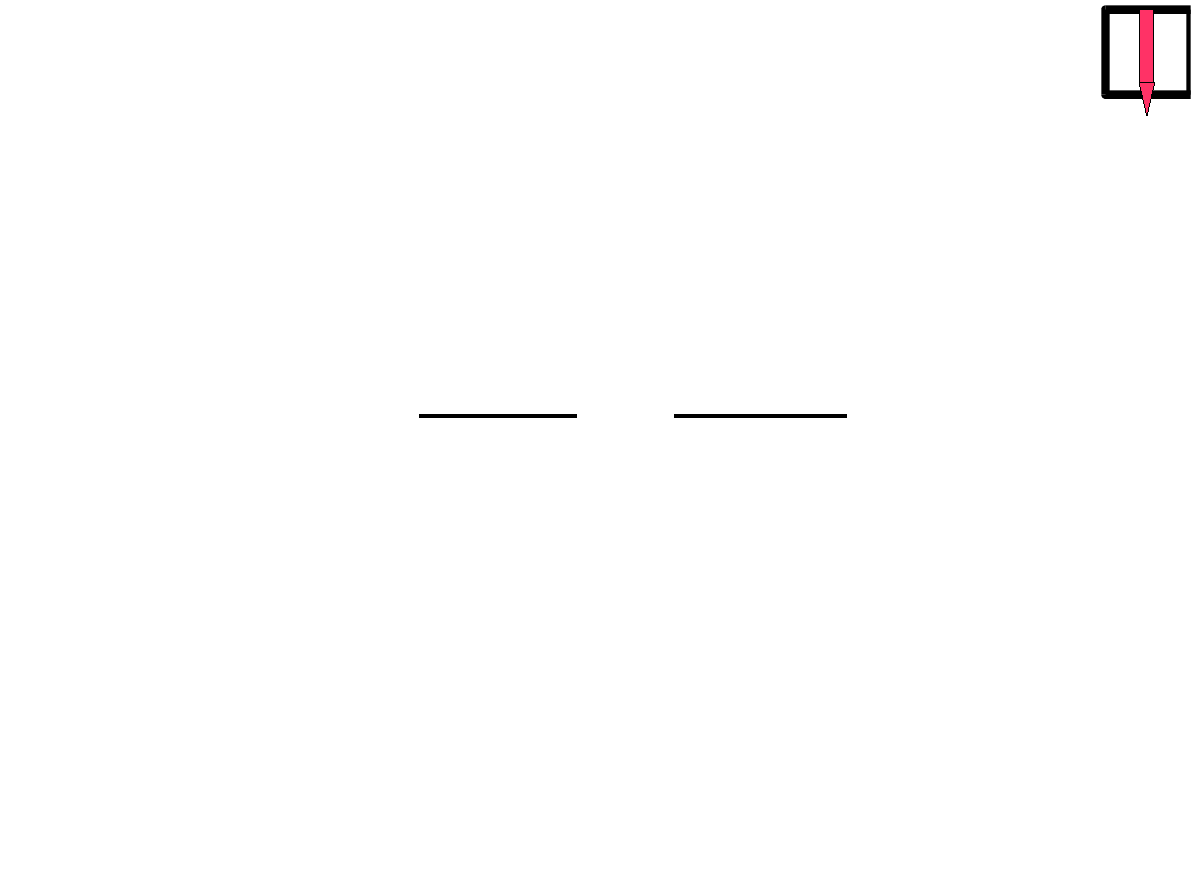
V
=
E
p
r
m
= −
G M
r
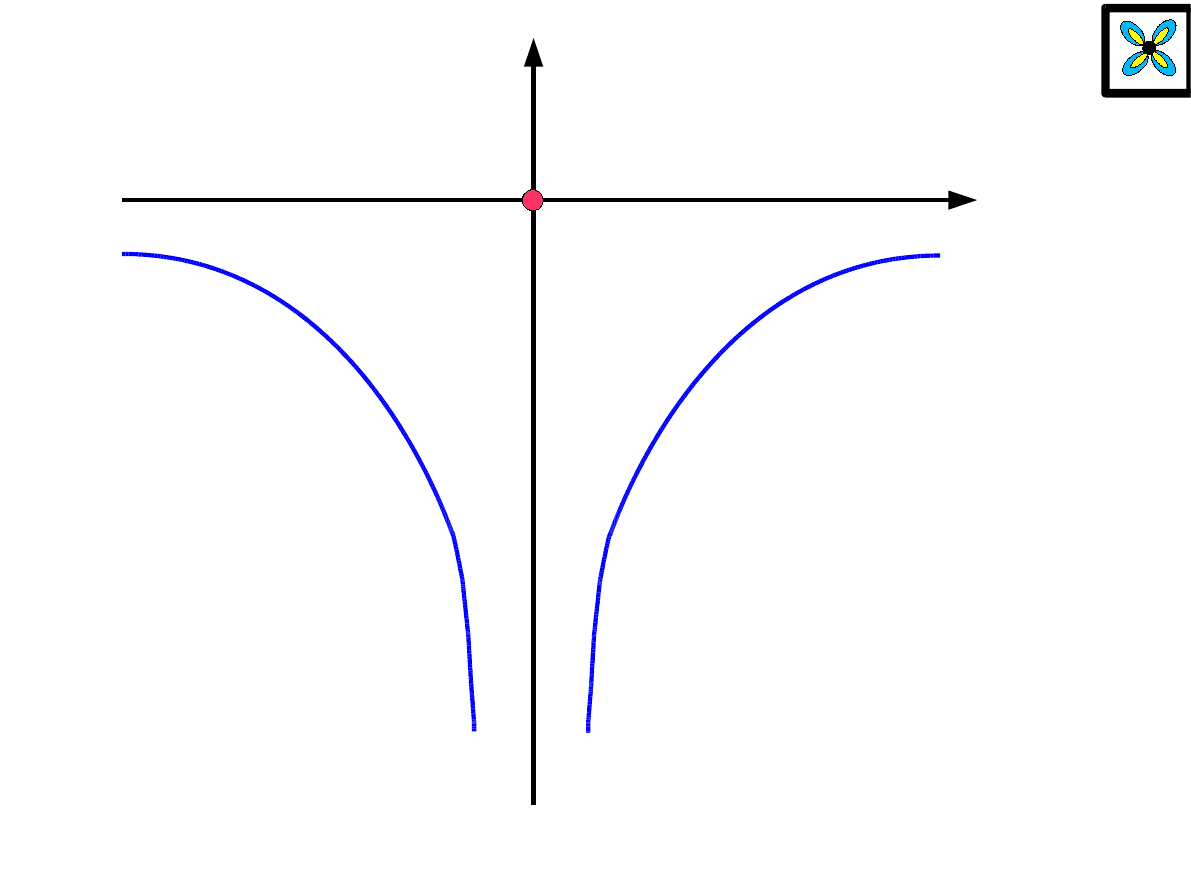
r
V
r
M
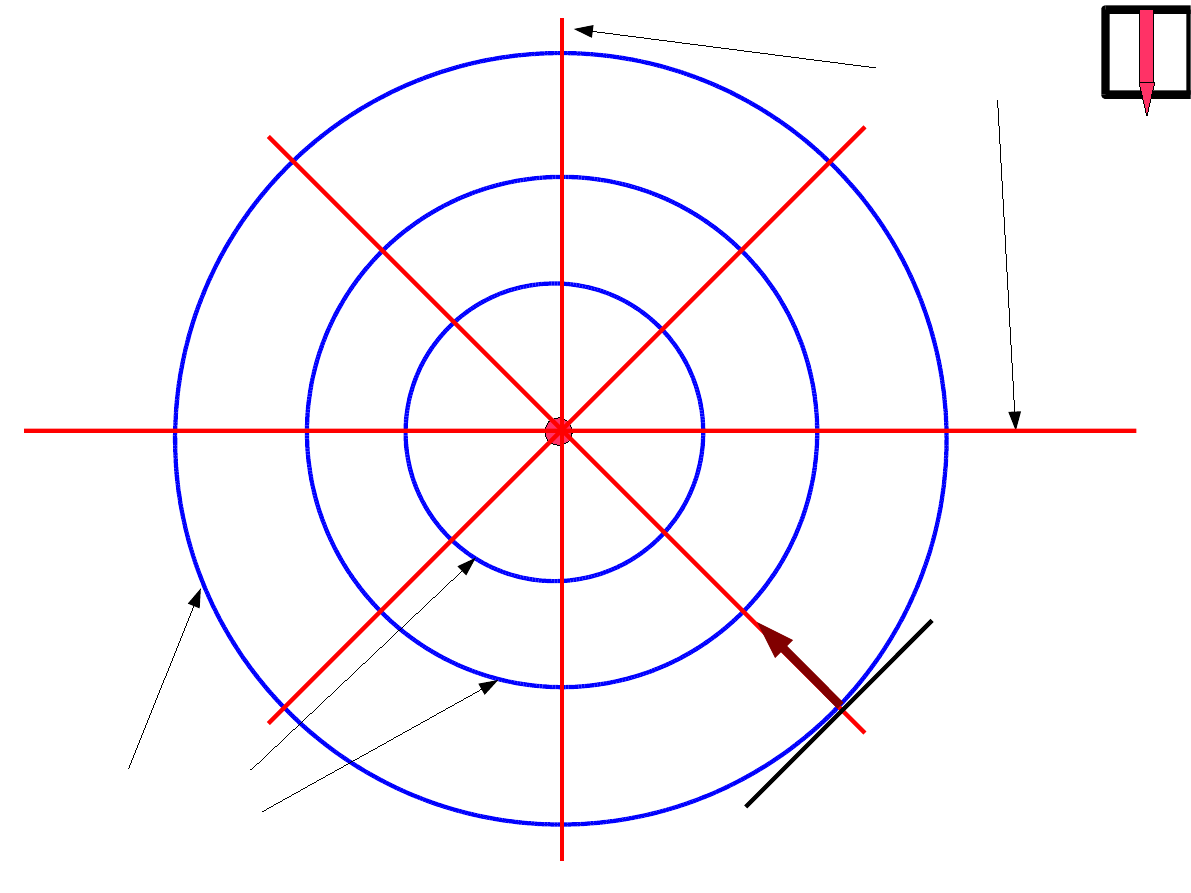
M
E
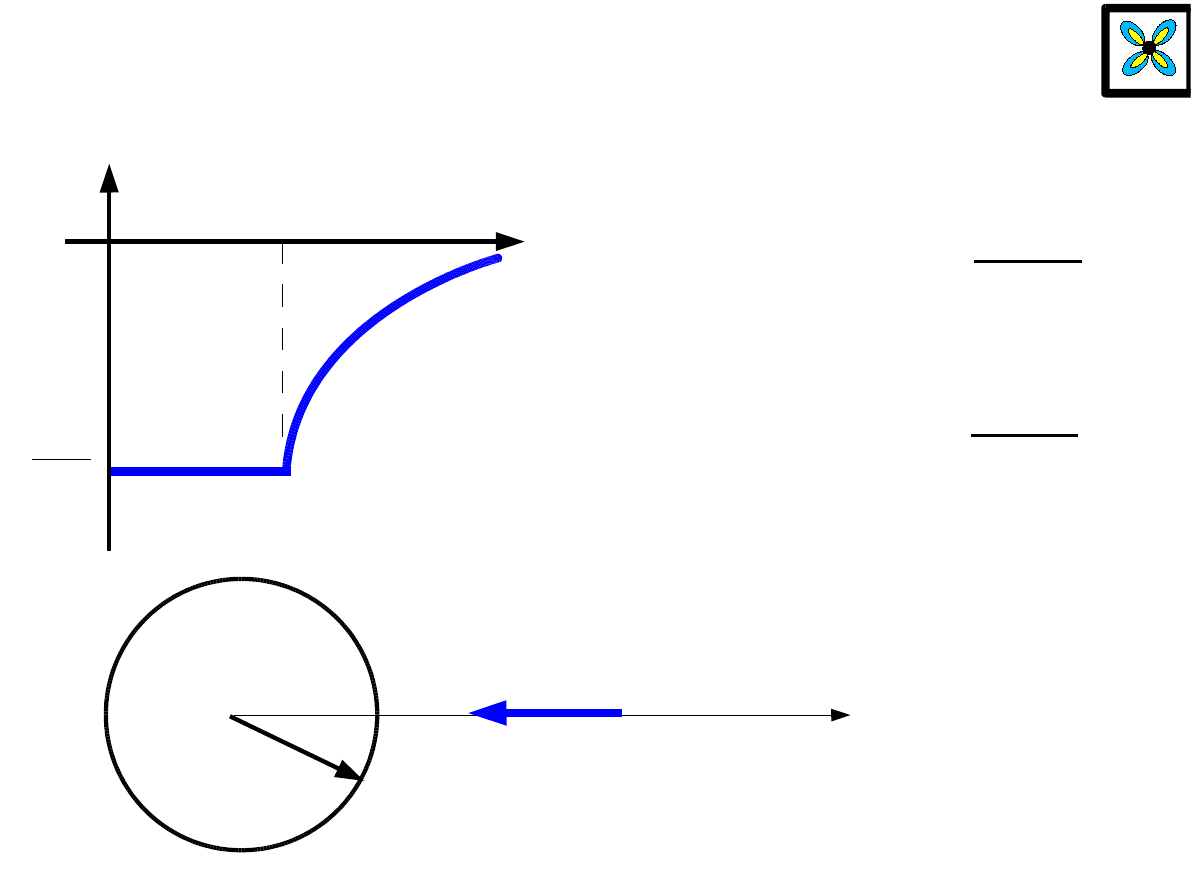
potencjał pola grawitacyjnego jednorodnej powłoki kulistej
M
R
V
r
R
x
R V = −
GM
R
x
≥R V = −
GM
r
r
F
−
GM
R
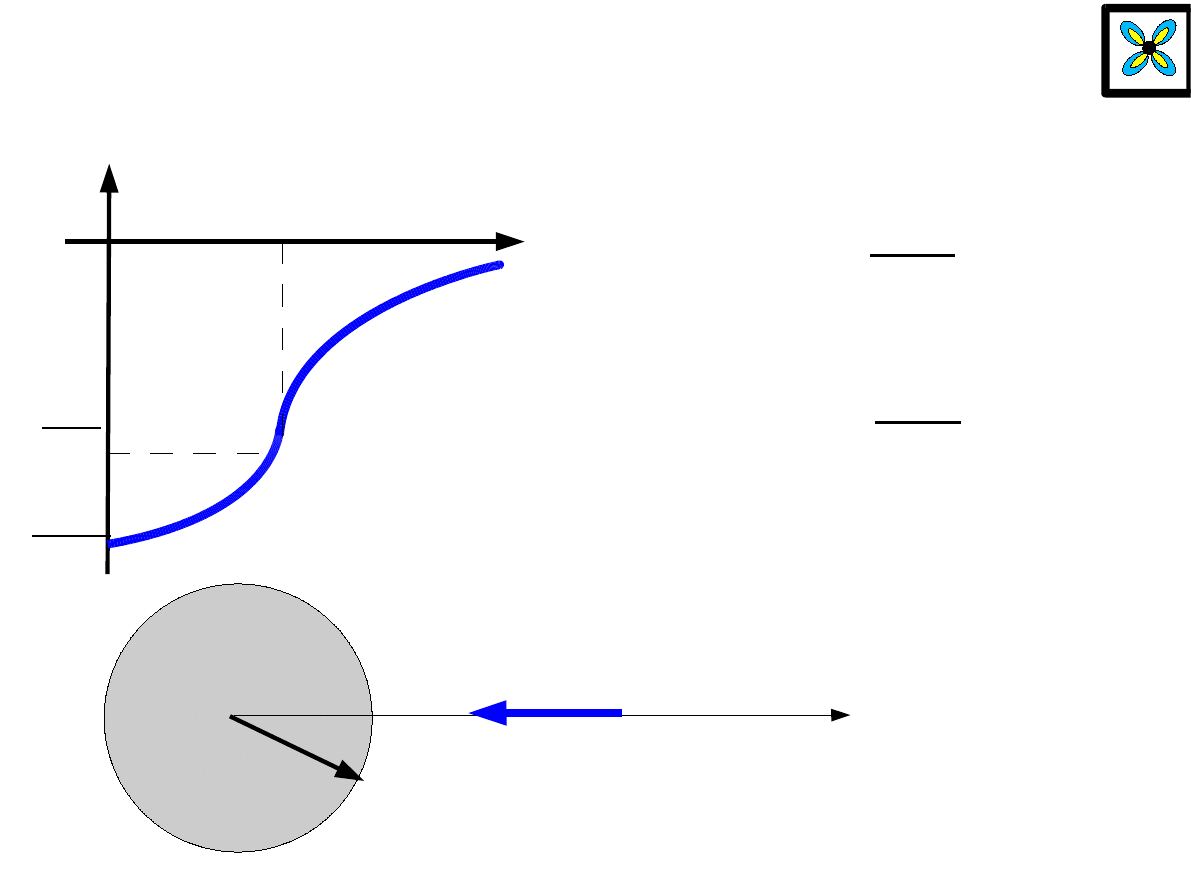
potencjał pola grawitacyjnego jednorodnej kuli
M
R
V
r
R
x
R V = −
GM
2 R
3
3 R
2
−r
2
x
≥R V = −
GM
r
r
F
−
GM
R
−
3GM
2 R
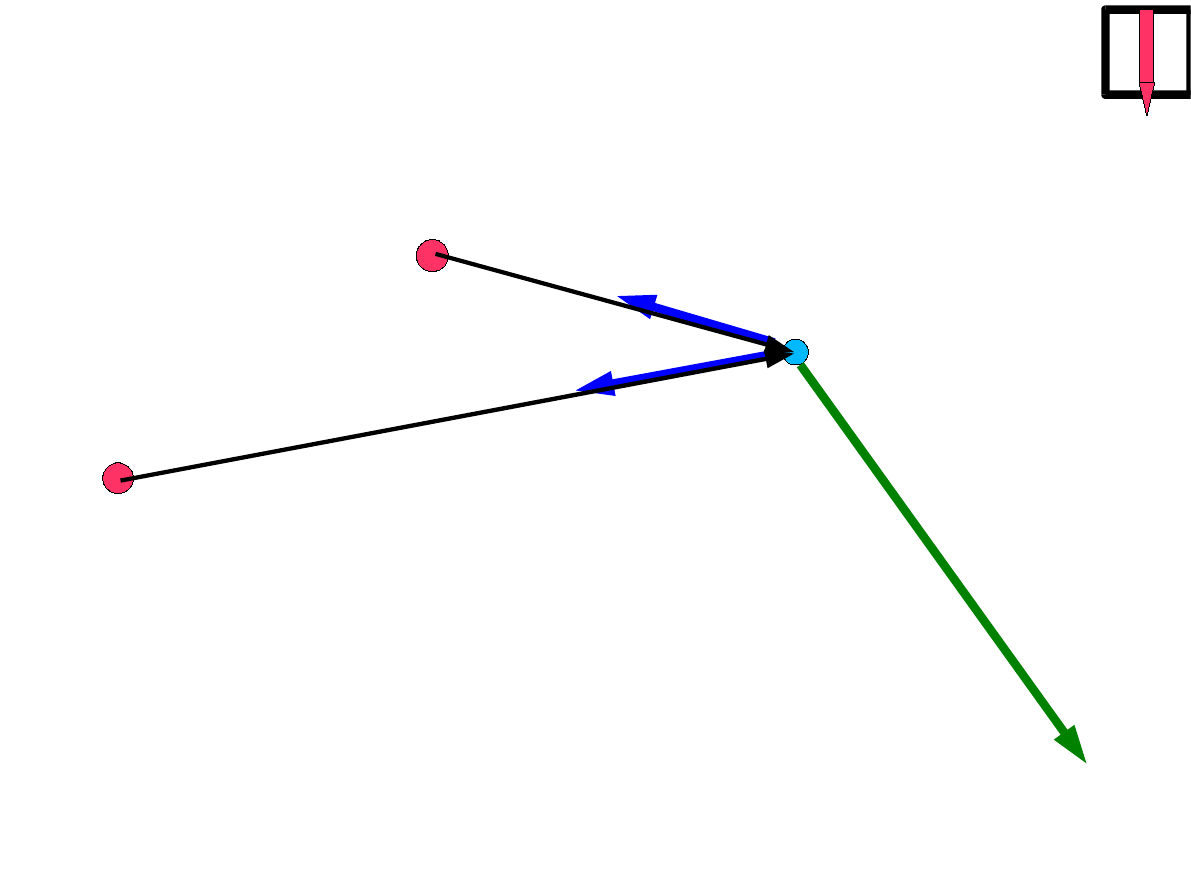
potencjał pola grawitacyjnego wielu mas punktowych
r
1
r
2
M
1
M
2
∞
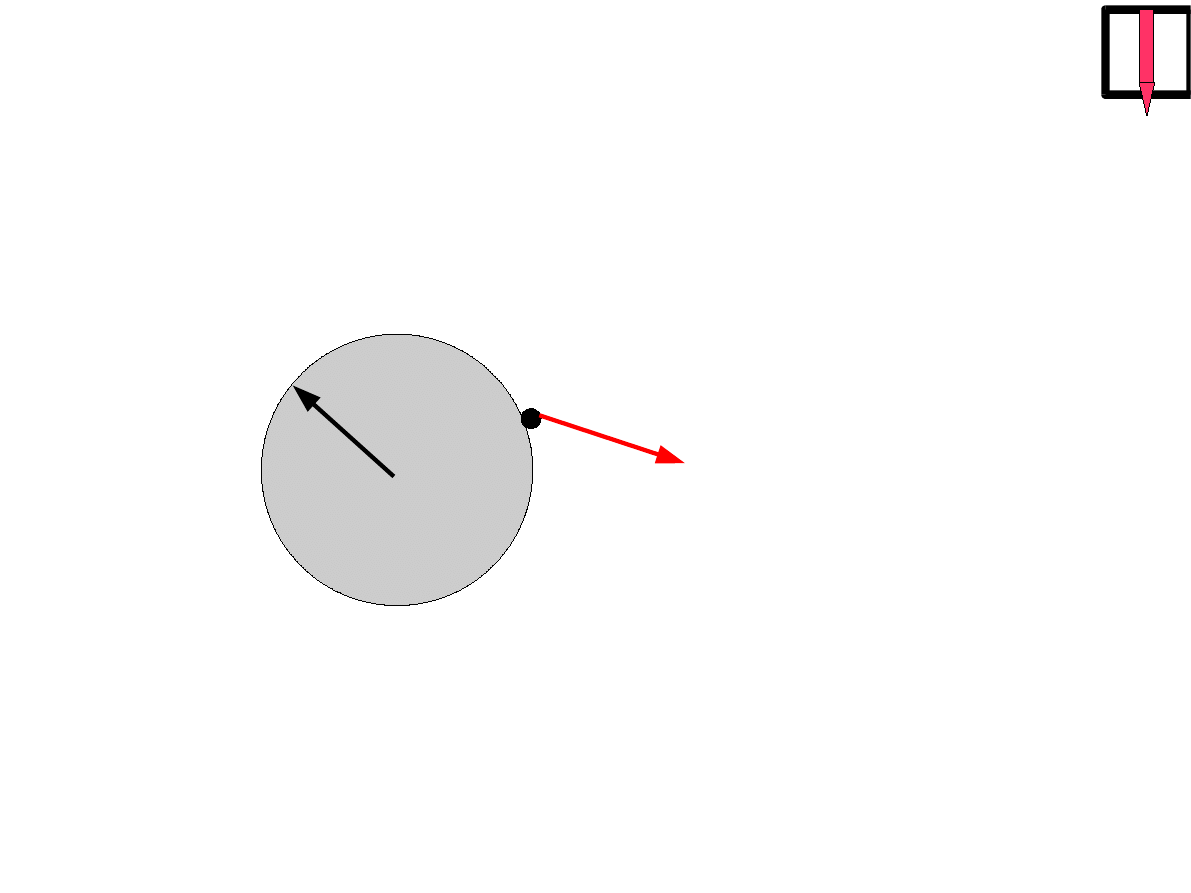
II prędkość kosmiczna
M
m
V
R
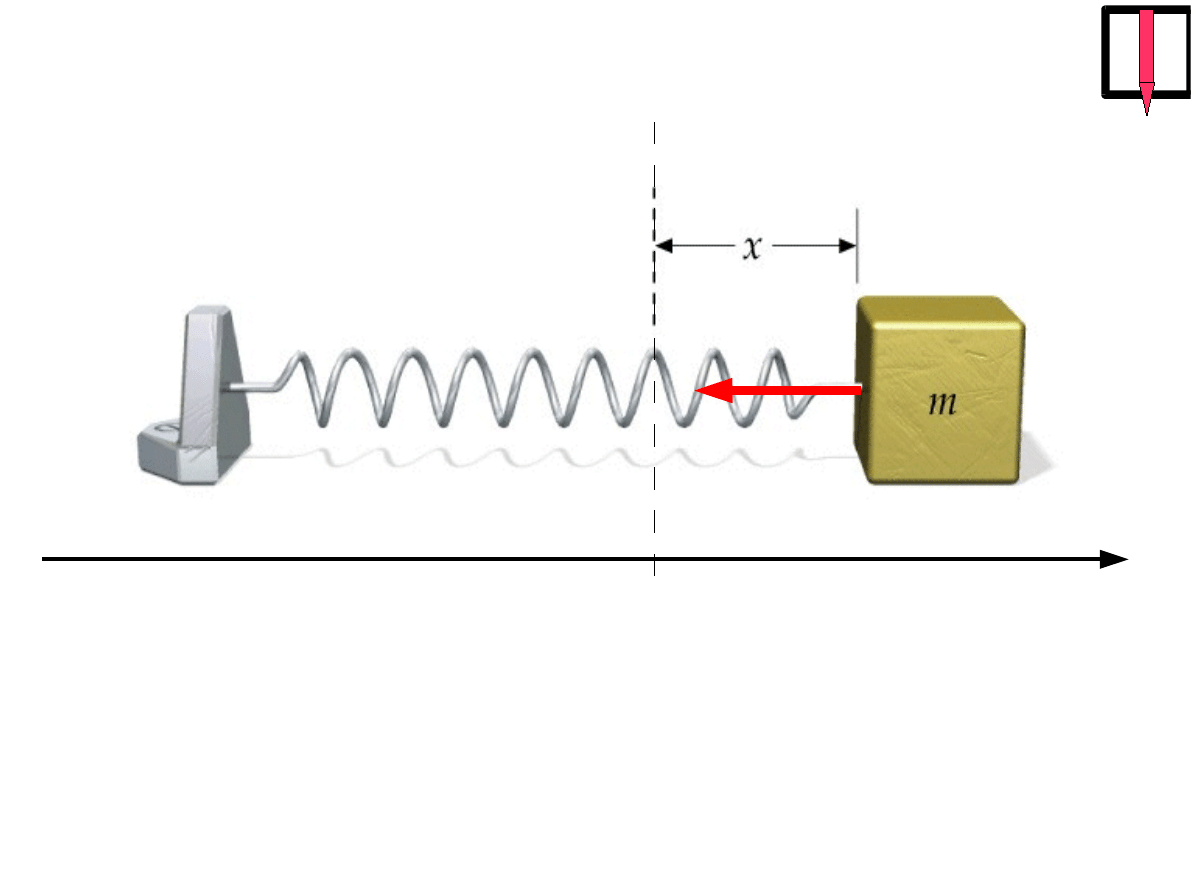
x
=0
X
F
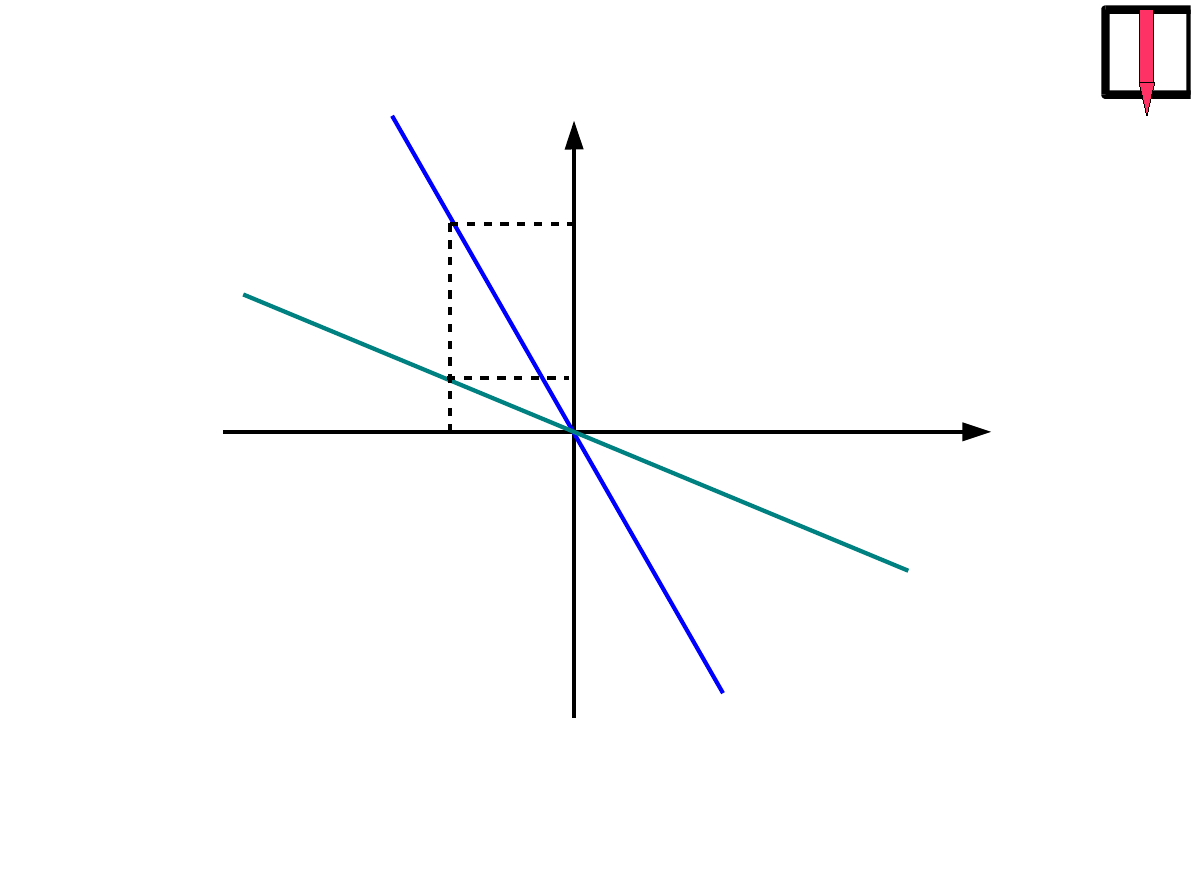
x
F

W
=
∫
0
x
F⋅
dx
=
∫
0
x
−kx dx=−k
[
x
2
2
]
0
x
W
= −
1
2
k x
2
praca siły sprężystości

W
=
∫
0
x
−dE
p
= −1[ E
p
x−E
p
0] = E
p
0−E
p
x
E
p
0 = 0
W
= −E
p
x
praca siły sprężystości
E
p
x = −W
E
p
x = −−
1
2
k x
2
=
1
2
k x
2

E
p
x =
1
2
k x
2
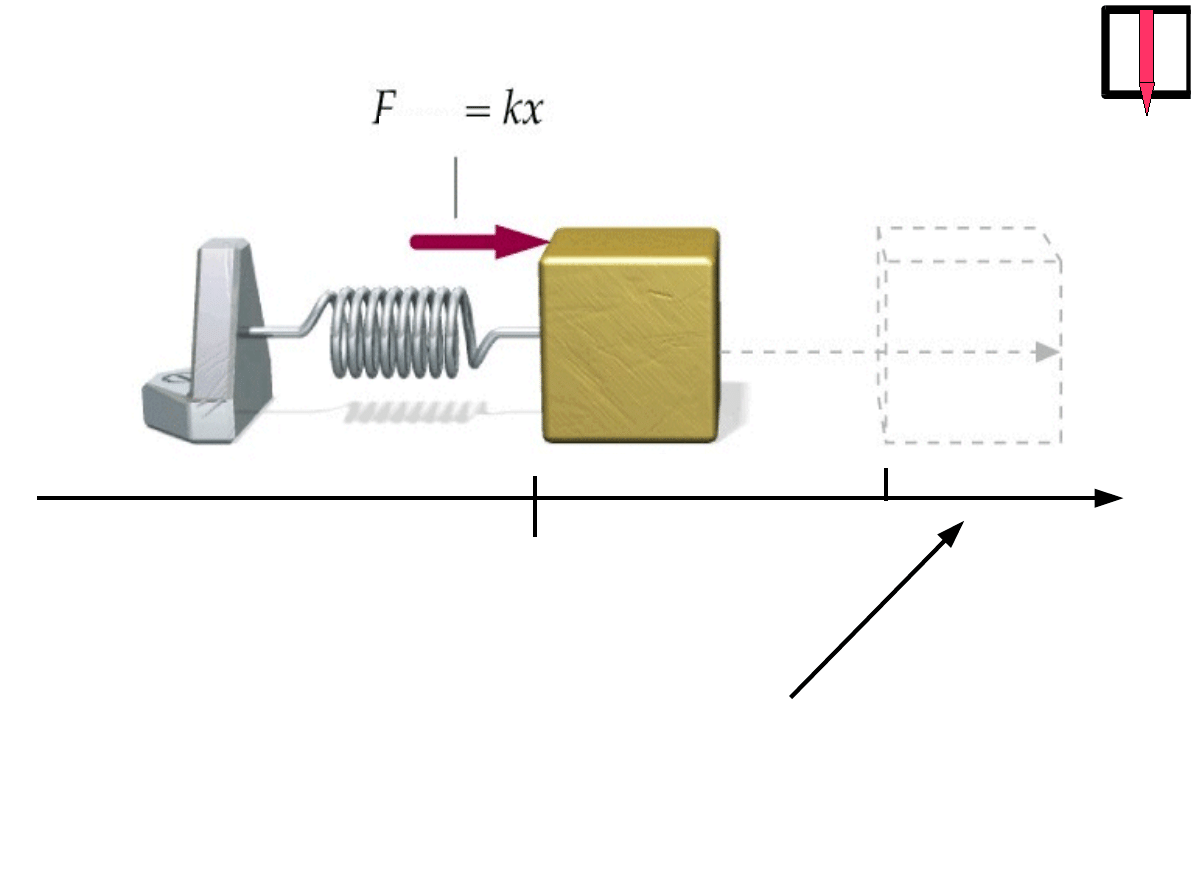
x
x
=0
z
siła zewnętrzna
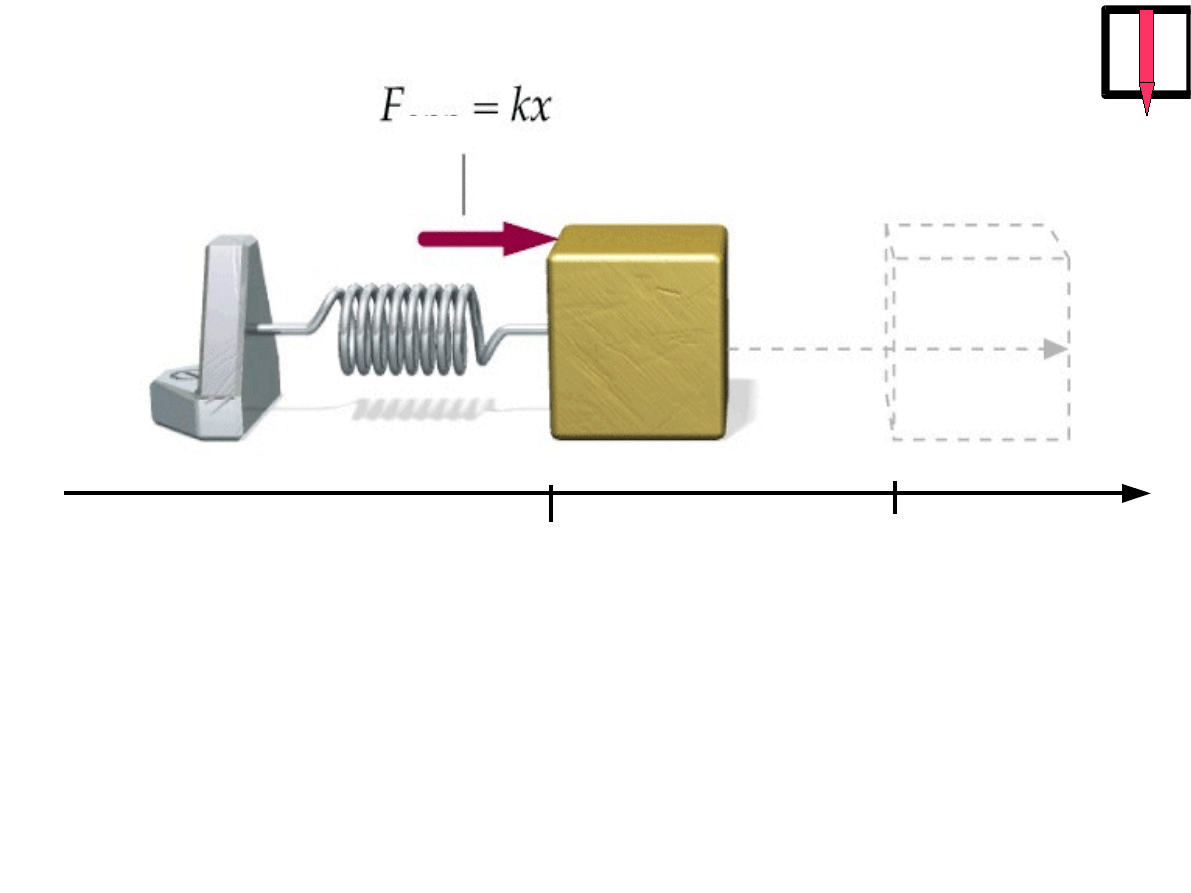
x
2
x
1
z
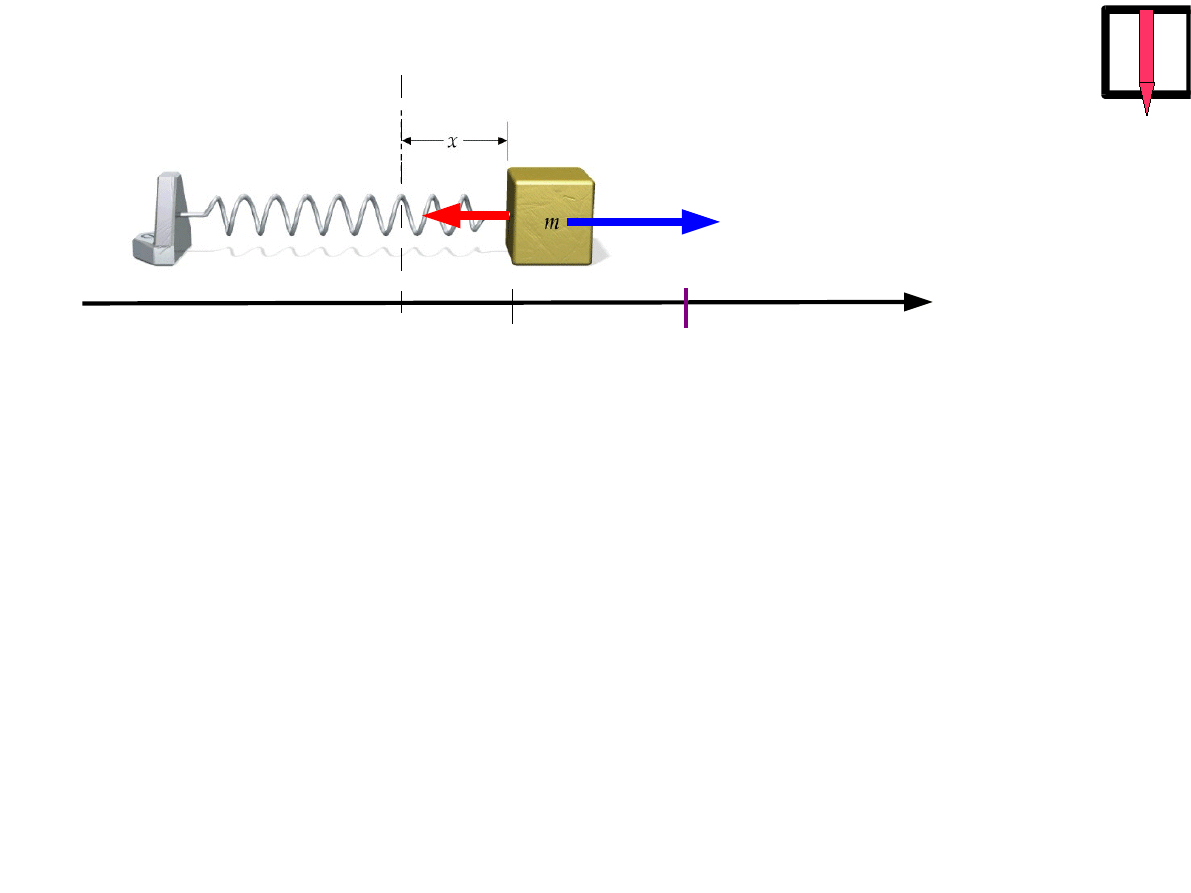
x
=0
X
F
V
A
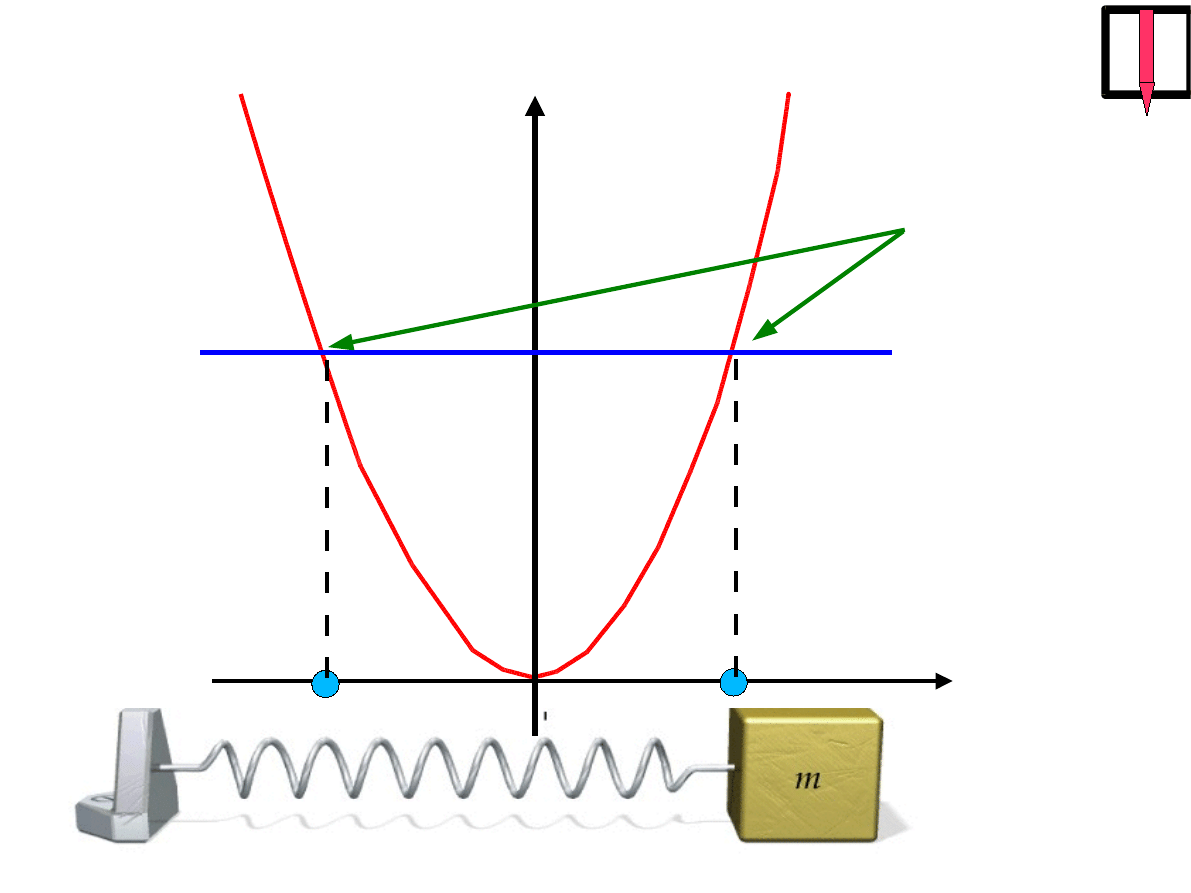
X
E
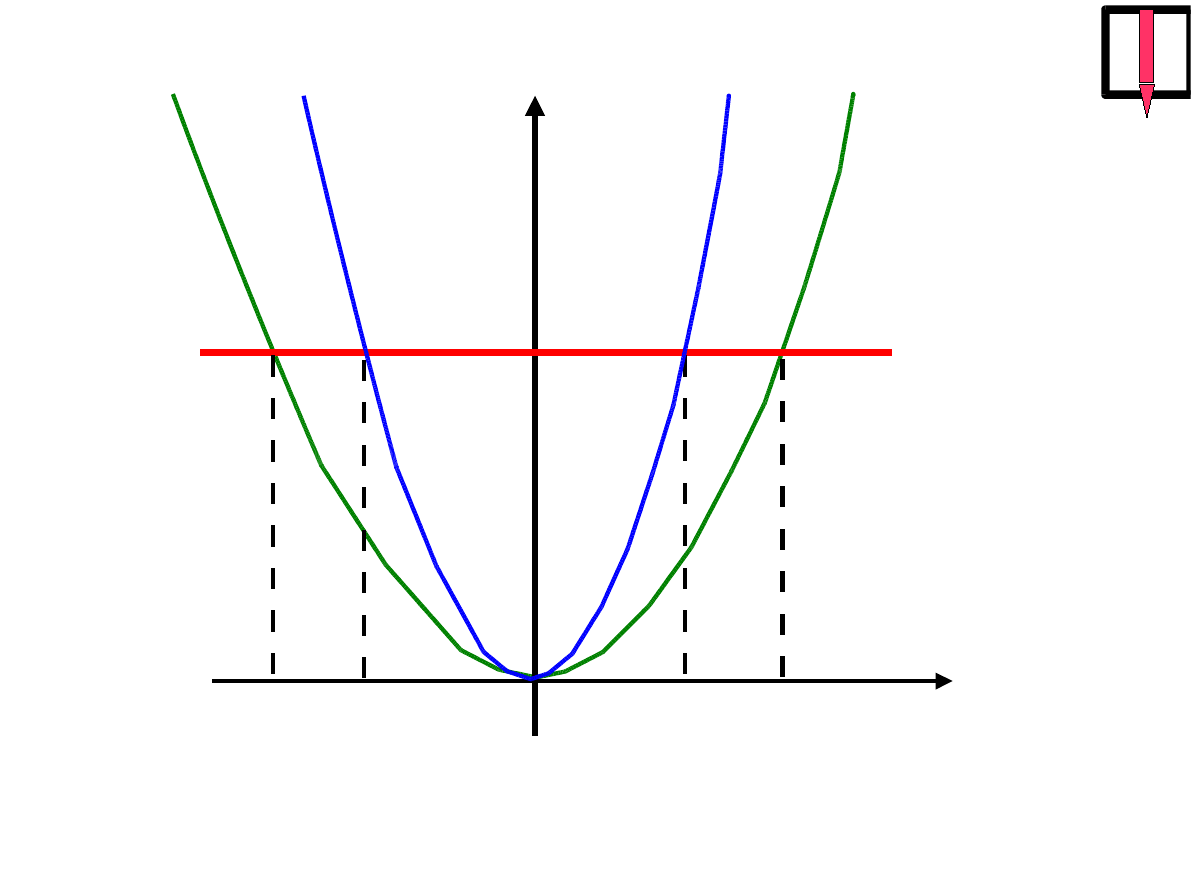
X
E
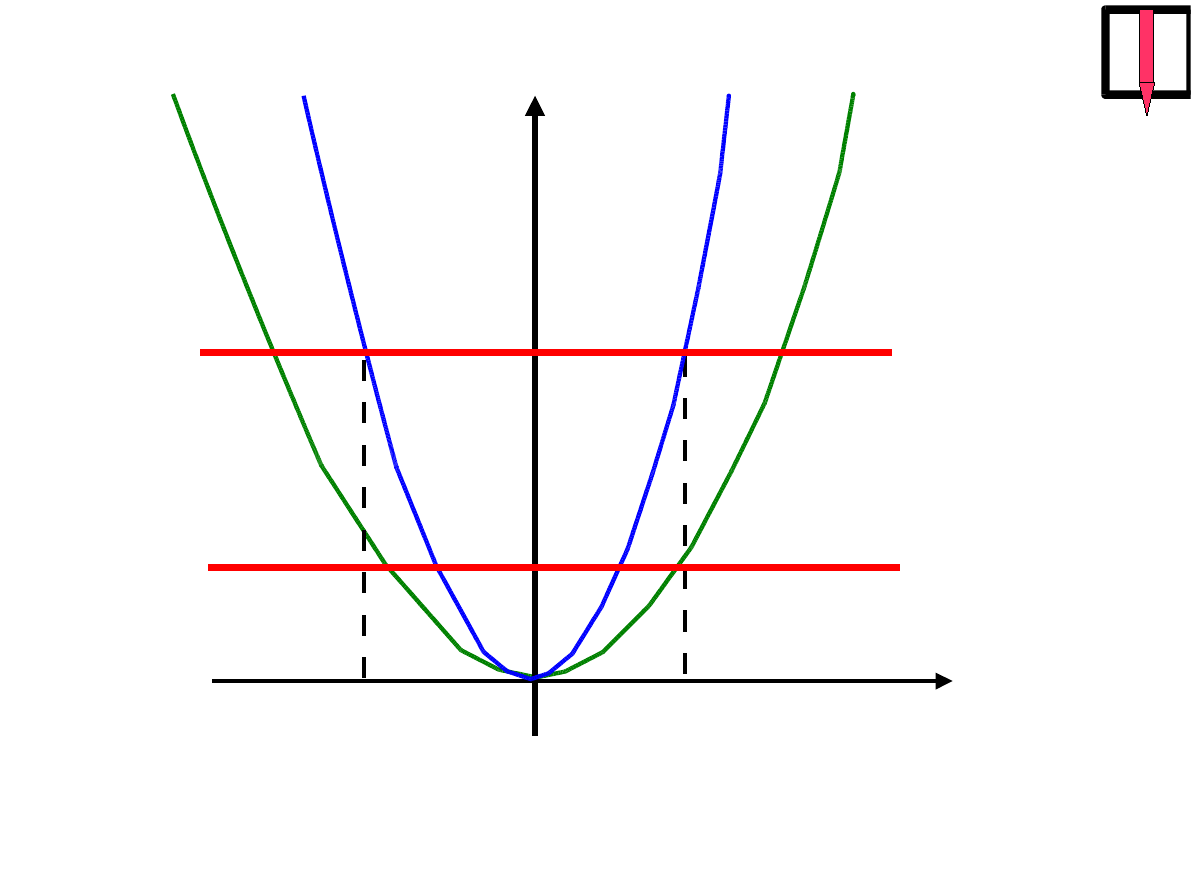
X
E
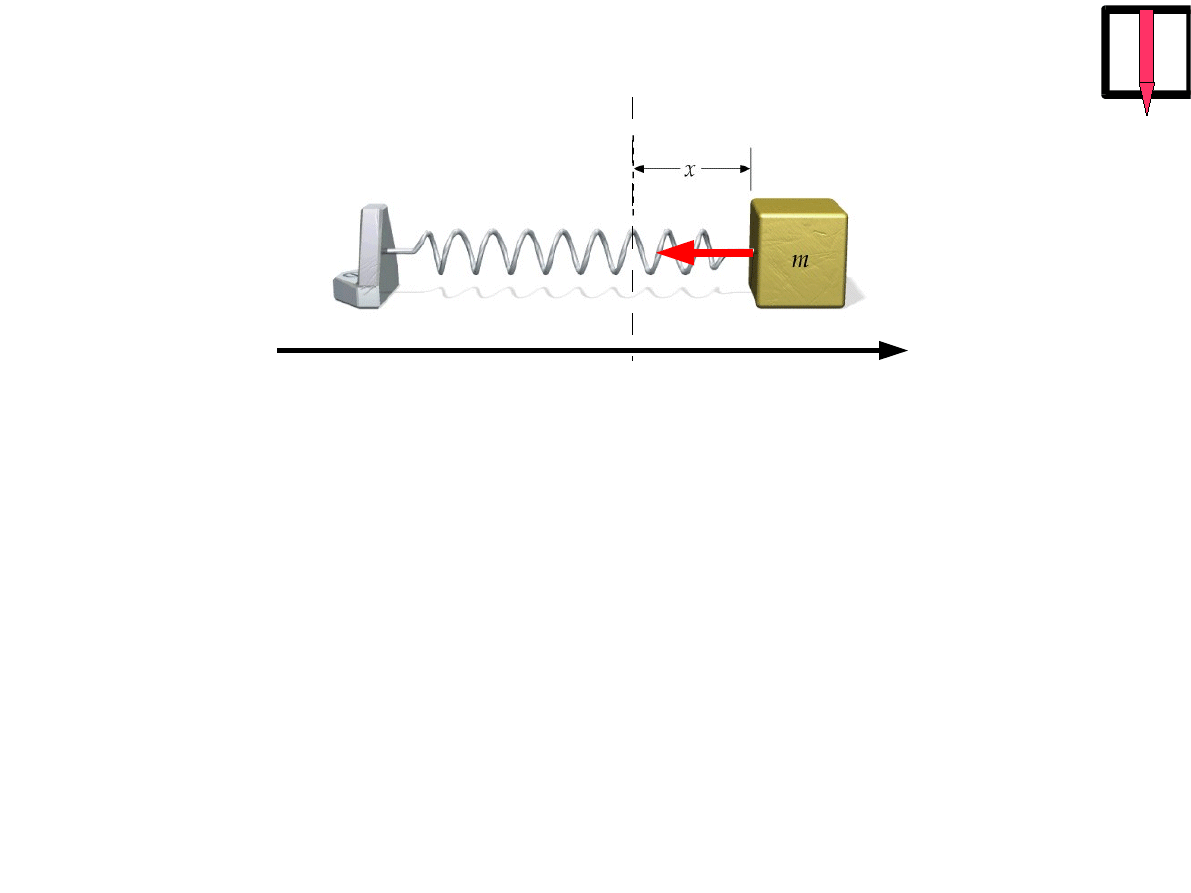
x
=0
X
F
dynamiczne równanie oscylatora harmonicznego

x
t = Asin t
kinematyczne równanie oscylatora harmonicznego
x
t
A
t
wychylenie z położenia równowagi
amplituda
faza
faza początkowa
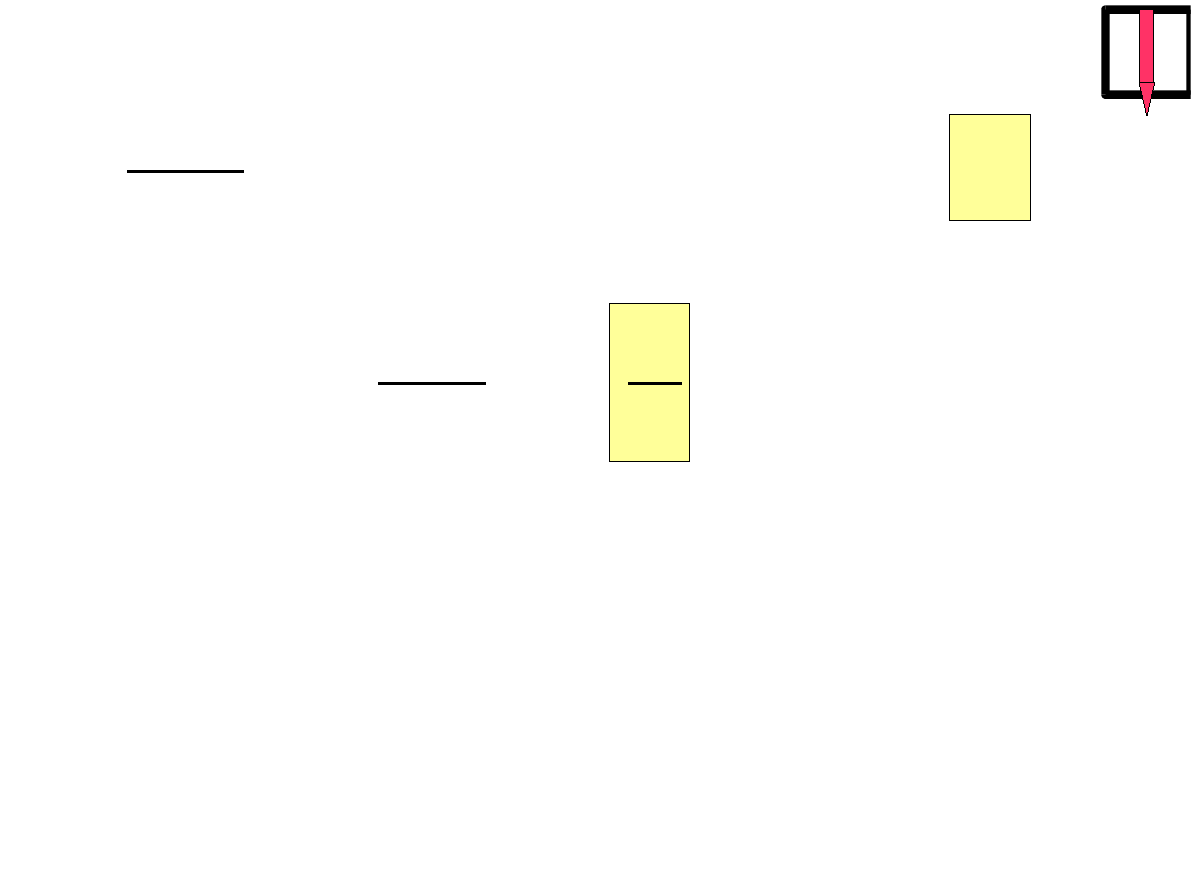
d
2
x
dt
2
= −
k
m
x
d
2
x
dt
2
= −A
2
sin
t = −
2
x
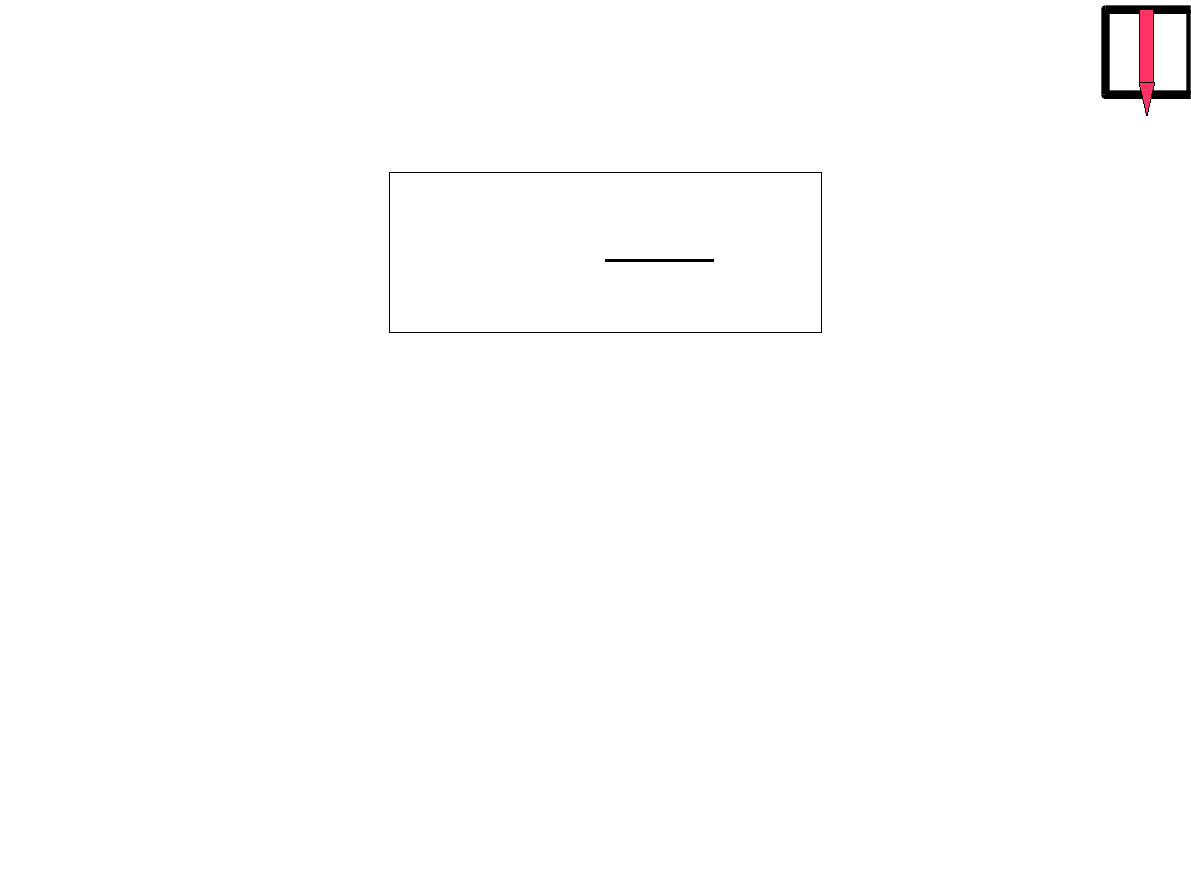
=
2
T
częstość kątowa (kołowa) drgania

f
=
1
T
=
2
T
= 2 f
częstotliwość drgania
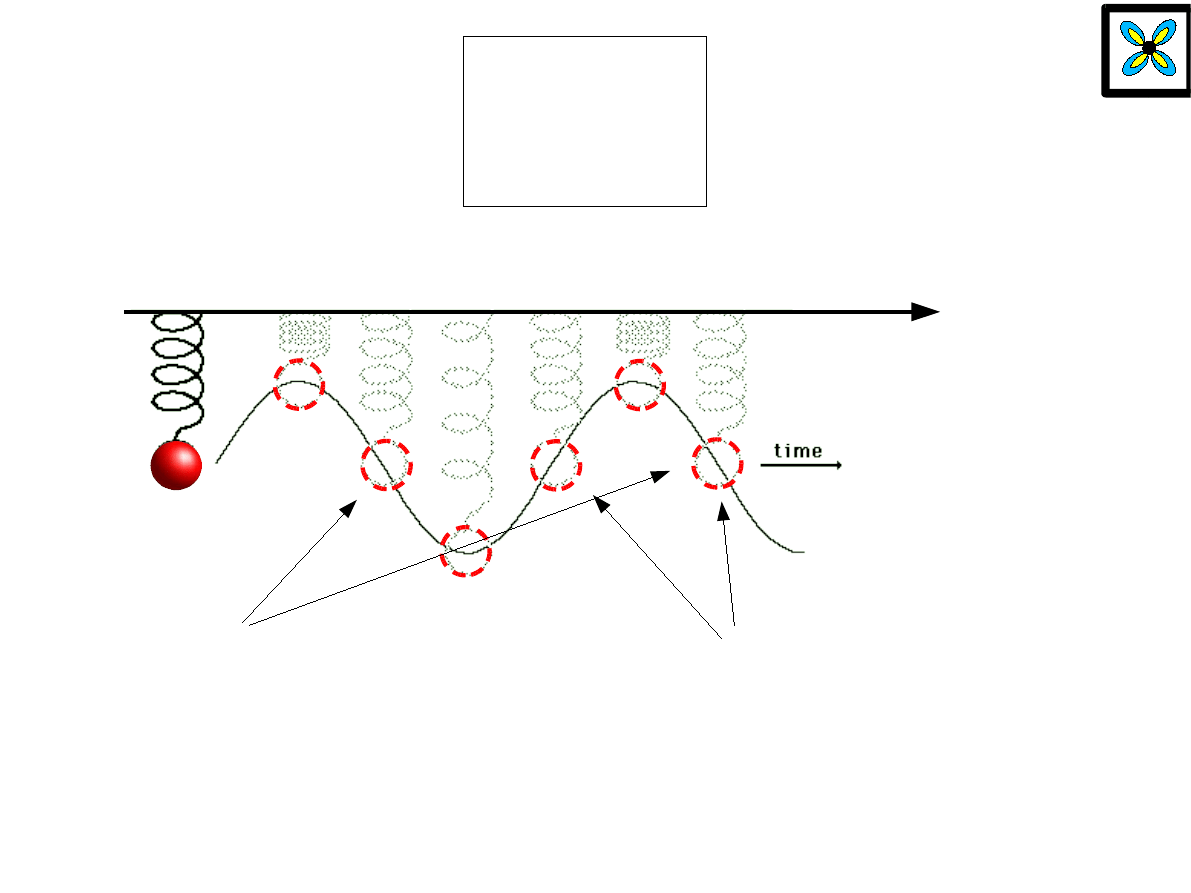
x
= Acost
t
zgodne
przeciwne
faza drgania
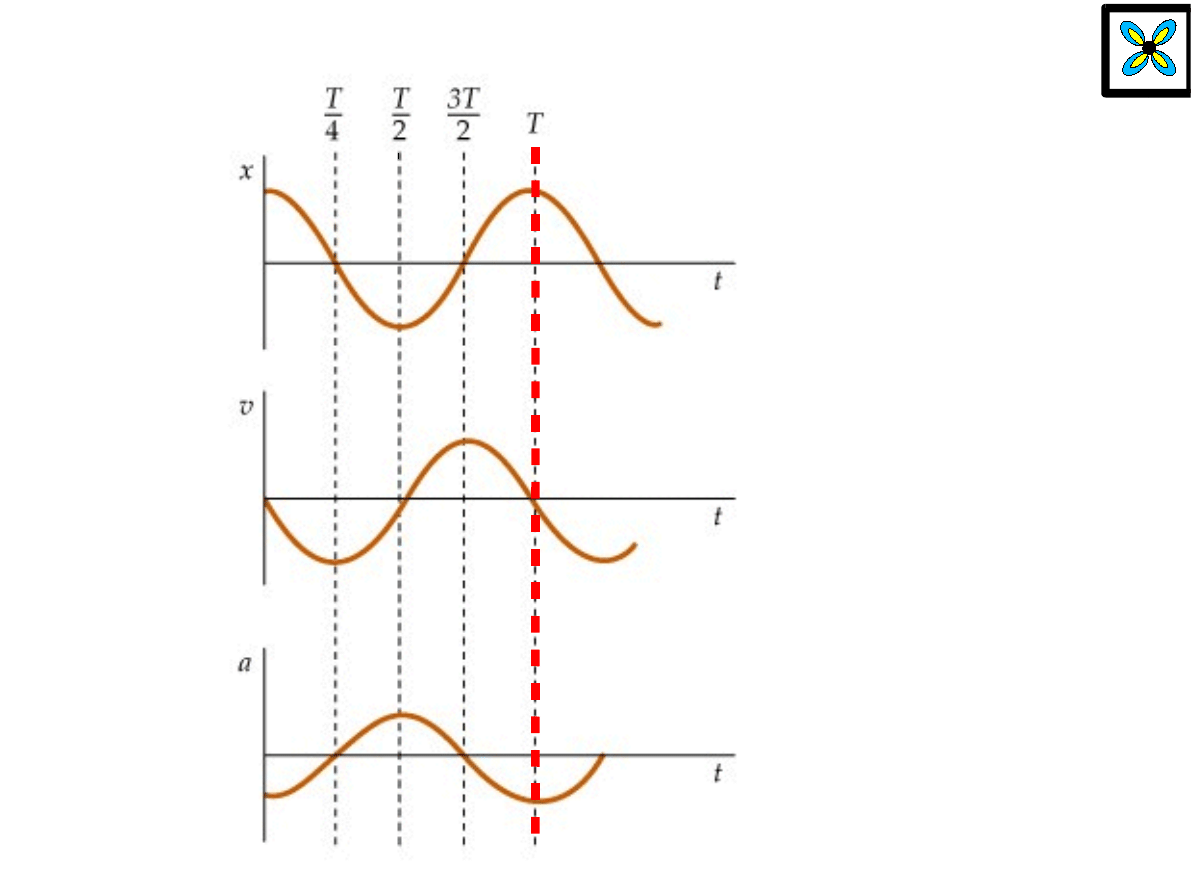

x
= Asin t
V
= A cost
a
= −A
2
sin
t = −
2
x
F
= −k x = −m
2
x
ruch harmoniczny prosty
siła
wychylenie z położenia równowagi
prędkość
przyspieszenie
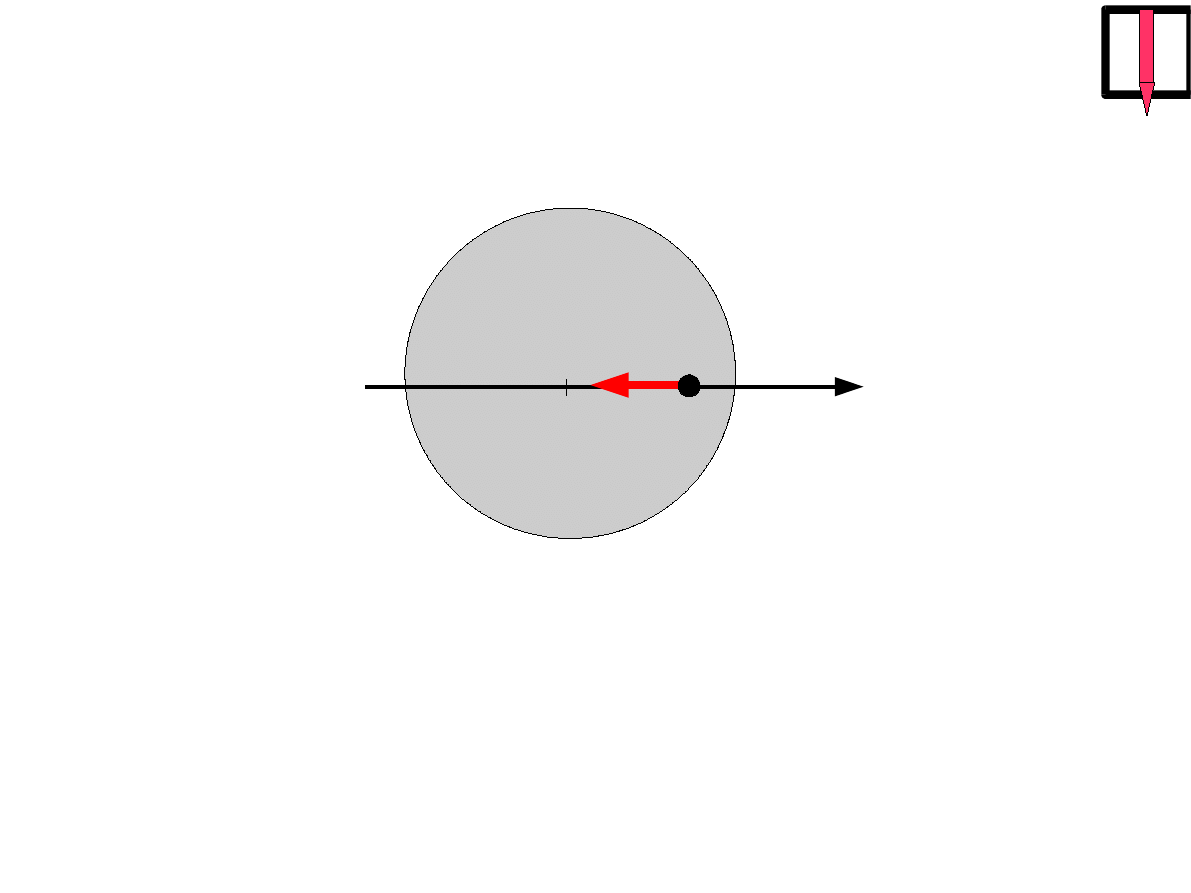
siły "sprężyste"
x
0
R
m
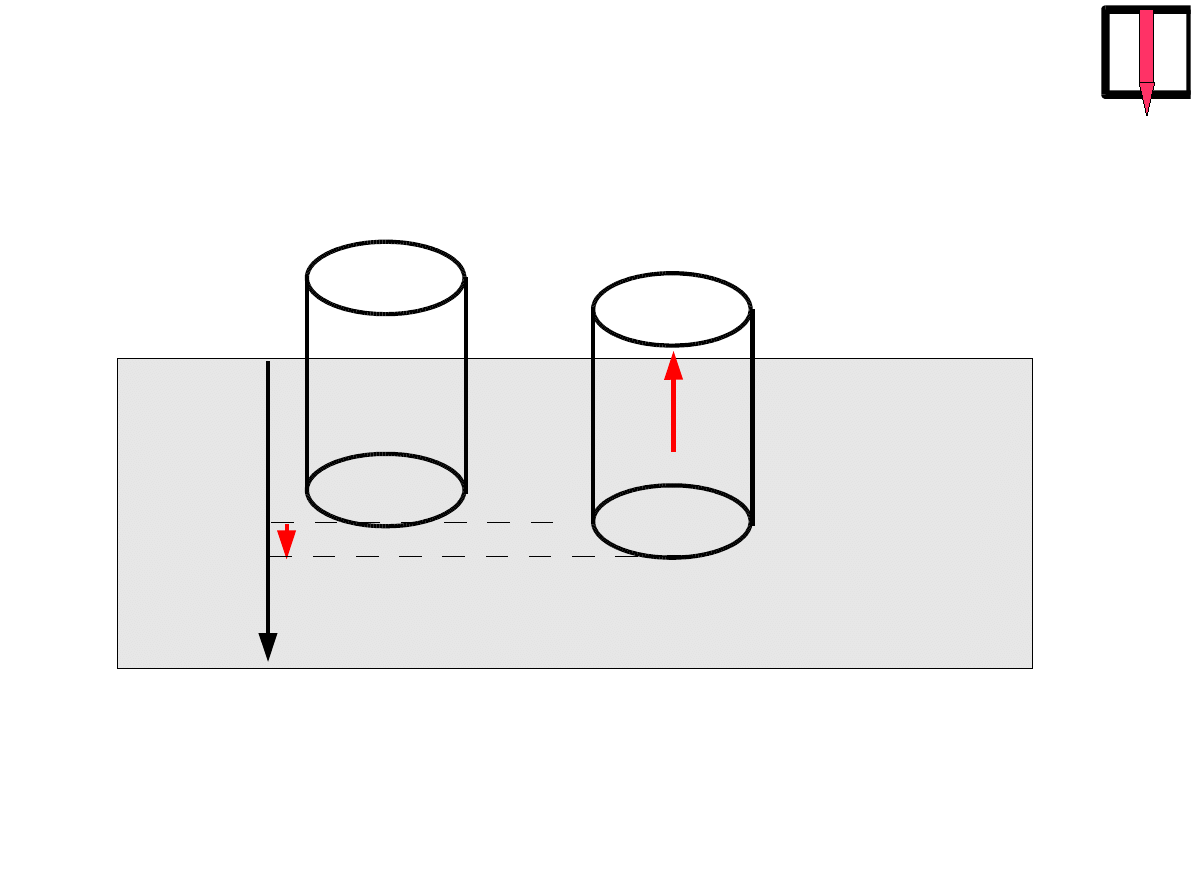
x
S
F
siły "sprężyste"
S
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron