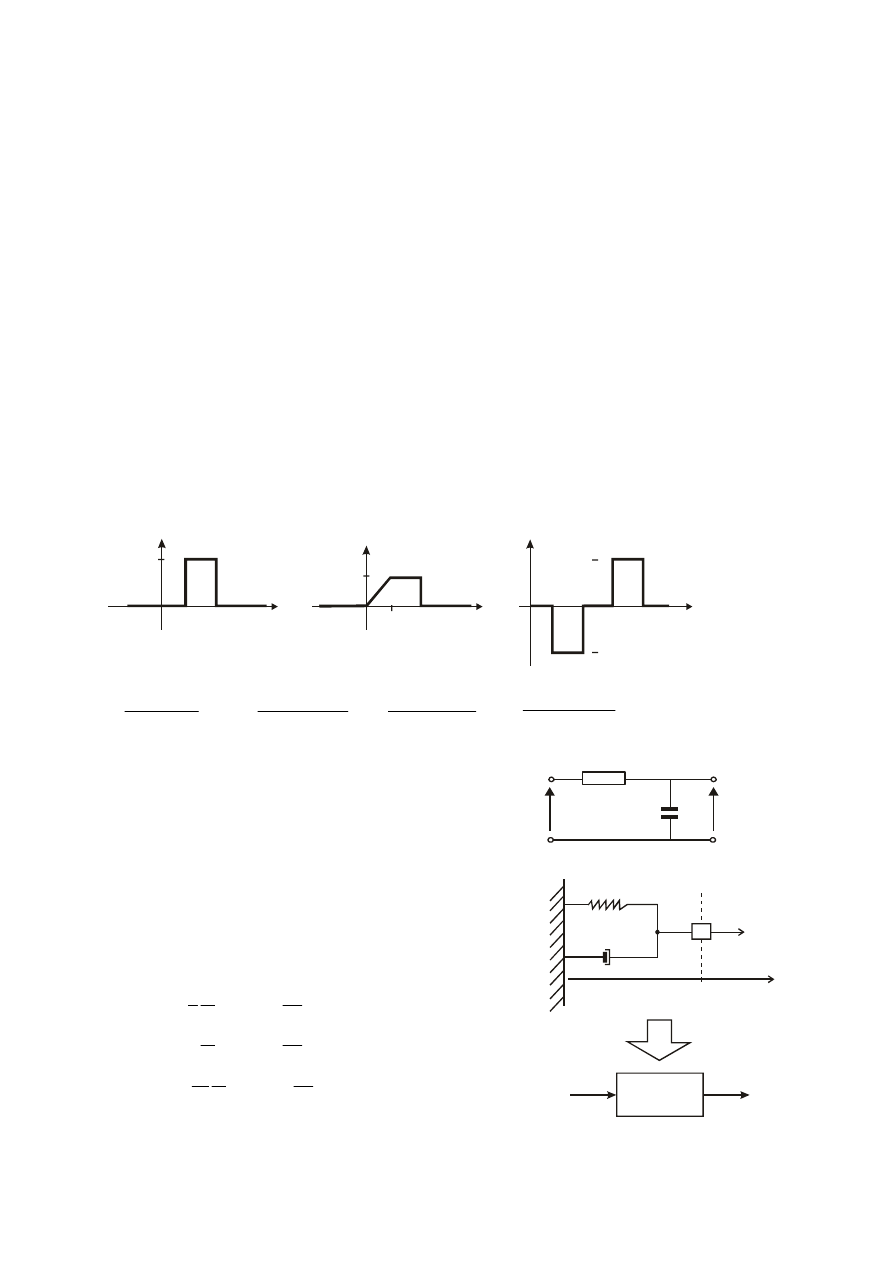
Sygnały i systemy
- Pytania i zadania -
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
maslowski@prz.edu.pl
Transformata Laplace’a
Transmitancja operatorowa i częstotliwościowa systemów
4.1. Wykreślić funkcje:
{
}
(
2)
2
3 ( ) 1;
(
2);
(
2); 2
(
/ 2)
(
/ 2)
2(
5
6)
t
t
u t
e u t
e
u t
u t T
u t T
t
t
−
− −
−
−
−
+
−
−
− +
4.2. Wyznaczyć transformatę jednostronną Laplace’a ciągłych sygnałów przyczynowych:
a) ( ); 2 ( ); 4 (
2);
u t
u t
u t −
b)
( ); 2 ( );
(
2);
t
t
u t
δ
δ
δ
−
c)
2
2
2(
2)
( );
( );
(
2)
t
t
t
e u t
e u t
e
u t
−
−
−
−
d)
[
]
0
0
0
(cos
) ( ); (sin
) ( );
sin(
) ( )
t u t
t u t
t
u t
ω
ω
ω
φ
+
e)
t
4
5
10
t
1
1
2
t
4
2
4
3
1
-4
4.3. Wyznaczyć transformatę odwrotna funkcji zespolonej
( ) :
F s
a)
10
7
3
2
+
+
+
s
s
s
;
b)
)
2
4
)(
1
(
4
2
+
+
+
s
s
s
s
;
c)
)
7
(
)
5
(
1
2
+
−
s
s
;
d)
)
13
4
(
52
38
2
+
+
+
s
s
s
s
4.4. Wyznaczyć transmitancję operatorową i częstotliwościo-
wą oraz odpowiedź skokową i impulsową systemu pierwszego
rzędu (filtr dolnoprzepustowy RC)
2
R
Ω
=
;
250
C
F
µ
=
4.5. Dla systemu drugiego rzędu pokazanego na rysunku:
a) wyznaczyć transmitancję operatorową i częstotliwościową
b) wyznaczyć i wykreślić charakterystykę amplitudową, fazową
(tzw. ch-ki Bode’go) oraz charakterystykę Nyquista (tzw. ch-ka
częstotliwościowo-fazowa)
c) wyznaczyć odpowiedź impulsowa i skokową dla różnych
wartości parametrów:
1)
kg
1
m
Ns
4
m
N
4
7
=
=
=
m
B
K
2)
kg
1
m
Ns
4
m
N
1
=
=
=
m
B
K
3)
kg
1
m
Ns
4
m
N
4
25
=
=
=
m
B
K
Wskazówka: Siła wypadkowa w układzie mechanicznym to siła wymuszająca
pomniejszona o siłę sprężystości
( )
Kx t
i siłę oporu
( )
Bv t
, gdzie
( )
( ) /
v t
dx t dt
=
C
R
u (t)
wy
u (t)
we
X(s)
m
Sprężyna
K
Tłumik
B
Ciężarek
F(t)
Siła
0
x
Położenie równowagi
H(s)
F(s)
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron