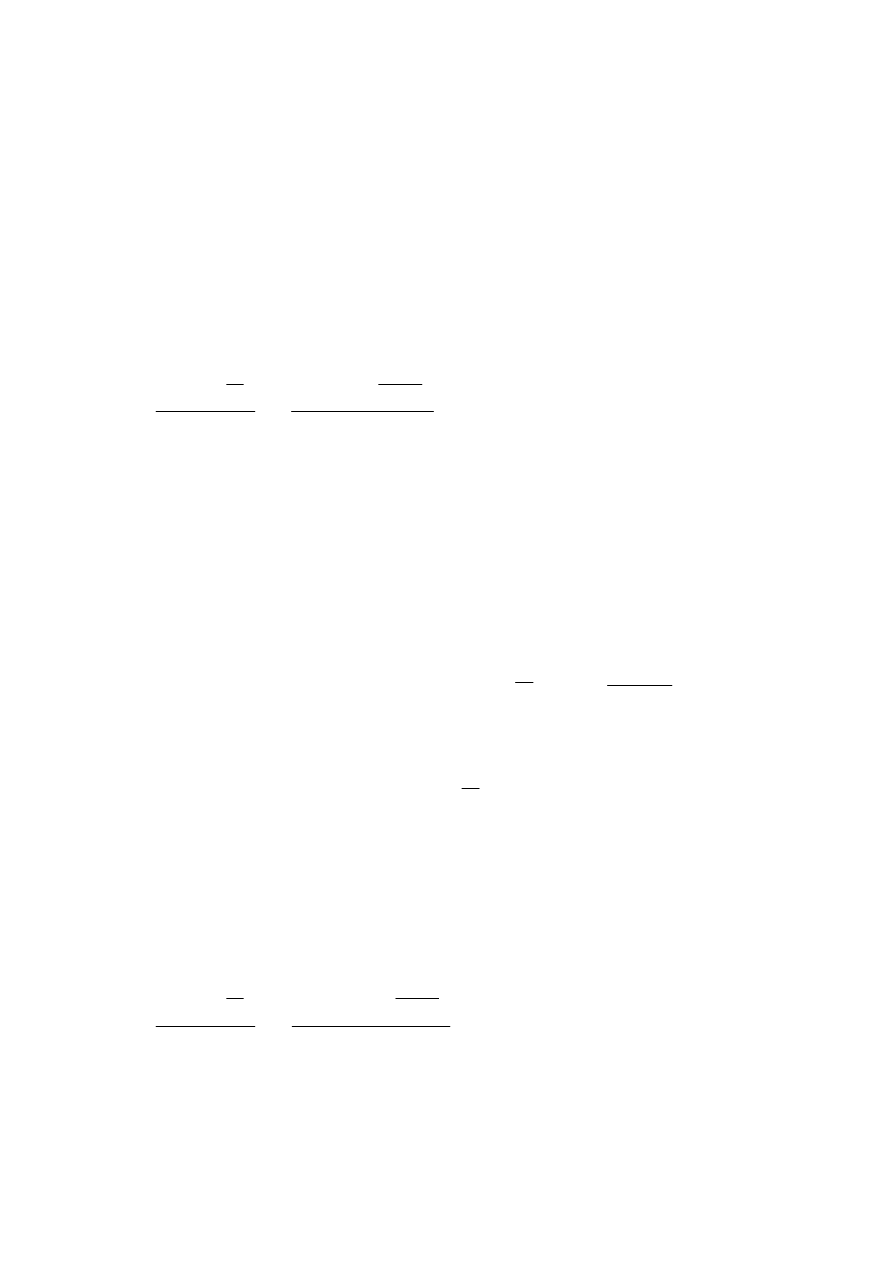
Przykład 8: Oprocentowanie rachunku wynosi 10% w skali roku. Na rachunku
znajduje się kwota 2400 zł. Na koniec każdego roku z rachunku będzie
wypłacana rata 300 zł. Ile rat w wysokości 300 zł można wypłacić z tego
rachunku? Jakie będzie saldo rachunku w rok po wypłaceniu ostatniej raty?
P=2400,
R=300,
i=10%,
n=?
∈
N
89
,
16
)
1
,
0
ln(1
300
2400
1
,
0
1
ln
i)
ln(1
R
P
i
1
ln
n
=
+
⋅
−
−
=
+
⋅
−
−
=
∉
N, n=NPER(10%; 300; -2400)
Maksymalna liczba wypłat:
*
n =16
Saldo po n
*
latach przy braku wypłat:
94
,
11027
1
,
1
2400
i)
(1
P
16
n
*
=
⋅
=
+
⋅
Warto
ść
ko
ń
cowa ci
ą
gu n
*
wypłat:
92
,
10784
1
,
0
1
1
,
1
300
s
R
16
i
|
n
*
=
−
⋅
=
⋅
Saldo po n
*
wypłatach:
02
,
243
92
,
10784
94
,
11027
s
R
-
i)
(1
P
i
|
n
n
*
*
=
−
=
⋅
+
⋅
Saldo po roku od ostatniej wypłaty: 243,02
⋅
(1+10%)=267,32 < 300 = R
Przykład 9: Oblicz liczbę rat renty, dla której R=200, i=5%, P=3600.
i)
ln(1
R
P
i
1
ln
n
+
⋅
−
−
=
19
,
47
)
05
,
0
ln(1
200
3600
05
,
0
1
ln
=
+
⋅
−
−
=

Problem sprzeczny, bo n=47,19
∉
N. Rozwi
ą
zanie stosowane w praktyce:
zaokr
ą
glenie n w dół lub w gór
ę
i korekta wysoko
ś
ci ostatniej raty.
1.
zaokr
ą
glenie n w gór
ę
, n=48
⇒
R
R
...
R
1
-
n
1
=
=
=
,
R
R
n
<
n
n
i
|
1
n
i)
(1
R
a
R
P
−
−
+
⋅
+
⋅
=
48
48
5%
|
47
5%)
(1
R
a
200
3600
−
+
⋅
+
⋅
=
⇒
49
,
39
R
48
=
2.
zaokr
ą
glenie n w dół, n=47
⇒
R
R
...
R
1
-
n
1
=
=
=
,
R
R
n
>
n
n
i
|
1
n
i)
(1
R
a
R
P
−
−
+
⋅
+
⋅
=
47
47
5%
|
46
%)
5
(1
R
a
200
3600
−
+
⋅
+
⋅
=
⇒
237,61
R
47
=
Praca domowa:
zadania 5.1-5.7, 5.9-5.14, 5.19 a-d, 5.20 (tylko oprocentowanie
składane), 5.22
Przykład 1: Dług w wysoko
ś
ci 1000 zł b
ę
dzie spłacony w trzech ratach 300,
400,
3
R . Jaka powinna by
ć
wysoko
ść
trzeciej raty, aby dług został spłacony
wraz z odsetkami obliczonymi przy stopie i=5%?
1000
300
400
3
R
0
1
2
3
j
n
1
j
j
0
i)
(1
R
K
−
=
+
⋅
=
∑
,
3
3
2
05
,
1
R
05
,
1
400
05
,
1
300
1000
+
+
=
⇒
3
R =406,88
j
n
n
1
j
j
n
0
i)
(1
R
i)
(1
K
−
=
+
⋅
=
+
⋅
∑
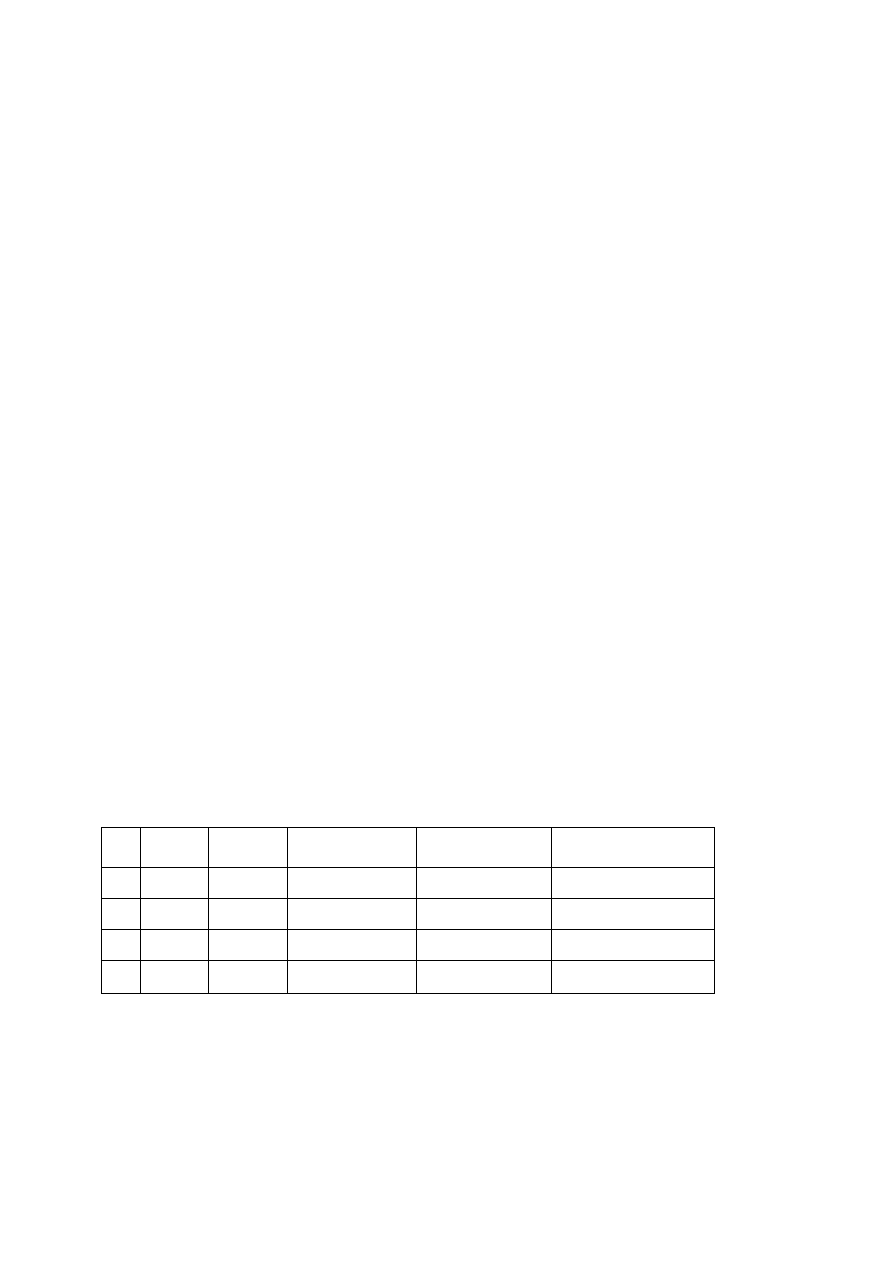
3
2
3
R
05
,
1
400
05
,
1
300
1,05
1000
+
⋅
+
⋅
=
⋅
⇒
3
R =406,88
j=1:
1000
K
0
=
,
1
1
0
0
K
750
300
0,05
1000
1000
R
i
K
K
=
=
−
⋅
+
=
−
⋅
+
j=2:
750
K
1
=
,
2
2
1
1
K
5
,
387
400
,05
0
750
750
R
i
K
K
=
=
−
⋅
+
=
−
⋅
+
j=3:
5
,
387
K
2
=
,
3
3
2
2
K
0
88
,
406
,05
0
5
,
387
5
,
387
R
i
K
K
=
=
−
⋅
+
=
−
⋅
+
Przykład 2: Dla spłaty długu z przykładu 1 oblicz cz
ęść
odsetkow
ą
i kapitałow
ą
rat oraz dług bie
żą
cy na koniec kolejnych okresów w zale
ż
no
ś
ci od
cz
ęś
ci kapitałowych rat.
j=1:
1000
K
0
=
50
0,05
1000
i
K
I
0
1
=
⋅
=
⋅
=
,
250
50
300
I
R
U
1
1
1
=
−
=
−
=
750
250
1000
U
K
K
1
0
1
=
−
=
−
=
j=2:
750
K
1
=
5
,
37
0,05
0
75
i
K
I
1
2
=
⋅
=
⋅
=
,
5
,
362
5
,
37
400
I
R
U
2
2
2
=
−
=
−
=
5
,
387
5
,
362
750
U
K
K
2
1
2
=
−
=
−
=
j=3:
5
,
387
K
2
=
,
38
,
19
I
3
=
,
5
,
387
U
3
=
,
0
K
3
=
j
1
j
K
−
j
R
i
K
I
1
j
j
⋅
=
−
j
j
j
I
R
U
−
=
j
1
j
j
U
K
K
−
=
−
1
1000
300
50
250
750
2
750
400
37,5
362,5
387,5
3
387,5
406,88
19,38
387,5
0
Σ
1000
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron