W.I.T., Egzamin z Podstaw Matematyki, rok 2008/2009

Rozwi ¾

azania (jednego wariantu) zada´n egzaminu 24 czerwca 2009

Przypominam, ·

ze egzamin w terminie 2 zaczynamy o 8:45 !!!! Zadania b ¾

ed ¾

a

podobne.

Zadanie 1

. Dla podanych ni·

zej funkcji zdaniowych '(x)

opisz podane

zbiory fx 2 R : '(x)g, stosuj ¾

ac ogólnie przyj ¾

ete oznaczenia na przedzia÷

y,

pó÷

proste, zbiory sko´nczone itp.

a) x > 3 ) x = 0 ,

b) x

2

> 9 ) x > 3

c) x

2

=

1 , x

2

= 1 .

Rozwi ¾

azanie. Implikacja jest fa÷

szywa, gdy jest postaci P ) F , inaczej

1 ) 0. Zatem zdanie x > 3 ) x = 0 jest fa÷szywe, gdy liczba x jest wi ¾

eksza od

3, a nie jest równa 0. W pozosta÷

ych przypadkach jest prawdziwa, a zatem zbiór

fx 2 R : '(x)g spe÷niaj ¾

acych t ¾

e form ¾

e zdaniow ¾

a, to ( 1; 3]. W przypadku b)

mo·

zna zastosowa´c podobne rozumowanie, ale lepiej jest rozumowa´c "wprost".

Z tego, ·

ze x

2

> 9 wynika, ·

ze x > 3 lub x <

3:Gdyby zatem "usun ¾

a´c" te

liczby mniejsze od minus 3, to wtedy mo·

zna by twierdzi´c, ·

ze je·

zeli x

2

> 9 to

x > 3. Inaczej mówi ¾

ac, w tym przypadku fx 2 R : '(x)g to [3; +1).

Zastanówmy si ¾

e nad dziwnie wygl ¾

adaj ¾

ac ¾

a równowa·

zno´sci ¾

a x

2

=

1 , x

2

=

1: Po lewej stronie mamy zawsze zdanie fa÷

szywe (bo x 2 R). Kiedy po lewej jest

zdanie fa÷

szywe? A, no, gdy nieprawda, ·

ze x

2

= 1, a zatem tylko dla x =

1.

Wniosek: fx 2 R : '(x)g = R n f 1; 1g:

Zadanie 2.

Spo´sród warunków a) - e) zaznacz, te, które s ¾

a warunkami

dostatecznymi do prawdziwo´sci zdania

9

x

2R

x

2

a

1 , a które s ¾

a warun

kami koniecznymi.

a) a

0

b) a =

1

c) a > 2009

d) a

1

e) j a j

1:

Jak to rozwi ¾

aza´c? Wystarczy si ¾

e zastanowi´c, co to znaczy „konieczny” i

"dostateczny" (=„wystarczaj ¾

acy”).

Je·

zeli z alf a wynika beta, to alf a jest

wystarczaj ¾

acy dla beta: Bo przecie·

z wystarczy, ·

zeby zasz÷

o alf a; ·

zeby beta te·

z

si ¾

e zdarzy÷

o. Z tego, ·

ze deszcz pada, wynika, ·

ze ulice s ¾

a mokre. A wi ¾

ec wystar-

czy, ·

zeby troch ¾

e popada÷

o i ju·

z jest mokro. Przeciwnie, beta jest konieczny dla

alf a:Na przyk÷

ad, z tego, ·

ze pada deszcz, wynika, ze ulice s ¾

a mokre. Je·

zeli

zobaczymy, such ¾

a ulic ¾

e, to znaczy, ·

ze deszcz nie pada. Ulice musz ¾

a by´c mokre

po deszczu.

Nst ¾

epnie, trzeba oswoi´c podany warunek z kwanty…katorem. Co znaczy po-

dany warunek: istnieje iks o tej w÷

asno´sci, ·

ze liczba przeciwna do jego kwadratu

spe÷

nia co´s tam? Otó·

z przecie·

z „liczb ¾

a przeciwn ¾

a do kwadratu”mo·

ze by´c ka·

zda

liczba ujemna (i zero) i odwrotnie, ka·

zda liczba ujemna (tak·

ze i zero) jest liczb ¾

a

przeciwn ¾

a do pewnego kwadratu. Na przyk÷

ad -2009 jest liczb ¾

a przeciwn ¾

a do

kwadratu liczby

p

2009: A zatem zdanie zamieszczone znaczy ni mniej ni wi ¾

ecej

tylko: a

1 jest liczb ¾

a ujemn ¾

a (b ¾

ad´z zerem). Jaki warunek wystarcza, by

a

1

0? Oczywi´scie jest to to samo, co a

1. Zatem ten warunek jest i

konieczny i dostateczny. Warunek a) nie jest konieczny, bo ·

zeby liczba by÷

a

mniejsza od 1 , niekoniecznie musi by´c mniejsza od zera.

Podobnie z b) .

1

Warunek c) jest, mo·

zna powiedzie´c, nie z tej opery. On nie ma nic wspól-

nego z nasz ¾

a w÷

asno´sci ¾

a, nie jest ani konieczny, ani dostateczny. Warunek e) te·

z

nie jest konieczny, bo w÷

asno´s´c z zadania ma liczba minus 2009, która na pewno

nie ma modu÷

u

1:

Zadanie 3

. Przez Z20 oznaczamy zbiór liczb naturalnych od 1 do 20 . Niech

A = fx 2 Z20 : 2 j (x + 1) g, B = fx 2 Z20 : 3 j xg, C = fx 2 Z20 : x < 10g:

Wylicz wszystkie elementy zbiorów A \ (B [ C) , A

(B \ C), A

B

C.

Odpowied´z. Po do´s´c ·

zmudnych wyliczeniach dostajemy:

A \ (B [ C) = f1; 3; 5; 7; 9; 15g; A (B \ C) = f1; 5; 6; 7; 11; 13; 15; 17; 19g

, A

B

C = f2; 3; 4; 8; 9; 11; 12; 13; 17; 18; 19g

Zadanie 4

. Metod ¾

a funkcji charakterystycznych rozstrzygn ¾

a´c, czy zawsze

a) A \ (B n A) = ? , b) A \ (A [ B) = A , c) A n (B [ C) = (A n B) n C

, d) A

B = (A [ B) n (A \ B) , e) A [ B = (A

B)

(A \ B):

Rozwi ¾

azanie. B ¾

edziemy pisa´c

a; b; c zamiast odpowiednio

A

;

B

;

C

.

Wtedy

a) Lewa strona to a (b (1 + a)) = ab

aba = ab + a

2

b = ab + ab = 0. Funkcj ¾

a

charakterystyczn ¾

a zbioru pustego jest oczywi´scie funkcja to·

zsamo´sciowo równa

zeru.

b) Lewa strona to a (ab + a + b) = a

2

b + a

2

+ ab = a =

A

:

c) Lewa strona to a (1+(bc+b+c)), prawa to a(1+b)(1+c) = a(1+bc+b+c),

obie strony s ¾

arówne.

e) Obie strony sa równe a + b + ab:
Zadanie 5

. Napisz dowód indukcyjny nierówno´sci 3

n

< n! (dla n

7).

Indukcj ¾

e zaczynamy od n = 7:Dla mniejszych n nierówno´s´c nie jest prawdziwa,

np. 3

6

= 729 > 720 = 6! - natomiast 3

7

= 2187 < 7! = 5040:Za÷

ó·

zmy teraz, ·

ze

nierówno´s´c jest spe÷

niona dla pewnego n

7. czyli 3

n

< n: Mamy wobec tego

3

n+1

= 3 3

n

< 3 n! < n n! = (n + 1)!:

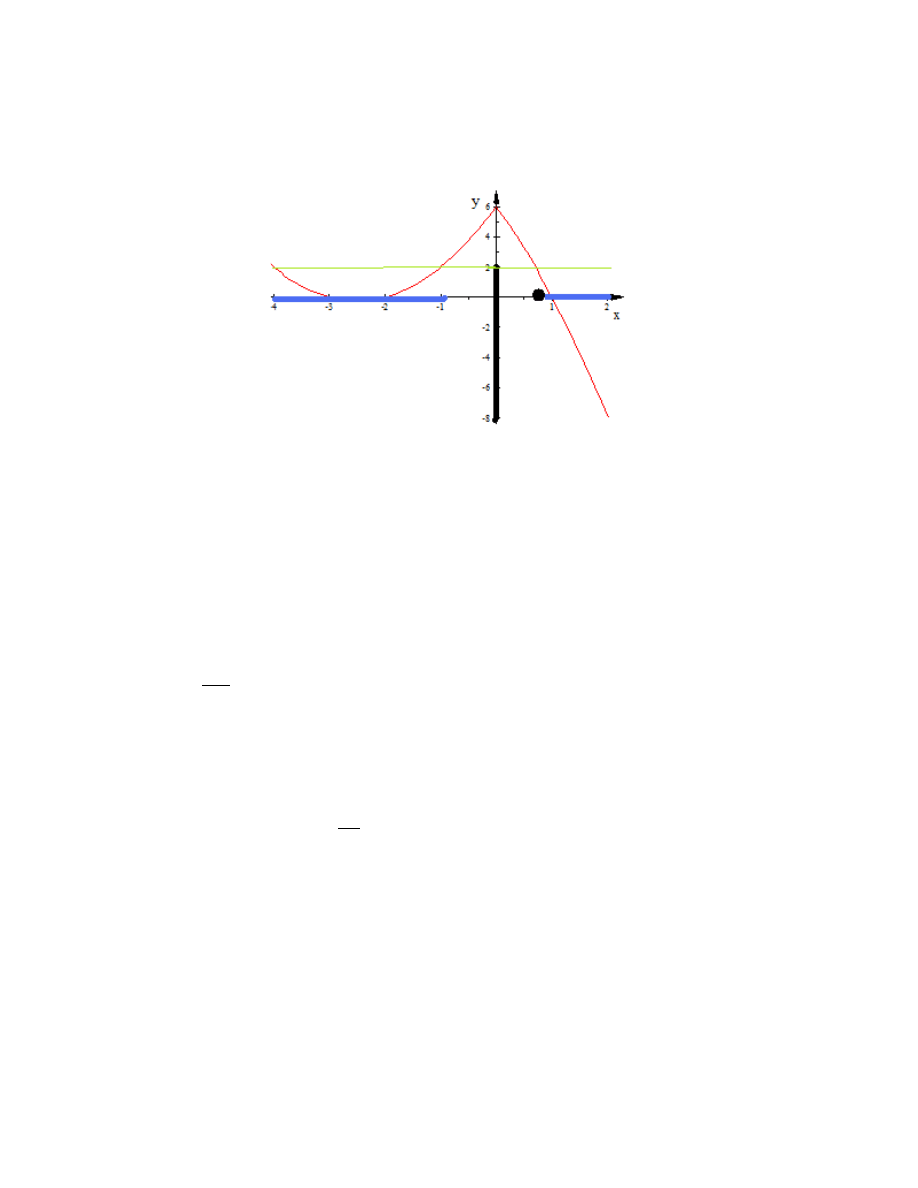
Zadanie 6

. Dla funkcji

f (x) =

x

2

5x + 6

dla

x > 0

x

2

+ 5x + 6

dla

x

0

wyznacz

obraz zbioru A i przeciwobraz zbioru B, gdzie A = ( 4; 1); B = ( 8;

2).

Rozwi ¾

azanie: patrz rysunek. Jest na nim wykres naszej funkcji oraz zaznac-

zony przedzia÷B (czarny pionowy odcinek). Jego przeciwbrazem jest suma od-
cinków zaznaczonych na osi x na niebiesko- pr przedzia÷

y ( 4;

1) oraz (a; 2),

gdzie warto´s´c musimy obliczy´c z równania f (a) = 2: Rozwi ¾

azuj ¾

ac równanie

kwadratowe

x

2

5x + 6 = 2, otrzymujemy dwa pierwiastki, z których dodatni

to

1
2

p

41

5
2

= 0; 701 56:::Sprawd´zmy rzutem oka, czy wynik jest poprawny.

Wyobra·

zamy siobie, ·

ze punkt x rusza si ¾

e po niebieskim odcinku. Czy wtedy y

jest mi ¾

edzy

8 a +2 ? A, no, jest.

Z tego samego rysunku - oraz po wyliczeniu minimu funkcji w punkcie

2; 5,

wida´c, ·

ze obrazem przedzia÷

u A = ( 4; 1) jest [

1
4

; 6]:

2

Zadanie 7.

Dane s ¾

a permutacje s = (12)(34) oraz t =

1

2

3

4

4

2

3

1

.

Oblicz t

1

s

4

:

Odpowied·

z. Poniewa·

z s

2

= id = t

2

; wi ¾

ec t

1

s

4

= t:

Zadanie 8.

Przez N oznaczamy zbiór liczb ca÷kowitych dodatnich. Zbiór

N

N porz ¾

adkujemy wed÷

ug porz ¾

adku leksykogra…cznego z gradacj ¾

a. Wyznacz

element, stoj ¾

acy na miejscu 222.

Rozwi ¾

azanie. Mamy

1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20 =

20 21

2

= 210:

Nasz element znajduje si ¾

e zatem w 21 rz ¾

edzie uko´snym na 12 miejscu. Jest

to (12, 10).

Zadanie 8a

Przez N oznaczamy zbiór liczb ca÷kowitych dodatnich. Zbiór

N N porz ¾

adkujemy wed÷

ug porz ¾

adku leksykogra…cznego z gradacj ¾

a. Na którym

miejscu w porz ¾

adku leksykogra…cznym z gradacj ¾

a znajduje si ¾

e (5,6)?

Rozwi ¾

azanie. W pierwszych 10 rz ¾

edach uko´snych jest ÷¾

acznie 1 + 2 + 3 + 4 +

5 + 6 + 7 + 8 + 9 =

9 10

2

= 45 elementów. Dziesi ¾

aty rz ¾

ad zawiera pary (1,10),

(2,9), (3,8), (4,7), (5,6), (6,5), (7,4), (8,3), (9,2), (10,1) . Z prostego rachunku
wynika, ·

ze na par ¾

e (5,6) przypada miejsce nr 50.

Zadanie 9

. Niech A = f1; 2; 3; 4; 5; 6; 7; 8g: W iloczynie kartezja´nskim A A

wprowadzamy relacj ¾

e R wzorem (a; b) R (c; d)

, max fa; bg = maxfc; dg.

Opisz podzia÷zbioru na klasy równowa·

zno´sci tej relacji, w szczególno´sci podaj,

ile jest tych klas i ile jest elementów w poszczególnych klasach.

Rozwi ¾

azanie. Pary liczb s ¾

a w relacji, gdy wi ¾

eksza z nich jest taka sama. Za-

tem na przyk÷

ad do tej samej klasy nale·

z ¾

a (1,5), (2,5), (3,5), (4,5), (5,5), (5,4),

3

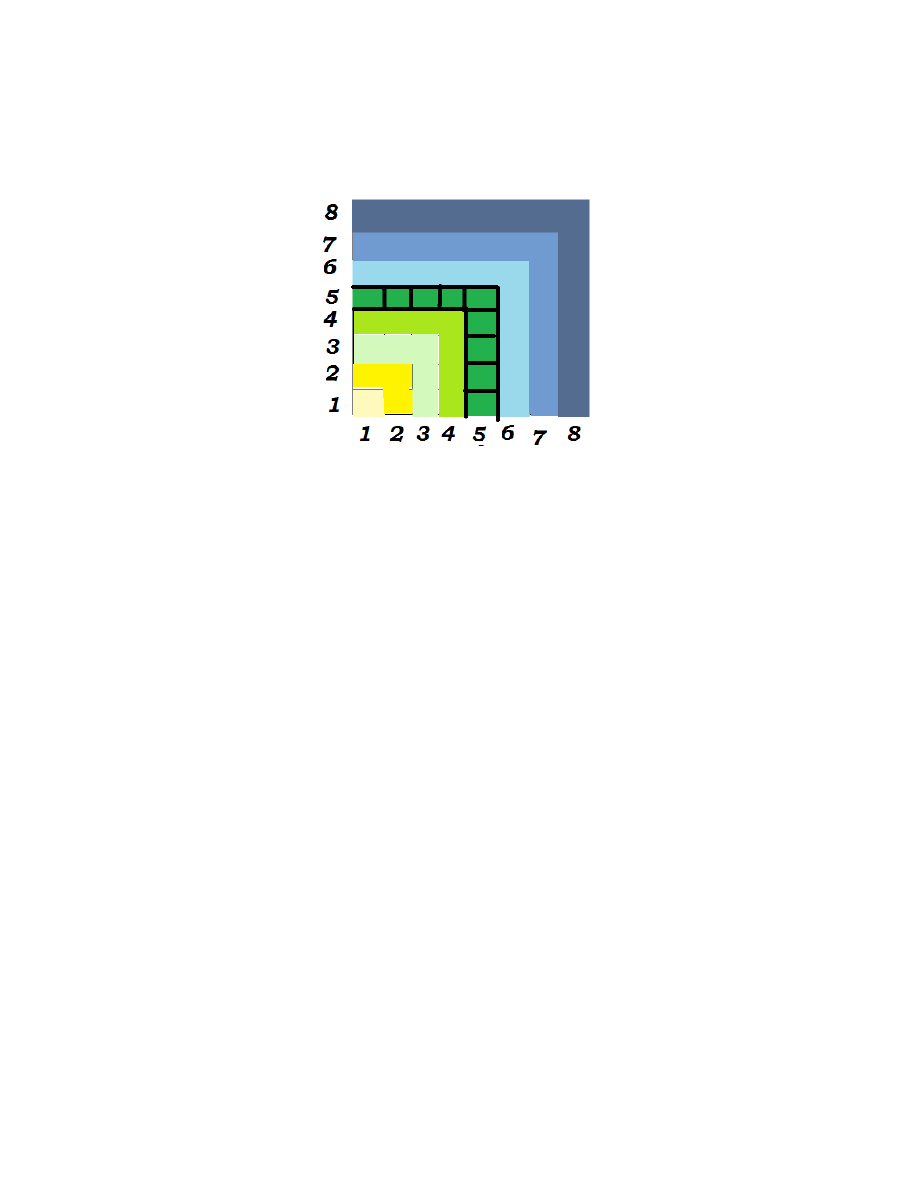
(5,3), (5,2), (5,1) - patrz rysunek. Jest 8 klas, maj ¾

a one 1,3,5,7,9,11,13, 17 ele-

mentów. Zauwa·

zmy, ·

ze pokazali´smy (nie: udowodnili´smy!) przy okazji, ·

ze suma

kolejnych liczb nieparzystych jest kwadratem liczby naturalnej. Wykorzystaj to

jako ´cwiczenie z indukcji matematycznej:

m

X

k=1

(2k

1) = m

2

.

Zadanie 10

. W zbiorze Z wszystkich liczb ca÷kowitych okre´slamy relacj ¾

e

J

w nastepuj ¾

acy sposób: m

J n wtedy i tylko wtedy, gdy

albo elementy te s ¾

a równe, albo n = 0 albo [(m n < 0 ^ m < n) _ (m n > 0 ^ j m j < j n j]

.

Który opis pasuje do tego porz ¾

adku:

a) Liczby ujemne s ¾

a nieporównywalne z dodatnimi, a na ka·

zdym z tych

zbiorów jest zwyk÷

y porz ¾

adek.

b) 0 jest nieporównywalne z innymi liczbami, liczby ujemne uszeregowane w

naturalnej kolejno´sci, nast ¾

epnie liczby dodatnie.

c) 0 jest elementem minimalnym, potem nast ¾

epuj ¾

a wszystkie liczby ujemne

uszeregowane w naturalnej kolejno´sci, nast ¾

epnie liczby dodatnie.

d) 0 jest nieporównywalne z innymi liczbami, wszystkie liczby ujemne usz-

eregowane s ¾

a w porz ¾

adku odwrotnym do naturalnej kolejno´sci, nast ¾

epnie liczby

dodatnie.

e) 0 jest elementem minimalnym, ale nie najwi ¾

ekszym, liczby ujemne s ¾

a

uporz ¾

adkowane w porz ¾

adku rosn ¾

acym, a liczby dodatnie w porz ¾

adku malej ¾

acym,

f) liczby ujemne sa uszeregowane w porz ¾

adku odwrotnym do naturalnego,

liczby dodatnie s ¾

a od nich wi ¾

eksze i s ¾

a uszeregowane rosn ¾

aco ,-1 jest elementem

najmniejszym, natomiast 0 jest elementem najwi ¾

ekszym, stoj ¾

acym za wszystkmi

liczbami dodatnimi.

Który z podanych ci ¾

agów jest ÷

a´ncuchem dla tego porz ¾

adku?

4

a)

1;

2;

3; 1; 2; 3; 0

b)

3;

2;

1; 0; 1; 2; 3

c) 3; 2; 1; 0;

1;

1;

3

d) 0; 1; 2; 3;

1;

2;

3

e) 1; 2; 3; 0;

1;

2;

3

f) 1;

1; 2;

2; 3;

3; 0

Rozwi ¾

azanie. Musimy si ¾

e wczyta´c w tre´s´c warunku [(m n < 0 ^ m < n) _ (m n > 0 ^ j m j < j n j] :

Jego pierwsza cz ¾

e´s´c

m

J n gdy m n < 0 ^ m < n

znaczy po prostu, ·

ze z liczb o ró·

znych znakach mniejsza w sensie relacji

J jest liczba "prawdziwie" mniejsza, a wi¾ec liczby ujemne sa mniejsze od
wszystkich liczb dodatnich. Porównujmy teraz liczby o tych samych znakach
(warunek m n

0 ^ j m j < j n j ): Dla liczb dodatnich, równych swojemu

modu÷

owi, jest to zwyk÷

a relacja. Liczby dodatnie s ¾

a uporz ¾

adkowane zgodnie

z naturaln ¾

a kolejno´sci ¾

a. Dla liczb ujemnych, przeciwnie, je·

zeli j m j < j n j ;

to m > n : Relacja

J ustawia liczby ujemne w porz ¾

adku odwrotnym.

Wreszczie, co z zerem? Z podanego warunku odczytujemy od razu, ·

ze 0 jest

wi ¾

eksze od wszystkich innych liczb.

Porz ¾

adek ten jest nast ¾

epuj ¾

acy:

1;

2;

3; ::::; 1; 2; 3; 4; :::::; 0 (opis f). ×a´ncuchem

jest tylko a). W sensie klasy…kacji typów porz ¾

adkowych (by÷

o na ostatnim

wyk÷

adzie) jest to typ 2! + 1:

5